Synchrotron X-ray and neutron diffraction study on the deformation and phase transformation mechanisms in TiAl alloys: a review

Origin and characterization of internal strains

In polycrystalline materials, plastic deformation typically initiates asynchronously across grains, with the deformation behavior varying depending on the crystallographic orientation of individual grains relative to the applied loading direction (LD). This asynchrony is especially pronounced in multiphase alloys, where the critical resolved shear stress (CRSS) values of different slip systems in the constituent phases differ significantly. As a result, neighboring grains must adapt to this inhomogeneous elastoplastic deformation to maintain interfacial continuity, which leads to the generation of elastic strains, commonly known as intergranular strains^[39-44]. These intergranular strains, fluctuating at the grain scale, are partially preserved as type II strains after unloading due to irreversible plastic deformation^[39]. The intergranular strain evolution is complex, collectively governed by multiple factors, including grain size, texture, and microstructure. These strains are crucial for understanding the deformation response of materials, as they contribute significantly to microstructural evolution by driving strain localization, damage initiation, and crack propagation during loading.

The lattice strain evolution of constituent phases within a polycrystalline material serves as an effective assessment for load partitioning and intergranular strain variation. The lattice strain for selected {hkl} reflections is estimated as^[45]:

Where d_hkl and $$ d_{{h} k l}^{0} $$ are the interplanar spacings of {hkl} lattice planes during loading and in the stress-free condition, respectively. These interplanar spacings are determined based on Bragg’s law. Lattice strain evolution reflects the intergranular strain distribution, which is influenced by grain orientation and thus fluctuates across different azimuth angle ranges.

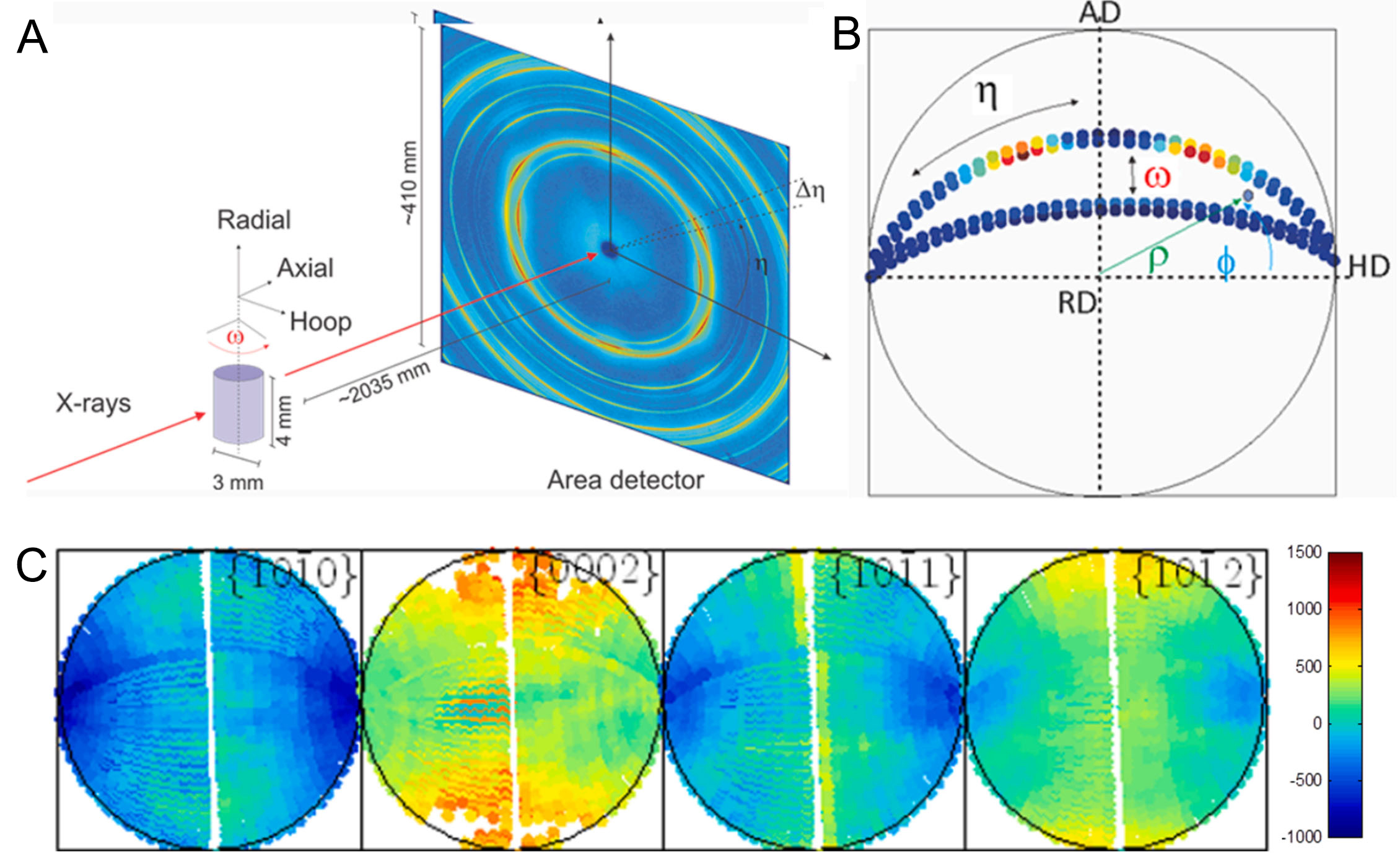
In synchrotron HEXRD experiments, strain states in deformed components can be comprehensively mapped by rotating the sample^[46-49]. As shown in Figure 2A, when the specimen is rotated around the radial direction (RD), more diffracting planes would satisfy the diffraction condition and contribute to the measurement^[50]. Specifically, this rotation extends the measurement range from the crystal plane normal being perpendicular to the incident beam to the crystal plane normal positioned on an arbitrary plane parallel to the RD, thereby facilitating a more comprehensive analysis of lattice strain in different directions. The acquired raw data are visualized by constructing generalized pole figures, which plot lattice strain or peak intensity as a function of azimuth angle ƞ and rotation angle ω. As shown in Figure 2B, each great circle projected along the hoop direction (HD) represents specific parameters (such as peak intensity and lattice strain) changing with ƞ at a fixed ω. Additionally, the position of each great circle shifts as ω changes, gradually establishing the pole figures (derived from intensity distribution) and strain pole figures (derived from lattice strain distribution, Figure 2C). First introduced by Wang et al.^[51-53], strain pole figures offer an overall visualization of the spatial distribution of intergranular strains by projecting them onto a three-dimensional space that reflects different grain orientations. This innovative method enables monitoring intergranular strain under different stress conditions and analyzing how stress states vary among differently oriented grains. However, it lacks visual intuitiveness when it comes to characterizing intergranular strain evolution during loading.

Figure 2. (A) Schematic illustration of the experimental configuration used for in situ HEXRD measurements. The sample is aligned with the axial direction (AD) parallel to the X-ray beam, the hooping direction (HD) horizontal, and the radial direction (RD) vertical. To analyze the peak profiles of grains with different orientations, the specimen rotates around the RD; (B) Construction of a stereographic projection, where each point encodes information such as peak intensity and lattice strain, defined by the azimuth angle (η) and the rotation angle (ω); (C) Experimental strain pole figures. (Reproduced from Ref.[50]^[50]). HEXRD: High-energy X-ray diffraction.

During uniaxial tension and compression experiments, lattice strains typically exhibit periodic variations as the crystal direction gradually shifts away from the LD. As the sample is rotated around the transverse direction (TD), the lattice strains exhibit similar changing trends at different rotation angles^[54]. Specifically, tensile stresses increase as grain orientations approach the LD, while the TD experiences the highest compressive stresses during tensile tests. In fact, this situation is widely applicable and also observed in multicomponent metallic glassy alloys, where the LD experiences the highest tensile stresses, and the TD endures the highest compressive stresses. Notably, crystal directions deviating 60° from the LD are almost unstrained^[55]. In general, lattice strains along the LD and TD reflect the most extreme stress conditions and are commonly used to investigate load partitioning behavior and internal stress evolution.

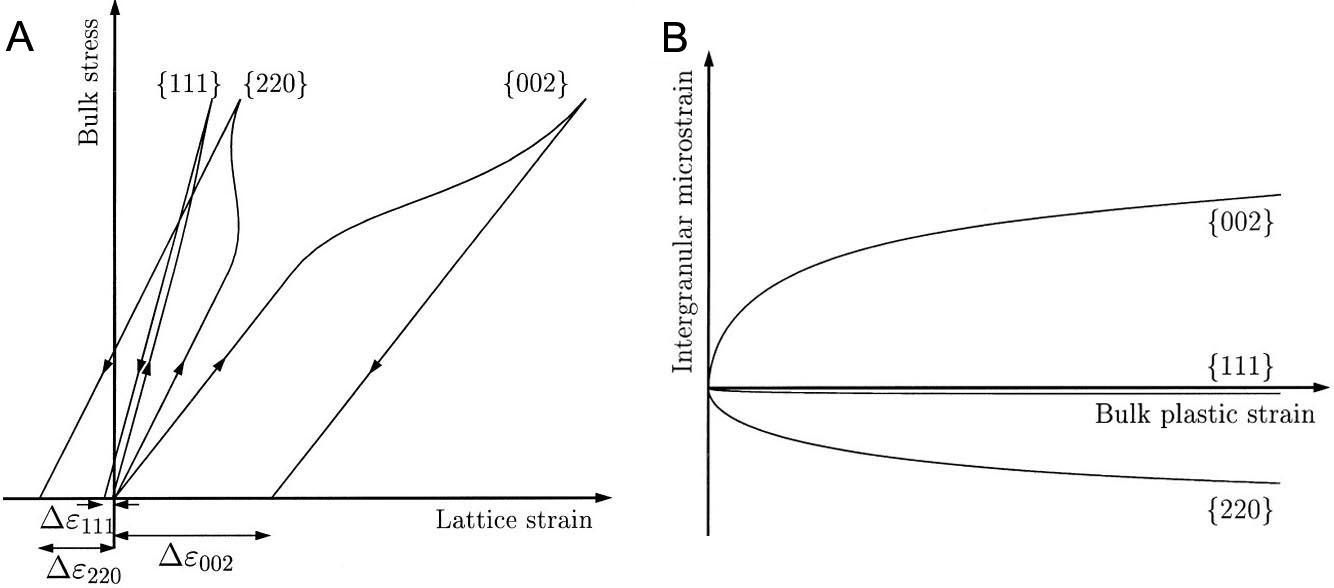
In face-centered cubic (FCC) metals, as demonstrated by Dye et al.^[39], the lattice strains of all reflections along LD respond linearly to bulk stresses during elastic deformation [Figure 3A]. Above macro-yielding, load partitioning between differently oriented grains becomes significant. At this stage, the lattice strains deviate from their initial linear elastic response and display distinct trends. The loads borne by plastically deformed grains no longer increase, and may even decrease, as evidenced by the reduction in the lattice strains of <220>//LD oriented grains with increasing bulk stress. Simultaneously, more load is transferred to elastically deformed grains, as indicated by an inflection point in the lattice strain evolution of <002>//LD oriented grains, followed by a rapid increase. This load partitioning is accompanied by intergranular strain accumulation, which is positively correlated with the degree of deviation from linear elastic behavior, as described by the following equation^[40]:

Figure 3. (A) Bulk stress vs. lattice strain curves for grains with normals parallel to the loading direction (LD) in face-centered cubic (FCC) metals; (B) Intergranular microstrain vs. bulk plastic strain curves in FCC metals. (Reproduced from Ref.[39]^[39]).

Where σ_app and E_hkl represent the applied stress and elastic diffraction constant, respectively, $$ \frac{\sigma_{a p p}}{E_{h k l}} $$ is linear elastic strains, and $$ \varepsilon_{{h} k l}^{i n t} $$ refers to intergranular strains. As illustrated in Figure 3B, the intergranular strain accumulation is rapid at the onset of plastic deformation, but this accumulation becomes retarded after a certain strain amount^[39]. In multiphase alloy systems, the interactions between different phases complicate this strain evolution, as phase boundaries and differences in mechanical properties lead to more complex load partitioning and strain distribution. To investigate the microscopic deformation mechanisms among constituent phases, a quantitative evaluation of the Von-Mises effective stress is commonly employed. References^[45,56,57] provide a detailed description of load partitioning between soft and hard phases that exhibit pronounced differences in plastic deformability. The Von-Mises stress σ_VM can be calculated as follows^[58]:

For cylindrical samples, σ₁₁ and σ₂₂ represent the principal stress along LD and TD, σ₃₃ is equivalent to σ₂₂. ε₁₁, ε₂₂ = ε₃₃ refer to the lattice strain along LD and TD, E and ν are diffraction elastic moduli and Poisson’s ratio, respectively.

Particularly, designing next-generation multiphase alloys such as TiAl alloys for high-performance applications, such as those in aerospace, automotive, and energy industries, presents a key challenge in controlling the microstructure to optimize internal stress distribution. Developing alloys that offer a balance of high strength, toughness, and fatigue resistance requires a thorough understanding of how these materials deform at the microstructural level, especially at grain boundaries where internal stresses accumulate.

Internal stress accumulation in the α₂ phase

In TiAl alloys, the α₂ phase with an ordered hexagonal structure plays a critical role in governing the overall deformation behavior. Due to its high strength and low plastic deformability, stress accumulation within the α₂ phase can accelerate crack initiation, particularly at α₂/γ interfaces, leading to premature failure of the alloy. Intergranular stress accumulation in the α₂ phase is mainly influenced by the activation of slip systems in the α₂ and γ phases, as well as by microstructure and texture formation. Plastic deformation in the α₂ phase is largely restricted to 1/3(1$$ \bar{1} $$00)[11$$ \bar{2} $$0] prismatic glide. Other slip systems, especially pyramidal glide with the Burgers vector b = 1/3[1$$ \bar{2} $$1$$ \bar{6} $$] on the {1$$ \bar{2} $$11} and {2$$ \bar{2} $$01} slip planes, are difficult to activate due to their significantly high CRSS^[18-20,59]. According to Song et al.^[60], <$$ \bar{1} $$014>{20$$ \bar{2} $$1} compressive and <$$ \bar{1} $$102>{1$$ \bar{1} $$01} tensile twins can also be activated in the α₂ phase. Though mechanical twins would alleviate the deformation anisotropy of the α₂ phase to some extent, their contribution to plastic deformation is limited due to a high CRSS for activation. As a result, plastic deformation is mostly accommodated by the γ phase, where dislocations primarily glide on the {111} slip planes^[43]. During in situ tensile experiments on equiaxed-grained TNM-TiAl (Ti-43.5Al-4Nb-1Mo-0.1B) alloys, Erdely et al.^[61] observed that plastic deformation in γ grains initiates sequentially depending on orientation, with more load being transferred to the elastically deformed α₂ and β_o grains, as shown in Figure 4A. Once all γ grains had deformed plastically, plastic deformation began in the α₂ phase. The great difference in plastic deformation between the constituent phases α₂ and γ results in substantial residual stresses preserved in the alloy after unloading. After cyclic deformation at 850 °C, Ding et al.^[62] found that the lattice strains of the α₂ and γ phases were opposite, with the compressive lattice strain in the α₂ phase being up to more than 8 times greater than the tensile lattice strain in the γ phase, as shown in Figure 4B. As reported by Appel et al.^[10], the α₂ phase exhibits significantly higher residual strains than the γ phase following roller indentation.

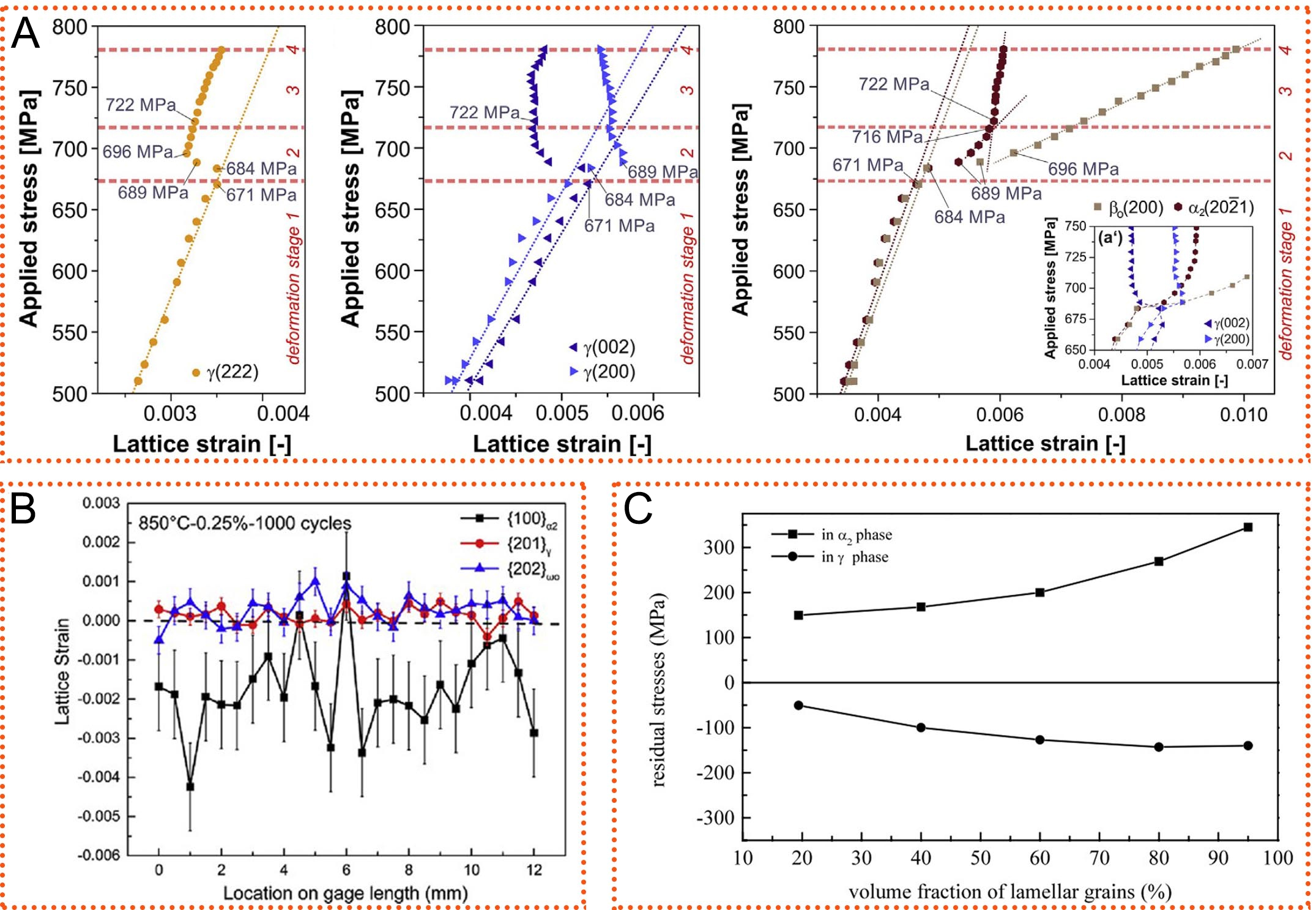
Figure 4. (A) True stress vs. lattice strain curves for the α₂, γ, and β_o reflections. Equiaxed grained TNM-TiAl alloys were stretched at room temperature. (Reproduced from Ref.[61]^[61]); (B) Development of the lattice strains revealed by sample gage length scanning interrupted at 1000 cycles in the fatigue deformation of high Nb-TiAl alloy at 850 °C. (Reproduced from Ref.[62]^[62]); (C) Residual stresses of the α₂ and γ phases varying with increasing volume fraction of the lamellar structures. (Reproduced from Ref.[11]^[11]).

The distribution and morphology of the (α₂+γ) lamellar structures in the microstructure strongly influence internal stress accumulation in the α₂ phase^[11,63,64]. In deformed TiAl alloys, Guo et al.^[11] found that residual stress in the α₂ phase is positively correlated with the volume fraction of the lamellar structures. The residual stress in the α₂ phase in a microstructure containing 95% lamellar structures is twice that of one with 20% lamellar structures, as shown in Figure 4C. During in situ HEXRD compression, Liu et al.^[65,66] found that the α₂ and γ phases in a nearly lamellar Ti-45Al-8Nb-0.2W-0.2B-0.02Y alloy exhibit different deformation behavior and internal stress evolution compared to those in the duplex microstructure (mainly consisting of equiaxed α₂ and γ grains) with the same composition. In the nearly lamellar microstructure, deformation in the γ phase proceeds through sequential activation of ordinary dislocations and mechanical twinning at stress levels of 200 MPa and 585 MPa, respectively. In contrast, plastic deformation of the α₂ phase occurs within a relatively narrow stress window of 775-850 MPa during the late strain hardening stage, as illustrated in Figure 5A. At 850 MPa, the Von-Mises stress in the α₂ phase is nearly three times higher than that in the γ phase [Figure 5B]. In the duplex microstructure, plastic deformation in the γ and α₂ phases initiates at stresses of 370 and 670 MPa, respectively [Figure 5C]. The Von-Mises stress in the α₂ phase is at most 2.5 times higher than that in the γ phase. These differences in internal stress accumulation between microstructures mainly originate from the strong deformation anisotropy of the lamellar structure.

Figure 5. Compression behavior of Ti-45Al-8Nb-0.2W-0.2B-0.02Y alloys with (A and B) nearly lamellar and (C) duplex microstructures at 800 °C. (A) True stress-lattice strain curves for α₂ and γ reflections; a detailed view of the α₂ lattice strain evolution in stage III is provided below. (Reproduced from Ref.[65]^[65]); (B and C) Von-Mises stress of α₂ and γ phases plotted against true stress for (B) the nearly lamellar (Reproduced from Ref.[65]^[65]) and (C) the duplex microstructure (Reproduced from Ref.[66]^[66]).

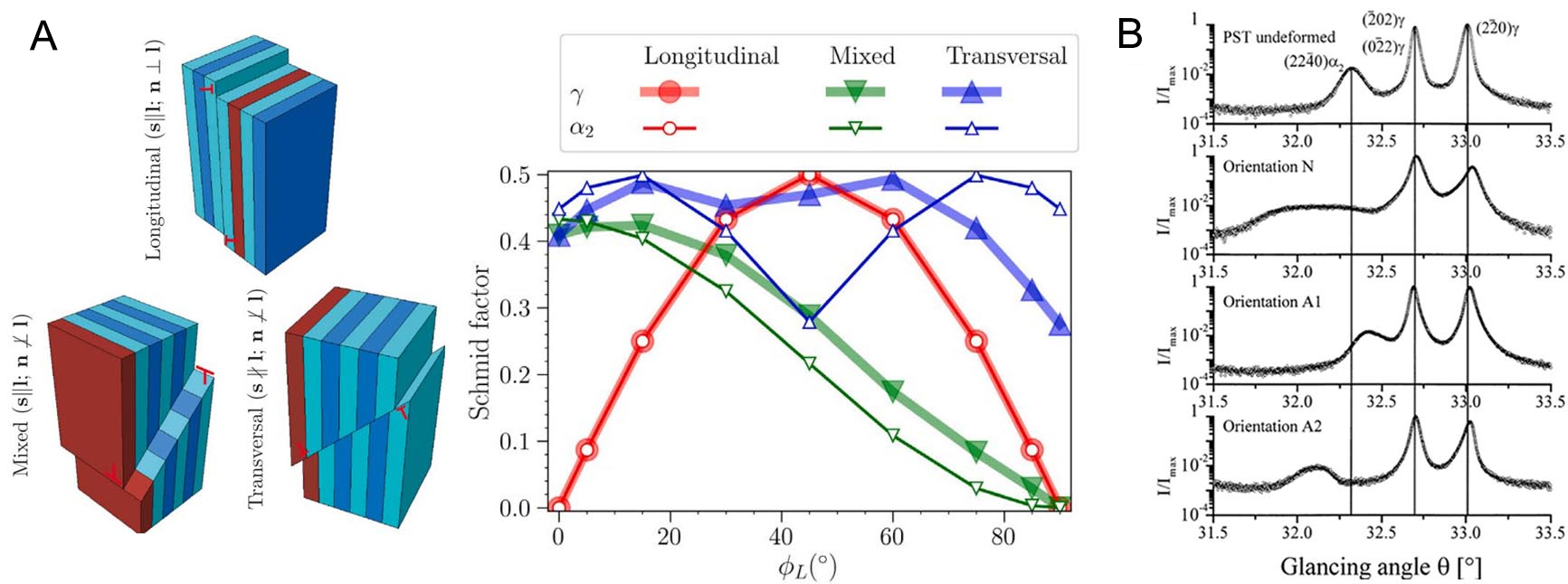
Within the lamellar structures, the α₂ and γ phases follow the well-known Blackburn OR: {111}_γ//(0001)_α2, <110]_γ//<11$$ \bar{2} $$0>α₂^[67]. The orientation of lamellar structures relative to the applied load greatly affects their deformation behavior by activating different slip systems in the γ and α₂ phases. As investigated in Ref.[68]^[68], the α₂/γ lamellar interfaces aligned at 45° (i.e. Φ_L = 45°) to the uniaxial loading direction are geometrically favorable for the activation of softer longitudinal slip systems where 1/3(0001)[11$$ \bar{2} $$0] basal glide has the highest Schmid factor [Figure 6A]. In contrast, lamellar structures with α₂/γ lamellar interfaces aligned vertically to applied loads (i.e. Φ_L = 90°) are difficult to deform plastically, as only the pyramidal glide in the α₂ phase can be activated in this orientation. The γ phase generally deforms more readily via multiple slip systems such as (1$$ \bar{1} $$1)[110] and twinning modes, making it more ductile than the hexagonal α₂ phase, which exhibits pronounced slip anisotropy. Due to this disparity, the γ lamellae primarily carry plastic deformation, while the α₂ lamellae accommodate strain predominantly through elastic distortion or by mediating the deformation of adjacent γ lamellae. As a result, significant intergranular strain accumulation occurs in the α₂ phase, which is directly reflected in the α₂ peak profiles. The peak shift of differently oriented α₂ phase in the PST-TiAl alloys is illustrated in Figure 6B^[14]. The α₂ lamellae within the (α₂+γ) lamellar structure are aligned with their [0001] directions either parallel (orientations A1 and A2) or perpendicular (orientation N) to the stress axis. Compared to the undeformed (22$$ \bar{4} $$0)_α2 diffraction peak, considerable peak shifts are observed after deformation, exhibiting notable differences across different orientations. Specifically, the (22$$ \bar{4} $$0)_α2 peak in the N orientation (i.e., α₂/γ lamellar interfaces aligned vertically to the load axis) shows the greatest peak shift and pronounced peak broadening, indicating that residual stress has accumulated substantially in the α₂ phase. In contrast, prismatic slip in the α₂ lamellae in the A1 and A2 orientations (i.e., α₂/γ lamellar interfaces aligned parallel to the load axis) is activated to some extent, which coordinates the plastic deformation of neighboring γ lamellae. Overall, the strong deformation anisotropy of the (α₂+γ) lamellar structures significantly influences internal stress accumulation in the α₂ phase. It is therefore reasonable to speculate that the texture evolution in the α₂ phase plays a crucial role in the deformation compatibility of TiAl alloys.

Figure 6. (A) Activation of different slip systems in differently oriented (α₂+γ) lamellar structures relative to the load axis (on the left) and Schmid factor variation of different slip systems in α₂/γ lamellar structures as they deviate from the load axis within an angle range of 0°-90° (on the right). (Reproduced from Ref.[68]^[68]); (B) XRD profiles of differently oriented PST-TiAl alloys deformed at room temperature. (Reproduced from Ref.[14]^[14]). XRD: X-ray diffraction.

The tilted basal and transverse textures, where the c axis is slightly misaligned from the LD and oriented along the TD, represent typical deformation textures in the α₂ phase^[69-74]. Stark et al.^[75] investigated the texture evolution of the α phase during hot compression at 1,230 °C. Initially, the intensity of the (0002)_α reflections is randomly distributed along the azimuth angle, indicating a weakly textured initial microstructure. As compression proceeds, the intensity of the (0002)_α reflections gradually shifts toward the LD. When the strain reaches 20 %, the intensity of the (0002)_α reflections becomes concentrated in a direction approximately 20° off the LD. The intensity evolution along the azimuth angle implicitly reflects the deformation texture evolution. The (0002)_α pole figures further confirm that the α phase develops a tilted basal fiber texture at a strain of 20%, although this texture is slightly weakened by flow softening in subsequent deformation. For hexagonal phases with a c/a ratio less than 1.63, the c axis tends to align with the compression direction, resulting in the formation of a basal texture^[76-78]. However, during hot rolling in the (α+β) or (α+β+γ) phase regions, TiAl sheets exhibit not only a basal texture but also a transverse texture component, as illustrated in Figure 7^[72]. This transverse texture is thought to form only in the presence of a softer secondary phase and is closely linked to the dominant activation of slip systems within that phase^[71,72]. It should be noted that the α₂ orientation in the basal texture refers to the c axis parallel to the load axis, which is the same case as the orientation N mentioned above. In other words, basal texture formation is unfavorable for subsequent deformation and would trigger a rapid internal stress accumulation in the α₂ phase.

Figure 7. Pole figures of the α₂ phase in a Ti-43Al-4Nb-1Mo-0.1B alloy hot rolled in different phase regions. The RD is aligned vertically, and the TD horizontally. (Reproduced from Ref.[72]^[72]). RD: Radial direction; TD: transverse direction.

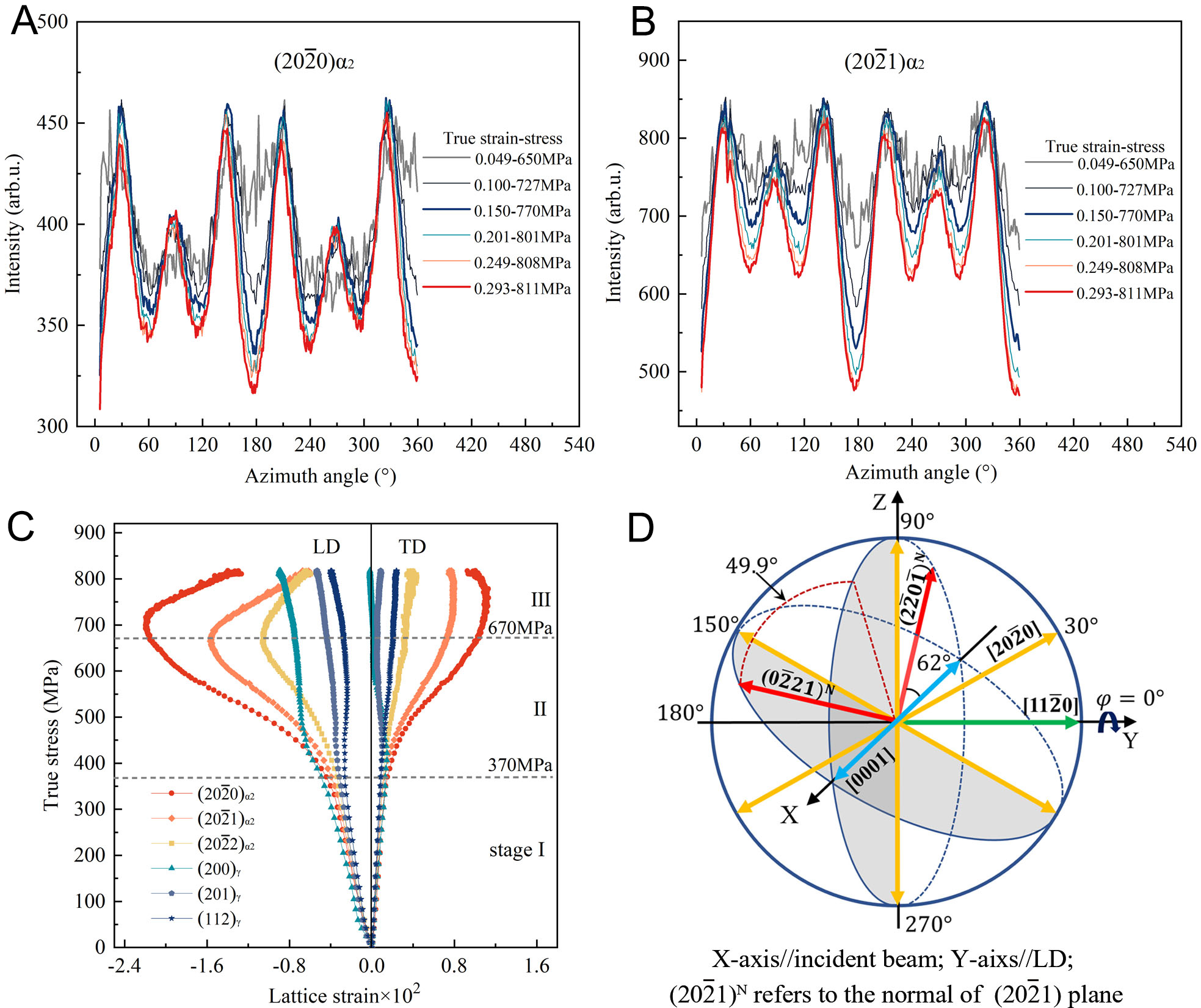
In practice, texture evolution and plastic deformation usually interweave during deformation, jointly influencing internal stress evolution in the alloy. Characterized by HEXRD, the microscopic deformation mechanisms of the α₂ phase in TiAl alloys during uniaxial compression have been investigated. At a stress level of 650 MPa, the intensity distribution of the α₂ reflections suggests that the development of α₂ texture is at an early stage. As visible in Figure 8A and B, the intensity of the (20$$ \bar{2} $$0)_α2 and (20$$ \bar{2} $$1)_α2 reflections is randomly distributed, while it fluctuates notably along the azimuth angle φ thereafter. Additionally, the peak intensities of the (20$$ \bar{2} $$0)_α2 and (20$$ \bar{2} $$1)_α2 reflections exhibit a similar arrangement and arise roughly at φ = 30°, 90°, and 150°. However, the lattice strain evolution indicates that the α₂ phase starts to undergo plastic deformation at a stress of 670 MPa [Figure 8C]. The intensity distribution of the α₂ reflections actually originates from the <11$$ \bar{2} $$0> fiber texture, in which the c axis is arranged transversely to the LD [Figure 8D]. This transverse texture component already forms during the elastic deformation stage of the α₂ phase and is facilitated by plastic deformation of the γ phase. The preferred orientation of the α₂ phase predominantly promotes double prismatic slip and additionally facilitates the activation of tensile twinning. The plastic deformation in the α₂ phase conversely affects the α₂ texture, as evidenced by the peak intensity of the (20$$ \bar{2} $$0)_α2 and (20$$ \bar{2} $$1)_α2 reflections decreasing at stresses above 727 MPa [Figure 8A and B]. In broad terms, the plastic deformation in the α₂ phase with the transverse texture is relatively easy to activate and coordinates the dislocation glide and twin activation in the γ phase to some extent.

Figure 8. A duplex Ti-45Al-8Nb-0.2W-0.2B-0.02Y alloy subjected to compression at 800 °C. (A and B) Azimuthal intensity distributions for the (20$$ \bar{2} $$0)_α2 and (20$$ \bar{2} $$1)_α2 reflections under different stress/strain conditions; (C) True stress-lattice strain relationships for α₂ and γ reflections; (D) Schematic illustration of the spatially preferential orientation of the α₂ phase, showing an <11 $$ \bar{2} $$0> fiber texture within a predefined rectangular coordinate system. (Reproduced from Ref.[66]^[66]).

In general, the deformation behavior of TiAl alloys exhibits significant complexity due to the anisotropic nature of the α₂ phase and the (α₂+γ) lamellar structures. The orientation-dependent deformation response of the lamellar structure makes the overall deformation behavior of TiAl alloys highly sensitive to both applied stress and temperature fluctuations. Further compounding this complexity, grain reorientation induced by texture development disrupts deformation coordination in the α₂ phase while simultaneously influencing internal stress accumulation. Additionally, the chemical composition of the α₂ phase generally deviates from the equilibrium state and has a strong disposition to decompose, such as α₂→γ and α₂→ω_o^[24-27]. This process is significantly accelerated by accumulated internal stress^[28-31]. The orthorhombic O phase, typically observed during long-term annealing, would precipitate from the α₂ phase under stressed conditions, further complicating the deformation dynamics. This phase not only generates additional internal stresses but also interacts with existing stress fields within the α₂ phase. These interactions highlight the critical need for detailed investigations into the coupled evolution of internal stresses and stress-induced phase transformations. Such research is essential for elucidating the fundamental deformation mechanisms governing TiAl alloys, particularly regarding the complex interplay between microstructural evolution and mechanical response.

Overview of O phase precipitation

Banerjee et al.^[32,79,80] first reported the existence of an ordered orthorhombic O phase with Cmcm symmetry in a Ti₃Al-based alloy with a high Nb content (Ti-25Al-12.5Nb). They suggested that the O phase originates from the slightly distorted α₂ phase with a nominal composition of Ti₂AlNb. Subsequently, Muraleedharan et al.^[38] discovered two different structures of the O phase, i.e., O1 and O2, which possess the same crystal structure and symmetry but differ in atomic occupancy. Ti and Nb atoms randomly occupy the Wyckoff positions 8g and 4c₂ in the O1 structure, while Ti atoms predominantly occupy the 8g position, and Nb atoms primarily occupy the 4c₂ position in the O2 structure. Except for the α₂ phase, the O phase could also transform from the β_o matrix. Bendersky et al.^[81] found that the addition of Nb affects the formation path of the O phase. In the Ti-25Al-12.5Nb alloy, the O phase originates directly from the α₂ phase, whereas in the Ti-25Al-25Nb alloy, the β_o phase transforms into the O phase via an intermediate B19 phase with Pmma symmetry.

Early studies on the orthorhombic O phase mainly focused on the Ti-Al-Nb ternary alloys with compositions of Ti-(12-31)Al-(12.5-37.5)Nb^[79-81]. In the 21^st century, researchers also observed the presence of the orthorhombic phase in γ-TiAl alloys. In Ti-(40-44)Al-8.5Nb alloys, Appel et al.^[82-84] found modulated microstructures composed of the β_o phase and an orthorhombic phase using transmission electron microscopy (TEM). The orthorhombic phase in this study was recognized as the B19 phase, transformed by a shuffle displacement of adjacent (110) planes along opposite [1$$ \bar{1} $$0] directions in the β_o phase. Song et al.^[85] also observed a modulated microstructure inside the α₂ phase within the lamellar structures in high-Nb TiAl alloys. The elongation of diffraction spots along the [1$$ \bar{1} $$00] direction under the [11$$ \bar{2} $$0] zone axis confirms the presence of the orthorhombic B19 phase. Furthermore, this phase was considered a transient phase of the α₂ to γ phase transformation. Taking advantage of HEXRD, the diffraction peaks belonging to the orthorhombic phase are observed in a quenched Ti-44Al-3Mo alloy after holding at 600 °C^[86]. A good quality of Rietveld refinement was achieved using the B19 structure model. TEM observations indicated that this B19 phase is transformed from the α₂ martensite. However, from a crystallographic perspective, Bendersky et al.^[87] suggested that the orthorhombic phase precipitating directly from the α₂ matrix is highly likely the O phase rather than the B19 phase. This argument is based on the structural similarities between the α₂ and O phases, particularly in terms of atomic occupancy and lattice arrangements. Specifically, the α₂ phase shares identical atomic occupancy at the 8g and 4c₁ Wyckoff positions with the O1 phase, while the O2 phase aligns with the α₂ phase at the 4c₁ position. These structural parallels render the transformation from α₂ to O1 or O2 more energetically favorable than the formation of the B19 phase, which requires a more complex atomic rearrangement since the atomic occupancy of the B19 phase at 4c₁ and 4c₂ positions is identical.

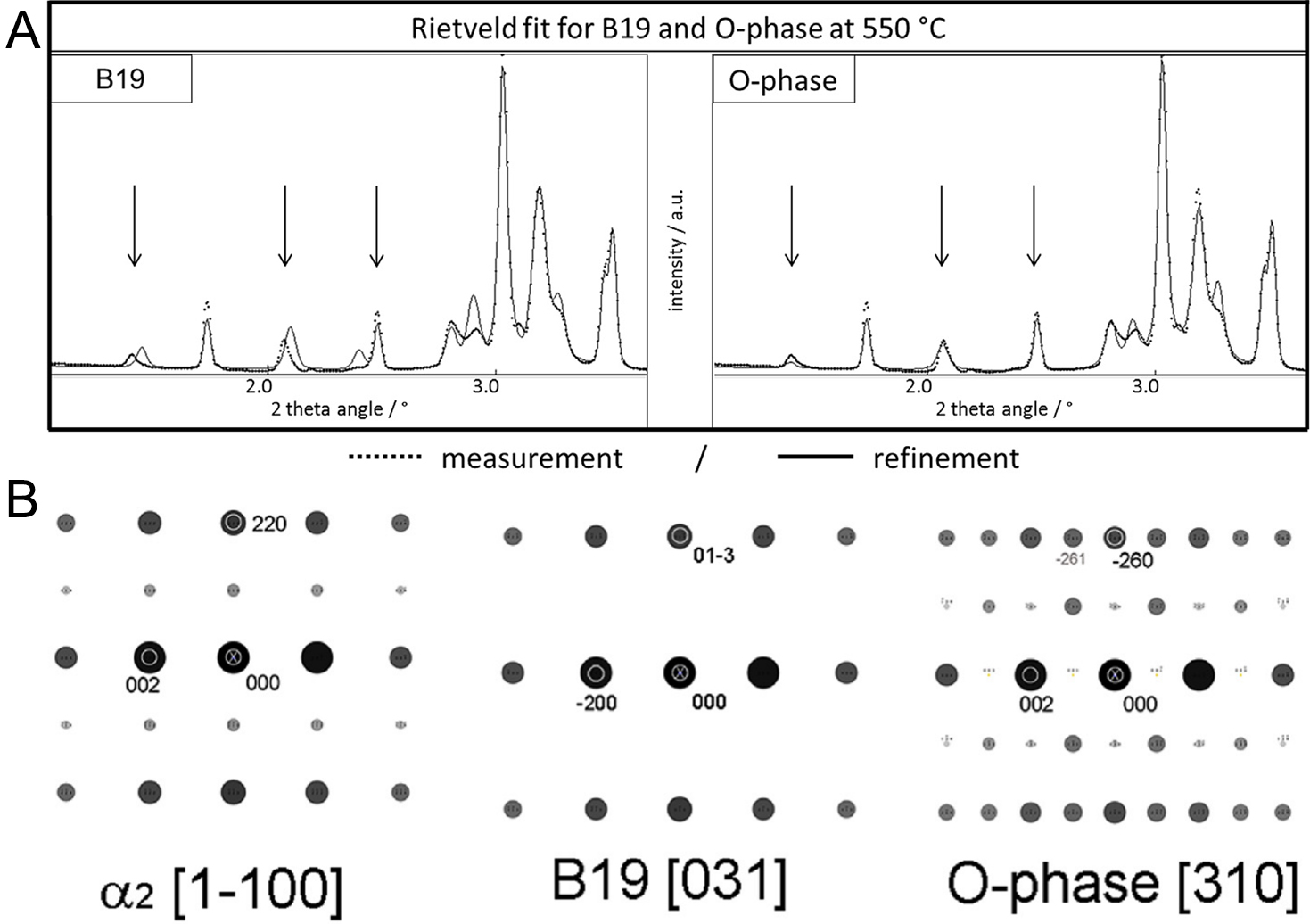
During in situ heating and cooling experiments in a lamellar Ti-42Al-8.5Nb alloy, Rackel et al.^[35] observed peak splitting of the α₂ reflections caused by orthorhombic phase precipitation. Employing both the B19 and O phase structural models for Rietveld refinement, the fitting results showed that the orthorhombic phase is structurally comparable to the O phase, as visible in Figure 9A. This indicates that the orthorhombic phase precipitating from the α₂ lamellae is, in fact, the O phase. Furthermore, the temperature range for the stability of the O phase was determined to be 500-700 °C. Additional evidence identifying the orthorhombic phase as the O phase was advanced by TEM observation^[33]. Theoretically, the O phase with lower symmetry should exhibit more diffraction spots compared to the B19 phase. Gabrisch et al.^[33] simulated the electron diffraction patterns of the α₂, B19, and O phases. Under the [1$$ \bar{1} $$00]_α2 zone axis, the (131)_O diffraction spot along the parallel [310]_O zone axis does not overlap with the diffraction spots of the other two phases, as visible in Figure 9B. After annealing at 550 °C, the experimental findings further confirmed that the O phase precipitates from the α₂ phase in a Ti-42Al-8.5Nb alloy^[33,35]. However, unlike the in situ HEXRD heating experiments, the O phase retransforms into the α₂ matrix at around 600 °C during in situ TEM heating experiments [Figure 10]^[33]. The discrepancy may originate from variations in specimen dimensions, specifically the utilization of bulk specimens for HEXRD experiments in contrast to thin foil samples employed for TEM characterization. This implies that volume and coherency stresses between the α₂ and γ phases within the lamellar structures are prerequisites for O phase precipitation.

Figure 9. (A) Rietveld refinement using structural models of the B19 and O phases. (Reproduced from Ref.[35]^[35]); (B) Simulated diffraction patterns in the [1$$ \bar{1} $$00]_α2 direction and the corresponding simulated diffraction patterns in the [031]_B19 and [310]_O directions. (Reproduced from Ref.[33]^[33]).

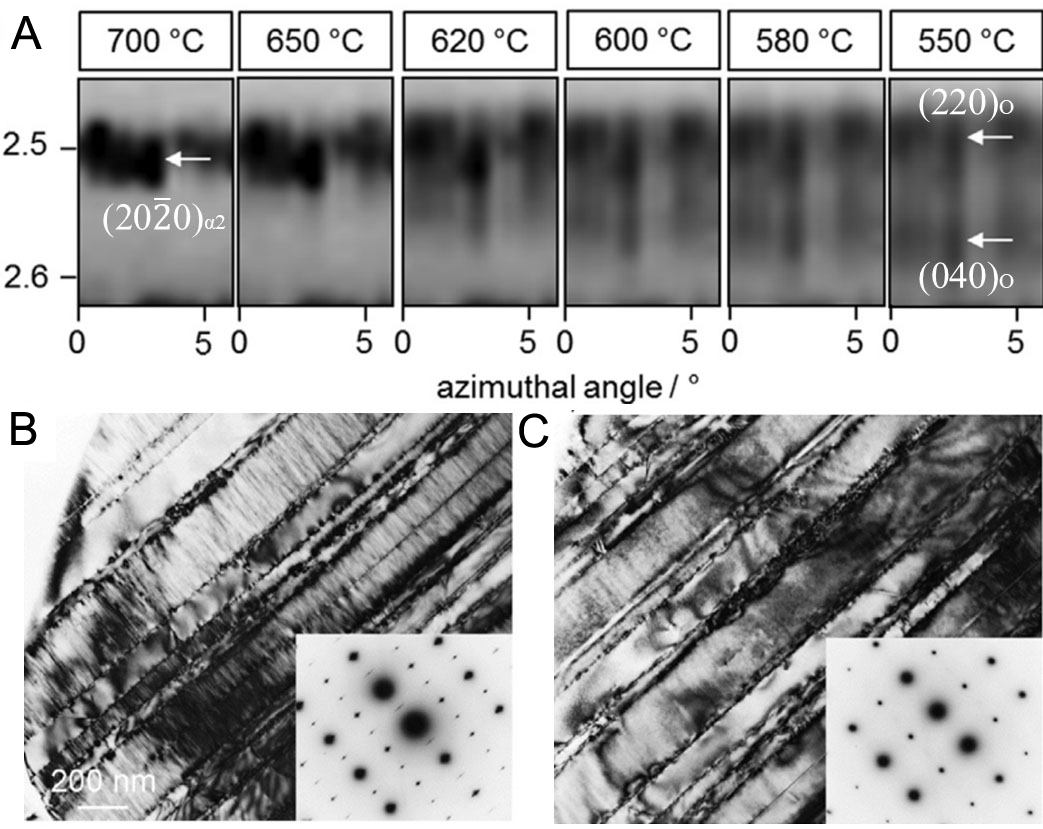
Figure 10. In situ (A) HEXRD and (B) and (C) TEM heating of a Ti-42Al-8.5Nb alloy: (A) the (20$$ \bar{2} $$0)_α2 reflections gradually split into the (220)_O and (040)_O reflections. (Reproduced from Ref.[35]^[35]); Modulated structures suggestive of O phase presence, observed at (B) room temperature and (C) after heating to 600 °C (Reproduced from Ref.[33]^[33]). HEXRD: High-energy X-ray diffraction; TEM: transmission electron microscopy.

Studies examining the temperature range of O phase formation across different alloy compositions have been conducted in γ-TiAl alloys. As evidenced by orthorhombic splitting of the α₂ reflections, the O phase forms out of the α₂ phase after annealing at 550 °C for 20 h when the Nb content exceeds 5-7.5 at.% and the Al content is below 46-47 at.%^[34]. In a Ti-42Al-8.5Nb alloy, TEM observations have directly identified nanoscale O phase domains embedded within the α₂ phase following annealing at 550 °C and 650 °C^[33]. In a lamellar Ti-45Al-8.5Nb alloy, modulated structures, associated with O phase formation within the α₂ lamellae, were observed after annealing at 650 °C and disappeared upon heating to 700 °C^[88,89]. A comparative study has been conducted to examine the effect of alloy composition on O phase formation in Ti-(43-47)Al-8.5Nb and Ti-45Al-(4-10)Nb alloys^[36]. The results demonstrated that while increasing Nb content and decreasing Al concentration elevate the dissolution temperature of the O phase, it remains below 750 °C. In general, the maximum temperature at which the O phase remains stable before dissolving is close to the typical service temperature of high Nb-containing TiAl alloys (i.e., above 800 °C).

Formation mechanisms of the O phase

The crystal structure of the O phase remains controversial. Previous studies suggested that two crystal structures, O1 and O2, can be differentiated by the ordered parameter (η), which quantifies the difference in Nb occupancy between the Wyckoff positions 4c₂ and 8g within Cmcm symmetry^[38]. Specifically, the O1 phase corresponds to η = 0 with Nb atoms randomly occupying the 8g and 4c₂ positions, while the O2 phase is defined by η > 0.2. Furthermore, η = 1 represents the fully ordered state, where the Nb atoms exclusively occupy the 4c₂ positions. In Ti-27.5Al-xNb ternary alloys, the O2 to O1 structural transition was once considered to take place during heating, as illustrated in Figure 11A^[38]. However, using in situ neutron diffraction heating experiments, Xu et al.^[90] found that only one crystal structure of the O phase exists, i.e., O2. The difference in atomic occupancy (i.e., different η) of the O1 and O2 structures causes intensity changes in the O reflections, as visible in Figure 11B. However, during continuous heating, especially within the structural transition temperature range of O2 to O1, the intensity of the O reflections remains the same (magnified view shown on the right in Figure 11C). Further Rietveld refinement demonstrated that the O phase maintains an O2 crystal structure. Additionally, within the stable temperature range of 750-950 °C of the O phase, the order parameter (η) fluctuates between 0.4 and 0.5, which aligns with the study reported by Mozer et al.^[91] (see Table 1). These results indicate that the β_o to O phase transformation involves not only a structural distortion but also a significant change in atomic ordering in Ti₃Al-based alloys. However, the situation becomes different when considering the α₂ to O phase transformation in γ-TiAl alloys. The Nb atoms of the O lattice show no preferential occupancy in the 4c₂ position, and this structure is identified as the O1 structure^[35]. Additionally, TEM evidence further supported the presence of the O1 structure in a Ti-45Al-8.5Nb alloy^[88]. In the convergent beam electron diffraction (CBED) pattern, the {110}_O and {002}_O reflections share the same intensity [Figure 12A], which indicates Ti and Nb atoms randomly occupy the Wyckoff positions at 8g and 4c₂. In general, the crystal structures of the O phase require further investigation, as they may vary depending on the chemical compositions of TiAl alloys and their parent phases (i.e., α₂ and β_o).

Figure 11. (A) Ternary Ti-27.5Al-xNb phase diagram. (Reproduced from Ref.[38]^[38]); (B) Simulated XRD patterns of the O phase with the chemical composition of Ti₂AlNb; (C) Variation of the Ti-24.8Al-24.3Nb neutron diffraction pattern at different temperatures. (Reproduced from Ref.[90]^[90]). XRD: X-ray diffraction.

Research has been conducted to explore the formation mechanisms of the O phase, particularly the compositional and structural transitions involved in the α₂→O phase transformation^{[33,88,89,92]}. In a Ti-25Al-12.5Nb alloy, Banerjee et al.^[79] proposed that a phase separation occurs within the α₂ phase, leading to the formation of Nb-lean and Nb-rich regions, with the O phase preferentially precipitating in the Nb-rich areas. This theory aligns with microscopic observations of the O phase with an extremely fine scale and dispersed distribution. Ren et al.^[88,89] further demonstrated that diffusion mechanisms play a dominant role in the thickening of the O phase. Energy dispersive X-ray spectroscopy (EDS) mapping of a Ti-45Al-8.5Nb alloy annealed at 600 °C for 500 h shows an enrichment of Nb and an almost homogeneous distribution of Ti and Al in the O phase, as visible in Figure 12B-D^[89]. The Nb partitioning coefficient between the α₂ and O phases was found to be around 2. However, different results were present during the early stages of the α₂→O phase transformation. In a Ti-42Al-8.5Nb alloy annealed at 650 °C for 2 h, small atomic shifts of the α₂ lattice along three {11$$ \bar{2} $$0}_α2 directions disrupt its hexagonal symmetry and form different O variants, as visible in Figure 12E^[33]. Furthermore, the Nb element exhibits a homogeneous distribution in the α₂ and O phases. This strongly suggests that structural transition precedes the compositional fluctuation for the α₂→O phase transformation. Nb diffusion plays a crucial role in the compositional transition from α₂ to O phase. However, this transformation can be sluggish, and factors such as annealing duration, temperature, Nb content, and other variables may lead to variations in Nb distribution within the O phase. Collectively, the experimental results suggest that minor atomic shifts are initially involved in the O phase precipitation and Nb distribution is crucial for the growth of the O phase in γ-TiAl alloys. Nevertheless, whether atomic ordering within the O lattice participates in the α₂→O phase transformation remains uncertain, and if so, how and when it occurs. In such a case, synchrotron X-ray and neutron diffraction techniques offer a powerful approach to address these scientific questions and are crucial for understanding the underlying mechanisms of the α₂→O phase transformation.

Figure 12. (A) CBED pattern of the O phase; (B-D) Atomic-resolution HAADF images showing the α₂ and O phases along the [0001]_α2/[001]_O zone axis in a Ti-45Al-8.5Nb alloy annealed at 600 °C for 500 h (reproduced from Ref.[89]^[89]); (E) HAADF image of a Ti-42Al-8.5Nb alloy annealed at 650 °C for 2 h, displaying the same crystallographic orientation relationship. (Reproduced from Ref.[33]^[33]). CBED: Convergent beam electron diffraction; HAADF: high-angle annular dark-field.

Crystallographic characteristics of O phase formation

Banerjee et al.^[79] proposed that the hexagonal α₂ and orthorhombic O phases should satisfy the OR as follows: [001]_O//[0001]_α2; [100]_O//[11$$ \bar{2} $$0]_α2; [010]_O//[1$$ \bar{1} $$00]_α2. Later, Muraleedharan et al.^[93] found that the O phase would slightly rotate around the invariant line [001]_O/[0001]_α2 to maintain undistorted habit planes. Correspondingly, this rotation enables a minor deviation of [100]_O from [11$$ \bar{2} $$0]_α2. Based on a phenomenological theory of martensitic transformation, the theoretical angle between the [100]_O and [11$$ \bar{2} $$0]_α2 directions is determined as 1.63°. Additionally, the habit planes of parent and precipitation phases are (4 ±7 0)_O and (8$$ \overline{11} $$30)_α2, respectively. The rigid rotation angle calculated by Ren et al.^[88] is 1.61° and the corresponding habit planes are (3 ±5 0)_O and ($$ \bar{1} $$4$$ \bar{3} $$0)_α2 [Figure 13A]. This theoretical calculation was confirmed by by high-resolution transmission electron microscopy (HRTEM) observation. Viewing along [0001]_α2, the (040)_O plane deviates from the (02$$ \bar{2} $$0)_α2 plane at an angle of 1.44° [Figure 13B], which approaches the calculation results. Simultaneously, this rotation enables [110]_O to be parallel to [11$$ \bar{2} $$0]_α2. Accordingly, the OR between the α₂ and O phases is determined to be (001)_O//(0001)_α2; [110]_O//[11$$ \bar{2} $$0]_α2, or equivalently, [001]_O//[0001]_α2; (110)_O//(1$$ \bar{1} $$00)_α2. This OR indicates a close alignment between specific crystallographic planes of the two phases. Among the six symmetrically equivalent {20$$ \bar{2} $$1}_α2 planes, four are closely aligned with the {221}_O planes, while the remaining two are oriented near the {041}_O planes. Notably, the (041)_O plane exhibits a deviation of approximately 2° from the (20$$ \bar{2} $$1)_α2 plane, as revealed by transmission measurements. This configuration is reflected in the orthorhombic splitting of the (20$$ \bar{2} $$0)_α2 and (20$$ \bar{2} $$1)_α2 reflections (which do not overlap with other reflections) in HEXRD profiles. That is, the (041)_O/(221)_O reflections slightly deviate from the (20$$ \bar{2} $$1)_α2 reflections in azimuth angle [Figure 13C]. The same goes for the (040)_O/(220)_O and (20$$ \bar{2} $$0)_α2 reflection doublets [Figure 13D]. Conversely, the reflection doublets of the α₂ and O phases observed in HEXRD originate from the O variants precipitating from the α₂ matrix [Figure 13E], and thus their intensity changes reflect the phase transformation process.

Figure 13. (A) [0001]_α2 superimposed pole figures showing the lattice correspondence between the α₂ and O phases, with the calculated habit planes being ($$ \bar{1} $$4$$ \bar{3} $$0)_α2; (B) HRTEM image recorded along [0001]_α2. (Reproduced from Ref.[88]^[88]); The [11$$ \bar{2} $$0]_α2/[110]_O superimposed pole figure exhibits the lattice correspondence of (C) equivalent {20$$ \bar{2} $$1}_α2 planes and {221}_O and {041}_O planes and (D) equivalent {20$$ \bar{2} $$0}_α2 planes and {220}_O and {040}_O planes; (E) Evolution of the (20$$ \bar{2} $$0)_α2 and (040)_O reflection doublet and (20$$ \bar{2} $$1)_α2 and (041)_O reflection doublet with increasing stress. (Reproduced from Ref.[37]^[37]). HRTEM: High-resolution transmission electron microscopy.

The α₂→O structural transition involves lattice deformation (shuffling along three <11$$ \bar{2} $$0>_α2 directions) and a small rigid body rotation (around the [0001]_α2 axis), leading to the formation of six possible O variants within the α₂ matrix. In the absence of external stress, the simultaneous precipitation of all O variants minimizes bulk elastic energy through mutual elastic interactions, resulting in an energetically favorable configuration^[94]. However, when stress is applied, selective nucleation of the O variants is induced^[95], which influences the deformation behavior of the alloy. HEXRD enables real-time observation of this transformation, revealing how stress drives variant selection and microstructural evolution. Additionally, HEXRD quantifies strain distribution across different O variants, providing insights into stress accommodation mechanisms. The selection of O variants not only determines the morphology and texture of the transformed regions but also directly influences the strength, ductility, and creep resistance of the alloy. Further investigation is required to enhance the performance of TiAl alloys in elevated temperature applications such as those in the aerospace and automotive industries.

Reversible stress-induced orthorhombic phase formation

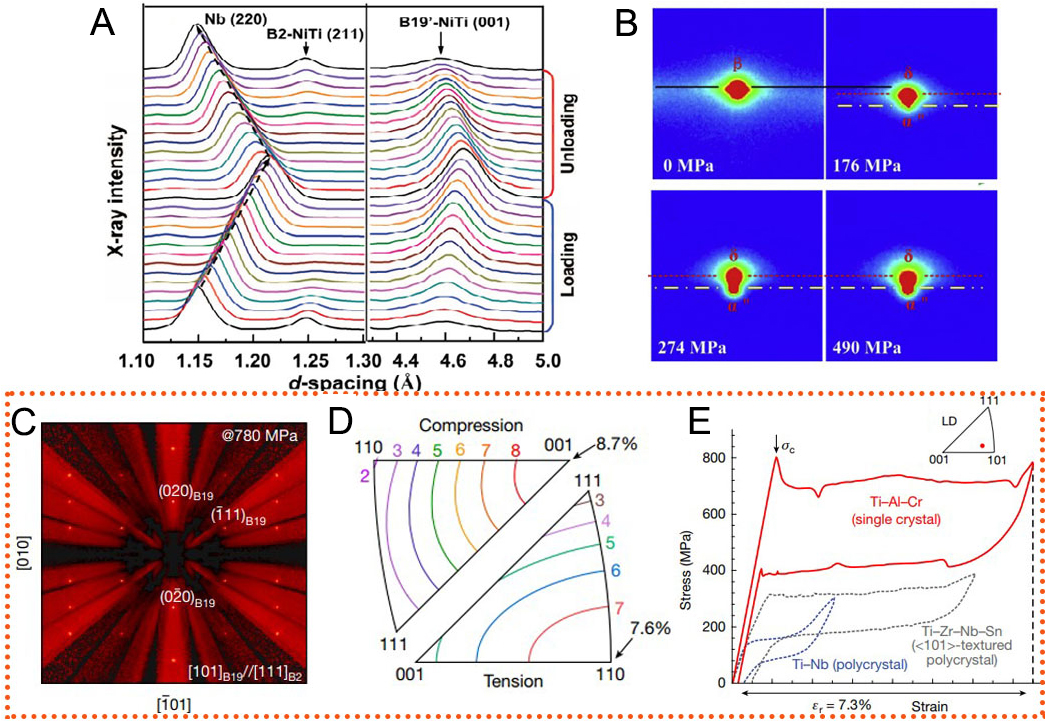
The stress-induced orthorhombic and martensite phases formation from body-centered β phase or B2 phase has been extensively observed in NiTi and β-Ti alloys^[96-101]. This transformation is highly reversible, enabling these alloys to withstand large elastic strains and thus exhibit promising practical applications. To elucidate the underlying mechanisms of this phase transition, in situ synchrotron or neutron diffraction techniques are essential for tracking the orthorhombic phase evolution under stress. In a Ni₄₁Ti₃₉Nb₂₀ alloy, the orthorhombic B19’ phase was observed to gradually precipitate from the B2 phase during loading and a reverse transformation took place during unloading, as visible in Figure 14A^[102]. However, some B19’ phase remains after unloading due to residual strain preserved from irreversible plastic deformation of Nb. Similarly, in a Ti-24Nb-4Zr-8Sn-0.1O single crystal, the diffraction spots of the β phase gradually split into those of the orthorhombic α” and δ phases during uniaxial tensile loading along the [110]_β axis [Figure 14B]^[103].

Figure 14. (A) Evolution of the diffraction peaks of (220)_Nb, (211)_B2 and (001)_B19′ during the tension of a Ni₄₁Ti₃₉Nb₂₀ alloy (Reproduced from Ref.[102]^[102]); (B) In a Ti-24Nb-4Zr-8Sn-0.1O single crystal, the (220)_β spot gradually splits into diffraction spots belonging to the orthorhombic α” and δ phases. (Reproduced from Ref.[103]^[103]); A Ti_75.25Al₂₀Cr_4.75 single crystal showing excellent superelasticity during tension: (C) B19 structure recorded at a stress of 780 MPa during in situ neutron diffraction; (D) calculated orientation dependence of transformation strain under tension and compression; (E) tensile loading-unloading stress-strain curves showing a large recovery strain of 7.3 %. (Reproduced from Ref.[104]^[104]).

Notably, a recent study on a specifically designed Ti₃Al-based alloy (Ti_75.25Al₂₀Cr_4.75) demonstrated exceptional superelasticity due to a reversible stress-induced orthorhombic phase transformation^[104]. In situ neutron diffraction tension on near-<110> single crystals captured the diffraction patterns of the B2 and B19 structures (see Figure 14C) under different stress conditions. Furthermore, lattice deformation theory was employed to calculate the orientation-dependent transformation strain using the equation^[105]:

Where x’ = Tx, x represents a given vector in the parent phase, x’ the corresponding vector in the precipitation phase, and T the lattice deformation matrix in the coordinates of the parent phase for the precipitate orthorhombic phase. For the B2 to B19 structural transition, normal strains along principal axes and shear strains are taken into account when calculating the lattice deformation matrix. For the α₂ to orthorhombic O phase transformation, orthogonal strains along the [11$$ \bar{2} $$0]_α2 and [1$$ \bar{1} $$00]_α2 directions, along with a rigid body rotation around the [0001]_α2 axis, are involved^[88]. The maximum recoverable transformation strain was calculated to be 7.6% as stretched along the [110]_β axis and 8.7% as compressed along the [001]_β axis [Figure 14D]^[104], aligning well with experimental results, which show a maximum recoverable strain of 7.3% [Figure 14E]^[104]. Additionally, the superelasticity in Ti₃Al-based alloys occurs over a broad temperature range due to the anomalous temperature dependence of transformation stresses, balancing lightness and enhanced mechanical properties.

The superelasticity of shape memory alloys is closely associated with transformation strain and crystallographic texture. In the Ti-Zr-Nb-Sn alloy system, transformation strains show similar distributions across different alloy compositions, reaching a peak of approximately 7% along the [011]_β direction^[106]. However, recoverable elastic strains vary significantly due to differences in the spatial distribution of the β phase. For instance, the Ti-18Zr-15Nb alloy exhibits a weak {112}_β<0$$ \bar{2} $$1>_β texture, whereas the Ti-18Zr-12.5Nb-2Sn alloy develops a strong {100}_β<011>_β recrystallization texture. As a result, the maximum recovery strain is 3.8% in Ti-18Zr-15Nb and increases to 6% in Ti-18Zr-12.5Nb-2Sn^[107]. It should be noted that a large recoverable elastic strain does not always correspond to uniaxial loading in the direction with the highest transformation strain. For instance, in a Fe_43.5Mn₃₄Al₁₅Ni_7.5 single crystal, although the highest transformation strains appear along the <100> directions, the superelastic strains reach 7.8% along the <123> orientation, significantly higher than the 3.6% observed along the <100> orientation^[108].

In a Ti-38Al-10Nb polycrystalline alloy, Liu et al.^[37] reported a reversible stress-induced O phase transformation occurring at 800 °C and even 900 °C, temperatures exceeding the temperature range of the O phase. The O phase formation is strongly correlated with stress levels and evolves synchronously with internal stress accumulation in the α₂ phase beyond a critical stress point. During the first loading, along with the rapid internal stress accumulation in the α₂ phase at stresses above ~1,055 MPa, the α₂ phase rapidly transforms into the O phase [Figure 15A and B]. During unloading and further holding, the O phase dissolves into the α₂ matrix as internal stress relaxes [Figure 15C and D]. The α₂→O phase transformation rapidly proceeds at stresses above ~1,220 MPa, where rapid internal stress accumulation takes place [Figure 15E and F]. Furthermore, the O phase formation exhibits a strong variant selection and preferentially precipitates from the α₂ matrix with the [0001]_α2 direction nearly unstrained and the [11$$ \bar{2} $$0]_α2 direction under the largest tension, facilitating the transition through small atomic shifts on the basal plane of the α₂ phase. This reversible stress-induced orthorhombic O phase formation highlights the potential for enhancing elastic strains in γ-TiAl alloys, especially in microstructural engineering for specific textures. Moreover, investigating the temperature dependence of stress-induced O phase formation and its reversibility in various alloy compositions is essential for optimizing the mechanical properties of TiAl alloys.

Figure 15. Lattice strain and intensity evolution in Ti-38Al-10Nb alloys subjected to double loading with an intermediate holding stage at 800 °C. (A) Lattice strain vs. true stress/holding time curves for α₂ and γ reflections during the first loading; (B) Intensity vs. true stress curves for the (20$$ \bar{2} $$0)_α2 and (040)_O reflections during the first loading; (C) Lattice strain vs. holding time curves for the α₂ reflections during the intermediate holding; (D) Intensity vs. holding time curves for the (20$$ \bar{2} $$0)_α2 and (040)_O reflections during the intermediate holding; (E) Lattice strain vs. true stress curves for the α₂ and γ reflections during the second loading; (F) Intensity vs. true stress curves for the (20$$ \bar{2} $$0)_α2 and (040)_O reflections during the second loading. The lattice strains of the γ reflections during the intermediate holding are omitted for clarity. (Reproduced from Ref.[37]^[37]).