Atomistic underpinnings for dislocation emission behaviors at the crack tips in FCC metals in light of thermo-kinetic synergy

Theoretical models

Herein, the continuum mechanics models within the ALEFM framework^[31] are used to obtain the stress distribution near the crack tips in FCC Al. When dislocations are emitted at the crack tips, various defects such as SFs, twinning, and free surfaces form near the crack tips^[22,32], triggering rearrangement of atoms near the crack tips to release the elastic strain energy, and thus enhancing the stability of crack tips. By analyzing the formation energy of these defects, the critical conditions for dislocation emission at the crack tips in FCC metals can be obtained from the thermo-kinetic variations.

Continuum mechanics models for twinning dislocation nucleation at the crack tips

Once the first partial dislocation is emitted at the crack tips, the local stress concentration spreads out^[6], which makes the atomic structure near the crack tips satisfy the critical condition for dislocation emission. In principle, there are three scenarios^[22] for subsequent dislocation emissions at the crack tips in FCC metals: (i) Trailing partial dislocation emission, where the second partial dislocation nucleates on the same slip plane as the first partial dislocation. The two partial dislocations react to form a full dislocation, moving away from the crack tips; (ii) Twinning partial dislocation emission, where the second partial dislocation nucleates on the adjacent slip plane of the first partial dislocation at the crack tips. This generates a twinning zone with a thickness of two atomic layers, which promotes the blunting phenomenon of the crack tips; (iii) Partial dislocation emission at non-adjacent slip planes, where the second partial dislocation nucleates on a non-adjacent slip plane of the first partial dislocation at the crack tips. This forms two separated SF regions, which can transform into a twinning zone with a thickness of three atomic layers during subsequent dislocation emission. In fact, the twinning partial dislocation emission is the most common in FCC Al^[28]. Following the Peierls concept^[12], a predictive model of the critical stress intensity factor $$ K_{Ie,tip}^{twin} $$^[22] for twinning dislocation emission was proposed based on Rice’s theory^[12], whereas the distinctions lies in: (i) for the twinning dislocation emission, the emission direction of the second partial dislocation φ_twin is consistent with that of the first dislocation emission φ_first, i.e., φ_twin = φ_first; (ii) the micro-twinning boundaries form via twinning dislocation nucleation on the adjacent slip planes rather than eliminating SF zone. Accordingly, the critical energy release rate for twinning dislocation emission at the crack tips depends on the twinning fault energy γ_utf. Meanwhile, the energy release rate before dislocation emission increases by γ_isf, since the first partial dislocation emission makes the initial state contain SF zone in the second partial dislocation before emission. As such, the critical stress intensity factor of the twinning dislocation emission at the crack tips^[22] was derived as:

(4) $$ K_{Ie,tip}^{twin}=\sqrt{(\gamma _{utf}-\gamma _{ssf})p(\theta ,\varphi _{first})} /F_{12}(\theta) $$

where F₁₂(θ) denotes the stress decomposition factor, which is a function of the angle θ between the slip plane and the crack plane, while the geometric factor p(θ,φ) is a function of θ and the angle φ between the Burgers vector of emitted dislocation and the crack propagation direction [Figure 1A]. In general, the critical stress intensity factor of twinning dislocation emission in FCC metals is smaller than that of trailing dislocation emission^[22], i.e., $$ K_{Ie,tip}^{twin}< K_{Ie,tip}^{trail} $$. Thus, the twinning dislocation emission was regarded as the primary mechanism of subsequent dislocation emission at the crack tips in FCC metals. However, the critical stress intensity factor predicted from the above model^[22] is significantly lower than that from atomistic simulations^[15]. For the twinning dislocation emission at the crack tips, the local stress on the twinning slip planes is lower than the stress at the crack tips, because the twinning slip planes do not directly intersect with the crack tips^[22]. By introducing an elastic correction factor f(C_ijkl) to quantitatively describe the enhancement effect of stress field required for twinning dislocation nucleation at non-crack tip locations, the above model^[22] was improved and the critical stress intensity factor of twinning dislocation emission^[27] was rewritten as:

(5) $$ K_{Ie,tip}^{twin}=f(C_{ijkl})\sqrt{(\gamma _{utf}-\gamma _{ssf})p(\theta ,\varphi _{first})} /F_{12}(\theta) $$

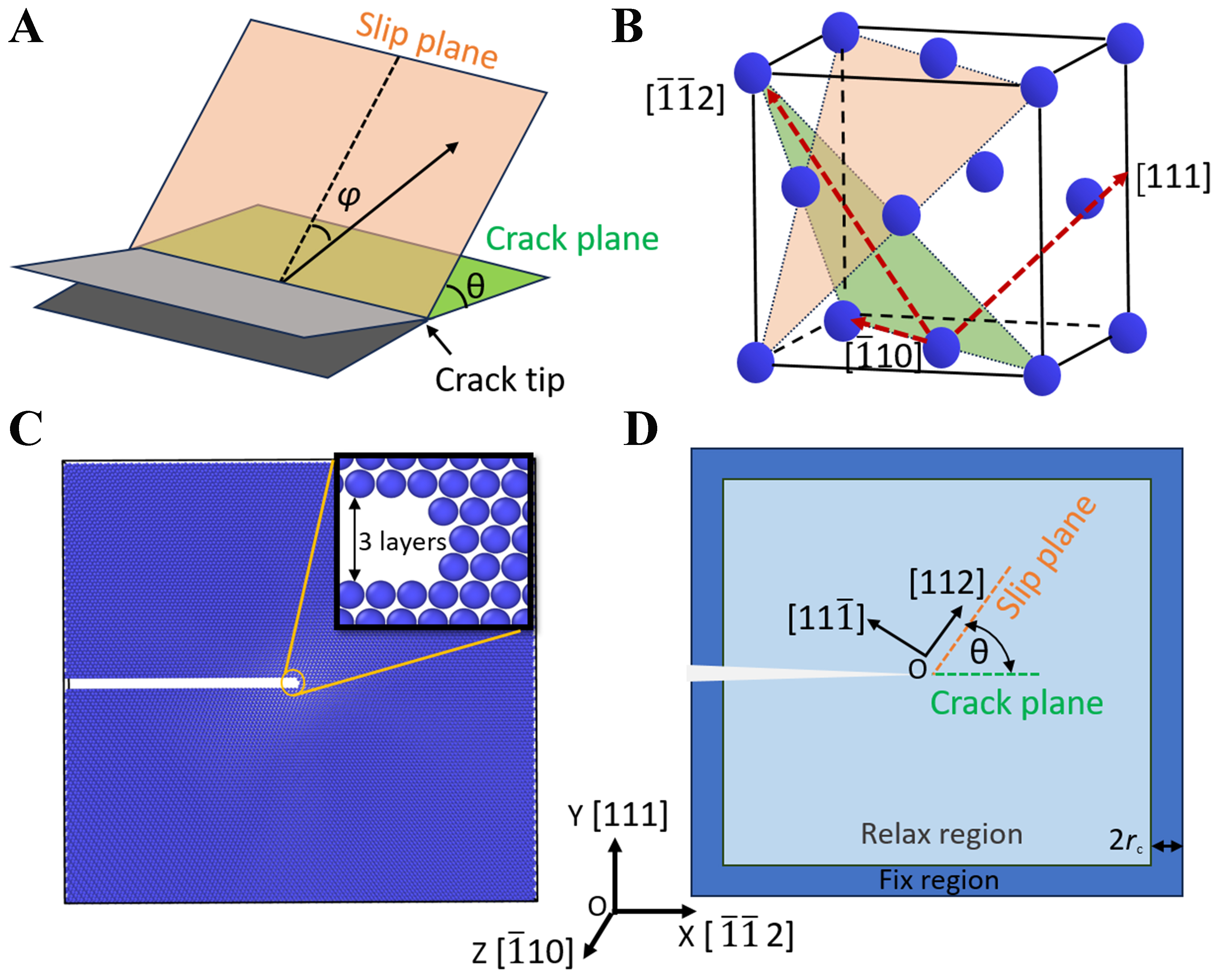
Figure 1. Schematic diagram for the structural model of FCC Al under the K-field loading conditions for atomistic simulations. (A) The direction of dislocation emission at the crack tips, where θ is the angle between the crack plane and slip plane, and φ is the angle between the dislocation emission direction and crack propagation direction; (B) The slip systems involved in dislocation emission at the crack tips, where the triangular region represents the {111} slip plane, and the direction of dislocation emission from the crack tips is along the <112> direction; (C) Atomic configuration of FCC Al with a marginal crack, where the X, Y, and Z axes of the simulation box are along the [$$ \bar{1}\bar{1} $$2], [111], and [$$ \bar{1} $$10] directions of FCC Al, respectively. A preset crack is introduced by removing three atomic layers on the XZ plane; (D) The K-field loading region, where the dark blue region represents the fixed region, while the remaining light blue region is the free zone to be relaxed. Note that the light green and orange planes denote the crack plane and dislocation slip plane, respectively. FCC: Faced-centered cubic.

where f(C_ijkl) is the elastic correction factor obtained via elastic analysis on the stress field at the crack tips, and C_ijkl is the elastic constant.

Equation (5) resolves the discrepancy of critical stress intensity factor at the crack tips between predictions and atomistic simulations, providing a robust foundation for understanding dislocation emission behaviors at the crack tips in FCC metals. Following thermodynamic extremal principle^[27], the dislocation emission at the crack tips always tends to the energy minimization while the defect formation is with the smallest energy barrier, regardless of the varied dislocation nucleation mechanism. Therefore, it is in urgent demand to identify the universal laws governing subsequent dislocation emission behaviors at the crack tips in FCC metals based on the thermo-kinetic synergy.

Computational procedures

Considering the slight deformations and plane strains of the ALEFM theory^[7], herein the applied load in the “K-field” loading model, i.e., the ALEFM-MD coupled model, is imposed via displacements near the crack tips generated by the “K-field” in the anisotropic continuum^[29]. For MD simulations, the magnitude of applied load is regulated by the stress intensity factor K, which enables an accurate description of atomic-scale behaviors of the crack tips and quantifies the critical stress intensity factor of cleavage/dislocation emission at the crack tips^[7]. The reasonability for such settings in MD simulations of the Mode I and Mode II loading conditions has been verified in previous work^[15,22,23].

As such, the atomistic configuration with a preset crack in FCC Al was constructed [Figure 1B], where the <112> direction on the ($$ \bar{1} $$11) slip plane is with the smallest interatomic separation of 2.86 Å. Extensive simulation works^[15,22,23] confirmed that the 1/6<112> Shockley partial dislocation dominates dislocation emission at the crack tips in FCC metals. For convenience of analyzing the dislocation emission behaviors, the X, Y, and Z axes of the simulation box with dimensions of 30 × 30 × 1 nm³ were along the [$$ \bar{1}\bar{1} $$2], [111], and [$$ \bar{1} $$10] directions of FCC Al, respectively. The normal direction of the ($$ \bar{1} $$11) slip plane is parallel to the dislocation slipping direction, which is perpendicular to Z axis of the simulation box, given that the dislocation emission direction is along the [112] direction. Besides, three atomic layers on the ($$ \bar{1} $$11) slip plane were removed from Y axis at position of the half box length to preset a marginal crack in the atomistic configuration, where the crack depth is the half box length of X axis [Figure 1C]. Such “blunted” crack can prevent the crack closing under stress during loading^[29].

For MD simulations, the free boundary condition was used for the X and Y axes, while the periodic boundary condition was used for the Z axis of the simulation box. The Mode I loading conditions for cracks in FCC Al were achieved by applying a displacement field, where all atoms move Δu_x and Δu_y along the X and Y axes at each loading time, respectively. The displacement increment Δu_x and Δu_y^[33] is given as:

where the initial value and the increment of the stress intensity factor are set as K_I = 0.1 MPa·m^1/2 and ΔK = 0.001 MPa·m^1/2, respectively. Figure 1D shows that after applying each displacement, those atoms within 2r_c (with r_c being cutoff radius of the interatomic potential) region from the simulation box boundary were fixed, while the remaining atoms were minimized to reach equilibrium. The simulations were carried out at 0 K to eliminate the influence of thermal vibrations on the dislocation emission behaviors at the crack tips. The embedded atom method (EAM) potential developed by Mishin et al.^[34], which has been used extensively to investigate dislocation nucleation behaviors^[25], was employed to describe the atomic interactions in FCC Al. The energy minimization includes three steps: (i) using the conjugate gradient method (CG)^[35] for coarse optimization (with energy tolerance of 1 × 10^-20 eV) to relax the long-range elastic strains rapidly; (ii) using the fast inertial relaxation engine (FIRE)^[36] algorithm (with energy tolerance of 1 × 10^-12 eV) for local atomic rearrangements at the crack tips to overcome the drastic oscillations of the potential energy surface; and (iii) using the high-precision CG optimization^[35] (with energy tolerance of 1 × 10^-25 eV) for eliminating the residual stress waves to ensure system at sub-angstrom scale displacement accuracy. Subsequently, the atoms were re-displaced and the cycle repeats 500 times with increasing the stress intensity factor from K_I = 0.1 to 0.6 MPa·m^1/2. The maximum atomic displacement was set as d_max = 0.05 Å to prevent system’s excessive relaxation. Such a three-step method can avoid the metastable states induced by traditional single minimization, and can precisely capture the critical state of dislocation emission at the crack tips by progressively tightening the convergence criteria^[37].

Characteristics of structural evolution during dislocation emission at the crack tips in FCC Al

Figure 2 shows the evolution of atomic structures perpendicular to [$$ \bar{1} $$10] direction at the cross-section of the crack tips in FCC Al with increasing stress intensity factor. The initial crack configuration with pre-loaded stress intensity factor of K_I = 0.1 MPa·m^1/2 is shown in Figure 2A, where the preset crack exhibits a regular wedge shape. This is attributed to that the magnitude of displacement δ for those non-boundary atoms is proportional to their radial distance r from the crack tips, as given in Equation (6). When the stress intensity factor increases to K_I = 0.281 MPa·m^1/2, a 1/6<112> partial dislocation appears along the [112] direction [Figure 2B], accompanied by a SF zone with width of d = 2.338 Å, i.e., the interplanar spacing of (111) plane in FCC Al. Meanwhile, a “surface step” forms on the plane where the dislocation is emitted from the crack tips, causing this plane to no longer be flat [Figure 3A]. With the stress intensity factor increasing to K_I = 0.433 MPa·m^1/2, the first partial dislocation slips continuously along the ($$ \bar{1} $$11) plane, resulting in the extension of SF zone [Figure 2C]. The angle between the dislocation emission direction and the crack plane is predicted as θ = 70°, which agrees well with 70.53° reported in previous work^[15,25].

Figure 2. Snapshots for evolution of atomic configurations along the direction perpendicular to [$$ \bar{1} $$10] of FCC Al with a marginal crack under the Mode I loading conditions. (A) The initial atomic configuration of the marginal crack; (B and C) The atomic configurations at stress intensity factor of K_I = 0.281 and 0.433 MPa·m^1/2, respectively, which correspond to the nucleation and emission of the first partial dislocation at the crack tips; (D and E) The atomic configurations at stress intensity factors of K_I = 0.434 and 0.482 MPa·m^1/2, respectively, which correspond to the second and third partial dislocation emission at the crack tips; (F) The atomic configuration at stress intensity factor of K_I = 0.545 MPa·m^1/2, which corresponds to the fourth partial dislocation emitted from the propagation plane at the front of crack tips. Note that the green line represents the 1/6<112> Shockley partial dislocation. The atomic configurations are denoted by the CNA, where the blue, red and white atoms represent the FCC, HCP and other structures, respectively. FCC: Faced-centered cubic; CNA: common neighbor analysis; HCP: hexagonal-close packed.

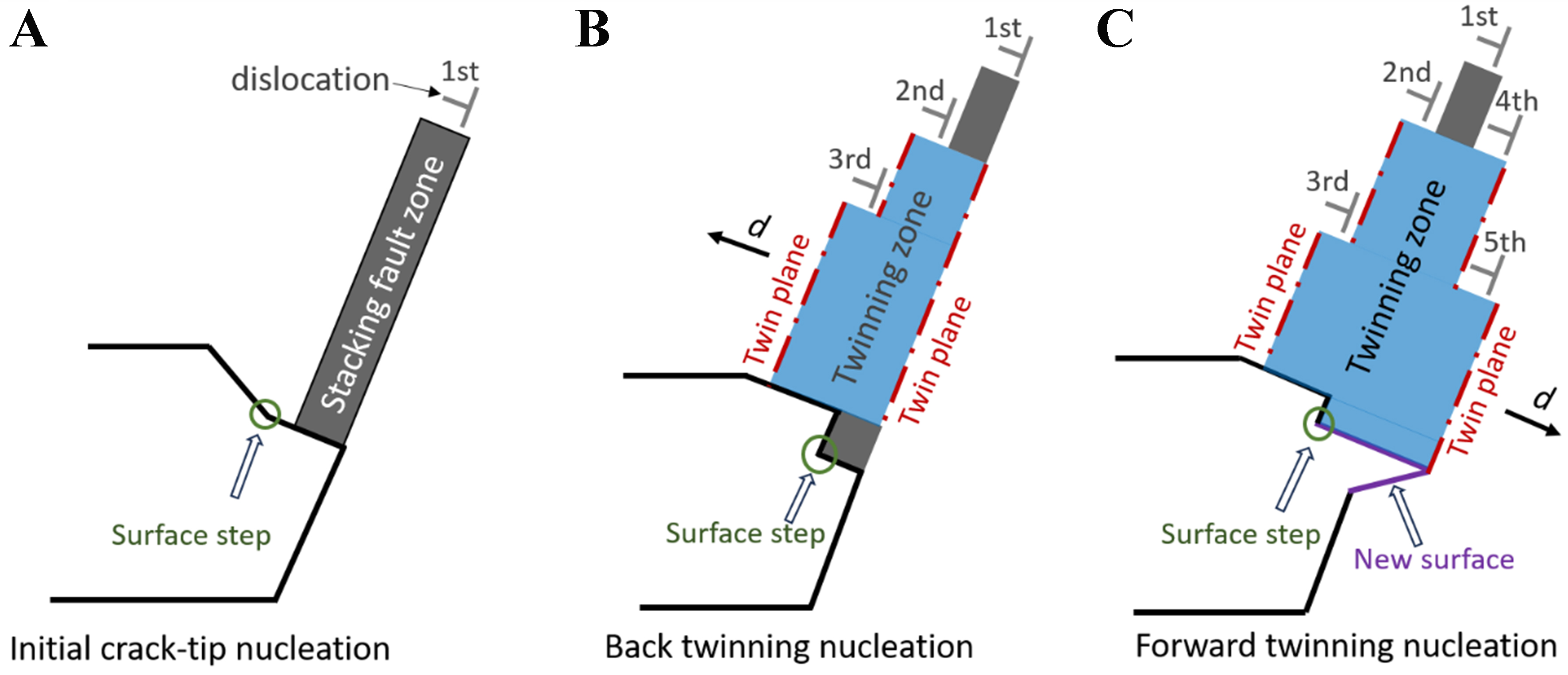
Figure 3. Schematic illustration for the formation and evolution of defects near the crack tips under different mechanisms of dislocation nucleation at the crack tips in FCC Al. (A) The initial dislocation nucleation at the crack tips accompanied by the formation of SF zone and a surface step on the dislocation propagation plane; (B) The back twinning dislocation nucleation at the crack tips, with the dislocation nucleation occurring on the slip plane adjacent to previous dislocation and the corresponding SF zone transforms into the twinning zone with stepwise shape due to the position distinctions in dislocation nucleation at the crack tips; (C) The forward twinning dislocation nucleation at the crack tips, with the dislocation nucleation occurring on the slip plane at the right of the first partial dislocation accompanied by instability of the crack tips and the corresponding twinning zone extended toward the crack tips. FCC: Faced-centered cubic; SF: stacking fault.

With the stress intensity factor increasing to K_I = 0.434 MPa·m^1/2, the second partial dislocation at the crack tips nucleates on the ($$ \bar{1} $$11) slip plane adjacent to the first partial dislocation [Figure 2D]. This broadens the plane region for dislocation emission at the crack tips, thus increasing curvature radius of the crack tips and promoting the crack blunting phenomenon. In principle, a SF zone composed of two ($$ \bar{1} $$11) atomic layers should be generated by the second partial dislocation emission. To prevent the overlap of the corresponding SF zones, a twinning zone with minimum thickness will be formed by reaction of SF zones corresponding to the above two partial dislocations. This signifies the beginning of the back twinning dislocation nucleation stage [Figure 3B], where the twinning boundaries correspond to the left boundary of the SF zone for the second partial dislocation and the right boundary of the SF zone for the first partial dislocation, the twinning zone thickness is 4.676 Å, i.e., two interplanar spacing of the ($$ \bar{1} $$11) plane for FCC Al.

With the stress intensity factor increasing to K_I = 0.482 MPa·m^1/2, the third partial dislocation appears at the crack tips [Figure 2E], where nucleation of this dislocation occurs on the adjacent slip plane of the second partial dislocation. The nucleation mechanism of this dislocation remains the same as the second partial dislocation, while the distinction lies in the nucleation position. Meanwhile, the SF zone related to the third partial dislocation forms an atomic step on the previous SF zone generated by the second partial dislocation. Besides, the twinning zone is extended via emerging the SF zones with the same width of the third partial dislocation and that of the first and second partial dislocations at the crack tips [Figure 3B]. Consequently, the twinning zone thickness along the crack ending direction increases to 7.014 Å, i.e., three times the interplanar spacing of the ($$ \bar{1} $$11) atomic layers. Compared with the second partial dislocation, the nucleation position of the third partial dislocation is closer to the crack plane. This signifies that the width w of the SF zone generated by the third partial dislocation is smaller, and a lower energy (i.e., E = γ_usf · S_SF, with S_SF being the area of the SF region) is required for this dislocation nucleation. Thus, nucleation of the third partial dislocation is easier than that of the second partial dislocation at the crack tips in FCC Al; see details in Section “Underlying mechanism of dislocation nucleation at the crack tips in FCC Al based on system energy evolution”. When the stress intensity factor increases to K_I = 0.545 MPa·m^1/2, the fourth partial dislocation appears at the crack tips [Figure 2F], where the atomic structures near the crack tips become no longer stable, and the crack tends to expand.

The nucleation of the fourth partial dislocation occurs on the right slip plane of the first partial dislocation, rather than on the left boundary of the twinning zone, while the newly formed SF zone merges with the SF zone related to the previous three partial dislocations to form a twinning zone with larger thickness. However, the twinning expansion direction is no longer toward the crack end, but along the crack expansion direction. This signifies that the mechanism transforms from the back twinning dislocation nucleation of the second and third partial dislocations to the forward twinning dislocation nucleation of the fourth partial dislocation [Figure 3C]. The predicted results have been confirmed by experimental characterization^[38] where certain crack propagation occurs through twinning nucleation ahead of the crack tips and the twinning serves as the nucleation sites for further cleavage.

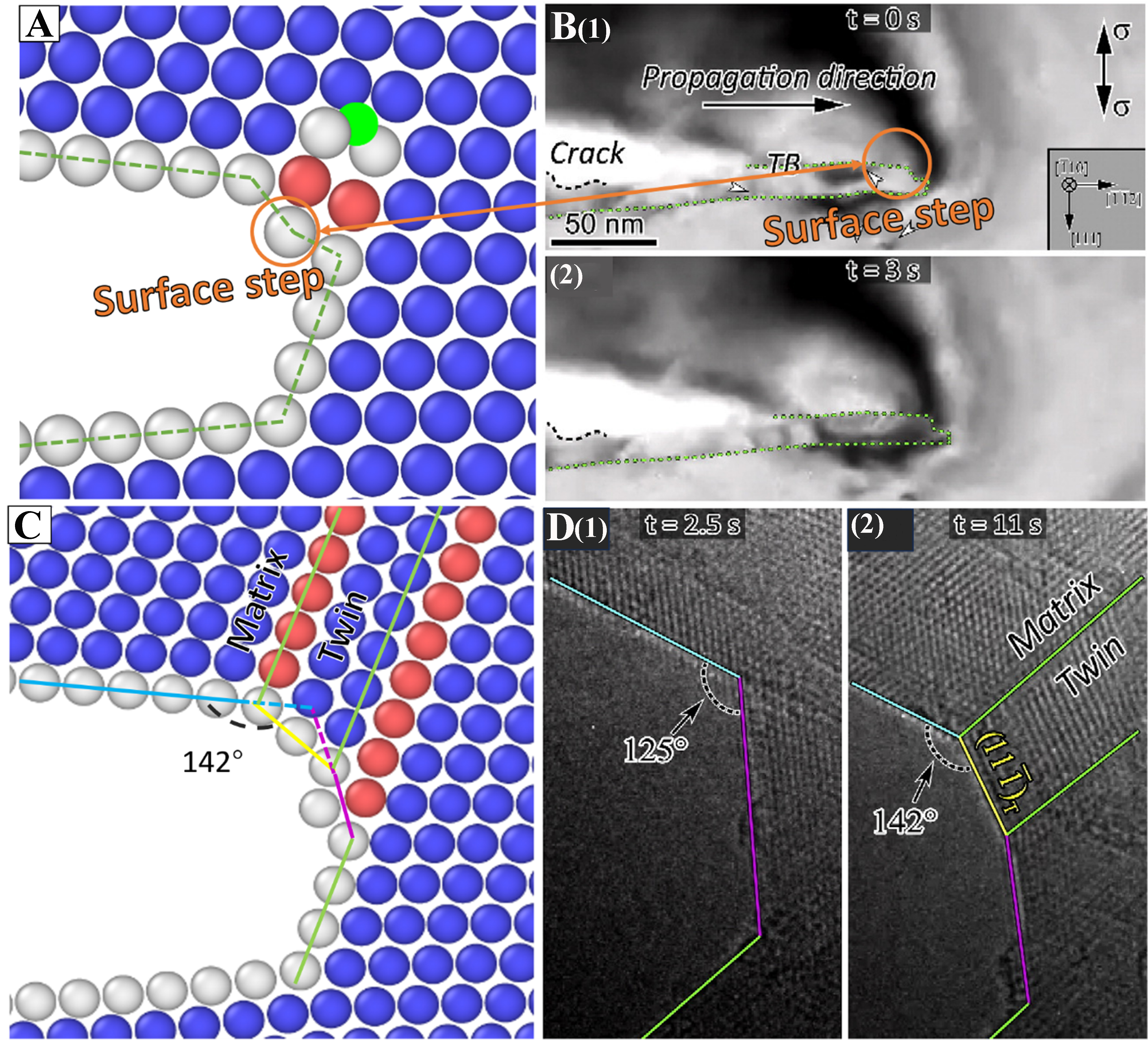
As shown in Figure 4, the predictions for emission behaviors and nucleation mechanisms of dislocations at the crack tips in FCC Al are in accordance with the experimental observations reported previously^[38]. For instance, the present MD simulations on the atomic behaviors of stress intensity factor of K_I = 0.281 MPa·m^1/2 [Figure 4A], agree well with the in-situ transmission electron microscopy (TEM) observations reported by Kou et al. that the first dislocation emission from the crack tips in FCC Al generates an atomic-scale surface step with a height equivalent to one {111} interplanar spacing [Figure 4B]^[38]. The twinning mechanism [Figure 4C] coincides with the TEM observations^[38] as well [Figure 4D]. Besides, these available experimental findings confirm the retraction behaviors along the crack edge during crack propagation in FCC Al, which agrees with the atomic-scale step formation during the initial dislocation emission at the crack tips captured in the present work. Meanwhile, subsequent dislocation emissions mainly initiated from the intersection of the crack tips and coherent twinning boundaries, which serve as favorable sites for dislocation nucleation due to the geometric constraints and stress concentration. Moreover, the in-situ TEM experiments^[38] confirmed that the twinning boundary migration is mediated by the glide of parallel Shockley partial dislocations on the {111} slip plane, which expands the twinning region progressively. This is consistent with the presently predicted back twinning mechanism of dislocation nucleation at the crack tips. As such, the present work demonstrates that the twinning formation and crack propagation are mediated by alternating slip of Shockley partial dislocations in FCC Al.

Figure 4. Comparisons between the present work and the TEM observations^[38] on the initial dislocation emission and back twinning dislocation emission at the crack tips in FCC Al. (A) MD simulation and (B) TEM characterization^[38] for surface step formation; (C) MD simulation and (D) TEM characterization^[38] for twinning dislocation formation. TEM: Transmission electron microscopy; FCC: faced-centered cubic; MD: molecular dynamics.

Thus, different combinations of various defects generated during dislocation emission reflect the different mechanisms of multiple dislocation nucleation at the crack tips in FCC Al. Specifically, the emission of the first partial dislocation is dominated by the crack-tip nucleation accompanied by the formation of surface steps. The emission of the second and third partial dislocations is dominated by the back twinning dislocation nucleation accompanied by the formation of twinning zones with stepwise shape. The emission of the fourth partial dislocation is dominated by the forward twinning nucleation and manifests as the crack propagation and thickening of the twinning zone along crack tip direction. The abovementioned defects originate from variations in displacement of atoms near the crack tips in FCC Al, because the atomic displacement exerts direct influences on the magnitude of local strain. Once the atomic displacement reaches the critical condition, various defects will form to maintain the system stability. Therefore, it is necessary to understand the structural characteristics of the crack tips and their evolution rule based on the atomic displacement.

Atomic displacement criteria for dislocation emission at the crack tips in FCC Al

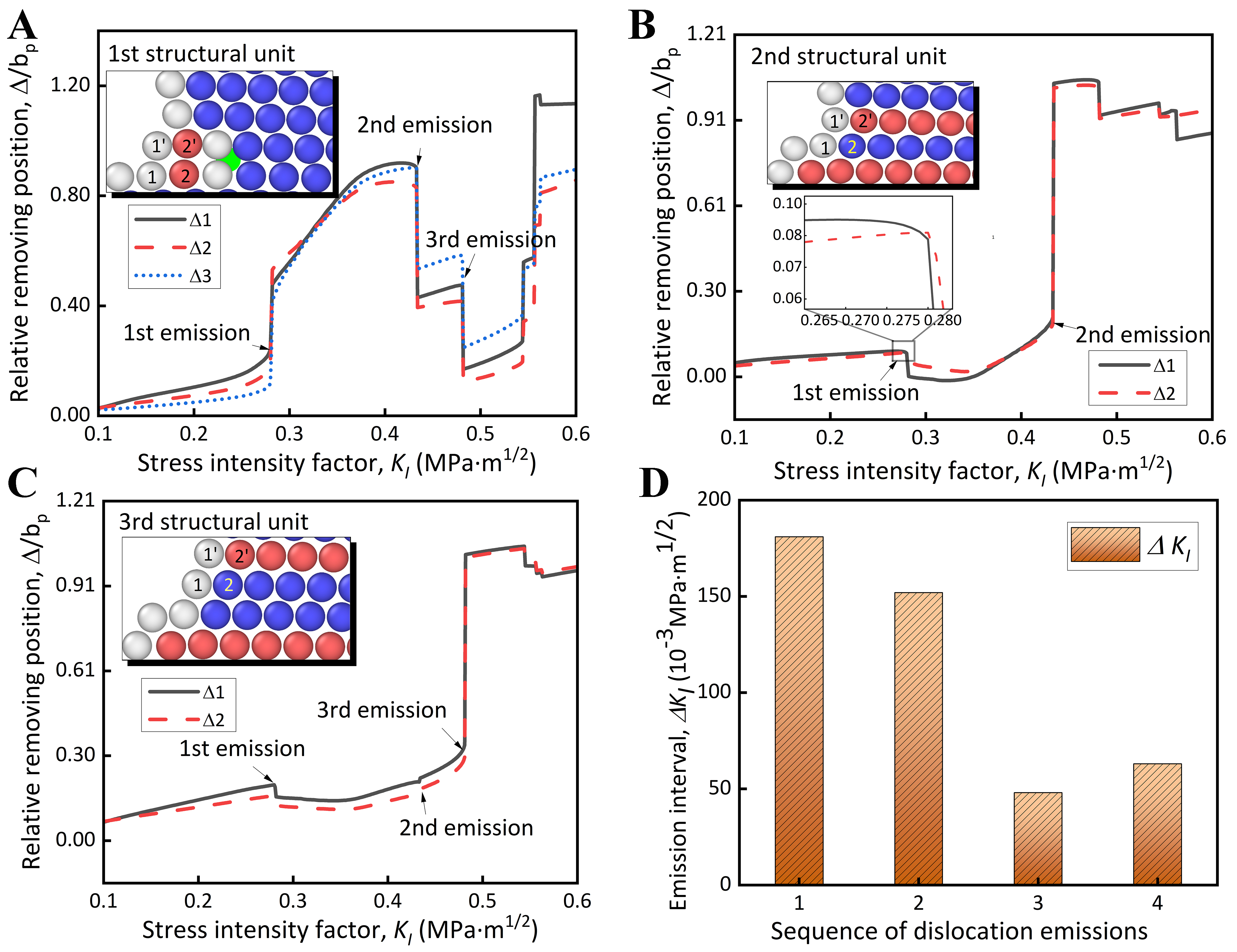
The critical conditions for dislocation emission can be determined from the displacement variations of atoms near the crack tips in FCC Al. In general, dislocation emission originates from the relative displacement of atomic pairs in the structural units at the crack tips. Specifically, the structural unit for dislocation emission at the crack tips in FCC Al under the Mode I loading conditions is defined as follows: (i) The two atoms overlapped between the SF zone formed by the first partial dislocation emission at the crack tips and the dislocation emission plane are denoted as the atomic pair 1 and 1’, and the corresponding displacement difference between these two atoms is denoted as Δ1; (ii) The two atoms adjacent to the atomic pair 1 and 1’ along the [112] direction are denoted as the atomic pair 2 and 2’, with the corresponding displacement difference as Δ2. When the first partial dislocation is emitted at the crack tips, the critical value of Δ1 (Δ1_c = 0.35 b_p) is smaller than that of Δ2 (Δ2_c = 0.36 b_p) [Figure 5A], which disagrees with Curtin’s theory^[15]. To this end, the displacement difference Δ3 between the atomic pair 3 and 3’ is obtained. The ratio of the critical displacement differences is Δ1_c/Δ3_c= 0.64, which is close to that from the statistical result^[15]. Figure 5B shows that when the second partial dislocation is emitted from the crack tips in FCC Al, the critical value for the displacement difference of the second structural unit, i.e., ΔI_c = 0.21 b_p, is smaller than that of the first structural unit, i.e., Δ1_c = 0.35 b_p. This indicates that the nucleation rate of the second partial dislocation is faster than that of the first partial dislocation. When the third partial dislocation is emitted at the crack tips in FCC Al [Figure 5C], the increment of displacement difference in the third structural unit approaches 0.68 b_p, which is smaller than that in the second structural unit (i.e., 0.83 b_p). This indicates that the energy required to dissipate for emission of the third partial dislocation is lower than that of the second partial dislocation.

Figure 5. The displacement curves of atomic pairs in different structural units near the crack tips in FCC Al with respect to the stress intensity factor, along with the interval variations in stress intensity factor for each dislocation emission at the crack tips. The differences in displacement of atomic pairs 1 and 1’, 2 and 2’, and 3 and 3’ as a function of stress intensity factor during dislocation emission of (A) the first structural unit, (B) the second structural unit, and (C) the third structural unit; (D) Incremental changes in stress intensity factor among emission of four partial dislocations at the crack tips. FCC: Faced-centered cubic.

The atomic displacement at the crack tips reflects the distribution and dissipation of energy within the crack tip stress field. Analysis of the first three dislocation emission events reveals that with rising distance between the structural units emitting dislocations and the crack tips, the critical displacement for dislocation emission increases progressively. This confirms that the crack tips have the highest energy, and the dislocation emission occurring far from the crack tips has to overcome a larger energy barrier. The atomic displacement associated with the three dislocation emissions reaches the maximum during the second dislocation emission, indicating that the SF zone formed by the second dislocation emission has the largest width and consumes the most energy. This suggests a potential transformation for the type of defects formed during dislocation emission at the crack tips compared to previous emissions. The emission of arbitrary partial dislocations at the crack tips in FCC Al can delay the emission of subsequent partial dislocations [Figure 5A-C]. Detailed analysis is provided in the Supplementary Materials.

The increment of stress intensity factor for each dislocation emission can be used to estimate the ease or difficulty of dislocation nucleation at the crack tips. Figure 5D shows that when the stress intensity factor increases to K_I = 0.282 MPa·m^1/2, the first partial dislocation emits at the crack tips in FCC Al. The interval of dislocation emission at the crack tips expands gradually as the applied load increases. The interval between the stress intensity factor for emission of the first and second partial dislocations is ΔK_I = 0.152 MPa·m^1/2, while that for emission of the second and third partial dislocations is only ΔK_I = 0.048 MPa·m^1/2. However, the interval between the stress intensity factor for emission of the third partial dislocation and the fourth partial dislocation increases to 0.064 MPa·m^1/2, which is attributed to the mechanism transition for dislocation nucleation at the crack tips. Thus, the ease or difficulty for dislocation emission at the crack tips in FCC Al is dominated by the synergistic effects of the applied stress intensity factor and the dislocation nucleation mechanism. Based on Equation (2), the system energy is a function of atomic displacement at the crack tips, and the critical conditions for dislocation emission can be captured from the abrupt changing points on the system energy evolution curve. Thus, the system energy dissipation can also serve as an indicator of dislocation emission at the crack tips. Moreover, the magnitude of energy dissipation can be used to estimate the ease or difficulty for defect formation, which corresponds to different dislocation nucleation mechanisms. As such, the mechanisms of dislocation nucleation at the crack tips can be understood from system energy dissipation, as analyzed in the following section.

Underlying mechanism of dislocation nucleation at the crack tips in FCC Al based on system energy evolution

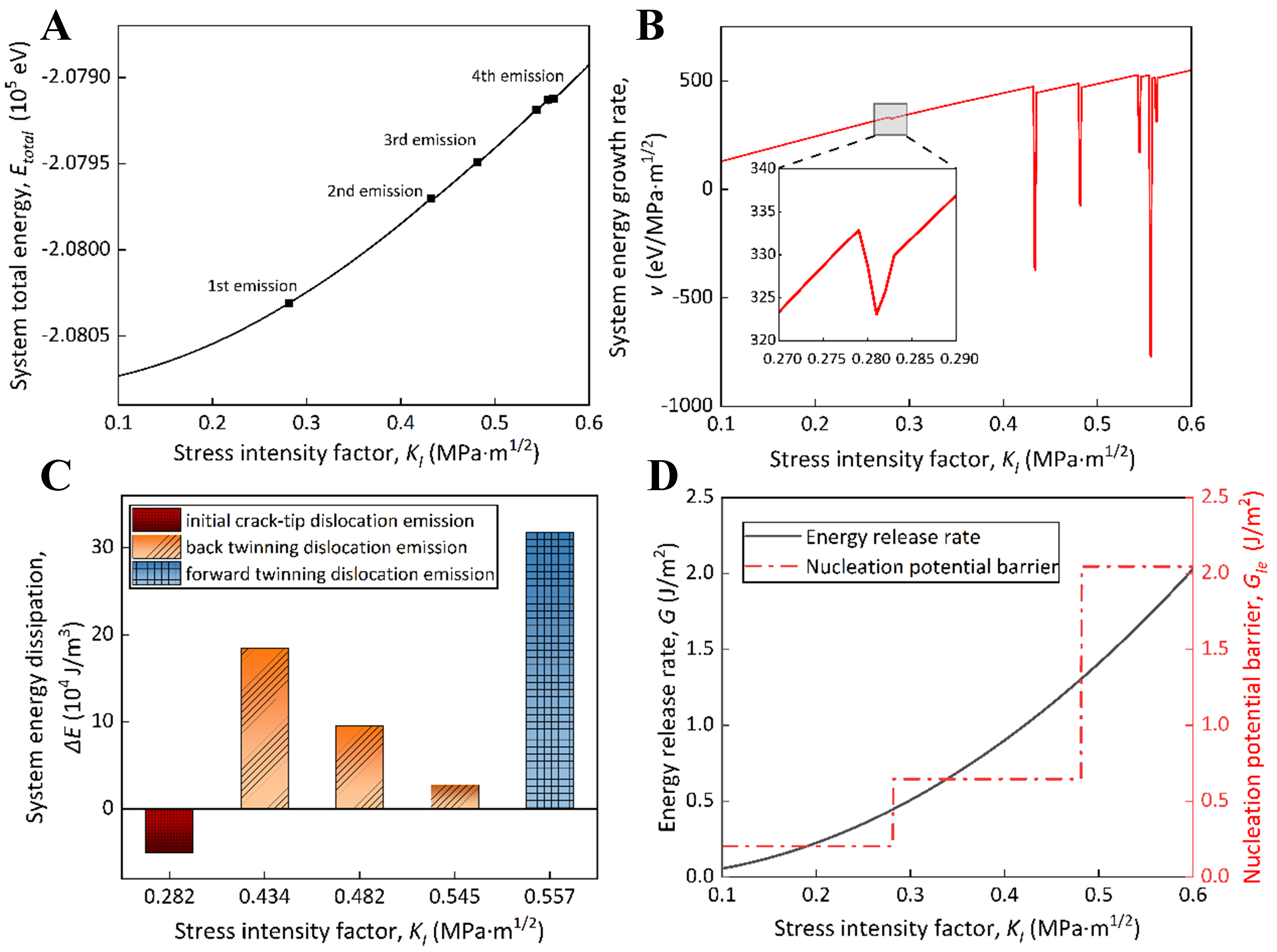
Figure 6 shows the system energy evolution curve of FCC Al with a marginal crack under the Mode I loading condition. The energy evolution curve presents an overall concave downward [Figure 6A], where the system energy increases from E_total = -2.081 × 10⁵ to -2.079 × 10⁵ eV with the stress intensity factor increasing from K_I = 0.1 to 0.6 MPa·m^1/2. By taking the derivative of the system energy with respect to the stress intensity factor, the energy evolution rate is denoted as: v = dE/dK_I. The results are shown in Figure 6B, where the system energy growth rate curve exhibits an overall linear upward trend. However, each dislocation emission gives rise to a decrease in the system energy growth rate and then an increase. When the first partial dislocation is emitted at the crack tips in FCC Al, the energy evolution rate decreases from v = 328 to 323 eV/MPa·m^1/2. When the second partial dislocation is emitted, the energy evolution rate suddenly drops from v = 474 to -358 eV/MPa·m^1/2. Such a decrease in system energy evolution rate is attributed to the high energy consumed by the twinning formation during the back twinning dislocation nucleation. When the third dislocation is emitted at the crack tips, the descender for system energy evolution rate slows down gradually. The SF zone width after dislocation emission decreases as dislocations continue to emit at the crack tips during the back twinning dislocation nucleation, and the released energy decreases due to the twinning boundary with respect to the twinning zone formation by merging SF zones. The fourth partial dislocation nucleation position is close to the crack tips, resulting in a smaller energy release compared to emission of the third one. Meanwhile, the crack surface is expanded due to instability of the crack tips, which consumes extra energy, and thus the descender for system energy evolution rate is smaller. When the fourth partial dislocation is emitted, the system energy evolution rate drops (with the largest descender) from v = 527 to -770 eV/MPa·m^1/2, but no new dislocations appear in the atomic configuration. Such variation in system energy evolution rate can be regarded as a continuation of the fourth partial dislocation emission, given that the mechanism of forward twinning dislocation nucleation at the crack tips can be divided into two stages: (i) In the 1st stage, the crack tip expands forward and dislocations are emitted from the crack tip plane accompanied by twinning formation; (ii) In the 2nd stage, the system is in a higher energy state due to formation of an uneven crack surface. To maintain stability, rearrangement of those atoms at the crack tips is triggered and the uneven crack surfaces merge, which reduces the surface energy and releases a large amount of system energy.

Figure 6. The system energy evolution of FCC Al with a marginal crack under Mode I loading conditions. (A) The system energy evolution; (B) Variations in growth rate of the system energy; (C) Variations in system energy dissipation during emission of different dislocations at the crack tips; and (D) Variations of system energy releasing rate and potential barrier of dislocation nucleation at the crack tips with respect to stress intensity factor. FCC: Faced-centered cubic.

The amount of system released energy during dislocation emission depends on the formation energy of defects at the crack tips. To further understand the dislocation emission behaviors at the crack tips, the energy evolution rule behind key segments for dislocation emission is analyzed, along with the characteristics of variations in potential energy distribution of atoms near the crack tip before and after dislocation emission [Figure 7]. By defining the second derivative of system energy E_total with respect to the stress intensity factor K_I, i.e., α = d²E_total/dK_I², as the acceleration of system energy evolution, it is found that when K_I = 0.281 MPa·m^1/2 (corresponding to the first partial dislocation emission), α < 0, indicating the system energy increasing rate slowing down [Figure 7A]. Actually, the rise in system energy is induced by the elevation of potential energy for those atoms near the crack tips. The slowdown for system energy increasing rate signifies that lattice distortion near the crack tips can be released by the SF zone formation, which can restrict the system energy increase further. For dislocation emission dominated by the back twinning dislocation nucleation mechanism [Figure 7B and C], before the second and third partial dislocation emissions at the crack tips, those high-energy atoms can aggregate at the SF zone generated by the first partial dislocation. After the twinning dislocation nucleation, the stratification phenomenon appears for the energy distribution of those atoms near the crack tips. Those atoms within the twinning zone maintain their original high-energy state; however, the energy of those atoms at the twinning boundary becomes lower in comparison to their counterparts within the twinning zone. Thus, the system energy released at the back twinning dislocation nucleation stage originates from the twinning boundary formation. Compared with the second partial dislocation, the third partial dislocation emission is accompanied by a smaller area of twinning boundary, and thus results in less energy release. This is consistent with the analysis in Sections “Characteristics of structural evolution during dislocation emission at the crack tips in FCC Al” and “Atomic displacement criteria for dislocation emission at the crack tips in FCC Al”. For the fourth partial dislocation emission, at the crack tip instability stage, the energy released due to twinning formation is similar to that at the back twinning dislocation nucleation stage [Figure 7D]. Meanwhile, the free surface formation increases the number of high-energy atoms near the crack tips, which slows down the system energy dissipation. When the forward twinning dislocation nucleation enters into the atomic rearrangement stage at the crack tips, the twinning zone expands slightly compared to the crack instability stage. However, the energy dissipates significantly due to the reduced energy of newly added atoms near the crack surface, resulting in an apparent energy decrease compared to previous dislocation emission at the crack tips.

Figure 7. The energy distribution of atoms near the crack tips, as denoted by system energy evolution curve during emission of different dislocations at the crack tips in FCC Al. (A) Emission of the first partial dislocation dominated by the crack-tip nucleation mechanism; (B and C) Emission of the second and third partial dislocations dominated by the back twinning nucleation mechanism; (D) Emission of the fourth partial dislocation dominated by the forward twinning nucleation mechanism. FCC: Faced-centered cubic.

Accordingly, the decrease in system energy evolution rate can serve as a criterion for dislocation emission at the crack tips, while the different mechanisms of dislocation nucleation are determined by the amount of system energy dissipation. For the first partial dislocation nucleation, the system energy remains almost unchanged because there is no rearrangement of atoms near the crack tips. During subsequent back twinning dislocation nucleation at the crack tips, which corresponds to nucleation of the second and third partial dislocations, the SF zone transforms into a twinning zone due to atomic rearrangement, resulting in considerable system energy dissipation. During the forward twinning dislocation nucleation at the crack tips, which corresponds to the fourth partial dislocation nucleation, the system energy dissipates due to the twinning formation and the reduced crack surface derived from atomic rearrangement. This results in multiple peak points in system energy evolution curve, among which the energy decreasing amplitude caused by the surface energy reduction is the largest.

Thermo-kinetic criterion for mechanism transition of dislocation nucleation at the crack tips in FCC metals

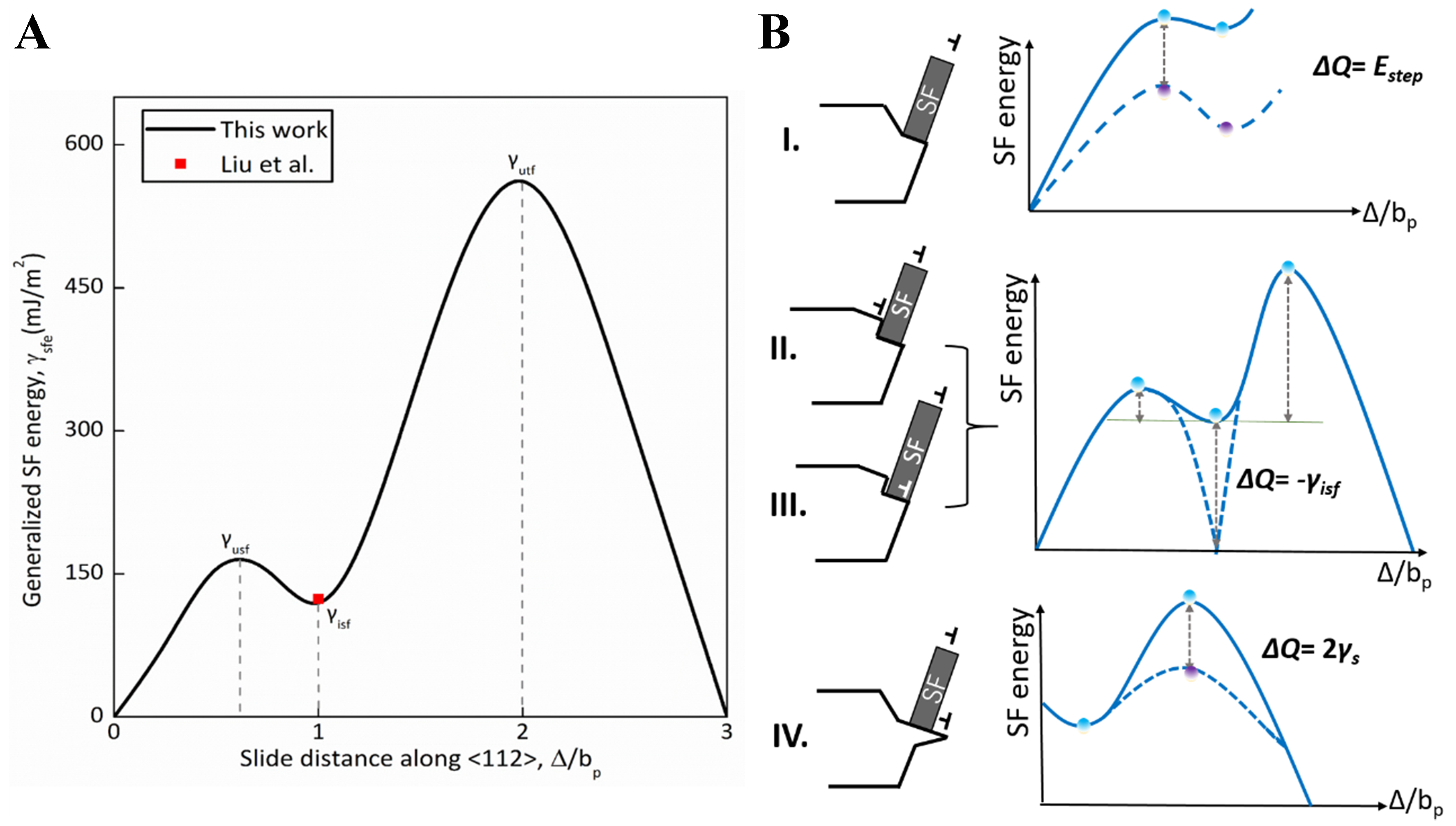
Following the results of Section “Underlying mechanism of dislocation nucleation at the crack tips in FCC Al based on system energy evolution”, the dislocation emission behaviors and the dislocation nucleation mechanism depend on system energy evolution, as dominated by the thermo-kinetic synergy. Specifically, the thermodynamic driving force is provided by the elastic strain energy accumulated at the crack tips, which is proportional to the energy release rate G at the crack tips. In contrast, the thermodynamic resistance is the dislocation nucleation energy Q, which depends on the potential barrier for dislocation nucleation G_Ie and the distance of dislocation emission (i.e., the SF zone width w). The kinetic energy barrier is determined by the thermodynamic driving force and resistance. The variations in energy release rate G and the potential barrier G_Ie for dislocation nucleation at the crack tips in FCC Al under the Mode I loading conditions is shown in Figure 6D, where G is obtained from K_I based on the Irwin relation^[39] (i.e., G = Y·K_I², where Y is the Young’s modulus), while G_Ie is calculated from the continuum mechanics model^[15,27]. As the applied load under the Mode I loading conditions rises, the energy release rate G of dislocation emission grows in a parabolic manner, while the potential barrier for dislocation nucleation G_Ie increases in a stepwise manner. Notably, G_Ie can be expressed as a linear combination of the SF energy and surface energy γ_s:

where γ_usf, γ_isf and γ_utf correspond to the extreme points of the generalized SF energy curve [Figure 8A]. The stages I, II, and III represent the initial crack-tip dislocation nucleation, the back twinning dislocation nucleation, and the forward twin dislocation nucleation, respectively. Under different dislocation nucleation mechanisms [Figure 8B], the dislocation nucleation position and the accompanying defects exert a direct effect on G_Ie. The potential barrier for dislocation nucleation at different stages can be obtained as: G_Ie = 0.2038, 0.6458, and 2.046 J/m² for the initial dislocation nucleation stage, the back twinning dislocation nucleation stage, and the forward twinning dislocation nucleation stage, respectively. Details on calculating potential barrier for dislocation nucleation at the crack tips are provided in the Supplementary Materials.

Figure 8. Schematic illustration for correlations between the SF energy γ and the potential barrier G_Ie of dislocation nucleation at the crack tips in FCC Al. (A) Generalized SF energy curve for FCC Al along the <112> direction on {111} slip plane, where the first peak point, the saddle point, and the second peak point represent the unstable SF energy γ_usf, intrinsic SF energy γ_isf, and unstable twinning fault energy γ_utf, respectively. Note that the values of SF energy calculated in this work are denoted by black solid line, while the red point represents the value reported by Liu et al.^[50]; (B) Correlation between dislocation nucleation barrier and position of dislocation nucleation at the crack tips, including (I) dislocation nucleates at the crack tips, where the nucleation barrier G_Ie increases due to the formation of surface steps, (II and III) dislocation nucleated at the SF region and/or the boundary of the SF region, where the nucleation barrier G_Ie decreases by γ_isf, and (IV) dislocation nucleated on a new surface generated after crack instability, where the nucleation barrier G_Ie increases by 2γ_s. SF: Stacking fault; FCC: faced-centered cubic.

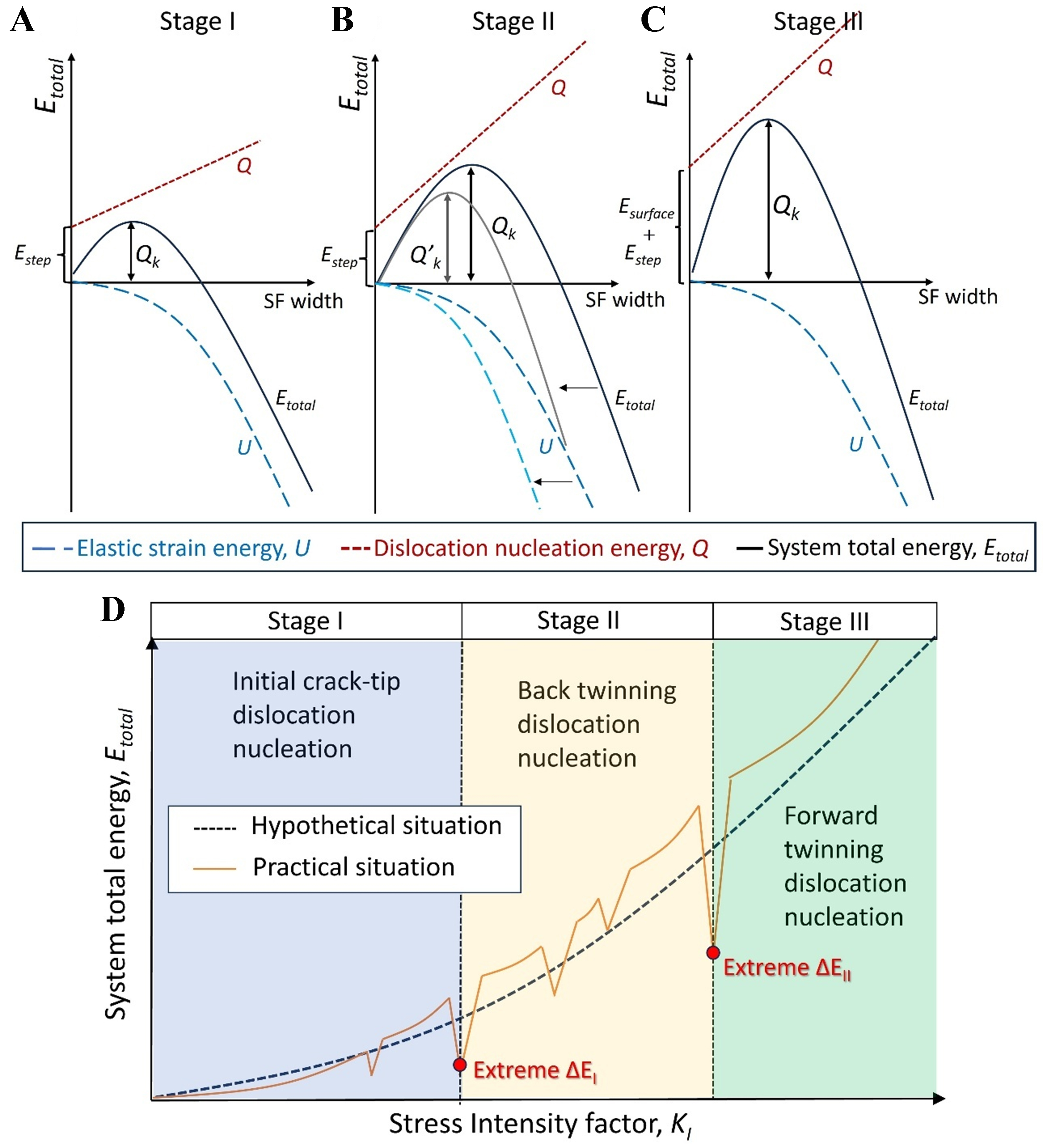
According to the variations in energy release rate G and potential barrier G_Ie, the system energy evolution of dislocation emission at the crack tips in FCC metals is schematically illustrated in Figure 9, where the elastic strain energy U accumulated at the crack tips (the blue dashed line) decreases as the SF zone width w increases, while the dislocation nucleation energy Q (the red dashed line) grows linearly with increasing SF region. The synergy of the elastic strain energy U and the dislocation nucleation energy Q determines the system total energy E_total (the black solid line) to increase firstly and then decrease. When the first derivative of the system total energy E_total with respect to the SF width w becomes zero, i.e., dE_total/dw = 0, the system energy evolution reaches a peak point, and the according energy is regarded as the activation energy for dislocation at the crack tips, i.e., the energy barrier Q_k of dislocation emission, with its physical meaning analogous to the critical nucleation energy for a new phase during phase transition. When the elastic strain energy U accumulated at the crack tips (i.e., the driving force) equals the energy barrier Q_k for dislocation emission, the system has to dissipate energy to reach a stable state, where the amount of released energy ΔE is proportional to dislocation activation energy Q_k.

Figure 9. System energy evolution with respect to the stress intensity factor, reflecting the different mechanisms of dislocation nucleation at the crack tips in FCC metals, along with the thermo-kinetic variations during dislocation emission. (A) Nucleation mechanism of the crack-tip dislocation, where the nucleation energy is required to overcome the step formation energy E_step, and subsequently the energy dissipated by the formation of SF zone increases with increasing the width w of SF zone; (B) Nucleation mechanism of the back twinning dislocation, where there is no new surface formation and the intercept of energy axis remains unchanged, although the slope of nucleation energy curve increases with the potential barrier for dislocation nucleation; (C) Nucleation mechanism of the forward twinning dislocation, where there is a new crack surface formation; thus, the nucleation potential barrier requires a surface energy contribution, while the growth rate for dislocation nucleation energy remains the same as that for the back twinning dislocation. Note that the red and blue dashed lines represent the contribution of the nucleation potential barrier as resistance to system total energy, and the contribution of the energy release rate as driving force to system total energy, respectively; (D) System energy evolution with respect to stress intensity factor under Mode I loading conditions, where the dashed line represents the hypothetical situation by assuming the crack tips without dislocation emission and propagation, and the solid line represents the practical situation scenario that there are dislocation emission and propagation at the crack tips. Two peaks appear in the amount of system energy dissipation curve, which corresponds to mechanism transition of dislocation nucleation at the crack tips. Appearance of the first peak indicates the dislocation emission at the crack tips transforming from the first stage (i.e., the initial dislocation nucleation mechanism) to the second stage (i.e., the back twinning dislocation nucleation mechanism), while that of the second peak indicates that dislocation emission steps into the third stage (i.e., the forward twinning dislocation nucleation mechanism). FCC: Faced-centered cubic; SF: stacking fault.

Different dislocation nucleation mechanisms correspond to varying driving forces and energy barriers for dislocation emission, which in turn affect the system energy evolution. For the dislocation crack-tip nucleation mechanism [Figure 9A], the initial value of the dislocation nucleation energy Q originates from the step formation energy E_step. When the nucleation mechanism is dominated by the back twinning dislocation, the rise in potential barrier for dislocation nucleation G_Ie can cause the curve slope to increase [Figure 9B]. When the mechanism transforms from the back twinning nucleation to the forward twinning nucleation, the contribution associated with the SF zone to the G_Ie remains unchanged, but the surface energy γ_s should be overcome, which is reflected as the unchanged slope of the line for Q but an increased intercept along the energy axis [Figure 9C]. It is worthwhile to mention that the energy barrier for dislocation nucleation is associated with the geometric shape of the crack tips and the loading conditions. For instance, the sharp crack tips exhibit a higher nucleation barrier for initial dislocation emission than the blunted crack tips due to the larger difficulty in surface step formation. Besides, the temperature increase can reduce the activation energy for dislocation motion, thus decreasing the dislocation nucleation barrier. Notably, while these factors can influence the critical stress intensity factor for different dislocation nucleation at the crack tips, the fundamental energy evolution rules governing the mechanism transition of dislocation nucleation at the crack tips in FCC Al are not affected.

When the dislocation nucleation mechanism undergoes transition, the elastic strain energy U curve remains unchanged. However, the dislocation nucleation energy suddenly rises with respect to the mechanism transition as follows: (i) the enhanced contribution from SF energy for potential barrier G_Ie induces a steeper slope of the Q line; (ii) the elevated contribution from surface energy for potential barrier G_Ie leads to the increase in intercept of the Q line along the energy axis. Accordingly, the energy barrier Q_k for dislocation emission escalates in a stepwise manner with respect to the dislocation nucleation mechanism transition, leading to a sudden amplification in energy dissipation ΔE. Figure 6C shows the system energy dissipation during dislocation emission at the crack tips in FCC Al. The amount of system energy dissipation rises from ΔE = -0.5 × 10⁵ to 1.85 × 10⁵ J/m³ when the initial dislocation nucleation stage transforms into the back twinning dislocation nucleation stage. Whereas from the back twinning dislocation nucleation stage to the forward twinning dislocation nucleation stage, ΔE grows from 0.28 × 10⁵ to 3.18 × 10⁵ J/m³. It is noteworthy that the fourth partial dislocation emission at the crack tips in FCC Al belongs to the back twinning dislocation nucleation stage, given that this dislocation emission occurs before atomic rearrangement, while the corresponding defect formation and system energy change characteristics remain similar to those of the back twinning dislocation nucleation, with distinctions in their nucleation location.

When the dislocation emission is dominated by the back twinning nucleation mechanism, there are multiple dislocations successively emitted from the crack tips, while the potential barrier G_Ie for dislocation nucleation remains unchanged during each dislocation emission [Figure 9B], resulting in a constant dislocation nucleation energy Q. However, the system energy release rate G increases continuously during dislocation emission at the crack tips. According to the expression for system energy release rate^[40], i.e., G = -dU/dA, where A represents the area of crack surface, the slope of elastic strain energy curve also rises, with accelerated curve descent rate. This results in the continuous decrease of energy barrier Q_k, along with the decrease in width w of SF zone generated by dislocation nucleation at the crack tips. The decrease in Q_k corresponds to the gradual decrease in the amount of system energy dissipation ΔE [Figure 6D], where the energy release rate G associated with the driving force for dislocation emission increases from U = 0.44 to 1.30 J/m² during emission of the second, third, and fourth partial dislocations (all dominated by the back twinning dislocation nucleation) at the crack tips in FCC Al, while the ΔE associated with Q_k for dislocation emission decreases from 1.85 × 10⁵ to 0.28 × 10⁵ J/m³. Hence, the increase in driving force U for dislocation emission at the crack tips in FCC Al is accompanied by the decrease in energy barrier Q_k, thus promoting dislocation emission, which is manifested as the reduced interval for dislocation emission at the crack tips. These analyses are in accordance with the results of Section “Atomic displacement criteria for dislocation emission at the crack tips in FCC Al” regarding the increment of applied load required for different dislocation emission [Figure 5D].

Following the above analysis, the correlation between different dislocation nucleation mechanisms and the system energy evolution during dislocation emission at the crack tips in FCC metals is schematically illustrated in Figure 9D. Under the Mode I loading conditions, the system energy evolution curve exhibits an overall parabolic upward trend, but there are several abrupt points (where the system energy firstly drops and then rises), which corresponds to the dislocation emission. As such, the dislocation nucleation mechanism transition can be examined in combination with the amount of system energy dissipation at the dislocation emission points. As shown in Figure 6C and 9D, when the dislocation nucleation mechanism transforms from the initial crack-tip nucleation (Stage I) to the subsequent back twinning nucleation (Stage II) and the forward twinning nucleation (Stage III), the amount of system energy dissipation increases progressively. Meanwhile, the sequential emission of multiple dislocations appears in the back twinning dislocation nucleation stage, where each dislocation emission is accompanied by gradual decrease in the amount of system energy dissipation. The system energy dissipation associated with dislocation emission at the crack tips can be treated as a discrete function of the stress intensity factor. Considering that there are three dislocations sequentially emitted at the crack tips with the corresponding stress intensity factor as K_n-1, K_n and K_n+1, when the system energy dissipation E(K) associated with these emission events satisfies: E(K_n) > E(K_n+1) and E(K_n) > E(K_n-1), and then K_n marks the critical stress intensity factor for the mechanism transition of dislocation nucleation at the crack tips in FCC metals [Figure 9D].

Before crack-tip instability, the number of dislocations emitted at the crack tips is restricted. As such, the fracture toughness can be adjusted by regulating the difficulty or ease of dislocation emission at the crack tips. In combination with system energy evolution, the process of dislocation emission can be slowed down by reducing the driving force (elastic strain energy U) and/or increasing the energy barrier Q_k for dislocation emission, and thus the dislocation emission interval decreases. This is favorable for delaying fracture so as to enhance the fracture toughness. For example, the intrinsic SF energy γ_isf of Al alloys can be decreased by adding alloying elements^[41] such as Cu, Mg, and Si, which can enhance the energy difference between the peak and saddle points on the generalized SF energy curve, corresponding to an increase in the potential barrier G_Ie for dislocation nucleation at the crack tips. Thus, the energy barrier Q_k for dislocation emission can be enhanced, which makes the dislocation emission slower and more sustainable, thus delaying the crack propagation.

It is noteworthy that the present thermo-kinetic criterion for dislocation emission behaviors and dislocation nucleation mechanisms of FCC Al can be extended to other FCC metals. The distinctions lie in the magnitude of driving force and energy barrier for dislocation emission at the crack tips of different FCC metals, which is attributed to the differences in their characteristics of SF energy and surface energy^[42]. Furthermore, it is certain that other defects can affect the dislocation emission behaviors at the crack tips of FCC metals. For instance, the solute atoms exert influences by changing the SF energy with respect to potential barrier of dislocation nucleation at the crack tips^[43]. The existence of grain boundary can serve as a pathway for crack propagation, and thus affect the deformation mechanisms at the crack tips^[44]. The precipitates that existed along the dislocation emission direction can introduce additional energy barriers for dislocation motion^[45]. Accordingly, the design for high-toughness FCC metallic alloys can be achieved by adjusting composition/processing dependent thermo-kinetic synergy during dislocation emission at the crack tips in FCC metals^[46-49]. Our continuous investigations along these directions are still in progress to acquire the general rule for dislocation nucleation with respect to the critical conditions for dislocation emission at the crack tips in FCC metallic alloys, and the results will be reported in further work.