A phase search-enhanced Bi-RRT path planning algorithm for mobile robots

3.1. Fundamentals

The basic principle of the Bi-RRT algorithm is to construct a randomized tree in space with the target point and the initial point as the root node simultaneously, respectively, and generate connected paths by expanding the two randomized trees alternately in relative directions to save path search time. The pseudo-code of Bi-RRT algorithm is shown in Algorithm 1 as follows.

The basic steps of the algorithm are as follows:

(1) In the known state space $$ M $$, initialize the random tree $$ T_1, T_2 $$, and set the start point and target point as $$ x_{start} $$ and $$ x_{goal} $$, respectively. Set the root nodes of the random trees $$ T_1 $$ and $$ T_2 $$ to $$ x_{start} $$ and $$ x_{goal} $$, respectively. Define and assign the relevant parameters, such as the number of iterations i, the step size is $$ StepSize $$, and so on;

(2) Use the random function to generate a random point in global space $$ x_{rand} $$, then denote the point on the random tree $$ T_1 $$ with the smallest distance from $$ x_{rand} $$ as $$ x_{near1} $$, then start from $$ x_{near1} $$ and extend a point along the direction pointing to $$ x_{rand} $$ in steps of $$ StepSize $$, denoted as $$ x_{new1} $$, and indicate the path connecting $$ x_{near1} $$ and $$ x_{new1} $$ as $$ E_1 $$;

(3) Detect whether there is an obstacle between $$ x_{near1} $$ and $$ x_{new1} $$ through the collision detection function $$ CollisionFree() $$, if it passes the detection, add $$ x_{new1} $$ to the set of nodes of the random tree $$ T_1 $$, and add $$ E_1 $$ to the set of edges of the tree $$ T_1 $$;

(4) Similar to the above process, generate $$ x_{new2} $$ and $$ E_2 $$ and add them to the node set and edge set of $$ T_2 $$;

(5) When the spacing between two nodes on the random tree $$ T_1 $$, $$ T_2 $$ is less than the set value and passes the collision detection, it indicates that the path search is successful and the expansion of the random tree will be stopped;

(6) Perform path backtracking to find and connect its parent node forward from the goal point, repeat this process until it connects to the start point, and generate a feasible path connecting the goal and start points.

3.2. Balancing exploration strategies with three stage search strategies

Aiming at the problem that the Bi-RRT algorithm has a long sampling time and produces too many redundant nodes, this paper introduces a balanced exploration strategy that effectively improves the efficiency of path search by generating the search tree from two directions simultaneously.

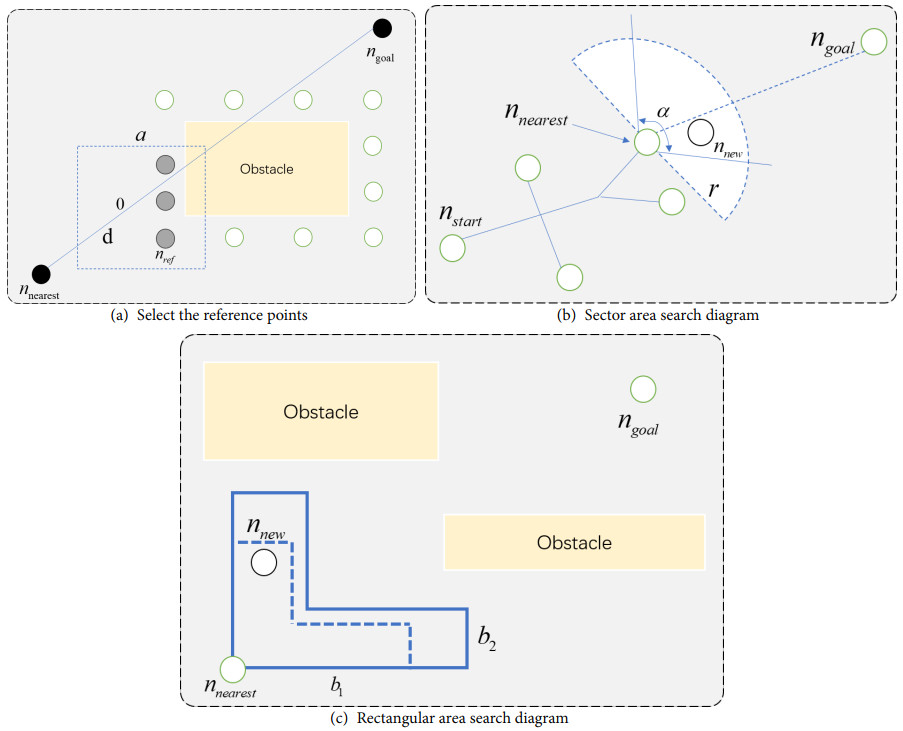
This paper uses a three-stage search strategy based on the real-time sampling failure rate. The novel search methodology adjusts the extension of $$ x_{rand} $$ and $$ X_{near} $$ within the Bi-RRT framework in response to environmental data, enabling the algorithm to accommodate environments of varying complexity. The choice of the search strategy is given in

where $$ p_1 $$ and $$ p_2 $$ are the search failure rate thresholds (SFRTs), $$ p_1 , p_2 \in (0, 1) $$, and $$ p $$ is the real-time sampling failure rate. SFRT is obtained by dividing the number of failed samples by the total number of samples. The search strategy for each sample is determined by $$ p $$. When $$ p \leq p_1 $$, the adaptive sector search is selected for the sampling points; When $$ p_1 < p < p_2 $$, the dynamic right angle search is run for the sampling points. Otherwise, switch to the target biased RRT search strategy.

The creation of the reference points is illustrated in Figure 2. The light gray point labeled $$ n_{ref} $$ represents the reference point, which is generated by expanding outward near each vertex of the obstacle. The dark gray point $$ n_{ref} $$ in Figure 3A indicates the returned reference point, which is located around the square lefted at $$ n_{nearest} $$ and $$ n_{goal} $$. Here, $$ O $$ marks the left of the square, $$ d $$ signifies the distance from $$ n_{nearest} $$ to $$ O $$, and $$ a $$ denotes the side length of the square area. The fan-shaped sampling area is depicted in Figure 3B. The line segment connecting the vertices of the sector at $$ n_{nearest} $$ and the endpoint at $$ n_{goal} $$ determines the central angle of the sector, denoted as $$ \alpha $$. Both the central angle $$ \alpha $$ and the radius $$ r $$ are functions of the real-time sampling failure rate $$ p $$. As the failure rate increases, the central angle widens and the radius diminishes. $$ \alpha $$ and $$ r $$ are respectively calculated by

Figure 2. Reference point extension diagram.

Figure 3. Diagram of reference point selection and search area.

where $$ \alpha $$ is the left angle, $$ r $$ is the radius, $$ k $$ is the scale factor, and $$ L $$ is the robot's extended step size.

The Dynamic Right Angle Search (DRAS) strategy and the Adaptive Sector Search (ASS) strategy exhibit identical algorithmic flows. The distinction lies in the DRAS policy, which substitutes the sector sampling region with a dynamic right-angle sampling region. This right-angle sampling region propels itself toward $$ n_{goal} $$, with $$ n_{nearest} $$ serving as the vertex of the right angle. An acute angle is defined as the angle formed between any right-angled edge and the line segment connecting $$ n_{nearest} $$ and $$ n_{goal} $$. When $$ n_{goal} $$ is situated in the upper right quadrant relative to $$ n_{nearest} $$, the configuration of the right-angle sampling region is illustrated in Figure 3C. The right-angle region comprises two congruent rectangles, mutually perpendicular and superimposed, with the longer side $$ b_1 $$ and the shorter side $$ b_2 $$ of these rectangles calculated by

where $$ k_1 $$, $$ k_2 $$ are the gain coefficients, $$ L $$ is the $$ AGV $$ expansion step, $$ e $$ is the Euler number, and $$ p $$ is the expansion failure rate. With the increase of $$ p $$, the sample area in Figure 3C gradually shrinks from solid to dashed areas.

3.3. Path pruning strategy

The RRT and Bi-RRT algorithms generate an excessive number of redundant nodes in narrow channel environments, leading to the algorithms' high path cost. In this paper, we optimize the node redundancy problem in the RRT algorithm from two aspects. First, referring to the idea of the RRT* algorithm, the paths can be pruned by comparing the costs of the paths to remove the unnecessary high-cost parts to obtain a better path. Secondly, a triangular pruning strategy will be applied after receiving the feasible paths.

Upon identifying a feasible path, the algorithm employs a triangular pruning strategy, which hinges on the principle that the sum of the lengths of any two sides of a triangle exceeds the length of the third side. The path pruning process is depicted in Figure 4. When the non-collision point $$ n_2 $$ in the original path is pruned, a new path is yielded, namely, $$ n1 - n3 - n4 $$.

Figure 4. Triangle pruning diagram.

3.4. Improvement of Bi-RRT

The RRT algorithm is based on boundary information, and the improved Bi-RRT algorithm is fused to ensure the overall operational efficiency and stability of the algorithm. First, a two-dimensional grid map is created by Light Detection and Ranging (Lidar), and the value obstacles in the map are labeled using the RRT algorithm based on boundary information. Second, the fusion of the improved Bi-RRT algorithm improves the convergence speed of the algorithm by reducing the generation of redundant nodes through the balanced exploration strategy and the three-stage search strategy. Further, the path pruning strategy is used to optimize the generated paths, effectively improving the overall efficiency of path planning. The algorithmic flow of the convergence algorithm is shown in Figure 5. The specific steps are summarized as follows:

Figure 5. Algorithm flowchart for boundary-information RRT with NCB-RRT. RRT: Rapidly-exploring random tree; NCB-RRT: nonholonomic constraints-based rapidly-exploring random tree.

(1) Add the initial point $$ x_{start} $$ to $$ \tau .init $$ as the growing root node of the tree, set the value of the iteration number $$ i $$ to 0, and set the exploration point $$ x_{temp} $$ of the value obstacle detection function $$ DetectValObs $$ to the starting point $$ x_{start} $$. Define two Boolean variables $$ collisionFree1 $$ and $$ collisionFree2 $$ to record the return value of the collision detection function $$ Checkcollision(x_{near}.x_{new}) $$ (Algorithm 2, lines 1-4).

(2) The maximum number of iterations the user can set max iteration. If the algorithm fails to find a feasible path within the specified maximum number of iterations, it will return to failure (Algorithm 2, line 27). Within the number of iterations, the value obstacle detection function $$ DetectValObs $$ generates any point around the obstacle (value obstacle) that the start/end line crosses, denoted as $$ x_{mid} $$. Proximity node function $$ NearNeighbor $$ will be generated from the tree $$ \tau $$ to search for a distance of $$ x_{mid} $$ the nearest node as $$ x_{near} $$. At this point, it grows along $$ x_{mid} $$ to $$ x_{near} $$ in a specific step to generate a new node $$ x_{new} $$. The collision detection function $$ Checkcollision $$ detects whether there is any obstacle between $$ x_{near} $$ and the newly generated node $$ x_{new} $$ and stores the result as a boolean value in the variable $$ collisionFree1 $$. (Algorithm 2, section 5, paragraph 5) (Algorithm 2, lines 5-9).

(3) The three-stage search strategy is run. First, the algorithm finds the closest point to the endpoint in the search tree denoted as $$ n_{nearest} $$. At line 10, Algorithm 2 returns the set of reference points between $$ n_{nearest} $$ and $$ n_{goal} $$. Then, the reference point in the set that does not collide with $$ n_{nearest} $$ is labeled $$ n_{new} $$ (line 12), and $$ n_{new} $$ is added to the search tree. If the result returned by $$ collisionFree1 $$ is true, $$ x_{new} $$ is added to the tree nodes. The new branch generated between $$ x_{near} $$ and $$ x_{new} $$ is added to the tree (Algorithm 2, lines 14-16); If $$ x_{new} $$ falls within the end range $$ x_{goal} $$, the search can be terminated and the path planning task is completed. If the line between the newly generated node and the endpoint does not cross any obstacle, then $$ x_{new} $$ can be assigned to $$ x_{temp} $$ to update the value obstacle (Algorithm 2, lines 18-22).

(4) Repeat the above process until a collision-free path is found from the start to the target point.

4.1. Algorithm simulation and analysis

To assess the efficacy of the proposed algorithm, it was compared against the RRT algorithm, the Bi-RRT algorithm, and the boundary information-based RRT algorithm. The superior performance of the proposed algorithm was evaluated in terms of path length, the number of nodes generated, and the computational time required.

The search component of the proposed algorithm in this paper consists of three distinct stages. The SFRT serves as the critical indicator for delineating these stages. To optimize the algorithm's performance across varying environments, it is essential to select appropriate SFRT values accordingly. Therefore, we systematically traverse the SFRT parameter space from 0 to 1 with a step size of 0.1. A cost function is specifically designed to select the optimal threshold configuration by identifying the group with the lowest average cost in each environment, as given in

where $$ Cost $$ denotes the total cost, $$ {node} $$ represents the average number of nodes, $$ {node} $$ indicates the average path length, $$ {len} $$ corresponds to the average iteration count, and $$ {iter} $$ signifies the average runtime.

The hardware environment used for simulation is a computer with Intel Core(TM) i5-1135G7 CPU @3.5GHz.16GB RAM with Windows 10 system, and the software environment is Matlab R2018b. The simulation experimental environment adopts the 600 $$ \times $$ 600-pixel ratio region of complex block-type obstacles as the two-dimensional simulation environment, where the black pixels denote the obstacle region and the white pixels represent the free region without barriers. Pixels denote the obstacle region, while white pixels denote the free region without barriers. The initial parameters of the algorithm are as follows: initial position $$ x_s=(50, 400) $$, target position $$ x_s=(440, 50) $$, step size $$ step = 40 $$, distance threshold $$ disTh = 40 $$, i.e., nodes within the distance threshold are considered as the same point.

Figure 6 shows the simulation comparison of the algorithm in the complex obstacle environment. Figure 6A presents the simulation of the RRT algorithm, which causes the algorithm to explore blindly due to the random selection of sampling points, resulting in the generation of more redundant nodes. Figure 6B shows a feasible path planned by Bi-RRT, which makes the search rate much higher and generates a better path by growing the tree in both directions. However, the algorithm still generates many redundant nodes. Figure 6C demonstrates the RRT algorithm based on boundary information from the figure. The number of nodes of the algorithm can be significantly reduced, and the planning efficiency is further improved. Figure 6D depicts the simulation of the proposed algorithm at the SFRT = 0.2. Thanks to the path-pruning strategy, the node utilization of the algorithm is further improved, and the search performance is significantly enhanced.

Figure 6. Simulation in the crowded environment. RRT: Rapidly-exploring random tree; Bi-RRT: bidirectional-rapidly-exploring random tree.

Due to the three-stage search strategy, the proposed algorithm can significantly improve the convergence speed of the algorithm by evaluating the real-time sampling failure rate p associated with the threshold SFRT as a measure of the complexity of the current environment. From the data analysis in Figure 7, it can be seen that in terms of path length, it is improved by about 37.32$$ \% $$ compared to the RRT algorithm, and about 0.31$$ \% $$ and 0.29$$ \% $$ compared to the Bi-RRT and boundary information-based RRT algorithms, respectively; in terms of number of nodes, it is improved by about 50.06$$ \% $$ and 50$$ \% $$.In terms of number of nodes, it is improved by about 50.06$$ \% $$ and 50.20$$ \% $$ over the RRT and Bi-RRT algorithms, respectively, and by about 50.06$$ \% $$ and 50.20$$ \% $$ over the boundary information-based RRT algorithm. information-based RRT algorithm by about 15.02$$ \% $$; in terms of running time, it is improved by about 19.23$$ \% $$, 10.50$$ \% $$ and 23.32$$ \% $$ over the RRT, Bi-RRT and boundary information-based RRT algorithms, respectively. In summary, when compared with RRT algorithm, Bi-RRT algorithm and boundary information-based RRT algorithm, the proposed algorithm shows significant superiority in terms of path length, number of nodes and running time, which proves its robustness and practicality in complex environments.

Figure 7. Performance comparison.

4.2. Real environment experiment

To deeply verify the effect of the algorithms proposed in this paper in practice, the authors decided to use a highly realistic and operable software experimental platform, ROS. ROS is an open-source software platform and a general platform widely accepted by most robot developers^[23]. The experiments in this paper use a customized mobile robot with a differentially driven motor on each side to control its forward motion. The front of the robot is also equipped with an auxiliary wheel whose main function is to provide balancing support to ensure that the robot remains stable and non-slip during its movement.

The homemade mobile robot based on the above was experimented in a complex indoor environment to verify the effectiveness and robustness of the algorithm. The complex indoor environment is shown in Figure 8A. The dimensions of the environment in the laboratory are 10.8 $$ \times $$ 5.8 meters. The floor smoothness of the experimental site is consistent, while on the raster map, the black circle represents the robot's position, and the block graphic indicates static obstacles. First, a 2D map of the indoor environment is created based on the Hector SLAM algorithm, and the resulting raster map is imported into RViz; as shown in Figure 8B, the resolution of the raster map is set to 20 cm $$ \times $$ 20 cm. Next, an adaptive Monte Carlo localization algorithm is applied to accurately determine the position and direction of the mobile robot, which tracks the robot's movement by particle filtering method. With iterations, all the particles will converge gradually so that the robot's current position can be accurately determined.

Figure 8. Experimental environment.

In this paper, a comparison experiment between the proposed algorithm and the RRT algorithm based on boundary information is carried out in a complex indoor environment as shown in Figure 9. The proposed algorithm is used in the experimental scenario. The proposed algorithm introduces a balanced exploration strategy, which effectively improves search efficiency by generating the search tree from two directions simultaneously. In addition, the introduced three-stage search strategy also enhances the quality of sampling points. As for the improved RRT algorithm based on boundary information, since the selection of sampling points near the obstacles is randomized, in real experimental scenarios, the robot will turn in place and move backward around the obstacles (as shown in Figure 9).

Figure 9. Results of the RRT algorithm using boundary data. (A) Schematic showing the robot spinning around an obstacle; (B) Schematic of the robot spinning during operation; (C) Schematic of the robot spinning near the target point; (D) Rviz interface showing the schematic of the robot spinning near an obstacle; (E) Rviz interface showing schematic of robot spinning near an obstacle; (F) Rviz interface showing schematic of robot spinning near a target point. RRT: Rapidly-exploring random tree.

In contrast, the algorithm proposed in this paper introduces a balanced exploration strategy, which effectively improves the search efficiency by simultaneously generating the search tree from two directions. In addition, the introduced three-stage search strategy also improves the quality of the sampling points, which significantly reduces the in-situ steering and backward phenomenon of the boundary RRT algorithm. According to the actual measurement, the deviation of the final position of the robot from the expected target point is less than 0.1 meter, which basically meets the requirements of actual robot navigation [Figure 10].

Figure 10. Experimental results of the improved RRT algorithm. (A) Diagram of the robot's movement process; (B) Diagram of the robot reaching the target point; (C) Rviz interface during the movement process; (D) Rviz interface when the robot reaches the target point. RRT: Rapidly-exploring random tree.

Combined with the experimental results in Figure 11, the proposed algorithm in this paper improves the running time by 13.4$$ \% $$ and the planning path length by 9.51$$ \% $$ compared with the RRT algorithm based on boundary information. The proposed algorithm shows stronger robustness in complex indoor environments.

Figure 11. Experimental results comparison.

Authors' contributions

Made substantial contributions to the research, idea generation, algorithm design, simulation, wrote and edited the original draft: Sun, Y.; Zhu, H.; Liang, Z.

Performed data acquisition and provided administrative, technical, and material support: Ni, H.; Liu, A.; Wang, Y.

Availability of data and materials

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Financial support and sponsorship

This work has been funded by the Key Research and Development Program of Zhejiang Province (Project No. 2023C01224).

Conflicts of interest

Liu, A. is the Junior Editorial Board Member of the journal Intelligence & Robotics. Liu, A. was not involved in any steps of editorial processing, notably including reviewer selection, manuscript handling, or decision-making. The other authors declare that there are no conflicts of interest.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Copyright

© The Author(s) 2025.