In-situ real-time monitoring of muscle energetics with soft neural-mechanical wearable sensing

Fabrication of the neural-mechanical sensor

The sensor was constructed by first laminating a 0.1 mm-thick copper/nickel-coated polyester conductive fabric (20 mm diameter, conductivity approximately 7.4 × 10⁵ S/m) with a 0.2 mm polyvinyl chloride (PVC) encapsulation layer, followed by screen-printing a flexible silver nanoparticle electrode [NSPP composite: nano silver/polydimethylsiloxane (PDMS)/kerosene 8:2:1 mass ratio, cured at 160 °C for 3 h] onto a 0.2 mm PDMS substrate to achieve a 0.1 mm conductive layer (conductivity about 6.5 × 10⁶ S/m), interconnected via silver-welded joints (7 mm × 6 mm) to copper wires. A 3 mm-thick CCTO and polyurethane sponge (CCTPS) dielectric layer was integrated by immersing a 60 par per inch (PPI) polyurethane sponge (20 mm diameter) in an ultrasonically homogenized CCTO/3-amino-propyl-triethoxysilane (APTES) suspension (mass ratio 35:10:75:1), dried at 60 °C for 8 h to enhance particle adhesion. Finally, a double-sided adhesive patterned with 2 mm apertures (3 mm spacing) filled with conductive cream was applied to optimize skin-electrode contact impedance.

Weight lifting with single muscle

The protocol focused on controlled weight lifting by a target muscle (e.g., biceps brachii, BIC) to quantify its mechanical work output [Supplementary Note 1]. Participants stabilized their upper arm on a 115 mm vertical support, lifting a 1.25 kg mass until the forearm reached the vertical orientation (γ = 90°) perpendicular to the table surface, then lowering it back to the initial resting position (γ = θ - 180°). This motion facilitated BIC-specific concentric (lifting) and eccentric (lowering) contractions, with equivalent mechanical work during elevation due to the identical vertical displacement of the mass. For active trials (fast and slow speeds), the BIC performed work to rotate the forearm from a stationary position (zero initial velocity) to a stationary state (zero final velocity), while passive trials (gravity-driven release) eliminated active muscle tension, resulting in a non-zero terminal velocity as the mass accelerated under unopposed gravitational force.

Weight lifting with multiple muscles

The second weight-lifting test was designed to assess mechanical work performed with multiple upper-limb muscles. Participants leaned forward with their upper arm angled at θ relative to the torso and aligned parallel to the table. To minimize compensatory motion of the upper body, the left hand stabilized the right shoulder. The forearm executed a forward lift of weight from the initial resting state (γ = -π/2) to γ = -θ, a phase dominated by mechanical work from the BIC thus termed the BIC phase. Subsequently, the weight was lifted backward from γ = -π/2 to γ = -π + θ, a transitioned to the triceps brachii (TRI) dominance, referred to as the TRI phase.

Muscle work sensing with neural-mechanical sensor

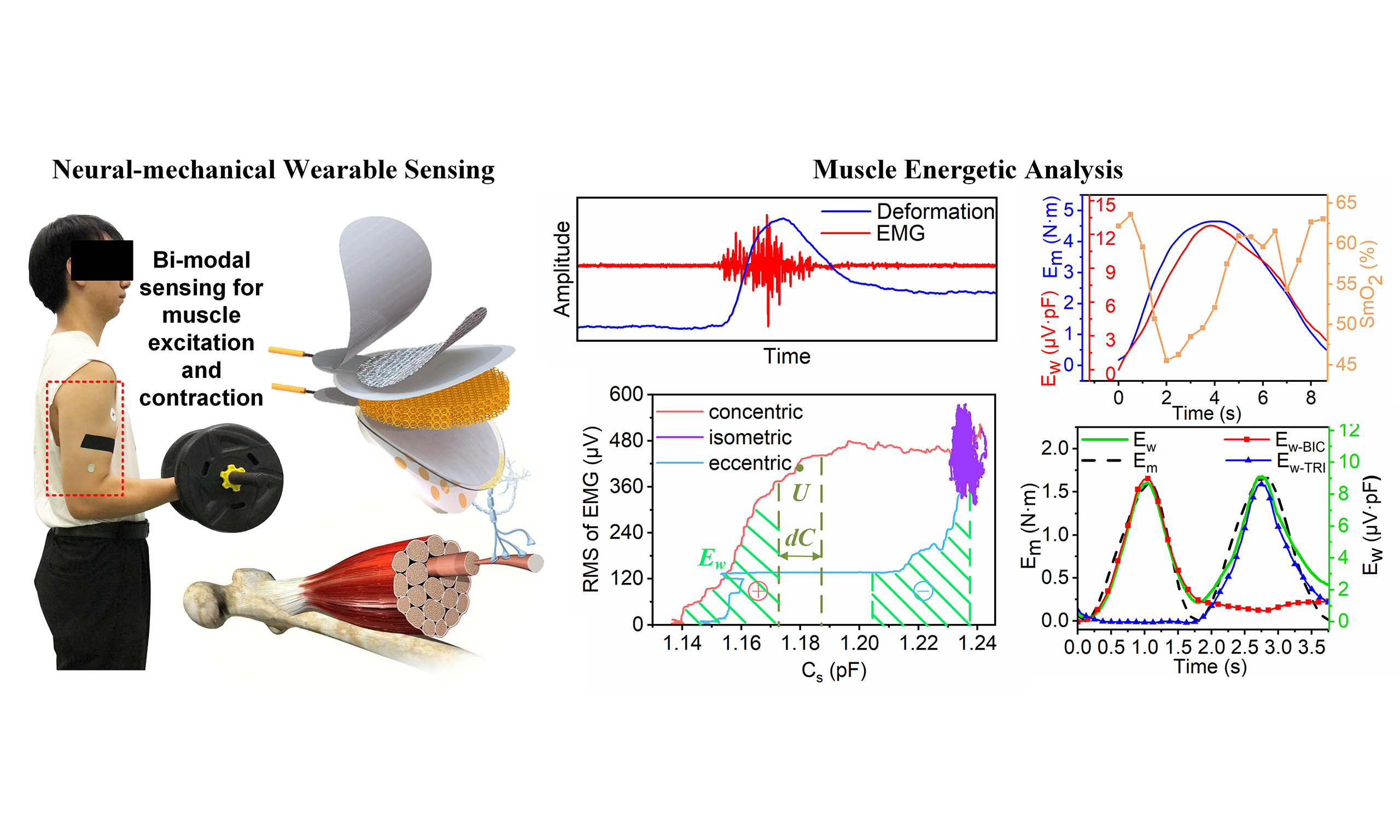
Motor neurons transmit action potentials along nerve fibers to generate the EMG in muscles [Figure 1A], which further causes muscle contractions, limb motions and energy consumption. Inspired by the excitation and contraction signatures of muscles, the neural-mechanical sensor is designed by integrating a capacitive sensing component and an EMG electrode. The sensor is composed of the PVC film, conductive fabric electrode, CCTPS dielectric layer, flexible silver nanoparticle electrodes, and conducting layer [Figure 1B]. The conductive fabric and flexible silver nanoparticle electrodes together with the CCTPS dielectric layer form the capacitance C_s. The conductive fabric electrode is encapsulated by PVC films to prevent a short circuit between the two electrodes. The flexible silver nanoparticle electrode is used to monitor muscle EMG in terms of the voltage U with reference to the commercial gel electrode. The conducting layer, a double-sided adhesive foam with a planar array of circular holes (PACH) containing conductive cream, provides low and stable contact impedance between the flexible silver nanoparticle electrode and human skin. PDMS was chosen for its unique mechanoelectrical stability, overcoming limitations of hydrogels (ionic drift/dehydration) and Ecoflex (interfacial delamination due to < 100 kPa modulus). Its 1-2 MPa modulus balances mechanical support and elasticity, enabling durable signal fidelity across 30%-100% strain ranges during dynamic monitoring. Silver nanoparticles overcome the limitations of liquid metals (processing challenges) and carbon nanotubes (humidity sensitivity and non-screen-printable properties), achieving high conductivity [signal-to-noise ratio (SNR) > 46 dB] and flexible compatibility when compounded with PDMS. CCTO, with a dielectric constant three times that of barium titanate (BaTiO₃) and 30 times that of strontium titanate (SrTiO₃), enhances capacitive sensitivity when integrated into polyurethane sponge while retaining flexibility (compression resilience > 98%) and thermal stability (250 °C). These two materials synergistically achieve the integration of high sensitivity and wearable reliability. In practice, the neural-mechanical sensor is secured in place and preloaded using an adhesive tape made of non-stretchable acetate cloth. The sensor prototype has a diameter of 24.5 mm and a thickness of 4.5 mm [Figure 1C]. The capacitive deformation signal is acquired via an AD7746 analog-to-digital converter (21-bit resolution, ±4 pF range, expandable to 0-21 pF), while the EMG signal is processed through an AD8422ARMZ instrumentation amplifier (±3,300 μV range, 16-bit resolution), sampled at 2,000 Hz, and denoised using a fourth-order Butterworth low-pass filter (450 Hz cutoff frequency). A hardware-triggered synchronization protocol ensures temporal alignment between modalities, with EMG RMS values downsampled to 100 Hz via a cubic spline algorithm. Real-time processing includes EMG active segment detection (sliding window threshold method, 250 ms window) and deformation signal baseline compensation (moving average filtering, 50 ms window).

Figure 1. Neural-mechanical sensor. (A) Comparison between deformation and EMG during voluntary muscle contraction; (B) Schematic of the neural-mechanical sensor; (C) Appearance of the sensor prototype with labeled dimensions; (D) Experiment of weight lifting. The volunteer subject performed the weight lifting with muscle concentric, isometric, and eccentric contractions; (E) Responses of the measured EMG and C_s under different muscle contractions for testing muscle fatigue; (F) Illustration of E_w calculation. The E_w is calculated with integration of the RMS of EMG and C_s for different muscle contraction modes during the fatigue testing. EMG: Electromyography; RMS: root mean square.

Since the muscle work can be estimated by the inner product of muscle contraction forces and deformation displacements, its equivalent index can be formulated as the area under the relation curve between U_R and C_s [Figure 1F]

with the assumptions: (1) The displacement of muscle contraction ΔL is linear with change of the measured C_s in ΔL = k₁ΔC_s; (2) the muscle force F is linear with the root mean square (RMS) of EMG, namely U_R, processed with a sliding window via F = k₂U_R; and (3) the muscle strain energy determined by E_s = ∫F(t)dL can be expressed as

where K = k₁k₂, and L and F are evaluated by the kinematic and dynamic analysis in Supplementary Note 1.

For a musculoskeletal system consisting of n muscles, it performs the total mechanical work

where the strain energy E_s⁽ⁱ⁾ for each muscle transforms into mechanical work and dissipative energy with the efficiency of 0 < η_i < 1 for i = 1, 2, …, n. Substitution of Equations (2) into (3) gives rise to

where η_i and K_i vary with different muscles. The above illustrates the overall mechanical work for the musculoskeletal system as an algebraic summation of each muscle work.

To validate the muscle work sensing model, the overall work performed by the musculoskeletal system is quantified with the weight lifting test [Figure 1D] in terms of the mechanical energy of the weight m

where g is the gravitational acceleration, L₁₂ is the forearm length, γ is the angle between the forearm and the horizontal X-axis, and ω is the angular velocity of forearm rotation.

Calculation of E_w with U_R and C_s using Equation (1) is illustrated for different modes of muscle motions in the weight lifting test. The measured BIC went through concentric, isometric, and eccentric contractions when the tested subject lifted a 6-kg weight to a position where the forearm was parallel to the ground, and held still before releasing to the initial state [Figure 1D]. The neural-mechanical sensor simultaneously captures both EMG and muscle deformation [Figure 1E]. During concentric and eccentric contractions, the measured EMG occurred and vanished earlier than the muscle deformation, and the mean power frequency (MPF) of the EMG gradually decreases while the measured capacitive deformation stays stable during isometric contraction with fatigue [Supplementary Figure 1]. Figure 1F shows the change in the area under the E_w curve in the lifting condition. When the muscle undergoes isometric contractions, E_w remains approximately constant with little change of the area spanned by U_R and C_s [Figure 1F]. It further shows isometric contractions (purple) yield far less cumulative E_w over 50 s than brief, high-intensity concentric/eccentric contractions (lasting for couple seconds). The EMG-to-deformation latency (20-50 ms) is negligible compared to typical muscle contraction duration (> 1 s). During this brief delay, no deformation occurs despite initial EMG surges in concentric contractions [Supplementary Figure 1A], whereas deformation persists after EMG stops during passive stretching [Supplementary Figure 1B]. These transient differences have minimal impact on integration of muscle work (E_w) due to smooth strain progression and limited EMG fluctuations. Given the positive U_R, the sign of E_w increment is the same as that of C_s change for different muscle contractions. As the muscle performs positive work to lift the weight, E_w increases with U_R and C_s. When the muscle undergoes isometric contractions, E_w remains approximately constant with little changes of U_R and C_s. After a prolonged isometric contraction, the fatigue muscle was unable to maintain enough tension and started to be passively stretched by the weight descending. In this way, the area E_w slightly decreases [Supplementary Figure 1D] with the dramatic vanishing of the measured EMG as visualized by the blue curve for the eccentric contraction [Figure 1F].

Mechatronic design and performance specification

Before leaping into neural-mechanical coupling, electrical and mechanical performance for the patchable electrodes were investigated for different designs in terms of contact impedance, SNR, sensitivity, and fatigue resistance. To achieve a low and stable contact impedance for EMG sensing with a high SNR, the flexible silver nanoparticle electrode was fabricated with a PDMS film printed with the mixed material that consisted of nanosilver powder dispersed in PDMS liquid with industrial kerosene (NSPP). The measured contact impedance of the sensor on the human skin decreases with the excitation frequency of the inductance-capacitance-resistance (LCR) digital bridge and is on average 46% lower than the contact impedance of commercial gel electrodes in the range within 1 kHz [Figure 2A]. This is attributed to the excellent conductivity and high conformability of the conductive gel and nano silver powder in the flexible silver nanoparticle electrode. In a 12 kg weight lifting test, SNR of the EMG collected on the BIC was 46.8 dB for the proposed sensor compared to 42.8 dB for a commercial gel electrode [Figure 2B]. The low contact impedance and high SNR justify the developed electrode as a competent candidate for EMG sensing.

Figure 2. Mechatronic design and performance characterization of the sensor. (A) Comparison of the neural-mechanical sensor and commercial gel electrode. Impedances are analyzed for the two electrodes adhered to the skin on the BIC; (B) EMG characterization for the two electrodes. The measured EMG captured by the neural-mechanical sensor and commercial gel electrode were compared in terms of SNRs; (C) Effect of muscle deformations on the impedance of the skin-electrode interface; (D) Impedance variation with cyclic compression. The maximum impedance change was only 1.05% with a cyclic loading for 750 times; (E) Mechanical properties of the polyurethane sponges. In comparison of polyurethane sponges with different pore sizes, the pore density of 60 PPI exhibited the highest sensitivity in the compression test; (F) Effects of CCTO on the sensitivity of muscle deformation measurements. The sensitivity of the sensor with CCTO is three times higher than that without CCTO; (G) Cyclic compression test. During 14,000 cycles of compression, the measured capacitive deformation exhibited a drift of approximate 0.85%; (H) SNR of the capacitive sensing for a tender touch. BIC: Biceps brachii; EMG: electromyography; SNRs: signal-to-noise ratios; PPI: par per inch; CCTO: copper calcium titanate.

To investigate the stability of electrode contact impedance when the muscle deforms and compresses the neural-mechanical sensor, compression tests (the compression machine ZQ-990) were conducted on pig skin. When the CCTPS dielectric layer of neural-mechanical sensor was compressed by 1.8 mm using a custom-made formaldehyde fixture, the impedance change of the skin-electrode interface is 0.111 kΩ (red line) and 0.043 kΩ (black line) for cases with conductive cream alone and a double-sided foam adhesive with PACH, respectively [Figure 2C]. The double-sided foam adhesive with PACH reduces the contact impedance variation by holding the conductive cream in place without leaking from the skin-electrode interface. In addition, the maximum impedance change is only 1.05% with a cyclic loading for 750 times [Figure 2D]. This means that during cyclic muscle deformations, the changes in the contact impedance at the skin-electrode interface are small enough that there is no significant distortion in the EMG data captured by the neural-mechanical sensor [Supplementary Figure 2].

Sensitivity of the capacitive measurements is characterized by comparing six polyurethane sponges (3.1 ± 0.15 mm in thickness) of 10 to 60 PPI. The 60 PPI design has the highest sensitivity with the steepest slope for the loading curve [Figure 2E]. The CCTPS dielectric layer exhibits high dielectric performance with the CCTO attached on the porous inner surface of the polyurethane foam. The sensor sensitivity for the design with CCTO is larger than 7 and three times of that for the case without CCTO [Figure 2F]. In addition, the measured capacitance change exhibits a linear relationship of the compression displacement with the square of the correlation coefficient (R²) greater than 0.93 for both loading and unloading at different step sizes of 0.2, 0.3 and 0.45 mm. The fatigue performance was investigated with a compression test of more than 14,000 cycles, during which the drift of 0.083 pF was observed throughout the process (approximately 0.85% of the amplitude change of 9.736 pF in Figure 2G). Furthermore, the SNR of muscle deformation sensing is estimated as 23.26 dB for a tender touch [Figure 2H].

Coupling muscle deformation and EMG

The neural-mechanical sensor, by coupling the bipolar plate capacitor with EMG electrodes, simultaneously measures muscle deformations and EMG in-situ. To analyze neural and mechanical motions of a muscle, lifting tests were conducted with various muscle contraction modes and speeds. As shown in the single muscle lift [Figure 3A].

Figure 3. The measured EMG, capacitive deformation and muscle work for different muscle contractions. (A) Weight lifting test with single muscle. The volunteer lifted a weight with muscle CC and released it with EC at different speeds. Each column of plots corresponds to different muscle motions: slow CC - slow EC, fast CC - fast EC, slow CC - passive EC, and fast CC - passive EC. The muscle was under tension during slow and fast movements, and was without tension during passive movement; (B) Measurements of EMG and C_s during muscle contractions. RMS of EMG is also calculated for different contractions; (C) Combination of the C_s and the RMS of EMG for different muscle contractions; (D) Illustration of E_w for weight lifting tasks. EMG: Electromyography; CC: concentric contraction; EC: eccentric contraction; RMS: root mean square.

Within one motion cycle, the muscle eccentric contraction facilitated by the gravity produced a weaker EMG than the concentric contraction. In the muscle concentric contraction, slow lifting of 9.3 s produced a weak EMG with its RMS of 203 μV and a large capacitive change of 0.113 pF, while the fast lifting of 1.4 s had a strong EMG with RMS of 262 μV and a small capacitive change of 0.076 pF (the first two plots in Figure 3B). Considering the positive correlation between the RMS of EMG and muscle force levels [Supplementary Figure 3], it is indicated that fast muscle motions require for larger contraction forces and recruit more muscle fibers than slow movements. For a certain contraction displacement of the whole muscle, the increased recruitment of muscle fibers gives rise to reduced axial and lateral fiber deformations at the muscle belly thus a reduced capacitive measurement.

For eccentric contractions with muscle tension, the blue area is approximately equal to the red one as the muscle performed negative work and E_w returns to the baseline near zero (the first and second plots in Figure 3C and D). The integration with Equation (1) provides approximately the same maximum E_w for concentric muscle contractions at different speeds (around 17 μV·pF in Figure 3D), because a similar amount of muscle work was performed to raise the weight to the same height. In this way, E_w increases with positive muscle work and decreases with negative muscle work. On the other hand, for eccentric contractions without muscle tension, the muscle performed little work during the passive stretching, and little decrement is observed in E_w due to the small blue area (the third and fourth plots in Figure 3D).

Muscle work estimation

Assumptions (1-3) are validated by investigation of E_w via comparison with the change of mechanical energy E_m of the lifted weight and the muscle oxygen saturation SmO₂ captured by the NIRS technique (MOXY-3). NIRS was used to measure changes in oxygenated/deoxygenated hemoglobin concentrations at the BIC belly via the principle of diffuse reflection, employing dual-wavelength light sources (730 and 850 nm). The system included a single-channel photoelectric detector operating at the sampling frequency of 2 Hz, with temporal synchronization to EMG signal acquisition. During the weight lifting and releasing with only BIC, the measured capacitance matches with the muscle deformation displacement [Figure 4A], and the linear regression of R² = 0.96 [Figure 4B] validates the assumption (1). Variation of the RMS of EMG is consistent with the muscle force [Figure 4C], and it validates the assumption (2) with their linear relation of R² = 0.91 [Figure 4D]. Integration of (5) produces E_w increasing with the weight lifting and decreasing with the weight releasing, which is consistent with variation of E_m [Figure 4E]. Oxygen consumption decreases as indicated by SmO₂ when the muscle performed positive work during the concentric contraction, and it gradually returns to the normal level during the eccentric contraction. The linear relation between E_w and E_m with R² = 0.95 [Figure 4F] validates assumption (3). With the measured EMG and capacitive deformation for three cycles of weight lifting and releasing [Figure 4G], E_w is calculated with its baseline drift suppressed by the high-pass filter with the cutoff frequency of 1 Hz. The calculated E_w closely relates to E_m [Figure 4H and Supplementary Movie 1] with R² = 0.95. Additionally, robustness of the proposed method for single muscle work sensing was justified by the same tests on six healthy volunteers [Supplementary Figure 4].

Figure 4. The work of a single muscle. (A and B) Relationship between the measured capacitive deformation and muscle contraction displacement. The change of C_s is consistent with the variation in muscle contraction displacement with the linear regression of R² = 0.96; (C and D) Relationship between the muscle contraction force and RMS of EMG. The RMS of EMG matches the variation of muscle contraction force with the linear regression of R² = 0.91; (E) Comparison of muscle work E_w, mechanical energy E_m of the weight, and muscle oxygenation SmO₂; (F) Linear regression between E_m and E_w with R² = 0.95; (G) Characterization of the measured C_s and EMG during multiple cycles of weight lifting with one single muscle; (H) Validation of muscle work during repeated weight lifting with one single muscle. The high-pass filtered E_w is consistent with Ew_mith the linear regression of R² = 0.95. RMS: Root mean square; EMG: electromyography.

Assumptions (1-3) are further validated for the case involving multiple muscles of the BIC and TRI where n = 2 for Equation (4) [Supplementary Note 1]. As shown in the multi-muscle lift [Figure 5A]. Two neural-mechanical sensors monitored motions of the BIC and TRI muscles by measuring EMG and C_s for E_w, and an IMU tracked the arm rotational angle to calculate the muscle force and contraction displacement for E_m. The BIC generates both EMG and deformations during the BIC phase, while it passively deforms with a weak EMG during the TRI phase [Figure 5B]. A similar phenomenon can be observed for the TRI [Figure 5C]. Changes of the measured capacitance match with the muscle contraction displacements for the BIC and TRI muscles [Figure 5D and E], where linear regression with R² = 0.98 and 0.85 [Supplementary Figure 5A and B] validates assumption (1) for collaborative muscle motions. The RMS of EMG is consistent with the muscle force [Figure 5F and G], and their linear regression with R² = 0.98 and 0.91 [Supplementary Figure 5C and D] also validates assumption (2) for collaborative muscle motions. Combining the RMS of EMG with capacitive measurements, the BIC muscle performed the same amount of positive and negative work during the BIC phase given the overlapped loading and unloading curves, and it performed little work during the TRI phase [Figure 5H]. Similarly, the TRI went through the same loading and unloading process during the TRI phase and performed no work during the BIC phase [Figure 5I]. The positive work performed by the BIC and TRI muscles, E_w-BIC and E_w-TRI, reach the maximum of about 9 μV·pF corresponding to the same weight-lifting height during the BIC and TRI phases [Figure 5J]. It is observed that E_w = E_w-BIC + E_w-TRI closely matches E_m via the linear regression of R² = 0.92 [Figure 5K] which validates assumption (3). For multiple cycles of lifting and releasing, the summed E_w for both muscles linearly relates to E_m with R² = 0.89 [Figure 5L and Supplementary Movie 2], which is further validated by six healthy volunteers [Supplementary Figure 6].

Figure 5. The work performed by multiple muscles. (A) Weight lifting with both BIC and TRI muscles. The BIC phase refers to the period when BIC dominates in positive work performance, and the TRI phase denotes the period when TRI contributes to the major part of positive work; (B and C) Measurements of C_s and EMG on the BIC and TRI muscles throughout the lifting process; (D and E) Comparison of ΔC_s and the muscle contraction displacement for BIC and TRI. The regression of ΔC_s and muscle contraction displacement was characterized by R² = 0.98 and 0.85 for BIC and TRI, respectively, validating the capacitive sensing for muscle deformations during collaborative muscle motions; (F and G) Comparison of the RMS of EMG and the muscle contraction forces for BIC and TRI. The regression of RMS of EMG and muscle contraction force was characterized by R² = 0.98 and 0.91 for BIC and TRI, respectively, validating the feasibility of muscle force sensing with EMG during collaborative muscle motions; (H and I) Curves plotted with ΔC_s and the RMS of EMG measured on the BIC and TRI; (J and K) Comparison of E_m and E_w (= E_w-BIC + E_w-TRI) with their linear regression of R² = 0.92, where E_w-BIC and E_w-TRI are the muscle work performed by the BIC and TRI muscles, respectively; (L) Comparison of E_w and E_m for multiple lifting cycles. The E_w summed for both muscles linearly related to E_m with R² = 0.89. BIC: Biceps brachii; TRI: triceps brachii; EMG: electromyography; RMS: root mean square.

Discussion of experimental findings

Previous studies have captured muscle excitation-contraction characteristics with local coupling mechatronic interfaces to identify motion characteristics for human-robot interaction. Muscle strains and EMG signals were coupled to delineate the gait phase cycles of the lower limbs^[29]. The finger flexion speed and the gripping strength were qualitatively monitored by the muscle strain rate and the EMG amplitude, respectively^[28]. Product of the muscle forces and deformations can lead to an estimation of the effective work performed by the muscle. However, the prerequisite of muscle work sensing for coupled force and deformation quantification has not been well studied and established yet, because there exist spatiotemporal differences between action potentials and myofiber contraction^[33] rendering challenges of in-situ measurement and signal synchronization for numerical integration.

Inspired by the working principle of muscle motions, the coupled neural-mechanical sensing method has been developed to capture individual muscle work. It offers the advantages of (1) in-situ (2) real-time monitoring of muscle work and (3) quantitative neural-mechanical coupling of muscle forces and contraction deformations. It achieves the SNRs of 46.8 dB and 23.26 dB respectively for the deformation and EMG sensing [Figure 2B and H]. The robustness was justified by the negligible drift of 0.85% in capacitive measurements during 14,000 cycles of loading [Figure 2G]. Combining with the lift test [Supplementary Figure 7], the proposed method has been experimentally validated by comparing against the local physiological measurements of oxygenation SmO₂ [Figure 4E] and the overall dynamic analysis of mechanical energy [Figure 4F].

The coupled neural-mechanical sensing is able to fully capture muscle kinematics and dynamics. The capacitive sensing can discriminate the muscle motion modes of concentric, eccentric and isometric contractions with the increasing, decreasing and constant measurements, respectively. On the other hand, EMG sensing can identify active and passive motions by the existence of muscle tensions caused by action potentials [Figure 3B]. In this way, an active concentric contraction produces positive work, and an active eccentric contraction gives rise to negative work, while other motions such as isometric contractions or passive deformations do not exert effective work [Figure 3D].

The proposed method also provides an alternative way to study muscle synergy from the energetic viewpoint. A biological joint is typically driven by antagonistic motions among muscle groups. Common myoelectric signals could tell the neural state of a muscle such as activation, fatigue or at rest^[34]; however, they could hardly quantify the effective contribution of each muscle’s to overall joint motions. Figure 5J illustrates workload-specific neuromuscular activation patterns in the BIC (E_w-BIC, red line) and TRI (E_w-TRI, blue line), where the BIC generated symmetrical mechanical work during its active phase but showed minimal engagement in the TRI phase, while the TRI exhibited reciprocal behavior. Both muscles achieved the maximum external work output (approximately 9 μV·pF), consistent with similar lifting height during their respective phases. The calculated total multi-muscle work (E_w, green line) strongly correlated (R² = 0.92) with the mechanical energy change (E_m, black line) derived from IMU measurements. The coupled sensing method represents a significant breakthrough in the energy monitoring of muscle synergy, as compared with all existing techniques [Supplementary Table 1]. In addition, energetics of muscle synergy provide a practical metric to evaluate the performance of wearable robots and locomotion capabilities of human bodies on the muscle energy level instead of overall metabolic cost, which may in turn provide a detailed guideline to improve motion skills^[35,36], innovate robot designs^[6,37] and optimize feedback control^[38].

While the proposed neural-mechanical sensing method, which integrates myoelectric and capacitive measurements to quantify muscle work through voltage and capacitance rather than joules, demonstrates feasibility through its correlation with the mechanical energy expenditure during weight lifting, it represents one of many potential approaches for analyzing muscle synergy energetics. Existing alternatives for assessing muscle forces include phonomyogram^[39,40] and force myography^[41,42], while techniques such as ultrasound imaging^[25], resistive sensing^[26] and electrical impedance tomography^[27] capture muscle deformations. The current framework could thus be enhanced by integrating these complementary modalities, either for force/displacement sensing or both. In this work, upper-limb single-joint motions serve as a foundational demonstration of the coupled sensing paradigm. Future studies will extend this to complex and realistic scenarios, such as distributed sensor networks monitoring multi-joint dynamic movements of running and jumping with high energy expenditure, as well as long-term monitoring requiring robustness to sweat and temperature variations. Scaling to multi-joint and lower-limb applications, such as rehabilitation engineering, sports science and human-centered robotics, will demand adaptive sensor fusion architectures and advanced coupling strategies for force-displacement sensing, particularly under extreme dynamic conditions such as heavy loads, sustained activity or intense impulses, necessitating further methodological refinements.