Neutron imaging quantifying hydrogen diffusion and distribution in metallic materials - a review

INTRODUCTION

Neutron imaging has emerged as a non-destructive evaluation method, employing the distinctive interaction between neutrons and atomic nuclei to investigate material properties^[1,2]. Recent advancements in neutron source design, detector technology, and computational algorithms have facilitated advanced experimental capabilities, including high spatial resolution attenuation imaging^[3], Bragg-edge imaging^[4,5], and grating imaging^[6]. Attenuation imaging relies on the scattering and absorption of neutrons by materials. Variations in the neutron counts transmitted through different materials generate image contrast, reflecting differences in neutron attenuation coefficients. Bragg-edge imaging utilizes wavelength dependent diffraction between neutron beam and crystalline lattices. Intensity contrast arises at specific wavelengths, enabling phase identification. Additionally, lattice distortion induced by stresses alters Bragg-edge profiles, allowing for quantitative stress mapping in specific phases^[7]. Grating imaging, a recently developed technique, employs periodic grating structures to achieve sub-micrometer resolution^[6]. Through the design of user-oriented experimental setups, in situ monitoring under extreme conditions (e.g., high temperature, mechanical stress), as well as operando studies of dynamic processes (e.g., hydrogen diffusion, phase transformation), have become achievable^[8-10].

In comparison with X-rays, which exhibit strong penetration through light elements but limited efficacy in dense metallic systems, neutrons provide exceptional penetration depth up to several centimeters in metals while maintaining sensitivity to light elements such as hydrogen, boron and lithium^[11,12]. This complementary capability makes neutron imaging an indispensable tool for analyzing hydrogen in metallic materials, where conventional techniques cannot resolve hydrogen distribution without destructive characterization. The unique advantage of neutron imaging lies in its ability to generate hydrogen specific contrast via neutron interaction with hydrogen nuclei, enabling non-destructive visualization of hydrogen distributions within bulk metallic specimens. This is particularly crucial for hydrogen storage alloys, and high strength steels^[13,14].

Hydrogen is a common element with wide importance in many areas, such as nuclear energy and storing hydrogen^[8]. However, when it comes into contact with other materials, it can cause serious damage, known as Hydrogen-Induced Damage (HID). The destructive effect of hydrogen on materials is complex and gradual, affecting atomic-level interaction, microstructural changes, and overall material failure. These effects show up as hydrogen embrittlement (HE), hydrogen attack and HID, each of which contributes to the degradation of material properties and performance under hydrogen exposure. HE is the most damaging form of HID, causing brittle fractures in metals such as high-strength steel and titanium/zirconium alloys, even under stresses much lower than the material’s yield strength. In this process, hydrogen atoms gather at the tips of cracks under stress, weakening the bonds between atoms and leading to early fracture^[5]. In titanium and zirconium alloys, hydrogen reacts with the material to form brittle hydrides (e.g., ZrH_1.5), which can cause delayed cracking known as delayed hydride cracking (DHC). DHC failure in nuclear fuel cladding under high temperature, water-cooled conditions is a major safety concern. Hydrogen attack is commonly observed in steels exposed to high-temperature and high-pressure environments such as in petrochemical reactors^[10]. This type of damage is often hard to detect during service and can lead to catastrophic failures. Additionally, hydrogen-assisted cracking occurs during processes such as welding, electroplating, or in corrosive environments, where hydrogen enters materials through cracks or corrosive media. The sudden and hidden nature of HID presents serious risks to industries such as nuclear power and hydrogen storage, highlighting the importance of analyzing hydrogen distribution. This paper focuses on attenuation imaging, which is a type of neutron imaging, and reviews its applications in hydrogen containing metallic systems in recent years, while also offering perspective on future developments.

PRINCIPLES OF NEUTRON ATTENUATION IMAGING

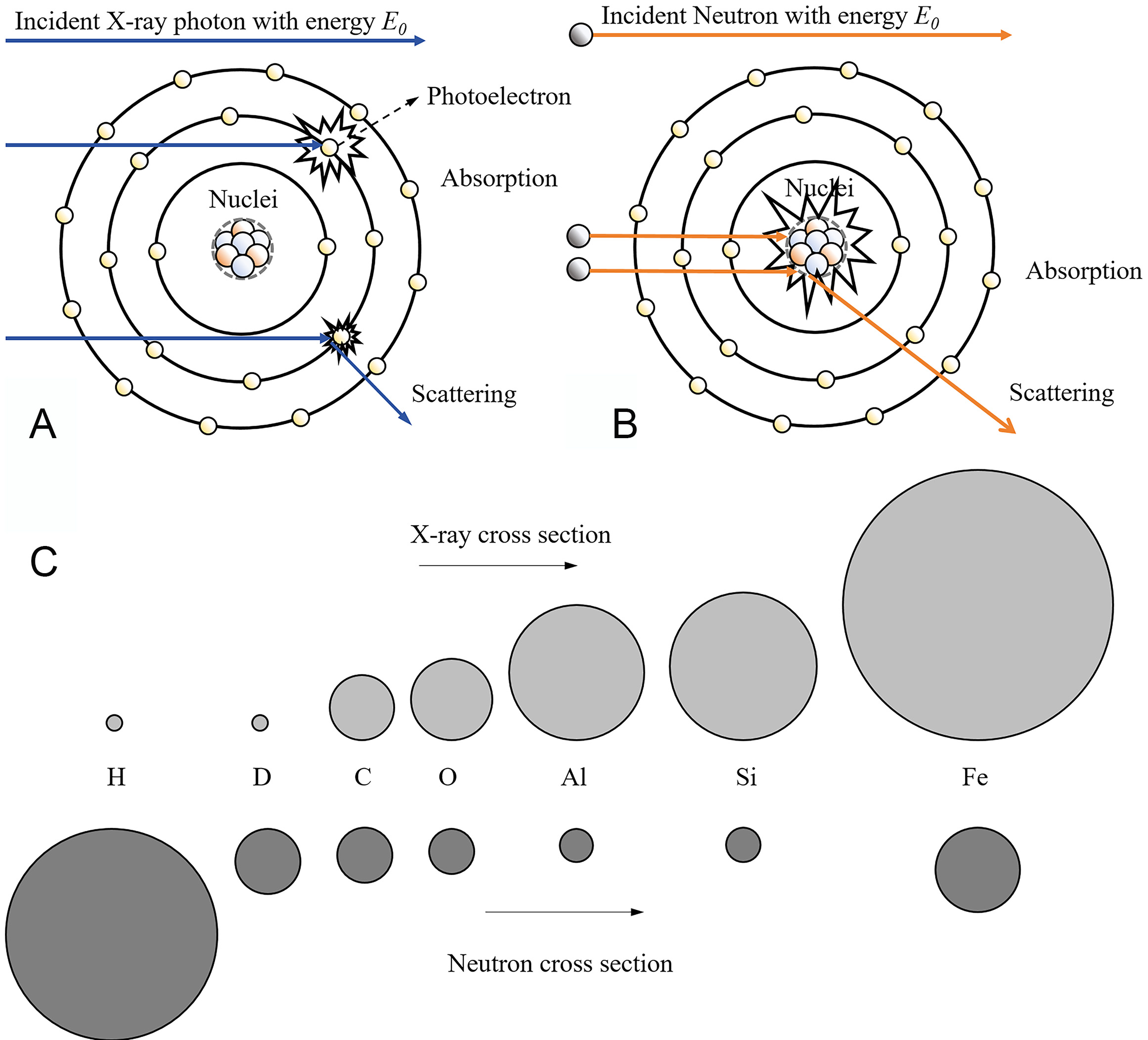
Neutrons have a unique property: they are electrically neutral. This allows them to form beams that carry no charge, making them highly useful for neutron imaging^[15]. Unlike X-rays, which interact with the electrons in atoms, neutrons only interact with atomic nuclei due to their neutral charge. While both X-ray and neutron imaging share some basic principles, such as the variation in mass attenuation coefficients across different materials, the interaction mechanisms of neutrons and X-rays with matter are different, leading to distinct mass attenuation coefficients. X-ray attenuation is directly related to the number of electrons outside the atomic nucleus, increasing as atomic number rises. In contrast, neutrons attenuation is influenced by more complex processes and their attenuation coefficients are not dependent on the atomic number. The distribution of neutron attenuation coefficients is independent of atomic number and can be utilized to distinguish isotopes (for instance, ¹H and ²H)^[16].

Research indicates that at a temperature of 473 K, the total neutron cross section of light water and heavy water, assessed using thermal neutrons at 25.3 meV, exhibits a considerable difference, nearly two orders of magnitude apart^[17]. The main reason for this discrepancy is that the atomic nuclei of the two substances have different masses, which influences how momentum and energy are transferred during elastic scattering. Inelastic scattering, on the other hand, is affected by changes in the energy levels of the nuclei. Additionally, in terms of absorption cross section, deuterium exhibits a lower neutron capture probability. This enables neutron techniques to distinctly differentiate between two materials, despite their identical electron configurations. Neutron-nucleus interactions can be divided into two fundamental categories that collectively determine the neutron cross section σ: (i) absorption cross section (σ_a), characterized by neutron capture via nuclear reactions; and (ii) scattering cross section (σ_s), which is governed by the exchange of momentum with atomic nuclei. The scattering cross section is further divided into coherent elastic scattering (similar to Rayleigh scattering of X-rays), incoherent elastic scattering (Thomson scattering), and inelastic scattering (Compton scattering). In liquid system with short-range order and long-range disorder, scattering dominates and behaves depending on energy. At low energy (E < 1 meV), elastic scattering occurs with minimal transfer; at intermediate energies (1 meV < E < 0.1 eV), quasi-elastic scattering prevails, especially in liquids containing light elements; and at higher energies (E > 0.1 eV), inelastic scattering, which causes molecular vibrations, becomes important. Additionally, light elements have a greater impact on these interactions due to their large scattering cross section^[18]. In multiphonon (solid) state, the inelastic scattering component of neutron interactions is predominantly modulated by the phonon density of states (DOS). The scattering cross section increases with the DOS, as seen in metals and their hydrides. Also, higher temperatures lead to more thermally excited phonons, increasing multiphonon scattering cross section^[19]. X-rays interact with matter in several ways, including the photoelectric effect, Rayleigh scattering, Compton scattering, and electron-positron pair formation, all of which are caused by interactions with electrons in atoms. Neutrons, on the other hand, interact directly with atomic nuclei. Figure 1A and B shows how X-rays and neutrons interact with matter in different ways^[2]. Table 1 demonstrates that hydrogen has a much greater neutron cross-section than other materials. Thus, it is theoretically demonstrated that neutron attenuation imaging has an extremely strong characterization capability for hydrogen in metals^[20]. The comparison between the reaction ability of X-rays with matter and the cross section of the interaction between neutron beams and matter is depicted in Figure 1C.

Figure 1. Comparison of the interaction of X-rays and neutron beams: (A) interaction with atom, (B) the relative cross sections of common elements, (C) cross sections of common elements^[2].

There are two major ways in which neutrons interact with atomic nuclei: absorption and scattering. The total neutron cross section is the sum of these two interactions. When a neutron is absorbed by a nucleus, it usually emits gamma rays, which account for a definite portion of the total cross section. Scattering, on the other hand, occurs when a neutron collides with a nucleus and changes its energy and direction without being absorbed. The spin state of hydrogen molecules has an effect on scattering^[18]. Neutron energy also affects scattering; as neutron energy increases, i.e., from cold neutrons (μeV-meV) to epithermal neutrons (eV-keV), the scattering cross section changes from the bound-nucleus value to the free-nucleus value^[19].

Neutron beams irradiate objects and are attenuated through absorption and scattering by the objects. The attenuation of the incident neutron beam depends on the thickness and elemental composition of the sample. Neutron attenuation imaging is based on the Beer-Lambert law, as given below^[21]:

where I indicates the intensity of transmitted intensity, I₀ represents the incident intensity, ∑_t stands for the neutron attenuating cross section, and x denotes the thickness of the target material.

Neutron imaging has long been used to determine hydrogen content in metal samples by analyzing the attenuation of a neutron beam as it passes through the specimen. The extent of attenuation reflects the overall hydrogen concentration within the material. The attenuation coefficient is a critical parameter in neutron imaging studies. The mean attenuation coefficient of hydrogen is typically higher than that of metallic materials, primarily due to the incoherent scattering of hydrogen^[22]. The incoherent scattering cross section of neutrons with hydrogen nuclei is very large; therefore, the presence of hydrogen significantly increases the attenuation of materials to neutrons. Differences in attenuation coefficients enable the effective detection of hydrides by measuring neutron beam attenuation as it passes through a sample. In studies quantifying hydrogen concentration in metallic materials, the neutron transmission relationship defines T^[23]:

where I_dc indicates dark current, the detector signal in the absence of neutrons, I_ob denotes the open-beam intensity without the sample, ∑_total represents the total macroscopic neutron cross section of the material, and s signifies the neutron path length through the sample. In the confined state, strong external potential forces restrict the movement of hydrogen nuclei. Within the lattice of metal hydrides, hydrogen nuclei oscillate around their equilibrium positions. In contrast, in water molecules, hydrogen nuclei form strong covalent bonds with oxygen atoms and weaker hydrogen bonds with neighboring molecules, which limit their mobility. The bound-state scattering cross-section (σ_bound) exhibits a strong environmental dependence. The σ_bound of hydrogen in zirconium hydride (ZrH_X) varies with the peak position of the lattice phonon DOS and is lower than the scattering cross-section in the free state. In the free state, hydrogen nuclei are completely unbound from external constraints and exist as freely mobile atoms. At this stage, the interaction between neutrons and hydrogen nuclei is dominated solely by nuclear forces, with the influence of confining potentials becoming negligible. The free-state scattering cross-section (σ_free) thus exhibits a significantly simplified energy dependence. In general, the neutron cross section shows an inverse dependence on energy, with distinct behaviors observed across three energy regimes: (1) In the lower energy range (E < 1 eV), the absorption cross section increases as the neutron velocity decreases, since the probability of absorption is inversely proportional to the neutron velocity (v). The scattering cross section in this regime is predominantly governed by coherent scattering, akin to Rayleigh scattering of photons, where the scattered waves maintain phase correlation. This phenomenon leads to diffraction effects due to the matching of neutron wavelengths with atomic spacing in crystalline structures; (2) In the medium energy range (1 eV < E < 0.1 MeV), the probability of neutron capture is significantly enhanced when the neutron energy matches the energy of the nuclear excited state, resulting in the formation of highly unstable compound nucleus. In resonant scattering, neutrons are temporarily captured by the nucleus and subsequently re-emitted (inelastic scattering), causing the scattering cross section to vary sharply with energy; (3) At high energies (E > 0.1 MeV), the interaction time between the neutrons and atomic nuclei is reduced, which leads to lower probability of interaction, thereby decreasing the neutron cross section^[17]. The empirically determined macroscopic cross-section in Equation (2) facilitates quantitative hydrogen characterization in materials. Then, for the hydrogen-containing materials^[24]:

where ∑_metal denotes the cross section of metal, σ_H represents the microscopic cross section of hydrogen, and N_H stands for the atomic number density of hydrogen. To enhance statistical efficiency and simplify the neutron transmission and hydrogen concentration relationship, uniform the thickness of metal for both calibration and experimental specimens^[25]. This refinement not only improves statistical accuracy but also yields a simplified exponential model:

where a denotes the neutron transmission of the hydrogen-free material, b represents the neutron sensitivity coefficient which depends on material and c_H signifies hydrogen concentration in wppm.

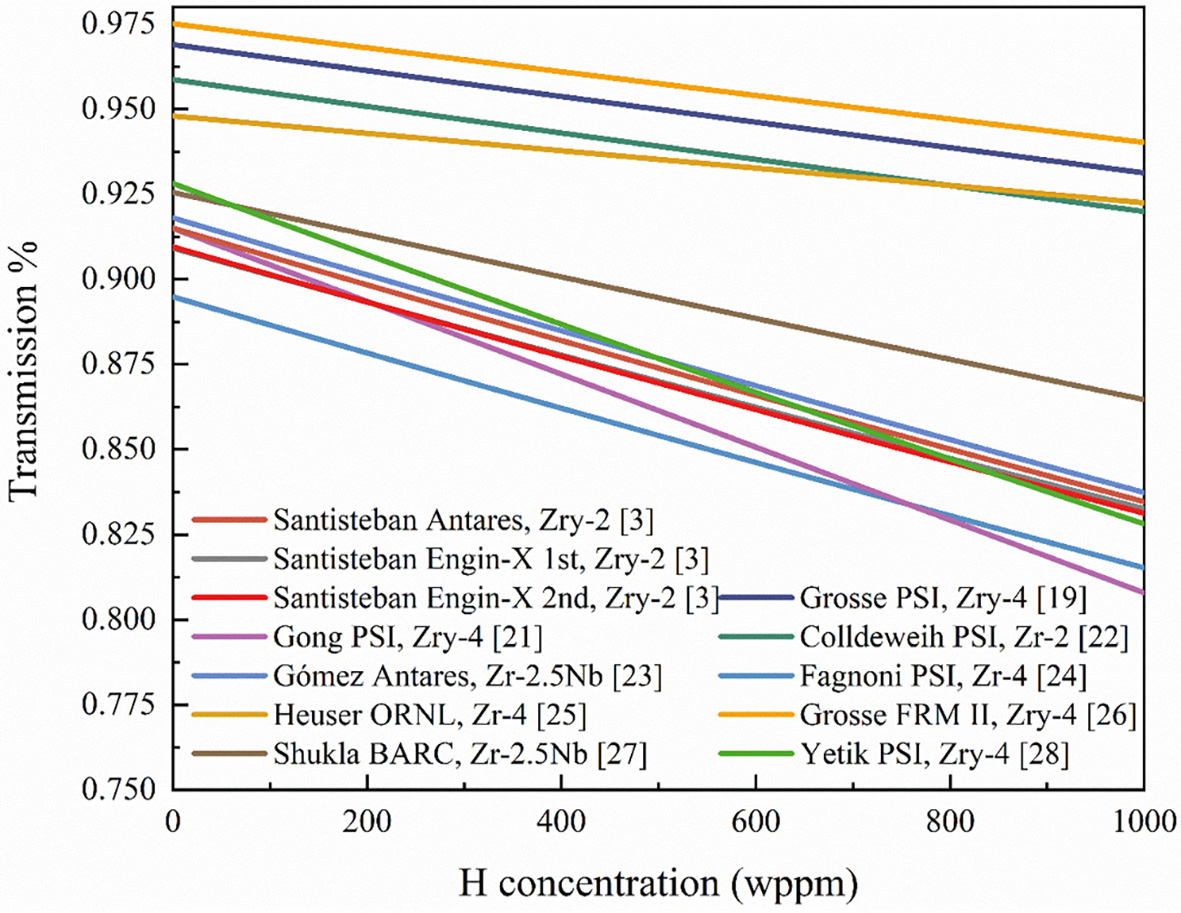
Numerous quantitative studies on hydrogen in zirconium alloys have shown that the calibration formulas used may exhibit minor deviations from Equation (4) when applied as calibration curves. In this review, experimental data are organized according to Equation (4), assuming a sample thickness of 4 mm unless otherwise specified. Figure 2 shows that the relationship between transmission and hydrogen concentration is nearly linear in the range of 0-1,000 wppm. The intercept indicates the absence of hydrogen in the material, while the slope reflects the sensitivity of the material to neutrons. Variations in material properties affect both the initial neutron transmission and the attenuation caused by hydrogen. Likewise, changes in material thickness influence its sensitivity to hydrogen. This conversion formula facilitates the description of hydrogen distribution and concentration in metals and hydrogen storage systems.

Figure 2. Exponential relationships of transmission and hydrogen concentration in zirconium from different papers^[3,23,25-32].

The attenuation coefficient is an intrinsic property of the material and is related to the neutron energy E or the equivalent neutron wavelength λ. For zirconium hydride, when λ 0.2 Å, its incoherent scattering behaves as the inelastic scattering of nearly free protons, and the attenuation coefficient remains basically constant. As the wavelength increases, oscillations appear. The thermal neutron interaction in zirconium hydride (ZrH_x) is dominated by the dynamics of bound hydrogen in the lattice, primarily through incoherent inelastic scattering from hydrogen. Its characteristics are determined by the vibrational modes of hydrogen in the lattice (acoustic and optical branches)^[17]. For λ 3 Å, the attenuation of hydrogen strongly depends on temperature due to the inelastic scattering process in which neutrons gain energy during collisions^[3]. Under identical testing conditions, variations in the attenuation coefficient for hydrogen concentration between different materials are primarily governed by disparities in hydrogen density within their hydride phases. For instance, titanium, which has a similar crystal structure to zirconium, exhibits distinct macroscopic cross sections at the same hydrogen concentrations^[13]. Consequently, material-specific calibration procedures are essential during quantitative measurements. These wavelength-related characteristics provide more evidence for the precise detection of hydrides. For instance, by choosing a neutron beam of an appropriate wavelength for the experiment, the presence and distribution of hydrides can be detected more sensitively^[3]. The primary source of variation in the attenuation coefficients of different hydride phases is the disparity in hydrogen density. Under identical conditions, hydride phases with higher hydrogen density exhibit stronger neutron attenuation and higher attenuation coefficients. This difference is crucial in practical research. For example, in the analysis of zirconium alloys containing different hydride phases, variations in hydrogen density can lead to significant differences in neutron imaging results^[7]. By measuring and analyzing the attenuation coefficient, both the presence and concentration of different hydride phases can be inferred.

HYDROGEN IN METALLIC STRUCTURAL MATERIALS

Zirconium alloys

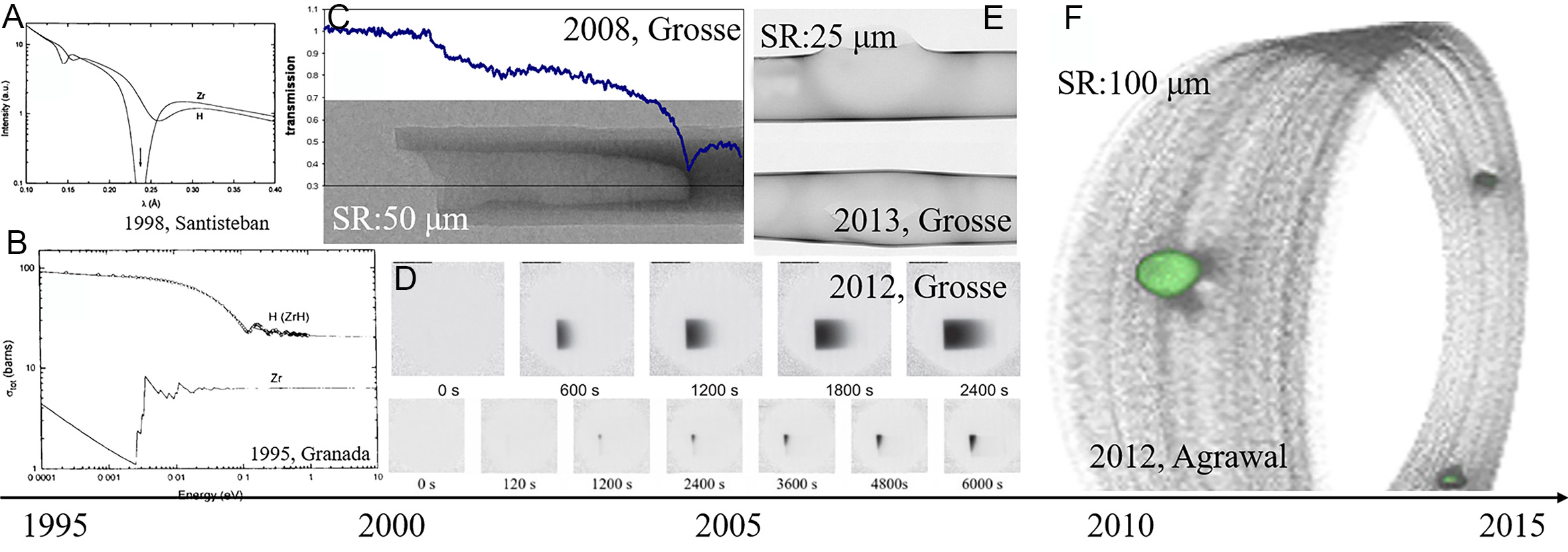
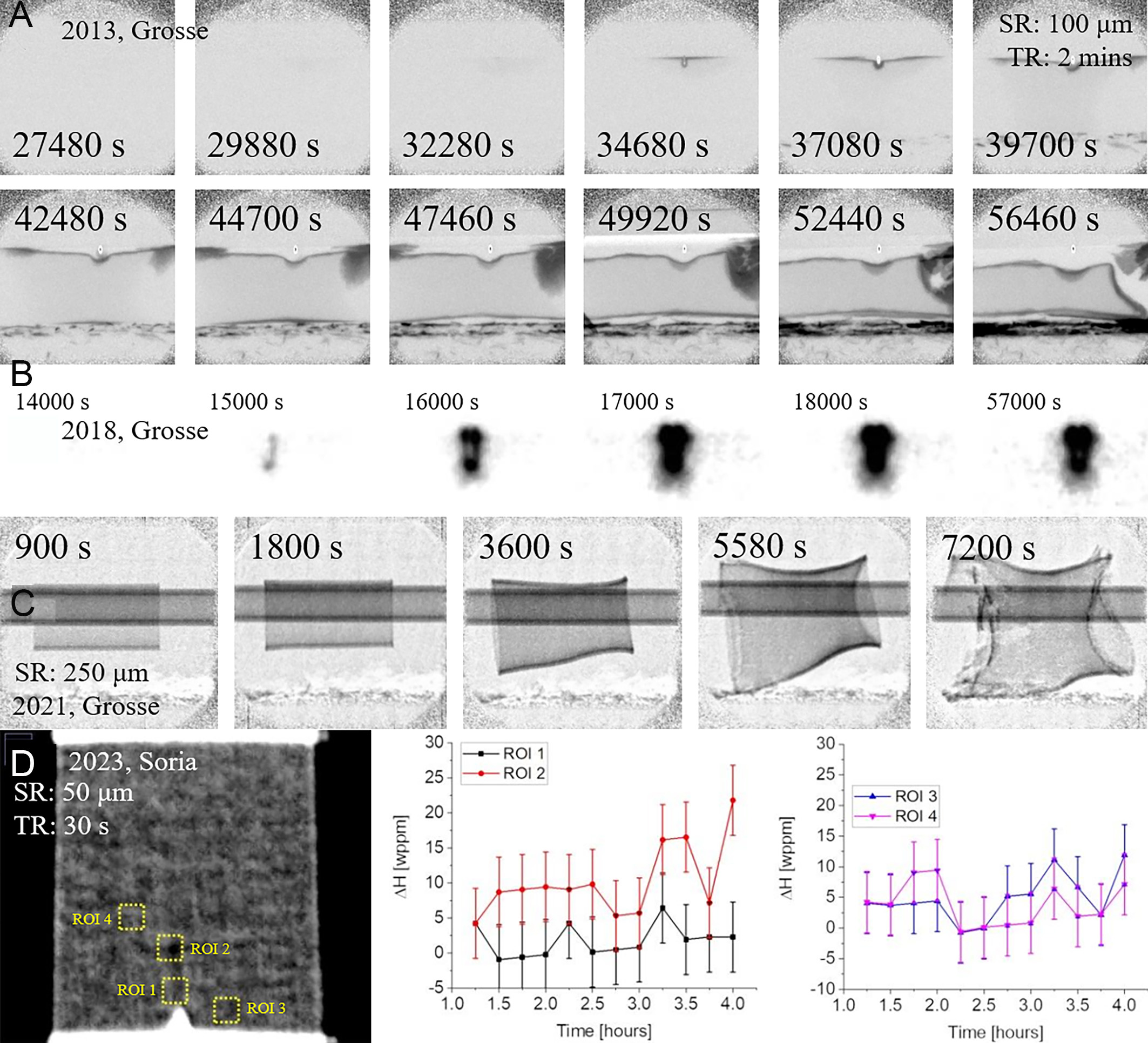
Zirconium alloys are widely employed as nuclear fuel cladding tubes and pressure tubes in reactor systems due to their exceptional corrosion resistance and neutron transparency. Under in-service conditions, these alloys are subject to waterside corrosion when exposed to coolants, generating hydrogen that penetrates through the protective oxide layer and into the matrix. As hydrogen accumulates at the cladding surface, it exceeds the local solubility limit, leading to hydride precipitation. This process significantly compromises the mechanical integrity of the cladding by inducing embrittlement and volume expansion, which increases the risk of nuclear fuel leakage. Therefore, investigating the behavior of hydrogen dissolution and diffusion in zirconium alloys is crucial for predicting the thresholds for hydride formation, optimizing cladding performance, and ensuring the operational safety of nuclear reactors. Neutron imaging has become an essential tool in addressing critical issues such as hydrogen diffusion and HID in zirconium alloys, offering unique advantages due to its sensitivity to light elements, strong penetration capabilities, and non-destructive detection methods^[2]. The characterization of hydrogen in zirconium using neutron beams was first validated by Bennun et al.^[33] through neutron cross section measurements, diffraction studies^[10], and imaging experiments on zirconium alloys and hydrides conducted between 1995 and 2004, as shown in Figure 3A-C^[34-36]. The pioneering work by Grosse et al. further demonstrated the potential of neutron imaging for in-situ studies under high-temperature conditions, providing qualitative characterizations of hydrogen pickup and redistribution processes^[37,38]. These studies examined hydrogen diffusion at elevated temperatures, steam oxidation dynamics, and Loss of Coolant Accidents (LOCA), highlighting the technique’s advancement in hydrogen detection, achieving high hydrogen concentrations up to 2,600 wppm and spatial resolutions ranging from 25 to 100 μm, as shown in Figure 3D and E^[39-42]. Agrawal et al. expanded on this work by using neutron imaging to map hydride blister distributions in zirconium alloys, distinguishing tomography images of samples with hydrogen concentrations of 25, 50, 75, and 100 wppm at a spatial resolution of 100 μm^[43]. This marked an early quantitative analysis of hydrogen concentration with a resolution of 25 wppm. Agrawal et al. also localized blister morphology, laying the groundwork for further quantitative hydrogen concentration analysis, as shown in Figure 3F^[43]. Since Grosse et al. established the quantitative relationship between hydrogen concentration and neutron cross section in 2008^[23], neutron imaging has progressed from static characterization to dynamic in-situ analysis, achieving sub-micron resolution. Over the past 15 years, breakthroughs in spatial resolution, hydrogen detection limits, temporal resolution, and multi-physics coupling capabilities have redefined the technology’s role in materials science.

Figure 3. Neutron imaging development from 1995 to 2015: (A) the neutron scattered time of flight spectra by H and Zr^[35], (B) cross sections of Zr and H in ZrH alloy^[34], (C) neutron images of Zr-1Nb rod^[23], (D) hydrogen diffusion at 1,273 K and 823 K in Zr-4^[39], (E) 3D volume of pressure tube with blisters^[37], (F) 3D tomography of the hydride blister in Zr-2.5Nb^[43].

Grosse et al. found the linear association between neutron cross section and hydrogen concentration between 2008 and 2014. Although the relationship is subject to the influence of multiple factors, it establishes the physical foundation for quantitative neutron imaging^[23]. Agrawal et al. transitioned from qualitative observation to quantitative application in zirconium hydride research, achieving a detection accuracy of 25 wppm^[43]. Smith et al. rebuilt three-dimensional hydrogen distributions in Zr-4 alloys subjected to temperature gradients (13-1,096 wppm) to illustrate temperature-induced hydrogen segregation mechanisms as in Figure 4A^[44].

Figure 4. Neutron imaging resolution of hydrogen in Zr alloys optimizing with time: (A) 3D uneven hydrogen distribution in Zr-4^[45], (B) hydrogen concentration of hoop stress tube^[29], (C) tomographic hydrogen concentration distribution of clad segment^[45], (D) hydrogen concentration in two inhomogeneous Zr-2.5Nb^[3], (E) transmission of thermo-mechanical tested Zr-4 and stress field near the notch^[46], (F) transmission imaging of the duplex cladding tubes^[25], (G) annealed Zr-2.5Nb for displaying hydrogen diffusion^[31], (H) hydrogen concentration maps for samples after annealed^[27], (I) DHC in Zr-2 with integral 200 wppm hydrogen^[26], (J) optical micrograph of Zr-2.5Nb annealed samples for diffusion rate and hydrogen concentration obtained by quantitative neutron imaging^[32], (K) transmission imaging of the images of Zr-2 based cladding^[49], (L) strain and hydrogen distribution maps of Zr-4 tensile samples^[51].

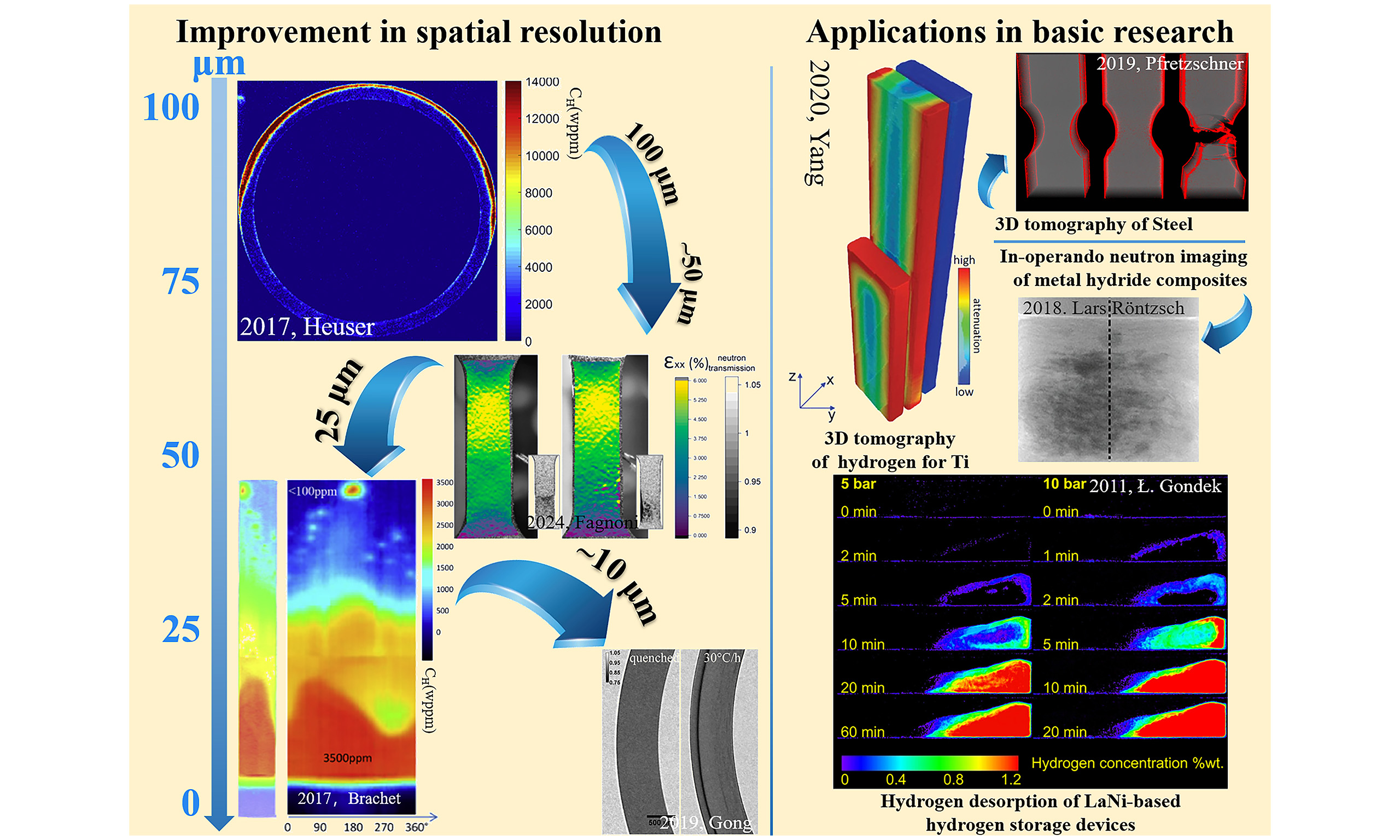
The resolution of pictures and the sensitivity to hydrogen were improved between 2015 and 2020. Brachet took 25 μm photos of clad hydrogen pick up in LOCA in Figure 4B and 4C. Heuser, on the other hand, employed 100 μm resolution imaging to explore stress-induced anisotropic hydrogen diffusion under hoop stress^[29,45]. A milestone emerged in 2018 when Santisteban integrated multi-beamline data to achieve 25 μm spatial resolution and hydrogen resolution (HR) of 5 wppm, proving the technique’s reliability for low-concentration samples (< 10 wppm) in Figure 4D^[25]. Meanwhile, Gong attained 10 μm spatial resolution and 9 wppm in sensitivity [Figure 4E and F] in hydrogen diffusion studies under stress and chemical potential gradient, enabling hydrogen behavior analysis at micron-scale level and in 2022 revealed the influence of stress-driven conditions on hydride precipitation, demonstrating the inhibitory effect of compressive stress on hydride formation^[3,25,46]. Additionally, the results of finite element modeling (FEM), which analyzes stress distribution, can demonstrate the distribution states of tensile and compressive stress. The hydride redistribution integrates with stress distribution, better corroborating the interactive effect of tensile and compressive stresses during hydride formation^[47].

In the past five years, breakthroughs in neutron imaging have significantly advanced the quantitative characterization of hydrogen behavior in metallic systems, particularly in terms of spatial resolution, detection sensitivity, and multi-physics coupling. One notable example is Shukla’s pioneering high-resolution diffusion studies, which achieved a spatial resolution of 100 μm and a hydrogen detection limit of 17 wppm. These advances enabled accurate tracing of hydrogen diffusion rates. Neutron imaging also revealed fine-scale hydrogen gradients [Figure 4G], providing five times more data compared to conventional metallography^[31]. In 2023, Gómez et al. & Stella et al. improved dynamic hydrogen monitoring by achieving a spatial resolution of 33 μm and a hydrogen quantification sensitivity of 10-25 wppm. This advancement enabled direct observation of hydrogen migration during diffusion cycles [Figure 4H]^[27,48]. Furthermore, in the context of microscale hydrogen-induced delayed hydride cracking (DHC), Colldeeweih reached an unprecedented spatial resolution of 8.1 μm, allowing micron-scale visualization of hydrogen aggregation fronts [Figure 4I]^[26]. Weick & Grosse pushed spatial resolution below 10 μm with hydrogen quantification limitation approaching a few wppm, setting new benchmarks for nanoscale hydrogen mapping^[7]. The quantification limitation improvement achieved by Shukla employed advanced signal processing algorithms to as low as 5 wppm, enhancing sensitivity for low-concentration hydrogen analysis in complex alloys in Figure 4J^[32]. Multi-physics coupling capabilities in hydrogen quantitative characterization: Duarte et al. combined 10 μm spatial resolution with 10 wppm hydrogen quantification resolution to uncover interface-induced hydrogen diffusion barriers in Zr-2 alloys, linking microstructural features to hydrogen trapping efficiency in Figure 4K^[49]. In 2023, Konarski et al. further characterized such diffusion barriers using neutron imaging and developed a modeling approach, which clearly revealed hydrogen diffusion, hydride dissolution/precipitation, and the hydrogen solubility difference between the substrate and liner^[50]. In addition, Fagnoni et al. integrated hardness mapping in 9.6 μm resolution and hydrogen-strain field synchronization (47 μm/9 wppm) to correlate hydrogen distribution quantitatively with mechanical degradation during plastic deformation, offering mechanistic insights into HE [Figure 4L]^[51].

In the advancement of neutron imaging technology, improvements in scintillator materials and upgrades in detector design have played a pivotal role. The new scintillator ¹⁵⁷Gd₂O₂S:Tb, combined with iridium coating materials, can improve light output efficiency while maintaining resolution and neutron absorption capacity^[52]. Moreover, enlarging the numerical aperture of magnifying optical instruments can improve resolution by 30%, attaining a spatial resolution of 5 μm^[53]. Recent studies indicate that a high numerical aperture enhances spatial resolution, whereas variable optical magnification mitigates inelastic and incoherent Moiré effects arising from varying pixel sizes for distinct events^[54].

In 2013, LOCA simulations highlighted the trade-off between short exposure times (2 min) and spatial resolution degradation, with ex-situ studies achieving 100 μm, whereas in-situ studies reached 25 μm, as shown in Figure 5A. Subsequent optimization of the optical system enabled in-situ oxidation monitoring at 25 μm spatial resolution^[40]. Grosse et al. further demonstrated the non-destructive advantage of neutron imaging by dynamically characterizing hydrogen distributions under coupled mechanical stress-thermal-gas field conditions at 350 °C, achieving a spatial resolution of 25 μm in Figure 5B^[55]. However, increasing the sample-detector distance to 225 mm was found to degrade the resolution to 250 μm [Figure 5C]^[56], emphasizing the importance of optimized beamline design in multi-physics experiments. By 2023, Gómez et al. advanced real-time neutron imaging capabilities, achieving 33 μm spatial resolution, 10 wppm sensitivity, and 30 s time resolution in hydrogen diffusion studies^[27]. In the same year, Soria et al. maintained 50 μm spatial resolution with 30 s imaging intervals to analyze DHC in Zr-2.5Nb, as shown in Figure 5D^[57]. Stella et al. later developed a 15-min effective temporal resolution via 30-frame image stacking while retaining 33 μm spatial resolution, enabling long-term monitoring of DHC processes^[48]. Additionally, ancillary equipment for neutron imaging is evolving rapidly. Notably, a mobile imaging system based on accelerator-driven neutron sources has been developed to perform both thermal and fast neutron imaging and tomography^[58], significantly enhancing experimental versatility across diverse conditions.

Figure 5. In-situ neutron imaging of Zr alloys: (A) mechanical stress-Ar/H₂ and 350 °C conditions coupling for Zr-4^[38], (B) mechanical stress-inert annealing in Ar/H₂ at 350 °C for hydrogen diffusion^[55], (C) nitrogen/steam atmosphere for Zr-4 swelling^[56], (D) end image of in-situ DHC test for Zr-2.5Nb^[57].

In summary, neutron imaging technology has advanced rapidly. Continuous improvements in in-situ characterization equipment have enabled precise control of stress and temperature during experiments, while also significantly enhancing image quality and hydrogen detection resolution^[59]. Spatial resolution has improved more than 30-fold, from above 100 μm in 2008 to below 10 μm in 2024, and hydrogen detection limits have decreased fivefold, from 25 wppm to less than 5 wppm. Despite these advances, trade-offs remain: for example, Stella’s 33 μm resolution required compromising sensitivity at 25 wppm, reflecting persistent limitations in neutron flux and detector efficiency^[3]. In addition, multi-field interferences - such as thermally and mechanically induced geometric distortions - reduced resolution by up to 40% in the 2024 study by Grosse. Hydrogen continues to exert a profound influence on metals, particularly in clean energy applications, where accurate characterization of hydrogen in metallic materials remains a major challenge. Neutron imaging has therefore emerged as a powerful and rapidly evolving tool to address this issue^[60]. Furthermore, the concept of hydrogen concentration resolution has recently been introduced. Derived from transmission measurements, it allows detection of hydrogen concentrations down to approximately 5 wppm, although this represents a statistical average over bulk material rather than variations at individual local points.

Titanium alloys

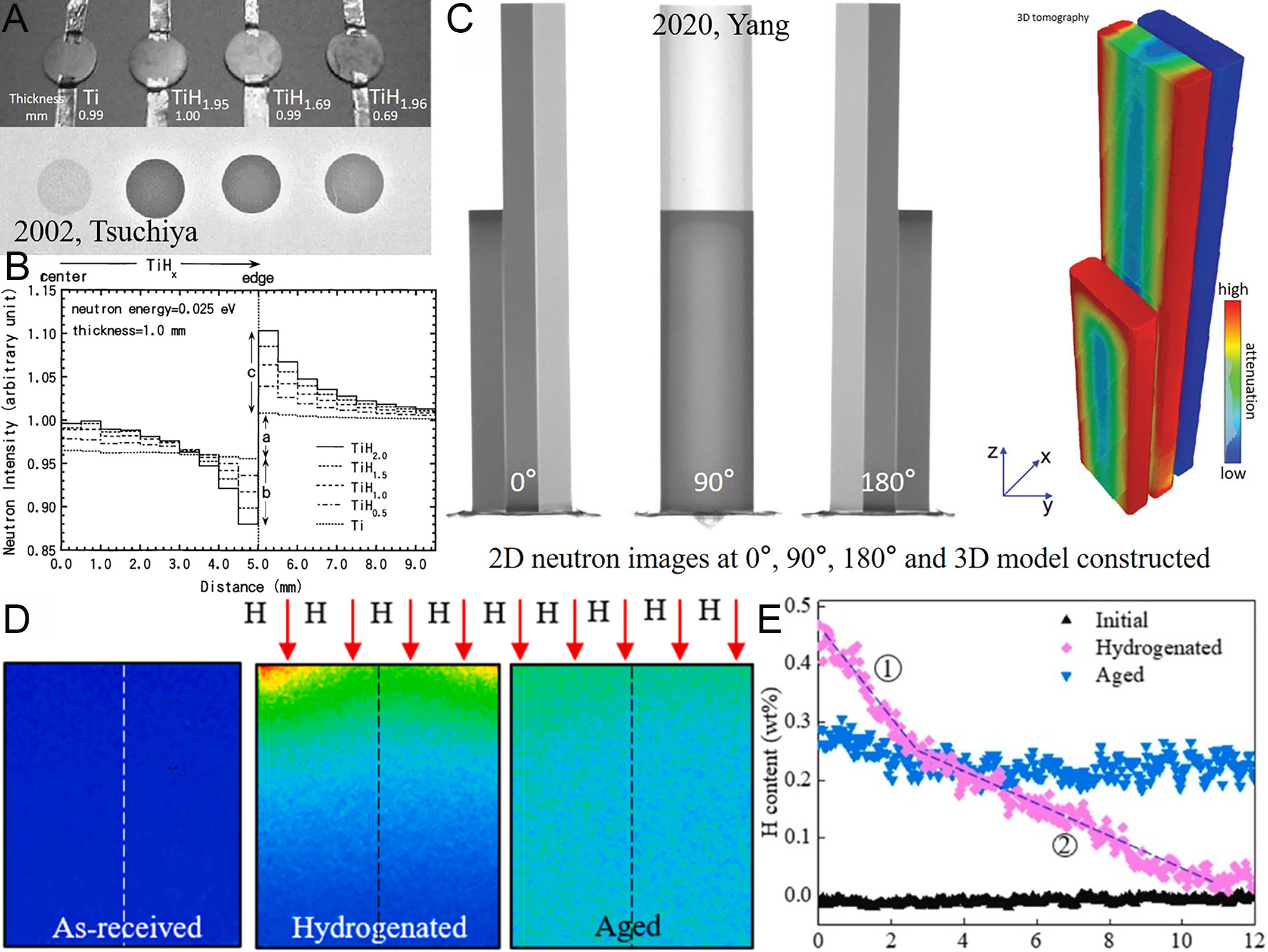
Titanium, extensively applied in aerospace, biomedical engineering, marine exploration, and the nuclear industry^[61-64], exhibits hydride formation behaviors similar to those observed in zirconium alloys. Hydrogen in titanium alloys degrades mechanical properties through the formation of hydride phases^[65]. However, targeted heat treatments can partially restore mechanical performance. These thermal processes facilitate hydrogen desorption while promoting the dissolution and redistribution of hydride phases. Therefore, understanding hydrogen distribution and diffusion kinetics in titanium alloys is crucial for optimizing post-hydrogenation recovery strategies and ensuring structural reliability^[66]. The relatively low neutron cross-section of titanium further enhances its suitability for neutron imaging studies^[2]. Initial experiments on titanium hydrides in 2002 demonstrated a systematic decrease in neutron transmission with increasing hydrogen concentration, accompanied by edge effects, wherein peripheral regions exhibited higher brightness compared to central areas and background. These effects intensified with increasing hydrogen content as shown in Figure 6A and B^[67]. In 2020, 3D neutron tomography enabled quantitative characterization of hydrogen gradient distributions in titanium alloys, revealing higher hydrogen concentrations at surfaces compared to interiors and dynamically tracking hydrogen diffusion pathways during thermal hydrogenation processing (THP) [Figure 6C]^[68]. By 2025, neutron imaging elucidated the dominant role of β-phase in early-stage hydrogen diffusion, with rapid hydrogen migration through β-phase channels resulting in non-uniform distribution at diffusion fronts. Quantitative comparisons of hydrogen concentrations before and after aging treatments [Figure 6D and E] provided experimental evidence of phase-transition-diffusion coupling mechanisms in titanium-hydrogen systems^[69]. Kumar et al.’s 2025 study further characterized the radial uniformity of hydrogen distribution and the decreasing concentration gradient from surface to interior in hydrided titanium alloys during corrosion, demonstrating that MgZnCa coverage at the center impedes hydrogen diffusion^[70]. Thermal neutrons (energy < 0.5 eV) and cold neutrons (energy < 5 meV) can be employed for imaging metallic materials at a centimeter scale or smaller. With technological advancements, neutron imaging has progressed from qualitative observations to a multiscale, quantitative analytical tool^[71].

Figure 6. 2D neutron images and 3D tomography of titanium: (A) transmission images^[67], (B) neutron intensity on the imaging plate^[67], (C) 2D imaging projections and reconstructed 3D model^[69], (D) hydrogen distribution maps^[68], (E) hydrogen concentration curves along diffusion distance^[68].

Future research should integrate neutron imaging with phase-field simulations and synchrotron-based characterization to elucidate the dynamic evolution of titanium hydrides. Such multimodal approaches will connect mesoscale hydrogen distribution patterns with atomic-scale structural changes, ultimately enabling predictive modeling of hydrogen-induced degradation in titanium alloys under service conditions.

Steels

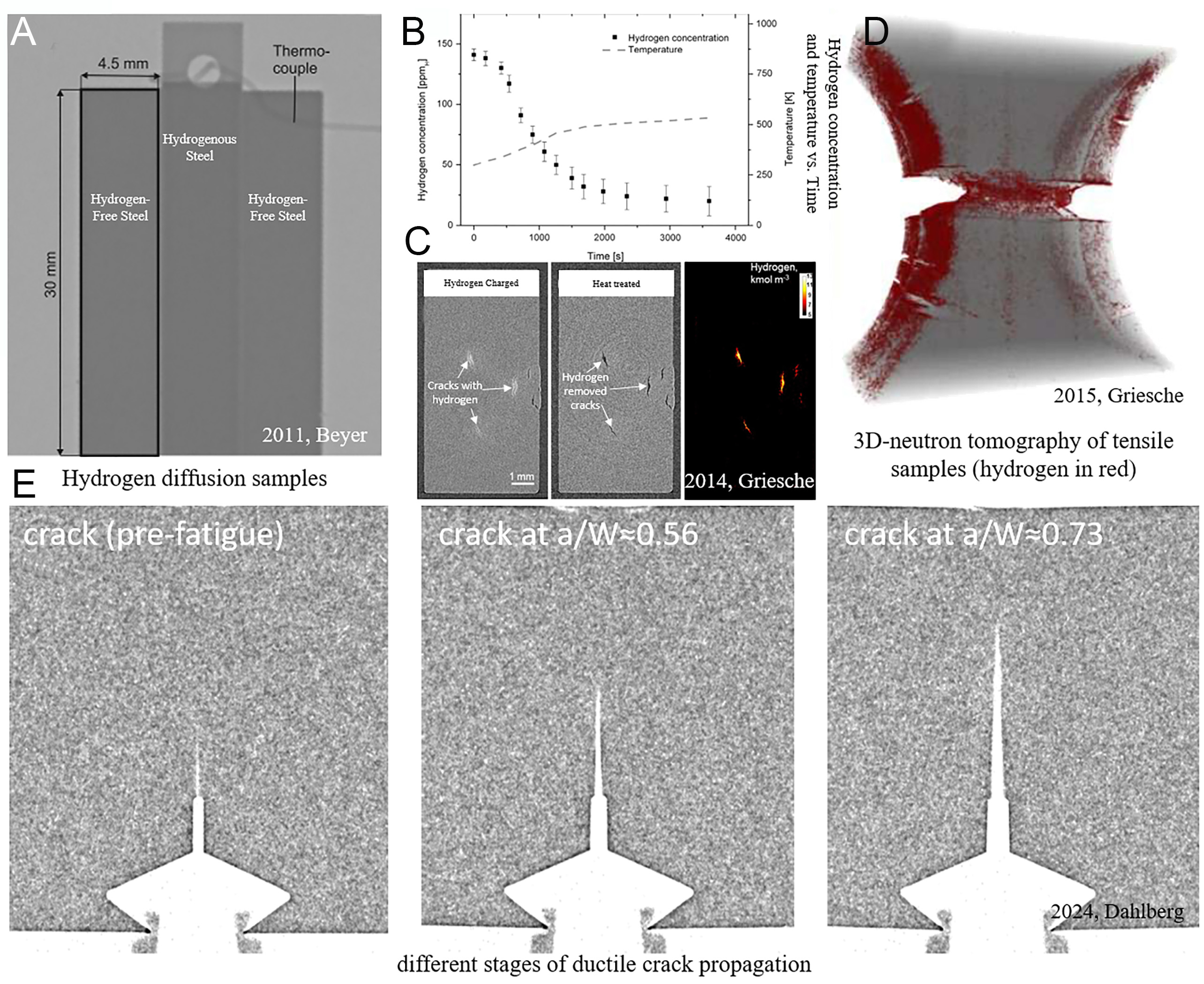
Steel components operating in hydrogen-rich environments, such as hydrogen storage tanks, absorb hydrogen through mechanisms involving hydrogen transport, stress fields, and localized accumulation, resulting in significant deterioration of mechanical properties^[72]. During welding, hydrogen dissociated from protective gases diffuses into the weld pool and becomes trapped upon solidification. When hydrogen exceeds local solubility limits, material degradation accelerates markedly. The combined influence of hydrogen and stress on defects promotes crack initiation and propagation, a phenomenon particularly pronounced in high-strength alloys. In these materials, hydrogen segregation at grain boundaries and precipitates substantially reduces fracture toughness, facilitating crack growth. A comprehensive understanding of these hydrogen-material interactions is therefore essential for optimizing welding protocols and developing effective corrosion mitigation strategies^[73]. HE in steels arises from the synergistic effects of lattice-dissolved hydrogen and hydrogen trapped at microstructural sites such as dislocations, grain boundaries, and carbide particles. Resolving these mechanisms critically depends on mapping hydrogen spatial distributions, a task for which neutron imaging offers unique advantages due to its non-destructive and hydrogen-specific detection capabilities^[74]. In 2011, neutron imaging was first applied to study hydrogen effusion rates in austenitic stainless steel^[75]. By integrating a heating unit, this study achieved synchronous in-situ monitoring of hydrogen concentration and temperature, overcoming the limitations of conventional carrier gas hot extraction (CGHE), which only measures lattice-diffusible hydrogen [Figure 7A and B]. Subsequent work in 2013 further validated the technique’s ability to capture cavity-trapped hydrogen^[76], offering a novel approach to investigate multi-state hydrogen interactions.

Figure 7. Neutron images of steels: (A) neutron images of hydrogenous and hydrogen-free steels^[75], (B) Hydrogen concentration change with time and temperature^[75], (C) hydrogen in cracks before and after heat treatment^[73], (D) 3D tomography of martensitic tensile sample (hydrogen in red)^[79], (E) different stages of ductile crack propagation^[72].

In the characterization of hydrogen-induced cracks, neutron imaging non-destructively reveals crack morphology and internal hydrogen retention. Studies on steels with high hydrogen concentrations show persistent hydrogen signals within internal cracks even after thermal treatment, providing insights into hydrogen distribution and crack geometry [Figure 7C]^[73,77,78]. Tensile experiments on austenitic and martensitic stainless steels further demonstrate hydrogen accumulation in stress-concentrated regions [Figure 7D]^[79]. However, apparent hydrogen enrichment at sample surfaces and crack edges may partially result from neutron imaging edge effects reduces penetration efficiency at boundaries rather than true hydrogen segregation^[3]. Although neutron imaging has successfully visualized delayed crack propagation in steels, analogous to DHC in zirconium alloys [Figure 7E]^[72], its detection capability faces limitations in low-hydrogen-solubility, high-mobility systems. Rapid hydrogen diffusion at crack tips often prevents the accumulation of detectable concentrations (> 10 wppm), highlighting current challenges in capturing dynamic, low-concentration hydrogen. Future research must focus on enhanced detector sensitivity and the integration of complementary techniques, such as synchrotron X-ray diffraction, to overcome spatial-hydrogen concentration resolution limits. Such advancements will enable mechanistic analysis of hydrogen aggregation at crack tips and contribute to a deeper understanding of hydrogen-assisted fracture dynamics.

SOLID-STATE HYDROGEN STORAGE MATERIALS

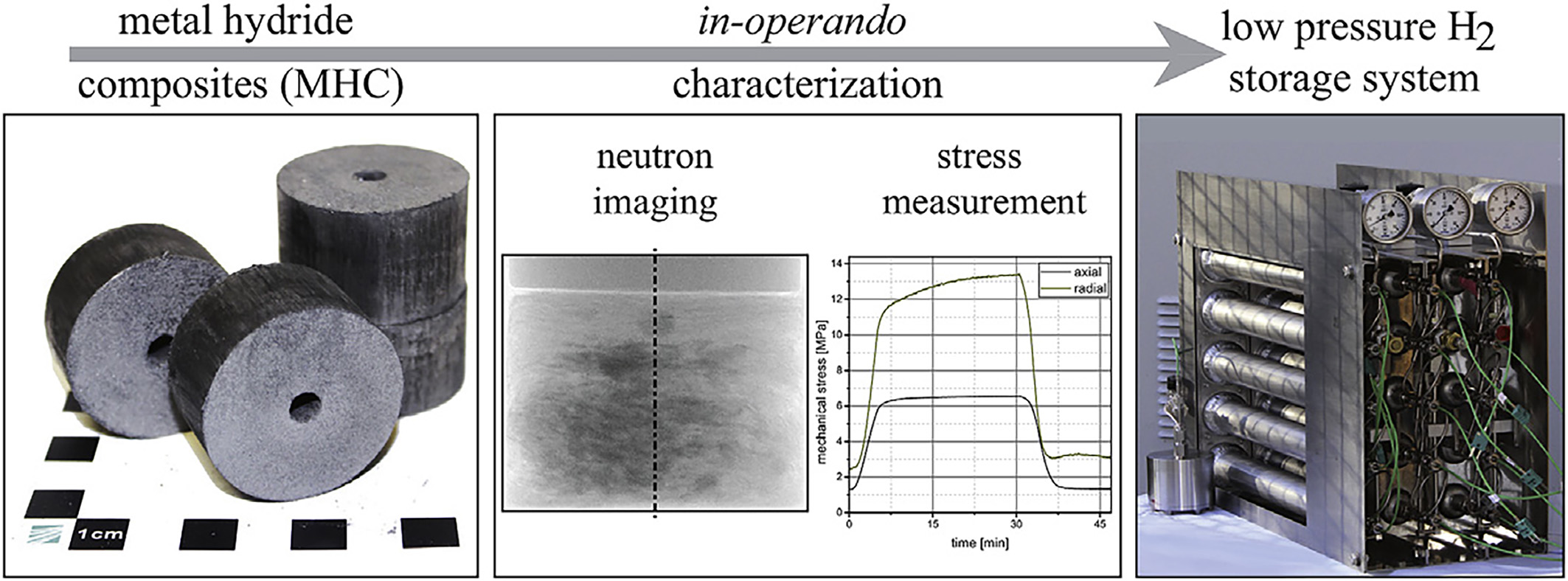
Solid-state hydrogen storage materials, which offer a promising solution for safe and efficient hydrogen storage, have garnered significant attention in recent years^[80]. These materials are generally capable of reversibly absorbing and desorbing hydrogen, rendering them ideal candidates for applications in fuel cells and other hydrogen-powered technologies. A critical challenge, however, lies in fully understanding the hydrogen evolution behavior within these storage materials - a problem particularly well-suited for investigation using neutron imaging^[81]. The design of neutron imaging systems for hydrogen storage materials requires careful consideration of factors such as neutron flux, spatial resolution, and the experimental chamber, which must accommodate the high-pressure environments typical of hydrogen storage conditions. Furthermore, neutron imaging can be integrated with complementary techniques, such as X-ray imaging and thermal analysis, providing a more comprehensive understanding of material behavior under varied operating conditions. Beyond microscopic studies, neutron imaging also informs the design and optimization of hydrogen storage tanks and enables the examination of entire hydrogen tanks filled with storage materials.

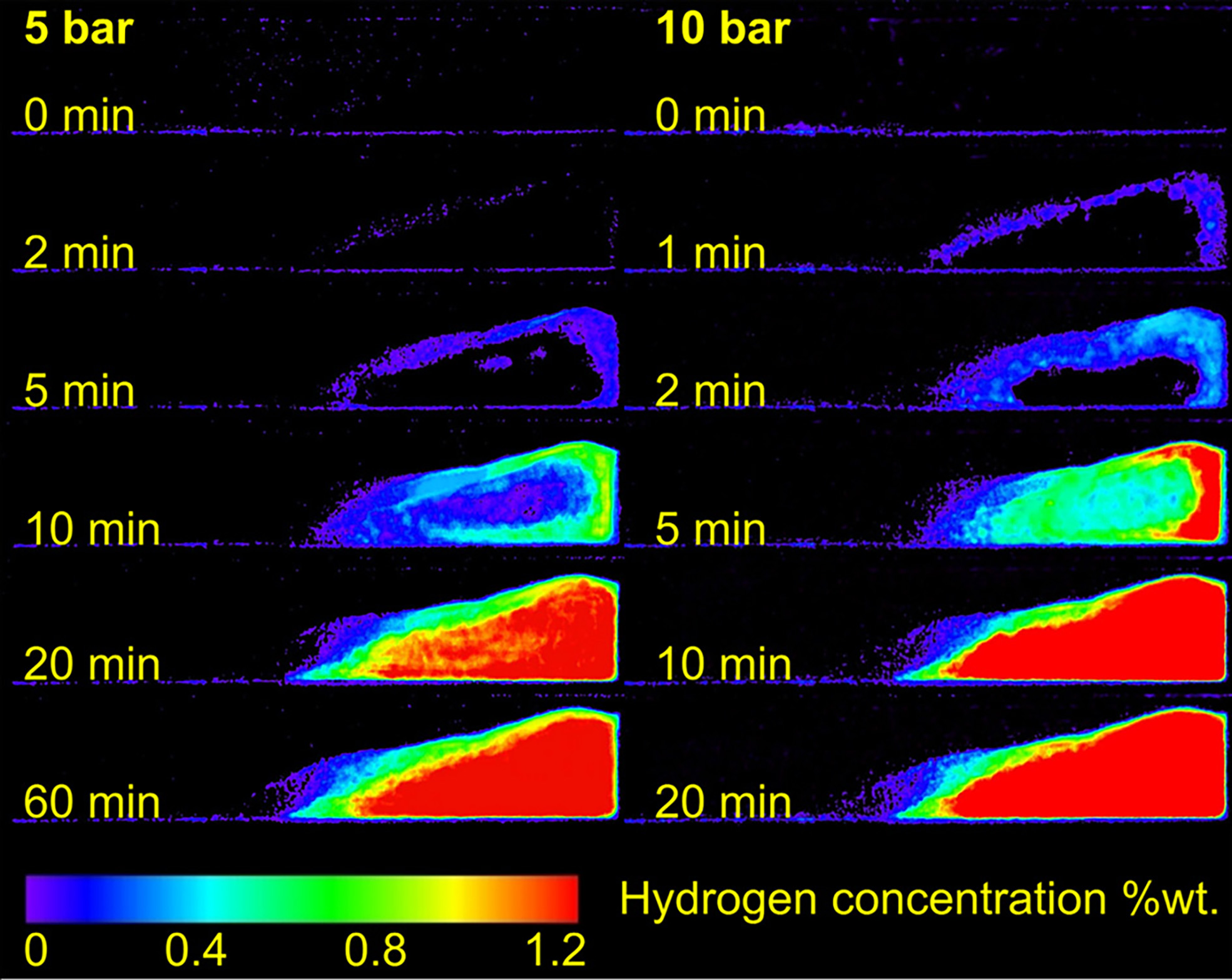
In hydrogen storage alloys, Sakaguchi et al. employed neutron radiography (NRG) and neutron computed tomography (NCT) to visualize hydrogen distribution in the hydrogenated solid solution of Mg-Ni alloys. The studies revealed that Mg₃Ni was more prone to pulverization compared to Mg₂Ni due to the formation of the MgH₂ phase^[82,83]. These investigations provided both qualitative and quantitative insights into hydrogen absorption [Figure 8] and the desorption kinetics of LaNi-based hydrogen storage materials within specific storage devices, offering valuable guidance for industrial design and the future application of onboard hydrogen storage tanks^[84-86]. In metal hydrides, Garlea demonstrated that NRG effectively captures LiH behavior, including its hydrolysis products and the thermal conversion of LiOH to Li₂O^[87]. Similarly, Röntzsch employed neutron imaging to study the structural stability and spatiotemporal hydrogen concentration in graphite-containing metal hydride composites (MHC) with diameters of 40 mm. This approach allowed observation of reaction fronts within the MHC and powder bed, which were strongly influenced by heat transfer^[88]. Börries further established the utility of neutron imaging for precise quantitative analyses of time-dependent hydrogen distribution in metal hydride systems, exemplified through investigations of sodium alanate inside hydrogen storage tanks^[89]. For composite systems, the LiBH₄-MgH₂ system, with and without ScCl₃ additives, was characterized using both synchrotron- and neutron-based probing methods, providing complementary insights into the hydride matrix^[90]. Furthermore, neutron tomography of a hydrogen storage tank filled with NaAlH₄/TiF₃ was employed to demonstrate the hydrogenation process and the distribution of hydrides within the composite hydride system in the tank^[91].

Figure 8. Neutron images of hydrogenating process kinetics at different pressures^[85].

In addition to studies on hydrogen storage materials, neutron imaging has proven to be a critical tool for visualizing the internal states of large-scale hydrogenated containers and informing the design of efficient hydrogen storage tanks^[92]. The optimization of such tanks necessitates precise, time-resolved investigations of hydrogen distribution within large-scale metal hydride beds. In this context, researchers have proposed that in-situ fission neutron imaging can provide unique insights into hydrogen spatial distributions, enabling direct examination of hydrogen storage tanks even in large-scale compact configurations^[93]. Baruj et al. conducted in-situ neutron imaging experiments on a hydrogen container employing hydride-forming materials. This setup facilitated tracking of heat-induced hydrogen release, wherein hydrogen evolved from initially fully hydrided material, and a reaction front propagated outward from the central heater. Beyond hydrogen release dynamics, neutron imaging offers a distinctive method for studying operando reaction fronts^[94]. Pohlmann et al. pioneered the use of neutron imaging and tomography, with a spatial resolution of 7 mm, to perform comprehensive operando analyses of hydride-graphite composites (HGCs) based on Ti-Mn hydrogen-absorbing alloys and expanded natural graphite^[95]. During the initial hydrogenation, regions exhibiting enhanced reactivity were identified, and these active zones expanded progressively with successive hydrogenation-dehydrogenation cycles, ultimately engaging the entire HGC volume uniformly in the hydrogen absorption reaction. Since volume expansion of MHC can generate mechanical stresses on the vessel walls and internal components, Heubner utilized neutron imaging to in-operando characterize HGCs with varying metal particle morphologies under axial free expansion. This approach enabled detailed analysis of spatiotemporal hydrogen distributions, reaction front propagation, and the evolution and stability of volume expansion within the MHC system, as illustrated in Figure 9^[96]. It should be noted that the characterization of metal-organic framework (MOF) hydrogen storage materials using neutron imaging presents specific challenges. The inherent organic network structures of MOFs strongly influence neutron transmission, reducing effective signal intensity and introducing substantial data interference. Consequently, detecting variations in hydrogen concentration becomes considerably more difficult. Similar limitations are encountered in materials containing light elements with large neutron cross sections, such as lithium.

Figure 9. In-operando characterization of the volume expansion and mechanical stress measurement of MHC for the design of safe metal hydride storage systems^[96].

BLACK BODY GRID CORRECTION OF BACK SCATTERING NEUTRON

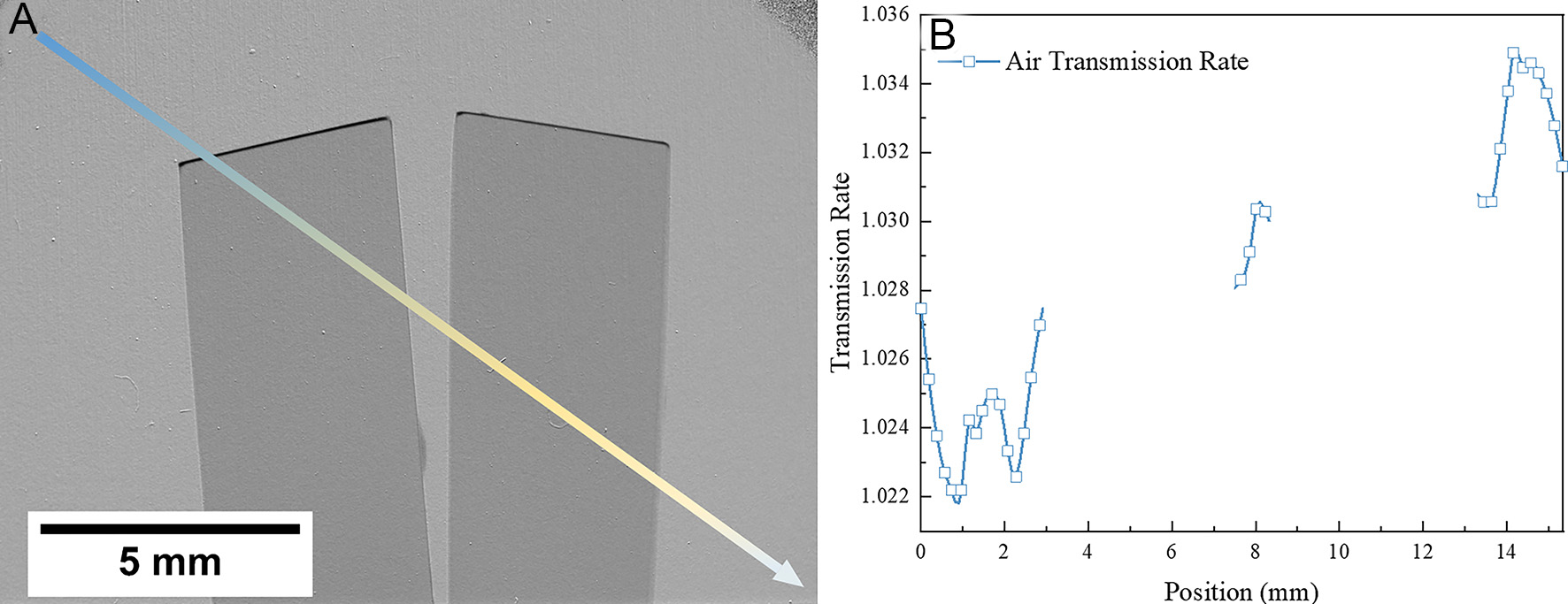
In the quantitative determination of hydrogen concentration, data processing reveals spatially inconsistent air transmission profiles, as obtained using Equation (2) and illustrated in Figure 10A. To systematically assess this phenomenon, a width of 0.2 mm along a diagonal path from the upper-left to the lower-right of the image was analyzed, deliberately avoiding regions influenced by the sample to isolate background effects. The measured transmission exhibited an initial increase followed by a slight decrease [Figure 10B], a trend attributed to background scattering caused by the presence of the sample rather than to edge effects. Specifically, neutron beams passing near the sample edges interact with post-imaging optical components, such as mirrors, and scatter back toward the scintillator screen, generating extraneous counts across the entire image. This effect alters the recorded counts from the sample itself and was first identified by Hassanein et al.^[97], introducing systematic biases in hydrogen quantification.

Figure 10. (A) The diagonal path and region of interest (ROIs); (B) the air transmission of 7 ROIs.

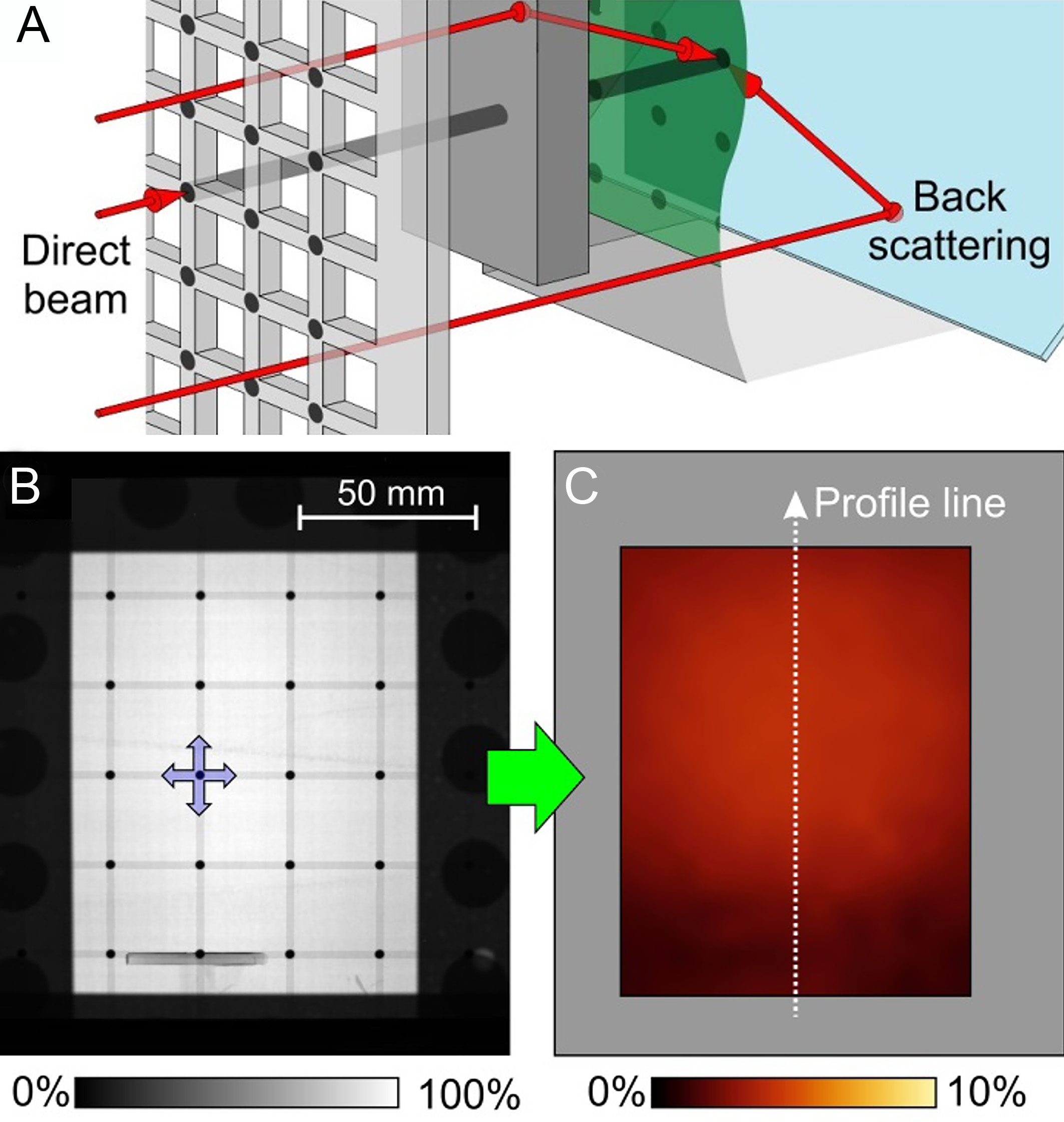
Boillat et al.^[98] proposed a correction method employing a black body grid to address this issue. The protocol involves two steps: firstly, grid-only reference images use a grid framework consisting of the high transmission material as a cross grid with low transmission material in the junctions [Figure 11A]. Secondly, sample and grid composite images are the measurements combining the sample and grid to isolate backscattering neutron contributions. The absorbers occupy only 0.8% of the total imaging area, minimizing beam attenuation while enabling full-field characterization of the point spread function (PSF) [Figure 11B]. The deconvolution correction was applied to the entire image using the measured PSF, reconstructing bias-free transmission profiles [Figure 11C].

Figure 11. (A) The schematic of black body grid and the back scattering neutron; (B) measurement of black body grid; (C) resulting interpolated background image by the black body grid^[98].

Yetik et al. advanced quantitative neutron imaging methodology by integrating a black body grid into hydrogen redistribution studies^[99]. This approach employs a high-transmission substrate, such as aluminum, embedded with periodic, uniformly distributed low-transmission circular absorbers across both the sample area and background in the same image^[99]. Background intensity variations are observed in regions unaffected by neutron scattering, with background intensities at approximately 2% of the nominal beam flux, while in affected regions, intensities increase to 4%. Prior to deconvolution correction, an additional 2% intensity bias arises, further compounding quantification errors. Post-processing corrections for backscattered neutron contributions, yielding transmission correction magnitudes between 0.264% and 2.603%, were implemented using the software KipTool^[100]. In 3D tomography, precise alignment of the black body grid with the sample is crucial to minimize thickness-dependent biases, particularly for low-transmission samples such as hydrogen-rich alloys, high-thickness materials, or elements of relatively high atomic mass. These corrections are essential because transmission fluctuations within this range caused by factors unrelated to hydrogen concentration can significantly distort quantitative analysis, especially for hydrogen concentrations below 1,000 wppm.

Although neutron imaging has achieved spatial resolutions of ~10 μm, this remains approximately three orders of magnitude lower than that of synchrotron X-ray imaging, which can reach resolutions as fine as ~30 nm. While optical paths can be readily adjusted for X-rays using lenses, collimation of neutron beams is inherently challenging, limiting their achievable spatial resolution. Temporal resolution is similarly constrained: time-resolved synchrotron radiation can acquire 8,000 projection images within 1-2 s^[101], whereas neutron imaging typically requires one minute to three hours per complete image. Each neutron image results from averaging and stacking multiple filtered data points, and successive data collection periods are needed to ensure neutron beam stability, further extending experimental durations.

These limitations arise primarily because neutrons interact randomly with atomic nuclei, resulting in multiple scattering events that cause image blurring. Additionally, the photon flux of synchrotron X-rays can reach up to 10¹² ph/cm²/s^[102], which is 6-8 orders of magnitude higher than typical neutron fluxes (~0.5 × 10⁶ to 6 × 10⁸ n/cm²/s). Consequently, X-ray imaging exhibits far superior efficiency. Differences in optical components and focusing further exacerbate the disparity: neutrons are electrically neutral and weakly interacting, making effective focusing difficult and limiting spatial resolution. Scintillator detectors convert neutron signals into optical signals, which are then amplified and transformed into information-bearing electrical signals^[103]. Despite these limitations, neutron imaging offers a unique advantage in distinguishing light elements, making it indispensable for research in nuclear materials, batteries, hydrogen storage materials, and metal defect studies. To fully leverage its potential, neutron imaging should combine high composability with resolution improvements, integrating neutron beamlines with other research facilities or complex experimental environments (e.g., gas, pressure, electromagnetic fields, or mechanical loading) to enable unprecedented technological advancements^[51].

SUMMARY AND FUTURE DIRECTIONS

Due to its non-destructive nature, high penetrability, and exceptional sensitivity to hydrogen, neutron imaging has emerged as a powerful tool for the quantitative analysis of hydrogen diffusion and distribution in metallic materials. The methodology is grounded in the Beer-Lambert law, which relates the microscopic cross-section of a material to its hydrogen concentration, forming the theoretical foundation for quantitative characterization. Ex-situ and in-situ studies have demonstrated the capability of high-resolution neutron imaging to resolve hydrogen distribution with remarkable precision. In particular, in-situ investigations of hydrogen absorption and desorption kinetics in hydrogen storage materials, coupled with the development of dedicated characterization equipment, have enabled detailed monitoring of dynamic processes in real time. Advancements in imaging instrumentation, alongside improvements in data processing techniques, have further enhanced spatial resolution and hydrogen quantification accuracy.

Despite these achievements, several challenges remain in optimizing neutron imaging for hydrogen detection in metals and hydrogen storage materials. Future research directions include the development of enhanced neutron monitoring systems to improve imaging precision and hydrogen sensitivity, particularly within large or complex experimental setups. Integrating neutron imaging with complementary characterization techniques, such as differential scanning calorimetry (DSC), will provide more comprehensive insights into solid-state hydrogen storage phenomena. Additionally, establishing a standardized, cross-facility database that documents neutron beam parameters, sample thickness, material composition, and transmission data will be critical for enabling reproducible experiments and robust data sharing. Collectively, these advancements are expected to improve the descriptive characterization of hydrogen behavior, enhance detection capabilities, and optimize the design and performance of hydrogen storage technologies.