Multi-directional attention: a lightweight attention module for slender structures
Abstract
The segmentation of slender structures in images faces challenges of discontinuous segmentation and insufficient recognition. These slender structures, such as arteries and veins, are particularly important in 3D medical images that are sensitive to the computational complexity of segmentation networks. Therefore, in order to balance the computational complexity of the network and adaptive perception of slender structures, this paper proposes a multi-directional attention module for slender structures, which is a lightweight attention module that can be inserted into the encoder or decoder unit. At the same time, we propose a contour loss function to address the class imbalance phenomenon that may arise in the joint segmentation task of slender and ordinary structures. This function improves the balance by converting traditional class mask labels into contour mask labels. The effectiveness of our proposed module has been validated through training on segmentation tasks on 2D and 3D images.
Keywords
1. INTRODUCTION
Our goal is to perform image segmentation on three-dimensional (3D) medical images containing slender structures such as arteries and veins, as well as irregular structures such as endogenous tumors, while designing lightweight networks as much as possible to ensure computational efficiency and lower device requirements, which is vital for clinical applications[1].
For the above structure, we face many challenges when performing segmentation, as shown in Figure 1. Taking blood vessels as an example, their narrowest part is only 2-3 mm, occupying only a small number of pixels in the image, which is easily overlooked in the segmentation process. In addition, although these structures require high continuity, the impact of occlusion or small gaps cannot be ignored.
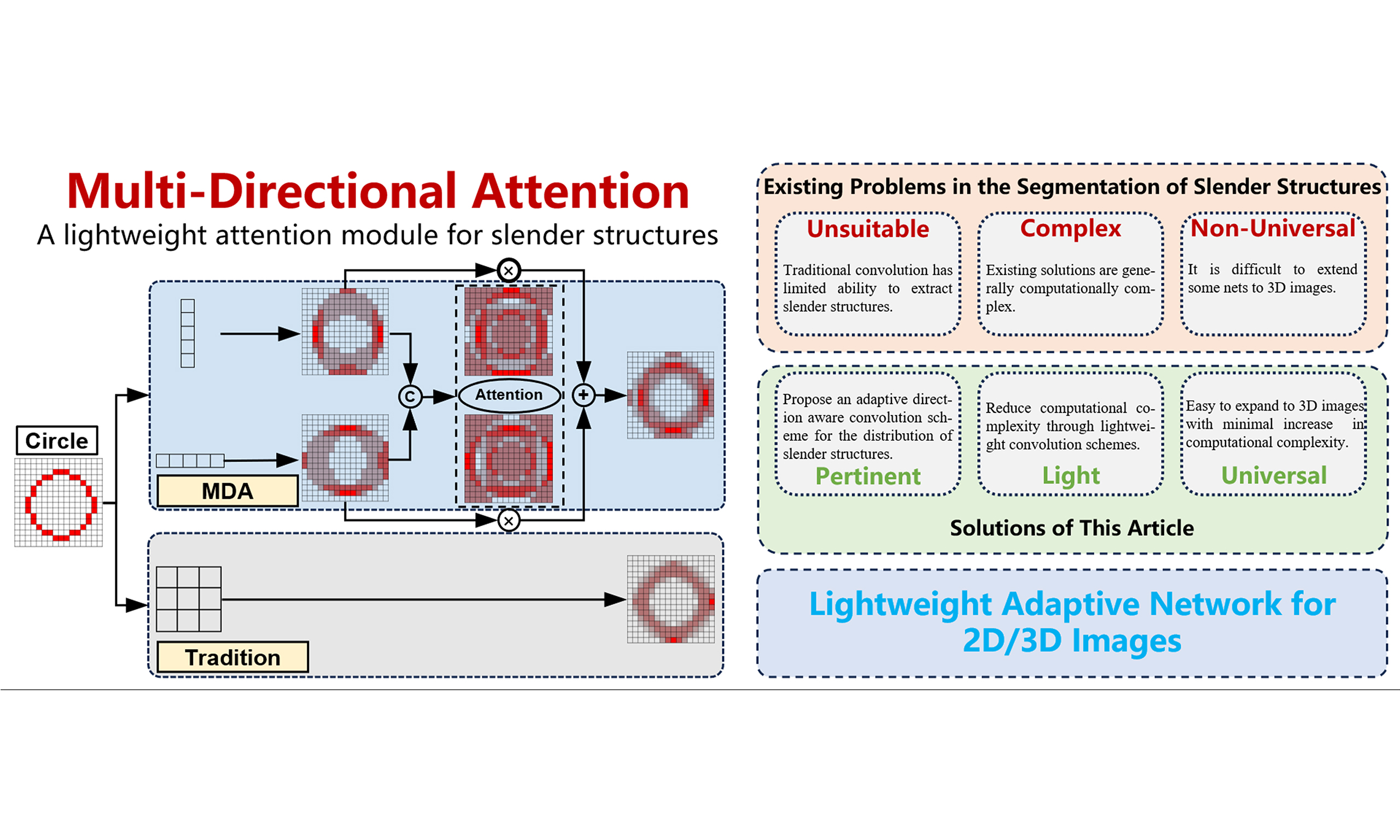
The current problems in the segmentation of slender structures mainly include the following aspects. First, for slender structures, due to their small number of pixels, traditional convolution operations may be affected by complex backgrounds, resulting in limited feature recognition. Especially when all parts of the image share the same convolution weight parameters, some structures with special shapes may be submerged as a result. Second, due to the fixed and regular calculation method of convolution, it cannot achieve adaptive and coherent feature extraction along slender structures. Third, especially in U-Net structured networks, multiple downsampling operations may cause the original pixels to fold or overlap, making them difficult to distinguish. Besides, in the training process of multi classification tasks, the loss function does not pay sufficient attention to the slender structures with fewer pixels, which causes class imbalance and affects the overall training process.
In addition, the segmentation ability of slender structures also represents the network’s ability to understand topological features. In segmentation tasks such as tumors that require strict requirements for morphological features and contour extraction, the ability to adaptively extract contours is particularly important.
To address the aforementioned challenges, some studies have made improvements to slender structures. We can divide these studies into three dimensions: (1) Improvements from the perspective of convolution itself, such as dilated convolution[2], deformable convolution[3], dynamic snake convolution[4], etc. These convolutions adapt to the shape of the target structure by changing the way of obtaining context; (2) Improvements from the perspective of network architecture, such as all-scale feature fusion[5], dual chain fusion U-Net[6], encoder-dual-decoder-based network[7], graph convolutional networks[8], etc., aim to enhance the perception ability of slender structures by changing the form of the network; (3) Improvements from the perspective of loss functions, such as introducing centerline-Dice similarity measurement[9], geometric measurement[10], etc. These studies have some targeted designs for us to learn from, but some methods that introduce huge computational complexity are not suitable for our applications.
From the perspective of network structure alone, networks designed for slender structures often increase model complexity in order to ensure long-range dependencies and multi-resolution perception. This not only increases the number of parameters and computational costs of the model, but also puts higher demands on the quality and quantity of training data and its annotations. For small batch datasets, although lightweight networks such as Dilated Convolution Net (DCNet)[11] and Slim UNEt Transformers (UNETR)[12] sacrifice some of the complexity and depth of the model, resulting in lower feature expression ability than large models when dealing with complex scenes or fine structures, it is necessary to use lightweight networks for small datasets to ensure the trainability of the model. This also puts forward certain requirements for the design of training frameworks and methods.
Unlike the above research, in order to target some segmentation application scenarios that require low computational complexity, we propose a lightweight multi-directional attention mechanism on the basic encoder-decoder structure network. By changing the shape of the convolution and adding an attention fusion strategy, this attention mechanism can be well integrated into the encoder-decoder units of the network. In addition, we also propose a low computational complexity contour loss function method, which reduces the impact of class imbalance during training by converting segmentation labels into contour labels. In terms of network architecture, we have also made appropriate modifications to the skip connections and bottleneck layers to better perform feature fusion. To sum up, our contributions are as follows:
(1) A lightweight multi-directional attention module has been proposed, which can be integrated into various units of the network and has been validated in two datasets with different dimensions and tasks.
(2) A contour loss function is proposed to reduce class imbalance.
(3) Explored modifications to the skip connections and bottleneck layers in the network architecture, and provided some reference for network design.
2. RELATED WORK
The classic network for image segmentation is the U-Net network proposed by Ronneberger et al. in 2015[13]. It fuses high-level semantic information and low-level feature information through encoders, decoders, and intermediate skip connections, greatly preserving the original feature information of the image. Subsequently, convolutional neural networks (CNNs) represented by residual U-Net (ResU-Net)[14], U-Net++[15], U-Net3+[16], etc. have continuously improved their performance through cleverly designed residual or dense connections.
During this process, some studies explored segmentation of slender structures. For example, Li uses residual U-Net to simultaneously segment renal parenchyma, arteries, veins, ensemble systems, and abnormal structures[17]; the resulting Dice indices were 0.96, 0.86, 0.8, 0.62, and 0.29, respectively. It can be seen the difficulty level of segmenting slender tissues and some special shaped structures.
With the explosive popularity of Transformer structures in the natural language processing (NLP) field, networks represented by Vision Transformer[18] and Swin Transformer[19] have achieved remarkable results in image segmentation by better ensuring the perception and understanding of global features through self-attention mechanisms and moving windows. However, although this attention can help us establish associations between slender structures, due to the complex structure and the lack of inductive bias, its ability to process local information is not as good as pure convolutional networks, and it is difficult to train for good performance on some smaller datasets.
In order to improve the understanding ability of convolution on slender structures and make convolution better adapt to these structures, some deformable convolutions have been proposed[2-4]. Taking dynamic snake convolution as an example, they can change their convolution shape along slender structures and achieve excellent results in image segmentation tasks. However, due to the huge computational and memory consumption caused by convolution offset calculation and other operations, the network cannot be designed for deep multi-scale.
The methods for improving network architecture mostly rely on multi-scale feature fusion[5,8], which provides rich semantic information for the segmentation of these structures through multi-scale feature fusion of different spatial and semantic information. Similarly, the computation and fusion strategy of multi-scale features will also bring huge computational complexity, which is also not suitable for some application scenarios that require high real-time performance.
The method based on loss function[9,10] can indeed help the network strengthen its attention and constraints on the continuity and topological consistency of slender structures during network training, but it is not suitable for all classification tasks, especially for multi classification tasks involving conventional shapes.
3. METHODS
In order to provide a targeted introduction, we will first introduce our core contribution and then introduce the specific network architecture. At the same time, we use ellipses instead of specific image dimensions, such as “H × W × ···”, to adapt to images of more dimensions.
3.1. Pre-theoretical foundation
In conventional convolution, the new pixel value of the pixel with coordinates p0 in the image after convolution is calculated as follows.
Among them, p0 is the center point coordinate corresponding to the current convolution, pn is the offset of each position of the current convolution kernel compared to the center of the convolution kernel, R is all the image points within the scope of the current convolution, x(p) is the pixel value of the original image at point p, y(p) is the value of the p-point after convolution, and w(pn) is the weight of the convolution kernel at the offset position pn. Due to the fact that the weights of the convolution kernel are shared globally, this often brings about a problem that if a slender structure is encountered, the number of pixels it occupies in the corresponding convolution is often small and diverse in shape. After the shared weight calculation, the features of these pixels are likely to be weakened after multiple calculations, making it difficult to distinguish them.
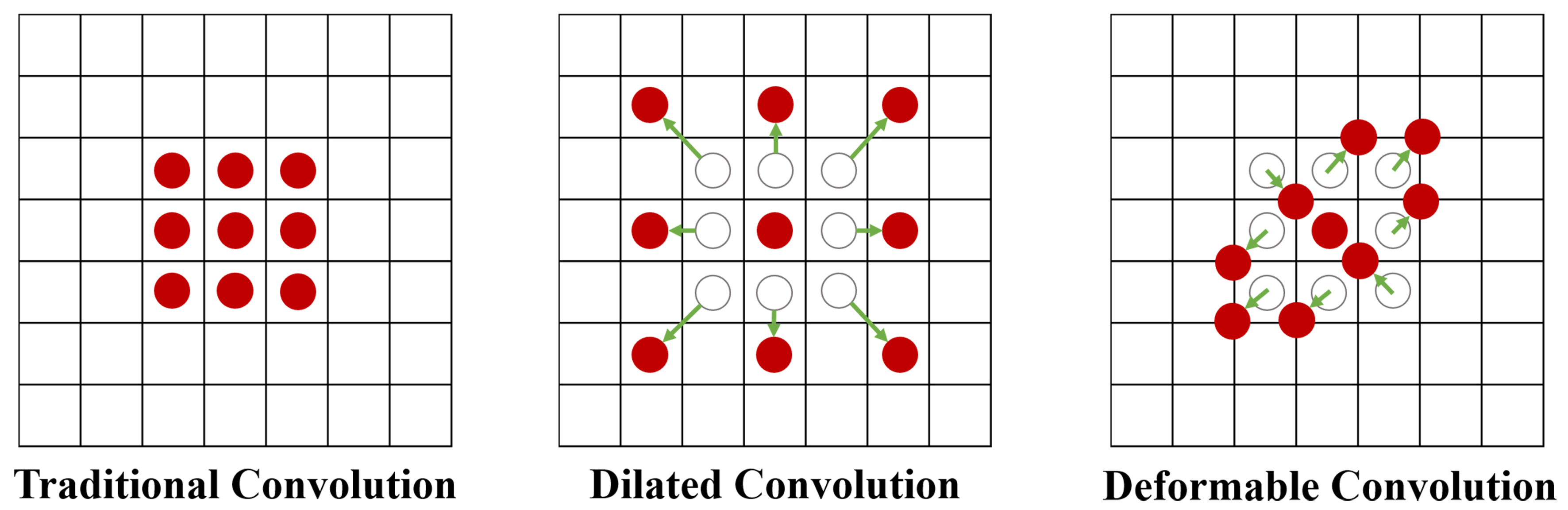
In order to target slender structure, some deformable convolutions have been proposed, as shown in Figure 2. These convolutions usually add a learnable offset ∆pn to the original image on the basis of the original convolution, as given in
However, the offset of pixels in this unit is often a decimal and an integer, so bilinear interpolation is needed to obtain the specific pixel value of the offset position. However, the huge computational and memory consumption brought by offset calculation and bilinear interpolation will occupy more resources, thereby reducing the running speed of the network and hindering feature extraction in deeper and more dimensional layers.
In fact, the essence of these convolutions is to break the constraint of weight sharing in convolution kernels, in order to better adapt to the shape of the target structure in the image. Therefore, our multi-directional attention mechanism is designed as follows.
3.2. Multi-directional attention and the units designed based on it
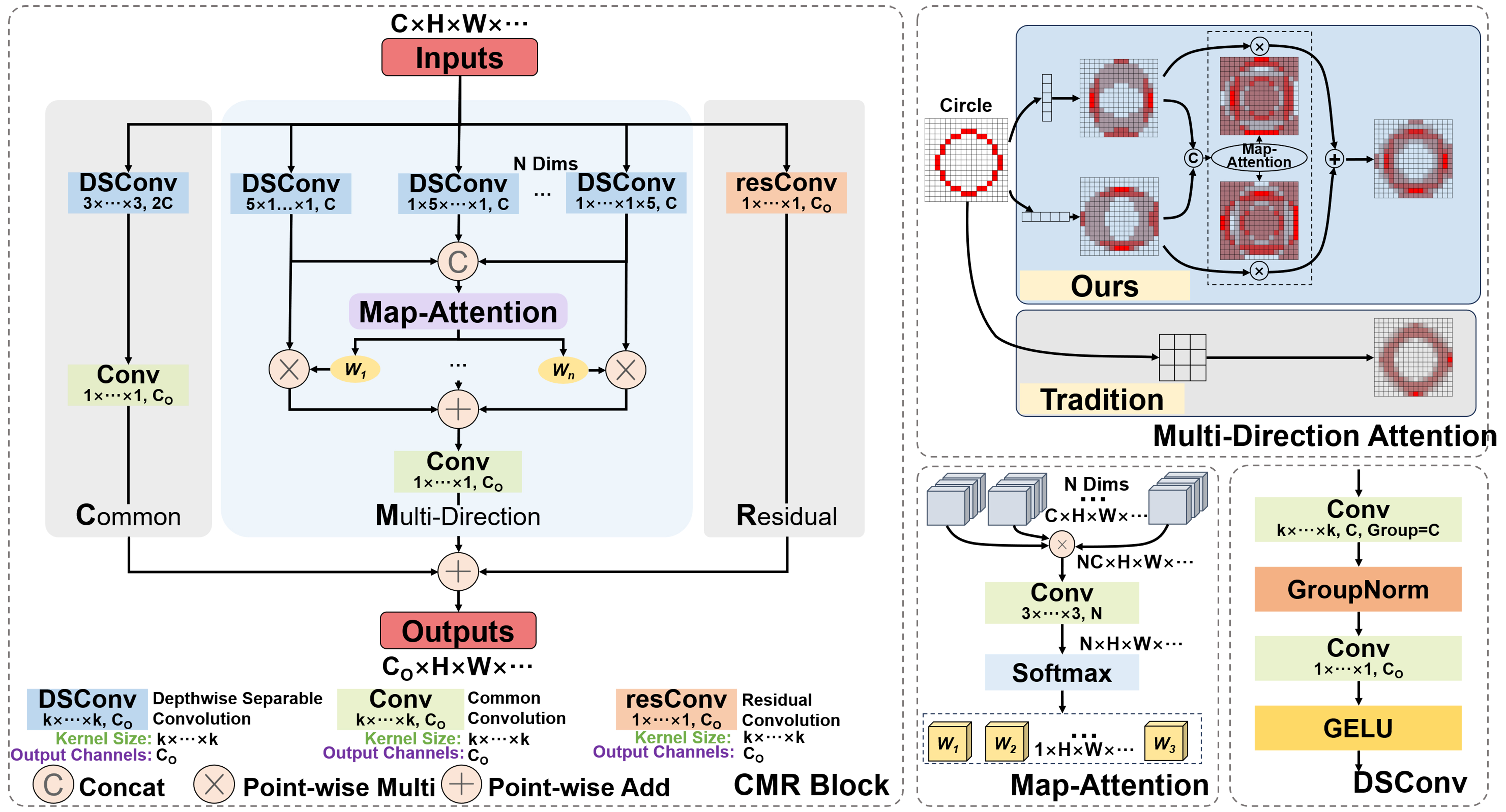
Unlike deformable convolution, which requires learning an offset, we directly design strip-shaped convolution modules in different directions to adapt to offsets representing the direction of slender structures. The attention mechanism we designed and the encoder-decoder module common and multi-direction with residual (CMR) Block integrated on it are shown in Figure 3.
Figure 3. Multi-directional attention module and CMR Block based on it. CMR: Common and multi-direction with residual.
Due to the uncertain shape of slender structures, block convolution without directional features is often difficult to extract effective coherent information of slender structures. In contrast, strip convolution with different axes is more conducive to adapting to slender structures. Therefore, in the early stage of the multi-directional attention unit, we first use a 5-pix strip convolution for feature extraction for different axes of the image. The convolution results obtained in different directions are as follows.
where k represents the different dimensional directions of the original image, yk indicates the convolution result in the k direction, and
Through this processing mechanism that integrates multi-directional strip convolution results, the multi-directional attention module can combine attention weights to overcome the impact of convolution kernel weight sharing on feature extraction, and better help pixels find the adjacent pixels with the highest correlation in their neighborhood, thus achieving adaptation to slender structures. As shown in the upper right corner of Figure 3, for a circular arc curve that can represent any direction of slender structures, the feature map processed by the multi-directional attention module better preserves the original features of the curve compared to the feature maps of traditional convolution, without being mixed by background pixels. Besides, in order to minimize computational complexity, we introduced the depthwise separable convolution[20] into the module instead of using traditional convolution method.
Compared with the traditional convolution, the deep separable convolution can significantly reduce the parameters and achieve a better effect by combining the deep convolution which is responsible for each channel by a convolution kernel and the point-wise convolution whose convolution kernel size is only 1 × 1. For a two-dimensional image with a length and width of H × W, the amount of computation required for a traditional convolution with a convolution kernel size of K × K is FLOPsstandard = Cin × Cout × H × W × K2, while the amount of computation required for a deep separable convolution is only FLOPsDS = Cin × H × W × K2 + Cin × Cout × H × W = Cin × H × W × (K2 + Cout), which is particularly significant when the number of output channels cout is large. Therefore, for a Multi-Directional Attention module, the overall computational cost is FLOPsMA = N × Cin × H × W × (K2 + Cin) + N × Cin × Cout × H × W = N × Cin × H × W ×
In addition, the CMR block is composed of three parts: regular convolution block, multi-directional attention block and residual convolution block. The function of common convolution blocks is to preserve the feature extraction capability of traditional convolution; The function of multi-directional attention blocks is to focus on the distribution of slender structures; The function of residual convolution blocks is to ensure better semantic coherence and alleviate the gradient vanishing/exploding problem caused by the network being too deep.
3.3. CMR U-Net: the segmentation network architecture based on CMR Block
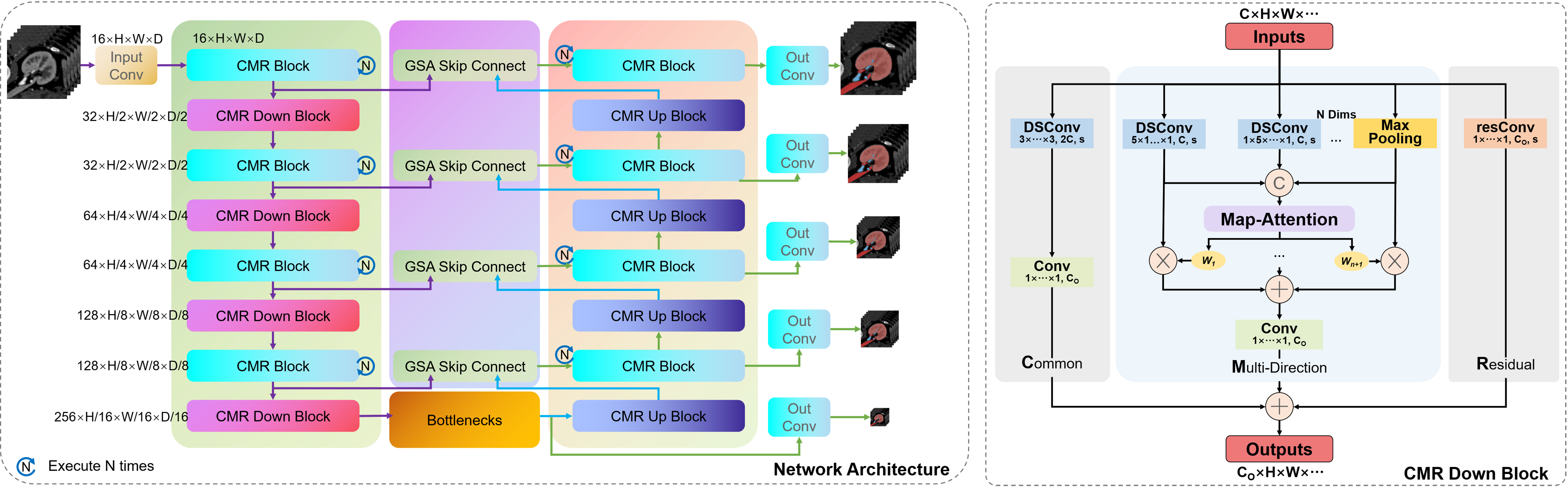
For segmentation task, we designed a network architecture as shown in Figure 4. It should be noted that the CMR Block is executed multiple times in a stage of the network. Because when the multi-directional attention module is executed only once, the receptive field range of the model is only on the coordinate axes of each dimension corresponding to the current pixel point, while multiple executions can expand the receptive field to the entire cube around it.
Figure 4. CMR U-Net: the network architecture based on CMR Block. CMR: Common and multi-direction with residual.
In addition, for the down-sampling and up-sampling units of the net, we use stride 2 convolution and transpose convolution, respectively, to replace the convolution settings of CMR Block. It is worth noting that we have also introduced max pooling operation in the multi-directional attention mechanism of the down-sampling unit, which can help avoid information loss of slender structures during the convolution down-sampling process with a stride of 2.
For the network, the skip connection mechanism and the bottleneck layer are also important units. Here, we have made improvements to these two units by proposing a skip connection fusion mechanism based on gated spatial attention (GSA) and a bottleneck layer based on axial attention. However, the only effective mechanism in practice is the skip connection fusion mechanism, which will be introduced in later experiments.
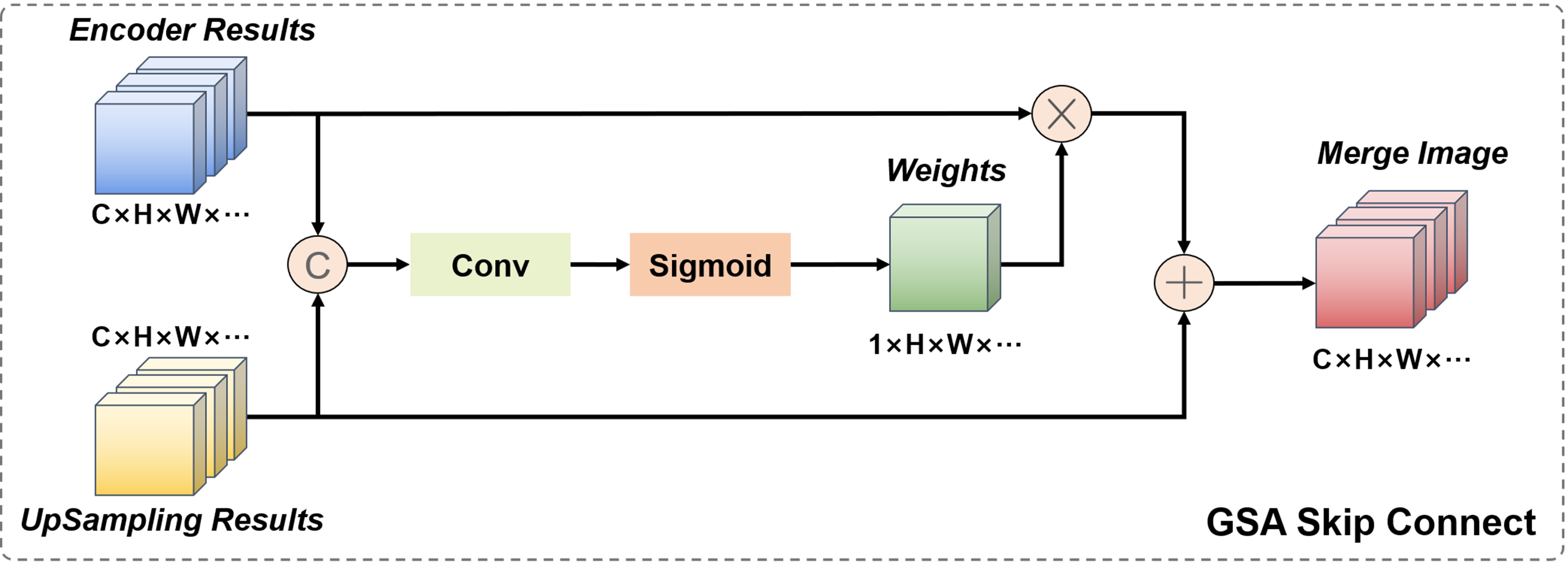
In the classic U-Net network model, the role of the skip connection layer is to fuse the low-level feature information of the encoder and the high-level semantic information of the decoder at the same resolution to ensure feature reusability, and to help the decoder stage recover the original pixel information of the up-sampled image, usually using channel concatenation for fusion. However, for 3D and even higher-dimensional images containing other information, the computational cost of channel concatenation cannot be ignored. Therefore, in medical images, the commonly used skip connection fusion strategy adopts the point-wise addition operation. It should be noted that although point-wise addition can reduce computation, this direct summation of high-level semantic information and low-level feature information without distinction may disrupt the coherence of the original semantic information, thereby reducing the reliability of the network. Therefore, here we propose a skip connection fusion strategy based on GSA, as shown in Figure 5.
This module combines the output image of the encoder part and the up-sampled image of the decoder part. Firstly, the two are concatenated in the channel dimension, and then the concatenated result is jointly fed into a regular convolution with a kernel size of 1. The output is a convolution result with 1 channel and a size equal to the input image size, which is activated by the Sigmoid function to become the spatial attention weight of the encoder image. This weight combines the information of low-level feature images and high-level semantic images, and is a learnable dynamically adjustable fusion weight. Finally, by weighting the encoder image and adding it point by point to the decoder image, the semantic coherence of the fused image is ensured.
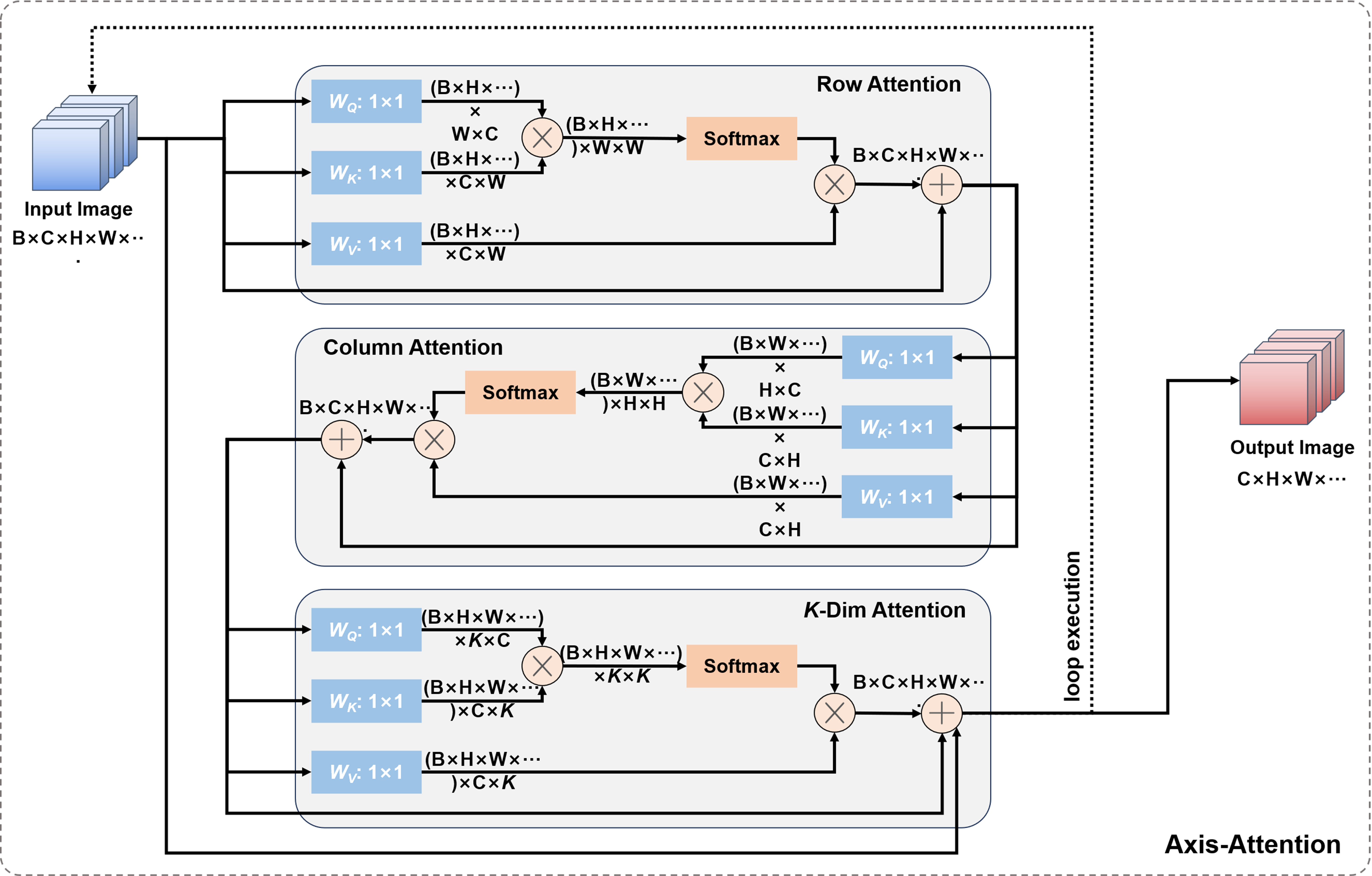
In addition, we also introduced axial attention mechanism to the bottleneck layer of the network, which was proposed by Ho et al.[21] [Figure 6]. Axial attention is used to extract relevant information between different parts of the image, and is applied in low-resolution images to reduce computational complexity.
3.4. The contour loss that can reduce class imbalance and the loss strategy
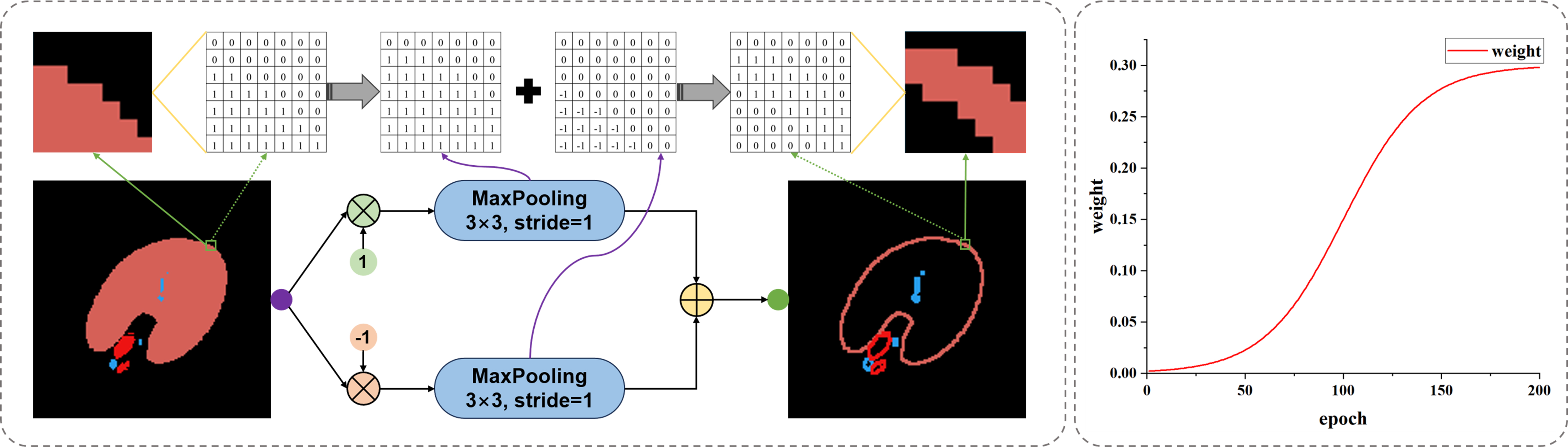
In order to target slender structures and weaken the influence of internal areas in ordinary classification structures, we designed contour loss LContour as given in Equation (5), which simplifies the classification results of all structures into contour labels. The calculation of contours depends on a maximum pooling function (MP) with a window size of 3 × 3 and a step size of 1. By calculating the MP results of positive and negative samples of the labels and summing them up, as shown in Figure 7, we effectively extract the classification edges of various types of segmented images and reduce the computational imbalance caused by too many internal pixels in the structures. By dividing the contour difference F norm between the true label and the predicted label by the F norm of the true label contour, we obtain a global contour error result.
where G represents the true value label, and P represents the predicted label. In addition, our total loss consists of three parts, including Dice loss LDice, Cross Entropy loss LCE, and Contour loss, as given in
It cannot be ignored that contour loss lacks directionality, which may bring significant uncertainty to the network in the early stages of training. Due to the above reason and the poor performance of the cross-entropy loss function in class imbalance situations, weights α and β are respectively set for the two, where α is set to 0.8 and β is set to
The variation of β during the training process is shown in the coordinate graph on the right side of Figure 7. Throughout the entire training process, the maximum value of β is 0.3, and it follows a pattern of slow growth, accelerated growth, and finally stable growth. This is because in the initial training process, the network is underfitting, and the predicted contour has a large degree of uncertainty. After the network reaches a certain segmentation ability, the weight is increased to optimize the segmentation contour.
In addition, for the task of renal medical image segmentation, based on the above loss functions, different tissues are weighted to focus on tumor, artery, and vein tissues, while weakening the segmentation results of normal renal parenchymal tissue with a larger area, as given in
Based on the above theory, we conducted experiments and applications in our proposed method.
4. RESULTS AND APPLICATION
To test the effectiveness of the above method on different types and dimensions of datasets, we conducted experimental tests on the kidney CTA medical image dataset KiPA 2022[22-25], retinal vessels dataset (including DRIVE[26], Stare[27] and CHASE DB1[28]) and the satellite road dataset[29]. At the same time, we made preliminary attempts to apply the kidney segmentation network into an augmented reality (AR)-guided surgery experiment.
4.1. Introduction to image segmentation experiments and evaluation indicators
On the dataset introduced above, we organized the training of the network. Note that the default network here is the CMR U-Net with the CMR Block as the bottleneck layer, as experimental results show that the effect of using axial attention mechanism in the bottleneck layer is not as good as using CMR Block. For the convenience of later description, we define the network used for training and its abbreviation [Table 1].
Network introduction and abbreviation
| Network description | Abbreviation |
| CMR U-Net with the CMR Block as the bottleneck | CMR U-Net (Ours) |
| CMR U-Net with the Axis Attention as the bottleneck | CMR-AAB (Ours but worse) |
| CMR U-Net without any bottleneck | CMR-NoBL |
| CMR U-Net without the GSA skip connection | CMR-NoGC |
| U-Net with the CMR Block as the bottleneck | U-Net-CMRB |
| CMR U-Net without the Contour Loss in training | CMR-NoCL |
| Other networks (such as DeeplabV3) | No abbreviation (such as DeeplabV3) |
In Table 1, the structure and parameters of all U-Net-base architecture networks are designed with reference to Figure 4, using the same initialization conditions and training hyperparameter settings. And the initialization learning rate is 0.01.
The training of the model was conducted on an Ubuntu server equipped with an NVIDIA T4 graphics card with 16 GB of video memory. The server uses an Intel Xeon (Cascade Lake) Gold 6240 8-core CPU, 64 GB of system memory, and Ubuntu 22.04. The training framework is a combination of Pytorch 2.2.2, Cuda 12.1, and Python 3.11. To address the issue of high memory usage in 3D images, the model uses the checkpoint gradient checkpoint function to implement breakpoint continuation training to optimize memory usage. Define a training cycle of 200 epochs, collect model parameters at 200 epochs to evaluate the model.
To evaluate the segmentation results, we use the following evaluation metrics, including dice similarity coefficient (DSC), 95%-Hausdorff distance (95%-HD or HD), and average Hausdorff distance (AVD). DSC is used to evaluate the area-based overlap index, HD, which is sensitive to outliers, is used to compare the segmentation quality of outliers, AVD, which is the average of total HD, reflects the coincidence of the surface for stable but less sensitive to outliers. Assuming that under a certain classification, the label is L, the predicted value is P, and the pixel values of the label and the predicted value at point i are li and pi, which are expressed as follows,
4.2. Segmentation results and comparative analysis
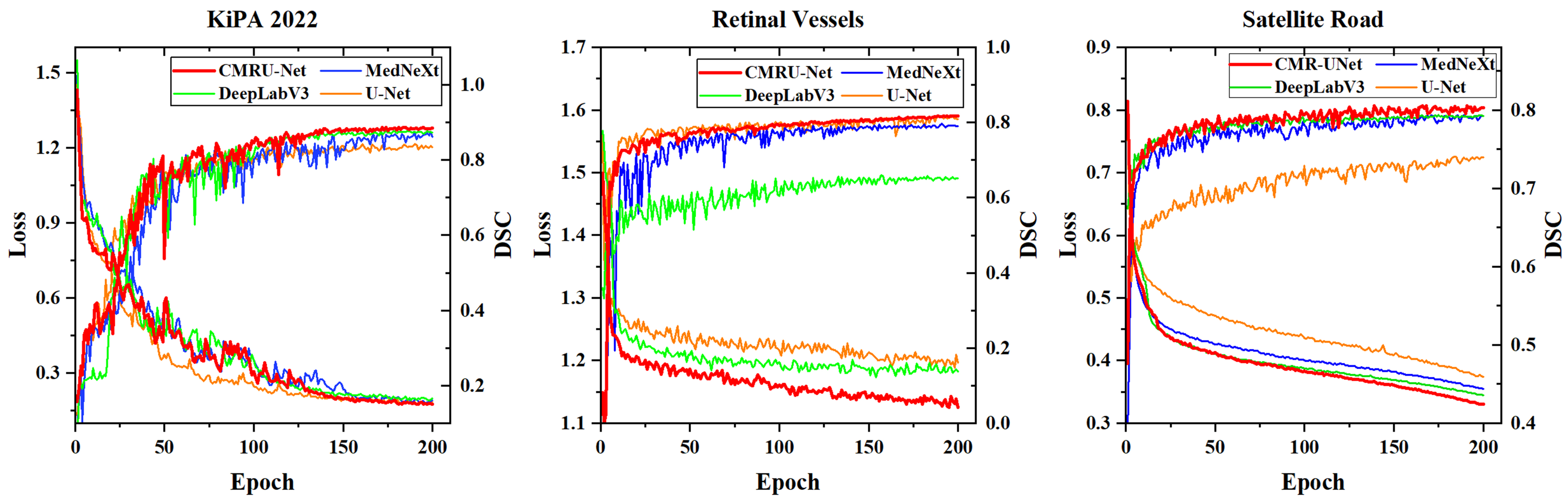
Before conducting numerical analysis, we first plot the loss curves and validation set DSC of CMR U-Net and other networks, as shown in Figure 8. It is not difficult to find that DeepLab V3 in retinal vessels segmentation tasks and U-Net in satellite road segmentation tasks achieved poor training results, while our CMR U-Net has achieved better training results compared to others.
Due to the small size of the KiPA 2022 medical image segmentation dataset, we can clearly see the advantages of CMR U-Net on the satellite road map dataset and retinal vessels dataset. In addition, due to the introduction and continuous increase of contour loss, we observed some shaking in the curve during the training process, but it gradually stabilized in the later stage.
The quantitative analysis results of different networks or losses are shown in Tables 2 and 3, and Figure 9 presents the segmentation results and heatmap effects of varying networks. By comparing the data and segmentation results between these networks, we can see that under the same network training conditions, our proposed CMR U-Net always outperforms in various classification situations and different dimensions. Through the AVD and HD index, it can be seen that its edge recognition ability is stronger than that of other networks.
Comparison of training results for different networks on 3D images
| Network | KiPA 2022 | |||||||||||
| Parenchyma | Tumor | Artery | Vein | |||||||||
| DSC | AVD/mm | HD/mm | DSC | AVD/mm | HD/mm | DSC | AVD/mm | HD/mm | DSC | AVD/mm | HD/mm | |
| CMR U-Net | 0.9536 | 0.6697 | 1.8234 | 0.8909 | 1.0511 | 2.3814 | 0.8697 | 0.8071 | 2.7139 | 0.8309 | 1.1942 | 1.4646 |
| DeepLabV3 | 0.9529 | 0.6952 | 1.9635 | 0.8821 | 1.8321 | 3.1927 | 0.8615 | 1.1129 | 3.9579 | 0.8291 | 1.2169 | 2.3313 |
| MedNeXt | 0.9479 | 0.8647 | 2.6892 | 0.8796 | 2.5114 | 6.2227 | 0.8619 | 1.1121 | 3.8817 | 0.8249 | 1.2215 | 2.4598 |
| U-Net | 0.9371 | 0.8349 | 2.8904 | 0.8596 | 2.9529 | 6.7964 | 0.8314 | 1.5510 | 5.8766 | 0.7906 | 1.2528 | 2.7992 |
| CMR-AAB | 0.9497 | 0.8354 | 2.4603 | 0.8694 | 2.0251 | 6.5212 | 0.8407 | 1.3765 | 5.3203 | 0.8035 | 1.5802 | 3.7216 |
| CMR-NoBL | 0.9533 | 0.6764 | 1.8987 | 0.8893 | 1.0962 | 2.6395 | 0.8679 | 0.8902 | 2.9693 | 0.8307 | 1.1973 | 1.5203 |
| CMR-NoGC | 0.9531 | 0.6921 | 1.9010 | 0.8867 | 1.3305 | 2.7879 | 0.8634 | 0.9234 | 3.2506 | 0.8314 | 1.1765 | 1.4298 |
| U-Net-CMRB | 0.9407 | 0.8053 | 2.5639 | 0.8683 | 2.4962 | 5.9653 | 0.8409 | 1.3805 | 5.3679 | 0.8195 | 1.3264 | 2.7981 |
| CMR-NoCL | 0.9459 | 0.7759 | 2.5112 | 0.8763 | 2.0535 | 7.2303 | 0.8468 | 1.4573 | 5.1845 | 0.8079 | 1.4508 | 3.0368 |
Comparison of training results for different networks on 2D images
| Network | Retinal vessels | Satellite road | ||||
| Vessels | Road | |||||
| DSC | AVD/pix | HD/pix | DSC | AVD/pix | HD/pix | |
| CMR U-Net | 0.8175 | 1.9859 | 4.5598 | 0.8154 | 5.2559 | 16.1461 |
| DeepLabV3 | 0.6523 | 5.3229 | 15.9988 | 0.8065 | 5.9270 | 16.3762 |
| MedNeXt | 0.7912 | 2.8317 | 8.1600 | 0.8046 | 6.0225 | 18.3740 |
| U-Net | 0.8087 | 2.2253 | 5.5255 | 0.7496 | 10.2342 | 33.0458 |
| CMR-AAB | - | - | - | 0.8073 | 5.6729 | 16.2896 |
| CMR-NoBL | 0.8155 | 2.0034 | 4.8863 | 0.8132 | 5.3158 | 16.2794 |
| CMR-NoGC | 0.8151 | 2.0106 | 4.8979 | 0.8134 | 5.3029 | 16.2142 |
| U-Net-CMRB | 0.8095 | 2.1342 | 5.3268 | 0.7743 | 8.6351 | 26.1852 |
| CMR-NoCL | 0.7953 | 2.5752 | 7.2152 | 0.7872 | 7.3564 | 22.8546 |
From the comparison of heat maps in Figure 9, we can more intuitively conclude that the coherence of RCM U-Net is much better. In contrast, DeeplabV3, which uses dilated convolutions, does not maintain continuous heat maps in angled structures. Additionally, MedNeXt and U-Net using traditional convolution are slightly inferior in edge recognition ability and feature extraction ability.
In the ablation experiment, we found that the use of the axis attention mechanism in the bottleneck layer of the network only had a positive effect on the satellite road dataset, which has a large sample size, while in the KiPA2022 dataset with a small sample size, this module did not work as well and had negative effects instead. If the bottleneck layer uses CMR Block, it will be much better, which also proves the flexibility of our CMR Block’s lightweight multi-directional attention.
Besides, through ablation experiments, we also evaluated the contributions of the GSA module and loss function. The largest one was our contour loss function, which improved the effect by about 1.79%, followed by our GSA skip connection module, which improved the effect by about 0.30%.
Overall, our module has significant advantages in capturing the topological continuity of structures, which is not only important for continuous segmentation of slender structures, but also has a crucial impact on edge recognition of ordinary structures.
The most significant contribution of our proposed innovation is the multi-directional attention mechanism, which adapts the module to recognize slender structures by changing the convolution calculation method. The second is the contour loss function, which, although it may introduce uncertainty in the early stages of network training, can help better optimize edge segmentation once the network has acquired a certain level of recognition ability. In addition, compared with traditional attention networks such as axial attention, our module demonstrates better adaptability in small datasets.
4.3. The network’s applications
With the help of the network proposed in this article, we can quickly segment medical images. This network not only shortens the segmentation time to within 30 s, but also has very clear edges such as arteries and veins, which is very important for clinical diagnosis. Taking the partial nephrectomy as an example, we can take CTA image of the patient’s kidney again shortly before the surgery and combine the segmentation results with other former preoperative diagnoses to guide the surgical implementation.
In addition, we also proposed an AR-guided intraoperative localization framework for laparoscopic partial nephrectomy, as shown in Figure 10. Using the segmentation results to reconstruct the kidney, and utilizing manual initial point selection and video point tracking techniques to overlay the kidney reconstruction model with intraoperative images through PnP algorithm, an initial registration error of approximately
Figure 10. Schematic diagram of AR guidance system for laparoscopic partial nephrectomy. AR: Augmented reality.
The effectiveness of this network has been verified not only on 3D medical images but also on 2D images. Furthermore, more applications can be developed and explored for multiple scenarios such as satellite image analysis and industrial scratch detection.
5. DISCUSSION
Despite the many advantages of our method, the uncertain impact of our proposed contour loss function in the early stages of network training cannot be ignored. In addition, we only trained the network on three datasets related to slender structures. Although we have demonstrated its effectiveness for slender structures, further exploration is needed to determine whether this method is equally applicable to some other morphological structures.
6. CONCLUSIONS
In this study, we focused on image segmentation of slender structures and proposed a multi-directional attention mechanism that can be embedded in the basic units of the network. This attention mechanism can adapt well to the morphological changes of slender structures and does not bring uncertain effects to the network in small datasets due to its simple structure. In addition, our proposed contour loss and GSA skip connections have also improved the network. Experimental verification has also demonstrated the advantages of our method.
DECLARATIONS
Authors’ contributions
Made substantial contributions to conception and design of the study and performed data analysis and interpretation: Liu, D.; Zhang, Y.; Cong, M.
Performed data acquisition and provided administrative, technical, and material support: Ren, Y.; He, X.; Yu, G.
Provided technical support and conducted reviews: Pan, D.
Secured funding and conducted the final proofreading: Liu, D.
Availability of data and materials
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Financial support and sponsorship
This work is supported by Ningbo’s “Science and Technology Innovation Yongjiang 2035” Key Technology Breakthrough Program Project under Grant 2024Z201 and the Dalian Life and Health Guidance Program Project under Grant 2022YG013.
Conflicts of interest
The authors of Ren, Y.; He, X. and Yu, G. are from Dalian Municipal Central Hospital, while other authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
As we are using an open-source dataset, there is no need for individual patient informed consent, and the aforementioned study is currently in the theoretical research stage and has not yet involved real clinical or animal trials, so ethical approval is not required at this time.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Shao, P.; Qin, C.; Yin, C.; et al. Laparoscopic partial nephrectomy with segmental renal artery clamping: technique and clinical outcomes. Eur. Urol. 2011, 59, 849-55.
2. Yu, F. , Koltun V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. https://arxiv.org/abs/1511.07122. (accessed 10 Sep 2025).
3. Dai, J.; Qi, H.; Xiong, Y.; et al. Deformable convolutional networks. In 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy. October 22-29, 2017. IEEE; 2017. pp. 764-73.
4. Qi, Y.; He, Y.; Qi, X.; Zhang, Y.; Yang, G. Dynamic snake convolution based on topological geometric constraints for tubular structure segmentation. In 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France. October 01-06, 2023. IEEE; 2023. pp 6047-56.
5. Zou, S.; Xiong, F.; Luo, H.; Lu, J.; Qian, Y. AF-Net: all-scale feature fusion network for road extraction from remote sensing images. In 2021 Digital Image Computing: Techniques and Applications (DICTA), Gold Coast, Australia. Novermber 29 - December 01, 2021. IEEE; 2021. pp 66-73.
6. Xian, Y.; Zhao, G.; Chen, X.; Wang, C. DCFU-Net: rethinking an effective attention and convolutional architecture for retinal vessel segmentation. Int. J. Imaging. Syst. Tech. 2025, 35, e70003.
7. Yang, C.; Zhang, H.; Chi, D.; et al. Contour attention network for cerebrovascular segmentation from TOF-MRA volumetric images. Med. Phys. 2024, 51, 2020-31.
8. Jalali, Y.; Fateh, M.; Rezvani, M. VGA-Net: vessel graph based attentional U-Net for retinal vessel segmentation. IET. Image. Processing. 2024, 18, 2191-213.
9. Shit, S.; Paetzold, J. C.; Sekuboyina, A.; et al. clDice - a novel topology-preserving loss function for tubular structure segmentation. In 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition(CVPR), Nashiville, USA. June 20-25, 2021. IEEE; 2021. pp. 16560-9.
10. Wang, Y.; Wei, X.; Liu, F.; et al. Deep distance transform for tubular structure segmentation in CT scans. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, USA. June 13-19, 2020. IEEE; 2020. pp. 3832-41.
11. Shang, Z.; Yu, C.; Huang, H.; Li, R. DCNet: a lightweight retinal vessel segmentation network. Digit. Signal. Process. 2024, 153, 104651.
12. Pang, Y.; Liang, J.; Huang, T.; et al. Slim UNETR: scale hybrid transformers to efficient 3D medical image segmentation under limited computational resources. IEEE. Trans. Med. Imaging. 2024, 43, 994-1005.
13. Ronneberger, O.; Fischer, P.; Brox, T. U-Net: convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention - MICCAI 2015, Munich, Germany. Springer, Cham; 2015. pp. 234-41.
14. Zhang, Z.; Liu, Q.; Wang, Y. Road extraction by deep residual U-Net. IEEE. Geosci. Remote. Sensing. Lett. 2018, 15, 749-53.
15. Zhou, Z.; Rahman, Siddiquee. M. M.; Tajbakhsh, N.; Liang, J. UNet++: a nested U-Net architecture for medical image segmentation. In: Stoyanov D, Taylor Z, Carneiro G, et al. editors. Deep learning in medical image analysis and multimodal learning for clinical decision support. Cham: Springer International Publishing; 2018. pp. 3-11.
16. Huang, H.; Lin, L.; Tong, R.; et al. Unet 3+: a full-scale connected UNet for medical image segmentation. In ICASSP 2020 - 2020 IEEE international conference on acoustics, speech and signal processing (ICASSP), Barcelona, Spain. May 04-08, 2020. IEEE; 2020. pp. 1055-9.
17. Li, J.; Lo, P.; Taha, A.; Wu, H.; Zhao, T. Segmentation of renal structures for image-guided surgery. In: Frangi AF, Schnabel JA, Davatzikos C, Alberola-López C, Fichtinger G, editors. Medical image computing and computer assisted intervention - MICCAI 2018. Cham: Springer International Publishing; 2018. pp. 454-62.
18. Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; et al. An image is worth 16 × 16 words: transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. https://arxiv. org/abs/2010.11929. (accessed 10 Sep 2025).
19. Liu, Z.; Lin, Y.; Cao, Y.; et al. Swin transformer: hierarchical vision transformer using shifted windows. In 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, Canada. October 10-17, 2021. IEEE; 2021. pp. 10012-22.
20. Chollet, F. Xception: deep learning with depthwise separable convolutions. In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, USA. July 21-26, 2017. IEEE; 2017. pp. 1251-8.
21. Ho, J.; Kalchbrenner, N.; Weissenborn, D.; et al. Axial attention in multidimensional transformers. arXiv 2019, arXiv:1912.12180. https://arxiv.org/abs/1912.12180. (accessed 10 Sep 2025).
22. He, Y.; Yang, G.; Yang, J.; et al. Meta grayscale adaptive network for 3D integrated renal structures segmentation. Med. Image. Anal. 2021, 71, 102055.
23. He, Y.; Yang, G.; Yang, J.; et al. Dense biased networks with deep priori anatomy and hard region adaptation: semi-supervised learning for fine renal artery segmentation. Med. Image. Anal. 2020, 63, 101722.
24. Shao, P.; Tang, L.; Li, P.; et al. Precise segmental renal artery clamping under the guidance of dual-source computed tomography angiography during laparoscopic partial nephrectomy. Eur. Urol. 2012, 62, 1001-8.
25. Grand Challenge. Kidney Parsing Challenge 2022. https://kipa22.grand-challenge.org/. (accessed 2025-09-10).
26. Staal, J.; Abràmoff, M. D.; Niemeijer, M.; et al. Ridge-based vessel segmentation in color images of the retina. IEEE. Trans. Med. Imaging. 2004, 23, 501-9.
27. Hoover, A.; Kouznetsova, V.; Goldbaum, M. Locating blood vessels in retinal images by piecewise threshold probing of a matched filter response. IEEE. Trans. Med. Imaging. 2000, 19, 203-10.
28. Fraz, M. M.; Remagnino, P.; Hoppe, A.; et al. An ensemble classification-based approach applied to retinal blood vessel segmentation. IEEE. Trans. Biomed. Eng. 2012, 59, 2538-48.
29. Kaggle. Satellite-road-segmentation-dataset. https://www.kaggle.com/datasets/timothlaborie/roadsegmentation-boston-losangeles/. (accessed 2025-09-10).
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data



















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].