Multimodal semantic communication system based on graph neural networks
Abstract
Current semantic communication systems primarily use single-modal data and face challenges such as intermodal information loss and insufficient fusion, limiting their ability to meet personalized demands in complex scenarios. To address these limitations, this study proposes a novel multimodal semantic communication system based on graph neural networks. The system integrates graph convolutional networks and graph attention networks to collaboratively process multimodal data and leverages knowledge graphs to enhance semantic associations between image and text modalities. A multilayer bidirectional cross-attention mechanism is introduced to mine fine-grained semantic relationships across modalities. Shapley-value-based dynamic weight allocation optimizes intermodal feature contributions. In addition, a long short-term memory-based semantic correction network is designed to mitigate distortion caused by physical and semantic noise. Experiments performed using multimodal tasks (emotion analysis and visual question answering) demonstrate the superior performance of the system. Under low signal-to-noise ratio conditions, the proposed BERT-ResNet and GCN–GAT enhanced deep semantic communication (BR-GG-DeepSC) model achieves higher accuracy than conventional methods, while reducing the total number of transmitted symbols to approximately 33% of that in conventional approaches. These results validate the robustness, efficiency, and potential of the proposed system for practical deployment in resource-constrained environments.
Keywords
1. INTRODUCTION
The exponential growth of multimodal data, which comprise text, images, audio, and videos, has fundamentally transformed communication systems. This has led to the requirement for efficient data transmission and advanced semantic understanding. Conventional communication frameworks based on Shannon’s syntactic-focused theory emphasize bit-level accuracy but fail to address the semantic richness and contextual dependencies of multimodal interactions. This limitation is particularly evident in bandwidth-constrained environments, where channel noise and resource competition compromise reconstruction fidelity and task performance. For example, in emotion analysis tasks, the transmission of raw pixels and text tokens without semantic compression results in significant redundancy. Moreover, the independent processing of modalities fails to leverage cross-modal correlations, leading to suboptimal accuracy. These challenges highlight the urgent requirement for a paradigm shift toward semantic-aware communication systems that prioritize “meaning” over “bits”.
Recent advancements in semantic communication have leveraged deep-learning architectures, such as transformers and recurrent neural networks, to extract and transmit task-relevant features. For example, research on semantic communication focusing on single-modal scenarios, such as text or images, has significantly improved system transmission performance compared to traditional communication[1-3]. Additionally, advanced multimodal frameworks typically integrate various modalities, including text, images, and videos[4,5]. However, fully harnessing the synergistic potential of multimodal data is also one of the areas that require further investigation. For instance, in visual question answering (VQA), spatial image regions must be aligned with contextual text phrases using adaptive interaction mechanisms that cannot be provided by current static fusion approaches. Additionally, transmission-induced distortions, including semantic noise from ambiguous symbols and physical noise from fading channels, are seldom addressed comprehensively. This results in error propagation, which adversely affects downstream tasks. These limitations highlight the requirement for more sophisticated and holistic approaches for multimodal semantic communication.
Graph neural networks (GNNs) have emerged as a promising solution to these challenges because they can model relational data through graph structures. Graph convolutional networks (GCNs)[6] and graph attention networks (GATs)[7] have been successfully applied to social network analysis and molecular modeling. For example, GNN-based fusion methods typically construct static graphs based on fixed heuristics, which has some drawbacks, such as the inability to adapt to the evolving semantic relationships in multimodal streams[8,9]. Moreover, the lack of integration with domain knowledge (ontologies or knowledge graphs) limits their ability to resolve semantic ambiguities, particularly in low signal-to-noise ratio (SNR) regions where partial data loss occurs.
This study proposes a novel multimodal semantic communication system based on dynamic graph learning and knowledge-aware fusion. Our study makes four key contributions:
• Dynamic graph construction: A context-aware graph initialization framework integrates knowledge graph embeddings to enhance node features, thereby enabling semantically grounded representation learning. Unlike static graphs, edges are dynamically formed based on real-time cross-modal correlations and Shapley interaction values, thus ensuring adaptive relationship modeling.
• GAT–GCN synergy: A hybrid fusion layer combines the attention mechanism of GATs with the neighborhood aggregation of GCNs to capture local and global dependencies across modalities. This design mitigates oversmoothing in deep GNNs while preserving structural semantics.
• Cross-modal correction network: A Shapley-value-based long short-term memory (LSTM) module rectifies transmission distortions by leveraging auxiliary semantic information from complementary modalities. This approach uniquely quantifies modality contributions through the cooperative game theory and enhances robustness in noisy channels.
• Task-oriented efficiency: A resource-aware encoding strategy reduces image transmission symbols and improves task accuracy.
The remainder of this paper is organized as follows. Section 2 reviews related work on semantic communication. Section 3 introduces the system architecture, including dynamic graph construction and the GAT–GCN fusion layer. Section 4 presents the system model. Section 5 reports the experimental results and comparative analyses. Section 6 concludes the paper.
2. RELATED WORK
Semantic communication began to be widely studied in the 21st century because of the development of machine learning and other technologies. The key to semantic analysis and communication is the feature-extraction technology, which is the foundation for efficiently processing semantic information.
2.1. Semantic communication systems
Shannon and Weaver[10] first used the term semantic communication and categorized the communication problem into three dimensions: (1) the technical dimension, which focused on the accurate transmission of communication symbols; (2) the semantic dimension, which explored how to accurately convey the meaning behind a symbol; and (3) the validity dimension, which examined whether transmitted symbols could achieve set goals as expected. They emphasized that valuable information for human beings was a perfect combination of its form (syntactic information), meaning (semantic information), and utility (pragmatic information), and semantic information was the core embodiment of this whole[11-15].
Subsequently, Cavagna et al. applied probability logic to conduct in-depth research on the semantic information contained in words and sentences, proposed the conceptual framework of semantic information theory, and suggested that the semantic information of sentences should be defined based on the logical probability of their content[16]. Barwise and Perry further defined semantic information using the principle of situation logic. However, Floridi noted a fundamental paradox in Carnap and Bar-Hillel’s semantic communication theory: contradictory sentences yield an infinite amount of information. To address this, he proposed the theory of strong semantic information[17]. In 2011, Alfonso introduced class distortion, providing a new perspective for the measurement of semantic information. Niu et al. used the trinity of information to systematically summarize the theory of semantic communication and proved the uniqueness of semantic information representation[13].
Although semantic information has been studied for decades, the theoretical framework of semantic communication remains immature compared with the well-established transmission framework in classical information theory. In recent years, data transmission rates have increased exponentially owing to the global deployment of 5G and the deep integration of the Internet of Things (IoT) with artificial intelligence. This growth has led to severe data redundancy, while channel capacity has gradually approached the Shannon limit[18-23]. In this context, semantic communication has attracted considerable attention, particularly with advances in machine learning that make its practical implementation feasible.
2.2. Text communication systems
The breakthrough of deep learning in natural language processing, particularly in machine translation, inspired Farsad et al. to design an innovative text-transmission system. In this system, a sender transmitted information to a receiver using limited bit resources by erasing a channel. Farsad et al. first used the pretraining tool of Global Vectors for Word Representation (GloVe)[19] to convert words into embedded vectors that could capture semantics and then used the sequence-to-sequence learning mode in machine translation[24,25] to build coders and decoders based on LSTM. The embedded word vectors were used as input, and the most likely word sequences were determined through the beam search algorithm[26], thereby embedding rich semantic content into sentence reconstruction.
Although word embedding models such as GloVe and Word2Vec can capture semantic connections between words, they are not well-suited for representing syntactic structures[1,27-29]. Consequently, Farsad
To address these challenges, researchers have proposed a new architecture known as the transformer, which has attracted widespread attention. This architecture can efficiently extract both semantic and syntactic information from complete sentences[30]. The transformer network employs a multihead attention mechanism that enables the parallel processing of multiple sentence features[31]. Compared with recurrent neural networks such as LSTM, the transformer has lower computational complexity, greater parallel processing capability, and the ability to capture long-term dependencies in input sequences. These advantages make it particularly effective for handling long text and complex grammatical structures[2]. Zhou et al. further proposed a flexible semantic-extraction method based on the general transformer, introducing an adaptive loop mechanism that broke the original fixed structure and stimulated extensive research on transformer optimization[32].
2.3. Image communication systems
Lee et al. proposed a basic image transmission environment for processing image data, in which IoT devices sent images to a server for recognition[3]. These devices communicated with the server through a direct point-to-point wireless connection. The additive white Gaussian noise (AWGN) and Rayleigh fading channels were used. In contrast to the conventional multilevel communication model, Lee et al. proposed a joint transmission recognition scheme based on deep learning, which used recognition accuracy as the main performance evaluation index and adopted the ResNet architecture[3], which is well known for its excellent performance and few parameters. To realize feature extraction before image transmission, the RESNET deep neural network (DNN) is divided into two parts. The first six layers serve as the feature extractor at the sending end to extract the semantic information of the image, and the remaining layers function as the recognizer at the receiving end.
To achieve adaptive semantic extraction in noisy channels, Lee et al. used a DNN as the channel encoder and decoder to achieve joint semantic channel coding[3]. To verify the practicality of this scheme, they compared it with three other series of compression identification schemes in analog and digital transmission modes. Experimental data showed that the proposed scheme exhibited the best performance in terms of recognition accuracy and computational complexity.
2.4. Multimodal communication systems
Multimodal communication refers to the use of multiple media for information transmission, such as text, voice, and video. Semantic communication effectively transmits information by analyzing the content of these media and understanding their meaning. Research on multimodal semantic communication focused on the integration of information in different modes and effective semantic analysis and communication.
Xie et al. designed a multimode data semantic communication system using memory, attention, and combined neural networks to answer visual questions. In addition, they unified the semantic coding architecture of an image transmitter and text transmitter based on the transformer and proposed a new semantic decoder network composed of a query module and an information fusion module[28]. Compared with another work, this scheme achieved extremely high response accuracy in terms of perfect and imperfect channel state information. Although the performance of task-oriented semantic communication has been significantly improved, the model must be updated once a task changes. To solve this problem, Zhang et al. developed a unified deep learning-enabled semantic communication system (U-DeepSC), which was the first unified semantic communication system to provide services for various tasks. U-DeepSC simultaneously handled numerous tasks in three modes: image, text, and voice[4]. In addition, channel noise was added to the training process so that U-DeepSC could realize the dynamic inference of an adaptive layer under different channel conditions.
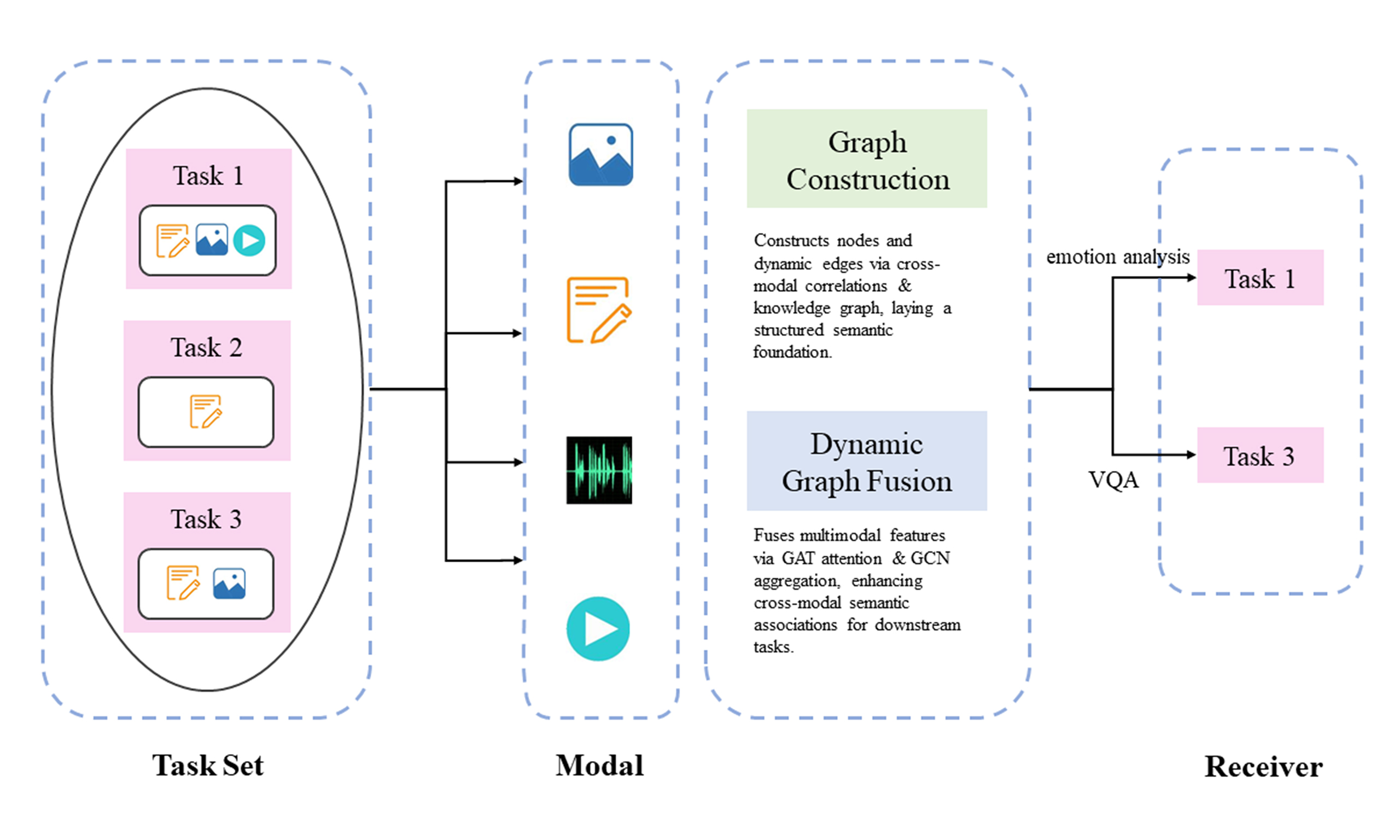
In summary, most existing research focuses on single-mode data. Cross-modal semantic communication is suitable for the interaction and integration of different modal data and expands the field and application scenarios of data applications. The architecture of multimodal semantic communication is shown in Figure 1.
3. MULTIMODAL
3.1. System model and problem formulation
The feature fusion of multimodal data is the core issue in semantic communication. Conventional methods tend to process images and text separately and then realize fusion through simple splicing or weighted summation. However, this method makes it difficult to deeply mine the correlation between modes.
To solve these problems, this study introduces a knowledge mapping mechanism and uses an external semantic knowledge base to assist in the understanding and fusion of multimodal features. A knowledge map contains concepts, entities, and their relationship information such as the history, style, and geographical location of buildings. This information can be combined with the visual features of the image and key phrases in the text in the semantic coding stage to generate an accurate semantic representation.
3.2. Multimodal feature fusion method
Assuming the semantic features of text, MT, and an image, MI, each text and visual unit is regarded as a graph node, and the node set is defined as V. Edges are defined according to the semantic and spatial relationships between nodes, such as between adjacent regions in the image, between semantically related words in the text, and between image regions and related text descriptions. The edges between nodes are determined in real time according to the input multimodal data. For example, when processing each pair of text image data, the connection relationship between edges is determined by calculating the correlation between the text and image features or by defining rules based on prior knowledge. If an object in the image is mentioned in the text, an edge is established between the corresponding text and image nodes. In addition, a knowledge map is introduced to assist feature fusion, and its rich concept, entity, and relationship information can help determine the connections between edges. For example, for images and related text containing specific objects, knowledge maps can provide additional information about objects. This makes the calculation of the correlation between text and image features more accurate and establishes the edges between nodes more reasonably.
A knowledge map is a graph structure used to represent and organize knowledge. It consists of entities, relationships, attributes, and other elements and is used to describe objects and their relationships in the real world. In the knowledge map, the structure and node characteristics of the graph remain unchanged throughout the training and reasoning process[1]. A knowledge map is defined as follows:
where G represents the knowledge map, E indicates the entity set, R denotes the relationship set, and F signifies the set of fact triples (E, R, F).
Entity E: This figure includes movies, directors, actors, and other entities. The movies include Oppenheimer, Don’t Look Up, Inception, and Interstellar; the director is Christopher Nolan; and the actors include Cillian Murphy, Leonardo DiCaprio, and Marion Cotillard.
Relationship R: Different entities are connected through specific relationships. There is a “direct” relationship between Christopher Nolan and Oppenheimer, Inception, and Interstellar. There is an “act” relationship between Cillian Murphy and Oppenheimer and Inception; Leonardo DiCaprio and Inception and Don’t Look Up; and Marion Cotillard and Inception. There is a “cooperate” relationship between Leonardo DiCaprio and Marion Cotillard in Inception.
Meaning F: Through this knowledge map, one can intuitively observe the relationship between characters and works in the film industry, which is convenient for information retrieval and knowledge reasoning, such as rapidly understanding the works of directors and co-actors.
Let the additional semantic information provided by the knowledge map be k, which can be integrated into the process when calculating the correlation between nodes i and j.
where s (i, j) is the correlation score of nodes i and j, Ti is the text node feature, Ij is the image node feature, and f is the correlation calculation function. The edge set is denoted as e, and the dynamically constructed graph is given as g = (V, e). This dynamic construction method allows the graph structure to change adaptively according to different input data and accurately reflects the real-time correlation between multimodal data. The feature fusion module based on GNN is shown in Figure 2. This figure is adapted from the multi-view sentiment analysis (MVSA) dataset (https://mcrlab.net/research/mvsa-sentiment-analysis-on-multi-view-social-data/). The MVSA dataset, developed by the Multimedia Communications Research Laboratory, is also used in the experiment.
3.3. Fusion feature representation initialization
For text node i (corresponding to MT), initial feature htext0 is the feature representation of the text unit. The information about related concepts in the knowledge map is adjusted to obtain
where g is the fusion function and Ktext is the text-related information in the knowledge map.
For image node j (corresponding to MI), initial feature himage0 is the feature representation of the image unit. In a similar manner, we obtain
where Kimage is the image-related information in the knowledge map.
In this manner, the semantic expression ability of the initial features is enhanced using the knowledge map so that the model can deeply mine the potential semantics of multimodal data in subsequent processing.
3.4. GAT–GCN fusion layer
GAT: In the fusion process of each layer, the attention mechanism of the GAT is first introduced to calculate the attention coefficient eij between nodes. For nodes i and j, the attention coefficient is calculated as follows:
where w is the learnable weight matrix, a is the attention function, and hil and hjl represent the characteristics of the nodes in layer l. Then, the attention coefficient is normalized using the softmax function.
where Ni is a collection of neighboring nodes. The information obtained from the knowledge map can be used in the calculation to make the model focus on the nodes that are closely related to the concepts in the knowledge map. A new formula for calculating the attention coefficient is obtained as follows[1]:
Feature enhancement (GCN part): Feature fusion is performed based on the calculated attention weight combined with the graph convolution operation of the GCN. First, we calculate normalized adjacency matrix
where
where
3.5. Cross-attention mechanism
To achieve more efficient feature fusion, we extend the idea of single-layer cross attention to realize a multilayer two-way cross-attention mechanism and capture rich associations between images and text through multiple interactions in each layer. This mechanism can cross learn image and text features at multiple levels and further improve the fusion of multimodal features.
Suppose there are image features hil ∈
3.5.1. Image-to-text multilevel learning
In the L-th layer, image hil interacts with text htl as a query through the cross-attention mechanism. For the image-to-text cross-attention mechanism, image feature hil is used to generate a query, followed by text feature htl.
The final output is obtained as
The output is combined with the original image features, as follows:
3.5.2. Text-to-image multilevel learning
In multilayer text-to-image learning, text feature htl is used to generate a query, and image feature hil is used to generate a key and value. Finally, the image and text features are combined to obtain the final features as follows:
Through the interaction of multiple attention layers, the multilayer two-way cross-attention mechanism not only improves the information flow between the images and text but also allows features to be refined and adjusted at multiple levels, thus providing strong modeling ability for multimodal learning tasks. This method can deeply mine the fine-grained semantic association between images and text and improve the effect of downstream tasks.
The multimodal feature fusion method based on the GNN and multilayer two-way cross attention can focus on important node relationships using the attention mechanism of the GAT and effectively fuse neighbor node information by utilizing the graph convolution operation of the GCN. Furthermore, it fuses features to accurately model the complex relationships in multimodal data and improve the performance of multimodal tasks.
4. SYSTEM MODEL
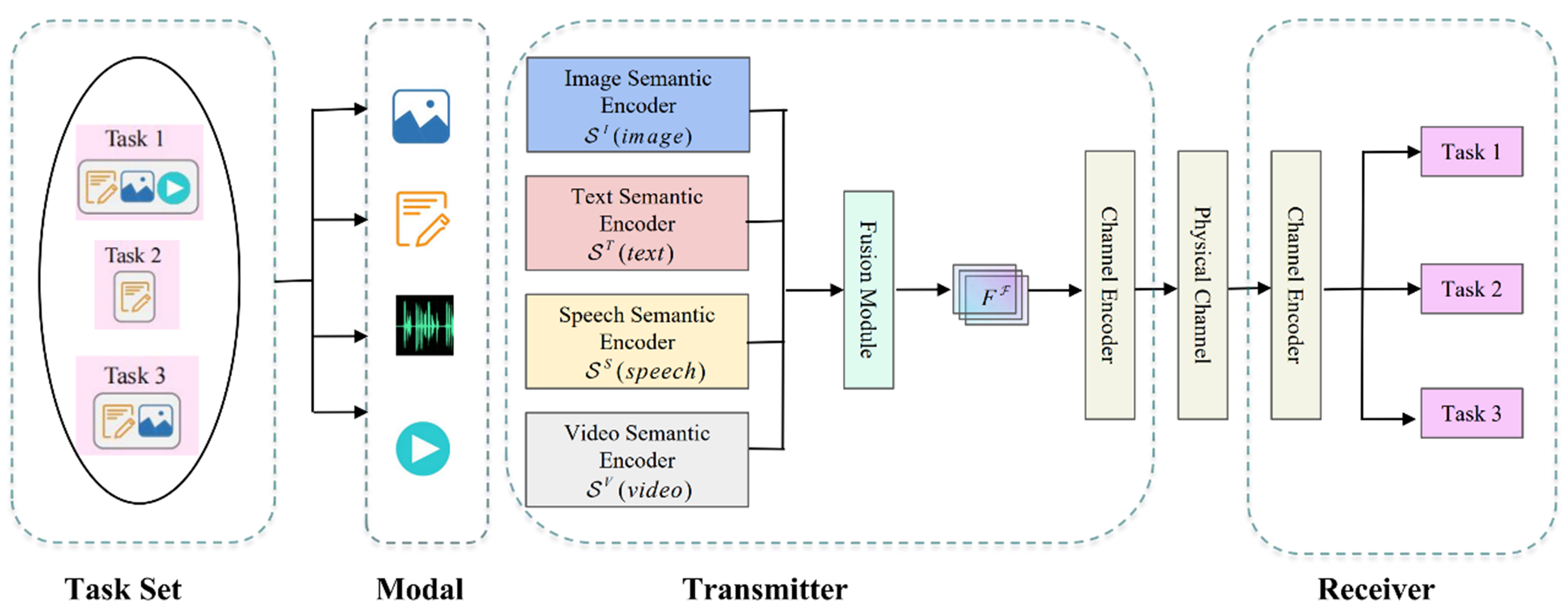
A multimodal semantic communication system model [BERT-ResNet and GCN–GAT enhanced deep semantic communication (BR-GG-DeepSC) model] based on a GNN is proposed for multimodal emotion analysis tasks, as shown in Figure 3.
Figure 3. BR-GG-DeepSC model. BR-GG-DeepSC: BERT-ResNet and GCN–GAT enhanced deep semantic communication.
4.1. Image transmitter
An image sender is an important module for processing image information in the multimodal-data semantic communication system, which mainly comprises a semantic encoder and channel encoder. When an image enters the image sender, it is preprocessed and adjusted to a uniform resolution (224 × 224) to ensure consistency and effectiveness in subsequent processing. Then, the image is input into the semantic encoder built by RESNET-101. The semantic encoder uses the powerful feature extraction ability of the pretraining model to deeply mine the semantic features in the image, as calculated by
where MI ∈
where XI ∈
4.2. Text transmitter
The text sender is responsible for processing text information in the multimodal-data semantic communication system. Its architecture uses the method described in Section 3 as the semantic encoder and the dense layer as the channel encoder. When text message sT = (s1,T, s2,T, …, sl,T) enters the text sender, where sl,T indicates the l-th word in the sentence to be transmitted, it is first processed by the embedding layer. The embedding layer maps the words in the text to numeric vectors, ST ∈
where MT ∈
where XT ∈
Similar to the image transmitter, the transmission signal must be converted into a complex signal by first using the shaping operation, xT ∈
4.3. Receiver
The receiver is the core of the multimodal-data semantic communication system. It mainly consists of a convolution layer of different units as the image channel decoder, a dense layer as the text channel decoder, and the GAT–GCN as the semantic decoder. When the receiver receives signal Y, it first estimates the signal. According to the system model, the relationship between received signal Y, channel H, transmission symbol X, and noise N is given by
where H is the channel status, X =
The system introduces channel estimation knowledge to improve the training speed and decision accuracy. Based on the channel gain and zero-forcing detector, the transmitted signal can be estimated as
which indicates the influence of the noise and introduces deviations between the estimated signal
Then, the semantic recovery of the signal is carried out through the image and text channel decoders. The calculation method is as follows:
Similarly,
where
After obtaining the semantic information of text
where SF(·; φ) is a semantic fusion network with trainable parameter φ.
Data are easily disturbed by noise during transmission in multimodal semantic communication, which leads to the distortion of different modal data and affects the accurate transmission of semantic information. A dynamic weight-allocation scheme based on cross-modal auxiliary semantic information and Shapley interactions is designed to solve this problem. An LSTM network is used to fuse the modal-specific and auxiliary semantic information to correct the distortion of different modal data. In addition, different modal-specific loss functions are used to train the network to improve the semantic quality of signal recovery. The Shapley interaction value is an index used to measure the overall contribution of each participant in a cooperative game. In multimodal semantic communication, it can be used to measure the correlation between different modal semantic features. Suppose there is a text semantic feature set, T = {t1,
where ϕ represents the Shapley value, which is calculated as follows:
Here, S represents all semantic feature sets involved in the game, R is any subset of S that does not contain feature k, v(R) indicates the contribution value to the multimodal semantic similarity of the overall goal when the semantic features cooperate in subset R, and v(R
After obtaining normalized weight ξij, the auxiliary semantic features are calculated as
The modal-specific and auxiliary semantic information are fused using the LSTM network. The forget gate, input gate, memory unit, and output gate of the LSTM network are calculated as follows:
where Wf, Wi, WC, and Wo are the weight matrices; bf, bi, bC, and bo are the bias terms; σ is the sigmoid function;
If
4.4. Loss function
The proposed system uses a design concept based on task orientation to accurately analyze the emotions of multimodal data. In this system, unlike conventional communication systems, images and text are not accurately restored but the emotion at the receiving end is directly analyzed. Therefore, the conventional loss function based on bit error or symbol error is not applicable. To improve the accuracy of emotion analysis, the system uses a loss function that is suitable for emotion classification tasks, namely, the cross-entropy (CE) loss function. The main function of CE is to measure the probability distribution difference between real and predicted emotional tags, which is calculated as follows:
Here, p(E) is the probability of real emotion tag e and p(
Joint learning is performed by defining joint loss function L containing multiple task-related loss items. In the multimodal emotion analysis task, in addition to the original CE loss function, a loss item is added to measure the effect of semantic feature extraction and fusion. A semantic consistency loss item, LKG, based on the knowledge graph is introduced to measure the consistency between the fused features and semantic information in the knowledge graph. Suppose the semantic representation obtained from the knowledge graph is yKG and the semantic features after model fusion are expressed as
An end-to-end training method is adopted during the training process, and the parameters of the image transmitter, text transmitter, receiver, and interaction part with the knowledge graph are simultaneously updated. We consider the optimization algorithm based on gradient descent as an example and calculate the gradient,
This improves the ability of the semantic feature extraction and fusion and the accuracy of emotion analysis. During back propagation, the loss items related to the knowledge map enable the model to utilize the information in the knowledge map and optimize the extraction and fusion of semantic features.
In semantic recovery, different modes adopt specific loss functions when training the network. For image modes, the weighted combination of the mean square error (MSE) loss and perceptual loss is used as the loss function, as given by
where α is the weight coefficient,
The following CE loss function is used for the text mode:
where q(wn) is the true probability of the n-th word appearing in the recovered sentence, p(wn) is the prediction probability, and N is the total number of words in the sentence.
By introducing knowledge mapping and joint learning, the model effectively mines semantic information and associations across different modalities during multimodal feature fusion. The knowledge map enriches the semantic depth of node feature initialization. The joint learning mechanism allows continuous optimization of semantic feature extraction and fusion during training. In multimodal emotion analysis, the model accurately captures emotional cues in images and text. When processing multimodal data with human expressions and related text, the knowledge map clarifies the relationship between expressions and emotions, enhancing the model’s understanding of emotional semantics. This understanding is further refined through joint learning, improving the accuracy of emotion analysis. Additionally, minimizing the loss function and updating network parameters with the backpropagation algorithm helps the cross-modal correction network accurately correct data distortion. This process enhances the semantic quality of signal recovery, leading to improved performance in multimodal semantic communication systems.
5. EXPERIMENTAL SETUP AND RESULTS
5.1. Experimental setup
Experiments are conducted to comprehensively evaluate the performance of the proposed multimodal-data semantic communication system in multimodal emotion analysis tasks, and the results are compared with those obtained using conventional communication methods. This dataset has multimodal characteristics and can present rich emotional expressions and simulate real scenes. Its labeling is of high quality and consistency, which is ensured through professional labeling and multilabeling mechanisms. Furthermore, it has a certain data scale and diversity, wide range of sources, and sufficient sample size. It is the standard benchmark dataset in the field of multimodal emotion analysis and can promote research in this field. The MVSA dataset comprises the MVSA-single dataset (5,129 text pairs) and MVSA-multiple dataset (19,600 text pairs), which have only one and three annotations for each text pair, respectively. The dataset contains rich image and text data and their corresponding emotion tags.
For text processing, the initialization of the text-embedding layer adopts a Gaussian distribution with zero mean and unit variance, and its shape is set as 300. C1, C2, K1, and K2 are set as the optimized values of 512, 128, 512, and 256, respectively, according to the experiment. The image channel encoder consists of carefully designed convolution layers. The numbers of filters in the four convolution layers are 256, 128, 256, and 512. The kernel size is 3 × 3, and the rectified linear unit (ReLU) activation function is employed. The text-channel encoder comprises five dense layers with 256, 256, 256, 256, and 512 neurons. The ReLU activation function is used, and the output of the channel decoder is processed using the LayerNorm method to stabilize the training process. The dynamic graph network is designed according to the requirements of the multimodal emotion analysis task, including multiple GCN and GAT processing units, and its parameters are optimized through training.
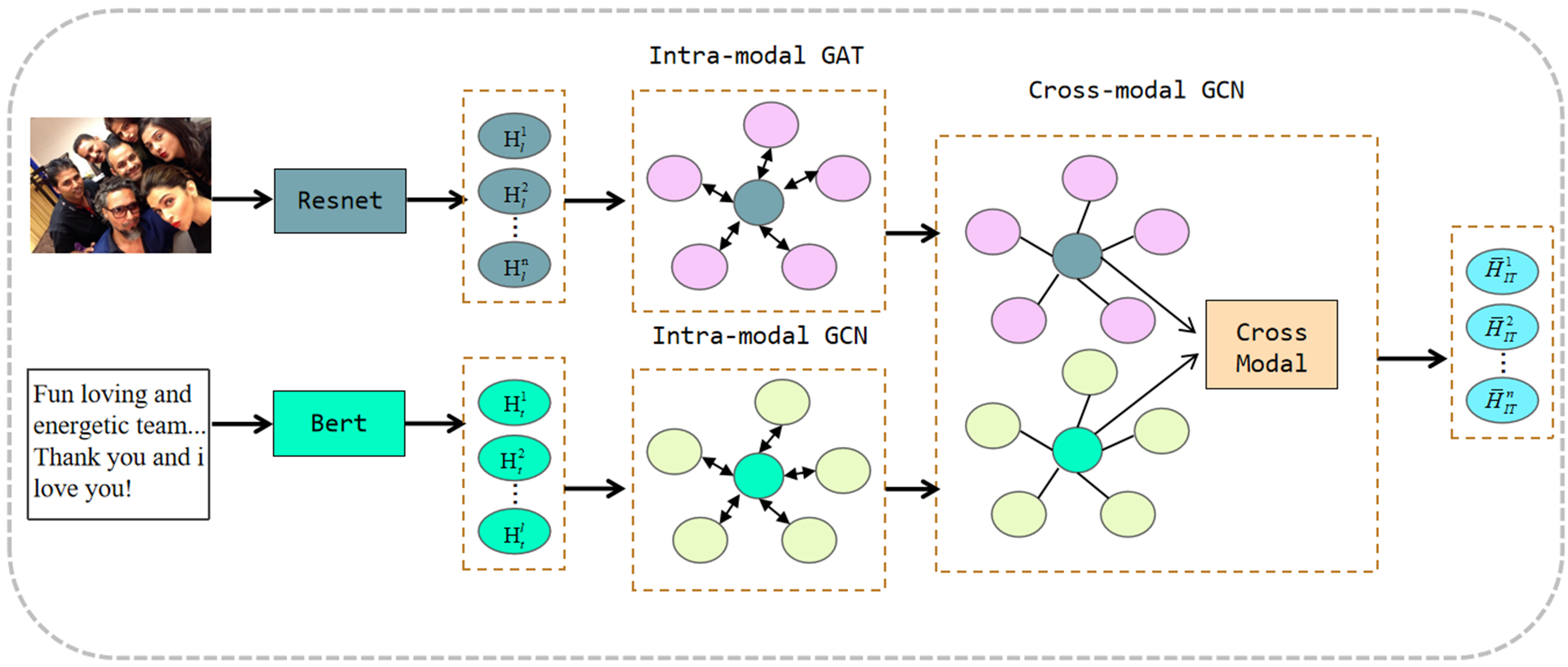
A dynamic graph network is a multimodal information fusion model based on a GNN, as shown in Figure 4. The figure is also adapted from the MVSA dataset (https://mcrlab.net/research/mvsa-sentiment-analysis-on-multi-view-social-data/). The image component uses the RESNET model to extract visual features from images, while the text component employs the Bert model for semantic analysis of phrases such as “fun-loving and energetic team”.
In the graph construction phase, nodes represent individuals in the image, with edges based on visual similarity and spatial relationships. In the text graph, nodes represent words, connected by grammatical or semantic associations.
During dynamic graph fusion, the image and text graphs combine, linking character nodes to relevant vocabulary in the text. This aids in integrating visual and semantic information for tasks such as image classification, efficient retrieval, and emotional analysis of visual and textual cues.
The Adam optimizer, with a learning rate of 0.0001, adjusts parameters to minimize the loss function. Evaluation methods include JPEG compression, Huffman coding, and low-density parity-check (LDPC) coding, alongside single-modality emotion analysis using classifiers[1].
Comparison algorithms include:
• Error-free transmission: Complete images and texts are input into RESNET-101 and Bi-LSTM without noise for performance benchmarking.
• Conventional methods: JPEG compression at 75% and LDPC coding at a 1/3 rate are applied for performance assessment.
• Single-modality prediction: The transmitter operates in single mode to highlight the advantages of multimodal fusion.
Methods are evaluated on emotion analysis accuracy, number of transmitted symbols, and computational complexity, indicating system performance and efficiency.
5.2. Results
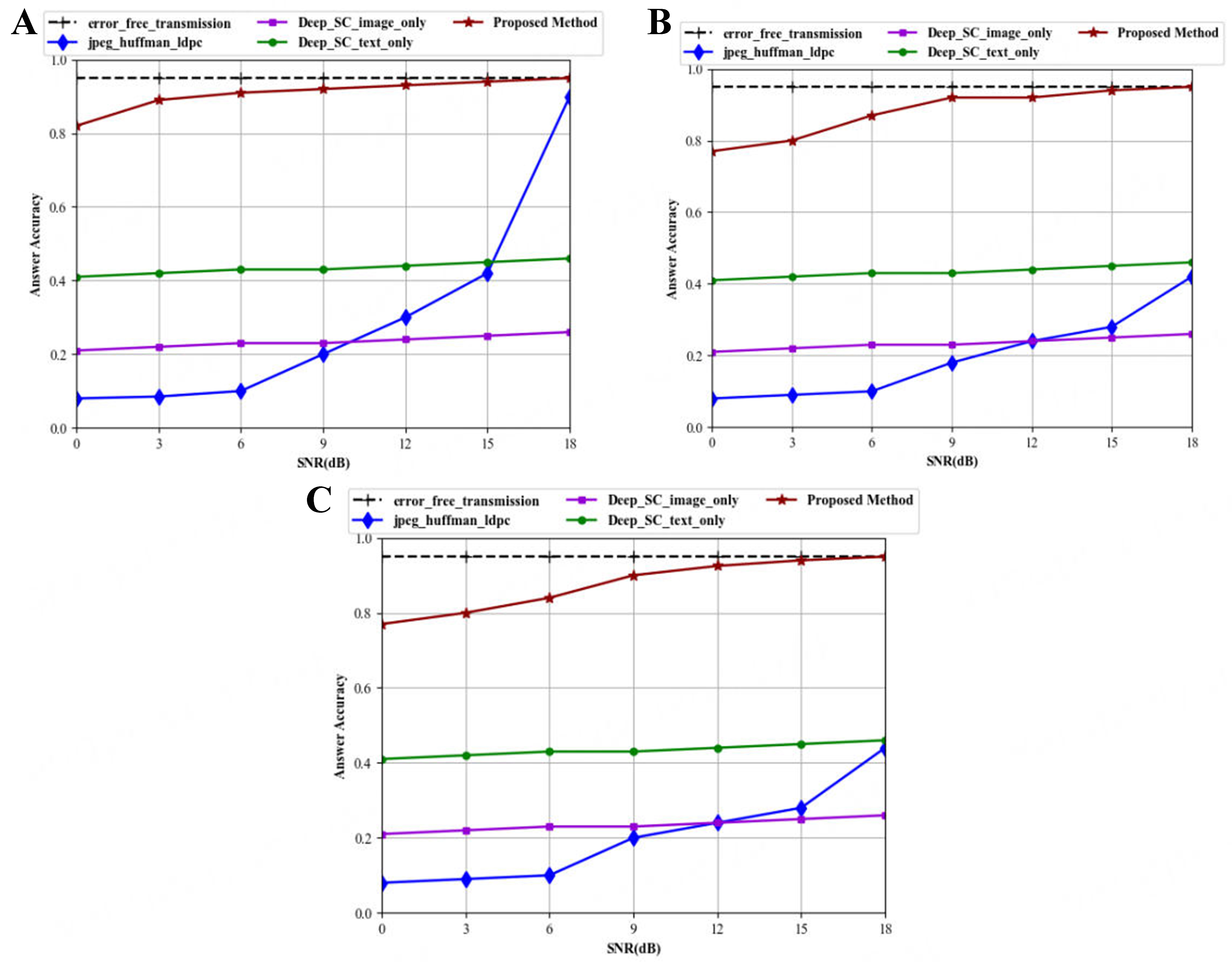
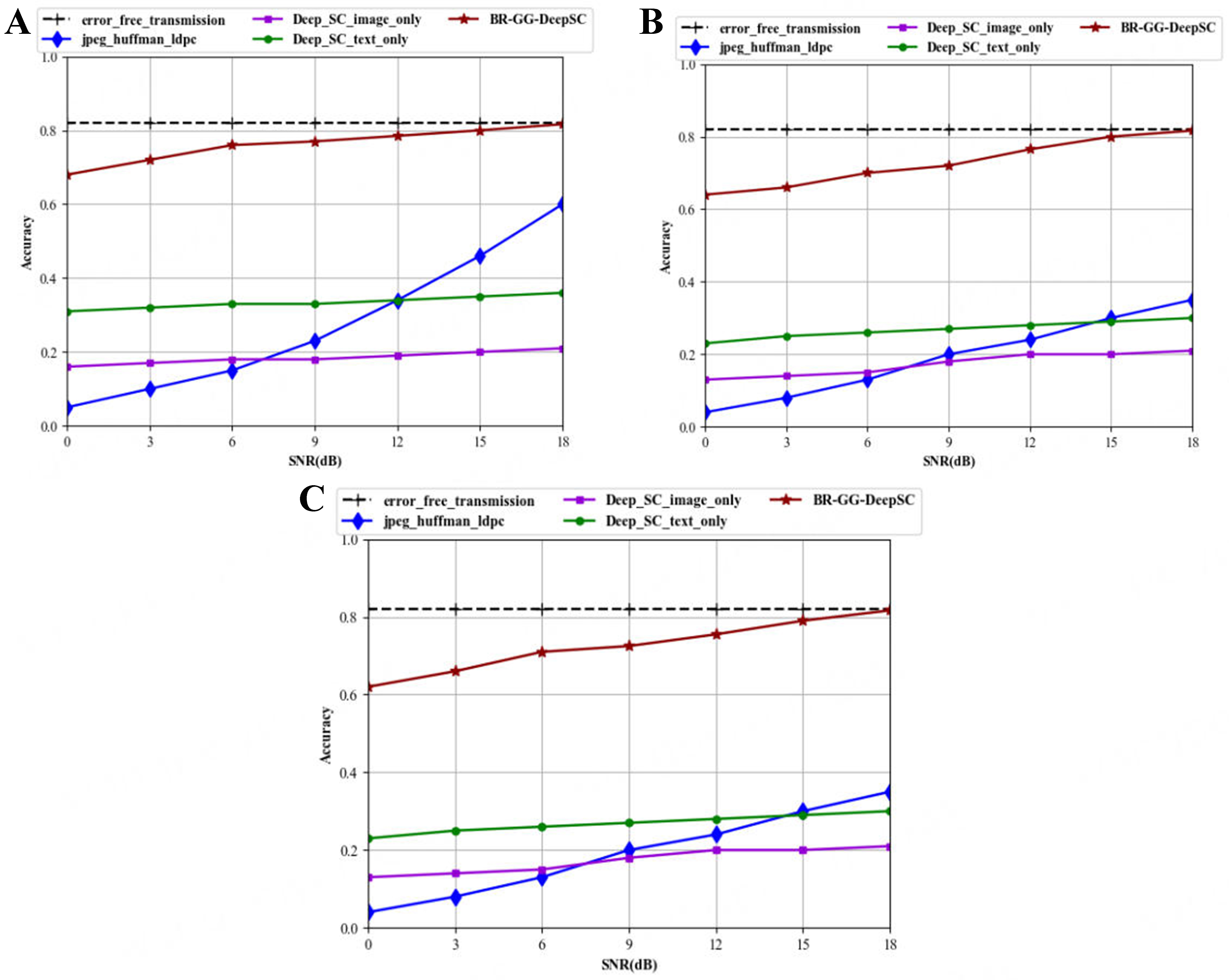
The accuracy of emotion analysis and the number of transmitted symbols for the proposed multimodal-data semantic communication system and conventional methods are obtained under different channel conditions [Figure 5].
Figure 5. Comparison of accuracy of different methods for emotion analysis task. (A) AWGN channel; (B) Rayleigh channel; (C) Rician channel. AWGN: Additive white Gaussian noise.
Figure 5 illustrates the performance of the proposed system under different channel conditions, including AWGN channel, Rayleigh channel, and Rician channel. From the figure, we can see that the proposed scheme exhibits high accuracy, especially in the low SNR region, where its accuracy is significantly better than that of conventional methods. When the SNR is low, conventional methods are susceptible to noise interference during the transmission of image and text information, leading to lower accuracy in emotion analysis. However, accuracy gradually increases as the SNR improves. For the single-mode emotion analysis methods (which use only images or text), accuracy remains relatively stable across different channel conditions, but it is still lower than that of the multimodal fusion system. In the high-SNR region, the emotional analysis accuracy of the proposed BR-GG-DeepSC system approaches its upper limit, indicating strong performance stability.
Similarly, we applied the proposed algorithm to the VQA task, and obtained similar results, as shown in Figure 6. The simulation results verify the performance in the AWGN channel, Rayleigh channel, and Rician channel respectively. The selection of these three channels is based on the channel models commonly used in the performance evaluation of semantic communication[28].
Figure 6. Comparison of accuracy of different methods for VQA task. (A) AWGN channel; (B) Rayleigh channel; (C) Rician channel. VQA: Visual question answering; AWGN: additive white Gaussian noise.
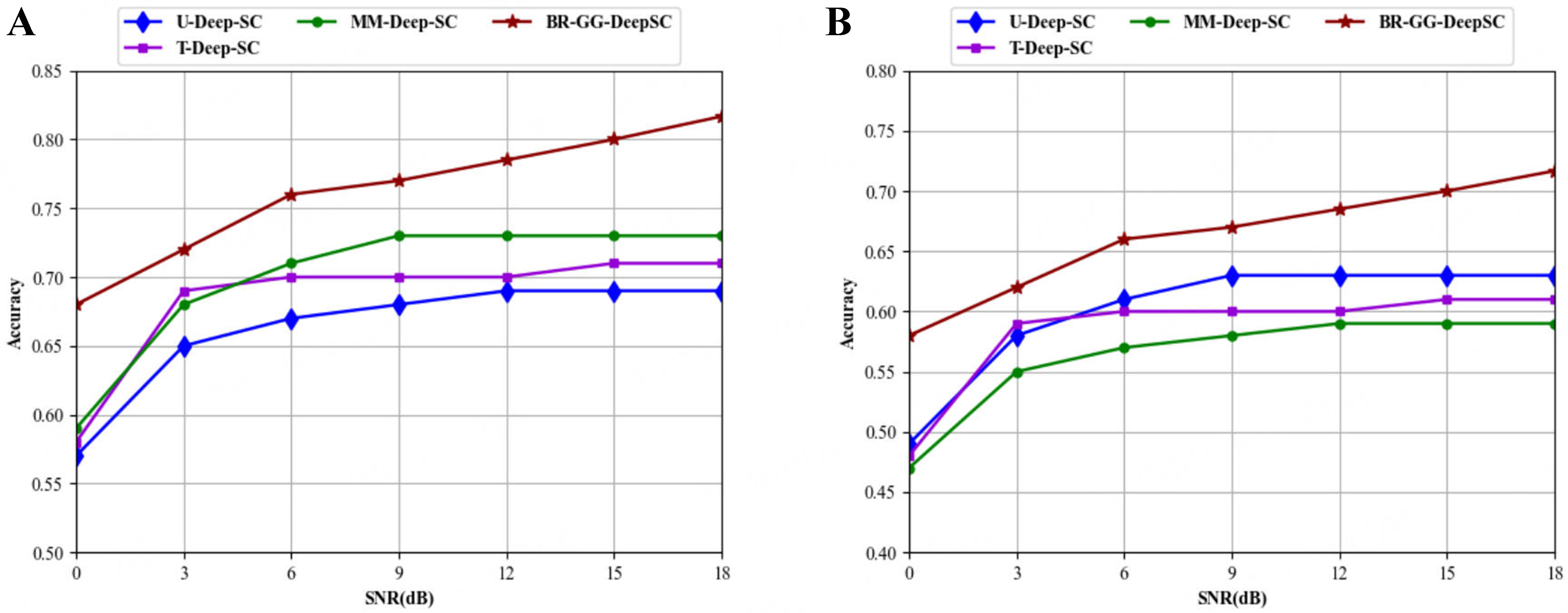
Figure 7 shows that the proposed model achieves better results compared with the mainstream deep-learning-based semantic communication systems. MM-IMDb (Multimodal IMDb) is an information system that integrates multimodal data with the traditional IMDb database. It is typically used in research within the fields of machine learning and computer vision to enhance the understanding and analysis of movies, TV shows, and other media content. VQA v2 is the second version of the VQA dataset, aimed at improving the accuracy and diversity of question answering. Figure 7 compares the accuracy of four deep-learning-based semantic communication systems (U-Deep-SC, MM-Deep-SC, T-Deep-SC, BR-GG-DeepSC) across varying SNR levels. For Figure 7A, as SNR increases from 0 to 18 dB, the BR-GG-DeepSC model shows a continuous and prominent rise in accuracy, outperforming U-Deep-SC, MM-Deep-SC, and T-Deep-SC. Figure 7B exhibits a similar trend: with the growth of SNR, BR-GG-DeepSC maintains a higher accuracy compared to the other three models, clearly demonstrating its superiority in different SNR environments for semantic communication tasks.
Figure 7. Comparison of the accuracy of different deep learning methods for various tasks. (A) VQAV2; (B) MM-IMDB. VQAV2: Visual Question Answering v2.0; MM-IMDB: MultiModal Internet Movie Database.
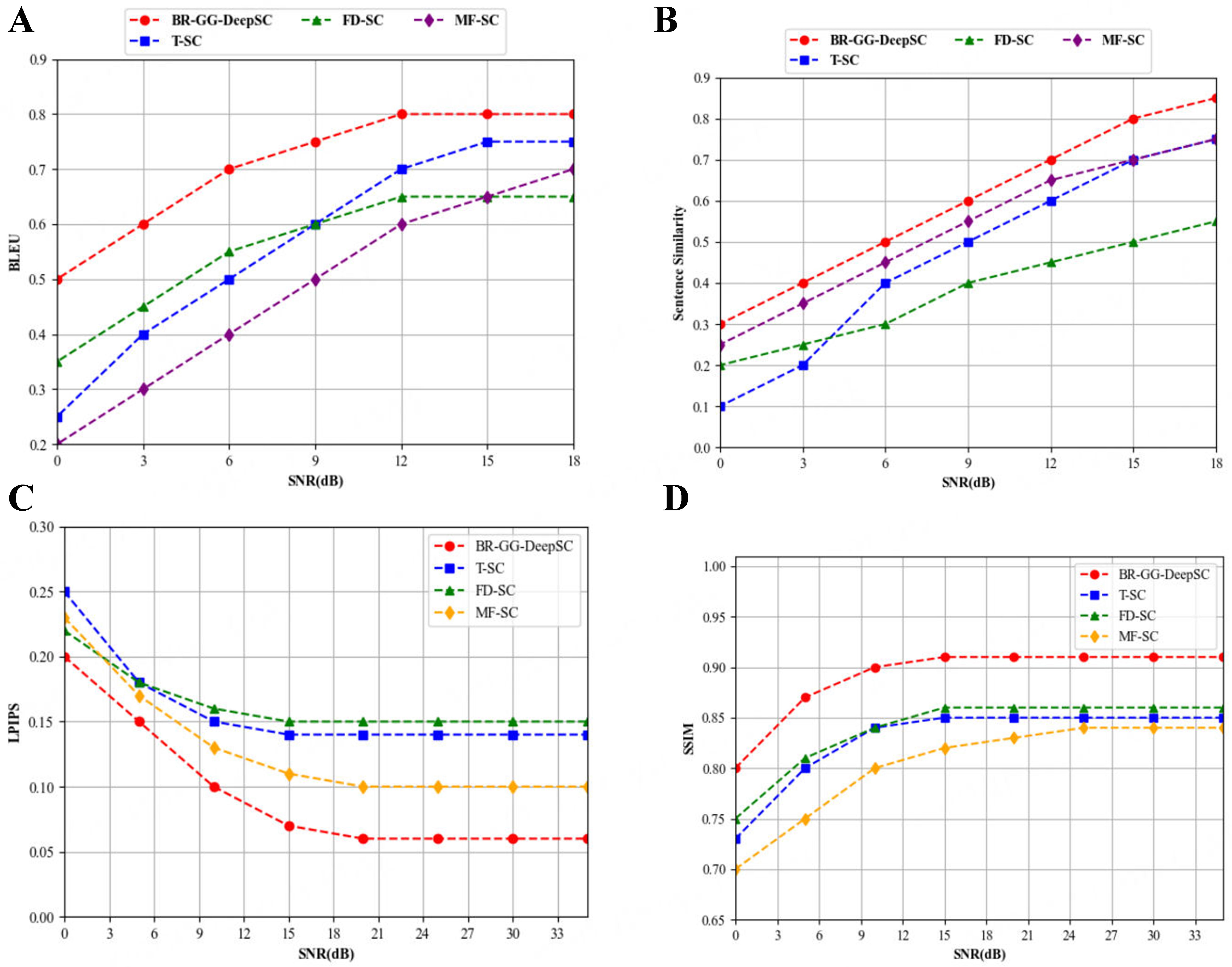
Figure 8 shows the experimental results obtained for text and image recovery. The performances of the different methods of multimodal semantic communication are compared under various SNRs. Figure 8A and B demonstrates the changes in sentence similarity and the Bilingual Evaluation Understudy (BLEU) score with the SNR, respectively, in the presence of semantic noise. The BR-GG-DeepSC method exhibits evident advantages at low SNRs and is superior to other models at high SNRs. Figure 8C and D presents the changes in the structural similarity index measure (SSIM) and learned perceptual image patch similarity (LPIPS) with the SNR when image semantic noise is present. BR-GG-DeepSC effectively reduces the impact of semantic noise at high SNRs. The semantic communication system better preserves image structural information at low SNRs. Its SSIM is the highest, outperforming other models at high SNRs. In addition, the proposed model achieves superior performance in terms of LPIPS compared with the other models.
Figure 8. Comparison of semantic recovery effects of different depth learning models for semantic recovery task. (A) BLEU score; (B) Sentence similarity; (C) LPIPS; (D) SSIM. BLEU: Bilingual Evaluation Understudy; LPIPS: learned perceptual image patch similarity; SSIM: structural similarity index measure.
Symbol transmission rate is typically an indicator of the performance of semantic communication. Table 1 compares the number of transmitted symbols between the proposed system and conventional communication methods when transmitting an image or text. For image transmission, the proposed system significantly reduces the number of transmitted symbols, indicating that the system has higher data compression efficiency and can utilize channel resources more effectively. For text transmission, although the number of symbols transmitted by the proposed system differs from that of the conventional method, its computational complexity and robustness under low SNR are advantageous. This implies that in text transmission, the proposed system can better balance the use of computing resources while ensuring transmission efficiency.
Comparison of the number of transmitted symbols
| Method | Source | Single symbols | Total symbols | Single ratio | Total ratio |
| BR-GG-DeepSC | Image Text | 12,544 128 | 62,720,000 6,400,000 | 30.1% 853.3% | 33% |
| Traditional communications | Image Text | 41,718 15 | 208,590,000 750,000 | / / | / |
For image transmission, BR-GG-DeepSC transmits 12,544 symbols, compared with 41,718 symbols for the conventional communication method. This demonstrates that BR-GG-DeepSC improves transmission efficiency and conserves resources. For text transmission, BR-GG-DeepSC and the conventional method transmit 128 and 15 symbols, respectively. Although BR-GG-DeepSC transmits more symbols for text, it provides greater robustness under complex channels and low SNR conditions. Overall, the numbers of transmitted symbols for image and text are approximately 30.1% and 853.3% of the conventional method, respectively. The increase in text symbols is considerably smaller than the reduction in image symbols. In total, BR-GG-DeepSC transmits roughly 33% of the symbols required by the conventional method, demonstrating its superior performance in reducing transmitted data - a fundamental advantage of semantic communication systems.
Table 2 presents the ablation experiment results of the BR-GG-DeepSC model on the multimodal MVSA and VQAv2 datasets in an AWGN channel at SNR = 0 dB, quantifying the independent contributions of each module. Values in parentheses indicate the percentage decrease compared to the full model. The results demonstrate that each component of BR-GG-DeepSC plays a crucial role in the system’s performance.
Ablation experiment
| Model variant | Emotion analysis | VQA | ||
| Acc (%) | F1-Score | Acc (%) | F1-Score | |
| Full model (BR-GG-DeepSC) | 85.2 | 0.841 | 78.6 | 0.772 |
| w/o Dynamic graph | 80.1 (-6.0%) | 0.789 (-6.2%) | 73.4 (-6.6%) | 0.718 (-7.0%) |
| w/o GAT-GCN fusion | 77.8 (-8.7%) | 0.761 (-9.5%) | 70.2 (-10.7%) | 0.683 (-11.5%) |
| w/o Shapley-LSTM | 82.3 (-3.4%) | 0.810 (-3.7%) | 75.1 (-4.5%) | 0.735 (-4.8%) |
| w/o Knowledge graph | 79.5 (-6.7%) | 0.781 (-7.1%) | 72.8 (-7.4%) | 0.705 (-8.7%) |
6. CONCLUSIONS
This study proposes the BR-GG-DeepSC multimodal semantic communication system, which implements knowledge mapping and joint learning to enhance the extraction and fusion of semantic features. The experiments utilize image and text information to conduct emotional analysis and VQA tasks. The system employs semantic and channel encoders to process semantic information and fuse different types of information for task accomplishment. Additionally, a cross-modal correction network based on the Shapley value is designed, utilizing an LSTM network to integrate information and correct distortions, with different loss functions applied for training in various modes.
In the multimodal emotional analysis tasks, the application of knowledge mapping and joint learning significantly enhances the system’s accuracy. At low SNR, the proposed system maintains high accuracy in the presence of noise compared to the original system. At high SNR, performance approaches the ideal upper limit, and the system also excels in tasks such as VQA, demonstrating the effectiveness of the proposed method and its potential to provide reliable support for practical applications.
Simulation results show that the BR-GG-DeepSC method outperforms other benchmark methods, particularly at low SNRs, with accuracy approaching the upper limit at high SNRs. The system performs well across different channels (AWGN, Rayleigh, and Rician). Compared with traditional systems, its advantages are especially pronounced when low SNR leads to increased errors in image transmission, demonstrating better robustness. The cross-modal correction network facilitates semantic recovery, reduces interference from semantic and physical noise, and enhances data recovery robustness. The system achieves high-precision semantic recovery by establishing correlations between multimodal signals.
Furthermore, the BR-GG-DeepSC system reduces the number of transmitted symbols in image transmission. Although the number of transmitted symbols for text transmission increases, the system demonstrates good robustness, effectively addressing the challenges posed by increased wireless data traffic while supporting intelligent tasks.
DECLARATIONS
Authors’ contributions
Made substantial contributions to the research, idea generation, algorithm design, simulation, wrote and edited the original draft: Ba, X.; Zhang, X.; Li, S.
Performed data acquisition and provided administrative, technical, and material support: Yuan, J.; Hu, J.
Availability of data and materials
The data are from the publicly available MVSA dataset, which can be downloaded at https://mcrlab.net/research/mvsa-sentiment-analysis-on-multi-view-social-data/.
Financial support and sponsorship
This work was supported by the National Natural Science Foundation of China No. 62371428 and the National Key R&D Program of China under Grant No 2023YFF0904605.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
The data are from the publicly available MVSA dataset; the dataset provider has obtained the necessary ethical approvals; and this study does not involve additional personal privacy risks. Therefore, no further ethical approval or informed consent is required.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Xie, H.; Qin, Z.; Li, G. Y.; Juang, B. H. Deep learning enabled semantic communication systems. IEEE. Trans. Signal. Process. 2021, 69, 2663-75.
2. Zhou, Q.; Li, R.; Zhao, Z.; Peng, C.; Zhang, H. Semantic communication with adaptive universal transformer. IEEE. Wirel. Commun. Lett. 2022, 11, 453-7.
3. Lee, C. H.; Lin, J. W.; Chen, P. H.; Chang, Y. C. Deep learning-constructed joint transmission-recognition for Internet of Things. IEEE. Access. 2019, 7, 76547-61.
4. Zhang, G.; Hu, Q.; Qin, Z.; Cai, Y.; Yu, G.; Tao, X. A unified multi-task semantic communication system for multimodal data. IEEE. Trans. Commun. 2024, 72, 4101-16.
5. Kipf, T. N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. Available online: https://doi.org/10.48550/arXiv.1609.02907. (accessed 29 Sep 2025).
6. Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. Available online: https://doi.org/10.48550/arXiv.1710.10903. (accessed 29 Sep 2025).
7. Han, Y.; Wang, P.; Kundu, S.; Ding, Y.; Wang, Z. Vision HGNN: an image is more than a graph of nodes. In 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France. October 01-06, 2023. IEEE; 2023. pp. 19821-31.
8. Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T. T-GCN: a temporal graph convolutional network for traffic prediction. IEEE. Trans. Intell. Transp. Syst. 2020, 21, 3848-58.
10. Bao, J.; Basu, P.; Dean, M.; Partridge, C.; Swami, A.; Leland, W. Towards a theory of semantic communication. In 2011 IEEE Network Science Workshop, West Point, USA. June 22-24, 2011. IEEE; 2011. pp. 110-7.
12. Shi, G.; Xiao, Y.; Li, Y.; Xie, X. From semantic communication to semantic-aware networking: model, architecture, and open problems. IEEE. Commun. Mag. 2021, 59, 44-50.
13. Niu, K.; Dai, J.; Zhang, P.; Yao, S.; Wang, S. Semantic communication for 6G. Mobile. Commun. 2021, 45, 85-90.
14. Liu, W.; Wang, M.; Bai, B. Efficient semantic communication method for bandwidth constrained scenarios. J. Xidian. Univ. 2024, 51, 9-18.
15. Lu, Y.; Dai, J.; Niu, K. Key technologies of semantic communication for industrial networks. Mobile. Commun. 2023, 47, 18-24.
16. Cavagna, A.; Li, N.; Iosifidis, A. Semantic communication enabling robust edge intelligence for time-critical IoT applications. In 2023 IEEE International Conference on Communications Workshops (ICC Workshops), Rome, Italy. May 28 - Jun 01, 2023. IEEE; 2023. pp. 1617-22.
17. Wang, L.; Wu, W.; Zhou, F.; Yang, Z.; Qin, Z.; Wu, Q. Adaptive resource allocation for semantic communication networks. IEEE. Trans. Commun. 2024, 72, 6900-16.
18. Luo, X.; Chen, H. H.; Guo, Q. Semantic communications: overview, open issues, and future research directions. IEEE. Wirel. Commun. 2022, 29, 210-9.
19. Farsad, N.; Rao, M.; Goldsmith, A. Deep learning for joint source-channel coding of text. In 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, Canada. April 15-20, 2018. IEEE; 2018. pp. 2326-30.
20. Pennington, J.; Socher, R.; Manning, C. GloVe: global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar. Association for Computational Linguistics; 2014. pp. 1532-43.
21. Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. Available online: https://doi.org/10.48550/arXiv.1409.0473. (accessed 29 Sep 2025).
22. Wu, Y.; Schuster, M.; Chen, Z.; et al. Google’s neural machine translation system: bridging the gap between human and machine translation. arXiv 2016, arXiv:1609.08144. Available online: https://doi.org/10.48550/arXiv.1609.08144. (accessed 29 Sep 2025).
23. Graves, A. Sequence transduction with recurrent neural networks. arXiv 2012, arXiv:1211.3711. Available online: https://doi.org/10.48550/arXiv.1211.3711. (accessed 29 Sep 2025).
24. Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. Available online: https://doi.org/10.48550/arXiv.1301.3781. (accessed 29 Sep 2025).
25. Sana, M.; Strinati, E. C. Learning semantics: an opportunity for effective 6G communications. arXiv 2021, arXiv:2110.08049. Available online: https://doi.org/10.48550/arXiv.2110.08049. (accessed 29 Sep 2025).
26. Dehghani, M.; Gouws, S.; Vinyals, O.; Uszkoreit, J.; Kaiser, L. Universal transformers. arXiv 2018, arXiv:1807.03819. Available online: https://doi.org/10.48550/arXiv.1807.03819. (accessed 29 Sep 2025).
27. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA. June 27-30, 2016. IEEE; 2016. pp. 770-8.
28. Xie, H.; Qin, Z.; Li, G. Y. Task-oriented multi-user semantic communications for VQA. IEEE. Wirel. Commun. Lett. 2022, 11, 553-7.
29. Xie, H.; Qin, Z.; Tao, X.; Letaief, K. B. Task-oriented multi-user semantic communications. IEEE. J. Sel. Areas. Commun. 2022, 40, 2584-97.
30. Antol, S.; Agrawal, A.; Lu, J.; Mitchell, M.; Batra, D.; Zitnick, L. VQA: visual question answering. In 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile. December 07-13, 2015. IEEE; 2015. pp. 2425-33.
31. Devlin, J.; Chang, M. W.; Lee, K.; Toutanova, K. BERT: pre-training of deep bidirectional transformers for language understanding. arXiv 2019, arXiv:1810.04805. Available online: https://doi.org/10.48550/arXiv.1810.04805. (accessed 29 Sep 2025).
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Special Topic
Copyright
Data & Comments
Data



















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].