Data-based dynamic event-triggered attitude control for helicopter with aperiodic denial-of-service attacks
Abstract
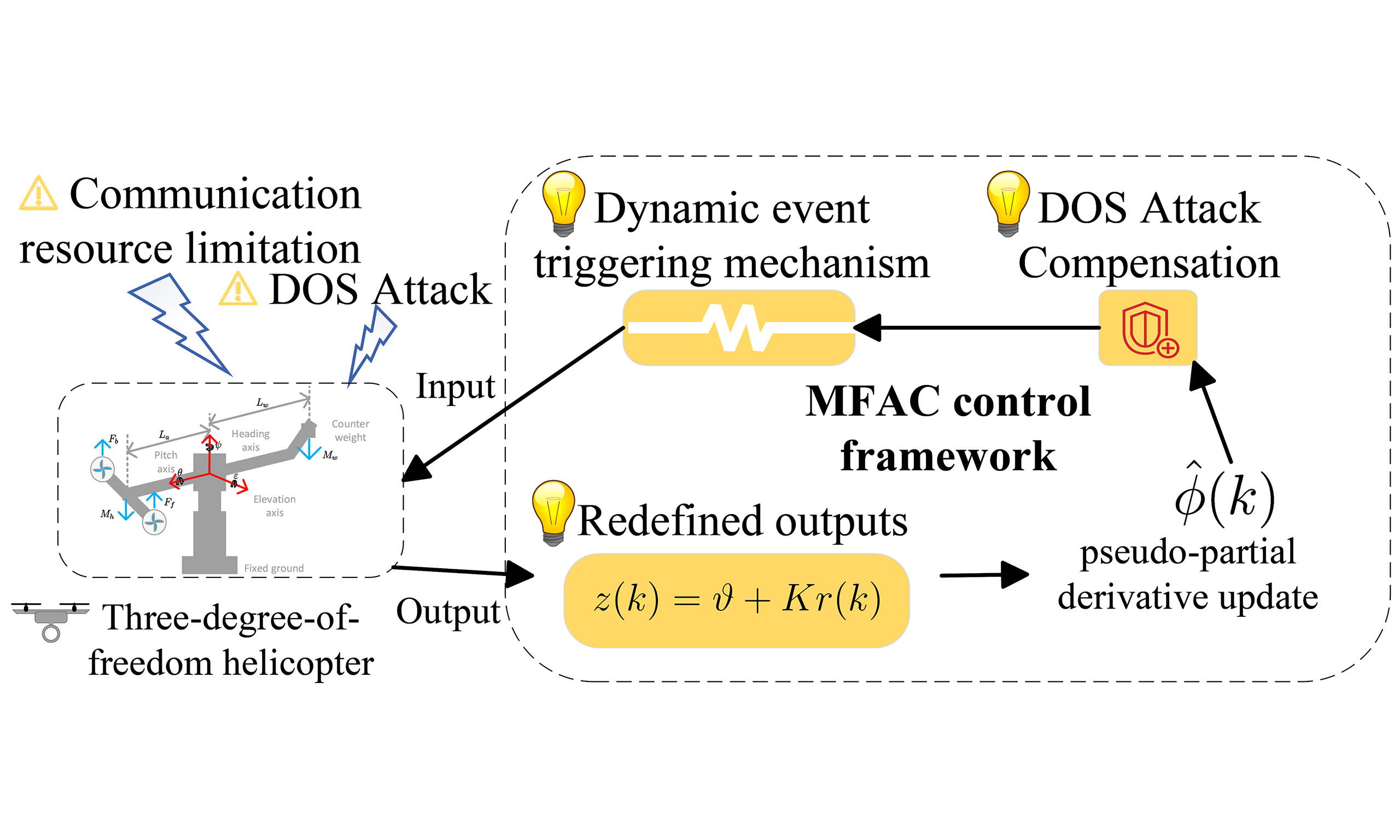
This paper investigates a dynamic event-triggered model-free adaptive control (MFAC) method for a three-degree-of-freedom helicopter subjected to aperiodic denial-of-service (DoS) attacks to perform attitude control tasks. Firstly, a redefined output is designed to satisfy a quasi-linearization requirement of MFAC theory. Meanwhile, a differential signal is designed to reduce the impact of the redefined output. Then, a dynamic event-triggered strategy is formulated, including a dynamic condition that reduces communication frequencies. Additionally, a DoS attack compensation method has been developed, which effectively mitigates the effects of aperiodic DoS attacks. Moreover, the convergence of the tracking error of the controlled helicopter with the designed method is strictly proven. Finally, simulation results further demonstrate the effectiveness of the designed scheme.
Keywords
1. INTRODUCTION
Recently, helicopters have garnered considerable attention due to their diverse range of applications in transportation[1], rescue[2], and military operations[3]. Much work has been done on linear/nonlinear controllers applied to helicopters. Among them, Zhao et al. designed a three-linear quadratic regulator-based attitude controller[4], Pandey et al. proposed a finite-time control strategy[5], and Mokhtari et al. designed a robust control scheme based on a third-order dynamic model[6]. Although the most mentioned methods are meaningful, those controller designs are based on a known mathematical model of the vehicle. Since the helicopter is easily influenced by environmental factors, such as wind speeds and humidity[7, 8], it is challenging to develop an accurate mathematical model. Hence, it is necessary to investigate a control method that is independent of the dynamics model of the controlled helicopter.
It is noted that data-driven control is a valuable method for solving the above problem, as it does not rely on accurate mathematical models. It instead directly employs the system's input and output data to obtain control strategies. Generally, data-driven control methods are categorized into iterative learning control[9], reinforcement learning control[10], model-free adaptive control (MFAC)[11], and so on. Among them, MFAC methods require fewer parameters to be adjusted and are less sensitive to changes in system parameters. Additionally, iterative learning control relies on repetitive tasks, whereas reinforcement learning control exhibits high computational complexity. In contrast, MFAC is simpler, less computationally burdensome, easier to implement, and more robust, making it more suitable for the nonlinear, dynamic, and real-time control needs of helicopters. Hou first proposed the MFAC method[12], which utilizes only the online input/output data of the controlled system to design the controller. In recent years, as the theory of MFAC has matured and the demand for controlling complex systems in engineering practice has grown, more researchers have applied it to control complex systems in aerospace[13], intelligent driving[14], and energy[15]. For instance, Liu et al. proposed an enhanced model-free adaptive attitude control method for a two-wheeled balance vehicle[16], Liu et al. proposed an MFAC scheme for a power converter system[17], and Ding et al. studied a model-free adaptive sliding mode control method for a quadrotor[18]. Notably, the mentioned results are valuable and significantly contribute to the development of the MFAC theory. However, they did not consider the influence of malicious cyberattacks, which can damage the stability of systems. Therefore, it is worthwhile to investigate the security issues of helicopter systems in the context of malicious cyberattacks.
Generally, cyberattacks can compromise system stability in several ways, including injection attacks[19], replay attacks[20], and denial-of-service (DoS) attacks[21]. Among them, DoS attacks are easy to implement and have become a common threat to network security. Recently, to reduce the impacts of DoS attacks, many meaningful strategies have been developed; for instance, Xiong et al. studied a model-free adaptive predictive control method for nonlinear systems with DoS attacks[22], Ma et al. designed a model‐free adaptive resilient control scheme for multi-agent systems with DoS attacks[23], and Li et al. investigated a model-free adaptive iterative learning controller for a nonlinear system against DoS attacks[24]. Although the existing methods are useful, most of them assume that DoS attacks satisfy a periodicity probability model, which is a strict requirement. Generally, it is more practical to investigate whether DoS attacks are aperiodic. Moreover, the methods mentioned above do not sufficiently consider the issue of limited communication resources. Helicopters are usually equipped with lightweight communication devices[25], where communication resources are limited. Hence, it is necessary to investigate a communication strategy to cut the frequency of communication and save communication resources.
It is noted that event-triggered control[26] is a standard solution to communication resource limitation issues. Roughly speaking, the event-triggered methods with different event-triggered conditions can be divided into static event-triggered methods[27] and dynamic event-triggered methods[28]. Recently, several event-triggered MFAC methods have been developed; to illustrate, Yu et al. designed a static event-triggered control strategy for nonlinear systems[29], Liu et al. studied an anti-interference event-triggered MFAC scheme for intelligent tugs[30], and You et al. proposed a static event-triggered background-impulse Kalman filter algorithm for wireless sensor networks[31]. Those studies effectively solve the communication limitation problem and reduce network communication resource consumption. However, most event-triggered MFAC methods rely on fixed thresholds. In contrast, the dynamic event-triggered mechanism has a dynamic event-triggered threshold, which can further reduce the communication burden. Hence, designing a dynamic event-triggered MFAC scheme for Helicopters is meaningful work.
Inspired by the studies mentioned above, this paper examines the attitude control issues of a helicopter subjected to aperiodic DoS attacks and limited communication resources. The main efforts are listed as:
(1) Develop a model-free adaptive attitude control method for the helicopter, which is a data-driven control method. Compared with existing methods[4–6], the dynamics model of the helicopter is no longer needed.
(2) Formulate a forgetting factor-based DoS attack compensation strategy. Compared with the existing method[23], the formulated compensation strategy effectively relieves the impact of aperiodic DoS attacks.
(3) Design a dynamic event-triggered communication mechanism. Compared to static event-triggered methods[29–31], the designed mechanism further reduces the communication frequencies.
The rest of this article is outlined as follows: Section 2 introduces the MFAC method and the controlled system. Section 3 gives the development of the designed method. Section 4 demonstrates the stability of the helicopter converged by the designed scheme. Section 5 demonstrates the effectiveness of the designed method through simulation studies. Finally, Section 6 gives conclusions.
Notations:
2. PRELIMINARY AND PROBLEM FORMULATION
2.1. MFAC method
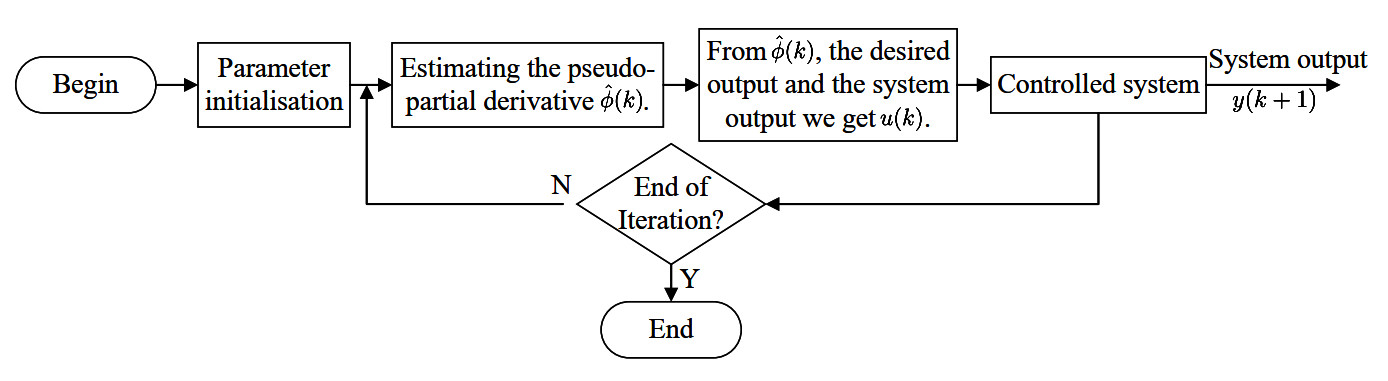
The core idea is to build an equivalent dynamic linearized model at each operating point, and to estimate the pseudo-partial derivative (PPD) parameters of the system online from the input and output data of the controlled system. In this case, the PPD parameter is a mathematical concept. It is a parameter that approximates the relationship between the system's input and output data to establish a dynamic linearization model, such as compact form dynamic linearization (CFDL), partial form dynamic linearization (PFDL), and full form dynamic linearization (FFDL). Subsequently, a MFAC method is proposed based on the established dynamic linearization model. The flowchart of the control algorithm is shown in Figure 1[32]. For complete theoretical foundations (e.g., stability proofs, algorithmic variants), refer to Refs.[33] and[34].
Considering a single-input single-output nonlinear system[35] satisfies that
where
Assumption 1[36] The partial derivative of
Assumption 2[37] The system, given in Equation (1), satisfies the generalized Lipschitz condition, if
Remark 1 Assumption 1 is a common condition of nonlinear systems. Assumption 2 is a restriction on the upper bound of the system output change rate. More deities of Assumptions 1 and 2 can be found in the reference[38].
Lemma 1[39] If Equation (1) satisfies Assumptions 1-2 and
where
Assumption 3[40] The sign of the PPD parameter remains unchanged for all
Remark 2 Assumption 3 implies that the system's output does not decrease when the input increases, also called a quasi-linearization requirement[41].
2.2. System descriptions
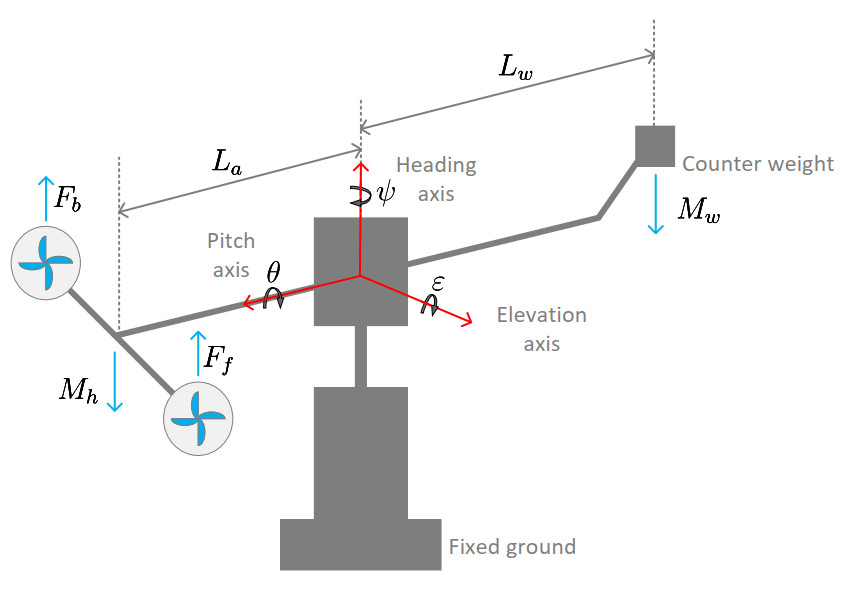
The three-degree-of-freedom helicopter features two direct current motors, one mounted at each end of a rectangular frame, which drive two propellers. The helicopter's attitude is controlled by the thrust forces
where
Remark 3 When helicopters are performing smooth hovering or slow attitude adjustment tasks, their pitch angle is usually in a small range. At this point, the Taylor series expansion of
Then it is obtained that
where
Remark 4 From the discrete-time model of the helicopter, given in Equation (4), it is found that the angular velocity of
Remark 5 Although the dynamics models of the helicopter are discussed in Equations (3) and (4), those models are only uncertainties and are employed to demonstrate the relationship between input data and output data of the controlled helicopter. It should be noted that the mentioned models are no longer required when designing the controller. This paper aims to design a data-driven control method for the helicopter to realize attitude control.
2.3. Aperiodic DoS attacks
DoS attacks aim to break system stability by blocking data transmission. Figure 2 illustrates a schematic diagram of the aperiodic DoS attack behavior. The
Then, the time interval without DoS attacks is given by
Assumption 4[42] Defining
where
Remark 6 Assumption 4 implies that the total duration of DoS attacks is bounded. In addition, the role of
2.4. Problem statement
The primary objective of this paper is to propose a data-driven, dynamic event-triggered attitude control method for helicopters to facilitate the implementation of attitude control tasks. To improve the control performance and resource utilization efficiency, it faces the following key challenges:
(1) Quasi-linearization Issue: The relationship between input and output data of the controlled helicopter does not satisfy the quasi-linearization requirement, which is a basic requirement for MFAC theory.
(2) Aperiodic DoS Attack Issue: The controlled helicopter system is subject to aperiodic DoS attacks, leading to the controller being unable to receive the feedback data.
(3) Limited Communication Resources: Generally, due to the restrictions on size and quality, helicopters are equipped with a lightweight communication device, which will cause communication jamming.
To summarize, this paper proposes a data-driven control scheme based on the MFAC theory, addressing the issues of aperiodic DoS attacks and limited communication resources.
3. CONTROLLER DESIGN AND ANALYSIS
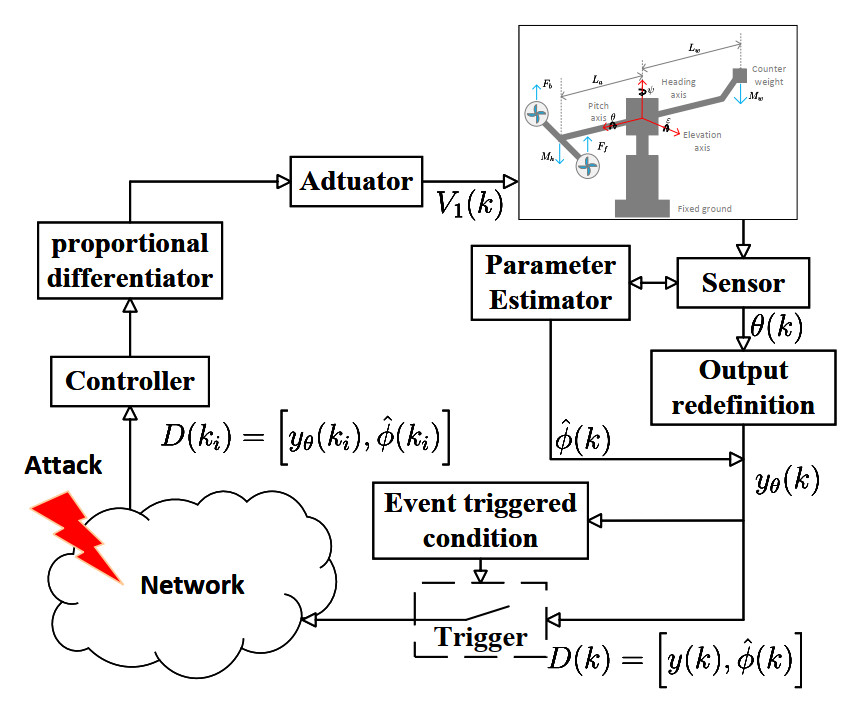
The schematic diagram of the formulated scheme is shown in Figure 3, which mainly includes a three-degree-of-freedom helicopter, output redefiner, trigger, and controller. The trigger keeps the value of the previous moment when the event-triggered condition is not met until the event is triggered, that is,
3.1. Output redefinition
It should be pointed out that the attitude angles of the helicopter have a characteristic of suddenly changing to the opposite extreme value (for example,
This article reconstructs the output signal using the angles and angular velocities of the three attitude angles and proves that the redefined output and the input satisfy Assumption 3. The output signal is redefined as
where
Redefine the reference signal for the system output as
where
As shown in Figure 4, the system introduces the angular velocity signal into the outer loop feedback system by redefining the output. This reflects the combined effect of interference on heading and angular velocity in a prompt manner. Thus, the controller can be adjusted more quickly to improve the system's anti-interference capability and dynamic response speed. Relevant details can be found in[43].
Theorem 1 The redefined output Equation (8) satisfies Assumption 3 when
Proof 1 The output increment satisfies:
Supposing
In actual systems, a dead zone exists in the controller's output, allowing the helicopter to take off. This means that when
Obviously, if
Substituting Equations (8) and (9) into
Considering
where
Substituting Equation (14) into Equation (13) yields
Defining
According to Equation (16),
It should be pointed out that although the control error converges when the design parameter
where
3.2. DoS attack compensation algorithm
Unmanned helicopters rely on network communications to send data to interact with ground terminals or other aircraft. For example, when performing missions, they need to upload flight attitude and position data and receive control commands in real-time. This exposes them to the risk of cyberattacks, especially DoS attacks, which are easy to implement. Hence, designing a DoS attack compensation algorithm for the helicopter is meaningful work.
DoS attacks can cause delays, data loss and interruption of communication between unmanned helicopters and ground control stations. These attacks consume network bandwidth and send large numbers of invalid packets. These issues significantly affect flight control, rendering it impossible to execute control commands promptly or provide accurate feedback on flight attitude data. This paper presents a compensation algorithm based on MFAC that aims to counteract the effects of DoS attacks. This algorithm compensates for the effects of a DoS attack on the communication system by dynamically adjusting control inputs to ensure flight stability and control accuracy.
Take the elevation channel as an example, a DoS attack compensation algorithm[44] is designed as
where
3.3. Dynamic event-triggered mechanism
Notably, the developed scheme is based on a continuous network communication condition. It should be pointed out that the helicopter's network resources are limited. To save communication resources, we introduce a dynamic event-triggered mechanism. Defining the set of event-triggered instants is
where
where
Then, an event-triggered condition is formulated as
When
Remark 7 As
3.4. Dynamic event-triggered MFAC approach development
Considering that the helicopter is an underactuated system, the first equation in Equation (4) is treated as a subsystem with control input
Combining Equations (17)-(22) and the DoS attack mechanism, the improved control scheme can be summarized as
where
Moreover,
The heading and pitch channels are single-input and two-output nonlinear systems. Similarly to the designed method in Equation (23), the controller
where
4. STABILITY ANALYSIS
Lemma 2[42] When the condition Equation (22) does not hold and without DoS attacks,
Theorem 2 If Assumptions 1-3 hold,
Proof 2 The following is an example of a proof of the elevation angle control law
Next, absolute values are taken on both sides of Equation (27). Then, we have
where
From Lemma 1, we have
Define
If
Hence, there exist constants
In summary,
During the event-triggered interval
Based on the above analysis, Theorem 2 is proved.
5. SIMULATION STUDIES
In this section, the MATLAB/Simulink software is employed to verify the validity of the designed control scheme. Referring to[45], the structural diagram of the three-degree-of-freedom helicopter is shown in Figure 5, where the corresponding parameters are listed in Table 1[45].
The parameters of the controlled helicopter
| Parameters | Values |
| DC motor voltage of the front and back motors | |
| Propeller force-thrust constant | |
| Distance | |
| Distance | |
| Equivalent gravitational moment | |
| Moment of inertia about elevation | |
| Moment of inertia about heading | |
| Moment of inertia about pitch |
In simulation, the sampling time is set to
5.1. Time-invariant angle tracking
Here, the three attitude angles are set as
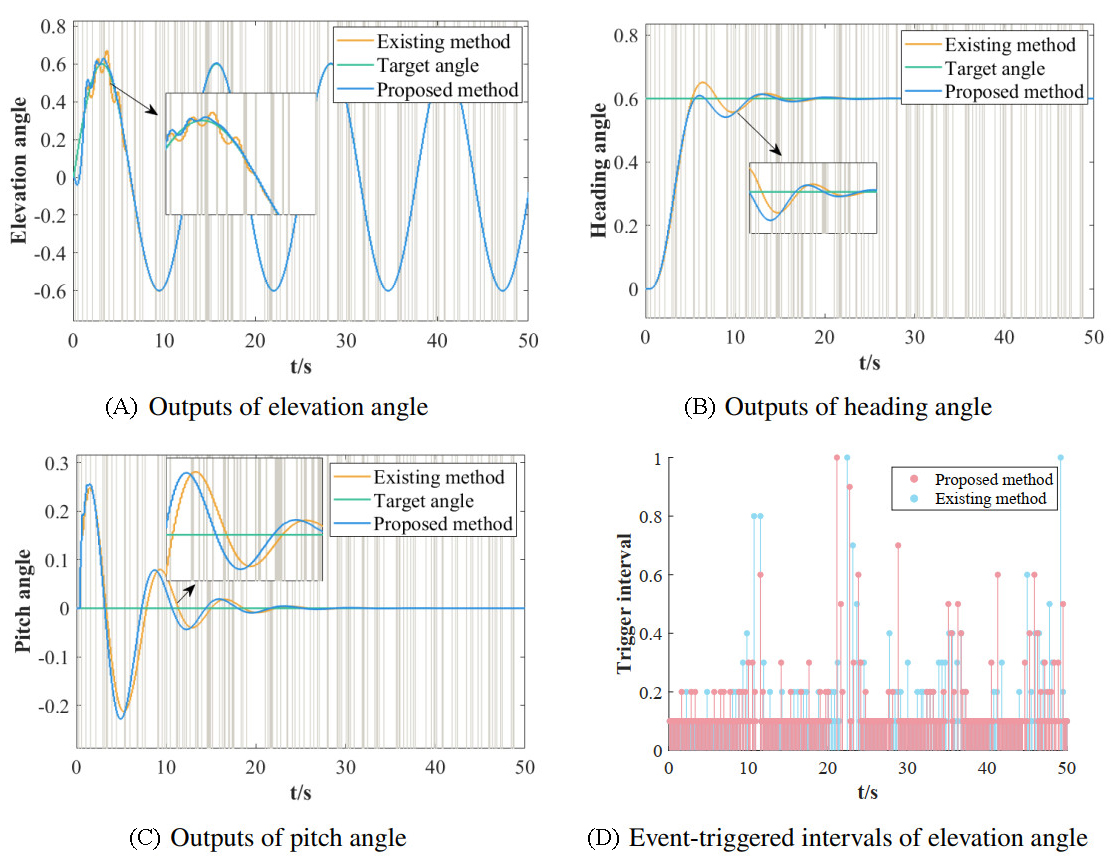
As shown in Figure 6A-C, the proposed method enables the helicopter system to efficiently track the desired angles by adjusting the control inputs in real-time, even under aperiodic DoS attacks. It should be pointed out that the gray bars denote the successive DoS attacks, as shown in Figure 6A-C. The designed method is effective against successive DoS attacks. Figure 6A shows that the dynamic event triggering strategy provides a slight improvement in response speed compared to the static event triggering strategy. Figure 6B and C illustrates that the dynamic event triggering strategy reduces overshooting by a greater amount than the static event triggering strategy. Figure 6D indicates that the dynamic event triggering strategy reduces the communication resources by 63.47%, while the static event triggering strategy reduces them by only 54.8%. This indicates that the dynamic event-triggering strategy can further reduce communication resources and load. Figure 6E demonstrates that the convergence rate slows down as the intensities of DoS attacks gradually increase.
Remark 8 To further validate the real-time potential of the proposed control method, the controller was deployed on a remote computer. The hardware configuration of the remote computer is as follows: it is equipped with an Intel Core i5-9300H processor (base frequency 2.4 GHz, maximum turbo frequency 4.1 GHz, four cores and eight threads), two 8GB DDR4 memories (frequency 2, 666 MHz), and an NVIDIA GeForce GTX 1650 graphics card. By executing a 50, 000-step simulation test, the average runtime per step was found to be 4.416 us.
5.2. Time-varying angle tracking
The desired angle of the elevation channel is set as
5.3. Parametric analysis
The results of the parameter analysis are shown in Figure 8, where the parameters involved in this section are tuned individually, and the other parameters are consistent with the time-invariant angle tracking experiment. First, the parameter
Then, as shown in Figure 8B, the parameter
6. CONCLUSIONS
This paper proposed a dynamic event-triggered model-free adaptive attitude control method for a three-degree-of-freedom helicopter with aperiodic DoS attacks. First, the outputs were redefined as a linear combination of angles and angular velocities, effectively solving the quasi-linearization requirements issue. Moreover, a dynamic event-triggered scheme has been developed. Compared with the existing scheme, the designed mechanism further reduces the communication frequencies. In the future, we will further consider extending the central algorithm of the current framework to multi-helicopter systems by combining it with distributed communication and decision-making mechanisms, and build a hardware-in-the-loop simulation system to verify the real-time performance and reliability of the algorithms in a real hardware environment.
DECLARATIONS
Authors' contributions
Made substantial contributions to conception and design of the study and performed data analysis and interpretation: Xu, Y.; Zhao, H.
Performed data acquisition and provided administrative and technical support: Gao, Y.; Yu, H.; Peng, L.
Availability of data and materials
The original contributions presented in this study are included in the article.
Financial support and sponsorship
This work was supported in part by the National Natural Science Foundation of China (62403216), in part by the Basic Research Program of Jiangsu Province (BK20241608), in part by the Wuxi Science and Technology Development Fund Project (K20231015), in part by the Wuxi Young Science and Technology Talent Support Program (TJXD-2024-114), in part by the 111 Project (B23008), and in part by the EU iMARs Project (HORIZON-MSCA-2023-101182996).
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Huang, J.; Yu, T.; Zhu, X.; et al. Energy efficiency maximization in UAV-assisted intelligent autonomous transport system for 6G networks with energy harvesting. IEEE. Trans. Intell. Transp. Syst. 2024, 1-11.
2. Sun, G.; He, L.; Sun, Z.; et al. Joint task offloading and resource allocation in aerial-terrestrial UAV networks with edge and fog computing for post-disaster rescue. IEEE. Trans. Mob. Comput. 2024, 23, 8582-600.
3. Pan, L.; Song, C.; Gan, X.; Xu, K.; Xie, Y. Military image captioning for low-altitude UAV or UGV perspectives. Drones 2024, 8, 421.
4. Zhao, T.; Li, W. LQR-based attitude controllers design for a 3-DOF helicopter system with comparative experimental tests. Int. J. Dynam. Control. 2024, 12, 1063-72.
5. Pandey, V.; Kamal, S.; Ghosh, S. Finite-time discrete control for two-DOF helicopter system. IEEE. Trans. Circuits. Syst. Ⅱ. Exp. Briefs. 2024, 71, 3800-4.
6. Mokhtari, M. A. Adaptive neural network-based dynamic surface control for a 3-DoF helicopter. J. Control. Autom. Electr. Syst. 2024, 35, 326-36.
7. Wang, C.; Li, W.; Liang, M. Event-triggered prescribed performance adaptive fuzzy fault-tolerant control for quadrotor UAV with actuator saturation and failures. IEEE. Trans. Aerosp. Electron. Syst. 2025, 61, 813-28.
8. Soleimani, E.; Sedigh, A. K.; Nikoofard, A. Data-driven reinforcement learning-based forgetting factor iterative learning control. IEEE. Trans. Autom. Sci. Eng. 2025, 22, 12245-56.
9. Shi, H.; Chen, Q.; Hong, Y.; Ou, X.; He, X. Adaptive fuzzy iterative learning control of constrained systems with arbitrary initial state errors and unknown control gain. IEEE. Trans. Autom. Sci. Eng. 2025, 22, 6439-50.
10. Cui, L.; Chakraborty, S.; Ozbay, K.; Jiang, Z. P. Data-driven combined longitudinal and lateral control for the car following problem. IEEE. Trans. Control. Syst. Technol. 2025, 33, 991-1005.
11. Xia, Z.; Dai, X.; Li, Y.; Wang, L.; Chen, F.; Ma, J. A data-driven control method for nonlinear characteristics of variable frequency regulation for wide-distance-range adaptive WPT system. IEEE. Trans. Power. Electron. 2025, 40, 10221-41.
12. Hou, Z.; Huang, W. The model-free learning adaptive control of a class of SISO nonlinear systems. In Proceedings of the 1997 American Control Conference (Cat. No. 97CH36041), Albuquerque, USA. June 06-06, 1997. IEEE; 1997. pp. 343-4.
13. Liu, L.; Han, X.; Fan, H.; Liu, L.; Wang, B. Model-free adaptive control of the combined aircraft with unknown multi-source disturbances and output saturation. Aerosp. Sci. Technol. 2025, 165, 110471.
14. Yu, Q.; Wu, S.; Bu, X.; Hou, Z. Model free adaptive predictive iterative learning cooperative control of multiple high-speed trains operation with disturbances. IEEE. Trans. Autom. Sci. Eng. 2025, 22, 19929-44.
15. Ding, H.; Shen, H.; Park, J. H.; Xie, Q. Model free adaptive control of strip temperature in continuous annealing furnace based on quantum-behaved particle swarm optimization. Nonlinear. Dyn. 2025, 113, 629-43.
16. Liu, S.; Yan, Y.; Ren, Y.; Jin, S.; Hou, Z. Attitude adjustment of a two-wheel balance vehicle based on an enhanced model-free adaptive control algorithm. IEEE. Trans. Circuits. Syst. II. Exp. Briefs. 2024, 71, 3885-9.
17. Liu, L.; Zhang, Z.; Zhao, Y.; et al. Data-driven model-free adaptive control for power converter under multiscenarios in microgrids. IEEE. Trans. Ind. Electron. 2025, 72, 8060-71.
18. Ding, Y.; Wang, J.; Zhang, J.; Luo, X. Design of quadcopter attitude controller based on data-driven model-free adaptive sliding mode control. Int. J. Dynam. Control. 2024, 12, 1404-14.
19. Xin, L.; He, G.; Long, Z. Stealthy false data injection attacks detection and classification in cyber-physical systems using deep reinforcement learning. IEEE. Trans. Autom. Sci. Eng. 2024, 22, 141-53.
20. Guo, J.; Zhang, Q.; Zhao, Y. Identification of FIR systems with binary-valued observations under replay attacks. Automatica 2025, 172, 112001.
21. Zhao, H.; Zhao, Z.; Xu, D.; Yu, H. Event-triggered automatic parking control for unmanned vehicles against DoS attacks. IEEE. Trans. Ind. Cyber. Phys. Syst. 2024, 2, 531-41.
22. Xiong, H.; Chen, G.; Ren, H.; Li, H. Broad-learning-system-based model-free adaptive predictive control for nonlinear MASs under DoS attacks. IEEE/CAA. J. Autom. Sinica. 2025, 12, 381-93.
23. Ma, Y. S.; Che, W. W.; Deng, C.; Wu, Z. G. Distributed model-free adaptive control for learning nonlinear MASs under DoS attacks. IEEE. trans. Neural. Netw. Learn. Syst. 2021, 34, 1146-55.
24. Li, Y.; Li, X. Improved nonlinear model-free adaptive iterative learning control in DoS attack environment. IET. Control. Theory. Appl. 2024, 18, 825-33.
25. Moloudian, G.; Hosseinifard, M.; Kumar, S.; et al. RF energy harvesting techniques for battery-less wireless sensing, industry 4.0, and internet of things: a review. IEEE. Sens. J. 2024, 24, 5732-45.
26. Dou, Y.; Xing, G.; Ma, A.; Zhao, G. A review of event-triggered consensus control in multi-agent systems. J. Control. Decis. 2025, 12, 1-23.
27. Pang, Y.; Zhuang, G.; Xia, J.; Xie, X. Fault detection and robust security control for implicit jump systems against random FDI attacks and packet loss under memorized output-perceptive event-triggered protocol. IEEE. Trans. Inf. Forensics. Secur. 2024, 19, 7362-73.
28. Liu, X.; Qiu, L.; Fang, Y.; Wang, K.; Li, Y.; Rodríguez, J. A two-step event-triggered-based data-driven predictive control for power converters. IEEE. Trans. Ind. Electron. 2024, 71, 13545-55.
29. Yu, J.; Ma, Z.; Li, K.; Chang, M. Event-triggered control of lag consensus for leader-following multi-agent systems with nonlinear dynamics. Circuits. Syst. Signal. Process. 2024, 43, 3500-15.
30. Liu, J.; Xu, C.; Li, S.; Dong, Z.; Hu, X. Event-triggered ADRC-MFAC for intelligent tugs in escort operations with a thrust re-allocation strategy. Control. Eng. Pract. 2025, 156, 106237.
31. You, X.; Xiao, K.; Wang, G. A static event-triggered background-impulse kalman filter for wireless sensor networks with non-Gaussian measurement noise. Inf. Fusion. 2025, 118, 102955.
32. Wen, Q.; Zhang, J.; Fan, H.; Liu, L.; Wang, B. Review on application of model-free adaptive control in flight control systems. Tact. Miss. Technol. 2024, 4, 41-52. https://caod.oriprobe.com/articles/67668280/wu_mo_xing_zi_shi_ying_kong_zhi_zai_fei_xing_kong_.htm (accessed 9 Sep 2025).
33. Hou, Z.; Jin, S. A novel data-driven control approach for a class of discrete-time nonlinear systems. IEEE. Trans. Control. Syst. Technol. 2010, 19, 1549-58.
35. Chang, L.; Chi, R.; Hou, Z. Coding-decoding protocol-based data-driven adaptive sliding mode control under energy-constrained DoS attacks. IEEE. Trans. Autom. Sci. Eng. 2025, 22, 16668-81.
36. Zhou, Q.; Ren, Q.; Ma, H.; Chen, G.; Li, H. Model-free adaptive control for nonlinear systems under dynamic sparse attacks and measurement disturbances. IEEE. Trans. Circuits. Syst. Ⅰ. Regul. Pap. 2024, 71, 4731-41.
37. Bu, X.; Yu, W.; Yu, Q.; Hou, Z.; Yang, J. Event-triggered model-free adaptive iterative learning control for a class of nonlinear systems over fading channels. IEEE. Trans. Cybern. 2022, 52, 9597-608.
38. Liu, S.; Lin, G.; Ji, H.; Jin, S.; Hou, Z. A novel enhanced data-driven model-free adaptive control scheme for path tracking of autonomous vehicles. IEEE. Trans. Intell. Transp. Syst. 2024, 26, 579-90.
39. Zhang, C.; Cen, C.; Huang, J. An overview of model-free adaptive control for the wheeled mobile robot. World. Electr. Veh. J. 2024, 15, 396.
40. Wang, J.; Wang, X.; Wang, X.; Zhang, Z.; Wang, J. Model free adaptive attitude control for a 3-DOF helicopter. IET. Control. Theory. Appl. 2023, 40, 2295-303.
41. Zhao, H.; Xu, D.; Zhou, Z.; Yu, H. Dynamic event-triggered resilient heading control for unmanned surface vehicle with encrypted data. IEEE. Trans. Intell. Veh. 2024, 9, 5718-27.
42. Ma, Y. S.; Che, W. W.; Deng, C. Dynamic event-triggered model-free adaptive control for nonlinear CPSs under aperiodic DoS attacks. Inform. Sci. 2022, 589, 790-801.
43. Liao, Y.; Jiang, Q.; Du, T.; Jiang, W. Redefined output model-free adaptive control method and unmanned surface vehicle heading control. IEEE. J. Ocean. Eng. 2020, 45, 714-23.
44. Pang, Z. H.; Liu, G. P.; Zhou, D.; Sun, D. Data-driven control with input design-based data dropout compensation for networked nonlinear systems. IEEE. Trans. Control. Syst. Technol. 2016, 25, 628-36.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data





















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].