Advancements in humanoid robot dynamics and learning-based locomotion control methods

doi:10.20517/ir.2025.32

Download PDF

Review | Open Access | 25 Jul 2025

Advancements in humanoid robot dynamics and learning-based locomotion control methods

Views: 63 | Downloads: 9 | Cited:

0

Shilong Sun

,

Haodong Huang

,

Chiyao Li

Intelligence & Robotics 2025, 5(3), 631-60.

10.20517/ir.2025.32 | © The Author(s) 2025.

Author Information

Article Notes

Cite This Article

Abstract

Humanoid robots are attracting increasing global attention owing to their potential applications and advances in embodied intelligence. Enhancing their practical usability remains a major challenge that requires robust frameworks that can reliably execute tasks. This review systematically categorizes and summarizes existing methods for motion control and planning in humanoid robots, dividing the control approaches into traditional dynamics-based and modern learning-based methods. It also examines the navigation and obstacle-avoidance capabilities of humanoid robots. By providing a detailed comparison of the advantages and limitations of various control methods, this review offers a comprehensive understanding of current technological progress, real-world application challenges, and future development directions in humanoid robotics. Key topics include the principles and applications of simplified dynamic models, widely used control algorithms, reinforcement learning, imitation learning, and the integration of large language models. This review highlights the importance of both traditional and innovative approaches in advancing the adaptability, efficiency, and overall performance of humanoid robots.

Graphical Abstract

Keywords

Humanoid robot, locomotion control, dynamics and machine learning, path planning

Download PDF 0 1

1. Introduction

Amid rapid technological advancements, humanoid robots have emerged as a key frontier in artificial intelligence and robotics, attracting significant research interest in recent years. Humanoid robots, characterized by their human-like form and functionality, have vast potential in industrial automation, healthcare, home services, and education. They also play irreplaceable roles in extreme or hazardous environments, such as planetary exploration, firefighting, and nuclear radiation scenarios^[1-5]. These diverse applications not only enhance the quality of life and improve work efficiency but also address unique challenges, highlighting their broad significance^[6].

Inspired by the human body, humanoid robots typically consist of a head, torso, two arms, and two legs, which allow them to perform human-like actions and tasks. Their development is a highly interdisciplinary endeavor that integrates mechanical design, sensor technology, motion control, and artificial intelligence. These technologies collectively enable humanoid robots to operate safely and effectively across various scenarios, including industrial production, medical procedures, rehabilitation, disaster response, and search-and-rescue operations.

Motion control is a fundamental aspect of humanoid robot technology that directly affects movement efficiency and operational safety. Effective control strategies enable robots to follow predefined gaits precisely and respond in real time to sudden changes or disturbances in balance. Key technical challenges include accurately modeling the dynamic characteristics of human walking, coping with environmental uncertainties, and optimizing the control algorithms. Addressing these challenges will improve both the functionality and safety of humanoid robots in complex environments.

Currently, electric motor drives dominate the control of humanoid robots. Hydraulic-driven robots, such as Boston Dynamics' Atlas^[7], which were once praised for their performance, have been retired, and research focus has shifted to electric actuation. In recent years, the field has witnessed rapid progress driven by emerging research initiatives and technological innovations.

The development of electric humanoid robots began with Japan's ASIMO^[8], which features 34 degrees of freedom, stands 130 cm tall, weighs 54 kg, and performs smooth walking, running, jumping, and stair climbing. In 2022, Tesla unveiled its Optimus prototype^[9], which was capable of single-leg balance and was equipped with self-correcting limbs. Agility Robotics' Digit, designed for warehouse logistics, is scheduled for commercial deployment in 2024. Figure AI launched Figure 02, a general-purpose humanoid robot integrated with ChatGPT for language understanding and task execution. China has also made significant advances, for example, Unitree's H1, which is widely deployed in universities, and Fourier Intelligence's GR-1, which features a unique structure optimized for bipedal locomotion and manipulation.

Although prior reviews have addressed reinforcement learning (RL) and teleoperation in humanoid robots, a comprehensive review specifically focusing on motion control and path planning is still lacking. This study aims to fill this gap by summarizing recent progress, highlighting motion control frameworks, and exploring future trends. The main contributions of this study are as follows: (1) A systematic review of dynamics-based and learning-based control methods for humanoid robots; (2) A detailed comparison of these approaches, emphasizing their strengths, limitations, and features; (3) A summary of path planning and obstacle avoidance techniques applicable to humanoid robots; (4) An analysis of existing challenges and prospects for future research.

The remainder of this paper is structured as follows: Section 2 introduces dynamics-based control methods; Section 3 reviews learning-based control approaches; Section 4 summarizes path planning and obstacle avoidance techniques; and Section 5 discusses current limitations and future directions. Finally, Section 6 concludes the paper.

2. Dynamics-Based Control Methods

Control methods based on dynamic models utilize the robot motion equations and dynamic constraints to design precise and reliable control strategies. By formulating the control problem within this dynamic framework, optimal control inputs can be computed to ensure that the robot achieves stable and desired motion under various conditions. This chapter introduces several widely used simplified dynamic models for humanoid robots, including the linear inverted pendulum model (LIPM), cart-table model, and spring-loaded inverted pendulum (SLIP) model. It also reviews common control methods based on these models, such as proportional–integral–derivative (PID) control, model predictive control (MPC), and zero moment point (ZMP) control, and discusses their roles in achieving effective and stable humanoid locomotion.

2.1. Simplified dynamic models of bipedal walking

Approximation is a practical approach for managing the complexity of humanoid-robot motion control. Complex robot models are often simplified to enable efficient computation. Several dynamic models have been widely adopted for bipedal gait planning, with the cart-table model and various inverted pendulum models being the most common.

Among these, two-dimensional (2D) and three-dimensional (3D) LIPMs are frequently used because of their balance between simplicity and accuracy. The 3D linear inverted pendulum plus flywheel (LIPPF) model extends this by incorporating the flywheel rotational inertia, offering a more complete depiction of dynamic stability. The SLIP model further introduces elastic components to mimic the spring-like behavior observed in natural locomotion, highlighting energy-efficient gait strategies.

The following sections examine the principles and features of these simplified models, discussing their contributions to humanoid gait planning and practical implementation in locomotion control. A brief overview is provided in Table 1.

Table 1

Common simplified models of humanoid robots

Model	Works	Characteristic
LIP: Linear inverted pendulum; 2D: two-dimensional; 3D: three-dimensional; LIPPF: linear inverted pendulum plus flywheel; CoM: center of mass; SLIP: spring-loaded inverted pendulum.
Cart-table model	^[10],^[11]	When the trolley moves at a specific acceleration, the table can maintain instantaneous balance and fall
LIP	^[12],^[13],^[14],^[15],^[16]	The 2D LIP can only generate the walking trajectory in the 2D plane; the 3D LIP is generalized to the 3D space based on the 2D LIP, and their center-of-mass height is constant
LIPPF	^[17],^[18],^[19],^[20],^[21]	LIPPF simulates the angular momentum of an object's CoM using a flywheel with a center-of-mass moment of inertia and rotation angle restrictions instead of a single particle
SLIP	^[22],^[23],^[24],^[25]	SLIP models can better simulate the vibration of the CoM and the smooth motion of the legs to adapt to the control of a humanoid robot in a high-speed running mode, such as jumping and trotting

2.1.1. Cart-table model

The cart-table model^[10] is a simplified representation commonly used to approximate the dynamics of bipedal-walking robots. In this model, the robot is abstracted as a massless table supported by a movable cart on a horizontal plane, which captures the fundamental principles of balance and motion. When the cart accelerates appropriately, the table remains balanced without tipping, which is a key behavior for understanding bipedal stability.

This model reduces the complex dynamics of bipedal walking to a 2D analysis. As shown in Figure 1, the robot operates in the z-x plane, with the x-axis representing the forward motion and the z-axis perpendicular to the ground. Movement of the cart along the x-axis shifts the force distribution on the table, determining the location of the center of pressure (CoP), also known as the ZMP.

Advancements in humanoid robot dynamics and learning-based locomotion control methods

Figure 1. Cart-table model

The ZMP is the point at which the net moment from the gravitational and inertial forces is equal to zero. By maintaining the ZMP within the support polygon - the area between the robot's feet - the robot achieves stable walking and avoids falling over. This model provides a foundational framework for balance control and guides the development of more advanced locomotion algorithms for humanoid robots.

The ZMP based on this model is given as follows:

(1)

$$ p = x - \frac{z_c}{g} \ddot{x} $$

ZMP has become an essential criterion for analyzing the dynamic balance. Figure 2 illustrates the principle of walking pattern generation based on ZMP. Given the target ZMP trajectory, the required center of mass (CoM) motion is calculated. Based on the calculated CoM trajectory, the actual ZMP trajectory can be computed. The overall goal is to minimize the error between the actual ZMP trajectory and the given ZMP trajectory to enhance the robot stability during motion (as deviations may lead to falls). This can be achieved through feedback control to track the target of the ZMP trajectory. In this control system, the input is the target position of the ZMP, denoted as $$ p^{ref} $$. The controller uses the feedback input of tracking errors to output an acceleration rate $$ u $$ for the CoM, which serves as the input to the actuator. The actuator determines the actual ZMP and CoM coordinates based on the system's state transition and motion equations. Using this control system, it is possible to generate the motion trajectory of the CoM while ensuring that the ZMP tracks the predefined reference position^[11].

Figure 2. Principle of walking pattern control based on ZMP. ZMP: Zero moment point

2.1.2. LIPM

The 2D LIPM proposed by Kajita et al.^[12] confines the robot dynamics to the sagittal (x–z) plane. By disregarding lateral motion, it models only the forward–backward translation and small vertical oscillation of the CoM and remains highly effective for basic gait planning. The 3D LIPM extends this formulation to include the lateral (y) degree of freedom, yielding more natural and stable walking patterns, and thus is preferred for full-body humanoid control. The 2D and 3D LIPM models share common characteristics, which can be summarized as follows: (1) All mass is lumped at the hip (CoM); (2) The legs are massless telescopic links; (3) The CoM height is constant.

Although the constant-height assumption linearizes the equations and simplifies the control design, it restricts gait versatility. Human biomechanics show that CoM height varies during locomotion, enabling faster movement^[26]. To relax this constraint, Zhang et al. introduced a wheel–leg switching strategy^[27], and Shafii et al. developed a variable-height LIPM with a dedicated height-trajectory generator^[14]. Simulations confirmed that variable-height gaits achieved higher walking speeds than fixed-height gaits, broadening the applicability of the LIPM framework.

2.1.3. LIPPF

Human motions, such as forward lunges or rapid arm swings, exploit angular momentum to maintain balance. The standard LIPM neglects rotational inertia and therefore cannot capture these behaviors. Pratt et al. addressed this shortcoming using the LIPPF, which replaces the point mass with a flywheel that embodies both the CoM inertia and bounded rotational angles^[17]. Consequently, the LIPPF reproduces the angular-momentum effects essential for human-like movement.

The key assumptions of the LIPPF are as follows: (1) All mass is lumped at the flywheel center (CoM); (2) The legs are massless telescopic rods; (3) The flywheel is free to rotate; therefore, its inertia can counteract the pendulum-like sway. Increasing this inertia improves stability and better mimics the human gait^{[18, 19]}. Several studies have further relaxed the constant height constraint on the CoM^{[20, 21]}, yielding an even more accurate dynamic model that enables humanoid robots to walk more stably and move similarly to humans.

2.1.4. SLIP

In his study^[22] of terrestrial biological jumping movements, Blickhan discovered that various insects and animals - whether jumping, trotting, or running at high speeds - exhibit dynamics closely matching those predicted by the SLIP model. The SLIP model excels at simulating the oscillations of the CoM and compliant behavior of leg movements, making it particularly suitable for controlling humanoid robots in high-speed locomotion modes, such as jumping and running.

1) The characteristics of the SLIP model can be summarized as follows:

2) All of the robot's mass is concentrated at its hip position, simplifying the dynamics to focus on leg behavior.

Legs exhibit different behaviors during different phases of movement.

● During the single support phase, the supporting leg maintains a constant length.

● During the double support phase, both legs undergo elastic extension and contraction, mimicking the spring-like behavior observed in natural locomotion.

3) The CoM can move vertically, allowing the model to capture vertical oscillations typical of dynamic movements such as jumping and running.

An increasing number of researchers have applied the SLIP model to study dynamic locomotion in legged robots. Wensing and Orin^[23] were the first to embed the SLIP model into a full-body humanoid model, simulating humanoid robots running stably at speeds of up to 6.5 m/s, which is comparable to the speeds of Olympic athletes in the 5, 000-meter race. Xiong et al. utilized a hybrid linear inverted pendulum (H-LIP)-based stepping controller to perturb periodic walking motions based on the 3D-driven spring-loaded inverted pendulum (3D-aSLIP) model^[24]. They integrated the dynamics of the 3D-driven SLIP model into the Atlas robot, successfully generating versatile walking behaviors, including periodic walking, fixed-position tracking, trajectory tracking, and walking with varying heights. This method provides a valuable reference for generating dynamic and versatile humanoid walking patterns with nonconstant CoM heights. Additionally, the SLIP model can be used to generate various motion patterns, such as walking, running, and walking-to-running transitions^[25].

2.1.5. Flexible linear inverted pendulum model

The flexible linear inverted pendulum model (FLIPM)^{[15, 16, 28]} enhances the basic LIPM by incorporating additional elements, such as springs and dampers. These components are used to simulate the flexibility of links, joints, and servomotors, which are essential for capturing the more nuanced and realistic dynamic behavior of humanoid robots. By adding these flexible elements, the FLIPM can accurately represent the compliant and adaptive nature of human-like movements.

This model accounts for the elasticity and damping characteristics inherent in real robotic systems, allowing a more detailed analysis of how these factors influence balance, stability, and motion control. The incorporation of flexibility enables the FLIPM to better handle dynamic interactions with the environment, such as walking on uneven surfaces or responding to unexpected perturbations. This leads to improved performance in tasks that require a high degree of adaptability and precision. Overall, FLIPM provides a more comprehensive and realistic framework for studying and designing control strategies for humanoid robots, bridging the gap between simplified theoretical models and the complex realities of physical robotic systems.

2.2. Control methodology

Based on a dynamic model, it is essential to design suitable control systems and algorithms to drive the robot joint actuators, ensuring balance and effective motion execution. Common control algorithms for humanoid robots include PID control^[29-31], which is simple and effective for precise joint position and velocity control; MPC^[32-35], which predicts future states using a robot dynamics model to optimize control inputs; ZMP control^[36-38], which is crucial for maintaining stable walking by keeping the ZMP within the support polygon; and inverse kinematics (IK)^[39-41] and inverse dynamics (ID)^{[42, 43]}, which compute the necessary joint angles and torques for desired motions. Additionally, central pattern generators (CPGs) generate rhythmic outputs for cyclic movements such as walking and running. Together, these algorithms improve the robot's ability to perform complex tasks with stability and precision.

2.2.1. PID control

PID control features a simple structure, strong robustness, and adaptability. In the field of industrial control, PID control algorithms are widely applied^[44]. A PID controller is a linear controller that computes an error signal e(t) as the difference between a desired setpoint $$ r(t) $$ and the actual output $$ y(t) $$, $$ e(t) = r(t) - y(t) $$. The controller adjusts the controlled object by combining proportional (P), integral (I), and derivative (D) actions of the error through linear combinations.

From a temporal perspective, the proportional action addresses the current error, the integral action accounts for the error's history, and the derivative action reflects the error's rate of change. Together, these components provide a balanced approach to managing past, present, and future system states^[45-47].

Alasiry et al. applied a PID control system to the humanoid dance robot ERISA, enabling it to walk stably on sloped surfaces without falling^[48]. Analog tilt sensors were installed on the robot's shoulders to measure terrain slope. Using the measured tilt values, they adjusted the robot's servo control equations via PID to automatically correct its posture opposite to the downward slope. The walking trajectories consist of gait position data sets. The study established an inverted pendulum model, from which IK computed joint angle setpoints $$ \theta_{set} $$. As the robot walks on slopes, the shoulder tilt sensor measures the actual body tilt angle $$ \theta_{tilt} $$. The joint angle command $$ \theta_{act} $$ is set based on the difference between $$ \theta_{set} $$ and $$ \theta_{tilt} $$, causing the servo to rotate and compensate for the tilt. The simulation results demonstrated that PID balance control with tilt sensor feedback effectively stabilized ERISA, allowing steady walking on sloped surfaces.

2.2.2. Hybrid zero dynamics

Hybrid zero dynamics (HZD) has become a popular framework for dynamic and underactuated bipedal walking. The principle of HZD is based on the analysis and control theory of nonlinear dynamical systems. The core idea is to transform the dynamic properties of the robot into a zero-dynamic system and design controllers to achieve these zero dynamics. For a system with constraints $$ y(q) = 0 $$, the zero dynamics are enforced as follows:

(2)

$$ \ddot{y} = L_f^2 y + L_g L_f y \cdot u = 0 $$

where $$ L_f $$ and $$ L_g $$ are the Lie derivatives that encode the system's nonlinear dynamics, and u is the control input. In a zero-dynamics system, when the input of the system is zero, the output remains zero or converges to values close to zero. This zero-dynamics behavior typically indicates system stability and convergence.

In the HZD controller, the goal of achieving an output function of zero is achieved through the design of virtual constraints. Virtual constraints are imposed via feedback control on the configuration variables of the robot, driving the output function to zero. The hybrid nature of walking requires additional conditions for impact events, expressed through the hybrid invariance condition:

(3)

$$ y^-(q) \cdot y^+(q) \leq 0 $$

where the superscripts − and + denote the pre- and post-impact states, respectively. Stable gait control was achieved by selecting appropriate control variables and constraint designs.

Jessy Grizzle at the University of Michigan has primarily adopted HZD^[49], which has been successfully applied to a series of robots, including MABEL^[50], Cassie^[51], and RABBIT^[52]. Hereid et al. combined trajectory optimization methods with a multi-domain HZD control framework and then applied this approach to the underactuated spring-legged humanoid robot DURUS^[53]. The experimental results demonstrate the ability to quickly and reliably generate efficient multi-contact robot walking gaits.

2.2.3. MPC

MPC is an online optimization control method used to achieve optimal control of dynamic systems. The principle of MPC can be summarized as follows: first, a mathematical model of the system needs to be established. In the context of humanoid robots, this typically involves building a control-oriented dynamic model based on the established kinematic and dynamic models of robots. Next, the system model is used for state prediction, iteratively predicting the system's future states and output variables based on future input variables. An optimization problem is then solved to select the optimal control strategy, considering constraints such as input limits and state-variable constraints.

The MPC optimization problem is formulated as follows:

(4)

$$ \begin{equation} \begin{aligned} & \min\limits_{u_{0:N-1}} \sum\limits_{k=0}^{N-1} \left( \|x_k - x_{\text{ref}}\|_Q^2 + \|u_k\|_R^2 \right) + \|x_N - x_{\text{ref}}\|_P^2 \\ & \text{s.t.} \quad x_{k+1} = f(x_k, u_k), \quad x \in \mathcal{X}, \quad u \in \mathcal{U} \end{aligned} \end{equation} $$

where $$ Q $$, $$ R $$, and $$ P $$ are weighting matrices that prioritize different aspects of the control performance, $$ N $$ is the prediction horizon, and $$ \mathcal{X} $$ and $$ \mathcal{U} $$ represent state and input constraints, respectively.

MPC is an iterative process in which the controller periodically predicts, optimizes, and controls the system to continuously and dynamically adjust it. A classic example of applying MPC to bipedal robots was presented by Li and Quan^[54], who proposed a new framework for dynamic legged robot MPC based on forces and torques. In their work, a 10-degree-of-freedom bipedal robot was simplified into a rigid-body dynamics model. Using this model, they established a predictive model for the MPC control system. By minimizing state errors and controlling input variations, an optimization problem was formulated to determine the optimal ground reaction forces and torques. These forces and torques were then mapped to the torque of the five actuators on each leg to generate the desired inputs. The optimal inputs computed via MPC help the robot achieve precise foot placement during swing-leg motion, thus avoiding instability and oscillations. The proposed MPC framework enables precise velocity tracking for 3D dynamic movements and is applicable to dynamic motions such as fast walking, jumping, and running using the same control parameters. This method also exhibits robustness on rugged terrains.

2.2.4. Whole-body control

Whole-body control (WBC) can be understood as a method for dynamically coordinating and controlling multiple tasks, or more explicitly, as prioritized multi-task control. The concept of executing prioritized multi-task control first appeared in the 1980s, pioneered by Sentis and Khatib, who applied this approach to humanoid robots and termed it WBC^{[55, 56]}. The fundamental WBC optimization problem is formulated as follows:

(5)

$$ \begin{equation} \min\limits_{\tau, f} \sum\limits_{i} w_i \| J_i \ddot{q} + \dot{J}_i \dot{q} - a_i^{des} \|^2 \end{equation} $$

subject to the following dynamic constraints:

(6)

$$ \begin{equation} M(q)\ddot{q} + C(q, \dot{q}) + g(q) = S^T \tau + J_c^T f \end{equation} $$

and contact constraints

(7)

$$ \begin{equation} J_c \ddot{q} + \dot{J}_c \dot{q} = 0 \end{equation} $$

where $$ M(q) $$ is the mass matrix, $$ C(q, \dot{q}) $$ represents Coriolis and centrifugal forces, $$ g(q) $$ is the gravity vector, $$ J_c $$ is the Jacobian for task $$ i $$, and $$ f $$ represents contact forces.

Luis Sentis and Oussama Khatib introduced WBC as a framework based on task and posture spaces to enable multitasking behaviors in humanoid robots. The task space refers to the specific objectives that the robot must accomplish, such as grasping or walking, whereas the posture space corresponds to the joint angles or positions that control the robot's posture. The relationship between these spaces is established through projection and mapping, where projection maps the robot dynamics into task-relevant spaces, and mapping transforms task-space commands into posture-space control inputs. The WBC aims to simultaneously control multiple tasks by prioritizing them according to their importance.

Moro and Luis further classified WBC controllers^[57] based on the output type and problem-solving method. Output-wise, controllers are velocity-based (producing joint velocities) or torque-based (producing joint torques), with these outputs ultimately converted into motor currents via low-level impedance or torque-feedback controllers. Regarding solution methods, the controllers are either closed-form or optimization-based. Closed-form controllers derive outputs through algebraic operations (such as projection and matrix inversion), allowing a fast hierarchical resolution of task priorities without heavy computation. Optimization-based controllers solve an optimization problem to find solutions, which generally requires more computation time.

Kim et al. proposed a controller combining WBC with MPC and applied it to the Mini-Cheetah quadruped robot^[58]. In this framework, the MPC computes the optimal distribution of reaction forces over an extended horizon using a simplified model, whereas the WBC generates joint torque, position, and velocity commands based on the MPC outputs. Unlike traditional WBC approaches, this controller emphasizes reaction force commands, thereby enabling high-speed dynamic maneuvers during aerial phases. It was validated with six different gaits in various environments, including outdoor and treadmill tests, and achieved a top speed of 3.7 m/s. Additionally, Zhu et al. proposed a dynamic cutoff frequency scheme to balance the speed and accuracy^[59].

2.3. Sum

This section presents a dynamics-based control framework for humanoid robots, leveraging simplified models such as the Cart-Table, LIP, LIPP, and SLIP to reduce computational complexity while maintaining stability in bipedal locomotion. Control strategies include PID for basic balance and three widely used approaches: HZD, MPC, and WBC. Table 2 provides a comparison of these three commonly used methods.

Table 2

Comparison of dynamic control methods in humanoid robots

Method	Key characteristics	Cases	Multidimensional insights
HZD: Hybrid zero dynamics; MPC: model predictive control; QP: quadratic programming; ALIP: angular momentum linear inverted pendulum; WBC: whole-body control; ID: inverse dynamics.
HZD	• Virtual constraint enforcement • Efficient with compliant legs (e.g., springs)	• Cassie walking at 2.1 m/s on flat terrain • Soft/uneven surfaces (sand)	• Low computational burden (offline trajectory optimization)
			• High energy efficiency
			• Limited adaptability to unknown disturbances
			• Requires accurate modeling of underactuated dynamics
MPC	• Receding-horizon QP solving • Real-time disturbance handling	• Terrain-adaptive walking (slope, gravel, steps) with ALIP-based • Fast walking at 1.6 m/s	• Strong robustness to terrain variations
			• High computational demand
			• Sensitive to model errors
			• Supports constraint-based planning
			• Enables complex coordinated behaviors
WBC	• Prioritized task-space optimization • ID + contact handling	• Atlas parkour (jumping, flipping, handstands) • Balance + manipulation synergy	• Requires full-body dynamic/contact models
			• Sensitive to latency and sensor delays
			• Less suitable for high-speed gaits

● High-speed, multi-task scenarios: Combine MPC for agile trajectory planning with WBC for coordinated whole-body execution.

● Challenging terrains: Use HZD with compliant mechanisms to enhance adaptability and energy efficiency.

● Hardware-driven choices: Prefer HZD for passive compliance; use MPC or WBC when active torque control is needed.

By combining simplified models with complementary control strategies, this integrated approach enables stable, efficient, and versatile locomotion for diverse humanoid robot applications.

3. Learning-Based Control Methods

Learning-based control methods for humanoid robots include RL^[60], imitation learning, phase-based methods, and large language models (LLMs). RL optimizes robot actions in complex environments through trial-and-error and reward feedback, thereby enabling autonomous adaptation and improvement. Imitation learning accelerates strategy acquisition by leveraging expert demonstrations and enhancing training efficiency through direct mimicry of human behavior. Phase-based methods capture periodic and pseudo-periodic patterns in human motion, allowing robots to replicate natural rhythmic locomotion with high fidelity. LLMs trained on vast datasets support multi-task and transfer learning, boosting robots' perception and decision-making by providing a broad contextual understanding. Integrating these advanced learning approaches significantly enhances the autonomy, adaptability, and intelligence of humanoid robots, enabling them to perform complex tasks with improved efficiency and accuracy.

3.1. RL

RL^[61-63], a key area within machine learning (ML), is fundamentally based on Markov decision processes (MDPs), defined by six main parameters $$ \langle S, A, T, R, C, \rho \rangle $$. Here, $$ S $$ and $$ A $$ denote the state and action spaces, respectively; $$ R $$ and $$ C $$ represent the reward and cost functions, respectively; $$ T $$ is the state transition function; and $$ \rho $$ is the discount factor. In humanoid robot research, RL is frequently combined with deep-learning techniques. Hybrid methods that integrate model-based and learning-based approaches have also been developed to exploit the advantages of both methods. According to^[64], deep RL frameworks for bipedal robots can be divided into two types: end-to-end and hierarchical, the latter featuring a layered control structure. Further details on this classification are beyond the scope of this study. The classification of RL methods is summarized in Table 3.

Table 3

Legged robot tasks using RL

Categorization	Method	Ref.	Pros	Cons
RL: Reinforcement learning; SARSA: state-action-reward-state-action; DQN: deep Q-network; DDPG: deep deterministic policy gradient; PPO: proximal policy optimization.
Model-free methods	Q-Learning	^[65],^[66],^[67]	• Simple, model-free	• High-dimensional inefficiency
			• Model-free learning	• Scalability issues
			• Simple and straightforward	• Exploration-exploitation dilemma
			• Convergence guarantees	• Learning rate sensitivity
			• Off-policy learning	• Temporal-difference error accumulation
			• Suitability for discrete action spaces	• Inefficiency in continuous spaces
	SARSA	^[71],^[72]	• On-policy learning	• Potentially slower learning
			• Policy-sensitive	• Exploration-exploitation trade-off
			• Convergence	• Scalability issues
			• Suitable for dynamic policies	• Sensitivity to learning parameters
			• Handles stochastic environments	• Suboptimal policies in certain cases
Model-based methods	Dyna-Q	^[71],^[72]	• Accelerated learning	• Model accuracy-dependence
			• Efficient use of data	• Computational overhead
			• Reduced exploration costs	• Complexity in implementation
			• Improved sample efficiency	• Scalability issues
			• Flexibility and adaptability	• Potential for overfitting
			• Better generalization	• Exploration-exploitation balance
			• Suitability for complex environments
Policy gradient methods	REINFORCE	^[73]	• Direct policy optimization	• Sample inefficiency
	REINFORCE	^[73]	• Continuous action spaces	• High-variance in gradients
	Actor-critic	^[74],^[75],^[76]	• Stochastic policies	• Sensitive to hyperparameters
			• Suitable for high-dimensional data action spaces	• Computationally intensive
			• Improved exploration	• Risk of suboptimal policies
			• End-to-end learning	• Implementation complexity
			• Efficient policy updates	• Bias in value estimation
Deep reinforcement methods	DQN	^[77],^[78]	• Handles high-Dim. state spaces	• Sample inefficiency
			• End-to-end learning	• Computationally-intensive
			• Experience replay	• Exploration challenges
			• Target networks	• Memory requirements
			• Scalability	• Stability issues
			• Improved performance	• Sensitivity to hyperparameters
				• Delayed rewards
				• Overfitting risk, data-hungry
	DDPG	^[79],^[80]	• Stable for continuous actions	• Increased complexity
			• Handles continuous action spaces	• Sample inefficiency
			• Deterministic policy	• Hyperparameter sensitivity
			• Efficient exploration with noise	• Exploration challenges
			• End-to-end learning	• Computational demands
			• Experience replay	• Stability issues
			• Actor-critic framework	• Risk of overfitting
			• Target networks	• Implementation complexity
	PPO	^[81],^[82],^[83]	• Stable, scalable	• Hyperparameter sensitivity
			• Stability and reliability	• Sample inefficiency
			• Improved sample efficiency	• Hyperparameter sensitivity
			• Ease of implementation	• Implementation complexity
			• Robust performance	• Exploration challenges
			• Continuous and discrete action spaces	• Scalability issues
			• Clipped surrogate objectives	• Long training times
			• Reduced computational complexity

3.1.1. Model-free methods

3.1.1.1. Q-Learning

Q-Learning^[65-67] is a classic model-free RL algorithm that learns discrete action-value mappings without requiring a model of the environment. For humanoid robots, Q-learning is suitable for discrete tasks such as basic navigation or simple motor control in environments with relatively simple dynamics. The Q-values are updated iteratively using

(8)

$$ Q(s, a) \leftarrow Q(s, a) + \alpha \left[ r + \gamma \max\limits_{a'} Q(s', a') - Q(s, a) \right] $$

where $$ Q(s, a) $$ denotes the value of taking action $$ a $$ in state $$ s $$, $$ \alpha $$ is the learning rate, $$ r $$ is the received reward, $$ \gamma $$ is the discount factor, $$ s' $$ is the next state, and $$ a' $$ is the next action.

3.1.1.2. State-action-reward-state-action

The state-action-reward-state-action (SARSA)^[68-70] is another model-free method that updates the action value function using the agent's current policy. In humanoid robots, SARSA is well-suited for on-policy learning tasks, such as real-time balancing or locomotion, where the current policy is continuously updated during execution. Its update rule is given by

(9)

$$ \begin{equation} Q(s, a) \leftarrow Q(s, a) + \alpha \left[ r + \gamma Q(s', a') - Q(s, a) \right] \end{equation} $$

The variables have the same meaning as in Equation 8, with the key difference being that SARSA uses the actual action $$ a' $$ chosen by the current policy instead of the maximum Q-value.

3.1.2. Model-based methods

Dyna-Q^{[72, 84]} is a hybrid method that integrates model-free Q-learning with a learned model of the environment. This enables both real and simulated experiences to update the policy, thereby improving the sample efficiency. In humanoid robotics, Dyna-Q has been applied to tasks such as dynamic balance and obstacle avoidance, where real-world interactions are combined with simulated rollouts to accelerate policy learning.

3.1.3. Policy gradient methods

3.1.3.1. REINFORCE

REINFORCE^[73] is a fundamental policy gradient algorithm used to directly optimize policies in continuous-action spaces. Humanoid robots are particularly suitable for tasks requiring smooth, high-dimensional motor control, such as walking, running, and executing complex movements. The algorithm updates the policy parameters via gradient ascent to maximize the expected return. The update rule is:

(10)

$$ \begin{equation} \theta \leftarrow \theta + \alpha \cdot \nabla_{\theta} \left[ \log \pi_{\theta} ( a_t \mid s_t ) \cdot G_t \right] \end{equation} $$

where $$ \theta $$ denotes the policy parameters, $$ \alpha $$ is the learning rate, and $$ \pi_\theta(a_t \mid s_t) $$ is the probability of selecting action $$ a_t $$ given state $$ s_t.$$ The return $$ G_t $$ is defined as a discounted cumulative reward:

(

$$ G_t = \sum\limits_{k=0}^{\infty} \gamma^k r_{t+k}, $$

where $$ \gamma $$ is the discount factor, and $$ r_{t+k} $$ is the reward at time $$ t+k $$.

3.1.3.2. Actor-critic

Actor-critic methods^[74-76] combine the strengths of value-based and policy-based approaches, making them well-suited for humanoid robots operating in high-dimensional continuous action spaces. These methods consist of an actor that updates the policy, and a critic that estimates the value function to guide the actor's learning.

The actor's update rule is given by

(11)

$$ \begin{equation} \theta_{\text{Actor}} \leftarrow \theta_{\text{Actor}} + \alpha_{\text{Actor}} \cdot \nabla_{\theta_{\text{Actor}}} \left[ \log \pi_{\theta_{\text{Actor}}} ( a_t \mid s_t ) \cdot \delta_t \right] \end{equation} $$

where $$ \theta_{\text{Actor}} $$ are the actor's parameters, $$ \alpha_{\text{Actor}} $$ is the learning rate, and $$ \delta_t $$ is the temporal difference (TD) error. The TD error serves as a feedback signal for adjusting the policy and is computed using the critic network as follows:

(12)

$$ \begin{equation} \theta_{\text{Critic}} \leftarrow \theta_{\text{Critic}} + \alpha_{\text{Critic}} \cdot \nabla_{\theta_{\text{Critic}}} \left[ \left( r_{t+1} + \gamma V(s_{t+1}) - V(s_t) \right)^2 \right] \end{equation} $$

Here, $$ \theta_{\text{Critic}} $$ are the parameters of the value function approximator, $$ \alpha_{\text{Critic}} $$ is the critic's learning rate, and $$ V(s_t) $$ estimates the expected return from state $$ s_t $$. The term $$ r_{t+1} + \gamma V(s_{t+1}) - V(s_t) $$ represents the TD error, which measures the discrepancy between the predicted and actual returns.

Actor-critic architectures are widely adopted in humanoid robotics owing to their sample efficiency and stability, particularly in dynamic and uncertain environments where real-time adaptation is essential.

3.1.4. Deep RL methods

3.1.4.1. Deep Q-network

The deep Q-network (DQN)^{[77, 78]} extends Q-learning by using deep neural networks to approximate the Q-function, enabling RL in high-dimensional state spaces. In the context of humanoid robots, DQN is suitable for tasks involving complex navigation and visual perception, such as obstacle avoidance and high-level decision-making. The Q-network is trained to minimize the difference between the predicted and target Q-values using the following loss function:

(13)

$$ \begin{equation} L = \mathbb{E} \left[ \left( y - Q(s, a; \theta) \right)^2 \right] \end{equation} $$

where $$ y = r + \gamma \max_{a'} Q(s', a'; \theta^{-}) $$ is the target Q-value, $$ \theta $$ are the current network parameters, and $$ \theta^{-} $$ represents the parameters of a target network updated periodically to stabilize training.

3.1.4.2. Deep deterministic policy gradient

Deep deterministic policy gradient (DDPG)^{[79, 80]} is an off-policy, actor-critic algorithm designed for continuous action spaces. It combines deterministic policy gradients with deep function approximators, making it particularly effective for humanoid robots performing complex motor tasks, such as manipulation, locomotion, and precise coordination. DDPG uses two networks: an actor $$ \mu(s; \theta_{\text{Actor}}) $$ to represent the policy and a critic $$ Q(s, a; \theta_{\text{Critic}}) $$ to estimate the action-value function. The critic is trained to minimize the following loss:

(14)

$$ \begin{equation} L_{\text{Critic}} = \mathbb{E} \left[ \left( r + \gamma Q(s', \mu(s'; \theta_{\text{Actor}}); \theta_{\text{Critic}}^{-}) - Q(s, a; \theta_{\text{Critic}}) \right)^2 \right] \end{equation} $$

The actor network is updated by maximizing the expected return using the deterministic policy gradient:

(15)

$$ \nabla_{\theta_{\text{Actor}}} J \approx \mathbb{E} \left[ \nabla_a Q(s, a; \theta_{\text{Critic}}) \nabla_{\theta_{\text{Actor}}} \mu(s; \theta_{\text{Actor}}) \right] $$

3.1.4.3. Proximal policy optimization

Proximal policy optimization (PPO)^{[81-83, 85-89]} is a widely used on-policy algorithm that stabilizes training by limiting policy updates through a clipped surrogate objective. It is well suited for humanoid robots performing tasks that demand robustness and adaptability, such as multijoint coordination, variable terrain walking, and dynamic interaction. The clipped objective function used by PPO is as follows:

(16)

$$ L_{\text{Clip}} = \mathbb{E}_t \left[ \min \left( r_t(\theta) A_t, \text{clip}(r_t(\theta), 1 - \varepsilon, 1 + \varepsilon) A_t \right) \right] $$

where $$ r_t(\theta) = \frac{\pi_\theta(a_t \mid s_t)}{\pi_{\theta_{\text{old}}}(a_t \mid s_t)} $$ is the probability ratio between the new and old policy, $$ A_t $$ is the advantage estimate, and $$ \varepsilon $$ is a hyperparameter that controls the update range to ensure conservative policy improvement.

3.1.4.4. Hierarchical reinforcement learning

Deep RL methods can be further categorized into end-to-end and hierarchical methods. Hierarchical reinforcement learning (HRL)^[90-97] decomposes complex tasks into simpler subtasks, each governed by a local policy, with a higher-level policy coordinating the overall behavior. This framework improves learning efficiency and task generalization, particularly for humanoid robots engaged in sequential or compound tasks, such as object manipulation, long-horizon navigation, and whole-body coordination.

3.2. Imitation learning

Imitation learning^{[98, 99]} enables humanoid robots to learn and perform complex tasks rapidly by replicating human demonstrations. Leveraging high-quality demonstration data allows robots to accurately imitate actions, significantly reducing the training time while enhancing control robustness and effectiveness. This approach improves the adaptability of robots in dynamic or unfamiliar environments, making it a vital technology for advancing robot intelligence. Key imitation learning methods include behavior cloning (BC),^[100] inverse RL,^[101] and generative adversarial imitation learning (GAIL)^[102]. The classification of imitation learning approaches for humanoid robots is presented in Table 4.

Table 4

Legged robot tasks using IL

Method	Ref.	Pros	Cons
IL: Imitation learning; BC: behavior cloning; IRL: inverse reinforcement learning; GAIL: generative adversarial imitation learning.
BC	^[103],^[104],^[105]	• Simplicity and ease of implementation	• Dependence on quality and quantity of data
		• Rapid learning	• Limited generalization
		• Efficiency in supervised settings	• Overfitting
		• Reduced risk	• Lack of exploration
		• High-quality performance	• Error propagation
			• Noisy or suboptimal expert demonstrations
IRL	^[101],^[106],^[107],^[108]	• Understanding of expert behavior	• High complexity and computational cost
		• Generalization	• Ambiguous reward functions
		• Robustness to suboptimal data	• Dependence on expert quality
		• Learning from sparse data	• Long training time
		• Transferability	• Overfitting risk
		• Interpretable reward discovery	• Sensitivity to demonstration variations
GAIL	^[102],^[109],^[110] ^[111],^[112],^[113],^[114]	• High-quality imitation	• Training instability
		• Robust to suboptimal demonstrations	• High computational complexity
		• No need for explicit rewards	• Mode collapse
		• Effective generalization	• Sensitive to expert quality
		• Efficient use of limited data	• Ambiguous learned behaviors
		• Learns from interactions	• Requires careful tuning

3.2.1. BC

BC^{[104, 105]} is a basic imitation learning approach formulated as a supervised learning problem. It models expert behavior by learning a mapping from the observed states to actions using expert trajectories. Given a discretized dataset of $$ n $$ expert demonstrations, the algorithm directly feeds state-action pairs into a neural network to train the policy. Although BC was initially applied to autonomous driving, it suffers from compounding errors owing to the lack of feedback, limiting its effectiveness in complex or long-horizon tasks. Consequently, BC has seen limited advancement in humanoid robot imitation learning.

3.2.2. Inverse reinforcement learning

Inverse reinforcement learning (IRL)^[101] reverses the typical RL process by first inferring the reward function from expert demonstrations and then learning a policy using that reward. This addresses a key limitation in traditional RL: the difficulty in designing effective reward functions, which significantly affects the control performance. The input to the IRL is a set of expert-generated trajectory samples, denoted as $$ T_E = \{ \tau_1, \tau_2, \dots \} $$, where each $$ \tau_i $$ is an ordered sequence of state-action pairs from expert demonstrations.

(17)

$$ T_E = \{ s_1, a_1, s_2, a_2, \cdots | \tau_i \} $$

IRL aims to derive a reward function from expert demonstration samples. It posits that trajectories generated by the expert policy yield maximal rewards, thereby necessitating the reward function $r^* $ to satisfy the inequality $$ E_{\pi_E} [r^*(s, a)] \geq E_{\pi} [r^*(s, a)] $$. By reformulating this inequality into an optimization problem, the process of determining the reward function unfolds as follows:

(18)

$$ \min\limits_{r} \max\limits_{\pi} E_{\pi} [r(s, a)] - E_{\pi_E} [r(s, a)] $$

Owing to the high-dimensional nature of humanoid robot control, computing reasonable reward functions using IRL requires significant computational power. Moreover, there is a possibility of deriving multiple reward functions that yield similar outcomes, necessitating further expert analysis. These challenges significantly limit the application of IRL in humanoid-robot control.

3.2.3. GAIL

Figure 3 illustrates the principle of GAIL^[102]. GAIL integrates imitation learning with generative adversarial networks (GANs)^[109], reformulating learning from expert demonstrations within the GAN framework. This approach addresses the compounding errors in BC caused by limited environmental interaction. In GAIL, the policy, which maps states to actions, acts as the generator, whereas the reward function, which evaluates state-action pairs $$ (s, a) $$ and outputs instantaneous rewards, serves as the discriminator. Policy optimization is performed based on the current reward function, which is analogous to generator training, whereas optimizing the reward function corresponds to training the discriminator. By adopting this GAN architecture, GAIL enhances robustness, representational power, and computational efficiency compared to traditional imitation learning methods^[102].

Figure 3. The general framework of GAIL. GAIL: Generative adversarial imitation learning

In addition, GAIL models the relationship between the generator and discriminator as an adversarial game process, thereby avoiding the explicit process of solving for the reward function. The objective function of this game is expressed as follows:

(19)

$$ \min\limits_{\pi} \max\limits_{D} E_{\pi}[\log D(s, a)] + E_{\pi_E}[1 - \log D(s, a)] - \lambda H(\pi) $$

where the discriminator $$ D(s, a) $$ aims to distinguish between decision trajectories $$ (s, a) $$ generated by the expert policy $$ E_{\pi_E} $$ and those produced by the policy being optimized, similar to the role of the discriminator in GANs. $$ H(\pi) $$ represents the entropy of the policy, maximizing the diversity of policy outputs to encourage exploratory behavior.

GAIL is the most widely used imitation learning method for humanoid-robot control. Peng^[110] used motion capture data from public Mocap datasets (CMU and SFU) for low-level control by mapping motions to robot joints, while high-level control set target tasks, enabling robots to perform predefined actions and mimic human motions. Combined with unsupervised RL, GAIL can train skill libraries from large datasets for diverse tasks^[111]. The adversarial motion priors (AMP) algorithm was validated on the Adam robot, tested in the Isaac Gym and Webots simulators, and deployed on hardware with highly human-like walking^[114]. Reference^[105] improved the rewards by combining task and imitation objectives using a multi-expert network for smoother behavior. Dai^[112] proposed a benchmark with expert datasets and multiple-robot platforms. Unlike most prior studies using full-body motions,^[115] mapped only upper-body motions onto the Unitree H1 robot, freeing the legs for diverse actions. Despite its successes, GAIL training can be unstable;^[116] addressed this by integrating diffusion models to enhance reward smoothness and robustness. GAIL has also been effectively applied to quadruped robots^{[97, 113, 117]}.

3.3. Representation learning

Reference trajectories (e.g., motion capture data) have greatly advanced motion learning^{[110, 118, 119]}, but these methods struggle to generalize beyond the training-data distribution^[117]. This limitation stems from imitation learning, which focuses on replicating trajectories rather than understanding the underlying dynamics, often resulting in memorization rather than true learning. Large distribution gaps between different motions hinder smooth transitions, and directly linking motion to the original trajectories leads to inefficient representations^[120]. A more systematic approach to leverage the spatial structure of motion is required.

Structured representations introduce inductive biases to manage complex motions efficiently by extracting fundamental features and temporal dependencies^{[121, 122]}. These representations enable the generation of continuous and diverse motions^[123]. Classical controllers often parameterize motion using cyclic sine-wave trajectories^[124] or CPGs. Self-supervised models, such as autoencoders, learn latent motion dynamics, enabling complex decision-making^[125], long-term tasks^[126], and motion imitation^[127].

Frequency domain methods, as shown in Figure 4, are another structured approach widely used in motion tasks. The periodic Autoencoder (PAE) applies frequency transformations as inductive biases to improve the smoothness and naturalness of motion transitions^[128]. The latent parameters of PAE serve as effective holistic states for downstream tasks^[123] but are limited to local frames. Fourier latent dynamics (FLD), an extension of PAE, models spatiotemporal relations in periodic motions via a predictive latent structure[Figure 4]^[129]. FLD efficiently represents high-dimensional trajectories in a continuous latent space, capturing fundamental features and temporal dependencies, and excels in robust long-term motion learning while avoiding unlearnable regions.

Figure 4. Structure diagram of PAE and FLD. PAE: Periodic Autoencoder; FLD: Fourier latent dynamics

3.4. LLMs

LLM technology is a deep learning–based natural language processing approach that trains large-scale models capable of understanding and generating natural language text. These models can produce codes or support common-sense reasoning, whereas visual language models enable open-vocabulary visual recognition^[130]. The key advantage of LLMs lies in their ability to learn rich linguistic knowledge and patterns from massive text corpora, allowing them to grasp semantics, grammar, and other language aspects with enhanced processing capabilities.

LLMs have achieved significant breakthroughs in both language and vision domains, exemplified by models such as BERT^[131], GPT-3^[132], Codex^[133], GPT-4^[134], SAM^[135], DALL-E 2^[136], and CLIP^[137]. In robotics, LLM applications can be broadly divided into direct robotic integration and related applications^[138]. This section focuses on research involving LLMs in legged robots.

The main applications of LLMs in legged robot tasks are summarized in Table 5, with robot policy learning and code generation being particularly important. In the previously mentioned GAIL research, adversarial imitation enabled robots to progressively align their motion trajectories with reference trajectories, although it often required task-specific strategies. To overcome this, combining LLMs with GAIL allows the pre-training of diverse motions via GAIL, while LLMs act as strategic planners to execute specific action sequences^{[139, 166]}. Moreover, LLMs play vital roles in semantic analysis and code generation. By leveraging their extensive knowledge, control tasks can be fully delegated to LLMs, which can be modularized into multiple specialized roles, such as task analysis, code generation, and debugging^[153].

Table 5

Legged robot tasks using LLM

Application scenarios	Tasks	Works
LLM: Large language model; RL: reinforcement learning.
Robotics	Language-conditioned imitation learning	^[139],^[140]
	Language-assisted RL	^[141],^[142],^[143],^[144],^[145],^[146]
	Language-image goal-conditioned value learning	^[147],^[148]
	High-level task planning	^[149],^[150],^[151]
	Code generation based on LLM	^[152],^[153],^[154],^[155],^[156],^[157],^[158],^[159]
Human-computer interaction	speech interaction	^[160],^[161],^[162],^[163],^[164],^[148],^[165]

3.5. Applications of learning-based methods in humanoid robots

Learning-based methods are widely used in humanoid robot motion control, with RL being the most common approach that processes proprioceptive observations (e.g., joint angles and velocities) and outputs joint actions through proportional-derivative (PD) control for locomotion. Supervised learning with encoders can further enable terrain adaptation by extracting the environmental features. For more human-like motions, imitation learning methods, such as GAIL, align robot movements with motion-capture data through adversarial training, as demonstrated by Tesla Optimus learning fine manipulation from human demonstrations. Representation learning (e.g., PAE, FLD) encodes motion primitives in latent space for efficient movement generation, whereas LLMs serve as high-level planners that interpret natural language commands to coordinate low-level controllers, effectively acting as the robot's "brain." As demonstrated in Table 6, we compiled real-world application examples of these methods.

Table 6

Representative cases of humanoid robot learning applications

Case	Method type	Key metrics/phenomena	Multidimensional insights
RL: Reinforcement learning; FLD: Fourier latent dynamics; LLM: large language model; IL: imitation learning; GPU: graphics processing unit.
DeepMind Soccer Robot (Deep RL)	End-to-end RL	Compared to scripted baseline: walking speed 181%, turning speed 302%, get-up time 63%, kicking speed 134%	• High autonomy & environmental adaptability
			• Large sample consumption (tens of millions of steps)
			• Zero-shot Sim-to-Real transfer proves the effectiveness of domain randomization
Tesla Optimus – Household Tasks	RL + Behavior Library	Already able to perform sequential actions such as "cut vegetables – plate – wipe table"	• Uses high-frequency visual closed-loop control; high computational load
			• Factory simulation helps shorten deployment time; better sample efficiency than pure RL
			• Safety mechanism: self-supervised detection of dangerous poses with co-control stop
FLD Representation Learning (MIT Humanoid)	Representation Learning	Latent space interpolation error < 0.04 rad; transitions smooth even for unseen trajectories	• Compression ratio ≈ 70%; inference latency < 1 ms
			• Significantly improves multi-action switching smoothness; enables long-horizon tasks
			• No need for reward engineering; minimal demonstration required
LUMOS – Language Conditioned Imitation	LLM + IL	CALVIN multi-task success rate improved from 47% 63%; zero-shot transfer to real robot arm	• Strong generalization; capable of understanding complex language
			• High sample efficiency: < 1% labeled language data
			• World model training narrows the sim-to-real gap, but inference requires GPU

3.6. Sum

The field of humanoid robot control has undergone a transformative shift from traditional rule-based approaches to data-driven learning paradigms. By integrating various ML techniques, modern control methods have significantly enhanced the environmental adaptability and task execution capabilities of robots. RL enables autonomous policy optimization in complex environments using reward mechanisms. Imitation learning rapidly acquires operational skills by mimicking the demonstrations of experts. Deep neural networks achieve high-precision control through big data training, whereas representation learning automatically extracts key features from raw data to support intelligent decision making. These cutting-edge technologies collectively advance humanoid robots toward higher levels of flexibility, autonomy, and intelligent performance.

Meanwhile, we compared four learning-based methods–RL, imitation learning, representation learning, and LLMs–across six dimensions: autonomy, sample efficiency, environmental adaptability, computational cost, interpretability, and safety, with the results shown in Figure 5. RL demonstrates outstanding performance in autonomous exploration and environmental adaptation but requires extensive trial and error and has lower safety. Imitation learning relies on high-quality demonstration data while maintaining a balanced overall performance. Representation learning exhibits high sample efficiency and good interpretability, making it suitable for structured tasks. LLMs show strong generalization and adaptability but suffer from high computational costs and limited interpretability. Therefore, these methods can be strategically combined across certain dimensions to leverage their respective strengths and compensate for their weaknesses.

Figure 5. Comparison of learning methods.

As shown in Table 7, although each control method has unique advantages, learning-based approaches demonstrate particularly promising potential. Although traditional methods (e.g., MPC and WBC) have certain advantages in motion control, learning-based methods are increasingly becoming the key solution for advanced challenges, such as navigating complex terrains, autonomous fall recovery, and dynamic object manipulation, as application scenarios continue to expand. Notably, learning-based methods also offer lower technical barriers and shorter development cycles, which not only reduce industry entry thresholds but also accelerate innovation across the humanoid robotics field. With continuous advancements in algorithms and computing hardware, learning-based control methods are poised to lead the next generation of technological revolutions in humanoid robotics.

Table 7

Control methods and their advantages/disadvantages for humanoid robots

Control method (category)	Basic principle	Refs.	Advantages	Disadvantages
IDC: Inverse dynamics control; ID: inverse dynamics; OSC: operational space control; CoM: center of mass; QP: quadratic programming; MPC: model predictive control; ZMP: zero moment point; RL: reinforcement learning.
IDC	Computes desired torques based on ID for tracking target trajectories	[167]	Simple implementation, high trajectory accuracy	Sensitive to model errors
Contact-constrained ID control	Models ground or arm contacts as force or position constraints	[168]	Supports multi-contact, improves steady-state control	Complex contact modeling
OSC	Defines targets in task space (e.g., CoM or end-effector), then maps to joint space	[169]	Supports task prioritization, yields natural motion	Relies heavily on accurate Jacobian and mass matrix
Optimization-based control (QP/MPC)	Formulates control as an online constrained quadratic programming problem	[170]	Unified handling of multi-task and multi-constraint control	High computational demands for real-time execution
Forward dynamics + feedback control	Treats the system as a known model and designs stabilizing feedback law	[171]	Strong stability guarantees, clear control design	Strong dependence on accurate system modeling
ZMP control	Maintains the projection of CoM within the support polygon for stability	[172]	Suitable for cyclic walking, mature and well-studied method	Not suitable for unstructured or highly dynamic tasks
MPC	Predicts future states and optimizes control inputs accordingly	[173]	Predictive capability, strong stability	High computational cost
State feedback control + estimation	Estimates system states via sensors for closed-loop feedback control	[174]	High robustness, suitable for real-world applications	Critically depends on state estimation accuracy
RL + imitation learning	Learns policy through trial-and-error or human demonstrations	[175]	Highly adaptive to unstructured environments	Safety concerns, high training cost
Hybrid control architecture (Hierarchical)	High-level policy planning combined with low-level optimization or feedback control	[176]	Flexible and modular structure, robust performance	Complex system integration and synchronization

4. Path Planning and Obstacle Avoidance

An essential capability of mobile robots is autonomous path planning and obstacle avoidance in complex dynamic environments^[177-179]. Path planning seeks an optimal route from a start to a target point, optimizing criteria such as the shortest distance, minimum travel time, or lowest operational cost while successfully avoiding obstacles. As effective path planning inherently requires obstacle avoidance, these two challenges are closely linked.

Environmental perception and autonomous localization are critical for motion planning. Robots employ sensors, such as laser scanners and cameras, to collect environmental data, build local maps, and simultaneously estimate their position within these maps using simultaneous localization and mapping (SLAM) technology^[180]. SLAM enables rapid and autonomous localization and mapping in unknown environments, thereby supporting precise path planning and obstacle avoidance. SLAM methods are classified based on the sensor type, as shown in Figure 6.

Figure 6. Classification of SLAM technology. SLAM: Simultaneous localization and mapping.

● 2D Laser SLAM:

Rotating laser scanners are used to measure the distance and direction in a plane. They enable localization and mapping but only capture 2D planar information, limiting their use to applications such as floor-cleaning robots or drones operating in a single plane and not suited for taller robots such as humanoids.

● 3D Laser SLAM:

It provides detailed 3D perception, including height and shape, but requires expensive equipment and significant computational resources^[181]. It is commonly used in indoor navigation, 3D modeling, and environmental monitoring.

● Visual SLAM:

Cameras are employed to extract image features and motion data for localization and mapping^[182]. It is cost-effective compared to lidar, but is sensitive to lighting changes and texture scarcity, which may cause localization errors.

● Fusion SLAM:

It combines multiple sensors [e.g., lidar, cameras, and inertial measurement units (IMUs)] to improve accuracy and robustness. For example, ETH's Anymal quadruped robot integrates IMUs, lidar, and cameras^[96], enhancing self-state perception and external environment mapping, respectively.

SLAM systems mainly consist of five components: sensor data acquisition, front-end odometry, loop closure detection, back-end nonlinear optimization, and map construction^[183], as shown in Figure 7.

Figure 7. SLAM system framework. SLAM: Simultaneous localization and mapping.

The overall system framework of SLAM is shown in Figure 7. The SLAM process typically consists of the following steps: acquiring sensor data [e.g., images, light detection and ranging (LiDAR) point clouds, IMU data, and wheel encoder measurements]; front-end odometry estimates poses using tightly coupled visual, LiDAR, and inertial data; loop closure detection relocates the current frame to reduce cumulative drift; the back-end performs nonlinear optimization to minimize global errors and ensure consistency of the estimated trajectory and map; finally, the mapping module integrates sensor observations into a coherent global map.

Extensive research has been conducted on path planning and obstacle avoidance techniques for mobile robots, resulting in various mature algorithms. These algorithms can be broadly classified into four categories: graph-based, sampling-based, optimization-based methods, and local obstacle avoidance strategies. Table 8 provides a summary of the representative algorithms in each category along with their respective advantages and limitations.

Table 8

Common path planning algorithms

Types	Algorithm	Description	Pros	Cons
RRT: Rapidly-exploring random trees; PRM: probabilistic roadmap; MPC: model predictive control.
Graph search	Dijkstra^[184]	Stepwise distance updates to find shortest paths	Guarantees shortest paths to all nodes	High computation; cannot handle negative edges
Graph search	A^*[185]	Heuristic search combined with Dijkstra	Efficient; finds optimal paths	Performance depends on heuristic design
Sampling-based	RRT^[186]	Random sampling to build exploration trees	Fast convergence; adapts to dynamic environments	Needs many samples
Sampling-based	PRM^[187]	Builds roadmap in map space	Suitable for complex, high-dimensional spaces; adaptive	Path quality affected by sampling density
Optimization-based	D^*[188]	Reverse search updating cost maps for path optimization	Efficient in dynamic environments	High memory usage for cost maps
Optimization-based	MPC^[189]	Predictive model optimizing path with dynamic constraints	Handles multiple goals and constraints simultaneously	High computation; needs accurate models
Local obstacle avoidance	Artificial potential field^[190]	Uses attraction and repulsion forces	Simple and real-time	Prone to local minima; parameter sensitive
Local obstacle avoidance	Dynamic window approach^[191]	Samples surroundings to determine next motion	Real-time; adaptable; easy tuning	May get stuck in local minima; unsuitable for large areas

Currently, research on humanoid robots primarily focuses on enhancing motion control and walking performance, with relatively little emphasis on trajectory planning. Humanoid robots can adopt trajectory-planning technologies from wheeled robots and autonomous vehicles^[192]. Unlike wheeled robots, which must navigate around obstacles, humanoid robots can step over or traverse obstacles, offering novel insights into trajectory planning.

Boston Dynamics' ATLAS robot^[193] uses LIDAR to scan the terrain, detect obstacles, and solve optimization problems for safe stepping region calculation and foot placement planning, which are fed into the controller. The Iterative Regional Inflation Semidefinite programming (IRIS) algorithm computes obstacle-free convex polygonal regions, enabling both trajectory planning and obstacle avoidance. The parkour perception algorithm converts the sensor data into actionable information, whereas a model predictive controller computes the optimal movements. Additionally, an off-template movement controller simplifies the behavior generation by invoking actions from an action library^[194].

Carnegie Mellon University's CHIMP humanoid robot constructs 3D environment models using multiview fusion and visual range systems, enhancing situational awareness with real-time texture mapping. Its geometric constraints are defined in Cartesian coordinates, and motion paths are generated using a constrained bidirectional rapidly exploring random tree algorithm^[195]. CHIMP's planning architecture includes multiple planning nodes with a request/response interface to ensure a high-speed system response.

Honda's ASIMO robot^[196] employs the A* search algorithm for optimal footstep sequencing and uses infrared sensors and CCD cameras for obstacle-avoidance. Delfin et al. proposed a vision-based navigation scheme integrating localization, planning, path tracking, and obstacle avoidance, focusing on 2D data to reduce computation^[197]. Sahu et al. developed an adaptive particle swarm optimization algorithm to optimize humanoid robot trajectories by determining the best next step position^[198]. Kusuma et al. applied the A* algorithm to a household assistant robot for indoor navigation, utilizing ultrasonic sensors for localization^[199]. Kuffner et al. designed a motion planning algorithm based on rapidly exploring random trees, emphasizing bipedal humanoids' unique ability to step over obstacles^[200].

These studies collectively demonstrate diverse approaches to navigation and obstacle avoidance in humanoid robots.

5. Challenges and Future Directions

5.1. Key challenges

Humanoid robotics faces three primary barriers to real-world deployment.

Cost Barriers: The sophisticated mechanical designs and sensor systems required^[201] result in prohibitively high production costs at current manufacturing scales.

Hardware Constraints: While platforms such as Atlas demonstrate basic mobility, their limited degrees of freedom and 1-2 hour operational endurance restrict complex task execution^[202].

Computational Demands: Implementing advanced controllers (e.g., Transformer-based approaches) requires substantial GPU resources^[175], while maintaining real-time performance remains challenging.

5.2. Future directions

The potential of humanoid robots has not been fully explored. The following vital technologies are poised to enhance their capabilities in the future:

(1) Unified Frameworks: Presently, control frameworks for humanoid robots span multiple platforms, including Isaac Gym^[203], Isaac Sim^[204], Unity^[205], MuJoCo^[206], MuJoCo Playground^[207], ROBOVERSE^[208], each with distinct advantages. Isaac Gym leverages GPU capabilities for superior simulation performance, Unity offers a more user-friendly GUI for adjustments, and MuJoCo excels in simulation accuracy. Integrating these platforms to harness their collective strengths could streamline the user experience and maximize their utility.

(2) Environment-Based Learning: Most current humanoid robots lack advanced environmental perception and rely predominantly on adaptive learning methods, such as knowledge distillation, for navigation across various terrains. Incorporating LIDAR or vision-based systems to enhance environmental awareness could significantly improve the adaptability of humanoid robots in human-centric spaces.

(3) Integration with LLMs: One challenge in RL is the design of reward functions. Utilizing LLMs to generate a repository of reward functions and iterating through sampling can identify the optimal reward function, surpassing those designed by the experts. Additionally, the superior code generation capabilities of LLMs can boost the efficiency of robot development.

(4) Sim2Real Transition: Despite promising results in simulations, transitioning from simulations to real-world applications remains challenging. Although some frameworks demonstrate effective sim-to-real transfer, many studies are confined to simulation environments, underscoring the need for more robust and reliable methods for real-world implementation.

(5) Control algorithm–system synergy: The fusion of control algorithms should be tightly coupled with the specific characteristics of the controlled system. A promising research direction would be to leverage a profound understanding of bipedal robot dynamics to enhance the current control performance. This approach could bridge the gap between theoretical control models and practical implementation.

(6) Manipulation Performance: In real world, humanoid robots still struggle with various legged locomotion tasks, making advanced manipulation tasks involving arms and dexterous hands even more distant.

6. Conclusions

Humanoid robots have made significant progress in motion control and planning, with two dominant approaches emerging: dynamic-based and learning-based methods. Dynamics-based techniques, such as MPC and ZMP, provide stable and predictable control through precise modeling, whereas learning-based methods, such as RL and LLM integration, enable adaptive and intelligent behaviors. However, key challenges remain in bridging the simulation-to-real gap and reducing development costs. Future advancements are likely to focus on integrating these approaches with enhanced perception systems and dexterous manipulation capabilities. As these technologies mature, humanoid robots are poised to transition from research laboratories to real-world applications in domestic and industrial settings; however, significant engineering hurdles must still be overcome to achieve reliable and cost-effective deployment. The field's progress suggests that we may be approaching an inflection point where humanoid robots become practical tools rather than just research prototypes.

Declarations

Authors' contributions

Funding acquisition: Sun, S.

Writing-original draft: Li, C.

Writing-review and editing: Huang, H.

Availability of data and materials

Not applicable.

Financial support and sponsorship

This work was supported in part by the Guangdong Basic and Applied Basic Research Foundation under Grants 2024A1515012041 and 2025A1515011710 and in part by the Shenzhen Higher Education Stability Support Plan under Grant GXWD20231130195340002.

Conflicts of interest

All authors declared that there are no conflicts of interest.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Copyright

REFERENCES

1. Bin, T.; Yan, H.; Wang, N.; Nikolić, M. N.; Yao, J.; Zhang, T. A survey on the visual perception of humanoid robot. Biomim. Intell. Robot. 2025, 5, 100197.

2. Wang, J.; Wang, C.; Chen, W.; Dou, Q.; Chi, W. Embracing the future: the rise of humanoid robots and embodied AI. Intell. Robot. 2024, 4, 196-9.

3. Kaneko, K.; Kaminaga, H.; Sakaguchi, T.; et al. Humanoid robot HRP-5P: an electrically actuated humanoid robot with high-power and wide-range joints. IEEE. Robot. Autom. Lett. 2019, 4, 1431-8.

4. Kakiuchi, Y.; Kojima, K.; Kuroiwa, E.; et al. Development of humanoid robot system for disaster response through team NEDO-JSK's approach to DARPA Robotics Challenge Finals. In 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Korea. Nov 03-05, 2015. IEEE; 2015. pp. 805–10.

5. Radford, N. A.; Strawser, P.; Hambuchen, K.; et al. Valkyrie: NASA's first bipedal humanoid robot. J. Field. Robot. 2015, 32, 397-419.

6. Faraji, S.; Razavi, H.; Ijspeert, A. J. Bipedal walking and push recovery with a stepping strategy based on time-projection control. Int. J. Robot. Res. 2019, 38, 587-611.

7. Boston Dynamics. Picking up momentum. https://bostondynamics.com/blog/picking-up-momentum/. (accessed 14 Jul 2025).

8. Hirose, M.; Ogawa, K. Honda humanoid robots development. Philos. Trans. R. Soc. A. 2007, 365, 11-9.

9. Shamsuddoha, M.; Nasir, T.; Fawaaz, M. S. Humanoid robots like Tesla Optimus and the future of supply chains: enhancing efficiency, sustainability, and workforce dynamics. Automation 2025, 6, 9.

10. Piperakis, S.; Orfanoudakis, E.; Lagoudakis, M. G. Predictive control for dynamic locomotion of real humanoid robots. In 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, USA. Sep 14-18, 2014. IEEE; 2014. pp. 4036–43.

11. Kajita, S.; Kanehiro, F.; Kaneko, K.; et al. Biped walking pattern generation by using preview control of zero-moment point. In 2003 IEEE International Conference on Robotics and Automation (Cat. No. 03CH37422), Taipei, Taiwan. Sep 14-19, 2003. IEEE; 2003. pp. 1620-6.

12. Kajita, S.; Tani, K. Study of dynamic biped locomotion on rugged terrain-derivation and application of the linear inverted pendulum mode. In Proceedings. 1991 IEEE International Conference on Robotics and Automation, Sacramento, USA. Apr 09-11, 1991. IEEE; 1991. pp. 1405-11.

13. Kajita, S.; Kanehiro, F.; Kaneko, K.; Yokoi, K.; Hirukawa, H. The 3D linear inverted pendulum mode: a simple modeling for a biped walking pattern generation. In Proceedings 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No. 01CH37180), Maui, USA. Oct 29 - Nov 03, 2001. IEEE; 2001. pp. 239–46.

14. Shafii, N.; Lau, N.; Reis, L. P. Learning a fast walk based on ZMP control and hip height movement. In 2014 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Espinho, Portugal. May 14-15, 2014. IEEE; 2014. pp. 181–6.

15. Urbann, O.; Schwarz, I.; Hofmann, M. Flexible linear inverted pendulum model for cost-effective biped robots. In 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Korea. Nov 03-05, 2015. IEEE; 2015. pp. 128–31.

16. Bae, H.; Jeong, H.; Oh, J.; Lee, K.; Oh, J. -H. Humanoid robot COM kinematics estimation based on compliant inverted pendulum model and robust state estimator. In 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain. Oct 01-05, 2018. IEEE; 2018. pp. 747–53.

17. Pratt, J.; Carff, J.; Drakunov, S.; Goswami, A. Capture point: a step toward humanoid push recovery. In 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy. Dec 04-06, 2006. IEEE; 2006. pp. 200–7.

18. Kashyap, A. K.; Parhi, D. R. Dynamic walking of humanoid robot on flat surface using amplified LIPM plus flywheel model. Int. J. Intell. Unmanned. Syst. 2022, 10, 316-29.

19. Kashyap, A. K.; Parhi, D. R. Optimization of stability of humanoid robot NAO using ant colony optimization tuned MPC controller for uneven path. Soft. Comput. 2021, 25, 5131-50.

20. Kasaei, M.; Lau, N.; Pereira, A. An optimal closed-loop framework to develop stable walking for humanoid robot. In 2018 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Torres Vedras, Portugal. Apr 25-27, 2018. IEEE; 2018. pp. 30–5.

21. Kasaei, S. M.; Lau, N.; Pereira, A.; Shahri, E. A reliable model-based walking engine with push recovery capability. In 2017 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Coimbra, Portugal. Apr 26-28, 2017. IEEE; 2017. pp. 122–7.

22. Blickhan, R.; Full, R. J. Similarity in multilegged locomotion: bouncing like a monopode. J. Comp. Physiol. A. 1993, 173, 509-17.

23. Wensing, P. M.; Orin, D. E. High-speed humanoid running through control with a 3D-SLIP model. In 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan. Nov 03-07, 2013. IEEE; 2013. pp. 5134–40.

24. Xiong, X.; Ames, A. D. Dynamic and versatile humanoid walking via embedding 3D actuated SLIP model with hybrid LIP based stepping. IEEE. Robot. Autom. Lett. 2020, 5, 6286-93.

25. Shahbazi, M.; Babuška, R.; Lopes, G. A. D. Unified modeling and control of walking and running on the spring-loaded inverted pendulum. IEEE. Trans. Robot. 2016, 32, 1178-95.

26. Kuo, A. D.; Donelan, J. M.; Ruina, A. Energetic consequences of walking like an inverted pendulum: step-to-step transitions. Exerc. Sport. Sci. Rev. 2005, 33, 88-97.

27. Zhang, C.; Liu, T.; Song, S.; Wang, J.; Meng, M. Q. H. Dynamic wheeled motion control of wheel-biped transformable robots. Biomim. Intell. Robot. 2022, 2, 100027.

28. Kwon, S.; Oh, Y. Real-time estimation algorithm for the center of mass of a bipedal robot with flexible inverted pendulum model. In 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, USA. Oct 10-15, 2009. IEEE; 2009. pp. 5463–8.

29. Jo, J.; Park, G.; Oh, Y. Robust walking stabilization strategy of humanoid robots on uneven terrain via QP-based impedance/admittance control. Robot. Auton. Syst. 2022, 154, 104148.

30. Mahapatro, A.; Dhal, P. R.; Parhi, D. R.; Muni, M. K.; Sahu, C.; Patra, S. K. Towards stabilization and navigational analysis of humanoids in complex arena using a hybridized fuzzy embedded PID controller approach. Expert. Syst. Appl. 2023, 213, 119251.

31. Zhou, Y.; Sun, Z.; Chen, B.; Huang, G.; Wu, X.; Wang, T. Human gait tracking for rehabilitation exoskeleton: adaptive fractional order sliding mode control approach. Intell. Robot. 2023, 3, 95-112.

32. Erez, T.; Lowrey, K.; Tassa, Y.; Kumar, V.; Kolev, S.; Todorov, E. An integrated system for real-time model predictive control of humanoid robots. In 2013 13th IEEE-RAS International Conference on Humanoid Robots (Humanoids), Atlanta, USA. Oct 15-17, 2013. IEEE; 2013. pp. 292–9.

33. Ishihara, K.; Morimoto, J. MPC for humanoid control. In Robotics Retrospectives-Workshop at RSS 2020; 2020. https://openreview.net/forum?id=-xj822-1KE. (accessed 14 Jul 2025).

34. Scianca, N.; Cognetti, M.; De Simone, D.; Lanari, L.; Oriolo, G. Intrinsically stable MPC for humanoid gait generation. In 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico. Nov 15-17, 2016. IEEE; 2016. pp. 601–6.

35. García, G.; Griffin, R.; Pratt, J. MPC-based locomotion control of bipedal robots with line-feet contact using centroidal dynamics. In 2020 IEEE-RAS 20th International Conference on Humanoid Robots (Humanoids), Munich, Germany. Jul 19-21, 2021. IEEE; 2021. pp. 276–82.

36. Kim, D. W.; Kim, N.-H.; Park, G.-T. ZMP based neural network inspired humanoid robot control. Nonlinear. Dyn. 2012, 67, 793-806.

37. Kagami, S.; Nishiwaki, K.; Kitagawa, T.; Sugihara, T.; Inaba, M.; Inoue, H. A fast generation method of a dynamically stable humanoid robot trajectory with enhanced ZMP constraint. In Proceeding of IEEE International Conference on Humanoid Robotics (Humanoid2000). 2000. http://www.humanoids2000.org/31.pdf. (accessed 14 Jul 2025).

38. Smaldone, F. M.; Scianca, N.; Modugno, V.; Lanari, L.; Oriolo, G. ZMP constraint restriction for robust gait generation in humanoids. In 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France. May 31 - Aug 31, 2020. IEEE; 2020. pp. 8739–45.

39. Lloyd, S.; Irani, R. A.; Ahmadi, M. Fast and robust inverse kinematics of serial robots using Halleyos method. IEEE. Trans. Robot. 2022, 38, 2768-80.

40. Dou, R.; Yu, S.; Li, W.; et al. Inverse kinematics for a 7-DOF humanoid robotic arm with joint limit and end pose coupling. Mech. Mach. Theory. 2022, 169, 104637.

41. Ma, H.; Song, A.; Li, J.; Ge, L.; Fu, C.; Zhang, G. Legged odometry based on fusion of leg kinematics and IMU information in a humanoid robot. Biomim. Intell. Robot. 2025, 5, 100196.

42. Ferrolho, H.; Ivan, V.; Merkt, W.; Havoutis, I.; Vijayakumar, S. Inverse dynamics vs. forward dynamics in direct transcription formulations for trajectory optimization. In 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi'an, China. May 30 - Jun 05, 2021. IEEE; 2021. pp. 12752–8.

43. Reher, J.; Ames, A. D. Inverse dynamics control of compliant hybrid zero dynamic walking. In 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi'an, China. May 30 - Jun 05, 2021. IEEE; 2021. pp. 2040–7.

44. Tang, H. A fuzzy PID control system. Electr. Mach. Control. 2005.

45. Guo, Q.; Jiang, D. Moving process PID control in robots' field. In 2012 International Conference on Control Engineering and Communication Technology, Shenyang, China. Dec 07-09, 2012. IEEE; 2012. pp. 386–9.

46. Zeng, J.; Wang, L. G.; Ye, M. J.; Hu, C. H.; Ye, T. F. Research of several PID algorithms based on MATLAB. Adv. Mater. Res. 2013, 760, 1075-9.

47. Tong, L.; Cui, D.; Wang, C.; Peng, L. A novel zero-force control framework for post-stroke rehabilitation training based on fuzzy-PID method. Intell. Robot. 2024, 4, 125-45.

48. Alasiry, A. H.; Satria, N. F.; Sugiarto, A. Balance control of humanoid dancing robot ERISA while walking on sloped surface using PID. In 2018 International Seminar on Research of Information Technology and Intelligent Systems (ISRITI), Yogyakarta, Indonesia. Noc 21-22, 2018. IEEE; 2018. pp. 577–81.

49. Wang, H.; Chen, Q. Adaptive robust control for biped walking under uncertain external forces. Intell. Robot. 2023, 3, 479-94.

50. Sreenath, K.; Park, H. -W.; Poulakakis, I.; Grizzle, J. W. A compliant hybrid zero dynamics controller for stable, efficient and fast bipedal walking on MABEL. Int. J. Robot. Res. 2011, 30, 1170–93. https://www.researchgate.net/publication/220122146_A_Compliant_Hybrid_Zero_Dynamics_Controller_for_Stable_Efficient_and_Fast_Bipedal_Walking_on_MABELs. (accessed 14 Jul 2025).

51. Reher, J.; Ma, W. -L.; Ames, A. D. Dynamic walking with compliance on a cassie bipedal robot. In 2019 18th European Control Conference (ECC), Naples, Italy. Jun 25-28, 2019. IEEE; 2019. pp. 2589–95.

52. Chevallereau, C.; Abba, G.; Aoustin, Y.; et al. Rabbit: a testbed for advanced control theory. IEEE. Control. Syst. Mag. 2003, 23, 57-79.

53. Hereid, A.; Cousineau, E. A.; Hubicki, C. M.; Ames, A. D. 3D dynamic walking with underactuated humanoid robots: a direct collocation framework for optimizing hybrid zero dynamics. In 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden. May 16-21, 2016. IEEE; 2016. pp. 1447–54.

54. Li, J.; Nguyen, Q. Force-and-moment-based model predictive control for achieving highly dynamic locomotion on bipedal robots. In 2021 60th IEEE Conference on Decision and Control (CDC), Austin, USA. Dec 14-17, 2021. IEEE; 2021. pp. 1024–30.

55. Khatib, O.; Sentis, L.; Park, J.; Warren, J. Whole-body dynamic behavior and control of human-like robots. Int. J. Humanoid. Robot. 2004, 01, 29-43.

56. Sentis, L.; Khatib, O. Synthesis of whole-body behaviors through hierarchical control of behavioral primitives. Int. J. Humanoid. Robot. 2005, 02, 505-18.

57. Moro, F. L.; Sentis, L. Whole-body control of humanoid robots. In: Goswami, A., Vadakkepat, P.; editers. Humanoid robotics: a reference. Springer, Dordrecht; 2018. pp. 1–23.

58. Kim, D.; Di Carlo, J.; Katz, B.; Bledt, G.; Kim, S. Highly dynamic quadruped locomotion via whole-body impulse control and model predictive control. arXiv 2019, arXiv: 1909.06586. https://doi.org/10.48550/arXiv.1909.06586. (accessed 14 Jul 2025).

59. Zhu, Z.; Ding, W.; Zhu, W.; et al. NP-MBO: a newton predictor-based momentum observer for interaction force estimation of legged robots. Biomim. Intell. Robot. 2024, 4, 100160.

60. Zhang, H.; He, L.; Wang, D. Deep reinforcement learning for real-world quadrupedal locomotion: a comprehensive review. Intell. Robot. 2022, 2, 275-97.

61. Peters, J.; Vijayakumar, S.; Schaal, S. Reinforcement learning for humanoid robotics. In Proceedings of the third IEEE-RAS international conference on humanoid robots. 2003. pp. 1–20. https://www.ias.informatik.tu-darmstadt.de/uploads/Team/JanPeters/peters-ICHR2003.pdf. (accessed 14 Jul 2025).

62. Hester, T.; Quinlan, M.; Stone, P. Generalized model learning for Reinforcement Learning on a humanoid robot. In 2010 IEEE International Conference on Robotics and Automation, Anchorage, USA. May 03-07, 2010. IEEE; 2010. pp. 2369–74.

63. Danel, M. Reinforcement learning for humanoid robot control. 2017. https://poster.fel.cvut.cz/poster2017/proceedings/Poster_2017/Section_IC/IC_021_Danel.pdf. (accessed 14 Jul 2025).

64. Li, Z.; Cheng, X.; Peng, X. B.; et al. Reinforcement learning for robust parameterized locomotion control of bipedal robots. In 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi'an, China. May 30 - Jun 05, 2021. IEEE; 2021. pp. 2811–7.

65. Le, T. D.; Le, A. T.; Nguyen, D. T. Model-based Q-learning for humanoid robots. In 2017 18th International Conference on Advanced Robotics (ICAR), Hong Kong, China. Jul 10-12, 2017. IEEE; 2017. pp. 608–13.

66. Liu, Y.; Zhou, M.; Guo, X. An improved Q-learning algorithm for human-robot collaboration two-sided disassembly line balancing problems. In 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Prague, Czech Republic. Oct 09-12, 2022. IEEE; 2022. pp. 568–73.

67. Tai, L.; Liu, M. A robot exploration strategy based on Q-learning network. In 2016 IEEE International Conference on Real-time Computing and Robotics (RCAR), Angkor Wat, Cambodia. Jun 16-10, 2016. pp. 57–62.

68. Tavakoli, F.; Derhami, V.; Kamalinejad, A. Control of humanoid robot walking by Fuzzy Sarsa Learning. In 2015 3rd RSI International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran. Oct 07-09, 2015. IEEE; 2015. pp. 234–9.

69. Xu, W.; Yu, B.; Cheng, L.; Li, Y.; Cao, X. Multi-fuzzy Sarsa learning-based sit-to-stand motion control for walking-support assistive robot. Int. J. Adv. Robot. Syst. 2021, 18.

70. Anas, H.; Ong, W. H.; Malik, O. A. Comparison of deep Q-learning, Q-learning and SARSA reinforced learning for robot local navigation. In Robot Intelligence Technology and Applications 6. Cham: Springer International Publishing; 2022. pp. 443–54.

71. Huang, J.; Zhang, Z.; Ruan, X. An improved Dyna-Q algorithm inspired by the forward prediction mechanism in the rat brain for mobile robot path planning. Biomimetics 2024, 9, 315.

72. Pei, M.; An, H.; Liu, B.; Wang, C. An improved Dyna-Q algorithm for mobile robot path planning in unknown dynamic environment. IEEE. Trans. Syst. Man. Cybern. Syst. 2022, 52, 4415-25.

73. GarcȪa, J.; Shafie, D. Teaching a humanoid robot to walk faster through Safe Reinforcement Learning. Eng. Appl. Artif. Intell. 2020, 88, 103360.

74. Zhao, X.; Han, S.; Tao, B.; Yin, Z.; Ding, H. Model-based actor?critic learning of robotic impedance control in complex interactive environment. IEEE. Trans. Ind. Electro. 2022, 69, 13225-35.

75. Wu, R.; Yao, Z.; Si, J.; Huang, H. H. Robotic knee tracking control to mimic the intact human knee profile based on actor-critic reinforcement learning. IEEE/CAA. J. Autom. Sinica. 2022, 9, 19-30.

76. Zhao, X.; Tao, B.; Qian, L.; Ding, H. Model-based actor-critic learning for optimal tracking control of robots with input saturation. IEEE. Trans. Ind. Electron. 2021, 68, 5046-56.

77. Gu, Y.; Zhu, Z.; Lv, J.; Shi, L.; Hou, Z.; Xu, S. DM-DQN: dueling munchausen deep Q network for robot path planning. Complex. Intell. Syst. 2023, 9, 4287-300.

78. da Silva, I. J.; Perico, D. H.; Homem, T. P. D.; da Costa Bianchi, R. A. Deep reinforcement learning for a humanoid robot soccer player. J. Intell. Robot. Syst. 2021, 102, 69.

79. Kuo, P.-H.; Hu, J.; Lin, S.-T.; Hsu, P.-W. Fuzzy deep deterministic policy gradient-based motion controller for humanoid robot. Int. J. Fuzzy. Syst. 2022, 24, 2476-92.

80. Tiong, T.; Saad, I.; Teo, K. T. K.; Lago, H. Deep reinforcement learning with robust deep deterministic policy gradient. In 2020 2nd International Conference on Electrical, Control and Instrumentation Engineering (ICECIE), Kuala Lumpur, Malaysia. Nov 28, 2020. IEEE; 2020. pp. 1–5.

81. Kuo, P.-H.; Yang, W.-C.; Hsu, P.-W.; Chen, K.-L. Intelligent proximal-policy-optimization-based decision-making system for humanoid robots. Adv. Eng. Inform. 2023, 56, 102009.

82. Melo, L. C.; Melo, D. C.; Maximo, M. R. Learning humanoid robot running motions with symmetry incentive through proximal policy optimization. J. Intell. Robot. Syst. 2021, 102, 54.

83. Liu, R.; Wang, J.; Chen, Y.; Liu, Y.; Wang, Y.; Gu, J. Proximal policy optimization with time-carying muscle synergy for the control of an upper limb musculoskeletal system. IEEE. Trans. Autom. Sci. Eng. 2024, 21, 1929-40.

84. Hayamizu, Y.; Amiri, S.; Chandan, K.; Zhang, S.; Takadama, K. Guided Dyna-Q for mobile robot exploration and navigation. arXiv 2020, arXiv: 2004.11456. https://doi.org/10.48550/arXiv.2004.11456. (accessed 14 Jul 2025).

85. Zhao, Z.; Huang, H.; Sun, S.; Jin, J.; Lu, W. Reinforcement learning for dynamic task execution: a robotic arm for playing table tennis. In 2024 IEEE International Conference on Robotics and Biomimetics (ROBIO), Bangkok, Thailand. Dec 10-14, 2024. IEEE; 2024. pp. 608–13.

86. Zhao, Z.; Huang, H.; Sun, S.; Li, C.; Xu, W. Fusing dynamics and reinforcement learning for control strategy: achieving precise gait and high robustness in humanoid robot locomotion. In 2024 IEEE-RAS 23rd International Conference on Humanoid Robots (Humanoids), Nancy, France. Nov 22-24, 2024. IEEE; 2024. pp. 1072–9.

87. Zhao, Z.; Sun, S.; Li, C.; Huang, H.; Xu, W. Design and control of continuous gait for humanoid robots: jumping, walking, and running based on reinforcement learning and adaptive motion functions. In Intelligent Robotics and Applications. ICIRA 2024. Singapore: Springer Nature Singapore; 2025. pp. 159–73.

88. Zhao, Z.; Sun, S.; Huang, H.; Gao, Q.; Xu, W. Design and control of continuous jumping gaits for humanoid robots based on motion function and reinforcement learning. Procedia. Comput. Sci. 2024, 250, 51-7.

89. Huang, H.; Sun, S.; Zhao, Z.; Huang, H.; Shen, C.; Xu, W. PTRL: prior transfer deep reinforcement learning for legged robots locomotion. arXiv 2025, arXiv: 2504.05629. https://doi.org/10.48550/arXiv.2504.05629. (accessed 14 Jul 2025).

90. Liu, Y.; Palmieri, L.; Georgievski, I.; Aiello, M. Human-flow-aware long-term mobile robot task planning based on hierarchical reinforcement learning. IEEE. Robot. Autom. Lett. 2023, 8, 4068-75.

91. Yang, X.; Ji, Z.; Wu, J.; et al. Hierarchical reinforcement learning with universal policies for multistep robotic manipulation. IEEE. Trans. Neural. Netw. Learn. Syst. 2022, 33, 4727-41.

92. Eppe, M.; Gumbsch, C.; Kerzel, M.; Nguyen, P. D.; Butz, M. V.; Wermter, S. Intelligent problem-solving as integrated hierarchical reinforcement learning. Nat. Mach. Intell. 2022, 4, 11-20.

93. Haarnoja, T.; Moran, B.; Lever, G.; et al. Learning agile soccer skills for a bipedal robot with deep reinforcement learning. Sci. Robot. 2024, 9, eadi8022.

94. Wei, W.; Wang, Z.; Xie, A.; Wu, J.; Xiong, R.; Zhu, Q. Learning gait-conditioned bipedal locomotion with motor adaptation. In 2023 IEEE-RAS 22nd International Conference on Humanoid Robots (Humanoids), Austin, USA. Dec 12-14, 2023. IEEE; 2023. p. 1–7.

95. Han, L.; Zhu, Q.; Sheng, J.; et al. Lifelike agility and play in quadrupedal robots using reinforcement learning and generative pre-trained models. Nat. Mach. Intell. 2024, 6, 787-98.

96. Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning quadrupedal locomotion over challenging terrain. Sci. Robot. 2020, 5, eabc5986.

97. Peng, T.; Bao, L.; Humphreys, J.; Delfaki, A. M.; Kanoulas, D.; Zhou, C. Learning bipedal walking on a quadruped robot via adversarial motion priors. In Towards Autonomous Robotic Systems. Cham: Springer Nature Switzerland; 2025. pp. 118–29. doi:.

98. Hua, J.; Zeng, L.; Li, G.; Ju, Z. Learning for a robot: deep reinforcement learning, imitation learning, transfer learning. Sensors 2021, 21, 1278.

99. Hussein, A.; Gaber, M. M.; Elyan, E.; Jayne, C. Imitation learning: a survey of learning methods. ACM. Comput. Surv. 2017, 50, 1-35.

100. Argall, B. D.; Chernova, S.; Veloso, M.; Browning, B. A survey of robot learning from demonstration. Robot. Auton. Syst. 2009, 57, 469-83.

101. Ng, A. Y.; Russell, S. Algorithms for inverse reinforcement learning. 2000. https://www.cl.cam.ac.uk/ey204/teaching/ACS/R244_2022_2023/papers/NG_ICML_2000.pdf. (accessed 14 Jul 2025).

102. Ho, J.; Ermon, S. Generative adversarial imitation learning. In 30th Conference on Neural Information Processing Systems (NIPS 2016), Barcelona, Spain. 2016. https://proceedings.neurips.cc/paper_files/paper/2016/file/cc7e2b878868cbae992d1fb743995d8f-Paper.pdf. (accessed 14 Jul 2025).

103. Bong, J. H.; Jung, S.; Kim, J.; Park, S. Standing balance control of a bipedal robot based on behavior cloning. Biomimetics 2022, 7, 232.

104. Florence, P.; Lynch, C.; Zeng, A.; et al. Implicit behavioral cloning. In Proceedings of the 5th Conference on Robot Learning. PMLR; 2022. pp. 158–68. https://proceedings.mlr.press/v164/florence22a.html. (accessed 14 Jul 2025).

105. Yang, C.; Yuan, K.; Heng, S.; Komura, T.; Li, Z. Learning natural locomotion behaviors for humanoid robots using human bias. IEEE. Robot. Autom. Lett. 2020, 5, 2610-7.

106. Gan, L.; Grizzle, J. W.; Eustice, R. M.; Ghaffari, M. Energy-based legged robots terrain traversability modeling via deep inverse reinforcement learning. IEEE. Robot. Autom. Lett. 2022, 7, 8807-14.

107. Liu, W.; Zhong, J.; Wu, R.; Fylstra, B. L.; Si, J.; Huang, H. H. Inferring human-robot performance objectives during locomotion using inverse reinforcement learning and inverse optimal control. IEEE. Robot. Autom. Lett. 2022, 7, 2549-56.

108. Kubík, J.; Čížek, P.; Szadkowski, R.; Faigl, J. Experimental leg inverse dynamics learning of multi-legged walking robot. In Modelling and Simulation for Autonomous Systems. Cham: Springer International Publishing; 2021. pp. 154–68.

109. Goodfellow, I. J.; Pouget-Abadie, J.; Mirza, M.; et al. Generative adversarial nets. In Advances in Neural Information Processing Systems. 2014. https://proceedings.neurips.cc/paper_files/paper/2014/file/f033ed80deb0234979a61f95710dbe25-Paper.pdf. (accessed 14 Jul 2025).

110. Peng, X. B.; Ma, Z.; Abbeel, P.; Levine, S.; Kanazawa, A. AMP: adversarial motion priors for stylized physics-based character control. ACM. Trans. Graph. 2021, 40, 1-20.

111. Peng, X. B.; Guo, Y.; Halper, L.; Levine, S.; Fidler, S. ASE: large-scale reusable adversarial skill embeddings for physically simulated characters. ACM. Trans. Graph. 2022, 41, 1-17.

112. Dai, H.; Tedrake, R. Planning robust walking motion on uneven terrain via convex optimization. In 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico. Nov 15-17, 2016. IEEE; 2016. pp. 579–86.

113. Escontrela, A.; Peng, X. B.; Yu, W.; et al. Adversarial motion priors make good substitutes for complex reward functions. In 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan. Oct 23-27, 2022. IEEE; 2022. pp. 25–32.

114. Zhang, Q.; Cui, P.; Yan, D.; et al. Whole-body humanoid robot locomotion with human reference. In 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates. Oct 14-18, 2024. IEEE; 2024. pp. 11225–31.

115. Cheng, X.; Ji, Y.; Chen, J.; Yang, R.; Yang, G.; Wang, X. Expressive whole-body control for humanoid robots. arXiv 2024, arXiv: 2402.16796. https://doi.org/10.48550/arXiv.2402.16796. (accessed 14 Jul 2025).

116. Lai, C. -M.; Wang, H. -C.; Hsieh, P. -C.; Wang, Y. -C. F.; Chen, M. H.; Sun, S. H. Diffusion-reward adversarial imitation learning. In 38th Conference on Neural Information Processing Systems (NeurIPS 2024). Curran Associates, Inc.; 2024. https://proceedings.neurips.cc/paper_files/paper/2024/file/ad47b1801557e4be37d30baf623de426-Paper-Conference.pdf. (accessed 14 Jul 2025).

117. Li, C.; Blaes, S.; Kolev, P.; Vlastelica, M.; Frey, J.; Martius, G. Versatile skill control via self-supervised adversarial imitation of unlabeled mixed motions. In 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK. May 29 - Jun 02, 2023. IEEE; 2023. pp. 2944–50.

118. Peng, X. B.; Abbeel, P.; Levine, S.; van de Panne, M. DeepMimic: example-guided deep reinforcement learning of physics-based character skills. ACM. Trans. Graph. 2018, 37, 1-14.

119. Bergamin, K.; Clavet, S.; Holden, D.; Forbes, J. R. DReCon: data-driven responsive control of physics-based characters. ACM. Trans. Graph. 2019, 38, 1-11.

120. Finn, C.; Tan, X. Y.; Duan, Y.; Darrell, T.; Levine, S.; Abbeel, P. Deep spatial autoencoders for visuomotor learning. In 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden. May 16-21, 2016. IEEE; 2016. pp. 512–9.

121. Lee, Y.; Wampler, K.; Bernstein, G.; Popović, J.; Popović, Z. Motion fields for interactive character locomotion. In ACM SIGGRAPH Asia 2010 Papers, New York, USA. Association for Computing Machinery; 2010. p. 1-8.

122. Levine, S.; Wang, J. M.; Haraux, A.; Popović, .; Z, .; Koltun, V. Continuous character control with low-dimensional embeddings. ACM. Trans. Graph. 2012, 31, 1-10.

123. Starke, P.; Starke, S.; Komura, T.; Steinicke, F. Motion in-betweening with phase manifolds. Proc. ACM. Comput. Graph. Interact. Tech. 2023, 6, 1-17.

124. Shafiee, M.; Bellegarda, G.; Ijspeert, A. Viability leads to the emergence of gait transitions in learning agile quadrupedal locomotion on challenging terrains. Nat. Commun. 2024, 15, 3073.

125. Aswin Nahrendra, I. M.; Yu, B.; Myung, H. DreamWaQ: learning robust quadrupedal locomotion with implicit terrain imagination via deep reinforcement learning. In 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK. May 29 - Jun 02, 2023. IEEE; 2023. pp. 5078–84.

126. Berseth, G.; Golemo, F.; Pal, C. Towards learning to imitate from a single video demonstration. J. Mach. Learn. Res. 2023, 24, 1-26.

127. Kim, N. H.; Xie, Z.; van de Panne, M. Learning to correspond dynamical systems. In Proceedings of the 2nd Conference on Learning for Dynamics and Control. PMLR; 2020. pp. 105–17. https://proceedings.mlr.press/v120/kim20a.html. (accessed 14 Jul 2025).

128. Starke, S.; Mason, I.; Komura, T. DeepPhase: periodic autoencoders for learning motion phase manifolds. ACM. Trans. Graph. 2022, 41, 1-13.

129. Li, C.; Stanger-Jones, E.; Heim, S.; bae Kim, S. FLD: Fourier latent dynamics for structured motion representation and learning. In The Twelfth International Conference on Learning Representations. 2024. https://openreview.net/forum?id=xsd2llWYSA. (accessed 14 Jul 2025).

130. Firoozi, R.; Tucker, J.; Tian, S.; et al. Foundation models in robotics: applications, challenges, and the future. arXiv 2023, arXiv: 2312.07843. https://doi.org/10.48550/arXiv.2312.07843. (accessed 14 Jul 2025).

131. Devlin, J.; Chang, M. -W.; Lee, K.; Toutanova, K. BERT: pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, Minnesota. Association for Computational Linguistics; 2019. pp. 4171–86.

132. Brown, T.; Mann, B.; Ryder, N.; et al. Language models are few-shot learners. In 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, Canada. Curran Associates, Inc.; 2020. pp. 1877–901. https://proceedings.neurips.cc/paper_files/paper/2020/file/1457c0d6bfcb4967418bfb8ac142f64a-Paper.pdf. (accessed 14 Jul 2025).

133. Xu, F. F.; Alon, U.; Neubig, G.; Hellendoorn, V. J. A systematic evaluation of large language models of code. In Proceedings of the 6th ACM SIGPLAN International Symposium on Machine Programming, New York, USA. Association for Computing Machinery; 2022. p. 1–10.

134. Egli, A. ChatGPT, GPT-4, and other large language models: the next revolution for clinical microbiology? Clin. Infect. Dis. 2023, 77, 1322-8.

135. Kirillov, A.; Mintun, E.; Ravi, N.; et al. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2023. pp. 4015–26. https://openaccess.thecvf.com/content/ICCV2023/html/Kirillov_Segment_Anything_ICCV_2023_paper.html. (accessed 14 Jul 2025).

136. Jhajaria, S.; Kaur, D. Study and comparative analysis of ChatGPT, GPT and DAll-E2. In 2023 14th International Conference on Computing Communication and Networking Technologies (ICCCNT), Delhi, India. Jul 06-08, 2023. IEEE; 2023. p. 1–5.

137. Radford, A.; Kim, J. W.; Hallacy, C.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the 38th International Conference on Machine Learning. PMLR; 2021. pp. 8748–63. https://proceedings.mlr.press/v139/radford21a.html. (accessed 14 Jul 2025).

138. Wang, J.; Shi, E.; Hu, H.; et al. Large language models for robotics: opportunities, challenges, and perspectives. J. Autom. Intell. 2025, 4, 52-64.

139. Kumar, K. N.; Essa, I.; Ha, S. Words into action: learning diverse humanoid robot behaviors using language guided iterative motion refinement. In 2nd Workshop on Language and Robot Learning: Language as Grounding. 2023. https://openreview.net/forum?id=K62hUwNqCn. (accessed 14 Jul 2025).

140. Chen, L.-H.; Lu, S.; Zeng, A.; et al. MotionLLM: understanding human behaviors from human motions and videos. CoRR 2024. https://openreview.net/forum?id=B7IGpMVPZU. (accessed 14 Jul 2025).

141. Shek, C. L.; Wu, X.; Suttle, W. A.; et al. LANCAR: leveraging language for context-aware robot locomotion in unstructured environments. In 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates. Oct 14-18, 2024. IEEE; 2024. pp. 9612–9.

142. Wang, Y. -J.; Zhang, B.; Chen, J.; Sreenath, K. Prompt a robot to walk with large language models. In 2024 IEEE 63rd Conference on Decision and Control (CDC), Milan, Italy. Dec 16-19, 2024. IEEE; 2024. pp. 1531–8.

143. Ma, Y. J.; Liang, W.; Wang, G.; et al. Eureka: human-level reward design via coding large language models. In The Twelfth International Conference on Learning Representations. 2024. https://openreview.net/forum?id=IEduRUO55F. (accessed 14 Jul 2025).

144. Yu, W.; Gileadi, N.; Fu, C.; et al. Language to rewards for robotic skill synthesis. In Proceedings of The 7th Conference on Robot Learning. PMLR; 2023. pp. 374–404. https://proceedings.mlr.press/v229/yu23a.html. (accessed 14 Jul 2025).

145. Song, J.; Zhou, Z.; Liu, J.; Fang, C.; Shu, Z.; Ma, L. Self-refined large language model as automated reward function designer for deep reinforcement learning in robotics. CoRR 2023.

146. Sun, S.; Li, C.; Zhao, Z.; Huang, H.; Xu, W. Leveraging large language models for comprehensive locomotion control in humanoid robots design. Biomim. Intell. Robot. 2024, 4, 100187.

147. Ingelhag, N.; Munkeby, J.; van Haastregt, J.; Varava, A.; Welle, M. C.; Kragic, D. A robotic skill learning system built upon diffusion policies and foundation models. In 2024 33rd IEEE International Conference on Robot and Human Interactive Communication (ROMAN), Pasadena, USA. Aug 26-30, 2024. IEEE; 2024. pp. 748–54.

148. Lykov, A.; Litvinov, M.; Konenkov, M.; et al. CognitiveDog: large multimodal model based system to translate vision and language into action of quadruped robot. In Companion of the 2024 ACM/IEEE International Conference on Human-Robot Interaction, New York, USA. Association for Computing Machinery; 2024. pp. 712–6.

149. Li, Y.; Li, J.; Fu, W.; Wu, Y. Learning agile bipedal motions on a quadrupedal robot. In 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan. May 13-17, 2024. IEEE; 2024. pp. 9735–42.

150. Xiao, Z.; Wang, T.; Wang, J.; et al. Unified human-scene interaction via prompted chain-of-contacts. In The Twelfth International Conference on Learning Representations. 2024. https://openreview.net/forum?id=1vCnDyQkjg. (accessed 14 Jul 2025).

151. Ouyang, Y.; Li, J.; Li, Y.; et al. Long-horizon locomotion and manipulation on a quadrupedal robot with large language models. arXiv 2024, arXiv: 2404.05291. https://doi.org/10.48550/arXiv.2404.05291. (accessed 14 Jul 2025).

152. Bärmann, L.; Kartmann, R.; Peller-Konrad, F.; Niehues, J.; Waibel, A.; Asfour, T. Incremental learning of humanoid robot behavior from natural interaction and large language models. Front. Robot. AI. 2024, 11, 1455375.

153. Luan, Z.; Lai, Y.; Huang, R.; et al. Automatic robotic development through collaborative framework by large language models. In 2023 China Automation Congress (CAC), Chongqing, China. Nov 17-19, 2023. IEEE; 2023. pp. 7736–41.

154. Tang, Y.; Yu, W.; Tan, J.; et al. SayTap: language to quadrupedal locomotion. In Proceedings of The 7th Conference on Robot Learning. PMLR; 2023. pp. 3556–70. https://proceedings.mlr.press/v229/tang23a.html. (accessed 14 Jul 2025).

155. Xu, M.; Huang, P.; Yu, W.; et al. Creative robot tool use with large language models. arXiv 2023, arXiv: 2310.13065. https://doi.org/10.48550/arXiv.2310.13065. (accessed 14 Jul 2025).

156. Yoshida, T.; Masumori, A.; Ikegami, T. From text to motion: grounding GPT-4 in a humanoid robot palter3q. Front. Robot. AI. 2025, 12, 1581110.

157. Chen, Y.; Ye, Y.; Chen, Z.; Zhang, C.; Ang, M. H. ARO: large language model supervised robotics Text2Skill autonomous learning. arXiv 2024, arXiv: 2403.15834. https://doi.org/10.48550/arXiv.2403.15834. (accessed 14 Jul 2025).

158. Chu, K.; Zhao, X.; Weber, C.; Li, M.; Lu, W.; Wermter, S. Large language models for orchestrating bimanual robots. In 2024 IEEE-RAS 23rd International Conference on Humanoid Robots (Humanoids), Nancy, France. Nov 22-24, 2024. IEEE; 2024. pp. 328–34.

159. Liang, J.; Xia, F.; Yu, W.; et al. Learning to learn faster from human feedback with language model predictive control. In First Workshop on Vision-Language Models for Navigation and Manipulation at ICRA 2024. 2024. https://openreview.net/forum?id=BdEnrtBlms. (accessed 14 Jul 2025).

160. Bien, S.; Skerlj, J.; Thiel, P.; et al. Human-inspired audiovisual inducement of whole-body responses. In 2023 IEEE-RAS 22nd International Conference on Humanoid Robots (Humanoids), Austin, USA. Dec 12-14, 2023. IEEE; 2023. p. 1–8.

161. Huang, J.; Yong, S.; Ma, X.; et al. An embodied generalist agent in 3D world. In Proceedings of the 41st International Conference on Machine Learning. PMLR; 2024. pp. 20413–51. https://proceedings.mlr.press/v235/huang24ae.html. (accessed 14 Jul 2025).

162. Habekost, J. -G.; Gäde, C.; Allgeuer, P.; Wermter, S. Inverse kinematics for neuro-robotic grasping with humanoid embodied agents. In 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates. Oct 14-18, 2024. IEEE; 2024. pp. 7315–22.

163. Kim, C. Y.; Lee, C. P.; Mutlu, B. Understanding large-language model (LLM)-powered human-robot interaction. In Proceedings of the 2024 ACM/IEEE International Conference on Human-Robot Interaction, New York, USA. Association for Computing Machinery; 2024. pp. 371–80.

164. Wang, H.; Chen, J.; Huang, W.; et al. GRUtopia: dream general robots in a city at scale. CoRR 2024. https://openreview.net/forum?id=T8d6Cd4p6X. (accessed 14 Jul 2025).

165. Miyake, T.; Wang, Y.; Yang, P.; Sugano, S. Feasibility study on parameter adjustment for a humanoid using LLM tailoring physical care. In Social Robotics, Singapore. Springer Nature Singapore; 2024. pp. 230–43.

166. Sun, J.; Zhang, Q.; Duan, Y.; Jiang, X.; Cheng, C.; Xu, R. Prompt, plan, perform: LLM-based humanoid control via quantized imitation learning. In 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan. May 13-17, 2024. IEEE; 2024. pp. 16236–42.

167. Sovukluk, S.; Englsberger, J.; Ott, C. Whole body control formulation for humanoid robots with closed/parallel kinematic chains: kangaroo case study. In 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, USA. Oct 01-05, 2023. IEEE; 2023. pp. 10390–6.

168. Lee, Y.; Hwang, S.; Park, J. Balancing of humanoid robot using contact force/moment control by task-oriented whole body control framework. Auton. Robot. 2016, 40, 457-72.

169. Yamamoto, K.; Ishigaki, T.; Nakamura, Y. Humanoid motion control by compliance optimization explicitly considering its positive definiteness. IEEE. Trans. Robot. 2022, 38, 1973-89.

170. Wensing, P. M.; Posa, M.; Hu, Y.; Escande, A.; Mansard, N.; Del Prete, A. Optimization-based control for dynamic legged robots. IEEE. Trans. Robot. 2024, 40, 43-63.

171. Li, Q.; Meng, F.; Yu, Z.; Chen, X.; Huang, Q. Dynamic torso compliance control for standing and walking balance of position-controlled humanoid robots. IEEE/ASME. Trans. Mechatron. 2021, 26, 679-88.

172. Onishi, Y.; Kajita, S. Understanding how a 3-dimensional ZMP exactly decouples the horizontal and vertical dynamics of the CoM-ZMP model. In 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates. Oct 14-18, 2024. IEEE; 2024. pp. 9036–42.

173. Elobaid, M.; Turrisi, G.; Rapetti, L.; et al. Adaptive non-linear centroidal MPC with stability guarantees for robust locomotion of legged robots. IEEE. Robot. Autom. Lett. 2025, 10, 2806-13.

174. Zhu, Z.; Zhang, G.; Li, Y.; et al. Observer-based state feedback model predictive control framework for legged robots. IEEE/ASME. Trans. Mechatron. 2025, 30, 1096-106.

175. Radosavovic, I.; Xiao, T.; Zhang, B.; Darrell, T.; Malik, J.; Sreenath, K. Real-world humanoid locomotion with reinforcement learning. Sci. Robot. 2024, 9, eadi9579.

176. Chen, Y.; Nguyen, Q. Learning agile locomotion and adaptive behaviors via RL-augmented MPC. In 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan. May 13-17, 2024. IEEE; 2024. pp. 11436–42.

177. Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path planning techniques for mobile robots: review and prospect. Expert. Syst. Appl. 2023, 227, 120254.

178. Zhu, H.; Gu, S.; He, L.; Guan, Y.; Zhang, H. Transition analysis and its application to global path determination for a biped climbing robot. Appl. Sci. 2018, 8, 122.

179. Chen, W.; Chi, W.; Ji, S.; et al. A survey of autonomous robots and multi-robot navigation: perception, planning and collaboration. Biomim. Intell. Robot. 2025, 5, 100203.

180. Khairuddin, A. R.; Talib, M. S.; Haron, H. Review on simultaneous localization and mapping (SLAM). In 2015 IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia. Nov 27-29, 2015. IEEE; 2015. pp. 85–90.

181. Xu, X.; Zhang, L.; Yang, J.; et al. A review of multi-sensor fusion SLAM systems based on 3D LIDAR. Remote. Sens. 2022, 14, 2835.

182. Mur-Artal, R.; TardȮs, J. D. ORB-SLAM2: an open-source SLAM system for monocular, stereo, and RGB-D cameras. IEEE. Trans. Robot. 2017, 33, 1255-62.

183. Shan, T.; Englot, B.; Ratti, C.; Rus, D. LVI-SAM: tightly-coupled lidar-visual-inertial odometry via smoothing and mapping. In 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi'an, China. May 30 - Jun 05, 2021. IEEE; 2021. pp. 5692–8.

184. Cormen, T. H.; Leiserson, C. E.; Rivest, R. L.; Stein, C. Introduction to algorithms. MIT press; 2022. https://mitpress.mit.edu/9780262046305/introduction-to-algorithms/. (accessed 14 Jul 2025).

185. Yao, J.; Lin, C.; Xie, X.; Wang, A. J.; Hung, C. -C. Path planning for virtual human motion using improved A* star algorithm. In 2010 Seventh International Conference on Information Technology: New Generations, Las Vegas, USA. Apr 12-14, 2010. IEEE; 2010. pp. 1154–8.

186. Vonásek, V.; Faigl, J.; Krajník, T.; Přeučil, L. RRT-path - a guided rapidly exploring random tree. In Robot Motion and Control 2009. Springer London; 2009. pp. 307–16. https://doi.org/10.1007/978-1-84882-985-5\_28.

187. Kavraki, L. E.; Svestka, P.; Latombe, J. C.; Overmars, M. H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE. Trans. Robot. Autom. 1996, 12, 566-80.

188. Kadry, S.; Alferov, G.; Fedorov, V.; Khokhriakova, A. Path optimization for D-star algorithm modification. AIP. Conf. Proc. 2022, 2425, 080002.

189. Liu, C.; Lee, S.; Varnhagen, S.; Tseng, H. E. Path planning for autonomous vehicles using model predictive control. In 2017 IEEE Intelligent Vehicles Symposium (Ⅳ), Los Angeles, USA. Jun 11-14, 2017. IEEE; 2017. pp. 174–9.

190. Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings. 1985 IEEE International Conference on Robotics and Automation, St. Louis, USA. Mar 25-28, 1985. IEEE; 1985. pp. 500–5.

191. Molinos, E. J.; Ángel Llamazares, .; Ocaña, M. Dynamic window based approaches for avoiding obstacles in moving. Robot. Auton. Syst. 2019, 118, 112-30.

192. Ni, J.; Chen, Y.; Tang, G.; Shi, J.; Cao, W.; Shi, P. Deep learning-based scene understanding for autonomous robots: a survey. Intell. Robot. 2023, 3, 374-401.

193. Kuindersma, S.; Deits, R.; Fallon, M.; et al. Optimization-based locomotion planning, estimation, and control design for the atlas humanoid robot. Auton. Robot. 2016, 40, 429-55.

194. Boston Dynamics. https://www.bostondynamics.com. (accessed 14 Jul 2025).

195. Haynes, G. C.; Stager, D.; Stentz, A.; et al. Developing a robust disaster response robot: CHIMP and the robotics challenge. J. Field. Robot. 2017, 34, 281-304.

196. Chestnutt, J.; Lau, M.; Cheung, G.; Kuffner, J.; Hodgins, J.; Kanade, T. Footstep planning for the Honda ASIMO humanoid. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain. Apr 18-22, 2005. IEEE; 2005. pp. 629–34.

197. Delfin, J.; Becerra, H. M.; Arechavaleta, G. Humanoid navigation using a visual memory with obstacle avoidance. Robot. Auton. Syst. 2018, 109, 109-24.

198. Sahu, C.; Kumar, P. B.; Parhi, D. R. An intelligent path planning approach for humanoid robots using adaptive particle swarm optimization. Int. J. Artif. Intell. Tools. 2018, 27, 1850015.

199. Kusuma, M.; Riyanto, ; Machbub, C. Humanoid robot path planning and rerouting using A-star search algorithm. In 2019 IEEE International Conference on Signals and Systems (ICSigSys), Bandung, Indonesia. Jul 16-18, 2019. IEEE; 2019. pp. 110–5.

200. Kuffner, J.; Nishiwaki, K.; Kagami, S.; Inaba, M.; Inoue, H. Motion planning for humanoid robots. In Robotics Research. The Eleventh International Symposium. Springer Berlin Heidelberg; 2005. pp. 365–74. https://link.springer.com/chapter/10.1007/11008941_39#citeas (accessed 2025-06-26).

201. Wang, J.; Chen, W.; Xiao, X.; et al. A survey of the development of biomimetic intelligence and robotics. Biomim. Intell. Robot. 2021, 1, 100001.

202. Castillo, G. A.; Weng, B.; Yang, S.; Zhang, W.; Hereid, A. Template model inspired task space learning for robust bipedal locomotion. In 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, USA. Oct 01-05, 2023. IEEE; 2023. pp. 8582–9.

203. Makoviychuk, V.; Wawrzyniak, L.; Guo, Y.; et al. Isaac Gym: high performance GPU based physics simulation for robot learning. In Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2). 2021. https://openreview.net/forum?id=fgFBtYgJQX_. (accessed 14 Jul 2025).

204. Mittal, M.; Yu, C.; Yu, Q.; et al. Orbit: a unified simulation framework for interactive robot learning environments. IEEE. Robot. Autom. Lett. 2023, 8, 3740-7.

205. Foxman, M. United we stand: platforms, tools and innovation with the unity game engine. Soc. Media. Soc. 2019, 5, 2056305119880177.

206. Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: a physics engine for model-based control. In 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal. Oct 07-12, 2012. IEEE; 2012. pp. 5026–33.

207. Zakka, K.; Tabanpour, B.; Liao, Q.; et al. Demonstrating MuJoCo playground. In Robotics: Science and Systems 2025. 2025. https://www.roboticsproceedings.org/rss21/p020.pdf. (accessed 14 Jul 2025).

208. Geng, H.; Wang, F.; Wei, S.; et al. RoboVerse: towards a unified platform, dataset and benchmark for scalable and generalizable robot learning. https://github.com/RoboVerseOrg/RoboVerse. (accessed 14 Jul 2025).

Cite This Article

Review

Open Access

Advancements in humanoid robot dynamics and learning-based locomotion control methods

How to Cite

Download Citation

If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click on download.

Export Citation File:

RIS BibTeX EndNote

Type of Import

Direct Import Indirect Import

Tips on Downloading Citation

This feature enables you to download the bibliographic information (also called citation data, header data, or metadata) for the articles on our site.

Citation Manager File Format

Use the radio buttons to choose how to format the bibliographic data you're harvesting. Several citation manager formats are available, including EndNote and BibTex.

Type of Import

If you have citation management software installed on your computer your Web browser should be able to import metadata directly into your reference database.

Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.

Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.

About This Article

Copyright

© The Author(s) 2025. Open Access This article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Data & Comments

Data

Views

63

Downloads

9

Citations

0

Comments

0

1

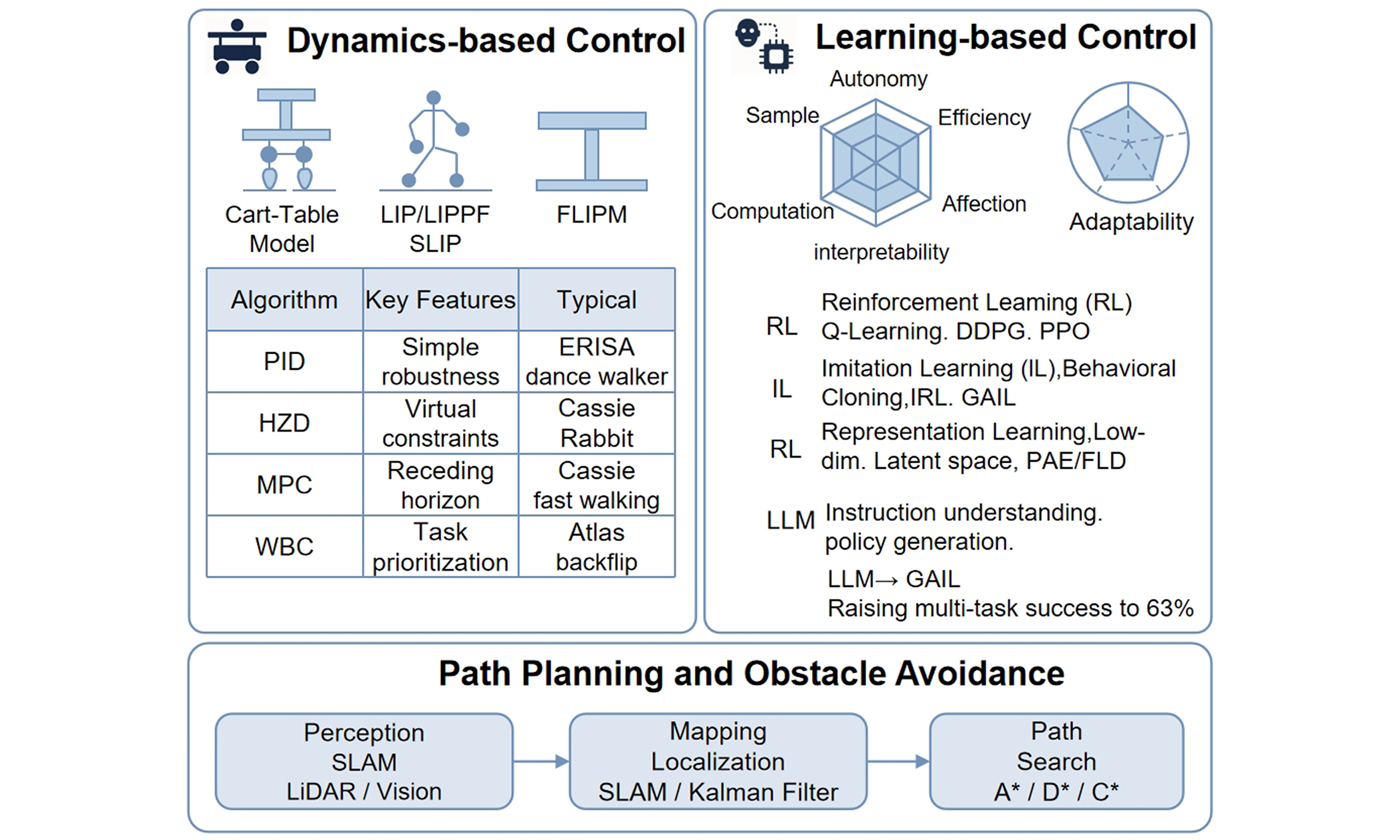
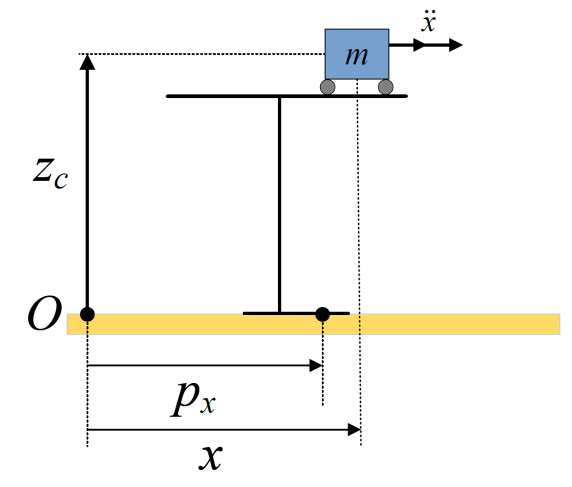
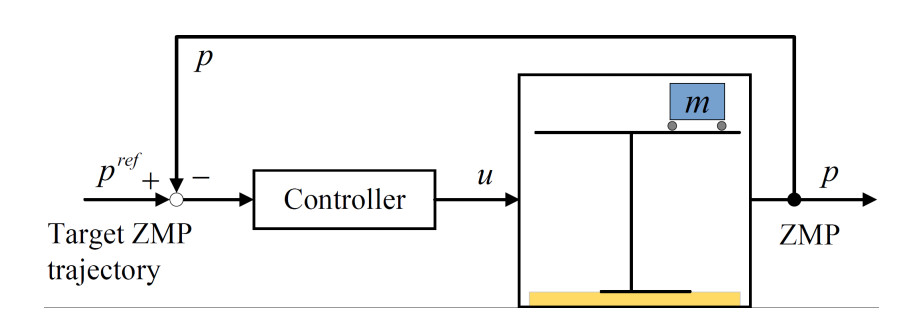
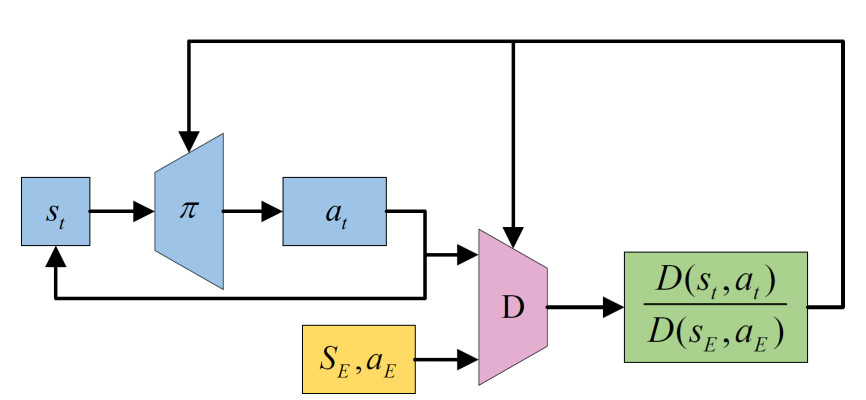
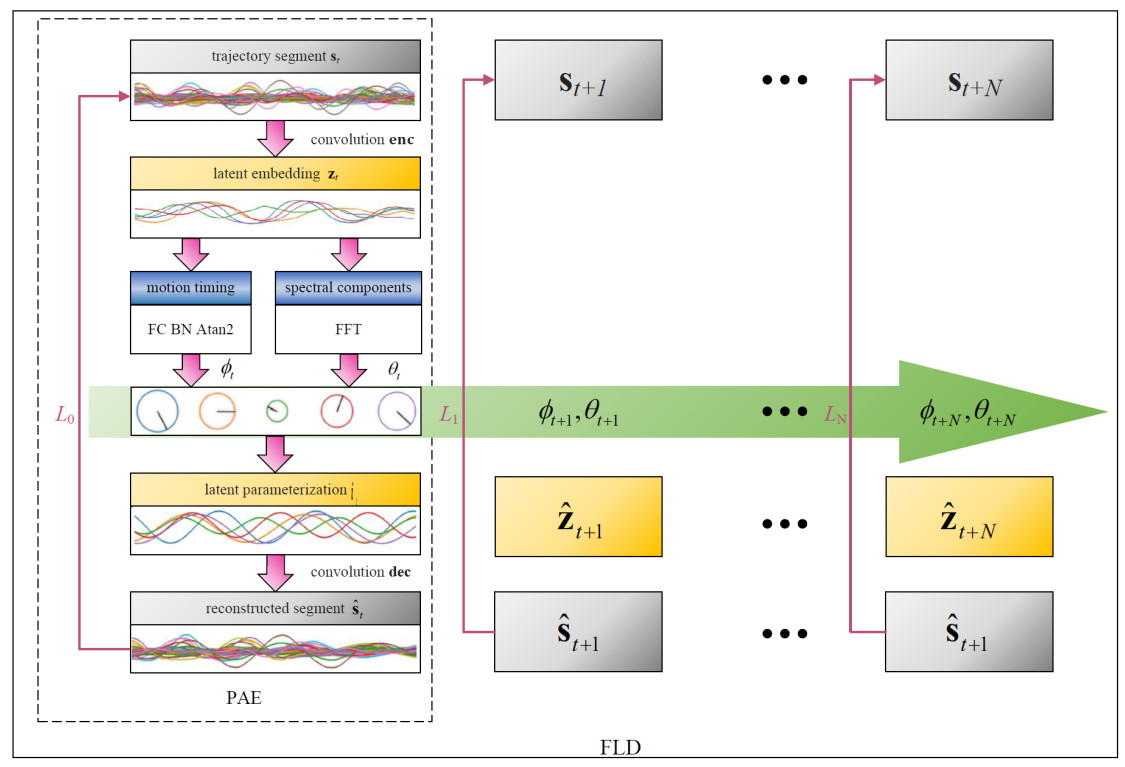
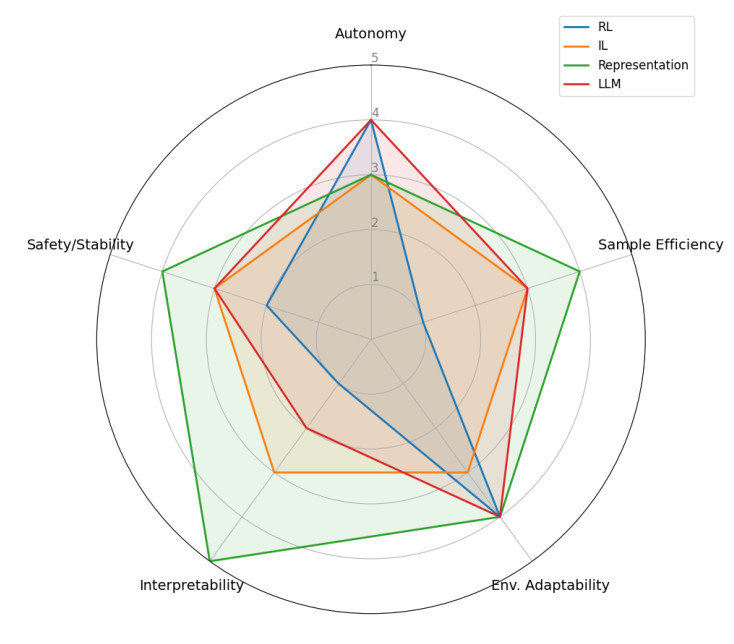
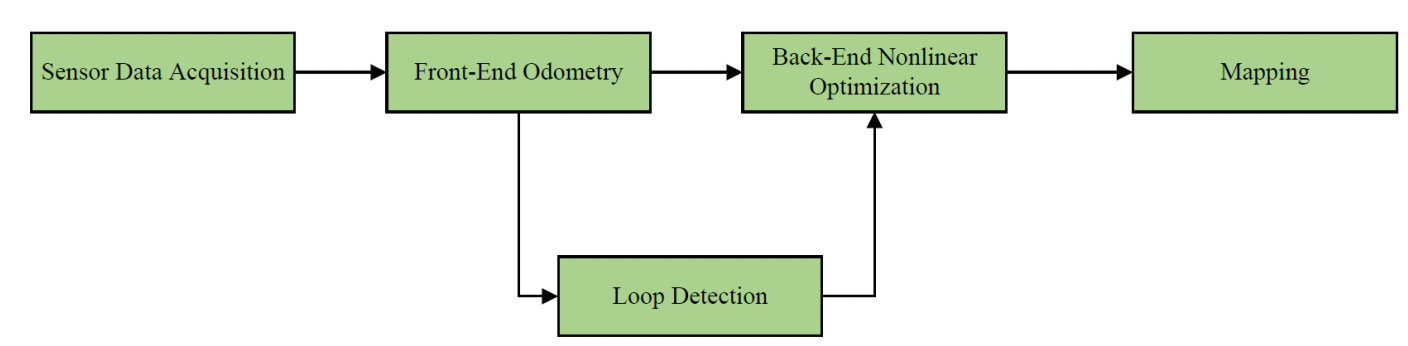
Comments

Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].

⁰

Download PDF

Download XML 0 downloads

Cite This Article 5 clicks

Export Citation 1 clicks

Like This Article 1 likes

Share This Article

https://www.oaepublish.com/articles/ir.2025.32

Scan the QR code for reading!

See Updates

Contents

Figures

Advancements in humanoid robot dynamics and learning-based locomotion control methods

Abstract

Graphical Abstract

Keywords

1. Introduction

2. Dynamics-Based Control Methods

2.1. Simplified dynamic models of bipedal walking

2.1.1. Cart-table model

2.1.2. LIPM

2.1.3. LIPPF

2.1.4. SLIP

2.1.5. Flexible linear inverted pendulum model

2.2. Control methodology

2.2.1. PID control

2.2.2. Hybrid zero dynamics

2.2.3. MPC

2.2.4. Whole-body control

2.3. Sum

3. Learning-Based Control Methods

3.1. RL

3.1.1. Model-free methods

3.1.1.1. Q-Learning

3.1.1.2. State-action-reward-state-action

3.1.2. Model-based methods

3.1.3. Policy gradient methods

3.1.3.1. REINFORCE

3.1.3.2. Actor-critic

3.1.4. Deep RL methods

3.1.4.1. Deep Q-network

3.1.4.2. Deep deterministic policy gradient

3.1.4.3. Proximal policy optimization

3.1.4.4. Hierarchical reinforcement learning

3.2. Imitation learning

3.2.1. BC

3.2.2. Inverse reinforcement learning

3.2.3. GAIL

3.3. Representation learning

3.4. LLMs

3.5. Applications of learning-based methods in humanoid robots

3.6. Sum

4. Path Planning and Obstacle Avoidance

5. Challenges and Future Directions

5.1. Key challenges

5.2. Future directions

6. Conclusions

Declarations

Authors' contributions

Availability of data and materials

Financial support and sponsorship

Conflicts of interest

Ethical approval and consent to participate

Consent for publication

Copyright

REFERENCES

Cite This Article

How to Cite

Download Citation

Export Citation File:

Type of Import

Tips on Downloading Citation

Citation Manager File Format

Type of Import

About This Article

Copyright

Data & Comments

Data

Comments

Share This Article

See Updates

Committee on Publication Ethics

Portico

Committee on Publication Ethics

Portico