Machine learning-driven new paradigm for Co-based superalloys
Abstract
Co-based superalloys exhibit exceptional high-temperature properties, granting them broad application prospects in the superalloy domain. However, constrained by the exorbitant trial-and-error costs and protracted research cycles inherent in their development, machine learning (ML) has emerged as the most pivotal research direction in this field. This review systematically examines ML-driven approaches for Co-based superalloys, progressing from fundamental regression models for property prediction to advanced multi-model, multi-scale computational paradigms-structured according to model sophistication and problem complexity. Furthermore, we discuss current challenges and future prospects in applying ML to Co-based superalloys, with particular emphasis on addressing data scarcity through the integration of high-throughput experimentation. This synergistic approach enables efficient establishment of standardized superalloy databases, accelerating research progress to meet evolving demands in aerospace applications.
Keywords
INTRODUCTION
With the advancement of modern aviation technology, the increasing thrust-to-weight ratio of aero engines demands higher temperature resistance for hot-section components, such as turbine blades, guide vanes, turbine disks, and combustion chambers. Superalloys serve as critical structural materials in the aerospace industry, exhibiting excellent microstructural stability, superior high-temperature strength, oxidation resistance, and creep properties[1]. Currently, widely used Ni-based superalloys strengthened by the L12-structured γ′-Ni3Al phase face limitations in further enhancing their temperature-bearing capacity due to inherent melting point constraints[2]. Consequently, the development of a new generation of superalloys with enhanced thermodynamic stability is essential for breaking through the limitations of existing material systems.
In 2006, Sato et al. first discovered the L12-structured γ′-Co3(Al, W) ordered precipitate strengthening phase in the Co-Al-W ternary alloy and successfully fabricated novel Co-based superalloys with a γ/γ′ dual-phase microstructure[3]. Unlike conventional Co-based superalloys, which primarily rely on solid-solution strengthening and carbide reinforcement at high temperatures, these γ′-strengthened novel Co-based superalloys demonstrate significantly enhanced strength. Furthermore, they exhibit higher solidus and liquidus temperatures, superior high-temperature strength, and improved thermal corrosion resistance relative to conventional Ni-based superalloys, positioning them as promising candidates for next-generation high-temperature structural materials[2,4-6].
With the rapid development of modern computer science and artificial intelligence fields, the design and application of machine learning (ML) algorithms continue to break through the traditional boundaries based on the significant improvement of algorithmic capabilities brought about by the deep integration and cross-innovation of various disciplines, such as computer science, statistics, and mathematics. With the deep intersection of materials science and artificial intelligence, the proposal and implementation of the concept of genetic engineering of materials has had a profound impact on the field of materials science, promoting the new development of data-driven materials research and development (R&D), in which artificial intelligence technology represented by ML algorithms has gradually entered into the R&D and application of advanced materials vision[7,8]. As mentioned earlier, in practical applications, multi-component superalloys are usually more likely to obtain excellent overall properties, such as high-temperature strength, oxidation resistance, creep resistance, corrosion resistance, and wear resistance. However, traditional materials science research is only based on the first paradigm of experimental science and the second paradigm of theoretical science[9-11], which is often inefficient and costly to optimize the alloy properties by repeated trial and error through experience and experiments. As the third paradigm of scientific research (computational science), ML methods have great advantages in analyzing and processing complex data compared with traditional research methods, which can deeply excavate the implicit laws between material knowledge and properties, and achieve fast and accurate prediction or analysis of unknown material properties and mechanisms, thus efficiently guiding material design, performance optimization, process optimization and mechanism investigation[12-16]. With the cross-development of ML in alloys in the last decade, the results of ML applications, whether in the fields of iron and steel materials[17], titanium alloys[18], shape memory alloys[19-21] or superalloys[22-25], have demonstrated the feasibility of the method and are quite mature.
Given the profound significance of interdisciplinary research on superalloys and ML, this review systematically outlines fundamental ML methodologies and principles from the perspective of Co-based superalloys. Progressing from fundamentals to advanced applications, we analyze and discuss recent five-year advances in ML for Co-based superalloys, structured according to implementation complexity and problem sophistication. Finally, we provide forward-looking perspectives on future developments within this research paradigm.
BASIC FRAMEWORK OF ML FOR Co-BASED SUPERALLOYS
The service environment for superalloys is extremely harsh (high temperature, high pressure, long-term operation), making experimental data acquisition costly and samples scarce. Moreover, the collected data may not even prove valuable-this is precisely the inherent flaw of the traditional trial-and-error method. Against this backdrop, ML demonstrates distinct advantages. Most of the data required for ML comes from the literature and unpublished experimental data. By scientifically learning the relationship between research objectives and material characteristics, relevant high-precision ML models are built to assist in the understanding of material mechanisms and achieve efficient and optimal design of materials. Figure 1 shows the overall research concept of ML for Co-based superalloys, which can be briefly summarized as follows: establish a database containing feature variables and target variables → build a model through ML → evaluate the model → interpret the model’s learning details → feed the learning results back into experimental validation → feed the validation data back into the ML model for iterative optimization → and so on until the problem is solved.
Establishment of Co-based superalloys datasets
ML algorithms belonging to the category of artificial intelligence are trained in the black box of various ML models through deep excavation of the unknowns and laws hidden inside the dataset, and provide the required results or laws to meet different design requirements. According to the model learning method and the characteristics of the corresponding datasets, they can be broadly categorized into supervised learning datasets, semi-supervised learning datasets, unsupervised learning datasets and reinforcement learning datasets.
Among them, supervised learning datasets are the most common in the field of superalloys and are often used in regression analysis and statistical classification in ML. Supervised learning algorithms are subdivided into two types: regression and classification[26,27]. In the case of regression algorithms, the collected dataset is artificially divided into inputs and outputs, and the mapping between the selected inputs and outputs is explored by appropriate ML algorithms, which provide predictions of the outputs for new inputs outside the dataset. As for the classification algorithm, by artificially labeling the collected dataset with different labels and predefining the categories to which it belongs, the ML model learns the relationship between the provided dataset and the labels to automatically predict the unknown data categories.
On the contrary, unsupervised learning datasets do not have outputs calibrated with labels, only features of the dataset itself, and the potential connections or laws of all data are mined by ML models learning autonomously instead of the human assignment of supervised learning. Unsupervised learning is mainly categorized into algorithms such as clustering and dimensionality reduction[28,29]. Clustering groups samples by similarity, maximizing intra-cluster likeness and inter-cluster differences, while dimensionality reduction identifies key feature combinations.
Semi-supervised learning lies between supervised and unsupervised learning, which utilizes a small amount of labeled data to guide the training of a large amount of unlabeled data[30,31]. This approach avoids the problem of costly data collection for supervised learning and also addresses the limitation of underutilized data resources for unsupervised learning. Reinforcement learning differs by having an agent interact with an environment through trial and error, using reward signals to iteratively optimize its policy and maximize cumulative reward.
In summary, the centrality of datasets as the foundation of ML is unquestionable. This also means that specialized databases for materials science must meet more stringent standards and unique requirements. At present, the Chinese Academy of Sciences has constructed a materials science database containing experimental data on metals, ceramics, composites, etc., the National Institute of Standards and Technology (NIST) of the United States has the NIST Materials Data Repository, and the National Institute for Materials Research (NIMS) of Japan has also set up the NIMS Materials Database. However, there is still a lack of specialized databases in the field of Co-based superalloys. The datasets in this field, except for a small amount of unpublished experimental data from subject groups, mainly rely on the scholars themselves to mine from the literature or obtain them through simulations. At present, the establishment of a unified global Co-based superalloy database faces two core challenges: First, data scarcity and inconsistent experimental standards across different countries; second, the application fields of superalloys are often sensitive, making data sharing difficult. Therefore, international collaboration is required to overcome issues such as divergent data standards, difficulties in data sharing, and even intellectual property protection. In particular, it is essential to promote joint research projects and open platforms among global research institutions, universities, and enterprises to share Co-based superalloy data and research findings.
Feature engineering of Co-based superalloys datasets
Before ML model training, it is also necessary to process the duplicate values, missing values, and outliers in the dataset, as well as a series of data standardization and normalization, so as to improve the quality of the dataset and reduce the noise. In general, the basic process of dataset processing includes data preprocessing, data transformation, and data dimensionality reduction.
Data preprocessing
For large sample datasets, direct deletion is a viable option if duplicates or missing data have negligible overall impact. For small sample datasets, it is possible to try to construct a supervised model to predict and interpolate missing values, but the practical implementation of this method is difficult; in addition, it is also possible to interpolate based on other characteristics, using statistical methods such as mean and median[32].
Data transformation
In order to eliminate the dominance effect caused by differences in feature sizes (features with large orders of magnitude overly affecting the model), it is often necessary to normalize or standardize the dataset, converting the data to dimensionless values that can be analyzed and weighted by the model. This process has become a prerequisite for many ML models for Co-based superalloys, because the characteristics of γ′ precipitates in Co-based superalloys are often determined by minute changes in trace alloying elements. For instance, γ′-forming elements such as Ti and Ta can significantly alter alloy properties with just single-digit percentage variations. Therefore, to accurately capture these critical feature variables, the datasets for Co-based superalloys frequently require data processing, and common data normalization or standardization methods are listed below[33,34]:
(1) Min-Max normalization
This normalization method scales the data to between 0 and 1 by linearly transforming the values based on the difference between the maximum and minimum values in the dataset with
where X* is the normalized value, X is the original value while Xmax and Xmin are the maximum and minimum values in the data set, respectively. As the simplest way of data normalization, this method ensures the data distribution and relative relationship between the datasets, but it is susceptible to the influence of extreme outliers in the datasets.
(2) Normalization of means
This method makes the data distribution centered on 0 by centering and scaling the data to a range using the same linear transformation as the Min-Max normalization, which is given as follows:
where μ is the mean value of the dataset. The method ensures the original distribution shape of the dataset and accelerates the convergence speed of the gradient descent by mapping the mean value to 0 while normalizing with the difference of the maximum value and minimum value, which improves the performance of the algorithm, but the method is also not friendly enough to the sparse data and is susceptible to the extreme outliers in the dataset.
(3) Z-score standardization
This standardization method maps the dataset to a normal distribution space with mean 0 and standard deviation 1 by performing mean and standard deviation calculations on the dataset, which are expressed as follows:
where Z* is the normalized value, σ is the standard deviation of the dataset, xi is the i-data point, and n is the total number of samples in the dataset. As a widely used data preprocessing method, this method effectively eliminates numerical differences in the dataset, but it is worth noting that the calculation of both the mean and the standard deviation is based on the overall dataset rather than on a single sample, which is due to the fact that standardization is targeted at a particular feature, and therefore requires the values on that feature in the entire dataset.
(4) Box-Cox transformation
The standardization of datasets is not only a linear transformation. For example, superalloy creep life and oxidation data often have skewed distributions, which can reduce the model’s generalization ability. For such datasets, we can consider adjusting the distribution pattern of data sets through power transformation to make them closer to normal distribution, so as to effectively solve the problem of nonlinear relationship, which is expressed as follows:
where λ is the transformation parameter. Remarkably, the Box-Cox transform is not an advanced form of normalization or standardization. The normalization or standardization focuses on unifying the different measures of the dataset, whereas the Box-Cox transformation focuses on transforming the distributional pattern of the dataset. In addition, not all non-normal data require Box-Cox transformations, models such as random forests that are not sensitive to the shape of the distribution do not need to force a transformation of the dataset.
Data dimension reduction
Data dimension reduction is the process of converting high dimensional data features to low dimensional data features. Since the original data contains a lot of redundant information, noise information, and sample sparsity in the high-dimensional space, which affects the model training and increases the training cost. For the dataset of Co-based superalloys, apart from data scarcity, another major characteristic is its high dimensionality, which further hinders the application and development of ML in this field. Due to the necessity of developing Co-based superalloys, their original datasets often contain multiple alloying elements, process parameters, and even structural features, with dimensionality frequently exceeding 20. To reduce learning costs and eliminate the impact of redundant data, the method of dimensionality reduction has been widely applied in this domain. The current data dimension reduction is mainly divided into two categories: feature selection and feature extraction.
(1) Feature selection
There are two types of cases to consider for feature selection: whether the features are dispersive or not and the correlation of the features with the target variable. If there are non-dispersive features in the dataset, such features are not useful for model training. In addition, if the features in the dataset have different relevance to the target variable, the higher the relevance, the higher the preference for features. The main methods for feature selection include Filter methods, Wrapper methods, etc.
(2) Feature extraction
Although feature selection and feature extraction are both dimensionality reduction methods with the same goal (dimension reduction), beginners are easy to confuse them; however, their principles are fundamentally different: feature selection filters important subsets from the original feature set, and after dimension reduction, the features remain the original attributes, with the feature space unchanged (only reduced to a subset); whereas feature extraction constructs brand-new features by combining or transforming the original features, thereby creating a new feature space. Common feature extraction methods include principal component analysis (PCA) and linear discriminant analysis (LDA).
Selection of ML models
Accompanied by the diversity of ML models and the continuous upgrading of algorithms, from the classical linear regression (LR) to deep neural networks, to integration learning and reinforcement learning and other models are emerging, the selection of ML models is not only a simple selection of algorithms, but also a systematic problem, which involves data characteristics, model objectives, computational resources, model explainability and other factors. From the perspective of the number and nature of models, ML models are typically categorized into single models and ensemble models. A single model refers to a ML model that consists of only one individual model, which is trained independently. Most models in supervised learning can be considered single models, including LR models, decision tree models, and so on. On the other hand, an ensemble model combines multiple single models to form a stronger model that leverages the strengths of all individual models, achieving relatively optimal performance. Commonly used ensemble models fall into two main categories: Boosting and Bagging, with representative examples including AdaBoost, XGBoost, and Random Forest, among others.
Considering the intrinsic data characteristics and developmental demands of superalloys - which typically involve multi-scale studies encompassing composition–process–microstructure–property relationships - regression models, as predictive modeling techniques capable of quantitatively describing and outputting dataset relationships, are widely applied in the field of superalloys. In this case, as mentioned before, Co-based superalloy datasets are often scarce and high-dimensional, and in studies of creep and oxidation there are also situations such as long-tail distributions. Apart from using data transformation to make the dataset more normally distributed, tree-based ensemble models are often more adaptable because they are insensitive to missing values and outliers, can automatically perform feature selection and dimensionality reduction, and can directly provide feature importance rankings.
Training of ML models
After the dataset has been processed and the models have been selected according to the requirements, it is also necessary to train the corresponding models to mine the potential laws in the processed dataset and to establish the functional relationships about the inputs and outputs with certain generalization ability. During model training, in order for the model to learn stably, the hyperparameters of different models need to be adjusted. Therefore, in this section, the training of ML models will be briefly described in terms of dataset partitioning and hyperparameter optimization.
For supervised learning models, the dataset is often divided into 2-3 subsets: the training set, validation set, and test set. Beginners often confuse these concepts. To illustrate, the training set can be compared to a textbook, the validation set to homework, and the test set to an exam. However, it is unnecessary to separate a validation set when the model has no hyperparameters that require manual tuning or when the dataset is very small. There are two main methods for dividing the dataset: the Hold-out Method and K-Fold Cross-Validation.
Hyperparameters directly affect the training speed, convergence and final performance of the model. In order to find the optimal combination of hyperparameters, it is usually necessary to conduct multiple experiments within a preset range to manually filter the best configuration. Currently, Grid SearchCV, Random Search and Bayesian Optimization are often used for hyperparameter tuning[35,36].
Model performance evaluation indicators
After completing the training of the model, it needs to be evaluated for generalization ability[37], which means the ability of the model to adapt to unknown new samples. Considering the superalloy dataset with small samples, many dimensional features and high noise, several types of classical regression model evaluation metrics will be introduced in detail in this section[38].
R2 score
As a statistical measure of how reliably the target variable of a regression model changes, it usually takes a value between 0 and 1, as determined by
where yi is the dataset value,
Mean absolute error
As an evaluation metric to measure the error between the predicted and actual values of the model, mean absolute error (MAE) is calculated by
Mean squared error
The mean squared error (MSE) measures the predictive performance of the model by calculating the average of the squared error between the predicted and actual values, which is given by
Compared with MAE, the MSE is more sensitive to larger errors by amplifying the error through the squared term, and the results of the MSE are of more significance considering the high risk of superalloy applications.
Root mean squared error
Based on MSE, the root mean squared error (RMSE) is obtained by taking the square root of it, as calculated by
As one of the most commonly used model evaluation metrics, such as MSE, RMSE is also able to reflect the model’s performance on larger errors by squaring the errors. Moreover, the RMSE, as the square root of the MSE, has the same magnitude as the original data, making the assessment more intuitive as in the case of the MAE. Comparing RMSE with MAE also reveals that RMSE is more sensitive to larger errors.
Model explainability
In previous research, ML models are often regarded as a kind of black box model, which means that the detailed processing steps of the dataset during the training process of the model are often invisible to the user, and even if the user understands the operation principle of the model, it is not possible to describe it in human-understandable terms. With the intersection of computer science with mathematics and statistics, there are already some ML models whose internal mechanisms are fully or partially understood, and users can not only understand the internal decision details, but also interpret the model outputs through the model parameters and the structure. Through explainability analysis, the feature engineering work in the pre-training stage of the model can be reverse-guided to further improve the generalization ability of the ML model. Therefore, this section will focus on several types of the most classical explainability methods that are applicable to all models and independent of the model itself.
Shapley additive explanation
Shapley additive explanation (SHAP) is a model-agnostic explainability method based on the Shapley value from game theory. This method provides a unified quantification of the marginal contribution of each feature variable to the model output. Grounded in rigorous mathematical theory, it enables analysis not only at the global level but also at the local level, thereby delivering consistent and interpretable assessments of feature importance. In short, SHAP analyzes the weights of feature variables by calculating the marginal contribution of adding a specific feature variable to the model, considering its contributions across different subsets of features, and taking the average to obtain the SHAP value for that feature[39].
Local interpretable model-agnostic explanations
Local interpretable model-agnostic explanations (LIME) is a local Explainability model that approximates the training behavior of a complex black-box model by constructing a local surrogate model, providing explanations for individual feature variables. Its core approach involves perturbing the data near the local feature variables to generate new feature variables. These newly generated data points are then fed back into the original black-box model to obtain new prediction results. Subsequently, an interpretable local surrogate model, such as a decision tree, is trained using these new feature variables and their corresponding new predictions. This results in a local approximation of the black-box model. Finally, the explainability analysis and feature weights derived from this weighted, interpretable local surrogate model are attributed as explanations for the black-box model.
APPLICATION OF MULTI-MODEL ML IN Co-BASED SUPERALLOYS
Multi-objective optimization of Co-based superalloys
In research within the field of materials science, the most widespread and fundamental application of ML lies in using traditional ML models to learn from raw datasets. This type of method is often suitable for performing simple importance screening of feature variables within the raw dataset, thereby obtaining the influence of different feature variables on the target variable[40-43]. This traditional ML approach is widely applied, particularly in alloy composition design, due to its high efficiency and ease of operation in practical applications.
As mentioned in the introduction section, novel Co-based superalloys have attracted significant attention due to their higher solidus and liquidus temperatures[2,4]. To further enhance the γ′ solvus temperature of novel Co-based superalloys, Sun et al. conducted ML-based dual-objective optimization targeting the γ′ solvus temperature and alloy density of Co-based superalloys, and the basic approach is illustrated in Figure 2[44]. By establishing and training eight traditional ML regression models, Sun et al. found that the support vector regressor (SVR) model exhibited the best fitting performance, and the evaluation metrics
Figure 2. Material design framework for dual-objective optimization of multi-component Co-based superalloys based on ML[44]. ML: Machine learning.
Figure 3. Evaluation metrics for eight traditional ML models. γ′ Solvus temperature (A) and alloy density (B); Fitting performance of the SVR model: γ′ solvus temperature (C) and alloy density (D)[44]. ML: Machine learning; SVR: support vector regressor.
Similar to the work of Sun et al.[44], Wang et al. combined ML with equilibrium phase diagrams[45]. By collecting published literature data and unpublished in-house data, and building upon Chen et al.’s prior work[46], they used a random forest model to predict multi-objective variables including γ′ precipitate volume fraction, Vickers hardness, γ′ solvus temperature, solidus temperature, and density. This ultimately yielded trend diagrams for the Co-30Ni-Al-Ta quaternary alloy after annealing at 800 °C for 48 h, as shown in Figure 4. Within these trend diagrams, Wang et al. selected optimal characteristic ranges according to different target variable requirements, successfully screening the Co-30Ni-10Al-6Ta alloy[45]. Experimental verification confirmed that its γ′ precipitate volume fraction, hardness, and γ′ solvus temperature matched the calculated results, significantly shortening the research cycle.
Figure 4. ML-calculated multi-objective variable relationships for the Co-30Ni-Al-Ta quaternary alloy system at 800 °C. (A) γ′ Precipitate volume fraction; (B) Vickers hardness; (C) γ′ Solvus temperature; (D) Density; (E) Relationship diagram between phase transformation temperature lines and pseudo-ternary isothermal sections; (F) Comparison of alloy properties between experimental and calculated results[45]. ML: Machine learning.
The significant improvement in thermal stability and high-temperature strength of novel Co-based superalloys over traditional counterparts primarily stems from the γ′ precipitates emphasized in previous studies. Traditional Co-based superalloys rely solely on solid-solution strengthening and carbide strengthening, lacking precipitate strengthening phases, resulting in lower temperature capability and inferior high-temperature strength. This limitation was overcome in 2006 when Sato et al. first discovered the L12-structured γ′-Co3(Al, W) ordered precipitate phase in a Co-Al-W ternary alloy[3]. However, beyond the primary γ/γ′ dual-phase microstructure, excessive alloying in novel Co-based superalloys may lead to precipitation of detrimental phases, such as β-CoAl, χ-Co3W, and μ-Co7W6 within the γ matrix, severely compromising microstructural stability[2,47-49]. Common phases in novel Co-based superalloys are summarized in Table 1.
Crystal structure parameters of common phases in Co-based superalloys
| Phase | Structure symbol | Prototype | Space group |
| γ | A1 | Co | Fm |
| ε | A3 | Co | P63/mmc |
| γ′ | L12 | Co3(Al, W) | Pm |
| χ | D019 | Co3W | P63/mmc |
| β | B2 | CoAl | Pm |
| μ | D85 | Co7W6 | R |
| Laves | C14 | MgZn2 | Fd |
Therefore, to ensure that the designed novel Co-based superalloys exhibit a more distinct γ/γ′ dual-phase microstructure with fewer detrimental phases while maintaining excellent high-temperature properties, Yu et al. proposed a two-stage ML strategy illustrated in Figure 5[50]. This strategy employs a classification model to predict the existence of γ′ precipitates, followed by a regression model to predict the γ′ solvus temperature. Consequently, it substantially reduces the workload and alloy search scope encountered by Sun et al. in composition screening, enabling the pre-selection of alloy ranges with potentially fewer γ′ precipitates and enhancing the efficiency of alloy composition design[44].
Figure 5. Two-stage design of the L12-strengthened Co-base superalloys. (A) Research framework; (B) Two-stage design: Stage 1 uses the RFC model to determine the existence of γ′ precipitates; Stage 2 employs the RFR model to predict the γ′ solvus temperature; (C) Prediction results of the RFC on the training dataset by 10-fold cross validation; (D) Prediction results of the regression models on the training dataset[50]. RFC: Random forest classifier; RFR: random forest regressor.
Similarly, Liu et al. adopted an analogous approach to optimize multi-objective properties of Co-based superalloys using ML, including γ′ solvus temperature, γ′ precipitate volume fraction, alloy density, and microstructural stability[51]. However, considering the difficulty in designing alloys with multiple desirable properties due to data scarcity in the field of novel Co-based superalloys, Liu et al. enhanced this method[51]. They introduced a framework integrating ML with the efficient global optimization (EGO) algorithm, utilizing a sequential filter and experimental feedback to screen alloy compositions. Ultimately, an alloy composition satisfying all target properties was identified within only three rounds of experimentation. This resulted in a new alloy achieving the highest possible γ′ solvus temperature while meeting other performance requirements; the workflow is shown in Figure 6.
Figure 6. Material design strategy for multi-property optimization of multi-component Co-based superalloys via ML and model iteration results. (A) Design strategy workflow; (B) ROC curve for evaluating classification models; (C) Regression results for γ′ solvus temperature; (D) Regression results for solidus temperature; (E) Regression results for liquidus temperature; (F) Regression results for density; (G) Variation of experimental values over three iterations[51]. ML: Machine learning; ROC: receiver operating characteristic.
Unlike Sun et al. who directly collected literature data for model training[44], Liu et al. combined existing experimental data with computational data from the thermodynamic software Pandat during the initial dataset construction[51]. Pandat, equipped with a thermodynamic database for Co-based superalloys, is widely used for phase equilibrium studies in these alloys due to its ability to generate large volumes of calculated phase diagram data. For instance, Li et al. employed this software to design multi-component Co-based superalloys free from detrimental phase precipitation after aging at 1,100 °C for 1,000 h[52]. Additionally, similar to Yu’s objective[50], to ensure designed alloy compositions exhibit only the γ/γ′ dual-phase microstructure without detrimental phases, Liu et al. established a classification model using physical parameters (e.g., valence electron number, first ionization energy) to predict phase composition[51]. This enabled preliminary screening of precipitate types in the microstructure, simultaneously reducing the subsequent composition search space and enhancing the classification model’s robustness. The gradient tree boosting (GTB) model was ultimately identified as the optimal classifier via receiver operating characteristic (ROC) curve analysis. For target properties such as γ′ solvus temperature and density, Liu et al. trained six regression models using MSE as the evaluation metric[51]. During training, data processing employed the hold-out method and bootstrap sampling as described in preamble, with final model performance shown in Table 2.
Evaluation results of different ML classification and regression models on test sets for γ′ solvus temperature (Tγ′-solvus), solidus temperature (Tsolidus), liquidus temperature (Tliquidus) and density of novel Co-based superalloys[51]
| Classification model | AUC | Regression model | MSE-Tγ′-solvus | MSE-Tsolidus | MSE-Tliquidus | MSE-density |
| LC | 0.82 | DTR | 3,210.9 | 995.7 | 664.0 | 0.04 |
| DTC | 0.90 | KNR | 4,123.8 | 2,754.4 | 1,080.0 | 0.11 |
| ABC | 0.93 | ABR | 2,148.0 | 877.2 | 724.7 | 0.04 |
| GTBC | 0.96 | SVR | 1,980.0 | 2,017.6 | 1,076.0 | 0.08 |
| RFR | 1,788.2 | 692.4 | 469.3 | 0.04 | ||
| GTBR | 1,610.3 | 737.4 | 469.2 | 0.03 |
In summary, ~97% of potential alloy compositions were screened out through initial data modeling. To further select new compositions with higher γ′ solvus temperatures, Liu et al. integrated bootstrap sampling with the acquisition function-based global optimization algorithm[51]. By repeating sampling 1,000 times to generate 1,000 training datasets (identical in size but differing in specific samples) and employing the expected improvement (EI) acquisition function-commonly used in Bayesian optimization-the screening process shown in Figure 6A was implemented to identify the optimal alloy composition.
Furthermore, γ′ precipitate volume fraction, as another critical property of Co-based superalloys, significantly impacts mechanical performance. Studies by Titus et al. revealed that creep resistance improves with increasing γ′ volume fraction[53]. Generally, the optimal γ′ volume fraction ranges between 50% and 70%, ensuring high thermal stability. However, excessively high fractions (> 70%) promote detrimental phase precipitation[54]. Compared to thermodynamic calculations[55], appropriate ML methods typically achieve higher prediction accuracy.
Building upon earlier work[50], Yu et al. proposed a ML-based ensemble strategy establishing predictive models for four key properties of novel Co-based superalloys: existence of γ′ precipitates, absence of detrimental phases, γ′ solvus temperature, and γ′ volume fraction[56]. This enabled efficient screening of potential compositions, as illustrated in Figure 7A. Similar to Liu et al.’s approach[51], these four models combined classification (for γ′/detrimental phase existence) and regression (for γ′ solvus temperature/volume fraction). The key advancement over Liu et al. lies in the dedicated γ′ volume fraction prediction model, which served as a screening criterion since precipitate fraction critically influences solvus temperature and secondary phase formation[51].
Figure 7. ML multi-model integration strategy and γ′ precipitate volume fraction predictions across different datasets. (A) ML workflow; (B) Training performance with 1st group features; (C) Training performance with 2nd group features[56]. ML: Machine learning.
In dataset processing, Yu et al. innovatively partitioned data using domain knowledge: recognizing that γ′ solvus temperature depends primarily on composition rather than processing parameters, while the latter significantly affects microstructure[56]. They applied a dataset with 14 alloying elements and 2 processing parameters (named 1st group features) to classification and γ′ volume fraction regression models. Conversely, a composition-only dataset (14 elements, named 2nd group features) was used for γ′ solvus temperature regression. Drawing inspiration from nickel-based superalloy design, Yu et al. introduced a new PHACOMP approach incorporating transition element descriptors: d-orbital energy level (Md) and bond order (Bo) to construct enhanced feature representations[56]. Final dataset features are summarized in Table 3.
Two groups of features
| 1st Group features | 2nd Group features |
| Aging temperature (°C) | Aging temperature (°C) |
| Aging time (h) | Aging time (h) |
| Co (at.%) | Atomic number |
| Al (at.%) | Melting point (°C) |
| W (at.%) | Boiling point (°C) |
| Ta (at.%) | Density (g/cm3) |
| Nb (at.%) | Relative atomic mass |
| Ti (at.%) | Atomic radius, non-bonded (Å) |
| V (at.%) | Covalent radius (Å) |
| Cr (at.%) | Electron affinity (kJ/mol) |
| Si (at.%) | Electronegativity (Pauling scale) |
| Mo (at.%) | 1st Ionization energies (kJ/mol) |
| Ni (at.%) | Md |
| Re (at.%) | Bo |
| Fe (at.%) | |
| Zr (at.%) |
Subsequently, considering the limited domain knowledge regarding the relationship between elemental micro-characteristics in 2nd group features and γ′ precipitate volume fraction, Yu et al. utilized both 1st and 2nd group features for regression model training[56]. K-fold cross-validation was implemented to prevent overfitting, with model training results shown in Figure 7B and C.
Comparison between ML-optimized alloys and classical W-free novel Co-based superalloys in Figure 8 reveals significantly enhanced γ′ solvus temperatures. The work of Sun et al. is particularly notable, with their designed 5Ti-3Cr-2Ta-2Mo alloy achieving a γ′ solvus temperature as high as 1,250 °C while maintaining an alloy density of only 8.2 g/cm3[44].
Based on the aforementioned analysis, it is evident that ML models demonstrate exceptional efficacy in predicting specific characteristics of Co-based superalloys, such as γ′ solvus temperature, alloy density, and so on. This success stems from two critical factors: the availability of sufficient training datasets to support model learning, and the relatively low-dimensional nature of these feature properties, which significantly enhances the efficiency of multi-objective alloy optimization.
However, as research progresses, the application of ML in Co-based superalloys will no longer be limited to common datasets with alloy composition, time, and temperature as the main feature variables. The integration of multi-scale methodologies is poised to advance ML applications in more complex domains, such as oxidation behavior and creep performance of Co-based superalloys.
ML driven by multi-scale datasets of Co-based superalloys
In recent years, driven by increasingly severe service conditions and maturing multi-scale methodologies, the study of Co-based superalloys based on ML has evolved beyond reliance on single ML models-particularly the traditional models discussed in preamble. While such models typically entail lower computational costs and accessibility barriers, their inherent limitations often constrain prediction accuracy. This discrepancy between theoretical ML results and practical applications hinders effective guidance for superalloy development. Additionally, some studies mechanically replicate existing model frameworks, merely replacing algorithms or tuning hyperparameters/datasets to achieve marginal improvements over prior work. To enhance ML’s applicability in superalloys and leverage domain knowledge for guiding ML design, multi-scale integrated ML research has emerged as the mainstream paradigm. This section therefore elaborates on multi-scale ML approaches for Co-based superalloys-incorporating domain knowledge, deep learning, CALPHAD, alloy phase diagrams, image processing, and phase-field simulations-building upon the preceding section.
Beyond temperature capability and high-temperature strength, oxidation behavior under elevated-temperature service conditions is critical for Co-based superalloys[63,64]. Poor oxidation resistance directly compromises surface integrity and severely degrades creep/fatigue resistance, posing unforeseen risks. For these alloys, the formation of stable Al2O3 or Cr2O3 oxide layers is essential for oxidation resistance. However, even disregarding other issues from high-Al alloying, Co-based superalloys with high Al content struggle to form continuous oxide layers during prolonged oxidation[65-68]. Understanding complex oxidation mechanisms in multi-component alloys presents significant challenges as compositions grow more intricate. ML has demonstrated feasibility in decoding these mechanisms embedded in oxidation kinetic data[69,70].
To overcome traditional models’ constraints by parabolic rate laws when simulating complex oxidation behaviors, Pei et al. proposed an ML framework integrating a 1D convolutional neural network (1D-CNN) with a long short-term memory network (LSTM), as illustrated in Figure 9[71]. This hybrid architecture accurately predicts multi-component Co-based superalloy oxidation behaviors under complex conditions (e.g., mass gain, kinetic parameters, oxidation mechanism transitions). The 1D-CNN extracts local features to decode nonlinear oxidation kinetics, while the LSTM models temporal dependencies to capture long-range correlations during oxidation, collectively enhancing predictive capability.
Figure 9. Flowchart of the ML model for predicting oxidation behavior in Co-based superalloys[71]. ML: Machine learning.
To ensure hourly data for each alloy was formatted into time-series sequences suitable for processing, Pei
Figure 10. Hybrid ML model and mass gain predictions. (A) 1D-CNN-LSTM model flowchart; (B) Comparison between model predictions and experimental data in the test set[71]. ML: Machine learning; 1D-CNN: 1D convolutional neural network; LSTM: long short-term memory.
Beyond mass gain prediction, the model’s critical capability lies in capturing oxidation curve profiles, specifically predicting oxidation rate (k) and exponent (n) from parabolic rate laws. Figure 11 compares experimental vs. predicted n values and normalized oxidation rates (kc). While minor deviations exist in n-value fitting (affecting kc accuracy), the model robustly adapts to diverse oxidation mechanisms. By classifying fitted data according to temperature and mass gain, Pei et al. observed distinct patterns[71]: higher n-values (> 0.5) predominantly occurred in high-temperature regions (> 1,000 °C), lower n-values (< 0.3) clustered in intermediate temperatures (900-1,000 °C), and medium n-values (0.3-0.5) dominated low-temperature zones (800-900 °C)-all consistent with parabolic oxidation principles[72,73].
Figure 11. Comparison of experimentally fitted vs. model-predicted oxidation kinetic parameters. (A) Comparison of oxidation index; (B) Comparison of oxidation rate; (C) Classification of oxidation index by temperature; (D) Classification of oxidation index by mass gain[71].
As established previously, although novel Co-based superalloys exhibit higher temperature capability potential compared to Ni-based superalloys, improving the γ′ precipitate processing window size - whether for the classical Co-Al-W ternary system discovered by Sato et al.[3] or its derivative multi-component alloys[52,74,75] - has become a critical direction for further enhancing their high-temperature strength[60,76].
To address this challenge, Ruan et al. proposed a strategy combining ML with CALPHAD (calculation of phase diagrams) for designing tungsten-free novel Co-based superalloys[77]. As a Gibbs energy database-driven design approach, CALPHAD is particularly suitable for multi-component alloy systems[52,78]. For instance, Zhuang et al. utilized this method to introduce Ni and Cr into the Co-7Al-8W-4Ti-1Ta pentenary alloy, developing a novel CoNi-based superalloy (Co-30Ni-8Al-2W-4Ti-1Ta-14Cr) with comprehensive properties rivaling nickel-based superalloy U720Li[79]. Similarly, Liang et al. employed CALPHAD to develop a new low-density γ′-strengthened CoNiCr-based superalloy with predefined high Ni content and Ti/Al ratio[80]. Ruan et al. first applied a pre-established ML model[50] to predict γ′ solvus temperature and γ′ precipitate volume fraction, generating composition-dependent maps for the Co-V-Ta ternary system after 800 °C/600 h annealing [Figure 12A and B][77]. Based on these predictions, Co-6V-2.5Ta and Co-10V-2.5Ta alloys were designed. Microstructural observation [Figure 12C and D] revealed abundant thermodynamically unstable intergranular Co3V phases that consumed γ′ precipitates. Consequently, as shown in Figure 12E-H, Ruan et al. calculated grain boundary segregation using the parallel tangent method[81,82] based on liquid-phase Gibbs free energy curves[77], supplemented by thermodynamic calculations via Thermo-Calc’s TTNI8 database[83]. These analyses confirmed Ta (not Co or V) segregation at grain boundaries. Integrating these insights, Ruan et al. ultimately fabricated the Ta-lean Co-12V-2Ta alloy[77]. Scanning electron microscopy (SEM) images [Figure 12I and J] demonstrate significant reduction of intergranular Co3V phases.
Figure 12. Alloy design workflow. Composition-dependent maps of (A) γ′ solvus temperature and (B) γ′ area fraction for Co-V-Ta ternary alloys after 800 °C/600 h annealing predicted by ML; SEM images of (C) Co-6V-2.5Ta and (D) Co-10V-2.5Ta alloys after
Microstructure characterization remains central to Co-based superalloy research. Compared to composition and processing parameters, microstructural information offers greater potential for ML applications[84]. As shown in Figure 13, Khatavkar et al.[85] quantified structural features in Co/Ni-based superalloy SEM images using two-point correlations[86,87] combined with advanced image processing. Binary phase-separated images yielded new feature variables, reduced via PCA and least absolute shrinkage and selection operator (LASSO) dimensionality reduction. A gaussian process regression (GPR) model successfully predicted Vickers hardness, enabling high-throughput design of high-hardness superalloys.
Figure 13. (A) Original SEM images; (B) Phase-separated binary images; (C) 2D point correlation functions; (D) Percentage variance of binarized micrograph captured as a function of number of principal components; (E and F) Microstructure and composition-based SVR predictions; (G) GPR fitting; (H) LASSO feature-reduced model fitting[85]. SEM: Scanning electron microscopy; SVR: support vector regressor; GPR: gaussian process regression; LASSO: least absolute shrinkage and selection operator.
This is exactly the opposite of Khatavkar’s approach[85], Taylor et al. combined physics-based methods with ML, using GPR to inversely predict Ni-based superalloy microstructures from composition and aging parameters[88]. In addition to this, in order to accelerate the prediction efficiency of atomic structures and mechanical properties in novel cobalt-based superalloys, Xi et al. proposed a multi-scale research methodology driven by ML and first-principles calculations[89]. By integrating unsupervised and supervised learning algorithms, this work enables predictions of atomic configurations in complex doped systems (e.g., occupancy trends and doping positions) and mechanical properties (bulk modulus B, shear modulus G, Young’s modulus E). As shown in Figure 14, Xi et al. established a closed-loop framework integrating first-principles calculations and ML[89]. This framework begins with unsupervised models predicting atomic structures through two distinct steps: accurately representing the occupancy trend and pinpointing the doping position of the TM elements. Subsequently, phase stability between L12 and D019 is compared using the stable formation enthalpy as the criterion. Where the L12 phase demonstrates superior stability, supervised learning algorithms predict its mechanical properties.
Figure 14. (A) Schematic workflow for an accelerated first-principles calculation; (B) The crystal structures of L12-ordered alloys in the Co-Al-W-M-X, Co-V-Ti-M-X, and Co-V-Ta-M-X (M = Nb, Ti) systems, as well as in the Co-Al-V-M-X-based system; (C) Ranking of prediction accuracy for the occupancy trend of doping elements based on a K-means cluster model and the clustering results for the occupancy trend of doping elements on the training set; (D) Model fitting results for L12 mechanical properties[89].
The training dataset originates from first-principles calculations, initially comprising 40 data points for Co-Al-W-Nb-X and Co-Al-W-V-X systems generated via the Vienna Ab initio Simulation Package (VASP). This dataset was iteratively extended to Co-Al-W-Ti/Ta-X, Co-V-Ti-M-X, Co-V-Ta-M-X, and Co-Al-V-M-X systems. Input features include eight microscopic characteristics of transition metal elements (e.g., electronegativity, covalent radius, melting point) alongside categorized occupancy trends and doping positions. The K-means clustering algorithm revealed that the combination of covalent radius and electronegativity accurately predicts occupancy trends, while melting and boiling points precisely classify doping positions [Figure 13C]. For mechanical property prediction, the random forest regressor (RFR) model exhibited optimal performance during 10-fold cross-validation [Figure 13D]. Xi et al. significantly accelerated the speed of traditional first-principles work through a closed-loop framework consisting of density functional theory (DFT) data generation, ML prediction, DFT verification, and iterative optimization[89].
Co-based superalloys often endure high temperatures and stresses during service, causing the alloy to undergo creep deformation, which affects the service life and safety of the equipment. Therefore, when designing high-temperature alloys, excellent creep performance is an important factor to consider[90-93]. Existing computational methods correlate creep properties with alloying elements, heat treatment, lattice parameters, shear modulus, and precipitate fraction[94-96], yet systematic integration remains challenging.
Creep life, as one of the most critical performance indicators in creep behavior, is primarily determined by alloy composition, heat treatment processes, microstructure, and loading conditions. Research centered on this metric often holds significant importance. However, given the inherent challenges in collecting creep life datasets, including scarcity and high acquisition costs, it is no longer feasible to simply study input-output relationships through standalone ML models. Consequently, multi-model and multi-scale fusion approaches have progressively emerged as the mainstream research direction[97-99]. Current theoretical methods for accelerated prediction of alloy creep rupture life fall into two primary categories: time-temperature parameter (TTP) methods and creep constitutive model (CCM) approaches. Among these, Dang et al. successfully predicted long-term creep life of alloys using low-temperature short-term creep data through the Larson-Miller and Manson-Haferd methods based on the TTP framework[100]. Meanwhile, Bolton et al. established an empirical stress-creep life relationship by leveraging steady-state creep rate and creep life datasets under identical temperatures but varying stresses, also within the TTP methodology[101]. However, both cases represent empirical fitting approaches that neglect actual microstructural evolution during creep deformation. Recently, with advances in crystal plasticity theory and continuum mechanics, CCMs have rapidly evolved. These models enable more precise description of creep behavior and life prediction[101-106].
In recent years, with continuous advancements in ML and materials science, research on predicting creep life of superalloys using ML has achieved notable progress. Among these developments, Venkatesh et al. pioneered the application as early as 1999 by employing a back-propagation neural network (BPNN) model to predict the creep life of INCONEL 690 Ni-based single-crystal superalloys at 1,000 and 1,100 °C[107]. Considering that there is much more research on Ni-based superalloys than on Co-based superalloys in terms of creep life and other aspects, we will explore new ideas for research on Co-based superalloys in this field based on some of the research on Ni-based superalloys.
However, given that superalloys exhibit distinct creep mechanisms under different conditions[108-112], it is challenging to address the relationship between relevant descriptors and creep properties in superalloys with mixed creep mechanisms using a single ML model. To address this, Liu et al. proposed a Divide-and-Conquer Self-adaptive ML strategy (DCSA), as illustrated in Figure 15[113]. This approach integrates multiple material descriptors with CALPHAD methodology while incorporating five microstructure parameters critical to creep processes (lattice parameter, mole fraction of γ′ precipitates, diffusion coefficient, and shear modulus[108,114,115]. The K-means clustering model then categorizes alloys by dominant creep mechanism. During processing, an adaptive function selects the optimal regression model for each cluster. These optimized models are subsequently integrated to form the final predictive framework.
Figure 15. DCSA model flowchart[113]. DCSA: Divide-and-Conquer Self-adaptive ML strategy.
To further enhance the prediction accuracy and efficiency of the DCSA strategy, Wu et al. improved upon the work of Liu[113] by addressing issues such as the high dimensionality of feature variables during model clustering and the heavy reliance on manual trial-and-error for model hyperparameter tuning[116]. As illustrated in Figure 16, Wu et al. first introduced PCA for dimensionality reduction prior to clustering, compressing the original 27-dimensional features into two principal components (PC1 and PC2)[116]. This effectively eliminated high-dimensional noise, resulting in physically clearer clustering outcomes. Secondly, Wu et al. replaced manual parameter tuning with fully automated Grid Search, which exhaustively explores the hyperparameter space and automatically selects the optimal combination using R2 as the evaluation metric, achieving true model self-adaptation[116]. Furthermore, Wu et al. extended this approach to construct a comprehensive “composition/processing-microstructure-creep life” framework, providing novel insights for the automated ML-driven design of Co-based superalloys[116].
Figure 16. Improved DCSA ML flowchart[116]. DCSA: Divide-and-Conquer Self-adaptive ML strategy; ML: machine learning.
Compared to Ni-based superalloys, creep datasets for Co-based superalloys are often characterized by smaller sample sizes, increasing the difficulty of aforementioned ML application. We have collected all available creep life data for novel Co-based superalloys since 2006, totaling barely over 100 datasets, The partly distribution characteristics in the datasets are concluded and arranged in Figure 17.
To address this, Qin et al. designed a prediction route for creep properties of Co-based superalloys integrating phase-field simulations with ML[117]. After processing the microstructure data obtained from phase-field simulations of Co-10Al-9W alloy, they employed convolutional neural networks (CNN) and support vector machines (SVM) to classify the creep stages of the alloy, followed by the use of several regression models to predict creep strain. Beyond creep life, Ohl et al. investigated the steady-state creep rate of Co-based superalloys[118]. As shown in Figure 18, they established seven intermediate ML models, taking alloy composition and Magpie elemental descriptors as inputs, and outputting seven material properties: solidus temperature, solidus temperature, liquidus temperature, hardness, γ′ precipitate volume fraction, lattice misfit, and yield strength. These outputs were then combined with the original dataset-including alloy composition, heat treatment process parameters, and γ′ precipitate microstructure parameters-and fed back into the ML model for training. During training, the dataset was partitioned into k groups via K-means clustering, and random forest regression was performed individually for each group. The dataset was then randomly split for iterative retraining to obtain the final results.
Figure 18. ML workflow for predicting steady-state creep rate of Co-based superalloys[118]. ML: Machine learning.
In summary, the development of ML in the field of creep behavior of Co-based superalloys currently faces certain difficulties. In addition to the high acquisition cost of creep life datasets, the application of ML under multiaxial loading conditions has rarely been explored. Compared to the uniaxial loading conditions discussed in previous studies, multiaxial loading involves higher experimental costs and more complex experimental procedures. These factors further exacerbate the issues that ML is most concerned about - data scarcity and high feature dimensionality - resulting in significant limitations for purely data-driven ML approaches. The current optimal solution combines data-driven methods with physical characteristics. This can be achieved through hybrid modeling, physics-informed neural networks (PINNs), and by incorporating transfer learning and active learning methods to further overcome bottlenecks such as data scarcity. These approaches provide powerful new tools and ideas for solving the long-standing engineering challenge of creep-fatigue life prediction.
In summary, the application of multi-scale and multi-model fusion approaches in the design and performance prediction of Co-based superalloys has enabled ML to achieve an organic integration of domain knowledge with alloy characteristics, thereby realizing high-precision predictions of complex evolutionary processes. This success stems from two key aspects: first, the availability of comprehensive and cross-scale training data that provides a solid foundation for model learning; second, the implementation of low-dimensional representation and dimensionality reduction techniques for features at different scales, which significantly enhances both the efficiency and interpretability of multi-objective optimization.
Regarding the scarcity of datasets for Co-based superalloys, generative adversarial networks (GANs) have emerged as one potential solution. However, currently, the primary challenge lies in how to incorporate constraints from the physical characteristics of superalloys, rather than merely generating numerical combinations, as existing Co-based superalloy datasets remain unsuitable for generative model training. In the future, further in-depth research is still required to advance this approach.
Explainable ML enabled deepening of Co-based superalloys
While the preceding two sections provide insights and demonstrate the feasibility of applying ML in the field of Co-based superalloys, Liu et al. points out that researchers must further investigate the learning behaviors of the employed models-specifically, the model explainability analysis described in preamble[119,120]. This necessity arises due to experimental costs, reliability concerns regarding model-generated data, and the disconnect between high-dimensional feature variables and small-sample datasets. Among explainability methods, SHAP analysis[39] has gained widespread adoption in alloy research owing to its strong explanatory power and model adaptability, and it has similarly attracted significant attention in the superalloy community. Therefore, this section will provide a detailed exposition on SHAP-based interpretable ML models for analyzing feature importance and interpreting mechanisms in the context of Co-based superalloys.
As illustrated in Figure 19, Huang et al. proposed a dimensionality reduction strategy integrating physical metallurgy models and the CALPHAD method, establishing an interpretable ML model for creep life[121]. Based on SHAP analysis, it was revealed that the γ′-solvus temperature exerts the most significant influence on creep life, with longer lifespans observed as the γ′-solvus temperature increases. Conversely, relevant processing parameters universally exhibited negative correlations with creep life. These findings align with empirical knowledge in the field of Co-based superalloys, allowing researchers to leverage such SHAP outcomes as a validation metric for model accuracy. However, when SHAP results deviate from conventional empirical conclusions, meticulous scrutiny of the entire modeling workflow is warranted. Huang et al. further discovered via SHAP that the γ/γ′ dual-phase lattice misfit exhibits an approximately positive correlation with creep life, yet excessive misfit proves detrimental[121]. This phenomenon may be attributed to the fact that excessively high misfit promotes instability at coherent interfaces and coarsening of γ′ precipitates, compromising microstructural stability and ultimately degrading creep performance. Additionally, SHAP analysis indicated a negative correlation between γ′ precipitate volume fraction and creep life-a finding inconsistent with prior studies. This discrepancy was reconciled through examination of the dataset characteristics: over 80% of the alloys in the dataset possessed γ′ volume fractions exceeding 60%, thus yielding this counterintuitive SHAP outcome.
Figure 19. Flowchart of an interpretable ML model applied to creep life prediction of superalloys[121]. ML: Machine learning.
Similarly, Zhang et al. introduced SHAP analysis into their work on predicting the creep-fatigue life of Inconel 617 alloy using PINNs[122-125]. The analysis revealed that strain amplitude and creep time constitute the two most critical feature variables influencing creep-fatigue life, both exhibiting negative correlations with lifetime. Furthermore, Co and Cr emerged as the most pivotal alloying elements affecting the creep-fatigue performance of Inconel 617. Specifically, Cr demonstrated a positive correlation with lifetime-a finding attributable to the role of Cr in forming a protective oxide layer on the alloy surface, thereby enhancing corrosion resistance and high-temperature oxidation resistance.
As previously discussed, the creep performance of superalloys is intrinsically linked to their precipitate phases. Under high-temperature service conditions, prolonged exposure or elevated temperatures induce systematic microstructural evolution in these precipitates, manifesting as the coarsening phenomenon. In Co-based superalloys, coarsening of γ′ precipitates compromises microstructural stability at elevated temperatures, thereby degrading alloy performance. While substantial progress has been made in understanding the underlying mechanisms and coarsening kinetics, traditional coarsening kinetic theories exhibit significant limitations when addressing excessive coarsening in certain advanced superalloys under increasingly demanding service conditions[126-129]. To deepen the investigation into key factors governing γ′ precipitate coarsening behavior, Sun et al. established an interpretable ML model illustrated in Figure 20[130]. This framework employs an XGBoost classifier to screen feature variables influencing γ′ coarsening behavior in Co-based and Co-Ni-based superalloys. Leveraging SHAP analysis, a final subset of critical features was identified. Subsequently, a symbolic classification approach was applied to derive an empirical formula, with experimental validation confirming the accuracy of the SHAP-derived insights.
Figure 20. Interpretable ML model for determining the key factors of γ′-phase coarsening behavior in Co- and Co-Ni-based superalloys[130]. ML: Machine learning.
In the model explainability section, Sun et al. formed SHAP analysis on the two filtered datasets shown in Figure 21[130]. Among them, the dataset constituent elements and processing parameters are named the CP dataset, while the dataset with nine atomic and electronic properties added to the CP dataset is named the CPAE dataset. For the CP dataset, the analysis identified aging temperature as the primary factor influencing γ′ precipitate coarsening. When temperatures exceed 900 °C, SHAP values shift from positive to negative, indicating the onset of significant coarsening, a conclusion substantiated by existing literature[131]. Furthermore, by examining SHAP value variations induced by changes in atomic fractions of alloying elements and integrating these findings with domain knowledge, researchers can delineate optimal compositional ranges for alloy design, such as constructing contour maps or heatmaps for compositional space exploration[132]. For the CPAE dataset, Sun et al. discovered that Young’s modulus exerts a more pronounced influence on coarsening behavior than other features and actively suppresses coarsening[130]. This phenomenon aligns with findings by Liu et al. who demonstrated that alloying elements with high Young’s modulus (e.g., Re and Mo) preferentially partition to the γ matrix, thereby reducing γ/γ′ dual-phase lattice misfit to inhibit coarsening[133,134].
Figure 21. The two datasets filtered through the modeling process. (A) Dataset CP: Contains atomic fractions of alloying elements and aging temperature; (B) Dataset CPAE: Augments CP with atomic and electronic descriptors based on domain knowledge[130].
Comparative analysis of SHAP results from the CP and CPAE datasets reveals that as feature selection progresses from fundamental parameters (alloy composition, heat treatment) to microstructural physicochemical properties, SHAP interpretations become progressively refined, significantly enhancing model reliability and explainability.
In summary, typical application examples of ML in Co-based superalloys are shown in Table 4.
Examples of ML-driven research on Co-based superalloys
| Year | Description | Model | Ref. |
| 2024 | Dual-objective optimization for γ′ solvus temperature and alloy density | SVR | [44] |
| 2022 | ML combined with phase diagrams to design alloys with high γ′ solvus temperature and volume fraction | RF | [45] |
| 2019 | Designing Co-based superalloys with more pronounced γ/γ′ biphasic microstructures through a two-stage ML strategy | RFC + RFR | [50] |
| 2020 | Introduced a framework integrating ML with the EGO algorithm, utilizing a sequential filter and experimental feedback to screen alloy compositions | GTB | [51] |
| 2020 | Innovative division of datasets based on domain knowledge (using component characteristics to predict γ′ solid solution line temperature, combining components and processing parameters to predict γ′ volume fraction) | RFC + GBR | [56] |
| 2025 | A ML hybrid structure framework was proposed to accurately predict the oxidation behavior of multi-component cobalt-based superalloys under complex conditions | 1D-CNN + LSTM | [71] |
| 2020 | ML was used to predict the alloy-composition-dependent solvus temperature and area fraction of γ′ phase in the Co-V-Ta ternary system | RFC + RFR | [77] |
| 2020 | Quantified structural features in Co/Ni-based superalloy SEM images using two-point correlations, and successfully predicted Vickers hardness | GPR | [85] |
| 2024 | Using unsupervised and supervised models, the integration of ML and first-principles calculations enables the prediction of atomic configurations and mechanical properties | RFR + K-means | [89] |
| 2020 | By adopting a Divide-and-Conquer Self-adaptive ML Strategy, the creep life is predicted | K-means + Regressor | [113] |
| 2023 | Proposed a dimensionality reduction strategy integrating physical metallurgy models and the CALPHAD method, establishing an interpretable ML model for creep life | RFR + SHAP | [121] |
| 2024 | Identifying determinants of γ′ phase coarsening behavior in Co/CoNi-based superalloys with explainable artificial intelligence | XGBoost + SHAP + SCA | [130] |
High-throughput experimental dataset driving application of ML
As established in the preceding sections, the foundation of ML lies in the dataset, and the quality of the dataset determines the quality of the final model. However, the current ML databases for novel Co-based superalloys suffer from a series of drawbacks that severely constrain the accuracy, reliability, and practical application value of the models.
(1) The majority of the data originates from published literature. However, there are significant differences in the experimental equipment, testing standards, and experimental conditions used by different research teams in the published studies. The data reported in the literature, such as hardness, yield strength, or oxidation mass gain, may have been obtained under vastly different conditions, resulting in a lack of direct comparability between data points.
(2) Academic journals tend to publish research results demonstrating breakthroughs or superior performance. This leads to literature databases predominantly featuring alloy compositions or process parameter combinations with relatively good performance. In contrast, a large amount of data on mediocre or even failed experiments - data crucial for understanding boundaries and failure modes - is selectively omitted or never published. ML models trained on such positive-sample-dominated datasets exhibit reduced prediction reliability.
(3) The core value of novel Co-based superalloys lies in their long-term service capability under extreme high-temperature conditions (creep, fatigue). However, obtaining reliable creep data or low-cycle/high-cycle fatigue data is costly and time-consuming. Published literature contains relatively little of this type of data. Consequently, models are forced to rely on short-term tests or accelerated tests for training. The reliability of the dataset remains questionable.
(4) Microstructural characterization in the literature is often limited to low-dimensional descriptions (e.g., average γ′ size, phase composition) and lacks high-resolution quantitative data [e.g., 3D electron back-scattered diffraction (EBSD) reconstructions, APT atom distribution maps, dislocation configuration statistics]. Furthermore, most SEM/transmission electron microscope (TEM) images are typically presented as representative micrographs, making the original image data difficult to obtain. This hinders the ability of ML to establish predictive models based on underlying micromechanisms.
In recent years, the approach of combining high-throughput experiment (HTE) with ML has gained increasing attention from researchers in relevant fields. HTE enables the simultaneous fabrication of dozens or even hundreds to thousands of samples, while high-throughput characterization allows for the concurrent assessment of composition, structure, or properties across a large number of samples, thereby facilitating the rapid establishment of material databases. Currently developed and mature high-throughput preparation methods include: laser additive manufacturing[135-137], co-deposition with multiple targets[138,139] and diffusion multiples[140].
As shown in Figure 22, Li et al. used mixtures of Fe, Ni, Co, and pre-alloyed GH3230 powder in varying proportions as raw materials[137]. They efficiently prepared samples with different elemental contents and laser parameters using laser additive manufacturing technology. Combined with a deep learning algorithm, they quantitatively investigated the influence of different elements and process ratios on cracking behavior.
Figure 22. High-throughput laser additive manufacturing system and prepared samples schematic diagram[137].
As shown in Figure 23A, Zhuang et al. employed the diffusion multiples method[140]. Using a Co-30Ni-8Al-3W-3Ti-1Ta-12Cr alloy as the base, they designed 10 sets of diffusion couples. Gradient diffusion yielded 1,053 sets of microstructural data with varying compositions. Subsequently, applying this data to a ML model enabled the precise prediction of the relationship between γ′ precipitate morphology and properties. This work not only addressed the challenge of TCP phase precipitation in high-chromium alloys but also provided a “Materials Genome” paradigm for multi-component alloy design, significantly accelerating the development process of new alloys. Additionally, as shown in Figure 23B, Shishkovsky et al. utilized laser cladding to prepare layered titanium matrix composites by adding several different volume fractions of TiB2 to a titanium matrix[141].
However, in reality, considering the inherent complexity of HTE itself, along with the numerous differences in process parameters, instrumentation, and experimental standards across different countries and laboratories, it is difficult to guarantee the consistency of the data itself - it is a universal and normal phenomenon. Nevertheless, we can still adopt various methods to verify the accuracy of high-throughput datasets. For example, we can employ domain knowledge such as first-principles calculations to validate relevant data. We can also use ML models to examine the distribution and fitting of datasets, comparing them with previous work to check for obvious anomalies. Furthermore, given that superalloys are often applied in sensitive fields such as aerospace, data sharing across laboratories is hindered, and currently there is no unified global database. To further advance this technological approach, we need to make efforts in multiple directions including technical standardization and establishing international industry collaboration mechanisms.
In the future, First, autonomous laboratories and HTE technologies can rapidly screen different alloy compositions and process combinations through large-scale parallel testing, substantially shortening the R&D cycle. This enables ML to analyze massive datasets, uncovering relationships between composition, processing, and properties to optimize alloy design. Second, through feedback from autonomous laboratories, ML can perform adaptive design, automatically adjusting alloy compositions or process conditions. Additionally, the combination of autonomous laboratories and ML can significantly reduce the probability of human-induced experimental failures, thereby improving the accuracy and efficiency of data acquisition. This substantially reduces unnecessary testing and accelerates the R&D process. Furthermore, reducing manual operations and trial-and-error processes can effectively lower R&D costs.
CONCLUSIONS AND PERSPECTIVES
This review systematically summarizes recent advances in ML applications for Co-based superalloys. While these developments clearly demonstrate the remarkable progress of ML in this field, significant challenges identified in this review demand further resolution. Consequently, we will focus on future prospects for ML in the field of novel Co-based superalloys, incorporating personal perspectives.
HTE enables standardization of experimental benchmarks. Utilizing standardized processes and characterization parameters, it synthesizes and characterizes hundreds to thousands of samples with varying compositions or processing conditions within a short timeframe, generating massive volumes of “composition-processing-structure-property” data. Furthermore, by employing HTE techniques such as diffusion multiples and combinatorial material chips, it actively explores compositional domains traditionally overlooked in literature while incorporating “failed” specimens, thereby providing comprehensive learning samples for ML. Additionally, through automated HTE techniques such as TEM tomography and 3D EBSD, quantitative datasets on nano-scale γ′ precipitate distribution, grain boundary elemental segregation, and dislocation networks are generated. These datasets enable ML to establish microstructure-property models and achieve in-depth analysis of micromechanisms.
Therefore, future research on novel Co-based superalloys should focus on HTE + ML technologies by pursuing the following objectives:
(1) Establishing a unified superalloy database that integrates experimental data, computational results, and service performance records to enable data sharing and efficient utilization.
(2) Integrating multi-scale modeling methods such as molecular dynamics, phase-field simulations, and finite element analysis to achieve comprehensive prediction and optimization of the microstructure and macroscopic properties of novel Co-based superalloys.
(3) Developing intelligent HTE platforms to achieve full-process automation from sample preparation and property testing to data analysis.
(4) Implementing “in-situ high-temperature 3D characterization of HTE”: Combining synchrotron X-ray tomography (observing γ′ rafting) and TEM (capturing dislocation climb) to generate dynamic structural evolution video datasets for training models to study failure mechanisms.
Through these developmental goals, the integration of HTE and ML for novel Co-based superalloys will deliver more efficient and precise solutions for aerospace, energy, and other critical sectors, propelling continuous innovation and advancement in superalloy technology.
DECLARTIONS
Authors’ contributions
References collection, content analysis, and manuscript drafting: Luo, J.; Liu, X.
Project conceptualization, methodology, supervision, manuscript revision, and funding acquisition: Gao, Q.
Discussion of the results: Luo, J.; Ma, Q.; Liu, X.; Pei, C.; Yao, H.; Xiong, J.; Gao, Q.
Availability of data and materials
Not applicable.
Financial support and sponsorship
The grants and financial support from the National Natural Science Foundation of China (Grant Nos. 52471004, 52401015, 52201203), the Industry-University-Research Cooperation Project of Hebei Based Universities and Shijiazhuang City (Grant No. 241791237A) are gratefully acknowledged.
Conflicts of interest
All authors declared that there are no conflicts of interests.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2026.
REFERENCES
1. Feng, Q.; Nandy, T.; Tin, S.; Pollock, T. Solidification of high-refractory ruthenium-containing superalloys. Acta. Mater. 2003, 51, 269-84.
2. Suzuki, A.; Inui, H.; Pollock, T. M. L12-Strengthened cobalt-base superalloys. Annu. Rev. Mater. Res. 2015, 45, 345-68.
3. Sato, J.; Omori, T.; Oikawa, K.; Ohnuma, I.; Kainuma, R.; Ishida, K. Cobalt-base high-temperature alloys. Science 2006, 312, 90-1.
4. Pollock, T. M.; Dibbern, J.; Tsunekane, M.; Zhu, J.; Suzuki, A. New Co-based γ-γ′ high-temperature alloys. JOM 2010, 62, 58-63.
5. Makineni, S. K.; Singh, M. P.; Chattopadhyay, K. Low-density, high-temperature Co base superalloys. Annu. Rev. Mater. Res. 2021, 51, 187-208.
6. Suzuki, A.; Denolf, G. C.; Pollock, T. M. Flow stress anomalies in γ/γ′ two-phase Co–Al–W-base alloys. Scr. Mater. 2007, 56, 385-8.
7. Hart, G. L. W.; Mueller, T.; Toher, C.; Curtarolo, S. Machine learning for alloys. Nat. Rev. Mater. 2021, 6, 730-55.
8. Jordan, M. I.; Mitchell, T. M. Machine learning: trends, perspectives, and prospects. Science 2015, 349, 255-60.
9. Curtarolo, S.; Hart, G. L.; Nardelli, M. B.; Mingo, N.; Sanvito, S.; Levy, O. The high-throughput highway to computational materials design. Nat. Mater. 2013, 12, 191-201.
10. Kalidindi, S. R.; Medford, A. J.; Mcdowell, D. L. Vision for data and informatics in the future materials innovation ecosystem. JOM 2016, 68, 2126-37.
11. Probert, M. Electronic Structure: Basic Theory and Practical Methods, by Richard M. Martin: Scope: graduate level textbook. Level: theoretical materials scientists/condensed matter physicists/computational chemists. Contemp. Phys. 2011, 52, 77.
12. Agrawal, A.; Choudhary, A. Perspective: Materials informatics and big data: realization of the “fourth paradigm” of science in materials science. APL. Mater. 2016, 4, 053208.
13. Zhang, H.; Fu, H.; Zhu, S.; Yong, W.; Xie, J. Machine learning assisted composition effective design for precipitation strengthened copper alloys. Acta. Mater. 2021, 215, 117118.
14. Tabor, D. P.; Roch, L. M.; Saikin, S. K.; et al. Accelerating the discovery of materials for clean energy in the era of smart automation. Nat. Rev. Mater. 2018, 3, 5-20.
15. Chen, G.; Shen, Z.; Iyer, A.; et al. Machine-learning-assisted de novo design of organic molecules and polymers: opportunities and challenges. Polymers 2020, 12, 163.
16. Zhou, T.; Song, Z.; Sundmacher, K. Big data creates new opportunities for materials research: a review on methods and applications of machine learning for materials design. Engineering 2019, 5, 1017-26.
17. Decost, B. L.; Francis, T.; Holm, E. A. Exploring the microstructure manifold: image texture representations applied to ultrahigh carbon steel microstructures. Acta. Mater. 2017, 133, 30-40.
18. Zou, C.; Li, J.; Wang, W. Y.; et al. Integrating data mining and machine learning to discover high-strength ductile titanium alloys. Acta. Mater. 2021, 202, 211-21.
19. Xue, D.; Balachandran, P. V.; Hogden, J.; Theiler, J.; Xue, D.; Lookman, T. Accelerated search for materials with targeted properties by adaptive design. Nat. Commun. 2016, 7, 11241.
20. Xue, D.; Xue, D.; Yuan, R.; et al. An informatics approach to transformation temperatures of NiTi-based shape memory alloys. Acta. Mater. 2017, 125, 532-41.
21. Gopakumar, A. M.; Balachandran, P. V.; Xue, D.; Gubernatis, J. E.; Lookman, T. Multi-objective optimization for materials discovery via adaptive design. Sci. Rep. 2018, 8, 3738.
22. Menou, E.; Ramstein, G.; Bertrand, E.; Tancret, F. Multi-objective constrained design of nickel-base superalloys using data mining- and thermodynamics-driven genetic algorithms. Modelling. Simul. Mater. Sci. Eng. 2016, 24, 055001.
23. Tancret, F. Computational thermodynamics, Gaussian processes and genetic algorithms: combined tools to design new alloys. Modelling. Simul. Mater. Sci. Eng. 2013, 21, 045013.
24. Hu, X.; Wang, J.; Wang, Y.; et al. Two-way design of alloys for advanced ultra supercritical plants based on machine learning. Comput. Mater. Sci. 2018, 155, 331-9.
25. Chandran, M.; Lee, S. C.; Shim, J. Machine learning assisted first-principles calculation of multicomponent solid solutions: estimation of interface energy in Ni-based superalloys. Modelling. Simul. Mater. Sci. Eng. 2018, 26, 025010.
26. Liu, X.; Zhang, F.; Hou, Z.; et al. Self-supervised learning: generative or contrastive. IEEE. Trans. Knowl. Data. Eng. 2023, 35, 857-76.
27. Huang, L.; Zhang, C.; Zhang, H. Self-adaptive training: bridging supervised and self-supervised learning. IEEE. Trans. Pattern. Anal. Mach. Intell. 2024, 46, 1362-77.
28. Bröker, F.; Holt, L. L.; Roads, B. D.; Dayan, P.; Love, B. C. Demystifying unsupervised learning: how it helps and hurts. Trends. Cogn. Sci. 2024, 28, 974-86.
29. Pagan, D. C.; Phan, T. Q.; Weaver, J. S.; Benson, A. R.; Beaudoin, A. J. Unsupervised learning of dislocation motion. Acta. Mater. 2019, 181, 510-8.
32. van Buuren, S.; Groothuis-Oudshoorn, K. mice: Multivariate imputation by chained equations in R. J. Stat. Softw. 2011, 45, 1-67.
33. Hu, M.; Tan, Q.; Knibbe, R.; et al. Recent applications of machine learning in alloy design: a review. Mater. Sci. Eng. R. Rep. 2023, 155, 100746.
34. Benarioua, M.; Amroune, S.; Alshahrani, H.; et al. Statistical normalization of mechanical properties of natural date palm biofibers using the Box-Cox transformation. J. Nat. Fibers. 2025, 22, 2544176.
35. Probst, P.; Boulesteix, A. L.; Bischl, B. Tunability: importance of hyperparameters of machine learning algorithms. J. Mach. Learn. Res. 2019, 20, 1934-65.
36. Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281-305.
37. Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning (still) requires rethinking generalization. Commun. ACM. 2021, 64, 107-15.
38. Khoshvaght, H.; Permala, R. R.; Razmjou, A.; Khiadani, M. A critical review on selecting performance evaluation metrics for supervised machine learning models in wastewater quality prediction. J. Environ. Chem. Eng. 2025, 13, 119675.
39. Lundberg, S. M.; Lee, S. I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, USA. Curran Associates Inc.; 2017. pp. 4768-77.
40. Zhang, H.; Fu, H.; He, X.; et al. Dramatically enhanced combination of ultimate tensile strength and electric conductivity of alloys via machine learning screening. Acta. Mater. 2020, 200, 803-10.
41. Wen, C.; Zhang, Y.; Wang, C.; et al. Machine learning assisted design of high entropy alloys with desired property. Acta. Mater. 2019, 170, 109-17.
42. Xiong, J.; Zhang, T.; Shi, S. Machine learning of mechanical properties of steels. Sci. China. Technol. Sci. 2020, 63, 1247-55.
43. Guan, Z.; Tian, H.; Li, N.; Long, J.; Zhang, W.; Du, Y. High-accuracy reliability evaluation for the WC–Co-based cemented carbides assisted by machine learning. Ceram. Int. 2023, 49, 613-24.
44. Sun, L.; Cao, B.; Ma, Q.; et al. Machine learning-assisted composition design of W-free Co-based superalloys with high γ′-solvus temperature and low density. J. Mater. Res. Technol. 2024, 29, 656-67.
45. Wang, C.; Chen, X.; Chen, Y.; et al. Accelerated design of high γ′ solvus temperature and yield strength cobalt-based superalloy based on machine learning and phase diagram. Front. Mater. 2022, 9, 882955.
46. Chen, Y.; Wang, C.; Ruan, J.; et al. Development of low-density γ/γ′ Co–Al–Ta-based superalloys with high solvus temperature. Acta. Mater. 2020, 188, 652-64.
47. Chung, D.; Toinin, J. P.; Lass, E. A.; Seidman, D. N.; Dunand, D. C. Effects of Cr on the properties of multicomponent cobalt-based superalloys with ultra high γ’ volume fraction. J. Alloys. Compd. 2020, 832, 154790.
48. Li, W.; Li, L.; Wei, C.; Zhao, J.; Feng, Q. Effects of Ni, Cr and W on the microstructural stability of multicomponent CoNi-base superalloys studied using CALPHAD and diffusion-multiple approaches. J. Mater. Sci. Technol. 2021, 80, 139-49.
49. Llewelyn, S.; Christofidou, K.; Araullo-Peters, V.; et al. The effect of Ni:Co ratio on the elemental phase partitioning in γ-γ′ Ni-Co-Al-Ti-Cr alloys. Acta. Mater. 2017, 131, 296-304.
50. Yu, J.; Guo, S.; Chen, Y.; et al. A two-stage predicting model for γ′ solvus temperature of L12-strengthened Co-base superalloys based on machine learning. Intermetallics 2019, 110, 106466.
51. Liu, P.; Huang, H.; Antonov, S.; et al. Machine learning assisted design of γ′-strengthened Co-base superalloys with multi-performance optimization. npj. Comput. Mater. 2020, 6, 334.
52. Li, W.; Li, L.; Antonov, S.; Feng, Q. Effective design of a Co-Ni-Al-W-Ta-Ti alloy with high γ′ solvus temperature and microstructural stability using combined CALPHAD and experimental approaches. Mater. Design. 2019, 180, 107912.
53. Titus, M. S.; Suzuki, A.; Pollock, T. M. Creep and directional coarsening in single crystals of new γ–γ′ cobalt-base alloys. Scr. Mater. 2012, 66, 574-7.
54. Xue, C.; Yu, H.; Liu, C.; Peng, T.; Ji, P.; Fang, W. Effect of Co content on precipitation behavior of γ′ phase strengthened CoNi-based alloys. Mater. Today. Commun. 2024, 40, 109877.
55. Fan, Z.; Wang, X.; Yang, Y.; Chen, H.; Yang, Z.; Zhang, C. Plastic deformation behaviors and mechanical properties of advanced single crystalline CoNi-base superalloys. Mater. Sci. Eng. A. 2019, 748, 267-74.
56. Yu, J.; Wang, C.; Chen, Y.; Wang, C.; Liu, X. Accelerated design of L12-strengthened Co-base superalloys based on machine learning of experimental data. Mater. Design. 2020, 195, 108996.
57. Liu, X.; Cai, W.; Chen, Z.; et al. Effects of alloying additions on the microstructure, lattice misfit, and solvus temperature of a novel Co–Ni-based superalloy. Intermetallics 2022, 141, 107431.
58. Cao, B.; Kong, H.; Ding, Z.; et al. A novel L12-strengthened multicomponent Co-rich high-entropy alloy with both high γ′-solvus temperature and superior high-temperature strength. Scr. Mater. 2021, 199, 113826.
59. Ohl, B.; Dunand, D. C. Effects of Ni and Cr additions on γ + γ’ microstructure and mechanical properties of W-free Co–Al–V–Nb–Ta-based superalloys. Mater. Sci. Eng. A. 2022, 849, 143401.
60. Pandey, P.; Mukhopadhyay, S.; Srivastava, C.; Makineni, S. K.; Chattopadhyay, K. Development of new γ′-strengthened Co-based superalloys with low mass density, high solvus temperature and high temperature strength. Mater. Sci. Eng. A. 2020, 790, 139578.
61. Li, L.; Wang, C.; Chen, Y.; et al. Effect of Re on microstructure and mechanical properties of γ/γ′ Co-Ti-based superalloys. Intermetallics 2019, 115, 106612.
62. Pandey, P.; Shankar Prasad, A.; Baler, N.; Chattopadhyay, K. On the effect of Ti addition on microstructural evolution, precipitate coarsening kinetics and mechanical properties in a Co–30Ni–10Al–5Mo–2Nb alloy. Materialia 2021, 16, 101072.
63. Klein, L.; Bauer, A.; Neumeier, S.; Göken, M.; Virtanen, S. High temperature oxidation of γ/γ′-strengthened Co-base superalloys. Corros. Sci. 2011, 53, 2027-34.
64. Pei, C.; Ma, Q.; Gao, Q.; et al. A critical review on oxidation behavior of Co-based superalloys. Chin. J. Aeronaut. 2025, 38, 103380.
65. Berthod, P.; Gomis, J. Addition of Co in Ni(Cr)-based cast superalloys for tantalum carbide stabilisation: consequences on the behaviour in oxidation at elevated temperatures. Can. Metall. Q. 2021, 60, 172-82.
66. Kubacka, D.; Weiser, M.; Spiecker, E. Early stages of high-temperature oxidation of Ni- and Co-base model superalloys: a comparative study using rapid thermal annealing and advanced electron microscopy. Corros. Sci. 2021, 191, 109744.
67. Li, W.; Li, L.; Antonov, S.; Lu, F.; Feng, Q. Effects of Cr and Al/W ratio on the microstructural stability, oxidation property and γ′ phase nano-hardness of multi-component Co–Ni-base superalloys. J. Alloys. Compd. 2020, 826, 154182.
68. Chen, Z.; Okamoto, N. L.; Chikugo, K.; Inui, H. On the possibility of simultaneously achieving sufficient oxidation resistance and creep property at high temperatures exceeding 1000 °C in Co-based superalloys. J. Alloys. Compd. 2021, 858, 157724.
69. Bhattacharya, S. K.; Sahara, R.; Narushima, T. Predicting the parabolic rate constants of high-temperature oxidation of Ti alloys using machine learning. Oxid. Met. 2020, 94, 205-18.
70. Pillai, R.; Romedenne, M.; Peng, J.; et al. Lessons learned in employing data analytics to predict oxidation kinetics and spallation behavior of high-temperature NiCr-based alloys. Oxid. Met. 2022, 97, 51-76.
71. Pei, C.; Ma, Q.; Zhang, J.; et al. A novel model to predict oxidation behavior of superalloys based on machine learning. J. Mater. Sci. Technol. 2025, 235, 232-43.
72. Sato, A.; Chiu, Y.; Reed, R. Oxidation of nickel-based single-crystal superalloys for industrial gas turbine applications. Acta. Mater. 2011, 59, 225-40.
73. Wang, Y.; Tan, Y.; Liu, L.; Li, P.; Li, X. Oxidation behavior and mechanism of GH4975 superalloy prepared electron beam smelting between 900 °C and 1100 °C in air. Vacuum 2024, 219, 112752.
74. Neumeier, S.; Freund, L.; Göken, M. Novel wrought γ/γ′ cobalt base superalloys with high strength and improved oxidation resistance. Scr. Mater. 2015, 109, 104-7.
75. Shinagawa, K.; Omori, T.; Sato, J.; et al. Phase equilibria and microstructure on γ′ phase in Co-Ni-Al-W system. Mater. Trans. 2008, 49, 1474-9.
76. Forsik, S. A. J.; Polar Rosas, A. O.; Wang, T.; et al. High-temperature oxidation behavior of a novel Co-base superalloy. Metall. Mater. Trans. A. 2018, 49, 4058-69.
77. Ruan, J.; Xu, W.; Yang, T.; et al. Accelerated design of novel W-free high-strength Co-base superalloys with extremely wide γ/γ′ region by machine learning and CALPHAD methods. Acta. Mater. 2020, 186, 425-33.
78. Zhu, J.; Titus, M. S.; Pollock, T. M. Experimental investigation and thermodynamic modeling of the Co-rich region in the Co-Al-Ni-W quaternary system. J. Phase. Equilib. Diffus. 2014, 35, 595-611.
79. Zhuang, X.; Lu, S.; Li, L.; Feng, Q. Microstructures and properties of a novel γ′-strengthened multi-component CoNi-based wrought superalloy designed by CALPHAD method. Mater. Sci. Eng. A. 2020, 780, 139219.
80. Liang, Z.; Neumeier, S.; Rao, Z.; Göken, M.; Pyczak, F. CALPHAD informed design of multicomponent CoNiCr-based superalloys exhibiting large lattice misfit and high yield stress. Mater. Sci. Eng. A. 2022, 854, 143798.
81. Hillert, M. Diffusion and interface control of reactions in alloys. Metall. Trans. A. 1975, 6, 5-19.
82. Ruan, J.; Ueshima, N.; Oikawa, K. Growth behavior of the δ-Ni3Nb phase in superalloy 718 and modified KJMA modeling for the transformation-time-temperature diagram. J. Alloys. Compd. 2020, 814, 152289.
83. Andersson, J.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273-312.
84. Chen, R.; Li, E.; Zou, Y. A survey of energies from pure metals to multi-principal element alloys. J. Mater. Inf. 2024, 4, 26.
85. Khatavkar, N.; Swetlana, S.; Singh, A. K. Accelerated prediction of Vickers hardness of Co- and Ni-based superalloys from microstructure and composition using advanced image processing techniques and machine learning. Acta. Mater. 2020, 196, 295-303.
86. Niezgoda, S. R.; Yabansu, Y. C.; Kalidindi, S. R. Understanding and visualizing microstructure and microstructure variance as a stochastic process. Acta. Mater. 2011, 59, 6387-400.
87. Latypov, M. I.; Toth, L. S.; Kalidindi, S. R. Materials knowledge system for nonlinear composites. Comput. Methods. Appl. Mech. Eng. 2019, 346, 180-96.
88. Taylor, P. L.; Conduit, G. Machine learning predictions of superalloy microstructure. Comput. Mater. Sci. 2022, 201, 110916.
89. Xi, S.; Yu, J.; Bao, L.; et al. Predicting atomic structure and mechanical properties in quinary L12-Strengthened cobalt-based superalloys using machine learning-driven first-principles calculations. Mater. Today. Commun. 2024, 38, 107774.
90. Zhao, Y.; Zhang, Y.; Zhang, Y.; et al. Deformation behavior and creep properties of Co-Al-W-based superalloys: a review. Prog. Nat. Sci. Mater. Int. 2021, 31, 641-8.
91. Weller, L.; M’saoubi, R.; Giuliani, F.; Humphry-Baker, S.; Marquardt, K. Void formation driven by plastic strain partitioning during creep deformation of WC-Co. Int. J. Refract. Met. Hard. Mater. 2025, 126, 106950.
92. Lu, S.; Luo, Z.; Li, L.; Feng, Q. Comparison of creep mechanisms between Co-Al-W- and CoNi-based single crystal superalloys at low temperature and high stresses. Metall. Mater. Trans. A. 2023, 54, 1597-607.
93. Rae, C.; Reed, R. Primary creep in single crystal superalloys: origins, mechanisms and effects. Acta. Mater. 2007, 55, 1067-81.
94. Wu, R.; Sandfeld, S. Insights from a minimal model of dislocation-assisted rafting in single crystal Nickel-based superalloys. Scr. Mater. 2016, 123, 42-5.
95. Wu, R.; Zaiser, M.; Sandfeld, S. A continuum approach to combined γ/γ′ evolution and dislocation plasticity in Nickel-based superalloys. Int. J. Plast. 2017, 95, 142-62.
96. Wu, X.; Dlouhy, A.; Eggeler, Y.; et al. On the nucleation of planar faults during low temperature and high stress creep of single crystal Ni-base superalloys. Acta. Mater. 2018, 144, 642-55.
97. Wang, C.; Wei, X.; Ren, D.; Wang, X.; Xu, W. High-throughput map design of creep life in low-alloy steels by integrating machine learning with a genetic algorithm. Mater. Design. 2022, 213, 110326.
98. Wang, J.; Fa, Y.; Tian, Y.; Yu, X. A machine-learning approach to predict creep properties of Cr–Mo steel with time-temperature parameters. J. Mater. Res. Technol. 2021, 13, 635-50.
99. Zhang, X.; Gong, J.; Xuan, F. A deep learning based life prediction method for components under creep, fatigue and creep-fatigue conditions. Int. J. Fatigue. 2021, 148, 106236.
100. Dang, Y. Y.; Zhao, X. B.; Yuan, Y.; et al. Predicting long-term creep-rupture property of Inconel 740 and 740H. Mater. High. Temp. 2016, 33, 1-5.
101. Bolton, J. Reliable analysis and extrapolation of creep rupture data. Int. J. Press. Vessel. Pip. 2017, 157, 1-19.
102. Maclachlan, D.; Knowles, D. Modelling and prediction of the stress rupture behaviour of single crystal superalloys. Mater. Sci. Eng. A. 2001, 302, 275-85.
103. Feng, L.; Zhang, K.; Zhang, G.; Yu, H. Anisotropic damage model under continuum slip crystal plasticity theory for single crystals. Int. J. Solids. Struct. 2002, 39, 5279-93.
104. Prasad, S.; Rajagopal, K.; Rao, I. A continuum model for the anisotropic creep of single crystal nickel-based superalloys. Acta. Mater. 2006, 54, 1487-500.
105. Fedelich, B.; Epishin, A.; Link, T.; Klingelhöffer, H.; Künecke, G.; Portella, P. D. Experimental characterization and mechanical modeling of creep induced rafting in superalloys. Comput. Mater. Sci. 2012, 64, 2-6.
106. Kim, Y.; Kim, D.; Kim, H.; Oh, C.; Lee, B. An intermediate temperature creep model for Ni-based superalloys. Int. J. Plast. 2016, 79, 153-75.
107. Venkatesh, V.; Rack, H. J. A neural network approach to elevated temperature creep-fatigue life prediction. Int. J. Fatigue. 1999, 21, 225-34.
108. Tian, N.; Tian, S.; Yan, H.; Shu, D.; Zhang, S.; Zhao, G. Deformation mechanisms and analysis of a single crystal nickel-based superalloy during tensile at room temperature. Mater. Sci. Eng. A. 2019, 744, 154-62.
109. Eggeler, Y.; Müller, J.; Titus, M.; Suzuki, A.; Pollock, T.; Spiecker, E. Planar defect formation in the γ′ phase during high temperature creep in single crystal CoNi-base superalloys. Acta. Mater. 2016, 113, 335-49.
110. Titus, M. S.; Eggeler, Y. M.; Suzuki, A.; Pollock, T. M. Creep-induced planar defects in L12-containing Co- and CoNi-base single-crystal superalloys. Acta. Mater. 2015, 82, 530-9.
111. Zhou, H.; Li, L.; Antonov, S.; Feng, Q. Sub/micro-structural evolution of a Co–Al–W–Ta–Ti single crystal superalloy during creep at 900 °C and 420 MPa. Mater. Sci. Eng. A. 2020, 772, 138791.
112. Lu, S.; Antonov, S.; Li, L.; et al. Atomic structure and elemental segregation behavior of creep defects in a Co-Al-W-based single crystal superalloys under high temperature and low stress. Acta. Mater. 2020, 190, 16-28.
113. Liu, Y.; Wu, J.; Wang, Z.; et al. Predicting creep rupture life of Ni-based single crystal superalloys using divide-and-conquer approach based machine learning. Acta. Mater. 2020, 195, 454-67.
114. Royer, A.; Bastie, P.; Veron, M. In situ determination of γ′ phase volume fraction and of relations between lattice parameters and precipitate morphology in Ni-based single crystal superalloy. Acta. Mater. 1998, 46, 5357-68.
115. Kassner, M.; Pérez-Prado, M. Five-power-law creep in single phase metals and alloys. Prog. Mater. Sci. 2000, 45, 1-102.
116. Wu, R.; Zeng, L.; Fan, J.; Peng, Z.; Zhao, Y. Composition, heat treatment, microstructure and loading condition based machine learning prediction of creep life of superalloys. Mech. Mater. 2023, 187, 104819.
117. Qin, Q.; Zhang, Z.; Long, H.; Zhuo, J.; Li, Y. Prediction of creep properties of Co–10Al–9W superalloys with machine learning. J. Mater. Sci. 2024, 59, 4571-85.
118. Ohl, B.; Campbell, C.; Dunand, D. C. Machine-learning prediction of creep strain rate in γ/γ′ cobalt-based superalloys. Mater. Sci. Eng. A. 2025, 934, 148304.
119. Liu, Y.; Guo, B.; Zou, X.; Li, Y.; Shi, S. Machine learning assisted materials design and discovery for rechargeable batteries. Energy. Stor. Mater. 2020, 31, 434-50.
120. Liu, Y.; Wu, J.; Avdeev, M.; Shi, S. Multi-layer feature selection incorporating weighted score-based expert knowledge toward modeling materials with targeted properties. Adv. Theory. Simul. 2020, 3, 1900215.
121. Huang, Y.; Liu, J.; Zhu, C.; et al. An explainable machine learning model for superalloys creep life prediction coupling with physical metallurgy models and CALPHAD. Comput. Mater. Sci. 2023, 227, 112283.
122. Zhang, S.; Wang, L.; Zhu, S.; et al. Physics-informed neural network for creep-fatigue life prediction of Inconel 617 and interpretation of influencing factors. Mater. Design. 2024, 245, 113267.
123. Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686-707.
124. Zhu, S.; Xu, W.; Hong, D.; et al. Rare-earth metal complexes supported by 1,3-functionalized indolyl-based ligands for efficient hydrosilylation of alkenes. Inorg. Chem. 2023, 62, 381-91.
125. Wang, L.; Chen, Y.; Mei, X.; Qin, W.; Qin, X. Lightweight sign transformer framework. SIViP 2023, 17, 381-7.
126. Luo, J. H.; Li, B. Q.; Sun, L. L.; et al. Effect of Ti/Cr ratio on coarsening behavior of γ′ precipitates in novel Co-based superalloys. Chin. J. Nonferrous. Met. 2025, 35, 2673-89. (in Chinese).
127. Philippe, T.; Voorhees, P. Ostwald ripening in multicomponent alloys. Acta. Mater. 2013, 61, 4237-44.
128. Pandey, P.; Kashyap, S.; Palanisamy, D.; Sharma, A.; Chattopadhyay, K. On the high temperature coarsening kinetics of γ′ precipitates in a high strength Co37.6Ni35.4Al9.9Mo4.9Cr5.9Ta2.8Ti3.5 fcc-based high entropy alloy. Acta. Mater. 2019, 177, 82-95.
129. Ardell, A. J.; Ozolins, V. Trans-interface diffusion-controlled coarsening. Nat. Mater. 2005, 4, 309-16.
130. Sun, L.; Ma, Q.; Zhang, J.; et al. Identifying determinants of γ’ phase coarsening behavior in Co/CoNi-based superalloys with explainable artificial intelligence (XAI). J. Mater. Inf. 2024, 4, 30.
131. Gan, W.; Gao, H.; Wen, Z. Based on damage caused by microstructure evolution during long-term thermal exposure to analyze and predict creep behavior of Ni-based single crystal superalloy. AIP. Adv. 2020, 10, 085301.
132. Duan, X.; Xu, H.; Wang, E.; et al. Design of novel Ni-based superalloys with better oxidation resistance with the aid of machine learning. J. Mater. Sci. 2023, 58, 11100-14.
133. Liu, P.; Huang, H.; Wen, C.; Lookman, T.; Su, Y. The γ/γ′ microstructure in CoNiAlCr-based superalloys using triple-objective optimization. npj. Comput. Mater. 2023, 9, 1090.
134. Liu, P.; Huang, H.; Jiang, X.; et al. Evolution analysis of γ' precipitate coarsening in Co-based superalloys using kinetic theory and machine learning. Acta. Mater. 2022, 235, 118101.
135. Marshal, A.; Pradeep, K.; Music, D.; Zaefferer, S.; De, P.; Schneider, J. Combinatorial synthesis of high entropy alloys: introduction of a novel, single phase, body-centered-cubic FeMnCoCrAl solid solution. J. Alloys. Compd. 2017, 691, 683-9.
136. Hofmann, D. C.; Kolodziejska, J.; Roberts, S.; et al. Compositionally graded metals: a new frontier of additive manufacturing. J. Mater. Res. 2014, 29, 1899-910.
137. Li, X.; Hou, Y.; Cai, W.; et al. Study on crack behavior of GH3230 superalloy fabricated via high-throughput additive manufacturing. Materials 2024, 17, 4225.
138. Ludwig, A. Discovery of new materials using combinatorial synthesis and high-throughput characterization of thin-film materials libraries combined with computational methods. npj. Comput. Mater. 2019, 5, 205.
139. Li, M. X.; Sun, Y. T.; Wang, C.; et al. Data-driven discovery of a universal indicator for metallic glass forming ability. Nat. Mater. 2022, 21, 165-72.
140. Zhuang, X.; Antonov, S.; Li, W.; Lu, S.; Li, L.; Feng, Q. Alloying effects and effective alloy design of high-Cr CoNi-based superalloys via a high-throughput experiments and machine learning framework. Acta. Mater. 2023, 243, 118525.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data






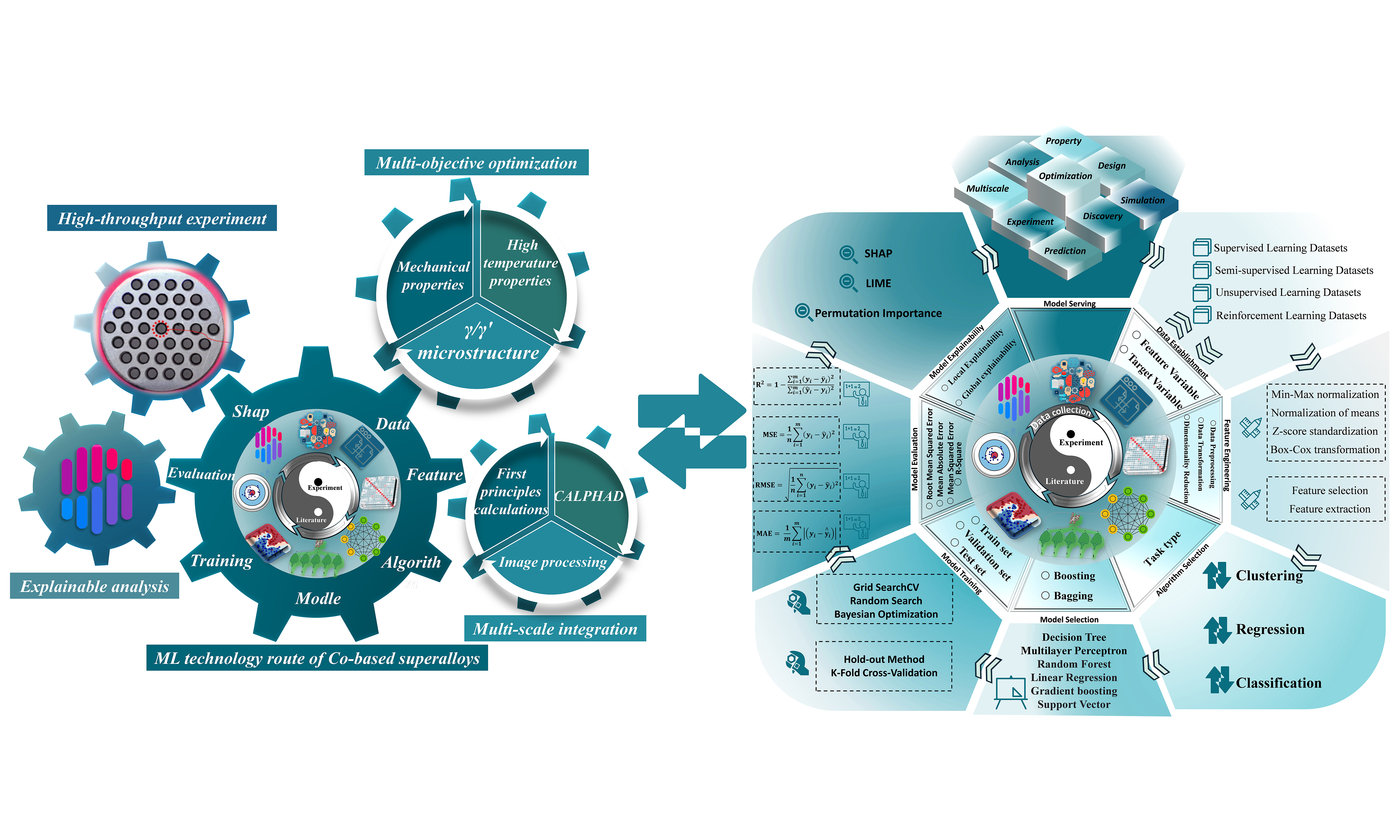
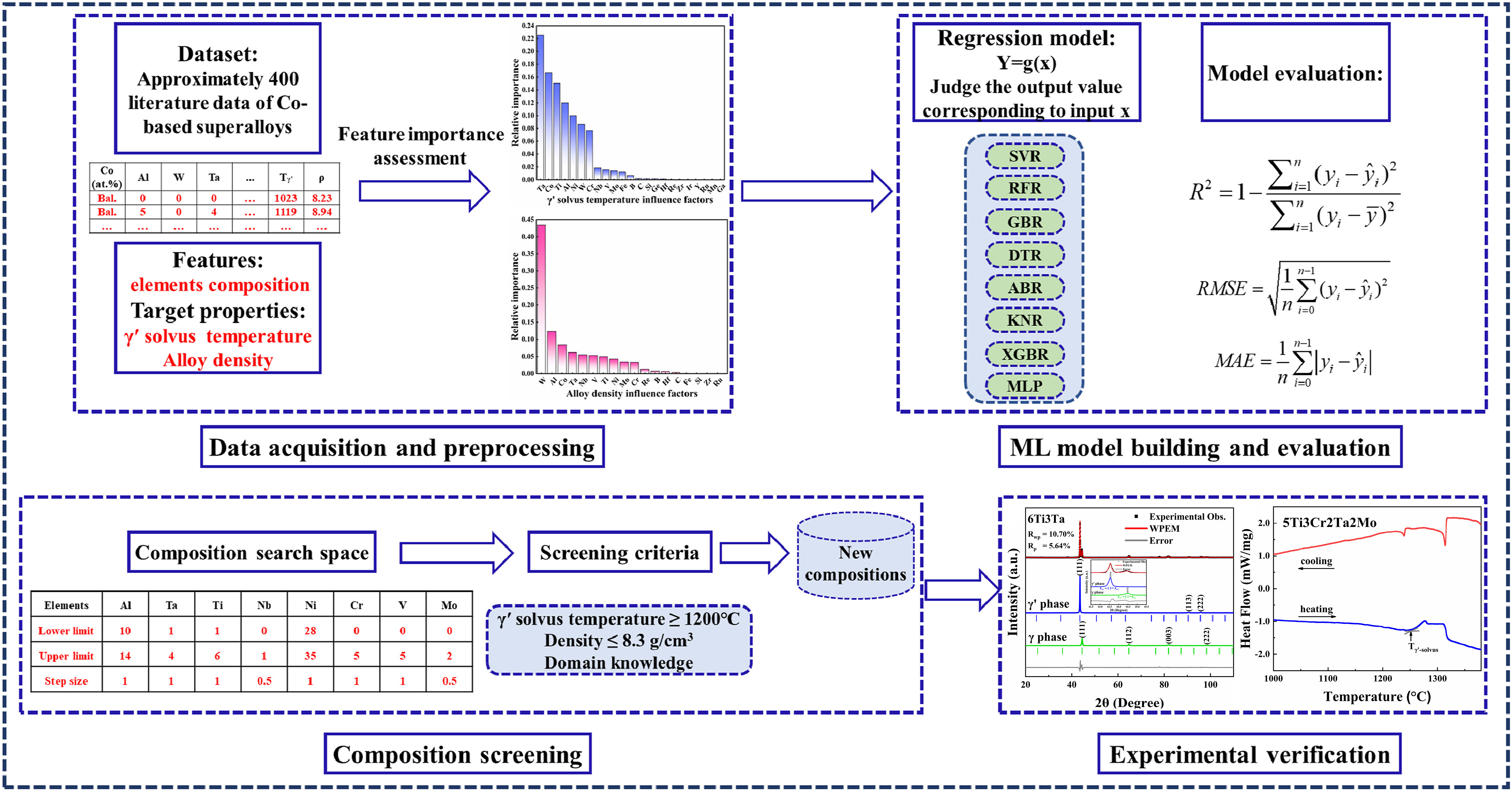
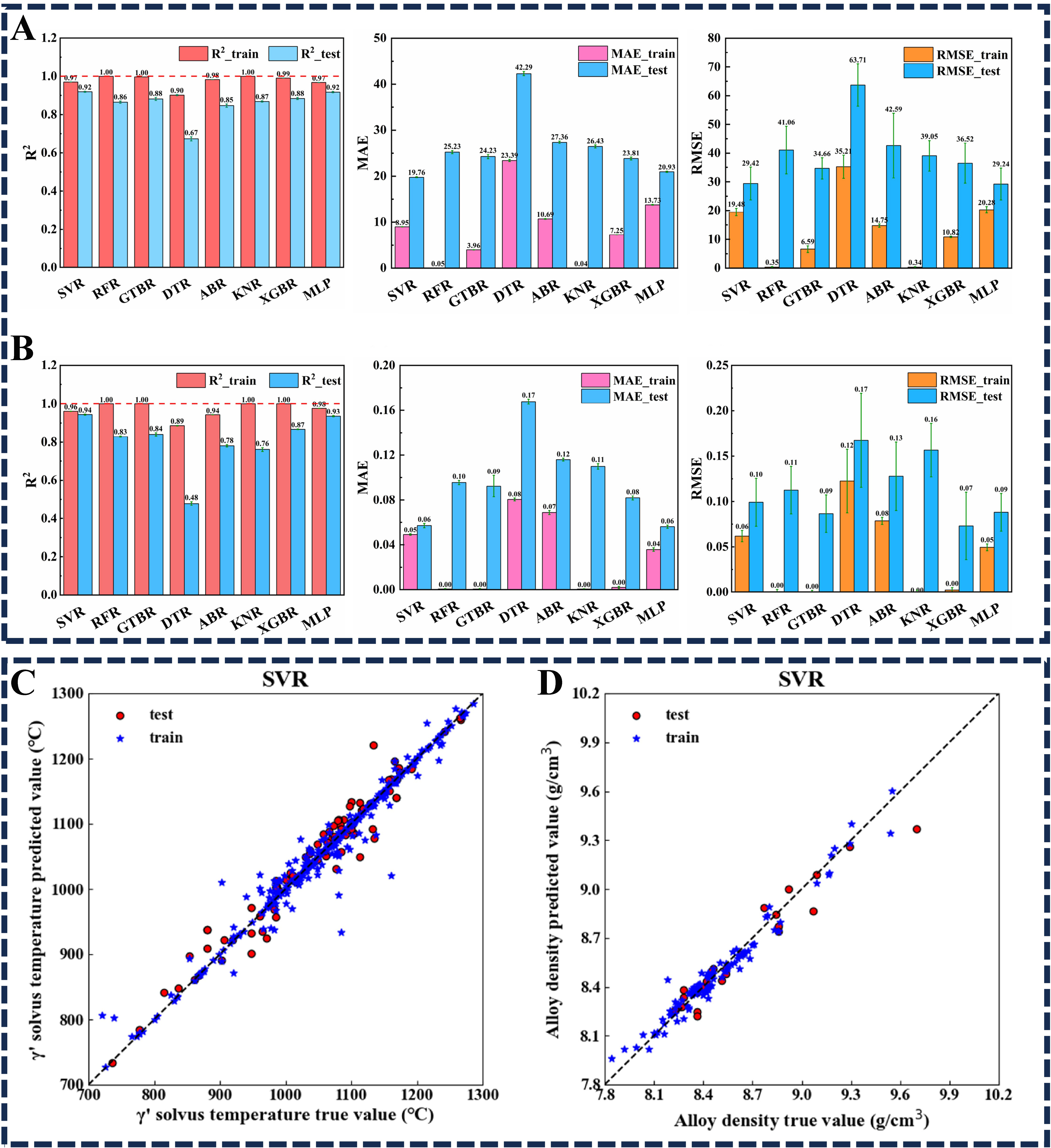
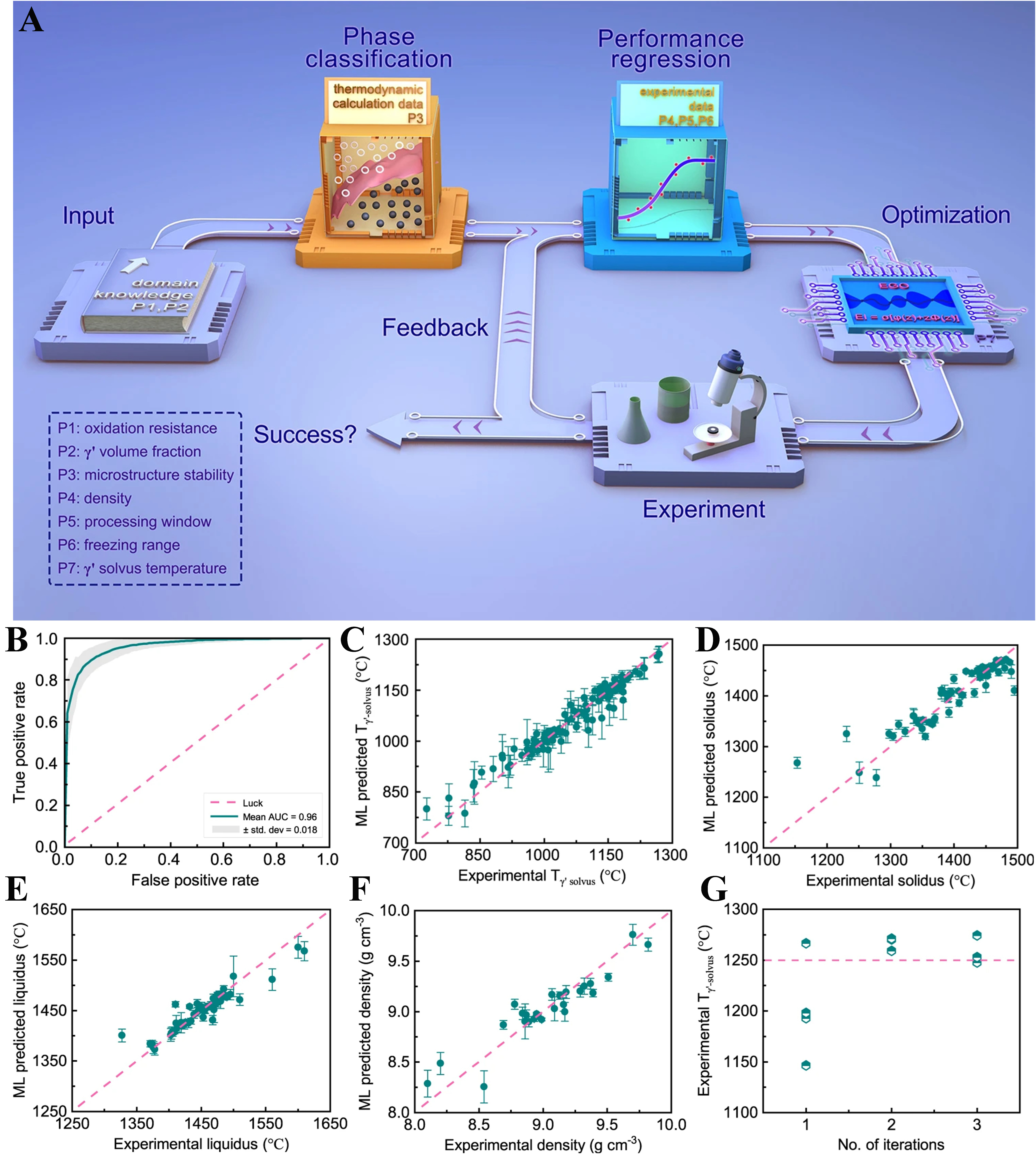
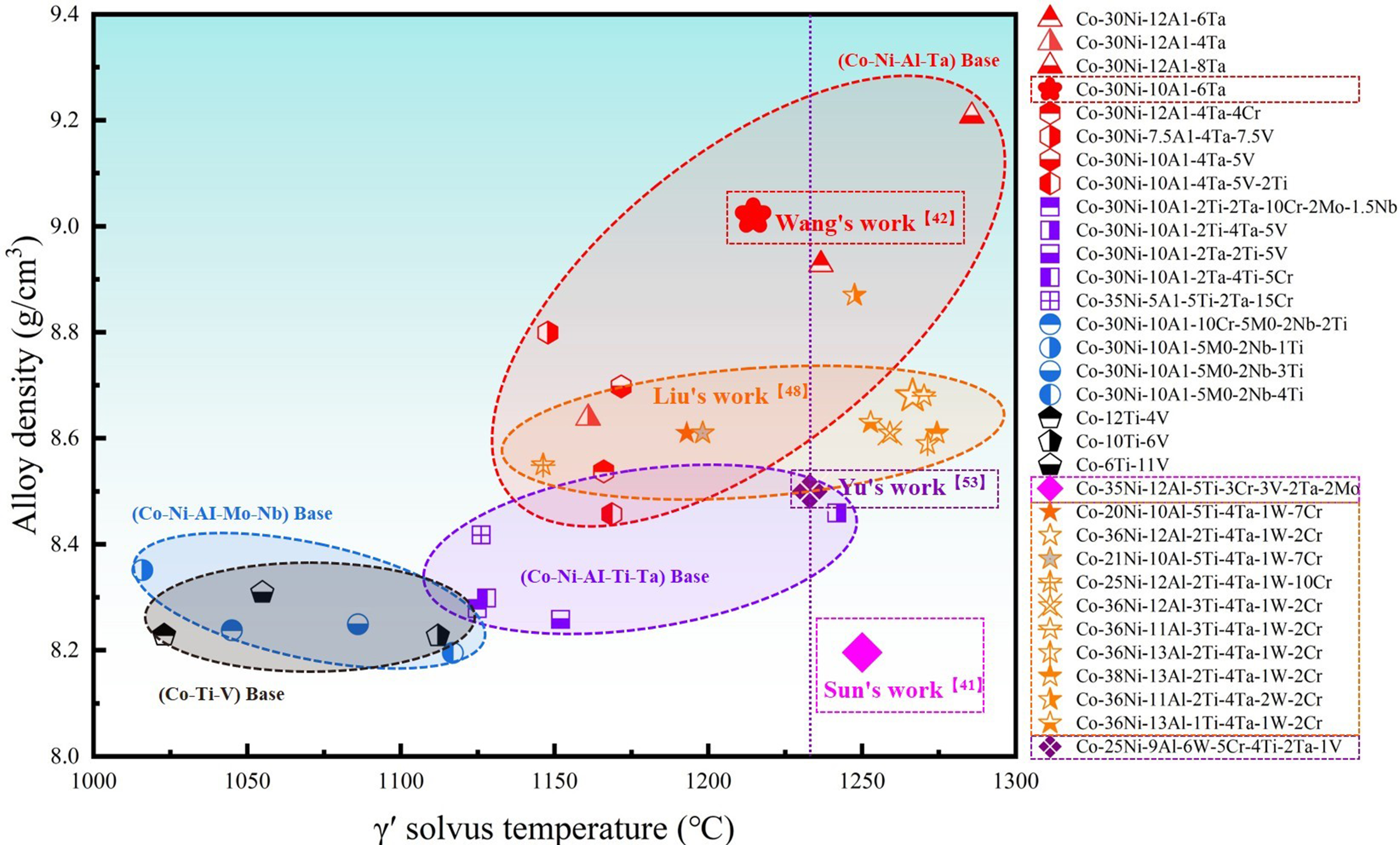
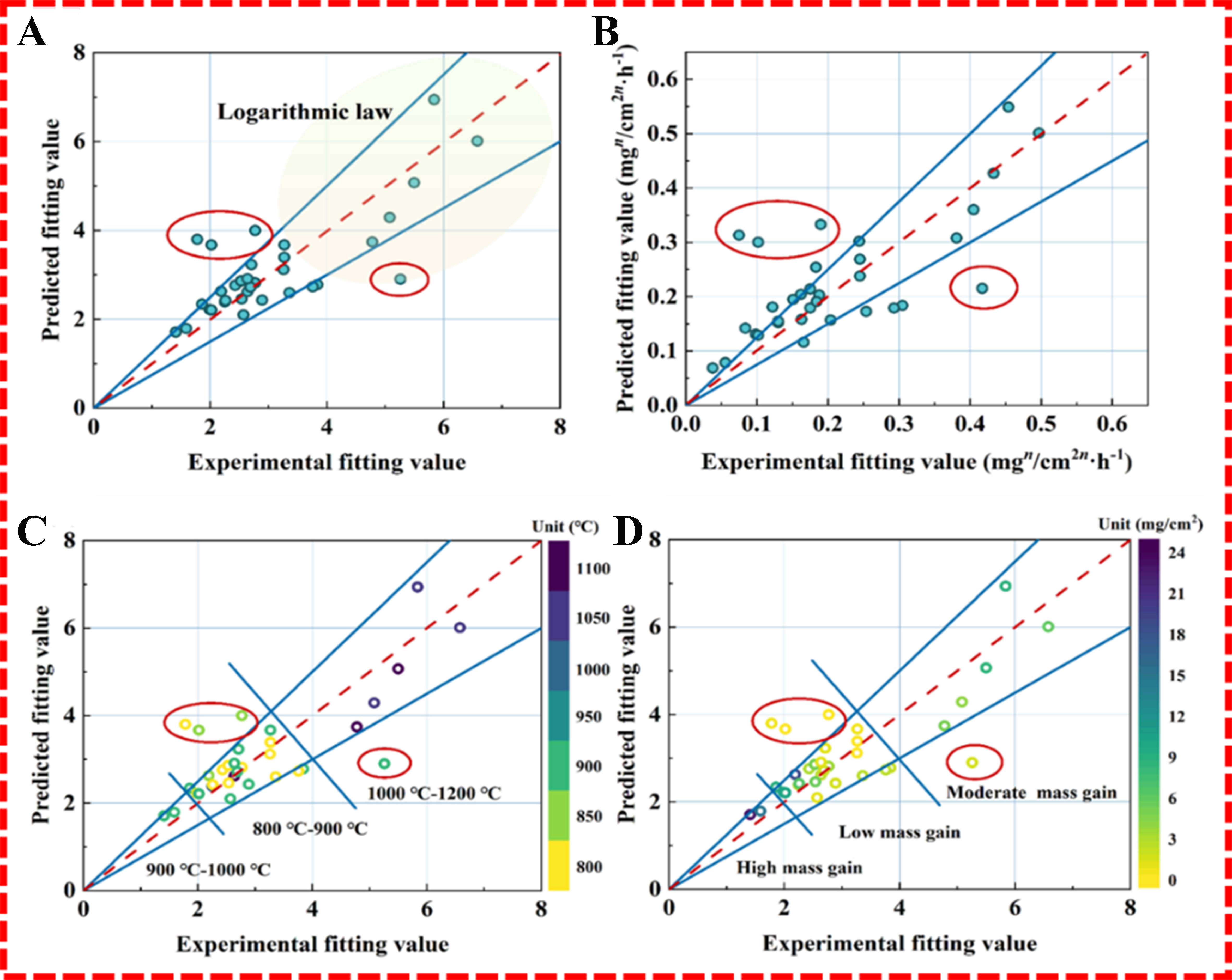
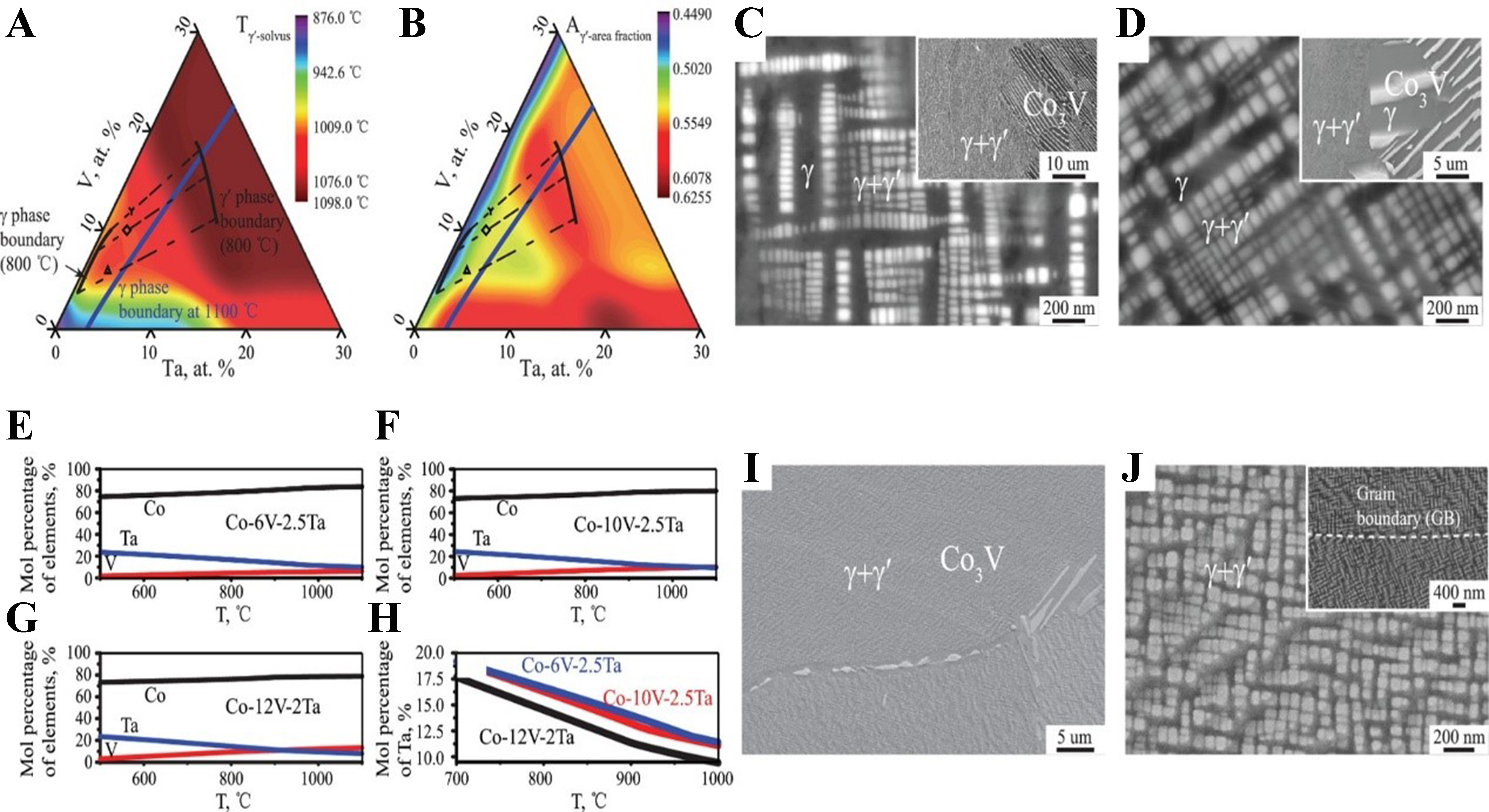
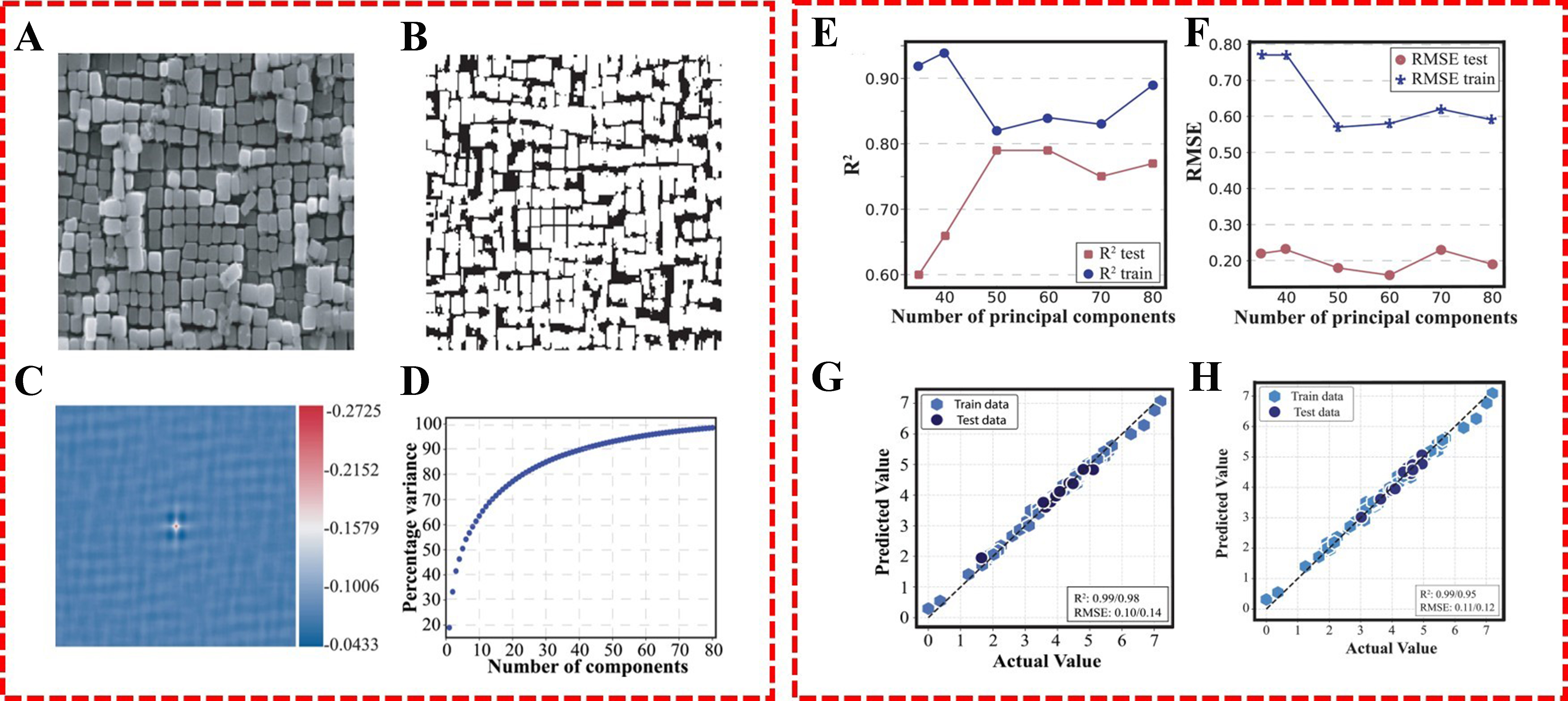
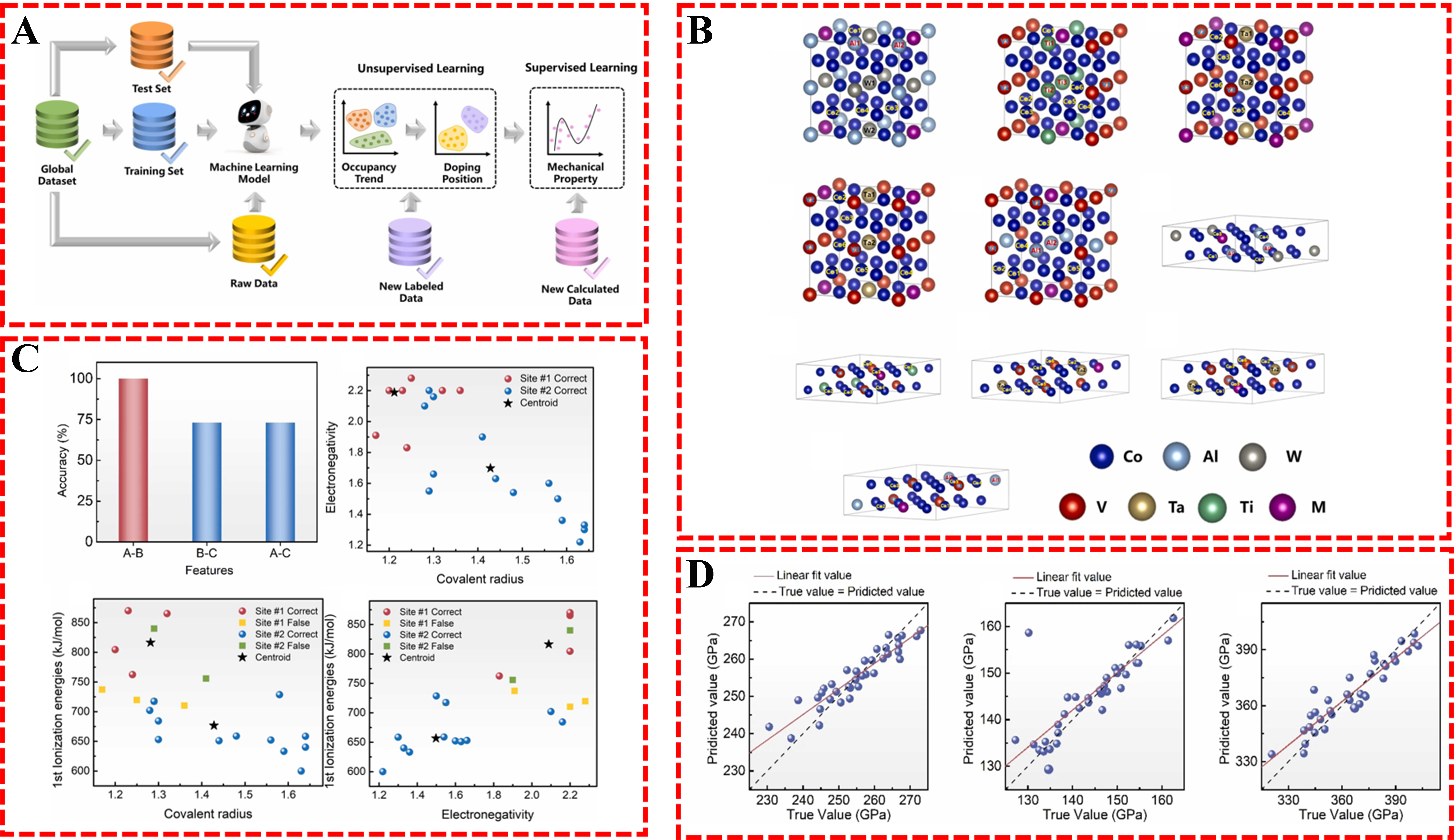
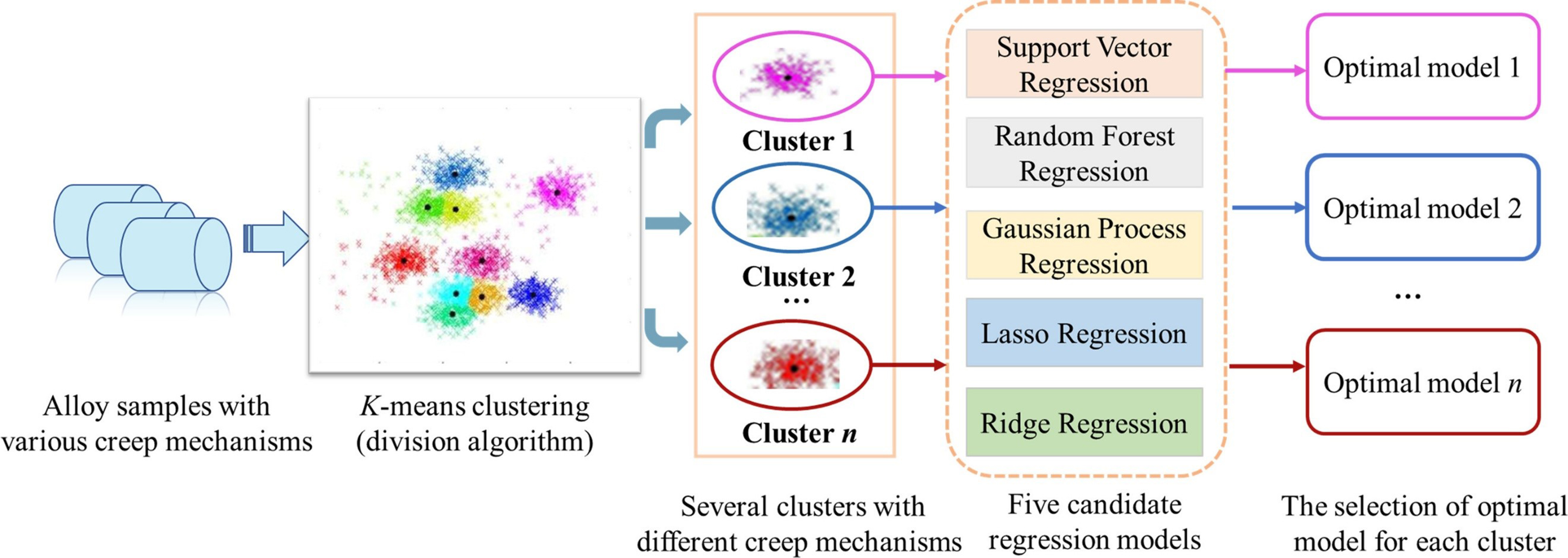
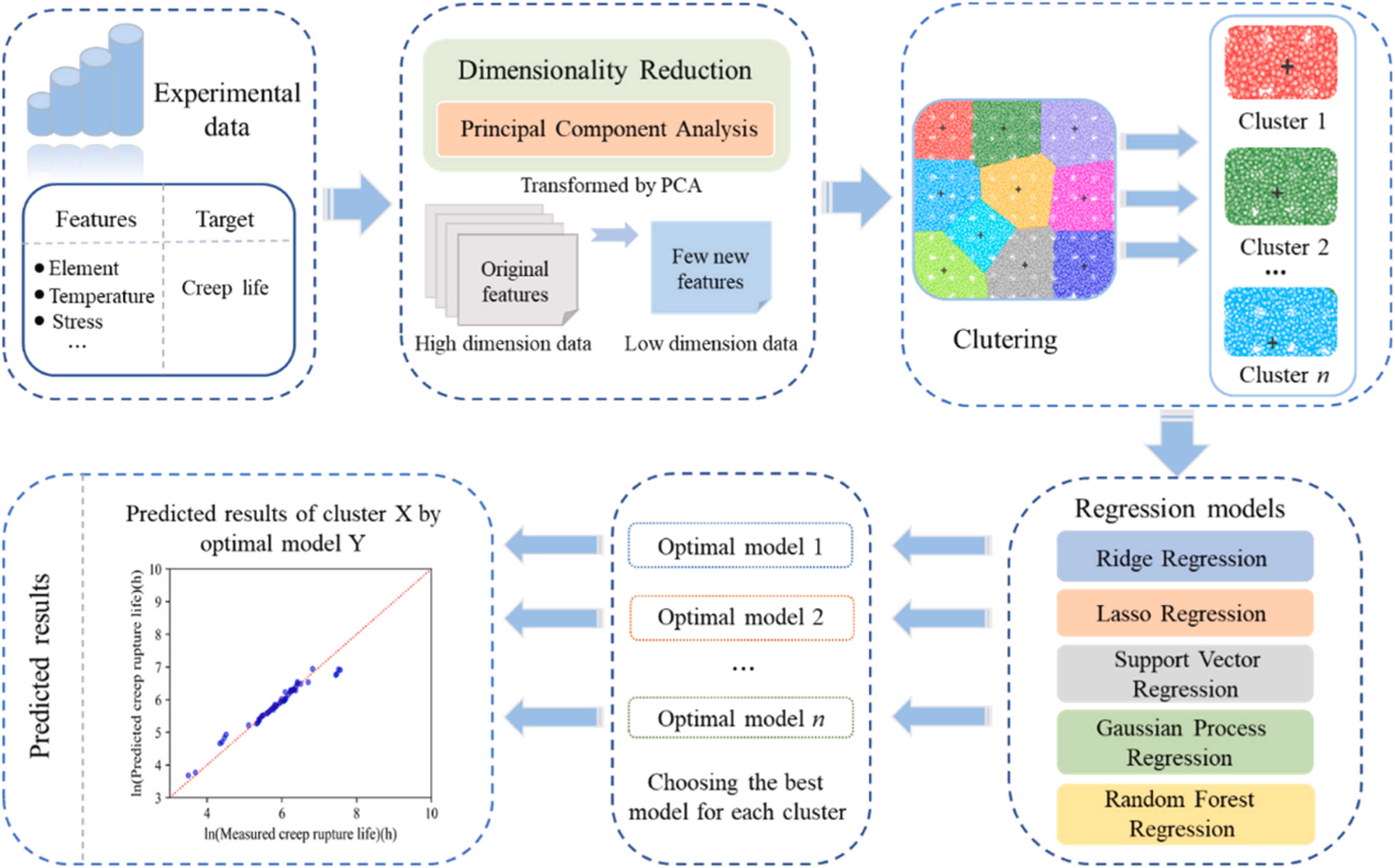
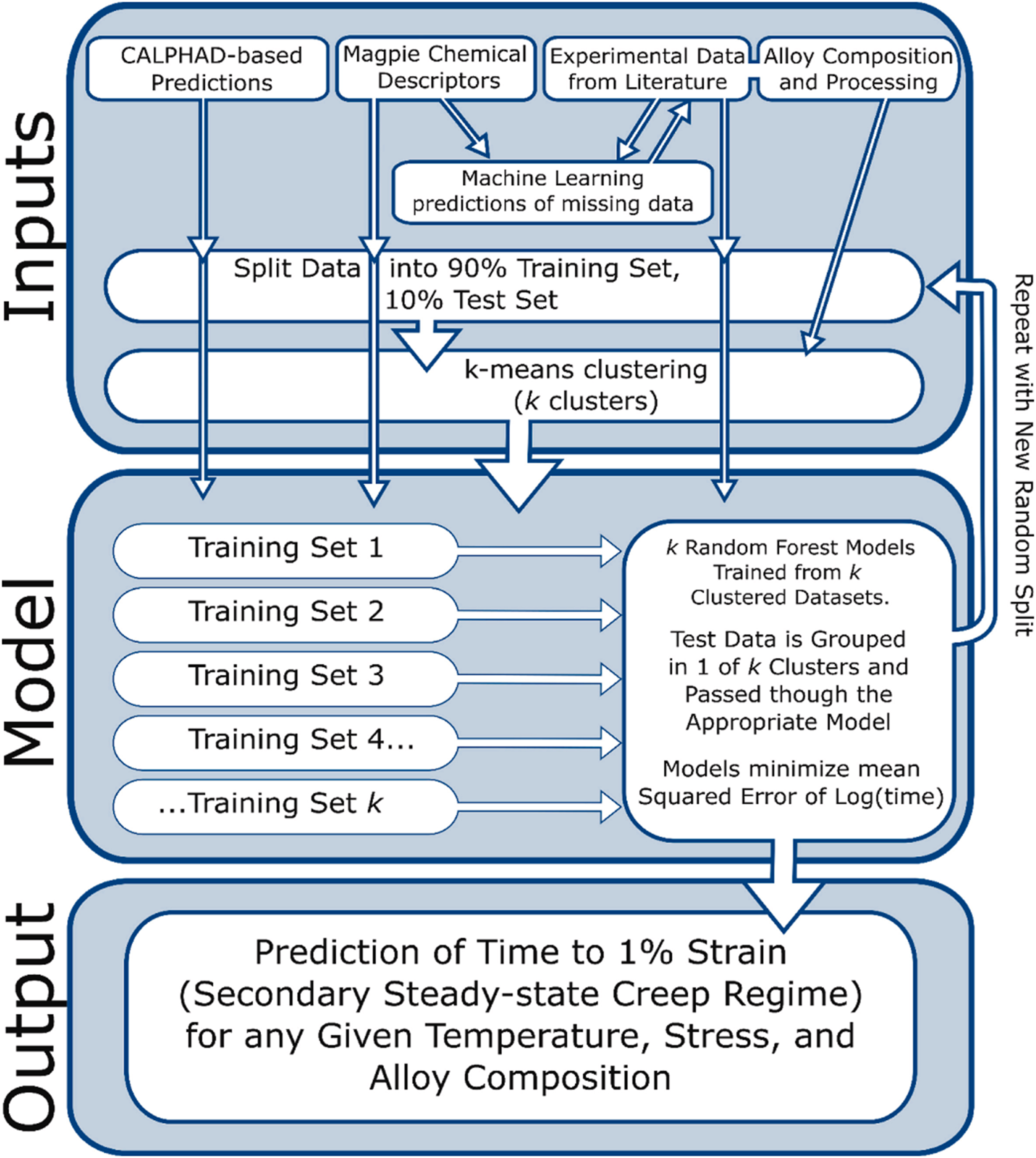
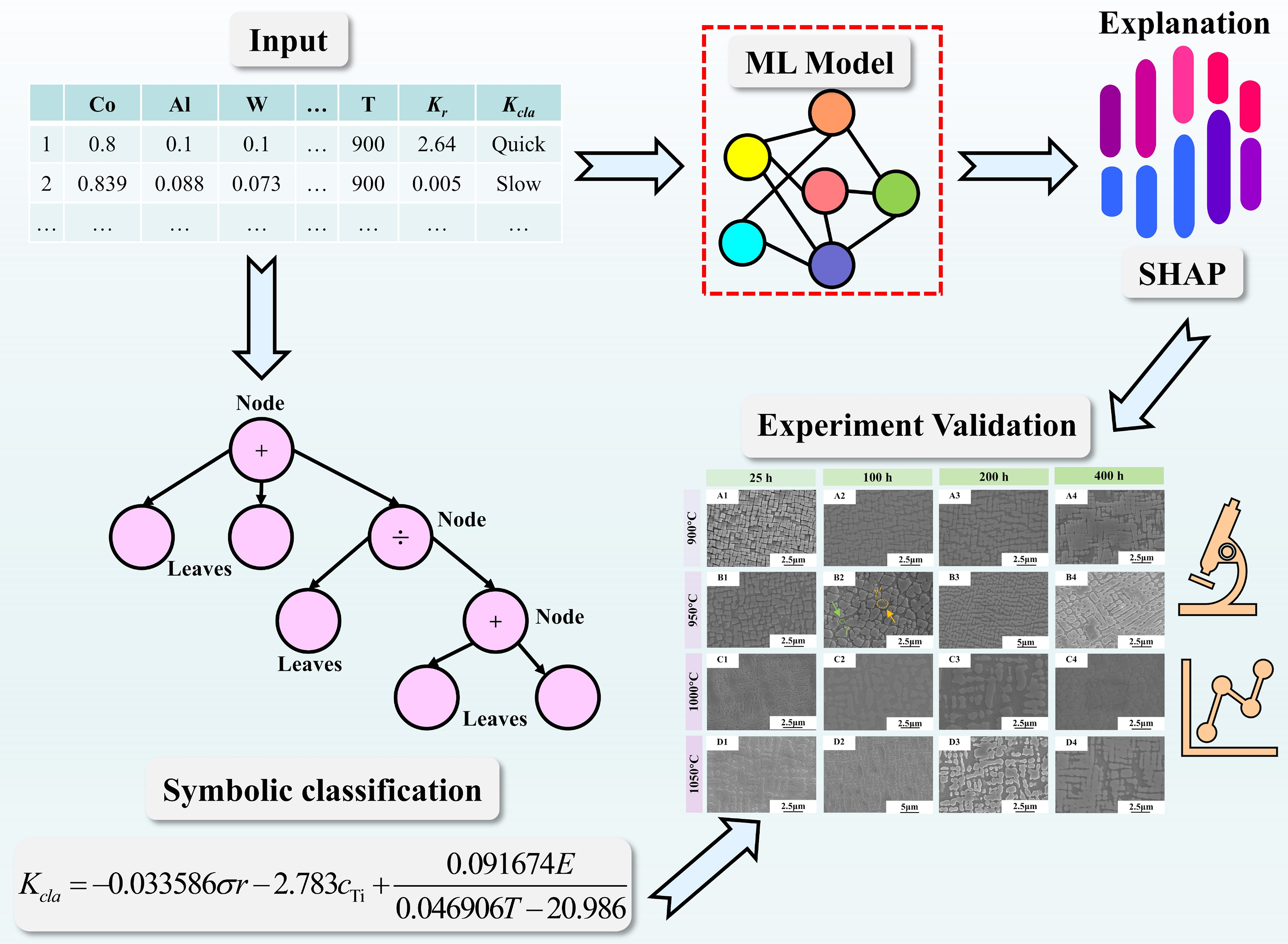
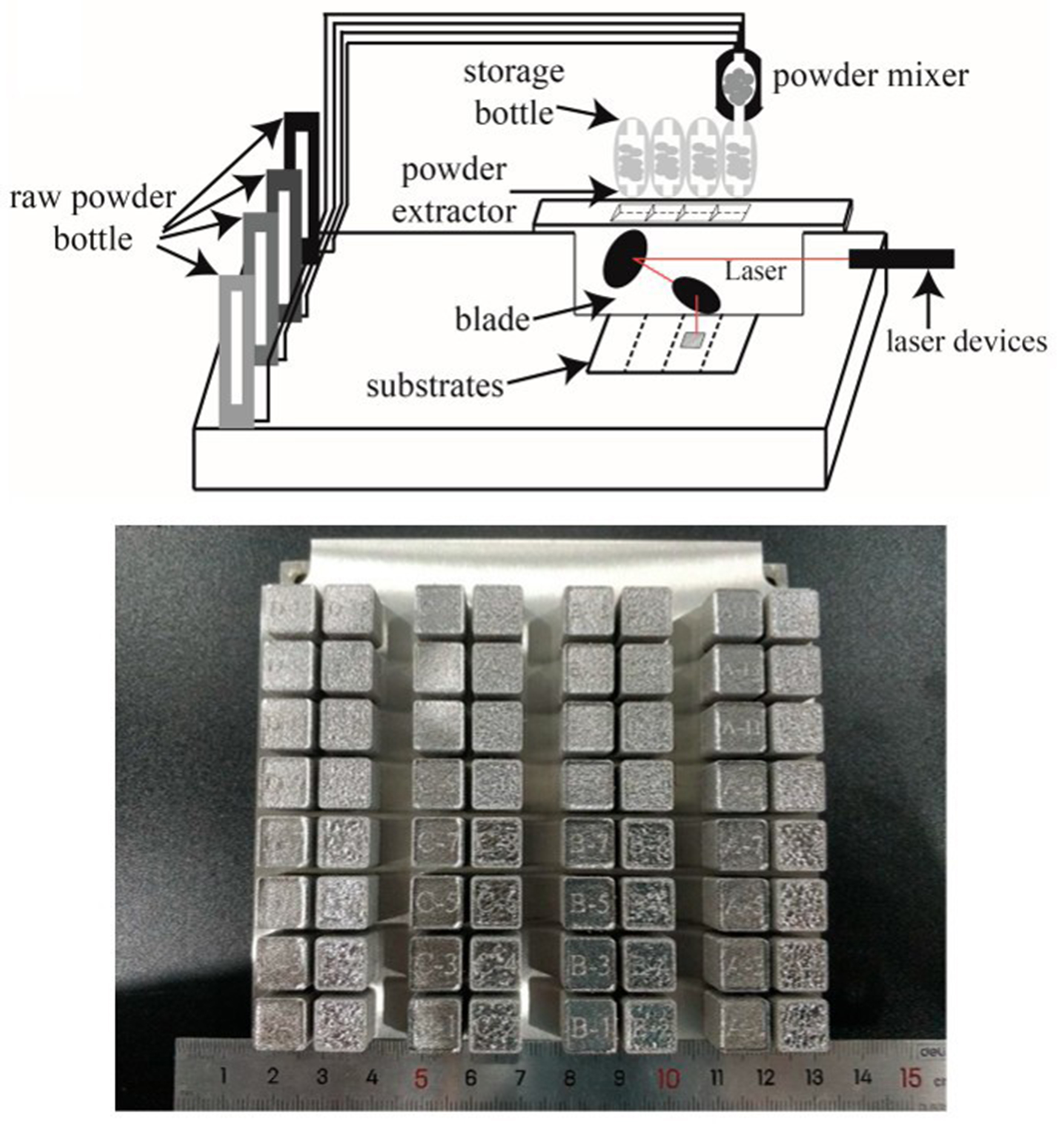
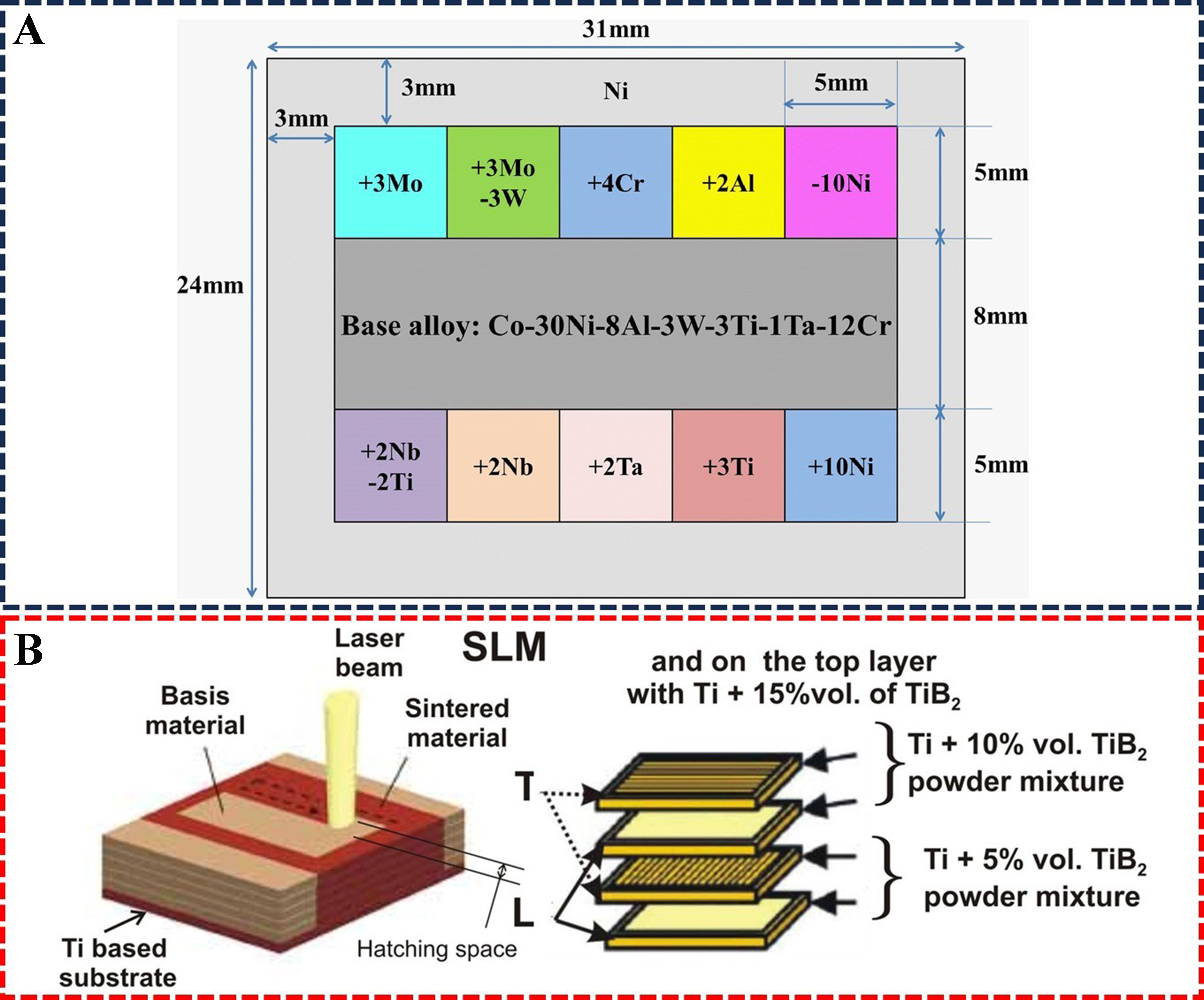











Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].