Morphing matter: from mechanical principles to robotic applications
Abstract
The adaptability of natural organisms in altering body shapes in response to the environment has inspired the development of artificial morphing matter. These materials encode the ability to transform their geometrical configurations in response to specific stimuli and have diverse applications in soft robotics, wearable electronics, and biomedical devices. However, achieving the morphing of intricate three-dimensional shapes from a two-dimensional flat state is challenging, as it requires manipulations of surface curvature in a controlled manner. In this review, we first summarize the mechanical principles extensively explored for realizing morphing matter, both at the material and structural levels. We then highlight its applications in the soft robotics field. Moreover, we offer insights into the open challenges and opportunities that this rapidly growing field faces. This review aims to inspire researchers to uncover innovative working principles and create multifunctional morphing matter for various engineering fields.
Keywords
INTRODUCTION
The remarkable adaptability of natural organisms fascinates us due to their ability to alter their body shapes in reaction to their environment[1-5]. Inspired by nature, artificial materials and structures that could change their geometrical configurations in response to specific stimuli, referred to as “morphing matter”, have been developed in diverse engineering fields, including soft robotics[4,6-10], wearable electronics[11-13], biomedical devices[14-16], etc.
While the morphing matter has demonstrated the potential to emulate the functionalities of living organisms and has made significant contributions across various engineering domains, attaining the ability for shape-morphing is not trivial[17,18]. The transformation from a two-dimensional (2D) flat sheet to intricate three-dimensional (3D) shapes requires a controlled manipulation of surface curvature[19-21]. Basic shape morphing forms (e.g., bending and rolling of flat sheets), which preserve the Gaussian curvature, can be achieved by leveraging the elasticity[22,23] and instabilities of materials and/or structures[24,25], such as strain-mismatch in bilayers and buckling of slender beams[21]. However, achieving more complex target shapes characterized by non-zero Gaussian curvature, such as spheres with positive curvature or hyperbolic shapes with negative curvature, requires approaches that generate localized extensional deformations of flat sheets[26,27]. To address this challenge, approaches based on origami/kirigami designs[28,29] and discrete element assemblies[30,31] have been exploited. Furthermore, inspiration has been drawn from the differential growth observed in plant morphogenesis, allowing for the programming of artificial materials to modify the surface metric tensor under external stimuli[32-36]. With a growing understanding of the mechanical principles governing shape morphing, the field of soft robotics is experiencing substantial benefits in its pursuit to replicate the remarkable adaptability seen in biological organisms[11,37-39].
In this review, we summarize recent developments in morphing matter, highlighting both the underlying mechanical principles and their applications in robotics. After providing an overview of the current challenges and methods for achieving morphing matter in the Introduction, we delve into the main mechanical principles utilized in morphing matter in Section “MECHANICAL PRINCIPLES UNDERLYING MORPHING MATTER”. These principles encompass strain-mismatch, instability, origami/kirigami, discrete elements, and morphogenesis. Section “MORPHING MATTER IN ROBOTIC APPLICATIONS” is dedicated to exploring the exciting applications of morphing matter in the field of robotics. Finally, we conclude with perspectives on potential future advancements and implications in Section “CONCLUSION AND OUTLOOK”.
MECHANICAL PRINCIPLES UNDERLYING MORPHING MATTER
Strain-mismatch
The intricate 3D deformation of a slender object can be decomposed into a combination of an in-plane stretching term and an out-of-plane bending term[40-43]. The out-of-plane bending is typically the consequence of a gradient in the planar stress distributed through the thickness of the material when subjected to a stimulus. Based on their dimensionality, slender bodies are commonly classified into beam elements and plate (shell) elements. One of the most straightforward strategies for creating morphing matter involves using a comparable bilayer composite with strain-mismatch between layers. To maintain the strain compatibility at the cohesive interface between the two layers upon activation, part of the composite is subjected to tension while the other undergoes compression. The curvature response of a bi-metal beam to changes in temperature can be studied using the Timoshenko beam theory[44]; the solution is directly proportional to the difference in the thermal expansion coefficients and inversely proportional to the thickness. Although this theory was initially derived from thermally activated metal strips, its general concept is also applicable to other responsive materials[45-47]. Various stimuli can be harnessed for activating these bi-layer structures, such as the swelling (or deswelling) of hydrogels[48], the evaporation or diffusion of polymer films[49,50], and light-induced extraction of liquid nematic elastomer[51], among others. An example is the use of bi-layer Polydimethylsiloxance (PDMS) films with inherent curvature[49], as illustrated in Figure 1A. The upper layer, containing controlled silicone oil, functions as the active layer when immersed in a chloroform bath due to the diffusion of the oil into organic solvents. After being left to dry at room temperature for several hours, the active layer tends to contract to restore its density. The mismatch in contraction between the top and bottom layers induces in-plane stress and bending moment in the film. Under the influence of the vertical gradient of the extraction strain, the film with a narrow width exhibits cylindrical deformation. The shape of the bilayer can be engineered through the manipulation of factors such as the volume fraction of the oil, the layer thickness, and the selective distribution of the active layer, enabling localized bending and alternative direction of out-of-plane deformation. Effective control of the interfaces within heterogeneous laminated systems is crucial for achieving the desired programmed configurations. To address this challenge, several strategies have been proposed to regulate interface bonding. These approaches encompass chemical surface modification[52-55] and the integration of surface microstructures[56,57]. Typical examples of application include electroadhesion and hierarchical cilia, both of which provide versatile pathways to facilitate the practical utilization of morphing matter.
Figure 1. Morphing matter based on strain-mismatch. (A) Bilayer PDMS films exhibiting inherent curvature. The top layer, containing silicone oil, undergoes drying and contraction, leading to bending behavior. The shape of the composite can be programmed through the selective patterning of the active layer. Reproduced with permission from[49]; Copyright 2016, The Royal Society of Chemistry; (B) Strain gradient induction via the peeling of plastic films. The interaction of peeling and adhesion force generates bending moments, and the plastic deformation can be precisely tailored by controlling peeling parameters and geometry. Reproduced with permission from[59]; Copyright 2022, Macmillan Publishers Limited; (C) Material gradient achieved by paraffin-diffused elastomer. Stretch-and-release procedures introduce residual strain in brittle paraffin crystals, while the elastomer tends to recover its initial shape. Reproduced with permission from[50]; Copyright 2022, Wiley-VCH; (D) The aspect ratio significantly influences deformation characteristics. Reducing the strip width within star polygons prevents the gripper from an axisymmetric cage-like configuration. Reproduced with permission from[64]; Copyright 2018, Wiley-VCH; (E) A network comprising multiplexed pairs of bilayer ribs yields a human face structure after swelling. Reproduced with permission from[66]; Copyright 2019, National Academy of Sciences, U.S.A; (F) Anisotropic strain-mismatch achieved by perpendicular shrinking of two layers results in a helical configuration with locally saddle geometry. Reproduced with permission from[67]; Copyright 2011, AAAS; (G) Programmed bilayer architectures demonstrating anisotropic swelling display complex 3D shapes of the underlying surface. Reproduced with permission from[46,68]; Copyright 2016, Macmillan Publishers Limited; (H) Radially curved ribbons, featuring geometrical frustration, assume bending or stretching-dominated configuration dependent on geometry. Reproduced with permission from[70]; Copyright 2021, American Physical Society; (I) An inverse design tool, utilizing hindered fabric contraction and bending of patterned ribbons, expands the range of achievable surfaces. Reproduced with permission from[72]; Copyright 2022, Wiley-VCH. PDMS: Polydimethylsiloxance.
The mechanism of inducing strain-mismatch in multi-layer composites can be extended to incorporate strain gradients within materials[58]. A commonly reported method for generating strain gradients along the thickness of films includes mechanically peeling plastic homogeneous materials[59] and utilizing external fields to activate graded material[50,60,61]. These methods mitigate delamination risks and streamline fabrication compared to laminated structures. Passive materials are inherently insensitive to external stimuli and resistant to configuration changes, while plastic yielding provides a clue for shape morphing[59] [Figure 1B]. Peeling adherent films from substrates can induce asymmetric plastic strains due to the interplay between peeling force and adhesion force. By carefully adjusting the peeling angle and deviation angle, precise control over the gradient of plastic strain and its orientation is achieved. This results in the transformation of the plastic film into intricate 3D shapes, such as curling, helices, and polygons. The method is versatile and applicable to plastic polymers, metals, and composite materials, thus enabling the creation of free-standing 3D electronics. Graded materials also find extensive use in creating morphing matter, with examples such as photocurable polymers[60], porous cationic poly membranes[61], and molecules diffused elastomers[50]. Photocurable polymers are exposed to specific wavelengths of light from one side, leading to a differential light absorption across the thickness and, consequently, an asymmetric cross-linking density in a swellable material[60]. Porous membranes are prepared by electrostatic complexation of an ionic solution coupled with the diffusion of ammonia into the membrane, promptly establishing a gradient cross-linking network instantly triggered by humidity[61]. Similar principles of diffusion are applicable to composite elastomers[50] [Figure 1C]. These elastomers are fabricated by immersing a soft elastomer film in a melted paraffin bath at high temperatures. Paraffin molecules diffuse into the elastomer, creating a concentration gradient along the thickness direction of the composite elastomer film, which is then locked in place by crystallization during cooling to room temperature. Stretch-and-release procedures introduce residual strains in brittle paraffin crystals while the elastomer recovers to its initial configuration. The geometrically programmed stretch-activated morphing behaviors can be achieved using patterned masks and reprogrammed with the assistance of the hexane solvent.
For isotropic slender structures, the response to mismatch strain has been elucidated through beam theory. Further research indicates that the aspect ratio (length to width ratio) significantly influences deformation characteristics[42,62,63]. Films with considerable aspect ratios approximate the surface of a sphere through a combination of bending and stretching deformation, eventually bifurcating into predominantly single curved shapes as strain increases[64,65]. Decreasing the strip width within star polygons results in axisymmetric cage-like configurations under significant mismatch strain, enabling the creation of self-folded grippers[64] [Figure 1D]. Tessellating beam elements into structured plane networks can markedly alter the linear growth factor, offering a method to design more complex shape-morphing structures by considering heterogeneous lattices as approximations of the underlying continuous surface profile[66]. Local metric tensor encoding is achieved by tailoring the bending deformation of ribs. Moreover, the extrinsic curvature necessitates multiplexed pairs of bilayers as ribs. By combining multiple materials and geometries, an inverse design strategy is presented to expand the range of achievable shapes, such as a complex human face constructed from swollen PDMS exposed to organic solvents [Figure 1E].
Anisotropic strain-mismatch is another programming strategy. This concept draws inspiration from the natural phenomenon of seed pods opening in Bauhinia variegate, and it involves investigating a mechanical analog comprised of stretched thin latex sheets to showcase the framework of incompatible elasticity[67] [Figure 1F]. When two layers are glued and shrink perpendicularly, the resulting composite tends to bend in two opposite directions, exhibiting locally saddle-shaped geometry. Notably, the initial flat sheet possesses zero Gaussian curvature, while the saddle configuration introduces non-zero Gaussian curvature. Consequently, residual stress is generated, causing the strip cut from the sheet to curl into helical configurations with reversible handedness, releasing stored elastic energy. The fabrication of bi-layer architectures with the abilities of anisotropic shrinking or swelling can be achieved through direct writing, offering precise control over mean and Gaussian curvatures in plane states by prescribing specific printing pathways[48,68]. The combination of patterns with simple geometry yields the complex shape of an orchid [Figure 1G]. Despite the ability of beam-based networks to approximate 3D shapes of the underlying surface upon activation, the creation of continuous double-curvature surfaces based on differential strain remains challenging. Emerging methodologies include the strategic placement of stretched or responsive ribbons/fibers onto passive sheets[69-71] and printed elastic ribbons on pre-stressed fabrics[72]. Typical examples involve the creation of helical shapes and complex 3D structures achieved through precise control of thermoplastic lines on stress-free films using extrusion shear printing[69,71]. The selective placement of these responsive lines can introduce geometrical frustrations[70,71], thereby enabling coarse-scale shape changes through different deformation mechanisms. For radially curved ribbons, the resulting shapes exhibit either bending-dominated toroidal configurations or stretching-dominated polygonal shapes composed of tubular regions and corners[70] [Figure 1H]. Computational design techniques for self-actuating deployable structures involve patterning ribbons on pre-stretched fabrics, leading to a wide range of versatile shapes[72] [Figure 1I]. The optimization of ribbon layouts inhibits fabric contraction, achieving the desired intrinsic curvature. Additionally, aligning the ribbons with the directions of principal extrinsic curvature helps resist torsion. This combination of the inverse design tool with the two shape-morphing effects paves the way for engineering applications.
Elastic instability
Elastic instability, encompassing phenomena such as buckling, wrinkling, and snapping, has undergone a paradigm shift from merely being avoided as a failure mode to being harnessed for the development of materials and devices with extreme properties and functionalities[73,74]. Structures comprising porous inclusions or flexible mechanisms experience substantial deformations, potentially surpassing the instability threshold when subjected to excessive external mechanical loading or multi-physical fields[42,75]. This rapid and profound transformation of structures can be effectively utilized in the design of morphing structures[21].
To construct reprogrammable one-dimensional (1D) morphing structures, an energy-efficient strategy has been proposed, leveraging the multistable unit cells inspired by drinking straws[76] [Figure 2A]. These unit cells can independently undergo deformation among deployed, retracted, and bent states. By combining optimized sequences of these units, complex 3D structures are demonstrated. Structures utilizing independent unit cells offer multiple configurations but come at the cost of distributed activation. To realize autonomous deployment, transition waves have emerged as a dependable method for switching bistable unit cells through a domino-like effect, achieved by carefully designing connectors[77,78]. By considering rigid bars joined at the ends with elastic next-nearest interactions using a stretched linear spring, stored potential energy in a flat configuration is sequentially released after a pulse is applied to one end, effectively exciting transition waves[79] [Figure 2B]. The behavior of these transitions can be easily controlled by adjusting spring stiffness and rest length. Combining bent configurations with opposite orientations generates curved profiles with inflection points, serving as the fundamental element for designing arbitrary 1D profiles.
Figure 2. Morphing matter based on elastic instabilities. (A) Reconfigurable flexible straws featuring stretched, compressed, and bent stable states. Through permutation and combination of these unit cells, the interconnected structure can present customized complex 2D and 3D configurations. Reproduced with permission from[76]; Copyright 2022, Elsevier Ltd; (B) Deployable linkages comprised of bistable joints support transition waves to trigger the curved configurations. Reproduced with permission from[79]; Copyright 2020, National Academy of Sciences, U.S.A; (C) Architected materials demonstrate a wide range of stable configurations through the use of bistable flexible mechanisms. The constituent triangular unit exhibits bistable behavior similar to symmetric inclined beams with fixed ends. By tessellating the beam elements in series or perpendicular directions, the multistable structures exhibit hysteresis under loading, enabling energy absorption. Reproduced with permission from[80]; Copyright 2022, Wiley-VCH; (D) Self-folding bistable elements comprised of an elastic layer bonded to a plate can assemble and transform into multimodal 3D structures under stepwise stretch-and-release procedures. Reproduced with permission from[81]; Copyright 2022, AAAS; (E) Multistable surfaces connected with 2D arranged snapping beams exhibit curved configurations in different directions resulting from displacements applied to the top plate and bistable units. Reproduced with permission from[83]; Copyright 2022, Elsevier Ltd; (F) Reconfigurable structures are constructed using novel multistable unit cells that combine elastic square frames with equi-biaxially pre-stretched soft membranes. Tuning the ratio of bending to torsional stiffness of anisotropic frames can control the number of multistable states. Applying out-of-plane force to intersection points of the grid causes the structure to snap into programmed states. Reproduced with permission from[84]; Copyright 2022, Wiley-VCH; (G) Snapping-induced morphing sheets with periodically tessellated spherical caps exhibit global curved states activated by popping individual shell elements. Hoop compression results in azimuthal buckling for single elements and introduces an interaction between snapping elements underlying the global curve shape. Reproduced with permission from[85]; Copyright 2023, Elsevier Ltd; (H) Inverse designed reconfigurable surfaces are discretized as Chebyshev nets. The discrete grid can change shape by the elongation or contraction of diagonal bistable units. Reproduced with permission from[86]; Copyright 2021, Elsevier Ltd; (I) Pixelated metamaterials with dense information embedded in programmed bistable kirigami-based units can be decoded sequentially by external stimuli such as stretching and temperature. Reproduced with permission from[87]; Copyright 2023, Wiley-VCH; (J) Complex 3D mesostructures with multiple layers of advanced materials popped up from releasable plane precursors via compressive buckling. Reproduced with permission from[89]; Copyright 2016, AAAS. FEM: Finite element method.
Extending snapping to the creation of multistable structures in 2D and 3D, the bistable unit cells can be assembled by the Cartesian tiling techniques[80] [Figure 2C]. The oblique beams within snapping triangular units collapse into closed configurations, while four hinge mechanisms tessellated in a diamond shape become a liner extension unit. By joining these linear unit cells in perpendicular planes, 3D extension units can be obtained. Periodic structures constructed with these flexible mechanisms exhibit rigged force-displacement responses and significant hysteresis, making them suitable for energy-absorbing applications. Materials with multimodal transformation properties often require fixed deformation sequences and complex actuation methods, such as biaxial experimental setups, which limit their practical use in real-world environments. To address this limitation and meet the demand for single-input actuation, an element is introduced, consisting of an elastic layer bonded to the plate with a bistable perforated joint[81] [Figure 2D]. The element can fold upon release after stretching due to the eccentric recovery force from the elastic membrane[82]. By combining bistable elements with distinct transition forces, programmed strips are created, allowing for multistep transformations into 2D or 3D shapes. To modify the encoded transformation pathways, responsive bistable elements are introduced, enabling the adjustment of transition forces and simplifying the recovery procedure. The integration of multistable elements into morphing surfaces offers significant advantages, particularly in the realm of tunable functionalities, such as adaptive optics[83] [Figure 2E]. This design strategy revolves around a compliant plate connected with independent snapping building blocks capable of flipping and altering the local height or curvature. The curved configuration of the surface can mimic various morphologies, including parallel states in diagonal directions, corrugated patterns, and irregular configurations. To predict snap-through transitions, an analytical model is developed to serve as guidance for manipulating stability by tuning geometric parameters.
A novel snapping element, combined with a pre-stretched membrane and an elastic boundary strip, is introduced to construct multistable structures capable of locomotion under selective inflatable actuation[84] [Figure 2F]. The stable state of snapping units is characterized by inflection points of carbon fiber composite strips, and stable behaviors are strongly influenced by the ratio of bending to torsional stiffness, which is dictated by the anisotropic properties of strips. The multistable states of the unit cell are preserved after tessellation, introducing a new stable state in unit cells capable of exhibiting a global cylinder configuration. When interactions between neighboring elements in a system are strong, the system can exhibit exceptionallly frustrated global deformation[85]. Silicone molds provide an interesting case for investigating elastic sheets integrated with multiple bistable hemispherical shells [Figure 2G]. The elastomer constituents are reversible under cyclic snapping, allowing for reprogrammable configurations. The dimpled sheet exhibits global deformations induced by the sequential popping of embedded elements. The bistability of a single element is primarily governed by the lateral size, and the global shape bifurcation can be controlled by modifying the tessellation lattice or lattice constants.
The inverse design of a planar sheet using snapping elements to deploy or transform into a target surface requires a basic unit cell to encode target surface information in material or geometry. A quadrilateral grid with deployable diagonal bonds is presented to overcome this challenge by modifying bond lengths to deform and feature the surface with positive or negative Gaussian curvature[86] [Figure 2H]. The inverse design procedure starts with using a Chebyshev net to mesh the target surface and then flattening the quadrilateral elements to a plane configuration by changing the interior angles of each element. Encoding the bond lengths of four diagonal beams in each element with the desired angle changes presents a design principle for physical bistable snapping specimens that can be fabricated using a multi-material printer. Pixelated metamaterials provide an alternative method to program dense target geometry information through decoupled multistable building blocks[87,88]. For example, different pixel heights, when subjected to a stretch-and-release procedure, result in responsive building blocks exhibiting specific deformation dependent on target heights stored in the geometry and materials of kirigami-based bistable units [Figure 2I]. By increasing the number of units in series, stored multiple layers of information can be displayed by sequential stimuli, including mechanical loading and temperature.
Elastic buckling of slender structures provides access to large, reversible deformations useful for designing morphing architectures. Buckled ribbons and plates exhibit out-of-plane mesostructures induced by contraction of elastomer support, playing an important role in fabricating flexible electronics[13,89]. Multilayered precursors enable complex shapes with stacking strategies and enhance functionalities [Figure 2J]. More inverse design strategies based on buckling assembly will be further illustrated in the next section concerning kirigami.
Origami and kirigami principles
Morphing into complex 3D structures with intricate curvature variations requires substantial distortion, posing challenges when working with rigid materials. To create intricate surface features that can be used with such rigid materials, researchers have turned to the old art forms of origami and kirigami[17]. These techniques involve folding and transforming planar sheets using crease and cut patterns, leading to the creation of 3D structures at both macro and micro scales. In the case of origami, deformations are primarily localized along the folding line, and rigid-foldable structures undergo continuous transformations without involving bending or stretching of the plates during the folding process. Although folding a flat sheet along crease lines does not alter the Gaussian curvature of the folded sheet, connecting multiple sheets through fold lines results in a global configuration exhibiting apparent Gaussian curvature. The geometric approach to achieving specific 3D profiles has attracted interest from multidisciplinary researchers, giving rise to the field of computational origami, which combines mathematics, algorithms, and manufacturing techniques[90]. Various approaches have been developed to approximate complex configurations, such as crease pattern tessellation[91-94] and origami tube assembly[92,95,96].
To control the apparent curvature of the target surface, a freeform tessellation is built based on Resch’s patterns with folded tucks[94]. The strategy generates plane patterns from a given polyhedral surface represented as triangular mesh and then optimizes the pattern to avoid the interactions between neighboring patterns using a penalty function. Consequently, the plane sheet could change its global Gaussian curvature without bending and stretching facets through the implementation of tucks within the Resch pattern. However, the approximated curved surfaces are mainly limited to surfaces with positive Gaussian curvature because saddle shapes might involve some crease bending and facet distortion that obstruct smooth, rigid folding. Early studies mainly focus on folding flat sheets to achieve specific 3D shapes. Subsequent research has indicated that deploying a predefined origami tessellation from a fully folded 2D state can also produce intricate configurations[91] [Figure 3A]. The development of explicit finite particle methods and optimization techniques for adjusting the neutral angles of the triangular Resch pattern across various locations provide potential for inverse designing. The Miura-ori pattern, akin to the spontaneous wrinkling of stiff films on soft bulk substrates subjected to biaxial compression, has been extensively studied. A generalized Miura-ori pattern is proposed to approximate folded complex surfaces, considering flat-foldability conditions and the bending energy of facets[92] [Figure 3B]. The optimized pattern tessellation indicates that both the flat state and the folded state of intrinsically curved surfaces are energetically preferable, and the barrier between these states is reduced when the flat-foldability residual is minimized. Furthermore, the refinement of the pattern allows for an approach to the target surface with a trade-off between accuracy and effort.
Figure 3. Morphing matter based on origami and kirigami. (A) An origami tessellation based on Resch’s patterns is showcased, optimizing the developable pattern while eliminating local collisions. Reproduced with permission from[91]; Copyright 2023, Elsevier Ltd; (B) A Generalized Miura-ori obtained from constrained optimization algorithms exhibits surfaces with negative, positive, and mixed Gauss curvature, aligning well with manually folded physical paper. Reproduced with permission from[92]; Copyright 2022, Macmillan Publishers Limited; (C) Magnetic Kresling units capable of folding/deploying and ominidirectional bending are interconnected with a robotic arm, displaying multimodal behaviors under rotating magnetic fields. Reproduced with permission from[100]; Copyright 2022, National Academy of Sciences, U.S.A; (D) Nonperiodic modular origami structures are proposed for volumetric 3D spatial curvilinear geometries. Reproduced with permission from[95]; Copyright 2022, Macmillan Publishers Limited; (E) Reconfigurable kirigami with optimized quadrilateral tiles can morph from an initial compact configuration to a customized deployed state and finally to another compact configuration. Reproduced with permission from[105]; Copyright 2021, American Physical Society; (F) A computational wrapping method enables nonstretchable and even brittle materials to conform to curved surfaces. Reproduced with permission from[106]; Copyright 2020, AAAS; (G) A quad kirigami tessellation is extended to fit curved surfaces with complex Gaussian curvature. Reproduced with permission from[107]; Copyright 2019, Macmillan Publishers Limited; (H) Auxetic kirigami sheets, comprising spatial varying motifs, exhibit stable morphing surfaces with optimized compressive stiffness. Reproduced with permission from[111]; Copyright 2021, Association for Computing Machinery; (I) Elastic tapered patterns are cut from a sheet to form axisymmetric structures with programmed profiles under compressive load at their edges. Reproduced with permission from[112]; Copyright 2020, The Royal Society of Chemistry; (J) Perforated kirigami exhibits a programmed apple-shaped structure with potential applications in grippers or packaging. Reproduced with permission from[114]; Copyright 2022, Elsevier Ltd; (K) A Cellular triangular microlattice design strategy is presented to reconstruct biomimetic surfaces resembling the blueberry flower. Reproduced with permission from[115]; Copyright 2023, AAAS; (L) Functionally graded composites using multi-materials voxel-based 3D printing are employed to constitute the divided elastic strip for morphing structures. Reproduced with permission from[116]; Copyright 2023, Elsevier Ltd.
Beyond flat origami structures such as Resech’s patterns[91,94], Miura-ori[92], and waterbomb[97], the Kresling origami has garnered significant interest[98,99]. This foldable tubular structure, featuring crease patterns reminiscent of the buckling of thin shell cylinders, offers multiple degrees of freedom for deployment and bending. An origami robotic arm, composed of a series of Kresling units and magnetic panels, has been developed, showcasing various deformation modes resembling octopus arms[100] [Figure 3C]. This robotic arm can execute grasp and manipulation tasks under remote magnetic fields. The scale-independent and untethered design of this approach presents potential applications in miniaturized medical devices, such as endoscopy and catheterization procedures. Stacking basic foldable modules is an effective method for constructing volumetric 3D structures[96]. However, periodic tessellation using constant building blocks poses limitations on 3D geometries, particularly those with curved edges. To address this challenge and enable the inverse design of architected structures with curvilinear geometries, a modular origami strategy known as geometric and topological reconstruction has been proposed[95] [Figure 3D]. The synthesis process starts with selecting a unit cell composed of polyhedrons, followed by the presentation of a nonperiodic tessellation aimed at defining the curvilinear geometry using an optimum transport algorithm. Origami structures are then constructed by spatially shrinking and extruding prismatic tubes inside the template. The geometric modification procedure allows these origami structures to have reconfigurable motion through the application of foldable constraints for the extruded tubes. This top-down approach significantly expands the design space of 3D geometries of origami structures. It is noteworthy that creases play important roles in the folding and unfolding behaviors of origami structures. However, they may also lead to undesirable stress concentrations and uncertain plastic deformation states, which can be highly detrimental to functional performance, especially in the context of membrane-type electronic devices integrated into morphing matter[101,102]. In general, placing the device layer within the neutral mechanical plane can enhance bendability, while an upper layer can minimize light scattering and optical losses, crucial considerations for image sensors and optical devices[103,104]. Plasticized region on the top surface, serving as a damper and reflows, facilitates programmable transformations with mild stress accumulation, ensuring structural stability in transformed states. These transformable frameworks, in conjunction with origami structures, offer promising avenues for the development of high-performance electronic devices.
Kirigami, closely related to origami, allows for paper cutting, giving rise to complex 3D morphing structures. A framework for 2D reconfigurable kirigami patterns has been proposed, taking into account edge length constraints, the angle sum constraints, and dual pairs of geometry constraints[105] [Figure 3E]. Through an optimization routine, iteratively updated node coordinates are determined, leading to deployed kirigami that conforms to the target domain while admitting two compact configurations. Additional geometric constraints ensure rigid deployability, analog to planar mechanisms. These results provide a clear understanding of kirigami design with contractibility and rigid deployability, thereby paving the way for art-inspired science and engineering. To transform a developable sheet to a nondevelopable 3D surface, polyhedral mesh unfolding proves to be an effective operation, allowing arbitrary surfaces to be flattened into 2D patches[106] [Figure 3F]. By algorithmically determining a polyhedral net with minimal folding angles and subsequently erasing crease lines, a nonpolyhedral developable net is obtained, suitable for wrapping the 3D surface and conformal devices with metallic and ceramic materials. The refinement of the mesh of the target surface reduces the area difference between the polyhedron and the target surface while leading to decreases in the maximum in-plane principal stress of the materials. In addition to segmentation and unfolding of surfaces, deployable kirigami tessellations based on geometric constraints are presented to fit surfaces with complex Gaussian curvatures[107] [Figure 3G]. While the contractibility constraints are similar to the planar case, the non-overlapping constraints and surface matching constraints differ. A bicubic Bezier surface is generated to fit every hole in the deployed state, with a comparison of mean and Gaussian curvatures to match the target surface. Various periodic tiling patterns are used for kirigami, such as triangles[108,109] and hexagons[110], all showing significant negative Poisson’s ratio and deploying as kinematic mechanisms at the flexible hinge limit. Combining auxetic kirigami and conformal geometry, an inverse design algorithm is established to morph complex surfaces by modifying the geometric parameters of the unit cell to introduce spatially metric frustration[108]. A deployable structure, transforming from a flat sheet to a surface with a hole, is presented, consisting of bistable auxetic units derived from the local extensibility of hinges[111] [Figure 3H]. The algorithm indicates that multiple solutions exist for the inverse design of the target surface, and the deployable structure with the highest stiffness is selected.
On the other hand, compressive loads at edges also play an important role in morphing principles based on kirigami, typically involving the removal of material from an elastic sheet to form a tapered pattern[112,113]. The fundamental mechanism driving the morphing of elastic strips is the equilibrium of tapered elastica[112], which lies a solid foundation of a series of inverse designs of morphing matter. When the moment of inertia of the strip’s cross-section varies along the strip, the resulting buckled strip exhibits noticeable curvature variation [Figure 3I]. A constant thickness scheme leads to gaps in the deformed shape, and relaxation in thickness distribution ensures full tessellation[112]. Fabricating a planar sample with variable thickness may present challenges, which can be circumvented by utilizing varying porosity, a strategy known as perforated kirigami[114] [Figure 3J]. The porosity can be tailored by introducing small pores using techniques such as laser cutting and microfabrication. Mechanical stability investigations of tessellated axisymmetric structures upon indentation tests further explore the relationship between the measured geometric rigidity of morphed half-ellipsoids and different aspect ratios. The design strategy of perforated sheets is not limited to regular poles or structures with rotational symmetry. A similar bio-inspired cellular micro-lattice design strategy has been presented recently, aiming to reconstruct complex surfaces using an elastic model and machine learning approaches[115] [Figure 3K]. For complex surfaces, an artificial neural network based on point cloud data is utilized to obtain the coordinates of triangular nodes and their porosity from pre-strained numerical datasets of microlattice ribbons. Combined with stretched elastomer, inner bonding sites, and strain-limiting frames, these microlattices can be used to create bilayer structures and face masks, demonstrating functional application in electronic systems. The explicit relationship between the shape of the 2D cut pattern and the curvature of the 3D target structure illustrates that inverse design strategies can encode the moment of inertia and Young’s modulus along a strip[112]. With advancements in additive manufacturing technologies, local control of elastic properties in materials becomes achievable. A novel paradigm based on multi-material volumetric pixel-based 3D printing is proposed[116] [Figure 3L]. By determining the relationship between the longitudinal modulus and the volume fraction of materials, a functionally graded composite (FGC) strip is manufactured by assigning soft and rigid phases to each voxel according to theoretical modulus distribution along the strip. In addition to their shape-changing abilities, FGC-based morphing structures also exhibit excellent multi-functionality[116]. These methods leverage geometric analysis and mechanical behaviors to create shape-morphing structures with complex shapes and multiple functions.
Assembly of discrete elements
To approximate a targeted free-form surface, a computational method is proposed to tessellate the given surface into rigid convex blocks in regular topologies[117] [Figure 4A]. In this method, a 2D polygonal tessellation is mapped to the targeted 3D surfaces, and the mapped edges are augmented with normalized vectors for constructing 3D planes. Lastly, the targeted surface is offset to intersect the 3D planes for interlocking topology. A variety of 3D surfaces (e.g., blob, spindle, flower, and torus) are achieved utilizing this method via assembling particles [Figure 4A ii]. However, one drawback is that this method requires picking and placing these particles at designed locations, which is highly time-consuming. To address this, an alternative computational approach assembles the rigid tiles with pre-stretched sheets as the actuating material[31] [Figure 4B]. The tiles are tightly attached to two pre-stretched elastic sheets and, once released, will assemble the tiles to the targeted 3D shapes by restoring elastic force in the elastic sheets [Figure 4B i]. The distribution, shapes, and attachment regions of the 2D tile arrangements are optimized for both fabrication and closely resembling the desired curved up state. This method allows for the realization of complex surfaces (e.g., turtle, bump cap, mask, spot, etc.) from a flat state [Figure 4B]. Nevertheless, reversible shape morphing is unrealistic to achieve using this method as the elastic energy is hard to restore and keep once released. To overcome this limitation, a reversible shape morphing strategy is introduced[118] [Figure 4C]. The tessellated rigid blocks are concealed in the air-tight rubber envelope. Vacuum pressure is used to assemble the particles from the flat surface to the targeted 3D shape. Unlike traditional morphing materials relying on the intrinsic softness of underlying materials, the achieved 3D structure possesses high mechanical rigidity due to the contact of rigid particles under confining pressure [Figure 4C iii]. When the pressure is removed, the 3D structure will return to the initial shape due to the gravity and elasticity of the rubber envelope.
Figure 4. Morphing matter based on discrete elements assembly. (A) Tessellating free-form surfaces into interlocking blocks. (i) Schematic of a tessellation strategy; (ii) Demonstrations of the tessellation algorithms with various surfaces; (iii) Manually assembling process. Reproduced with permission from[117]; Copyright 2019, Association for Computing Machinery; (B) Actuating discrete blocks with tension force. (i) Schematic of assembling the blocks with pre-stretched membranes; (ii) Demonstrations with various surfaces from flat state to curved state. Reproduced with permission from[31]; Copyright 2017, Association for Computing Machinery; (C) Shape morphing structures based on discrete particles under vacuum pressure. (i) Illustration of design and actuation process under vacuum pressure; (ii) Demonstrations with positive and negative Gaussian curvatures; (iii) Stiffness tuning ability under confining pressure. Reproduced with permission from[118]; Copyright 2023, Wiley-VCH; (D) Hierarchical tessellation strategy and demonstrations with varying curvature surfaces and asymmetric surfaces (from top to bottom: gourd shape, vase shape, and mushroom chair shape)[120]; (E) Grains on an elastic sheet. The sheet first conforms to individual grains, and then wrinkles will occur to the sheet as the granular grains rearrange and get jammed under confinement. Reproduced with permission from[121]; Copyright 2023, Cell Press; (F) Chainmail structure consisting of topologically interlocked particles undergoes reconfigurations and shows high mechanical rigidity under vacuum pressure. Reproduced with permission from[122]; Copyright 2021, Macmillan Publishers Limited.
Despite the fact that the above-mentioned strategies can achieve shape morphing from a flat surface to a non-deployable surface, a whole, complex 3D surface remains challenging to realize due to the restrictions of Gauss’ Theorema Egregium[119]. To buffer the incompatibility between 3D and flat surfaces, a two-level, inverse-design framework called ‘hierarchical tessellation’ is proposed[120] [Figure 4D]. At the first level, a free-form 3D surface is tessellated into petaloid-topology surfaces via kirigami tessellation. At the second level, the subdivided surface is further tessellated into architectured particles to match the curvature distribution. Through assembling/disassembling the particles via tendon, general 3D structures (e.g., asymmetrical and varying curvature) could be achieved reversibly. Notably, the mechanical properties of the structures could be tuned by controlling the actuation force (the force in the actuating tendon), which is challenging in traditional soft morphing materials.
Furthermore, the use of identical particles on elastic sheets is explored for shape morphing. When identical grains populate an elastic sheet, two morphing states will arise as the grain-sheet interaction strength surpasses the bending rigidity of the sheet[121] [Figure 4E]. Initially, the sheet will exhibit local conformation to each individual grain. Subsequently, it will achieve a global conformation to the granular packing under two conditions: either through the application of a confining force (examined through granular self-coherence) or by jamming on the surface of the sheet [Figure 4E]. As for jamming transition, the chainmail structure consisting of topologically interlocked identical octahedral particles can be shaped into various geometries (e.g., load bearing structures) at a soft state and using a jamming transition to fix the shape[122] [Figure 4F]. The discrete characteristics of the chainmail structure allow the rigid particles to become soft at the structure level, while they can be stiffened and lock the shape on demand under confinement. This reconfigurable morphing ability is essential for applications where conformability is required.
In addition to the well-established morphing materials/structures involving programming localized strain or cuts/folds[4,123], there has been another innovative method recently developed - the assembly of discrete elements (e.g., architectured particles) from basic building blocks[31,117,118,121,122,124]. The discrete characteristics grant the building blocks more freedom of movement, enabling easy changes in Gaussian curvature[17,112]. Recent developments have used architectured blocks[117], rotating beams[125,126], and curved ribbons[127] as the basic building elements. Through designing the geometries of the discrete building elements and their interactions (e.g., assembling, sliding, rotating, etc.), structures with respectable morphing capability can be achieved.
Morphogenesis-inspired design
Morphogenesis, a fascinating phenomenon observed in biological systems, orchestrates the development of diverse functional organs[128-130]. In plants, while specific genes regulate programmable cell growth, biomechanical constraints (e.g., physical restrictions from adjoining cell walls) and the differential growth strain (e.g., varying cell growth rates in response to environmental stimuli) also significantly contribute to evolving into complex 3D configurations at the organ level[131,132].
To understand this from the perspective of biomechanics, a morphological phase diagram is presented, rationalizing four general geometrical configurations (twisting, helical twisting, saddle bending, and edge waving) in plants[133] [Figure 5A]. Specifically, using a narrow strip to represent the leaf, the growth strain along the axial direction of the strip can be taken as: εg(y) = β(y/W)n, where y and W are the distance from the leaf center and half width of the leaf, respectively. The growth strain εg(y) increases from zero at the center to a maximum value of β at the edge. The power-law exponent, n, characterizes the steepness of the differential growth strain profile. Four configurations emerge with different n and β. The large intermediate state between the saddle bending state and the edge waving state may arise from the structure instability and residual stresses in the center. The findings indicate that the shape development of maturing leaves is influenced by both the highest magnitude and the spatial arrangement of growth-induced strain. Guided by this phase diagram, artificial hydrogels that could mimic the morphing behaviors of leaves are presented by controlling the polymerization process [Figure 5A iii].
Figure 5. Morphogenesis inspired morphing matter. (A) Differential growth in plants and their principles of morphogenesis. (i) Morphogenesis of long orchid petals and their corresponding basic mechanical configurations; (ii) Morphologies phase diagram as functions of n and β; (iii) Reproduction of the plant leaf morphogenesis through controlling the hydrogel polymerization process. Reproduced with permission from[133]; Copyright 2018, National Academy of Sciences, U.S.A; (B) Design principles of the liquid crystal elastomer actuator. The actuator combines the morphogenesis of plant leaves and the motion of a ray during swimming and could generate autonomous wave motions under structured light. Reproduced with permission from[134]; Copyright 2022, American Chemical Society; (C) Principles of the pneumatic morphing elastomers with air channels inside. (i) The anisotropic deformation of the elastomer under pneumatic actuation and the mold used to cast the elastomer plate with air channels; (ii) Two morphing states under pneumatic actuation; (iii) Morphogenesis of the Acetabularia alga from positive Gaussian curvature to negative Gaussian curvature shape due to the differential growth. Reproduced with permission from[135]; Copyright 2019, Macmillan Publishers Limited; (D) Design and demonstration of inflatables. (i) Heating to seal the two inextensible sheets using a soldering iron. Through controlling the sealing path, various shapes could be achieved; (ii) Demonstration with a “waving man”. The sealing path is programmed to be the shape of a waving man; (iii) Demonstration with a “Hello”. The sealing path is programmed to be the contour of “Hello”. Reproduced with permission from[136]; Copyright 2018, National Academy of Sciences, U.S.A; (E) Design guidelines and demonstration of discrete strain-limiting patches on inflatables. (i) The inverse-design pipeline; (ii) Demonstration of the design with a hyperbolic paraboloid surface; (iii) Grasping and lifting two baskets using a designed loop knot geometry. Reproduced with permission from[137]; Copyright 2023, Wiley-VCH; (F) The responsive surface by halftone gel lithography. (i) Schematic of the fabrication process; (ii) Programmed patterned sheets generate a saddle surface, a saddle surface with a defect, a cap surface, and a cone surface. Reproduced with permission from[138]; Copyright 2012, AAAS.
Inspired by this biological morphogenesis, a wavy soft, light-actuated robot that could perform rhythmic motor patterns for locomotion is presented[134] [Figure 5B]. This locomotion robot combines the two shaping principles developed from plant morphogenesis and the ray fish undulatory motion. Firstly, liquid crystal elastomer (LCE) strips could achieve differential morphing into various wavy shapes from flat shapes under nonuniform structured light. Secondly, a rhythmic motor pattern is achieved through localized light-induced contracting/expansion. These autonomous wave behaviors enable artificial soft machines to mimic the complex peristaltic waves in biological organisms. Apart from achieving differential growth through photothermal effect, pneumatic actuation offers fast and reversible actuation. By incorporating a specialized network of airways within the rubber plate, the channels tend to inflate (deflate) anisotropically (i.e., the width changes while the length remains almost the same) when the inner pressure is increased (decreased)[135] [Figure 5C i]. As a result, negative pressure contracts the plate in the azimuthal direction, resulting in a bowl shape with positive Gaussian curvature, while positive pressure transforms the plate into a saddle shape with negative Gaussian curvature [Figure 5C ii]. The desired curvature tensor can also be programmatically achieved using a bilayer structure consisting of two separate networks of airways. This precise control of local growth enables effectively mimicking the anisotropic growth of Acetabularia
To overcome the limitations of intrinsic softness in elastomers, stiff inflatables are developed based on inextensible sheets sealed along desirable continuous paths on their edges[136] [Figure 5D i]. Through rationalizing the stress state and curvature under inflation, a reversed model is proposed to design arbitrary 2D shapes from flat sheets. Specifically, the cross-sectional shape exhibits singularities and a complex arrangement of wrinkles, causing the outline of the inflated curved balloon with unfixed ends to become more curved during inflation. The feasibility of the model is validated with the targeted “waving man” and “hello” shapes [Figure 5D ii and iii]. Similarly, another inverse-designed inflatable is developed based on 3D discretely placed strain-limiting patches[137] [Figure 5E]. In this design, starting with a user-defined spatial curve, the authors employ kinematics to create a preliminary strategy for the positioning and heights of strain limiters on the unexpanded structure. This preliminary strategy then serves as the starting point for a finite element method (FEM) simulation integrated into an optimization framework aimed at refining strain limiter placement and dimensions. The initial approach is derived from a simplified model that offers insights into the mechanics governing elongated hyperelastic inflatables adorned with distinct strain limiters. Moreover, employing this preliminary approach to initiate the FEM optimization process narrows down the design possibilities, enhancing the convergence rate towards valid parameters as compared to using FEM alone. Using this design pipeline, various shapes, such as hyperbolic paraboloid surfaces, are presented [Figure 5E ii ]. As for applications, the soft inflatable equipped with this inverse design framework could be shaped into a loop knot for grasping and lifting the object [Figure 5E iii].
Additionally, spatially nonuniform growth in soft materials is explored as an alternative way to mimic biological morphogenesis. To create smooth nonuniform growth in a sheet, an approach called “halftone gel lithography” based on a two-mask lithographic patterning is described[138] [Figure 5F]. The detailed process involves coating a sacrificial layer on a wafer, and then the temperature-responsive N-isopropylacrylamide copolymer is solution cast and exposed to a small dose of UV light through the first mask. And then a large dose through the second mask.
The benzophenone acrylamide unit in the copolymer under UV light can be converted into cross-links that can swell. Finally, the sample is immersed in an aqueous solution for swelling [Figure 5F i]. The arbitrary and uniform distribution of highly cross-linked dot patterns could generate various shapes, such as saddle surfaces, a cone with a center defect, a cap, and a cone shape [Figure 5F ii].
MORPHING MATTER IN ROBOTIC APPLICATIONS
The exploration of various shape morphing mechanisms over the past few decades has led to a demonstration of various sophisticated soft robotic applications[4,139-141]. In contrast to traditional rigid robots, soft robots are designed to emulate natural organisms and adapt to specific external environments. Therefore, the ability to undergo shape morphing becomes a crucial benchmark for evaluating their reconfigurability in diverse surroundings[142,143]. Various actuation strategies have been employed to achieve active shape morphing in soft robotics, including pneumatic[144-147], magnetic[140,148,149], light[150,151], and heat-based[152,153] methods. These approaches allow soft robots to change their shapes and configurations in response to specific stimuli, making them highly versatile and capable of performing a wide range of tasks.
Pneumatic actuation is one of the most common methods used to change the shape of soft robots. The channels inside the soft bodies allow converting the internal pressure in the voids to the strain easily. A simple bubble casting method is proposed to manufacture the soft robot with voids[146] [Figure 6A i]. An uncured elastomer is filled into the tubular mold, and then air is injected into the elastomer to form an elongated bubble acting as the inner void of the soft actuator. Interestingly, gravity and viscosity drive the formation of the eccentric void topology [Figure 6A i]. The asymmetric wall thickness distribution leads to bending motion under inflation. The bending motion can be readily used as a self-folding gripper
Figure 6. Robotic applications of morphing matter. (A) Soft robots fabricated by bubble casting. (i) Illustration of fabrication processes and demonstration of acting as a gripper; (ii) Spiral-shaped actuator fabricated by bubble casting method. Reproduced with permission from[146]; Copyright 2021, Macmillan Publishers Limited; (B) Entangling filaments. (i) Schematic of the eccentric design of the filaments and their actuating performance; (ii) 12 eccentric hollow filaments grasping a house plant under actuation. Reproduced with permission from[147]; Copyright 2022, National Academy of Sciences, U.S.A; (C) Soft kirigami gripper. (i) Design parameters of the kirigami sheet and its morphing ability under stretching; (ii) Grasping a raspberry using the kirigami gripper. Reproduced with permission from[154]; Copyright 2021, AAAS; (D) Kirigami sheet with prescribed boundaries as soft grippers. (i) 2D precursors before stretching and morphing into a dome shape under stretching; (ii) Grasping raw egg yolk; (iii) Grasping a swimming fish. (iv) Grasping shampoo bubble. Reproduced with permission from[155]; Copyright 2022, Macmillan Publishers Limited; (E) Soft magnetic robot. (i) Schematic of the printing process and the composite ink composition. The magnetic field generated by the permanent magnet/electromagnetic reorients the hard ferromagnetic particles in the soft matrix; (ii) A soft magnetic robot for delivery under magnetic actuation. Reproduced with permission from[156]; Copyright 2018, Macmillan Publishers Limited; (F) A self-propelling thermo-responsive soft robot. (i) Schematic of the printing, morphing, and rolling process on a hot plate; (ii) Morphing process and rolling process on a hot plate; (iii) The rolling direction depends on the curvature direction of the tubule. Reproduced with permission from[157]; Copyright 2021, Cell Press; (G) A pipeline robot. (i) Schematic of the structure of the pipeline robot; (ii) Two different types of pipeline robots. Type A: two anchoring units and one elongation unit. Type B: two elongation units with two anchoring units; (iii) Navigating into a pipe with variable internal diameters (10 to 9 to 10 mm). Reproduced with permisFEMsion from[159]; Copyright 2022, AAAS. FEM: Finite element method.
For delicate grasping, kirigami cut patterns designed on a flexible, thin shell transfer linear uniaxial tension into grasping motion[154] [Figure 6C]. The pattern is generated on a polyethylene terephthalate sheet (thickness: 0.127 mm) via laser cutting, and then the kirigami sheet is mounted on a cylinder and heated to form the initial curvature. The grasping performance under tension depends on the cut parameters, i.e., the holding force increases monotonically with lc(ly - tc)κ0/[4(1 + ν)lxsin(κ0Le)] where ν is the Poisson’s ratio. The demonstration shows the ability of a kirigami sheet to grasp a raspberry. Another kirigami sheet design achieves 3D morphologies by programming the curvature of cut boundaries instead of cutting patterns[155] [Figure 6D]. The kirigami sheet consists of parallel cuts enclosed by continuous boundaries. By prescribing the boundaries, the stretching of the sheet generates various 3D shapes. For applications, a soft gripper is presented for delicate grasping. The 2D kirigami precursor transforms into a gripper grasping raw egg, live fish, and shampoo bubbles under simple stretching.
Different from pneumatic or mechanical stretching actuated shape morphing structures, smart, responsive materials offer a feasible way for remote control. 3D printing of ferromagnetic soft materials for fast morphing robots is developed based on embedding ferromagnetic microparticles (neodymium-iron-boron alloy) into soft silicone polymer matrix[156] [Figure 6E]. The orientation of the particles is controlled via the magnetic field applied during printing. The programmable and desirable orientation enables precise control of the modes of transformation. The capability of the complex shape changing enables the construction of a hexapedal structure that can act as cargo for carrying an object and releasing it. Thermo-responsive materials do not require complex magnetic fields. As an example, an untethered self-propelling robot based on LCE is presented[157] [Figure 6F]. The LCE samples consist of two layers with a difference of 90° in printing directions. The strain mismatch between the two layers forces the planar sample to transform into a helix tubular structure under heating. When the tubular sample is placed on a hot plate, a temperature gradient causes contrasting changes at the bottom and top of the circle, with the bottom shrinking while the top extends. This disrupts the balance of forces and results in the sample experiencing rolling ability. Moreover, compared to existing light-controlled and magnet-controlled soft robots, which rely on varying the direction of light or magnetic fields to control motion, the proposed robot only needs a slight change in curvature direction without modifying environmental factors.
Apart from the magnetic-actuated and heat-driven robots, the electric field is also employed in soft robots for their fast actuation speed[158]. A pipeline inspection robot is designed based on the high-power density dielectric elastomer actuators (DEAs)[159] [Figure 6G]. The DEAs act as the elongation unit, and the Smart composite microstructure (SCM) based on carbon fiber laminates is used as anchoring units. Through modeling and dynamic analysis of the robot’s characteristics, the pipeline robot demonstrated exceptional performance coupled with precise adjustments to the frequencies and phases of activation voltages. It achieved rapid bidirectional motion, both horizontally and vertically, at speeds surpassing one body length per second within confined subcentimeter-sized pipelines. Notably, this motion was enabled by tethered cables originating externally to the pipe. Moreover, the robot exhibited remarkable adaptability, showcasing its capability to navigate pipes with changing diameters, complex geometries such as L-shaped and S-shaped pipes, spiral configurations, and pipes filled with various oils and constructed from diverse materials.
CONCLUSION AND OUTLOOK
In this review, we have briefly discussed the recent developments of morphing matter, focusing on its mechanical principles. The inherent softness of morphing matter at both the material level (in terms of elasticity[21]) and the structural level (involving characteristics such as instability[85] and discreteness[86]) has greatly facilitated its applications in the realm of soft robotics, where adaptive shape reconfigurations are essential for interaction with dynamic environments[160]. Despite the significant progress made in this field, several challenges remain to be addressed before these technologies can be fully integrated into practical applications:
(1) Firstly, A pivotal challenge lies in ensuring that the achieved morphed shape remains stable without continuous actuation, thus conserving energy expended to maintain the shape[80,161]. Current actuation methods, such as pneumatic[162], thermal[16], or light-based techniques[123], often necessitate sustained pressure or temperature to retain the desired shape. Developing multistable designs could enable morphing matter to transform among various configurations while saving the energy for maintaining the shape, opening up new possibilities for diverse applications[163,164].
(2) Secondly, achieving morphing into intricate 3D geometries poses a challenging inverse-design problem[116,165]. While analytical models can be developed for specific strain-driven morphing scenarios, they encounter difficulties when confronted with complex shapes that involve intricate interactions between actuating forces and nonlinear material deformations. Often, addressing such complexities requires solving intricate partial differential equations[166-168]. Overcoming this challenge may entail harnessing the capabilities of machine learning techniques and capitalizing on extensive data acquired from experiments or finite element simulations[115,169,170].
(3) Thirdly, given the diverse range of actuation strategies available for morphing matter - such as electric[171-173], magnetic[174,175], and thermal[176,177] methods - accomplishing multiphysics simulations and predictions for these systems is paramount[178]. This is especially true when combining inverse design methodologies with multiphysics actuation strategies. In addressing this challenge, machine learning presents a viable solution for tackling complex multiphysics interactions[179]. Employing machine learning can facilitate the development of intricately morphed shapes under the influence of multiple interacting physical fields.
(4) Lastly, selecting an actuation method for robotic applications depends on the desired morphing range, morphing speed, and the available power consumption[171,173]. Actuators with high energy density[180,181], power density[182,183], and high efficiency[172,184] are still in great demand to realize soft-morphing robots with remarkable performance. Therefore, a major challenge in the application of morphing matter in robotics is to combine the morphing mechanisms with appropriate actuators to achieve controlled morphing.
DECLARATIONS
Authors’ contributions
Literature review, the outline of the manuscript structure, and writing of manuscript draft: Yang X, Zhou Y, Liu M
Participated in the discussion of the review content: Zhao H, Huang W, Wang Y, Hsia KJ
Supervision, writing - review and editing, project administration: Liu M
All authors have read the manuscript and approved the final version.
Availability of data and materials
Not applicable.
Financial support and sponsorship
This work was funded by the Presidential Postdoctoral Fellowship from Nanyang Technological University, Singapore, and the Start-up Grant from the University of Birmingham (Liu M); the NAP award (020482) (Wang Y) and the Start-up Grant (002271-00001) (Hsia KJ) from Nanyang Technological University, Singapore.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2023.
REFERENCES
1. Pikul JH, Li S, Bai H, Hanlon RT, Cohen I, Shepherd RF. Stretchable surfaces with programmable 3D texture morphing for synthetic camouflaging skins. Science 2017;358:210-4.
2. de Espinosa LM, Meesorn W, Moatsou D, Weder C. Bioinspired polymer systems with stimuli-responsive mechanical properties. Chem Rev 2017;117:12851-92.
3. Apsite I, Salehi S, Ionov L. Materials for smart soft actuator systems. Chem Rev 2022;122:1349-415.
4. Kim H, Ahn S, Mackie DM, et al. Shape morphing smart 3D actuator materials for micro soft robot. Mater Today 2020;41:243-69.
5. Erol O, Pantula A, Liu W, Gracias DH. Transformer hydrogels: a review. Adv Mater Technol 2019;4:1900043.
6. Jiao D, Zhu QL, Li CY, Zheng Q, Wu ZL. Programmable morphing hydrogels for soft actuators and robots: from structure designs to active functions. Acc Chem Res 2022;55:1533-45.
7. Li S, Wang KW. Plant-inspired adaptive structures and materials for morphing and actuation: a review. Bioinspir Biomim 2016;12:011001.
9. Keneth ES, Kamyshny A, Totaro M, Beccai L, Magdassi S. 3D printing materials for soft robotics. Adv Mater 2021;33:2003387.
11. Manna RK, Shklyaev OE, Stone HA, Balazs AC. Chemically controlled shape-morphing of elastic sheets. Mater Horiz 2020;7:2314-27.
12. Zhu Z, Ng DWH, Park HS, McAlpine MC. 3D-printed multifunctional materials enabled by artificial-intelligence-assisted fabrication technologies. Nat Rev Mater 2021;6:27-47.
13. Xu S, Yan Z, Jang KI, et al. Assembly of micro/nanomaterials into complex, three-dimensional architectures by compressive buckling. Science 2015;347:154-9.
14. Zhang Y, Ding J, Qi B, et al. Multifunctional fibers to shape future biomedical devices. Adv Funct Mater 2019;29:1902834.
15. Ze Q, Kuang X, Wu S, et al. Shape memory polymers: magnetic shape memory polymers with integrated multifunctional shape manipulation (Adv. Mater. 4/2020). Adv Mater 2020;32:2070025.
16. Kirillova A, Ionov L. Shape-changing polymers for biomedical applications. J Mater Chem B 2019;7:1597-624.
17. Callens SJP, Zadpoor AA. From flat sheets to curved geometries: origami and kirigami approaches. Mater Today 2018;21:241-64.
18. Shah D, Yang B, Kriegman S, Levin M, Bongard J, Kramer-Bottiglio R. Shape changing robots: bioinspiration, simulation, and physical realization. Adv Mater 2021;33:2002882.
19. Hannard F, Mirkhalaf M, Ameri A, Barthelat F. Segmentations in fins enable large morphing amplitudes combined with high flexural stiffness for fish-inspired robotic materials. Sci Robot 2021;6:eabf9710.
20. Yokota K, Barthelat F. Stiff bioinspired architectured beams bend Saint-Venant’s principle and generate large shape morphing. Int J Solids Struct 2023;274:112270.
21. Holmes DP. Elasticity and stability of shape-shifting structures. Curr Opin Colloid Inter Sci 2019;40:118-37.
22. Zhao Q, Zou W, Luo Y, Xie T. Shape memory polymer network with thermally distinct elasticity and plasticity. Sci Adv 2016;2:e1501297.
23. Saleem M, Morlot S, Hohendahl A, Manzi J, Lenz M, Roux A. A balance between membrane elasticity and polymerization energy sets the shape of spherical clathrin coats. Nat Commun 2015;6:6249.
25. Nagarkar A, Lee WK, Preston DJ, et al. Elastic-instability-enabled locomotion. Proc Natl Acad Sci U S A 2021;118:e2013801118.
26. Van Meerbeek IM, Mac Murray BC, Kim JW, et al. Foams: morphing metal and elastomer bicontinuous foams for reversible stiffness, shape memory, and self-healing soft machines (Adv. Mater. 14/2016). Adv Mater 2016;28:2653.
27. Grönquist P, Wood D, Hassani MM, Wittel FK, Menges A, Rüggeberg M. Analysis of hygroscopic self-shaping wood at large scale for curved mass timber structures. Sci Adv 2019;5:eaax1311.
28. Rus D, Tolley MT. Design, fabrication and control of origami robots. Nat Rev Mater 2018;3:101-12.
29. Ning X, Wang X, Zhang Y, et al. Assembly of advanced materials into 3D functional structures by methods inspired by origami and kirigami: a review. Adv Mater Interfaces 2018;5:1800284.
30. Oliver K, Seddon A, Trask RS. Morphing in nature and beyond: a review of natural and synthetic shape-changing materials and mechanisms. J Mater Sci 2016;51:10663-89.
31. Guseinov R, Miguel E, Bickel B. CurveUps: shaping objects from flat plates with tension-actuated curvature. ACM Trans Graph 2017;36:1-12.
32. Mirabet V, Das P, Boudaoud A, Hamant O. The role of mechanical forces in plant morphogenesis. Annu Rev Plant Biol 2011;62:365-85.
34. Berleth T, Sachs T. Plant morphogenesis: long-distance coordination and local patterning. Curr Opin Plant Biol 2001;4:57-62.
35. Lee H, Kim H, Ha I, et al. Directional shape morphing transparent walking soft robot. Soft Robot 2019;6:760-7.
36. Wu S, Hong Y, Zhao Y, Yin J, Zhu Y. Caterpillar-inspired soft crawling robot with distributed programmable thermal actuation. Sci Adv 2023;9:eadf8014.
37. Han B, Ma ZC, Zhang YL, et al. Reprogrammable soft robot actuation by synergistic magnetic and light fields. Adv Funct Mater 2022;32:2110997.
38. Wang XQ, Chan KH, Cheng Y, et al. Somatosensory, light-driven, thin-film robots capable of integrated perception and motility. Adv Mater 2020;32:2000351.
39. Jing L, Li K, Yang H, Chen PY. Recent advances in integration of 2D materials with soft matter for multifunctional robotic materials. Mater Horiz 2020;7:54-70.
40. Efrati E, Sharon E, Kupferman R. Elastic theory of unconstrained non-Euclidean plates. J Mech Phys Solids 2009;57:762-75.
42. Chun IS, Challa A, Derickson B, Hsia KJ, Li X. Geometry effect on the strain-induced self-rolling of semiconductor membranes. Nano Lett 2010;10:3927-32.
43. Huang W, Koric S, Yu X, Hsia KJ, Li X. Precision structural engineering of self-rolled-up 3D nanomembranes guided by transient quasi-static FEM modeling. Nano Lett 2014;14:6293-7.
45. Liu Y, Genzer J, Dickey MD. “2D or not 2D”: shape-programming polymer sheets. Prog Polym Sci 2016;52:79-106.
46. Bauhofer AA, Krödel S, Rys J, Bilal OR, Constantinescu A, Daraio C. Harnessing photochemical shrinkage in direct laser writing for shape morphing of polymer sheets. Adv Mater 2017;29:1703024.
47. Liu K, Hacker F, Daraio C. Robotic surfaces with reversible, spatiotemporal control for shape morphing and object manipulation. Sci Robot 2021;6:eabf5116.
48. Arslan H, Nojoomi A, Jeon J, Yum K. 3D printing of anisotropic hydrogels with bioinspired motion. Adv Sci 2019;6:1800703.
49. Egunov AI, Korvink JG, Luchnikov VA. Polydimethylsiloxane bilayer films with an embedded spontaneous curvature. Soft Matter 2016;12:45-52.
50. Tang J, Chen Z, Cai Y, He J, Luo Y. Stretch-activated reprogrammable shape-morphing composite elastomers. Adv Funct Mater 2022;32:2203308.
51. Zhao T, Zhang Y, Fan Y, Wang J, Jiang H, Lv J. Light-modulated liquid crystal elastomer actuator with multimodal shape morphing and multifunction. J Mater Chem C 2022;10:3796-803.
52. Guo J, Xiang C, Rossiter J. A soft and shape-adaptive electroadhesive composite gripper with proprioceptive and exteroceptive capabilities. Mater Design 2018;156:586-7.
53. Deng H, Xu X, Zhang C, Su JW, Huang G, Lin J. Deterministic self-morphing of soft-stiff hybridized polymeric films for acoustic metamaterials. ACS Appl Mater Interfaces 2020;12:13378-85.
54. Li Q, Le Duigou A, Guo J, et al. Biobased and programmable electroadhesive metasurfaces. ACS Appl Mater Interfaces 2022;14:47198-208.
55. Tan P, Wang H, Xiao F, et al. Solution-processable, soft, self-adhesive, and conductive polymer composites for soft electronics. Nat Commun 2022;13:358.
56. Yang SY, Carlson A, Cheng H, et al. Elastomer surfaces with directionally dependent adhesion strength and their use in transfer printing with continuous roll-to-roll applications. Adv Mater 2012;24:2117-22.
57. Hwang Y, Yoo S, Lim N, et al. Enhancement of interfacial adhesion using micro/nanoscale hierarchical cilia for randomly accessible membrane-type electronic devices. ACS Nano 2020;14:118-28.
58. van Manen T, Janbaz S, Zadpoor AA. Programming the shape-shifting of flat soft matter. Mater Today 2018;21:144-63.
60. Jamal M, Zarafshar AM, Gracias DH. Differentially photo-crosslinked polymers enable self-assembling microfluidics. Nat Commun 2011;2:527.
61. Zhao Q, Dunlop JW, Qiu X, et al. An instant multi-responsive porous polymer actuator driven by solvent molecule sorption. Nat Commun 2014;5:4293.
62. Alben S, Balakrisnan B, Smela E. Edge effects determine the direction of bilayer bending. Nano Lett 2011;11:2280-5.
63. Holmes DP, Roché M, Sinha T, Stone HA. Bending and twisting of soft materials by non-homogenous swelling. Soft Matter 2011;7:5188-93.
64. Abdullah AM, Li X, Braun PV, Rogers JA, Hsia KJ. Self-folded gripper-like architectures from stimuli-responsive bilayers. Adv Mater 2018;30:e1801669.
65. Liu Y, Cao Y, Feng XQ, Cao C. Phase transition and optimal actuation of active bilayer structures. Extreme Mech Lett 2019;29:100467.
66. Boley JW, van Rees WM, Lissandrello C, et al. Shape-shifting structured lattices via multimaterial 4D printing. Proc Natl Acad Sci U S A 2019;116:20856-62.
67. Armon S, Efrati E, Kupferman R, Sharon E. Geometry and mechanics in the opening of chiral seed pods. Science 2011;333:1726-30.
68. Gladman AS, Matsumoto EA, Nuzzo RG, Mahadevan L, Lewis JA. Biomimetic 4D printing. Nat Mater 2016;15:413-8.
69. Jang HS, Yoo S, Kang SH, Park J, Kim GG, Ko HC. Extrusion shear printing: automatic transformation of membrane-type electronic devices into complex 3D structures via extrusion shear printing and thermal relaxation of acrylonitrile-butadiene-styrene frameworks (Adv. Funct. Mater. 5/2020). Adv Funct Mater 2020;30:1907384.
71. Yoo JI, Park D, Kim SH, et al. Thermal shape morphing of membrane-type electronics based on plastic-elastomer frameworks for 3D electronics with various Gaussian curvatures. Mater Design 2023;227:111811.
72. Jourdan D, Skouras M, Vouga E, Bousseau A. Computational design of self-actuated surfaces by printing plastic ribbons on stretched fabric. Comput Graph Forum 2022;41:493-506.
73. Hu N, Burgueño R. Buckling-induced smart applications: recent advances and trends. Smart Mater Struct 2015;24:063001.
74. Reis PM. A Perspective on the revival of structural (in)stability with novel opportunities for function: from buckliphobia to buckliphilia. J Appl Mech 2015;82:111001.
75. Kochmann DM, Bertoldi K. Exploiting microstructural instabilities in solids and structures: from metamaterials to structural transitions. Appl Mech Rev 2017;69:050801.
76. Liu Y, Pan F, Ding B, Zhu Y, Yang K, Chen Y. Multistable shape-reconfigurable metawire in 3D space. Extreme Mech Lett 2022;50:101535.
77. Nadkarni N, Arrieta AF, Chong C, Kochmann DM, Daraio C. Unidirectional transition waves in bistable lattices. Phys Rev Lett 2016;116:244501.
78. Jin L, Khajehtourian R, Mueller J, et al. Guided transition waves in multistable mechanical metamaterials. Proc Natl Acad Sci U S A 2020;117:2319-25.
79. Zareei A, Deng B, Bertoldi K. Harnessing transition waves to realize deployable structures. Proc Natl Acad Sci U S A 2020;117:4015-20.
80. Haghpanah B, Salari-Sharif L, Pourrajab P, Hopkins J, Valdevit L. Multistable shape-reconfigurable architected materials. Adv Mater 2016;28:7915-20.
81. Meng Z, Liu M, Yan H, Genin GM, Chen CQ. Deployable mechanical metamaterials with multistep programmable transformation. Sci Adv 2022;8:eabn5460.
82. Meng Z, Chen W, Mei T, Lai Y, Li Y, Chen CQ. Bistability-based foldable origami mechanical logic gates. Extreme Mech Lett 2021;43:101180.
83. Zhang Y, Tichem M, van Keulen F. Concept and design of a metastructure-based multi-stable surface. Extreme Mech Lett 2022;51:101553.
84. Risso G, Sakovsky M, Ermanni P. A highly multi-stable meta-structure via anisotropy for large and reversible shape transformation. Adv Sci 2022;9:e2202740.
85. Liu M, Domino L, Dupont de Dinechin I, Taffetani M, Vella D. Snap-induced morphing: from a single bistable shell to the origin of shape bifurcation in interacting shells. J Mech Phys Solids 2023;170:105116.
86. Chen T, Shea K. Computational design of multi-stable, reconfigurable surfaces. Mater Design 2021;205:109688.
87. Meng Z, Yan H, Liu M, Qin W, Genin GM, Chen CQ. Encoding and storage of information in mechanical metamaterials. Adv Sci 2023;10:e2301581.
88. Pan F, Li Y, Li Z, Yang J, Liu B, Chen Y. 3D pixel mechanical metamaterials. Adv Mater 2019;31:e1900548.
89. Yan Z, Zhang F, Liu F, et al. Mechanical assembly of complex, 3D mesostructures from releasable multilayers of advanced materials. Sci Adv 2016;2:e1601014.
90. Demaine ED, Demaine ML. Recent results in computational origami. In: Hull T, editor. Origami3. 2002. Available from: https://www.semanticscholar.org/paper/Recent-Results-in-Computational-Origami-Demaine-Demaine/8c67754ac41e1eaea7d68f6dd49945bd881067e9. [Last accessed on 17 Oct 2023].
91. Yu Y, Chen Y, Paulino G. Programming curvatures by unfolding of the triangular Resch pattern. Int J Mech Sci 2023;238:107861.
92. Dudte LH, Vouga E, Tachi T, Mahadevan L. Programming curvature using origami tessellations. Nat Mater 2016;15:583-8.
94. Tachi T. Designing freeform origami tessellations by generalizing resch’s patterns. J Mech Des 2013;135:111006.
95. Xiao K, Liang Z, Zou B, Zhou X, Ju J. Inverse design of 3D reconfigurable curvilinear modular origami structures using geometric and topological reconstructions. Nat Commun 2022;13:7474.
96. Filipov ET, Tachi T, Paulino GH. Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proc Natl Acad Sci U S A 2015;112:12321-6.
97. Hanna BH, Lund JM, Lang RJ, Magleby SP, Howell LL. Waterbomb base: a symmetric single-vertex bistable origami mechanism. Smart Mater Struct 2014;23:094009.
98. Yasuda H, Tachi T, Lee M, Yang J. Origami-based tunable truss structures for non-volatile mechanical memory operation. Nat Commun 2017;8:962.
99. Zhai Z, Wang Y, Jiang H. Origami-inspired, on-demand deployable and collapsible mechanical metamaterials with tunable stiffness. Proc Natl Acad Sci U S A 2018;115:2032-7.
100. Wu S, Ze Q, Dai J, Udipi N, Paulino GH, Zhao R. Stretchable origami robotic arm with omnidirectional bending and twisting. Proc Natl Acad Sci U S A 2021;118:e2110023118.
101. Xia ZM, Wang CG, Tan HF. Quasi-static unfolding mechanics of a creased membrane based on a finite deformation crease-beam model. Int J Solids Struct 2020;207:104-12.
102. Xue Z, Song H, Rogers JA, Zhang Y, Huang Y. Mechanically-guided structural designs in stretchable inorganic electronics. Adv Mater 2020;32:e1902254.
103. Jang HS, Kim GG, Kang SH, et al. 3D image sensors: a bezel-less tetrahedral image sensor formed by solvent-assisted plasticization and transformation of an acrylonitrile butadiene styrene framework (Adv. Mater. 30/2018). Adv Mater 2018;30:1870224.
104. Kim GG, Kim Y, Yoo S, Jang HS, Ko HC. Hexahedral LED arrays with row and column control lines formed by selective liquid-phase plasticization and nondisruptive tucking-based origami. Adv Mater Technol 2020;5:2000010.
106. Lee YK, Xi Z, Lee YJ, et al. Computational wrapping: a universal method to wrap 3D-curved surfaces with nonstretchable materials for conformal devices. Sci Adv 2020;6:eaax6212.
107. Choi GPT, Dudte LH, Mahadevan L. Programming shape using kirigami tessellations. Nat Mater 2019;18:999-1004.
108. Konaković M, Crane K, Deng B, Bouaziz S, Piker D, Pauly M. Beyond developable: computational design and fabrication with auxetic materials. ACM Trans Graph 2016;35:1-11.
109. Konaković-luković M, Panetta J, Crane K, Pauly M. Rapid deployment of curved surfaces via programmable auxetics. ACM Trans Graph 2018;37:1-13.
110. Rafsanjani A, Pasini D. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extreme Mech Lett 2016;9:291-6.
111. Chen T, Panetta J, Schnaubelt M, Pauly M. Bistable auxetic surface structures. ACM Trans Graph 2021;40:1-9.
112. Liu M, Domino L, Vella D. Tapered elasticæ as a route for axisymmetric morphing structures. Soft Matter 2020;16:7739-50.
113. Fan Z, Yang Y, Zhang F, et al. Inverse design strategies for 3D surfaces formed by mechanically guided assembly. Adv Mater 2020;32:e1908424.
114. Zhang Y, Yang J, Liu M, Vella D. Shape-morphing structures based on perforated kirigami. Extreme Mech Lett 2022;56:101857.
115. Cheng X, Fan Z, Yao S, et al. Programming 3D curved mesosurfaces using microlattice designs. Science 2023;379:1225-32.
116. Kansara H, Liu M, He Y, Tan W. Inverse design and additive manufacturing of shape-morphing structures based on functionally graded composites. J Mech Phys Solids 2023;180:105382.
117. Wang Z, Song P, Isvoranu F, Pauly M. Design and structural optimization of topological interlocking assemblies. ACM Trans Graph 2019;38:1-13.
118. Yang X, Wang Z, Zhang B, et al. Self-sensing robotic structures from architectured particle assemblies. Adv Intell Syst 2023;5:2200250.
120. Yang X, Liu M, Zhang B, et al. Hierarchical tessellation enables programmable morphing matter. 2023; In press.
122. Wang Y, Li L, Hofmann D, Andrade JE, Daraio C. Structured fabrics with tunable mechanical properties. Nature 2021;596:238-43.
123. Jeon SJ, Hauser AW, Hayward RC. Shape-morphing materials from stimuli-responsive hydrogel hybrids. Acc Chem Res 2017;50:161-9.
124. Tanjeem N, Minnis MB, Hayward RC, Shields CW 4th. Shape-changing particles: from materials design and mechanisms to implementation. Adv Mater 2022;34:e2105758.
125. Ren Y, Kusupati U, Panetta J, et al. Umbrella meshes: elastic mechanisms for freeform shape deployment. ACM Trans Graph 2022;41:1-15.
126. Panetta J, Konaković-luković M, Isvoranu F, Bouleau E, Pauly M. X-shells: a new class of deployable beam structures. ACM Trans Graph 2019;38:1-15.
130. Efroni I, Eshed Y, Lifschitz E. Morphogenesis of simple and compound leaves: a critical review. Plant Cell 2010;22:1019-32.
131. Guo K, Huang C, Miao Y, Cosgrove DJ, Hsia KJ. Leaf morphogenesis: the multifaceted roles of mechanics. Mol Plant 2022;15:1098-119.
132. Tsukaya H. Organ shape and size: a lesson from studies of leaf morphogenesis. Curr Opin Plant Biol 2003;6:57-62.
133. Huang C, Wang Z, Quinn D, Suresh S, Hsia KJ. Differential growth and shape formation in plant organs. Proc Natl Acad Sci U S A 2018;115:12359-64.
134. Zhao T, Fan Y, Lv J. Photomorphogenesis of diverse autonomous traveling waves in a monolithic soft artificial muscle. ACS Appl Mater Interfaces 2022;14:23839-49.
135. Siéfert E, Reyssat E, Bico J, Roman B. Bio-inspired pneumatic shape-morphing elastomers. Nat Mater 2019;18:24-8.
136. Siéfert E, Reyssat E, Bico J, Roman B. Programming curvilinear paths of flat inflatables. Proc Natl Acad Sci U S A 2019;116:16692-6.
137. Baines R, Patiballa SK, Gorissen B, Bertoldi K, Kramer-Bottiglio R. Programming 3D curves with discretely constrained cylindrical inflatables. Adv Mater 2023;35:e2300535.
138. Kim J, Hanna JA, Byun M, Santangelo CD, Hayward RC. Designing responsive buckled surfaces by halftone gel lithography. Science 2012;335:1201-5.
139. Laschi C, Mazzolai B, Cianchetti M. Soft robotics: technologies and systems pushing the boundaries of robot abilities. Sci Robot 2016;1:eaah3690.
140. Huang W, Liu M, Hsia KJ. Modeling of magnetic cilia carpet robots using discrete differential geometry formulation. Extreme Mech Lett 2023;59:101967.
141. Qin L, Peng H, Huang X, Liu M, Huang W. Modeling and simulation of dynamics in soft robotics: a review of numerical approaches. Curr Robot Rep 2023.
142. Shah DS, Powers JP, Tilton LG, Kriegman S, Bongard J, Kramer-bottiglio R. A soft robot that adapts to environments through shape change. Nat Mach Intell 2021;3:51-9.
143. Wang Y, Wang Q, Liu M, et al. Insect-scale jumping robots enabled by a dynamic buckling cascade. Proc Natl Acad Sci U S A 2023;120:e2210651120.
144. Rajappan A, Jumet B, Preston DJ. Pneumatic soft robots take a step toward autonomy. Sci Robot 2021;6:eabg6994.
145. Tawk C, Alici G. A review of 3D-printable soft pneumatic actuators and sensors: research challenges and opportunities. Adv Intell Syst 2021;3:2000223.
146. Jones TJ, Jambon-Puillet E, Marthelot J, Brun PT. Bubble casting soft robotics. Nature 2021;599:229-33.
147. Becker K, Teeple C, Charles N, et al. Active entanglement enables stochastic, topological grasping. Proc Natl Acad Sci U S A 2022;119:e2209819119.
148. Li M, Pal A, Aghakhani A, Pena-Francesch A, Sitti M. Soft actuators for real-world applications. Nat Rev Mater 2022;7:235-49.
149. Hines L, Petersen K, Lum GZ, Sitti M. Soft actuators for small-scale robotics. Adv Mater 2017;29:1603483.
150. Chen Y, Yang J, Zhang X, et al. Light-driven bimorph soft actuators: design, fabrication, and properties. Mater Horiz 2021;8:728-57.
151. Zeng H, Wasylczyk P, Wiersma DS, Priimagi A. Light robots: bridging the gap between microrobotics and photomechanics in soft materials. Adv Mater 2018;30:e1703554.
152. Yang Y, Terentjev EM, Zhang Y, et al. Reprocessable thermoset soft actuators. Angew Chem Int Ed Engl 2019;58:17474-9.
153. Won P, Kim KK, Kim H, et al. Transparent soft actuators/sensors and camouflage skins for imperceptible soft robotics. Adv Mater 2021;33:e2002397.
155. Hong Y, Chi Y, Wu S, Li Y, Zhu Y, Yin J. Boundary curvature guided programmable shape-morphing kirigami sheets. Nat Commun 2022;13:530.
156. Kim Y, Yuk H, Zhao R, Chester SA, Zhao X. Printing ferromagnetic domains for untethered fast-transforming soft materials. Nature 2018;558:274-9.
157. Zhai F, Feng Y, Li Z, et al. 4D-printed untethered self-propelling soft robot with tactile perception: rolling, racing, and exploring. Matter 2021;4:3313-26.
158. Hajiesmaili E, Clarke DR. Reconfigurable shape-morphing dielectric elastomers using spatially varying electric fields. Nat Commun 2019;10:183.
159. Tang C, Du B, Jiang S, et al. A pipeline inspection robot for navigating tubular environments in the sub-centimeter scale. Sci Robot 2022;7:eabm8597.
161. Chen Z, Guo Q, Majidi C, Chen W, Srolovitz DJ, Haataja MP. Nonlinear geometric effects in mechanical bistable morphing structures. Phys Rev Lett 2012;109:114302.
162. Sofla AYN, Meguid SA, Tan KT, Yeo WK. Shape morphing of aircraft wing: status and challenges. Mater Design 2010;31:1284-92.
163. Shi J, Mofatteh H, Mirabolghasemi A, Desharnais G, Akbarzadeh A. Programmable multistable perforated shellular. Adv Mater 2021;33:e2102423.
164. Aksoy B, Shea H. Multistable shape programming of variable-stiffness electromagnetic devices. Sci Adv 2022;8:eabk0543.
165. Forte AE, Hanakata PZ, Jin L, et al. Inverse design of inflatable soft membranes through machine learning. Adv Funct Mater 2022;32:2111610.
166. Wang C, Zhao Z, Zhang XS. Inverse design of magneto-active metasurfaces and robots: theory, computation, and experimental validation. Comput Method Appl Mech Eng 2023;413:116065.
167. Bai Y, Wang H, Xue Y, et al. A dynamically reprogrammable surface with self-evolving shape morphing. Nature 2022;609:701-8.
168. Zheng X, Zhang X, Chen TT, Watanabe I. Deep learning in mechanical metamaterials: from prediction and generation to inverse design. Adv Mater 2023;35:2302530.
169. Jiang C, Wang D, Zhao B, Liao Z, Gu G. Modeling and inverse design of bio-inspired multi-segment pneu-net soft manipulators for 3D trajectory motion. Appl Phys Rev 2021;8:041416.
170. Peng J, Schwalbe-koda D, Akkiraju K, et al. Human- and machine-centred designs of molecules and materials for sustainability and decarbonization. Nat Rev Mater 2022;7:991-1009.
171. Chen Y, Zhao H, Mao J, et al. Controlled flight of a microrobot powered by soft artificial muscles. Nature 2019;575:324-9.
172. Duduta M, Hajiesmaili E, Zhao H, Wood RJ, Clarke DR. Realizing the potential of dielectric elastomer artificial muscles. Proc Natl Acad Sci U S A 2019;116:2476-81.
173. Zhao H, Hussain AM, Duduta M, Vogt DM, Wood RJ, Clarke DR. Compact dielectric elastomer linear actuators. Adv Funct Mater 2018;28:1804328.
174. Alapan Y, Karacakol AC, Guzelhan SN, Isik I, Sitti M. Reprogrammable shape morphing of magnetic soft machines. Sci Adv 2020;6:eabc6414.
175. Cui J, Huang TY, Luo Z, et al. Nanomagnetic encoding of shape-morphing micromachines. Nature 2019;575:164-8.
176. Ford MJ, Ambulo CP, Kent TA, et al. A multifunctional shape-morphing elastomer with liquid metal inclusions. Proc Natl Acad Sci U S A 2019;116:21438-44.
177. Zhao Z, Kumar J, Hwang Y, et al. Digital printing of shape-morphing natural materials. Proc Natl Acad Sci U S A 2021;118:e2113715118.
178. Dudek KK, Martínez JAI, Ulliac G, Kadic M. Micro-scale auxetic hierarchical mechanical metamaterials for shape morphing. Adv Mater 2022;34:e2110115.
179. Karniadakis GE, Kevrekidis IG, Lu L, Perdikaris P, Wang S, Yang L. Physics-informed machine learning. Nat Rev Phys 2021;3:422-40.
180. Wood RJ, Steltz E, Fearing RS. Optimal energy density piezoelectric bending actuators. Sensor Actuat A Phys 2005;119:476-88.
181. Lin Z, Shao Q, Liu X, Zhao H. An anthropomorphic musculoskeletal system with soft joint and multifilament pneumatic artificial muscles. Adv Intell Syst 2022;4:2200126.
182. Li J, Ma W, Song L, et al. Superfast-response and ultrahigh-power-density electromechanical actuators based on hierarchal carbon nanotube electrodes and chitosan. Nano Lett 2011;11:4636-41.
183. Zhao H, Li Y, Elsamadisi A, Shepherd R. Scalable manufacturing of high force wearable soft actuators. Extreme Mech Lett 2015;3:89-104.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.






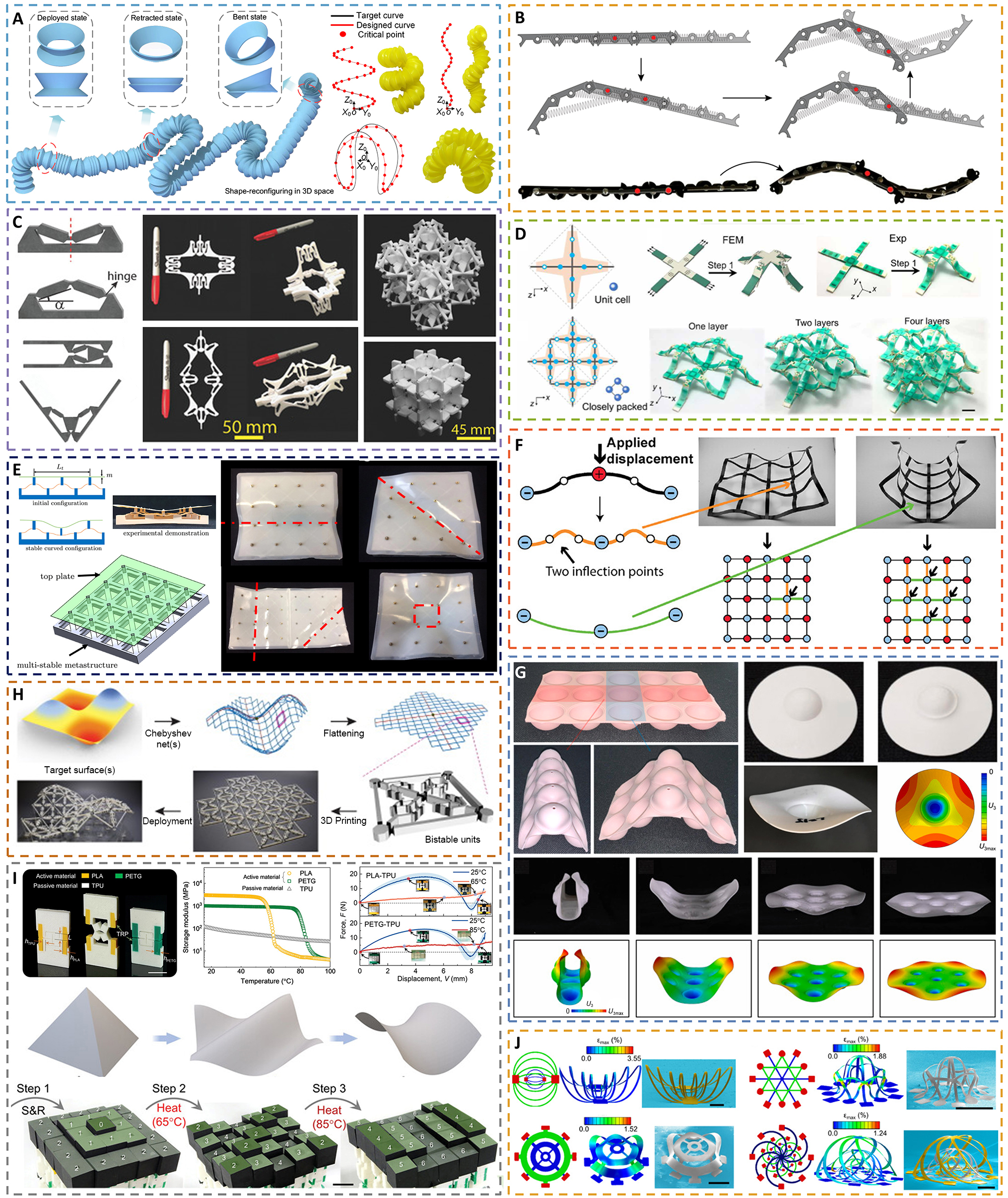



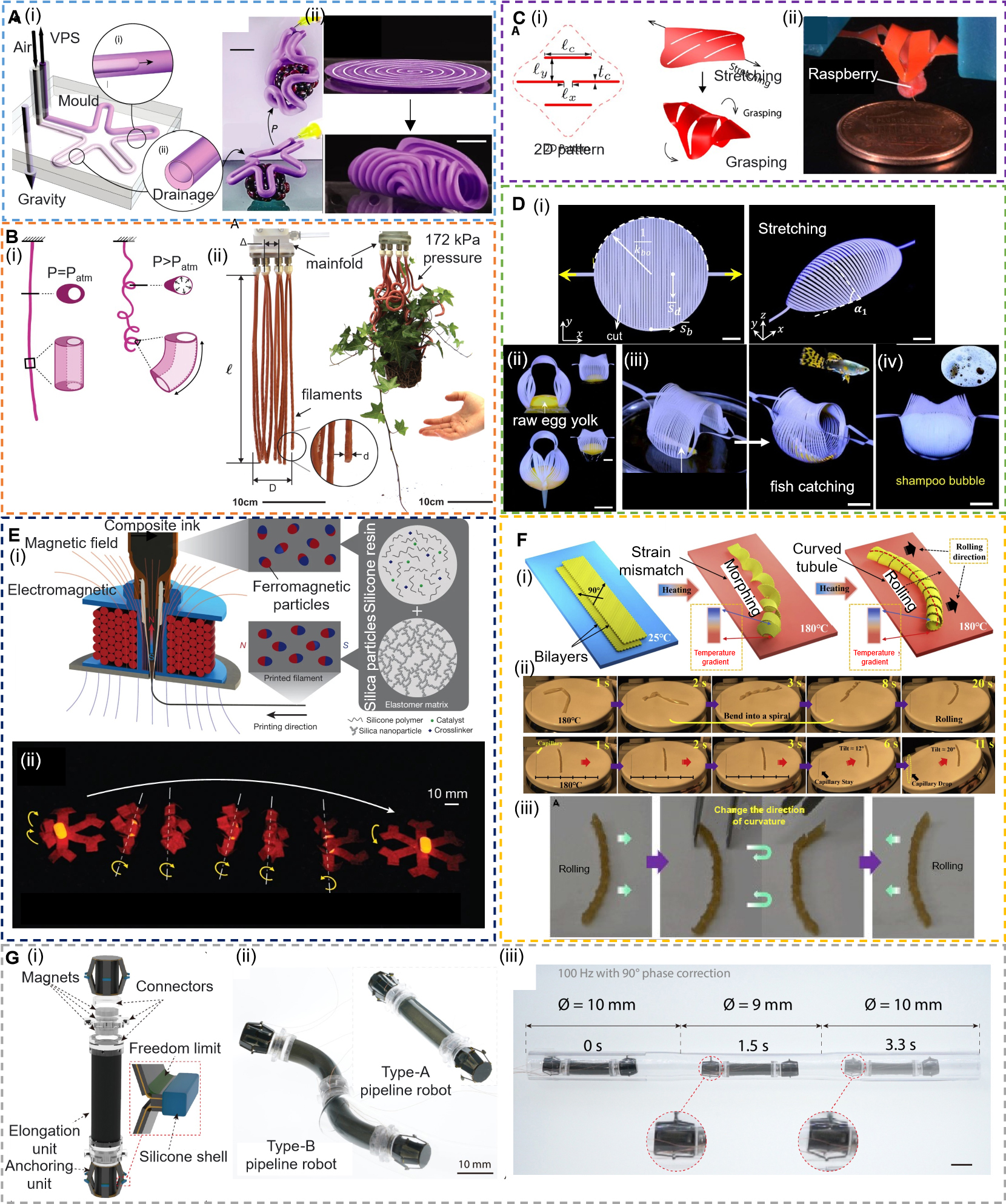













Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].