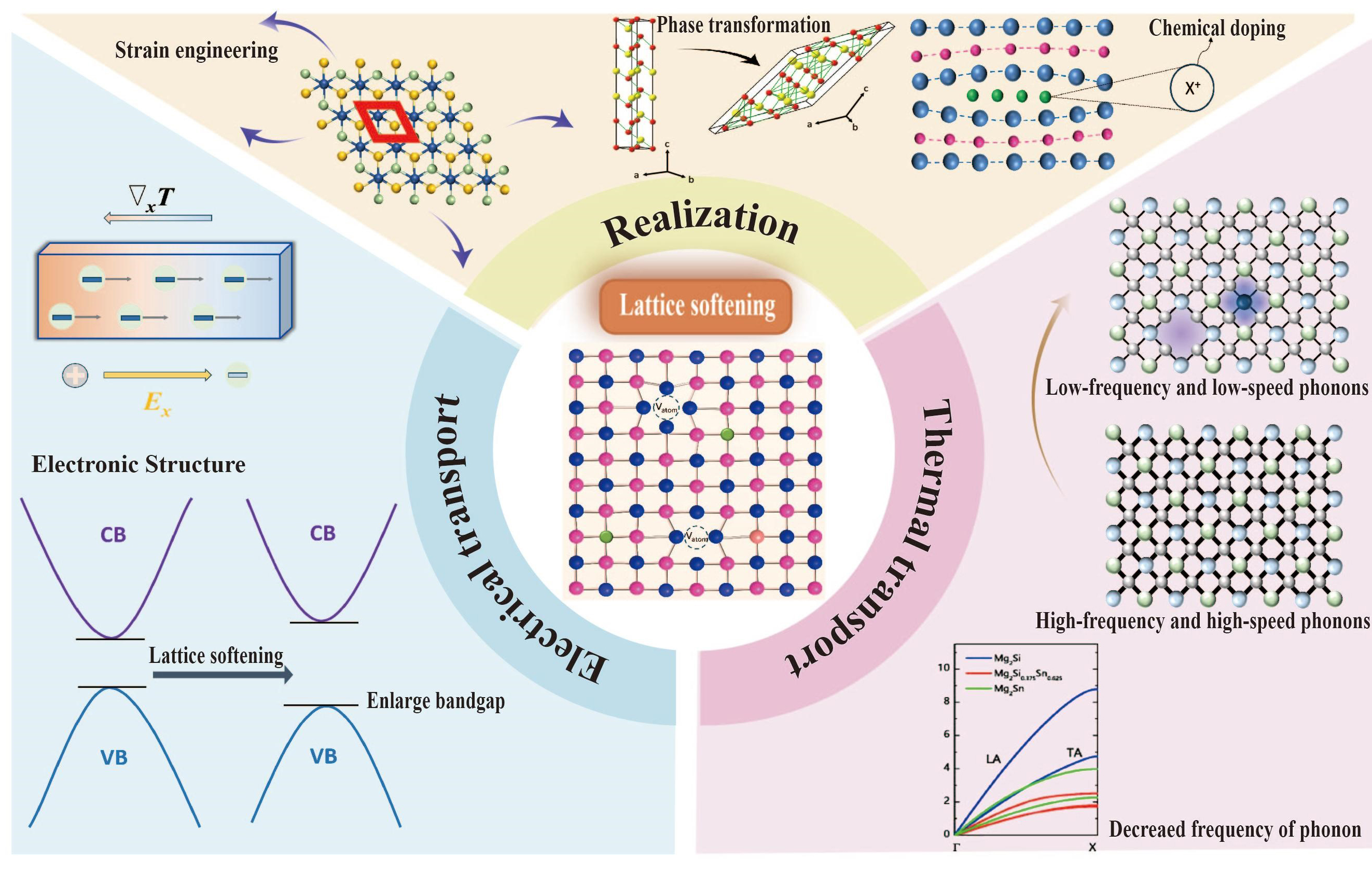
Lattice softening in thermoelectric materials
Abstract
Lattice softening refers to reducing the lattice stiffness of materials by weakening the binding force between atoms, thereby changing the electron and phonon transport characteristics. The advantage of lattice softening compared to other strategies for optimizing the properties of thermoelectric materials is that it can significantly reduce the lattice thermal conductivity by reducing the sound velocity without significantly affecting the electrical properties. Moreover, lattice softening shows a wide range of application potential in other material fields, such as magnetostrictive materials and intermetallic alloys. However, systematic reviews on the causes, effects, and specific applications of lattice softening in thermoelectric materials are still limited. This review introduces the recent progress of lattice softening in thermoelectric materials, focusing on how to achieve it and its mechanism in optimizing thermoelectric performance. Through mechanical strain engineering, chemical doping, and phase transition strategies to achieve lattice softening, one could lower the phonon speed, reduce the lattice thermal conductivity, and optimize the Seebeck coefficient and conductivity. In the outlook section, the potential applications of lattice softening in sustainable energy technologies are explored.
Keywords
INTRODUCTION
Since the beginning of the 21st century, the excessive exploitation and consumption of non-renewable energy sources have intensified the energy crisis. According to the International Energy Agency (IEA), one-third of the world’s energy is consumed by manufacturing, and 50% of this energy is emitted in the form of industrial waste heat. 60% of this waste heat can be utilized, but only 30% in China[1]. This inefficiency is further underscored by the fact that only around 30% of thermal energy[2] and 34% of fossil fuel energy is efficiently used, with the remainder released into the atmosphere as ineffective waste heat[3], leading to global warming and other environmental issues. This highlights the urgent need for efficient energy utilization and waste heat recovery. The exploration of novel substances concerning the creation and use of renewable energy sources is now crucial. Over the past few decades, research on thermoelectric (TE) materials has provided essential insights into their potential for sustainable energy applications[4-8], particularly in areas such as waste heat recovery[3,9,10], solar energy utilization[11,12], and thermal sensing[13-15]. TE materials can directly convert thermal energy into electricity, making them promising candidates for addressing environmental problems and the energy crisis[16,17].
The properties of TE materials[18] are measured using a dimensionless thermoelectric figure of merit ZT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and κ is the total thermal conductivity, consisting of electron thermal conductivity κe and lattice thermal conductivity κ1. To obtain high ZT, TE materials must have high S, high σ, and the lowest possible κ value. κl is related to phonon transport, and represents an inverse relationship between the S and the σ related by carrier concentration. Higher Seebeck coefficients occur at lower carrier concentrations, as fewer carriers enhance their response to temperature gradients. However, lower carrier concentration reduces electrical conductivity, while higher conductivity increases electronic thermal conductivity and total thermal conductivity, ultimately lowering ZT. Researchers need to optimize these parameters through material design and engineering to achieve excellent thermoelectric performance. Traditional methods for optimizing thermoelectric material performance, such as nanocomposite[19-23] and energy band engineering[24-26], make it possible to modify the parameters. Nanocomposites can introduce many interfaces, enhance phonon scattering, and reduce the lattice thermal conductivity of materials. The advantage of energy band engineering is to improve the electrical conductivity and Seebeck coefficient by adjusting the energy band structure, leading to improved power factor value (S2σ). However, these methods often involve parameter coupling, making it difficult to simultaneously optimize electrical and thermal performance.
Among the various optimization strategies, lattice softening has gradually emerged as a practical approach for enhancing thermoelectric performance. Lattice softening[27-32] refers to weakening the binding force between atoms, thereby changing the electron and phonon transport characteristics of the material, which is widely used in the fields of thermoelectric[31,33-35], magnetostrictive materials[36-38] and intermetallic alloys[39,40]. Lattice softening mainly reduces lattice thermal conductivity, thus improving thermoelectric efficiency without directly introducing additional phonon scattering, avoiding a significant impact on electrical performance.
Despite the rapid progress in this research field, there is still a lack of systematic evaluation of the specific applications of lattice softening, particularly regarding how lattice softening changes the thermal and electrical conduction performance of materials. This study aims to fill this gap by evaluating the practical application and mechanisms of lattice softening in various thermoelectric materials [Figure 1]. It provides an in-depth analysis of lattice softening on optimizing the coupled thermoelectric parameters, giving a theoretical foundation and practical reference for the design of high-performance thermoelectric materials.
ADVANTAGES OF LATTICE SOFTENING
Lattice softening changes the physical properties of the thermoelectric material [Table 1]. Its core is to increase lattice constants and weaken the bond strength between atoms. The reduction in bond strength leads to a decrease in the elastic modulus, lattice vibration frequency, and phonon velocity. Lattice softening can be achieved by mechanical strain engineering, chemical doping, and phase transition.
Physical property related to lattice softening in thermoelectric materials
| Physical property | Description |
| Lattice constant | Increased lattice constant weakens bonding among atoms |
| Elastic modulus | Lower elastic modulus makes lattice softer, affecting thermal and electrical properties |
| Thermal expansion | Lattice softening can directly or indirectly affect the thermal expansion behavior |
| Phonon group speed | Slower phonon speed due to lattice changes further reduces κl |
To illustrate the advantages of lattice softening, we minutely contrast it with other traditional strategies for optimizing the properties of thermoelectric materials. Common methods for optimizing the performance of thermoelectric materials include energy band engineering and nanocomposites. Energy band engineering[41] primarily focuses on optimizing electrical performance by modifying the material's band structure, such as band convergence and band flattening. For example, by increasing the band degeneracies, the Seebeck coefficient can be increased without significantly reducing the mobility. As for band flattening, Zhang et al.[42] realized that Gd doping flattens the conduction band edge of PbSe, thus resulting in a large Seebeck coefficient. However, its disadvantage is that the energy band structure of the material needs to be accurately adjusted, which puts forward high requirements for the design and synthesis of the material. Nanocomposites means introducing nanostructures into the matrix to optimize thermoelectric properties by nano-effects. The interface between the nanophase and the matrix can strongly scatter phonons, thus significantly reducing the thermal conductivity of the lattice. Bai et al.[43] used hydrothermal synthesis to bind functionalized multi-walled carbon nanotubes (f-MWCNTs) into the Bi2S3 matrix. The enhancement of phonon scattering results in the total thermal conductivity of Bi2S3/f-MWCNTs nanocomposites at 589 K being 0.27 W m-1 K-1, which is close to the lowest value of Bi2S3-based materials. However, the preparation of nanocomposites usually requires precise control of the size, distribution, and interface properties of the nanophase, which places high demands on the synthesis process.
Compared to the two methods [Table 2], lattice softening (1) can reduce the thermal conductivity of the lattice more directly while minimizing the negative impact on electrical properties; and (2) does not require complex preparation processes or expensive equipment. This makes the lattice softening strategy suitable for most thermoelectric material systems.
Advantages and disadvantages of three methods for optimizing the TE performance
| Method | Advantages | Disadvantages |
| Lattice softening | Structural changes lower lattice thermal conductivity | - |
| Softened lattice enlarges band gap | ||
| Band engineering | Band structure modulation increases carrier concentration and mobility | Requires sophisticated growth and doping techniques |
| Not all materials are suitable for band engineering | ||
| Nanocomposites | Interface scattering decreases lattice thermal conductivity | Interfaces in nanocomposites may be unstable |
| Better mechanical strength | Complex manufacturing processes increase costs |
REALIZATION METHOD OF LATTICE SOFTENING
Mechanical Strain engineering
Mechanical strain engineering[44-50] is a method of changing the lattice structure of a material by applying mechanical strain. Mechanical strain refers to the deformation of the material under the action of external forces, which can induce lattice softening [Figure 2A].
Figure 2. (A) Schematic diagram of lattice softening caused by mechanical strain; (B) Schematic diagram of ball milling; (C) The speed of sound (vs) measured by pulse-echo ultrasound versus the internal strain (CϵXRD) as measured. Copyright 2019, Wiley[28]. (D) Schematic diagram of graphene tensile test; (E) Evolution of the spectra of the 2D under strain. Copyright 2009, Wiley[51]; (F) Schematic of HPT instrument and method; insert is the picture of the as-processed sample and a schematic of how the stress is introduced; (G) Internal inhomogeneous strain characterization of as-sintered and HPT-processed silicon under 0-1/2 rotation, grain size, and mean strain (Cε) obtained from the analysis. Copyright 2023, Royal Society of Chemistry[52]. XRD: X-ray diffraction; HPT: high-pressure torsion.
Hanus et al.[28] synthesized stoichiometric PbTe samples under different internal strains induced by high-energy ball milling [Figure 2B]. Bulk PbTe particles with increasing internal strains showed significant phonon velocity reduction (lattice softening). By measuring sonic velocity (vs) and internal strain (CϵXRD), a linear relationship was found between the decrease in sound velocity and the increase in the internal strain of the material [Figure 2C], where ϵXRD is the internal strain determined via the Williamson-Hall method, and C is a constant related to the nature of the strain and details of the analysis method.
The relationship between strain and phonon frequency (and thus the speed of sound) is described through the Grüneisen tensor
which at small strains can be written as
where ω0 is the phonon frequency at zero strain. Recognizing that ω ∝ vs at low ω, it is possible to define an engineering Grüneisen parameter γint, which is associated with the internal-strain state of PbTe measured via X-ray diffraction (XRD). Then
This expression is consistent with the experimental observation of a linear dependence of the speed of sound on the strain. From a fit of Equation 3 to the experimental data in Figure 2C using C = 4, γint is estimated to be 5, which is similar to the thermodynamic Grüneisen parameter of PbTe.
Huang et al.[51] studied the graphene monolayer samples under mechanical stripping by Raman spectroscopy. With uniaxial stress to graphene [Figure 2D], 2D and G bands of graphene were significantly redshifted under strain [Figure 2E], which indicates the occurrence of phonon softening. Xu et al.[52] applied a moderate high-pressure torsion (HPT) process [Figure 2F] to nanocrystalline silicon by directly introducing finer nanostructures and internal strains, resulting in a global lattice softening and a significant boundary softening effect [Figure 2G], which reduced the phonon group velocity and enhanced phonon scattering at grain boundaries, respectively. A record low κl of 1.49 W m-1 K-1 was achieved.
Chemical doping
Chemical doping[31,53-57] can alter the lattice structure of the material by introducing doping atoms with mismatched dimensions, thus achieving lattice softening [Figure 3A]. For example, Zhang et al.[58] chose room-temperature cubic GeMnTe2 as the matrix to alloy Ag and Sb at the Ge/Mn site [Figure 3B]. Due to the huge difference [Figure 3C] in atomic electronegativity, mass, and radius, lattice softening would be caused, thereby reducing sound velocity and resulting in a significant reduction in lattice thermal conductivity. The introduction of certain doping atoms increases the number density of vacancies, which affects the stiffness of the lattice. In previous work, our group[59] modulated the number density of two-dimensional 2D Te vacancies in lead telluride (PbTe) by doping bismuth and indium [Figure 3D]. DFT calculations show that (Bi, In) co-doping reduces the formation energy of these defects, and increases the density of single-atom-layer two-dimensional vacancy (D2D-vac). 2D Te vacancy causes bond softening [Figure 3E], significantly reducing the phonon velocity and lattice thermal conductivity.
Figure 3. (A) Schematic diagram of lattice softening caused by chemical doping; (B) Schematic illustration of lattice anharmonicity due to the complexity of Ge sublattice; (C) Difference between elements (Ge, Mn, Ag and Sb) in atomic mass, radius, and electronegativity. Copyright 2025, Elsevier[58]; (D) Schematic diagram of single-atom-layer 2D Te vacancies, Bi and In doping in Pb0.988Bi0.007In0.005Te crystal structures; (E) Phonon group velocity as a function of frequency for PbTe (black) and PbTe with Bi/In next to 2D vacancy (blue). Copyright 2024, Elsevier[59]; (F) Crystal structure of Bi8Te9, Bi6Te7, Bi4Te5, and Bi2Te3; (G) A schematic illustration of the underlying mechanisms of the ultralow lattice thermal conductivity in the (Bi2)m(Bi2Te3)n (m/n = 3:9, 2:7, and 1:5) homologous series in comparison with Bi2Te3. The weak chemical bonding leads to low group velocity in the (Bi2)m(Bi2Te3)n homologous series compared to Bi2Te3. In addition, the Brillouin zone of the (Bi2)m(Bi2Te3)n homologous series shrinks as the number of atoms in the unit cell increases. Consequently, the high-frequency acoustic phonon modes are cut off because of the low group velocity of the acoustic phonon modes and the small volume of the first Brillouin zone in the (Bi2)m(Bi2Te3)n homologous series. Copyright 2021, American Chemical Society[60]; (H) Atomic-resolution HAADF-STEM image of Sn0.87Mn0.08Sb0.08Te-5%AgSbTe2 and EDS mappings of SnTe matrix (FFT image that corresponds to the HAADF-STEM image inset); (I) 2D map describing chemical bonds in solids. The map is spanned by the number of electrons transferred normalized by the oxidation state and electrons shared between adjacent atoms. Different chemical bonding mechanisms are demarcated by different colors. Copyright 2022, the Authors. Advanced Functional Materials published by Wiley-VCH GmbH[66]; (J) A schematic band diagram from simple chemical bonding (hybridization) arguments. The schematics of atomic orbital energies of Cu, S, Mn, Ag, In, Ga, Zn, Fe, and the molecular orbital energies of Mn-doped Cu2S and (K) Mn-doped Cu2S with hexagonal structures. The bonding (stabilizing) and antibonding (destabilizing) states could be well defined by the COHP values. The bonding orbital (grey area) has negative COHP. Copyright 2023, Elsevier[67]. HAADF-STEM: High-angle annular dark field-scanning transmission electron microscopy; FFT: fast Fourier transformation; EDS: energy dispersive spectrometer; COHP: crystal orbital hamilton populations.
Chemical doping can also soften the lattice by affecting the van der Waals bond, metavalent bonding, and bonding (stabilizing) and antibonding (destabilizing) states. Zhu et al.[60] investigated the high-temperature thermoelectric properties of (Bi2)m(Bi2Te3)n series compounds, revealing multiple mechanisms for their intrinsic low lattice thermal conductivity. (Bi2)m(Bi2Te3)n natural superlattice series compounds have layered structures [Figure 3F]. It consists of Bi2Te3 quintuple layers [Te-Bi-Te-Bi-Te] and a bismuth double layer (Bi2) stacked along the C-axis, with van der Waals bonds between the layers. Compared to Bi2Te3, the insertion of a bismuth bilayer in the (Bi2)m(Bi2Te3)n compound changes the interlayer van der Waals bond action, resulting in reduced longitudinal and transverse sound velocity. The decrease in sound velocity indicates the weakening of the interlayer bond (van der Waals bond). The weakening of the bond has an important effect on the lattice thermal conductivity. The (Bi2)m(Bi2Te3)n compound thus has extremely low lattice thermal conductivity [Figure 3G], such as κl of about 0.42 W m-1 K-1 for Bi8Te9 at 300K, much lower than the κl of Bi2Te3 at 300 K (about 1.6 W m-1 K-1). In the field of thermoelectric materials, metavalent bonding[61-65] (MVB), as a unique form of chemical bonding, describes a special semi-filled σ bond with only one electron between adjacent atoms, which is essentially a competition between electron localization and delocalization. Liu et al.[66] significantly improved the solid solubility of Ag in SnTe [Figure 3H] by combining with AgSbTe2 compounds with the same metavalent bond [Figure 3I]. Due to atomic size differences and other factors, the doping of Ag will produce lattice strain in the lattice. The related lattice strain softens the phonons and significantly reduces the lattice thermal conductivity, resulting in the lattice thermal conductivity of Sn0.87Mn0.08Sb0.08Te-5%AgSbTe2 being as low as 0.30 W m-1 K-1 at 873 K. Wang et al.[67] synthesized Cu1.98-2yMnyS and Cu1.98-2xMnxS0.985Se0.015 series polycrystalline samples by high-temperature melt-annealing combined with hot pressing. The DFT calculation shows that when Mn doping Cu2S, Mn’s 3d orbital interacts strongly with S’s 3p orbital [Figure 3J], weakens the Cu-S bond [Figure 3K], reduces the transition energy barrier and enthalpy change, and stabilizes the low-temperature cubic phase.
Phase transformation
Phase transition[67-70] refers to the phenomenon that a material changes from one phase (state) to another under different conditions (such as temperature, pressure, chemical environment, etc.), including structural phase transition[71-73], superionic phase transition[74-76], and topological transition[77-80]. It can significantly change the lattice structure of the material, thus affecting the physical properties of the material [Figure 4A].
Figure 4. (A) Schematic diagram of lattice softening caused by phase transition; (B) Powder XRD patterns for Bi2-xSbxSe3; (C) Lattice thermal conductivity as a function of the Sb content for Bi2-xSbxSe3. The solid and dashed lines are estimated based on the Klemens-Callaway theory, using different ε values. Copyright 2016, Royal Society of Chemistry[81]; (D)
Structural phase transition refers to the change of the crystal structure of the material, such as changing from a cubic system to a hexagonal system. For example, Wang et al.[81] achieved chemical bond softening and structural distortion in Te-free Bi2-xSbxSe3 by composition-induced (Sb alloying) structural transition from rhomboid phase to orthorhombic phase [Figure 4B], resulting in significant changes in electron band structure and phonon dispersion. At the same time, phonon softening and lattice disharmony caused by weak interchain interactions greatly hinder the heat-carrying phonons, resulting in a significant decrease in lattice thermal conductivity at 300 K [Figure 4C]. Yang et al.[82] quantitatively investigated the relationship between subtle changes in the statically disordered atoms across different CuTeI phases and κl during phase transitions. Specifically, α-CuTeI [Figure 4D] exhibits substantial lattice softening compared to β-CuTeI [Figure 4E], characterized by a 10.4% decrease in the vs and a ≈ 2 GPa reduction in the shear modulus at 273 K. The more significant reductions [Figure 4F] in vT compared to vL resulted in an increase in the average Grüneisen parameter, which further contributed to a more than 44% reduction in κl.
The superionic phase transition[83] refers to the phase transition process in which the mobility of ions in the lattice of the material is significantly increased under certain conditions, resulting in a substantial increase in the conductivity of the material. Shen et al.[84] study the case of a superionic phase transition in the Argyrodite Ag8GeSe6, where the soft mode does not freeze into a static distortion but rather triggers solid state diffusion upon crossing Tc. Consistently, no phonon hardening is observed in the superionic phase above Tc, and the soft mode maintains its over-damped character, as indicated in Figure 4G.
Two types of topological phase transition that can cause lattice softening are introduced here. Lifshitz phase transition[85-88] is a special topological Fermi surface transition, which occurs when the topological structure of the Fermi surface of the material changes and Fermi levels pass through the Van Hove singularity (VHS), resulting in a change in the density of the electronic states. Noad et al.[89] took an ultra-clean, quasi-two-dimensional correlated metal Sr2RuO4 single crystal, machined it into a neck and embedded it in an epoxy resin, and used custom equipment to synchronously monitor uniaxial stress and strain. They measured Young’s modulus. It is found that at Lifshitz transition strain, Young’s modulus decreases significantly
LATTICE SOFTENING AFFECTS ELECTRICAL TRANSPORT PROPERTIES
The electrical transport properties of thermoelectric materials include the conductivity and Seebeck coefficient. Conductivity is a parameter that measures the conductivity of a material, which is related to the carrier concentration and mobility within the material. The Seebeck coefficient describes the ability of a material to generate an electromotive force under temperature difference, which is related to the electronic structure of the material. The corresponding formula is as follows[18]:
where n, e, μ, h, kB, and m* stand for the carrier concentration, elementary charge, carrier mobility, Planck constant, Boltzmann constant, and carrier effective mass, respectively.
Lattice softening caused by chemical doping leads to increased vacancy density, thereby increasing the concentration of carriers and further optimizing the conductivity. Lattice softening can also lead to changes in the band structure [Figure 5A], which can affect the position of the Fermi level and the concentration of carriers.
Figure 5. (A) Schematic diagram of the effect of lattice softening on electrical transport properties of thermoelectric materials; (B) Temperature-dependent electrical transport properties for Cu3-3xAg3xSbSe4 (x = 0, 0.02, 0.03, 0.04, 0.05, 0.06) samples: electrical resistivity; (C) Room temperature carrier concentration nh and carrier mobility μ as a function of the Ag doping content. Copyright 2019, Royal Society of Chemistry[90]; (D) Top and side views of the crystal structure of 1T-SnSSe monolayer. The Heff in the side view represents the effective thickness of the 1T-SnSSe monolayer; (E) The calculated bandgaps (including the HSE06 + SOC and PBE + SOC methods) as a function of biaxial tensile strains ranging from 0% to 8% and the calculated Sn-S/Sn-Se bond lengths versus the lattice parameters corresponding to the biaxial tensile strains. Copyright 2022, Elsevier[92]. HSE06: Heyd-scuseria-ernzerhof; SOC: spin-orbital coupling effect; PBE: perdew-burke-ernzerhof.
Zhang et al.[90]’s strategy of eliminating p-d hybridization by Ag substitution can achieve a high average ZT in Cu3SbSe4. Using density functional theory (DFT), it is proved that the weakening of Cu-Se bonds favors the formation of Cu vacancies, which increases carrier concentration and thus reduces resistivity [Figure 5B and C]. Liang et al.[91] prepared Mg3.2-xMnxSb1.5Bi0.49Se0.01 Zintl compounds co-doped with Se and Mn, in which Mn was doped at the Mg site. Since the electronegativity of Mn (1.55) is larger than that of Mg (1.31), the chemical bonds in Mn-doped samples are softened, leading to a significant increase in carrier concentration and mobility. As can be seen from Equation 5, the Seebeck coefficient is inversely proportional to the carrier concentration S ~ n-2/3. Therefore, at low temperatures (below 400 K), the Seebeck coefficient of the manganese-doped sample is significantly lower than that of the non-manganese sample. For example, at 323 K, it decreases from -284 μV K-1 in the Mn-free sample (3.92 × 1019 cm-3) to -250 μV K-1 in the x = 0.02 sample (4.7 × 1019 cm-3). Tang et al.[92] investigated the effect of strain engineering on the thermoelectric properties of asymmetric Janus 1T-SnSSe monolith. Figure 5D presents the top and side views of the 1T-SnSSe monolith, which is formed by the S-Sn-Se covalent bond. The band gap of 1T-SnSSe monolayers increases first and then decreases with the increasing biaxial tensile strain [Figure 5E]. The softened lattice structure (such as the increase in lattice constant) caused by strain is one of the reasons for the change in the band gap, leading to an increase in the Seebeck coefficient. At 300 K, the Seebeck coefficient is 94.60 μV K-1 at 0% strain and increases to 189.03 μV K-1 at 8% strain. At 900 K, the Seebeck coefficient is 213.37 μV K-1 at 0% strain and rises to 214.84 μV K-1 at 6% strain.
LATTICE SOFTENING AFFECTS THERMAL TRANSPORT PROPERTIES
The heat conduction of thermoelectric materials mainly includes the contribution of carrier and lattice vibration. Carrier thermal transport is closely related to electric transport, while lattice thermal transport involves phonon propagation. The effect of lattice softening on the lattice thermal conductivity (κl) is reviewed in detail below.
Assuming that phonon-phonon scattering dominates at temperatures well above the Debye temperature, the phonon group velocity (vg) is directly connected to κl, as shown by Equation 6[82]:
where
In Yang et al.’s study[82], they derived Equation 9 based on Equations 6-8:
The right part of the denominator in Equation 9, enclosed in parentheses, is related to the vs, while the left part is associated with the γ. Importantly, as the variables
Lattice softening decreases the speed of sound (vL and vT) and elastic modulus [Table 3], thus reducing κl. Most importantly, the softening of the material lattice can achieve the reduced thermal conductivity of the lattice without introducing additional phonon scattering mechanisms. Moreover, lattice softening also significantly increases the thermal expansion rate of materials by changing the lattice spacing and reducing the lattice rigidity.
Speed of sound and elastic properties of pristine and doped compounds
| Compound | Longitudinal/km s-1 | Transverse/km s-1 | Bulk/GPa | Shear/GPa | Young/GPa |
| GeTe | 3.445 | 1.965 | - | - | - |
| Ge0.8Sn0.2Te | 3.365 | 1.833 | - | - | - |
| Ge0.6Sn0.4Te | 3.179 | 1.632 | - | - | - |
| Ge0.4Sn0.6Te | 2.953 | 1.535 | - | - | - |
| Ge0.2Sn0.8Te | 3.331 | 1.876 | - | - | - |
| SnTe | 3.408 | 1.873 | - | - | - |
| CuGaTe2 | 3.84 | 2.08 | 53.1 | 25.4 | 65.8 |
| Cu0.95Li0.05GaTe2 | 3.77 | 2.05 | 50.0 | 24.4 | 63.1 |
| CuGaTe1.99Sb0.01 | 3.82 | 2.09 | 51.4 | 25.6 | 65.8 |
| Cu0.05Li0.05GaTe1.99Sb0.01 | 3.40 | 1.91 | 37.4 | 20.3 | 51.7 |
| Cu0.95Ag0.05InTe2 | 3.78 | 2.05 | 51.7 | 24.9 | 64.4 |
| Cu0.9Li0.05Ag0.05InTe2 | 3.44 | 1.81 | 43.8 | 19.3 | 50.5 |
| SrCuSb | 4.237 | 2.500 | - | - | - |
| SrAgSb | 3.803 | 2.236 | - | - | - |
| Sr2ZnSb2 | 3.767 | 2.174 | - | - | - |
Group velocity and frequency of phonons
Phonon group velocity[93-96] is a physical quantity that describes the speed at which phonons (the quanta of lattice vibrations) propagate through a material. The group velocity is closely related to the dispersion relation of phonons, which can be obtained by derivation of the dispersion relation. Specifically, the group velocity of phonons can be calculated by the following formula[95]:
where ω is the frequency of the phonon, q is the wave vector of the phonon, C is the elastic constant (Young’s modulus, shear modulus, or bulk elastic modulus) and ρ is the density of the material.
Research on the reduction of lattice thermal conductivity due to lattice softening is prevalent in the field of thermoelectrics. Jiang et al.[97] studied the mechanism of electron and phonon localization and found that the crystal symmetry of high-entropy materials improves the electron delocalization distribution [Figure 6A], optimizes the band structure, and improves the electrical properties. At the same time, the disordered distribution of elements produces lattice strain, destroys crystal symmetry, and affects phonons. Raman spectroscopy [Figure 6B] shows phonon mode splitting and transverse phonons are more affected by disorder; sound velocity measurements [Figure 6C] show that the transverse sound velocity vt drops faster than the longitudinal sound velocity vl, that is, phonon softening, which enhances the anharmonicity, significantly reduces the lattice thermal conductivity, and synergies with electron delocalization to optimize the thermoelectric properties. Han et al.[98] found that a 65% reduction in lattice thermal conductivity can be achieved with only 10% covalent Hf doping in a high-band NbFeSb system, compared to the fourfold higher isoelectronic Ta alloying concentration. Figure 6D shows the neutron-weighted phonon DOSs of Nb0.9X0.1FeSb at 5 K. Three phonon bands of 0-20 MeV, 20-30 MeV, and 30-45 MeV were observed, corresponding to one and two phonon bands, respectively. In the energy range of 30-35 MeV, significant softening of optical phonons was observed in Hf- and Zr-doped Nb0.9Hf0.1FeSb and Nb0.9Zr0.1FeSb, respectively. Softening of the phonon spectrum means that phonons have lower energies, which can lead to a decrease in the mean free path of phonons. Hanus et al.[28] found that lattice softening can significantly reduce thermal conductivity [Figure 6E]. The inset of Figure 6E shows the sound velocity reduction data of different samples; for example, the sound velocity of (Na,Sr)-PbTe is 1860 m s-1, and the sound velocity of (Na,Eu)-PbTe is 1719 m s-1. The decrease in sound velocity correlates with lattice softening. According to κl = Avs3T-1, a decrease in sound velocity leads to a decrease in κl. The highlighted region in Figure 6E represents the part of reduced κl caused by lattice softening only, which is obviously different from the part caused by an increase in the phonon-defect scattering center. Tang et al.[92] used density functional theory (DFT) and semi-classical Boltzmann transfer theory to study the effect of strain engineering on the thermoelectric properties of asymmetric Janus 1T-SnSSe monolides. As the biaxial tensile strain increases, the lattice thermal conductivity decreases significantly [Figure 6F]. For example, because of lattice softening, the thermal conductivity at room temperature of an unstrained 1T-SnSSe monolellar lattice is about 19.77 W m-1 K-1, and when a biaxial tensile strain of 8% is applied, the lattice thermal conductivity drops sharply to about 3.53 W m-1 K-1. Tan et al.[99] studied the phonon transport and thermal conductivity of Mg2Si1-xSnx solid solution by first-principles calculation and phonon Boltzmann transport equation. Compared with Mg2Si and Mg2Sn, the acoustic phonon branch along the direction of “Γ-X” of Mg2Si0.375Sn0.625 was significantly softened [Figure 6G-J]. The acoustic phonon of Mg2Si0.375Sn0.625 has a relatively lower frequency under the same wave vector, which means that the energy of the phonon is reduced and the
Figure 6. (A) Distribution of normal strains in the GeTe and high-entropy Ge0.61Ag0.11Sb0.13Pb0.12Bi0.01Te samples. Left images and green lines are from GeTe samples, and right images and pink lines are from the Ge0.61Ag0.11Sb0.13Pb0.12Bi0.01Te sample. The value of σ is the root mean square; (B) Raman intensity and FWHM of the GeTe (left) and high-entropy Ge0.61Ag0.11Sb0.13Pb0.12Bi0.01Te (middle) samples; (C) Measured sound velocities of the transverse (νt) and longitudinal (νl) waves and the calculated Grüneisen parameter (γ) and lattice thermal conductivity (κl) values at room temperature, where ν0 is the measured sound velocity of the GeTe sample. Copyright 2022, AAAS[97]; (D) Measured neutron-weighted phonon DOSs of the Nb0.9X0.1FeSb compounds. The error bars represent one standard deviation from counting statistics. Copyright 2023, Han et al.[98]; (E) A reduction of κl upon the introduction of micro/nano structural defects. The lines show the κl= Avs3T-1 model describing phonon thermal conductivity in the high-T limit where the only scattering mechanism is phonon-phonon scattering. A is normalized to the Na-PbTe sample and fixed. The shaded region shows the reduction in κl expected from lattice softening alone, without assuming an increase in phonon-defect scattering centers. Phonon scattering mechanisms could account for the remaining reduction in κl, depicted by the cross-hatched region. The speed of sound (vs) reduction, measured in this study, is given in the legend. The circles are data for a Na-doped (0.75% Na) sample synthesized and measured in this study. The square data points are a low dislocation density sample from reference (Na0.015Eu0.03Pb0.955Te). Copyright 2019, Wiley[28]; (F) Lattice thermal conductivity versus temperature under different biaxial tensile strains (δ = 0%, 2%, 4%, 6%, and 8%) of unstrained and strained 1T-SnSSe monolayers. Copyright 2022, Elsevier[92]; Phonon dispersion relations for (G) Mg2Si; (H) Mg2Si0.375Sn0.625; and (I) Mg2Sn; the gradually changing colors indicate the group velocity for the corresponding phonon branches; (J) shows their acoustic phonon branches along the “Γ-X” direction. Copyright 2017, AIP Publishing[99]. FWHM: Full width at half maximum.
Thermal expansion coefficient
The thermal expansion coefficient[100-103] is a physical quantity related to the size of materials, which describes the volume change degree of the material when the temperature changes [Figure 7A]. Lattice softening may directly or indirectly affect the thermal expansion behavior of materials through a variety of mechanisms. These mechanisms include increased phonon scattering, enhanced anharmonic effects, changes in the Grüneisen constant, modifications of material properties, and the influence of
Figure 7. (A) Diagram of the effect of lattice softening on the coefficient of thermal expansion; (B) The XRD patterns of SPS-treated Cu1.8S-x% AgCl bulk specimens with different x values; (C) The enlarged patterns between 45.5° to 46.5° and the relative mass density of the samples; (D) The thermal expansion rate of Cu1.8S and Cu1.8S-2% AgCl in 300 K to 773 K. Copyright 2021, Elsevier[104]. SPS: Spark plasma sintering; XRD: X-ray diffraction.
Zhang et al.[104] investigated the effects of introducing AgCl into Cu1.8S. With the addition of AgCl, the (110) diffraction peak of Cu1.8S moves to the left [Figure 7B and C]. This is because the larger Ag+(1.15 Å) replaces the site of Cu+(0.96 Å), resulting in an increase in lattice volume. The change of lattice volume is an external manifestation of lattice softening, indicating that the distance and interaction between atoms have changed, reducing the rigidity of the lattice, making it more prone to deformation, and thus reflecting the trend of lattice softening. Lattice softening also increases the thermal expansion rate of Cu1.8S, and the thermal expansion rate dL/L0 of the Cu1.8S-1% AgCl sample increases rapidly after 500 K [Figure 7D], which is due to the more serious volatilization of sulfur after the introduction of AgCl and the damage of chemical bond strength.
In the field of material design, the thermal expansion coefficient is of great significance. By controlling the thermal expansion coefficient of the material, the thermal stress can be effectively reduced and the temperature stability and reliability of the material can be improved.
CONCLUSION AND OUTLOOK
Lattice softening offers a universal way to optimize thermoelectric properties through material design. In this paper, we first conclude three ways to achieve lattice softening, including mechanical strain engineering, chemical doping, and phase transition, and then discuss their distinct softening mechanisms by showing related examples. In addition, the effects of lattice softening on the electrical and thermal transport properties of TE materials are summarized. We believe that the continuous development and improvement of lattice softening technology will provide strong support for the design and preparation of high-performance thermoelectric materials, and promote the wide application of thermoelectric technology in the fields of energy recovery, temperature difference power generation, and thermal management.
In the future, with the continuous deepening of research and technological progress, lattice softening is expected to make breakthroughs in many aspects. First, through precise strain engineering and chemical doping, the lattice structure of the material can be more precisely regulated, which may further reduce the thermal conductivity and increase the conductivity and Seebeck coefficient, significantly improving the ZT value. Secondly, by introducing nanoparticles and nanocomposite structures, not only can the flexibility of the lattice be optimized, but also the phonon scattering can be more effectively increased, leading to improved thermoelectric conversion efficiency of the material. In addition, combined with advanced characterization techniques such as in situ extended X-ray absorption fine structure (EXAFS), in situ transmission electron microscopy (TEM), and inelastic neutron scattering, a deeper understanding of the effect of lattice softening on the microstructure of materials can be achieved, enabling finer regulation. Finally, more novel lattice softening methods can be developed to expand their applications in semiconductor, optical and magnetic materials through interdisciplinary cooperation.
DECLARATIONS
Authors’ contributions
Design and conception of the study, literature search, reference organization, data collection, data analysis, and manuscript drafting: Li, C.; Zhou, Z.
Provision of technical and material support, scientific discussion consultation, and manuscript revision suggestions: Fu, L.; Lou, Y.
All authors participated in the composition of the manuscript.
Availability of data and materials
Not applicable.
Financial support and sponsorship
None.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Tan, Z.; Feng, X.; Yang, M.; Wang, Y. Energy and economic performance comparison of heat pump and power cycle in low grade waste heat recovery. Energy 2022, 260, 125149.
2. Lu, X.; Pan, G.; Shi, Z.; Xu, B.; Lou, Y. Recent advances in interface engineering of thermoelectric nanomaterials. Mater. Chem. Front. 2023, 7, 4707-22.
3. Chen, Y.; Hong, G.; Li, L.; et al. Enlightening thermoelectric mastery: bio-inspired cellulose gel containing eco-friendly deep eutectic solvents. Chem. Eng. J. 2024, 483, 149344.
4. Miao, L.; Zhu, S.; Liu, C.; et al. Comfortable wearable thermoelectric generator with high output power. Nat. Commun. 2024, 15, 8516.
5. Beretta, D.; Perego, A.; Lanzani, G.; Caironi, M. Organic flexible thermoelectric generators: from modeling, a roadmap towards applications. Sustain. Energy. Fuels. 2017, 1, 174-90.
6. Yang, S. E.; Han, H.; Son, J. S. Recent progress in 3D printing of Bi2Te3-based thermoelectric materials and devices. J. Phys. Energy. 2024, 6, 022003.
7. Muddasar, M.; Menéndez, N.; Quero, Á.; et al. Highly-efficient sustainable ionic thermoelectric materials using lignin-derived hydrogels. Adv. Compos. Hybrid. Mater. 2024, 7, 863.
8. Li, C.; Jiang, F.; Liu, C.; Liu, P.; Xu, J. Present and future thermoelectric materials toward wearable energy harvesting. Appl. Mater. Today. 2019, 15, 543-57.
9. Du, K.; Wu, C. An innovative tubular thermoelectric generator (TTEG) for enhanced waste heat recovery in industrial and automotive applications. Appl. Sci. 2024, 14, 685.
10. Wang, J.; Chen, Y.; Liu, Y.; Liu, G.; Cai, R. Harvesting waste heat based on thermoelectric generation to drive LED car lamps. J. Therm. Anal. Calorim. 2024, 149, 3427-42.
11. Su, H.; Lin, P.; Lu, H.; Chen, Y. Efficient solar-thermal conversion and thermal energy storage towards personal thermal management and thermoelectric power generation enabled by massive screen printing of carbon nanotube dopped energy storage gels. J. Energy. Storage. 2024, 76, 109782.
12. Lewis, N. S. Research opportunities to advance solar energy utilization. Science 2016, 351, aad1920.
13. Chen, C.; Xu, F. Q.; Wu, Y.; et al. Manipulating hetero-nanowire films for flexible and multifunctional thermoelectric devices. Adv. Mater. 2024, 36, e2400020.
14. Han, Y.; Wei, H.; Du, Y.; et al. Ultrasensitive flexible thermal sensor arrays based on high-thermopower ionic thermoelectric hydrogel. Adv. Sci. (Weinh). 2023, 10, e2302685.
15. Gu, H.; Kang, S.; Fu, Y.; et al. High seebeck coefficient inorganic Ge15Ga10Te75 core/polymer cladding fibers for respiration and body temperature monitoring. ACS. Appl. Mater. Interfaces. 2023, 15, 59768-75.
16. Gupta, A.; Agrawal, S.; Pal, Y. Effect of thermoelectric materials in electrical and thermal performance of photovoltaic thermal (PVT) collector. IOP. Conf. Ser:. Mater. Sci. Eng. 2019, 691, 012036.
17. Zhang, Y.; Wang, W.; Zhang, F.; et al. Soft organic thermoelectric materials: principles, current state of the art and applications. Small 2022, 18, e2104922.
18. Shi, X. L.; Zou, J.; Chen, Z. G. Advanced thermoelectric design: from materials and structures to devices. Chem. Rev. 2020, 120, 7399-515.
19. He, J.; Xu, J.; Tan, X.; et al. Synthesis of SnTe/AgSbSe2 nanocomposite as a promising lead-free thermoelectric material. J. Materiomics. 2016, 2, 165-71.
20. Zhang, C.; de, M. M.; Li, Z.; et al. Enhanced thermoelectric performance of solution-derived bismuth telluride based nanocomposites via liquid-phase Sintering. Nano. Energy. 2016, 30, 630-8.
21. Chen, Y.; Nisar, M.; Qin, W.; et al. Integration of boron nitride into tin-enriched SnSe2 for a high-performance thermoelectric nanocomposite with optimized electrical transport and mechanical properties. Adv. Funct. Mater. 2025, 202425050.
22. Liu, W.; Yin, L.; Li, L.; et al. Grain boundary re-crystallization and sub-nano regions leading to high plateau figure of merit for
23. Gordillo, J. M.; Morata, A.; Sierra, C. D.; Salleras, M.; Fonseca, L.; Tarancón, A. Recent advances in silicon-based nanostructures for thermoelectric applications. APL. Materials. 2023, 11, 040702.
24. Yao, G.; Chen, Y.; Wang, S.; et al. Boosting thermoelectric performance of PbBi2Te4 via reduced carrier scattering and intensified phonon scattering. Small 2024, 20, e2400449.
25. Tan, X.; Wang, L.; Shao, H.; et al. Improving thermoelectric performance of α-mgagsb by theoretical band engineering design. Adv. Energy. Mater. 2017, 7, 1700076.
26. Yu, L.; Wei, S. T.; Wang, L. J.; et al. Band engineering and phonon engineering Effectively improve n-type Mg3Sb2 thermoelectric material properties. ACS. Appl. Mater. Interfaces. 2023, 15, 53594-603.
27. Slade, T. J.; Anand, S.; Wood, M.; et al. Charge-carrier-mediated lattice softening contributes to high zT in thermoelectric semiconductors. Joule 2021, 5, 1168-82.
28. Hanus, R.; Agne, M. T.; Rettie, A. J. E.; et al. Lattice softening significantly reduces thermal conductivity and leads to high thermoelectric efficiency. Adv. Mater. 2019, 31, e1900108.
29. Tan, G.; Hao, S.; Hanus, R. C.; et al. High thermoelectric performance in SnTe-AgSbTe2 alloys from lattice softening, giant phonon-vacancy scattering, and valence band convergence. ACS. Energy. Lett. 2018, 3, 705-12.
30. Muchtar, A. R.; Srinivasan, B.; Tonquesse, S. L.; et al. Physical insights on the lattice softening driven mid-temperature range thermoelectrics of Ti/Zr-inserted SnTe - an outlook beyond the horizons of conventional phonon scattering and excavation of heikes’ equation for estimating carrier properties. Adv. Energy. Mater. 2021, 11, 2101122.
31. Liu, M.; Guo, M.; Zhu, J.; et al. High-performance CaMg2Bi2-based thermoelectric materials driven by lattice softening and orbital alignment via cadmium doping. Adv. Funct. Mater. 2024, 34, 2316075.
32. Shen, X.; Zhang, B.; Chen, Q.; et al. Synergistically optimized thermoelectric properties of Ag1+xIn5Se8 alloys. Inorg. Chem. Front. 2019, 6, 3545-53.
33. Zhong, J.; Yang, X.; Lyu, T.; et al. Nuanced dilute doping strategy enables high-performance GeTe thermoelectrics. Sci. Bull. (Beijing). 2024, 69, 1037-49.
34. Tippireddy, S.; Azough, F.; Vikram; et al. Local structural distortions and reduced thermal conductivity in Ge-substituted chalcopyrite. J. Mater. Chem. A. 2022, 10, 23874-85.
35. Parashchuk, T.; Wiendlocha, B.; Cherniushok, O.; Knura, R.; Wojciechowski, K. T. High thermoelectric performance of p-type PbTe enabled by the synergy of resonance scattering and lattice softening. ACS. Appl. Mater. Interfaces. 2021, 13, 49027-42.
36. Chen, Y.; Fu, Z.; Wu, Y.; et al. Giant heterogeneous magnetostriction induced by charge accumulation-mediated nanoinclusion formation in dual-phase nanostructured systems. Acta. Materialia. 2021, 213, 116975.
37. Guan, C.; Chen, B.; Jiang, L.; et al. Atomic-scale insights into ω-variants in Galfenol triggered by displacive-diffusive transformation. Mater. Design. 2021, 205, 109745.
38. Rahman, N.; Gou, J.; Liu, X.; Ma, T.; Yan, M. Enhanced magnetostriction of Fe81Ga19 by approaching an instable phase boundary. Scripta. Materialia. 2018, 146, 200-3.
39. Guo, S.; Li, H.; Lu, Y.; Liu, Z.; Hu, X. Lattice softening enables highly reversible sodium storage in anti-pulverization Bi-Sb alloy/carbon nanofibers. Energy. Storage. Mater. 2020, 27, 270-8.
40. Mizoguchi, H.; Park, S. W.; Hosono, H. A view on formation gap in transition metal hydrides and its collapse. J. Am. Chem. Soc. 2021, 143, 11345-8.
41. Yang, J.; Zhang, X.; Ge, B.; et al. Effect of Zn migration on the thermoelectric properties of Zn4Sb3 material. Ceram. Int. 2017, 43, 15275-80.
42. Zhang, D.; He, P.; Liu, G.; et al. High thermoelectric performance of PbSe via a synergistic band engineering and dislocation approach. Scripta. Materialia. 2024, 244, 116003.
43. Bai, Y.; Li, X.; Ouyang, T.; et al. High thermoelectric performance in the n-type Bi2S3/f-MWCNTs nanocomposites prepared by hydrothermal method. Carbon 2023, 212, 118158.
44. Lv, H. Y.; Lu, W. J.; Shao, D. F.; Lu, H. Y.; Sun, Y. P. Strain-induced enhancement in the thermoelectric performance of a ZrS2 monolayer. J. Mater. Chem. C. 2016, 4, 4538-45.
45. Guo, Z.; Wang, J.; Yin, W. Atomistic origin of lattice softness and its impact on structural and carrier dynamics in three dimensional perovskites. Energy. Environ. Sci. 2022, 15, 660-71.
46. Zhang, G.; Zhang, Y. Strain effects on thermoelectric properties of two-dimensional materials. Mech. Mater. 2015, 91, 382-98.
47. Wu, Y.; Chen, Z.; Nan, P.; et al. Lattice strain advances thermoelectrics. Joule 2019, 3, 1276-88.
48. Sprague, L. W.; Huang, C.; Song, J.; Rubenstein, B. M. Maximizing thermoelectric figures of merit by uniaxially straining indium selenide. J. Phys. Chem. C. 2019, 123, 25437-47.
49. Yu, C.; Zhang, G.; Zhang, Y.; Peng, L. Strain engineering on the thermal conductivity and heat flux of thermoelectric Bi2Te3 nanofilm. Nano. Energy. 2015, 17, 104-10.
50. Song, X.; Wang, G.; Gan, S.; et al. Triaxial strain enhanced thermoelectric performance and conversion efficiency in Tl3TaSe4. J. Alloys. Compd. 2024, 1004, 175896.
51. Huang, M.; Yan, H.; Chen, C.; Song, D.; Heinz, T. F.; Hone, J. Phonon softening and crystallographic orientation of strained graphene studied by Raman spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 7304-8.
52. Xu, B.; Liao, Y.; Fang, Z.; et al. Extremely suppressed thermal conductivity of large-scale nanocrystalline silicon through inhomogeneous internal strain engineering. J. Mater. Chem. A. 2023, 11, 19017-24.
53. Moure, A.; Rull-bravo, M.; Abad, B.; et al. Thermoelectric skutterudite/oxide nanocomposites: effective decoupling of electrical and thermal conductivity by functional interfaces. Nano. Energy. 2017, 31, 393-402.
54. Mustafa, G.; Minhas, N.; Singh, H.; et al. Lattice softness regulates recombination and lifetime of carrier in Germanium doped CsPbI2Br perovskite: first principles DFT and NAMD simulations. J. Solid. State. Chem. 2023, 322, 123981.
55. Lee, S.; Esfarjani, K.; Luo, T.; Zhou, J.; Tian, Z.; Chen, G. Resonant bonding leads to low lattice thermal conductivity. Nat. Commun. 2014, 5, 3525.
56. Hu, J.; Zhu, J.; Dong, X.; et al. Breaking the minimum limit of thermal conductivity of Mg3Sb2 thermoelectric mediated by chemical alloying induced lattice instability. Small 2023, 19, e2301382.
57. Back, S. Y.; Cho, H.; Kim, Y.; et al. Enhancement of thermoelectric properties by lattice softening and energy band gap control in Te-deficient InTe1-δ. AIP. Advances. 2018, 8, 115227.
58. Zhang, Y.; Li, Y.; Mao, W.; Zhang, X.; Zhang, J.; Luo, J. Balancing structural stability and thermoelectric performance of GeMnTe2 by manipulating the complexity of cation sublattice. Mater. Today. Phys. 2025, 52, 101693.
59. Zhang, C.; Jin, K.; Dong, H.; et al. Synergistic enhancement of thermoelectric performance of n-type PbTe by resonant level and single-atom-layer vacancies. Nano. Energy. 2024, 126, 109615.
60. Zhu, H.; Zhao, C.; Nan, P.; et al. intrinsically low lattice thermal conductivity in natural superlattice (Bi2)m(Bi2Te3)n thermoelectric materials. Chem. Mater. 2021, 33, 1140-8.
61. Yang, W. J.; Ha, T.; Park, B. C.; et al. Switching to hidden metallic crystal phase in phase-change materials by photoenhanced metavalent bonding. ACS. Nano. 2022, 16, 2024-31.
62. Zhang, W.; Zhang, H.; Sun, S.; et al. Metavalent bonding in layered phase-change memory materials. Adv. Sci. 2023, 10, 2370094.
63. Guarneri, L.; Jakobs, S.; von, H. A.; et al. Metavalent bonding in crystalline solids: how does it collapse? Adv. Mater. 2021, 33, e2102356.
64. Sarkar, D.; Roychowdhury, S.; Arora, R.; et al. Metavalent bonding in gese leads to high thermoelectric performance. Angew. Chem. Int. Ed. Engl. 2021, 60, 10350-8.
65. Pathak, R.; Joseph, A.; Dutta, P.; et al. Impact of pressure on metavalent bonding in bite influencing electronic topological transitions. Angew. Chem. Int. Ed. Engl. 2025, 64, e202422652.
66. Liu, Y.; Zhang, X.; Nan, P.; et al. Improved solubility in metavalently bonded solid leads to band alignment, ultralow thermal conductivity, and high thermoelectric performance in SnTe. Adv. Funct. Mater. 2022, 32, 2209980.
67. Wang, Y.; Long, Z.; Cheng, Y.; et al. Chemical bonding engineering for high-symmetry Cu2S-based materials with high thermoelectric performance. Mater. Today. Phys. 2023, 32, 101028.
68. Zhu, T.; Su, X.; Zhang, Q.; Tang, X. Structural transformation and thermoelectric performance in Ag2Te1-xSex solid solution. J. Alloys. Compd. 2021, 871, 159507.
69. Rundle, J.; Leoni, S. Layered tin chalcogenides SnS and SnSe: lattice thermal conductivity benchmarks and thermoelectric figure of merit. J. Phys. Chem. C. Nanomater. Interfaces. 2022, 126, 14036-46.
70. Guo, F.; Liu, M.; Zhu, J.; et al. Suppressing lone-pair expression endows room-temperature cubic structure and high thermoelectric performance in GeTe-based materials. Mater. Today. Phys. 2022, 27, 100780.
71. Shrestha, R.; Luan, Y.; Shin, S.; et al. High-contrast and reversible polymer thermal regulator by structural phase transition. Sci. Adv. 2019, 5, eaax3777.
72. Wang, Y.; Xiao, J.; Zhu, H.; et al. Structural phase transition in monolayer MoTe2 driven by electrostatic doping. Nature 2017, 550, 487-91.
73. Migliorini, A.; Kuerbanjiang, B.; Huminiuc, T.; et al. Spontaneous exchange bias formation driven by a structural phase transition in the antiferromagnetic material. Nat. Mater. 2018, 17, 28-35.
74. Xiao, C.; Xu, J.; Li, K.; Feng, J.; Yang, J.; Xie, Y. Superionic phase transition in silver chalcogenide nanocrystals realizing optimized thermoelectric performance. J. Am. Chem. Soc. 2012, 134, 4287-93.
75. Singh, B.; Gupta, M. K.; Mittal, R.; Chaplot, S. L. Ab initio molecular dynamics study of 1-D superionic conduction and phase transition in β-eucryptite. J. Mater. Chem. A. 2018, 6, 5052-64.
76. Lee, S.; Lin, Z.; Huang, J.; et al. Programmable devices based on reversible solid-state doping of two-dimensional semiconductors with superionic silver iodide. Nat. Electron. 2020, 3, 630-7.
77. Ruta, F. L.; Kim, B. S. Y.; Sun, Z.; et al. Surface plasmons induce topological transition in graphene/α-MoO3 heterostructures. Nat. Commun. 2022, 13, 3719.
78. Xie, Y.; Wang, C.; Fei, F.; et al. Tunable optical topological transitions of plasmon polaritons in WTe2 van der Waals films. Light. Sci. Appl. 2023, 12, 193.
79. Sinha, S.; Adak, P. C.; Chakraborty, A.; et al. Berry curvature dipole senses topological transition in a moiré superlattice. Nat. Phys. 2022, 18, 765-70.
80. Shen, X.; Heid, R.; Hott, R.; et al. Precursor region with full phonon softening above the charge-density-wave phase transition in 2H-TaSe2. Nat. Commun. 2023, 14, 7282.
81. Wang, S.; Sun, Y.; Yang, J.; et al. High thermoelectric performance in Te-free (Bi,Sb)2Se3 via structural transition induced band convergence and chemical bond softening. Energy. Environ. Sci. 2016, 9, 3436-47.
82. Yang, S.; Lin, C.; He, X.; et al. Unlocking ultralow thermal conductivity in α-CuTeI via specific symmetry breaking in Cu sublattice. Adv. Funct. Mater. 2025, 35, 2419776.
83. Guin, S. N.; Sanyal, D.; Biswas, K. The effect of order-disorder phase transitions and band gap evolution on the thermoelectric properties of AgCuS nanocrystals. Chem. Sci. 2016, 7, 534-43.
84. Shen, X.; Koza, M. M.; Tung, Y. H.; et al. Soft phonon mode triggering fast Ag diffusion in superionic argyrodite Ag8GeSe6. Small 2023, 19, e2305048.
85. Beaulieu, S.; Dong, S.; Tancogne-Dejean, N.; et al. Ultrafast dynamical Lifshitz transition. Sci. Adv. 2021, 7, eabd9275.
86. Jung, H.; Jin, K. H.; Sung, M.; Kim, J.; Kim, J.; Yeom, H. W. Quantum-confined lifshitz transition on weyl semimetal Td-MoTe2. ACS. Nano. 2024, 18, 23189-95.
87. Chi, Z.; Zhang, J.; Gong, Z.; et al. Pressure-induced Lifshitz transition in the type-II Weyl semimetal WP2. Mater. Today. Phys. 2024, 42, 101372.
88. Wu, W.; Shi, Z.; Du, Y.; et al. Topological Lifshitz transition and one-dimensional Weyl mode in HfTe5. Nat. Mater. 2023, 22, 84-91.
89. Noad, H. M. L.; Ishida, K.; Li, Y. S.; et al. Giant lattice softening at a Lifshitz transition in Sr2RuO4. Science 2023, 382, 447-50.
90. Zhang, D.; Yang, J.; Bai, H.; et al. Significant average ZT enhancement in Cu3SbSe4-based thermoelectric material via softening p-d hybridization. J. Mater. Chem. A. 2019, 7, 17648-54.
91. Liang, J.; Yang, H.; Liu, C.; et al. Realizing a high ZT of 1.6 in N-type Mg3Sb2-based Zintl compounds through Mn and Se codoping. ACS. Appl. Mater. Interfaces. 2020, 12, 21799-807.
92. Tang, S.; Bai, S.; Wu, M.; et al. Improving thermoelectric performance of asymmetrical Janus 1T-SnSSe monolayer by the synergistic effect of band convergence and crystal lattice softening under strain engineering. Mater. Today. Phys. 2022, 29, 100923.
93. Kim, H.; Park, G.; Park, S.; Kim, W. Strategies for manipulating phonon transport in solids. ACS. Nano. 2021, 15, 2182-96.
94. Zhao, Y.; Zhang, G.; Nai, M. H.; et al. Probing the physical origin of anisotropic thermal transport in black phosphorus nanoribbons. Adv. Mater. 2018, 30, e1804928.
95. Zhao, Y.; Yang, L.; Kong, L.; et al. Ultralow thermal conductivity of single-crystalline porous silicon nanowires. Adv. Funct. Mater. 2017, 27, 1702824.
96. Cappai, A.; Melis, C.; Marongiu, D.; et al. Strong anharmonicity at the origin of anomalous thermal conductivity in double perovskite Cs2NaYbCl6. Adv. Sci. (Weinh). 2024, 11, e2305861.
97. Jiang, B.; Wang, W.; Liu, S.; et al. High figure-of-merit and power generation in high-entropy GeTe-based thermoelectrics. Science 2022, 377, 208-13.
98. Han, S.; Dai, S.; Ma, J.; et al. Strong phonon softening and avoided crossing in aliovalence-doped heavy-band thermoelectrics. Nat. Phys. 2023, 19, 1649-57.
99. Tan, X. J.; Liu, G. Q.; Shao, H. Z.; et al. Acoustic phonon softening and reduced thermal conductivity in Mg2Si1-x Snx solid solutions. Appl. Phys. Lett. 2017, 110, 143903.
100. Chen, Z.; Tian, Z.; Zheng, L.; et al. (Ho0.25Lu0.25Yb0.25Eu0.25)2SiO5 high-entropy ceramic with low thermal conductivity, tunable thermal expansion coefficient, and excellent resistance to CMAS corrosion. J. Adv. Ceram. 2022, 11, 1279-93.
101. Kucinski, T. M.; Dhall, R.; Savitzky, B. H.; et al. Direct measurement of the thermal expansion coefficient of epitaxial WSe2 by four-dimensional scanning transmission electron microscopy. ACS. Nano. 2024, 18, 17725-34.
102. Onodera, Y.; Kohara, S.; Masai, H.; Koreeda, A.; Okamura, S.; Ohkubo, T. Formation of metallic cation-oxygen network for anomalous thermal expansion coefficients in binary phosphate glass. Nat. Commun. 2017, 8, 15449.
103. Kano, E.; Malac, M.; Hayashida, M. Substrate and contamination effects on the thermal expansion coefficient of suspended graphene measured by electron diffraction. Carbon 2020, 163, 324-32.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data


























Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].