Machine learning-accelerated transition state prediction for strain-engineered high-entropy alloy catalysts
Abstract
The hydrogen evolution reaction represents a critical bottleneck in renewable energy conversion, with transition state (TS) identification being essential for rational catalyst design. While strain engineering offers powerful pathways to modulate catalytic activity in high-entropy alloys (HEAs), conventional density functional theory (DFT) calculations face prohibitive computational costs due to inherent atomic-level disorder and expanded configurational space. Here, we present a fine-tuned graph neural network EquiformerV2 (eqV2) framework that dramatically accelerates TS discovery in strain-engineered Ir-Pt-Rh-Pd-Ru HEA catalysts. Our lightweight 31-million-parameter model achieves pathway prediction from hours-scale DFT calculations to second-scale predictions while maintaining exceptional accuracy: mean absolute errors below 0.1 eV for reaction energies and structural predictions within 0.1 Å root mean square deviation for 88.8% of configurations across Volmer, Heyrovsky, and Tafel pathways under biaxial strain. This methodology establishes a scalable computational framework that overcomes traditional limitations in high-dimensional catalyst screening, offering a generalizable strategy for artificial intelligence-accelerated next-generation electrocatalyst discovery.
Keywords
INTRODUCTION
As a zero-carbon clean energy carrier, hydrogen plays a pivotal role in the transition toward a sustainable energy system[1]. Among various green hydrogen production pathways, water electrolysis stands as the most promising route, with the cathodic hydrogen evolution reaction (HER: 2H+(aq) + 2e- → H2(g), aq = aqueous) serving as the rate-determining step. However, sluggish HER kinetics severely limit overall energy conversion efficiency, underscoring the urgent need for high-performance electrocatalysts that combine efficiency, stability, and cost-effectiveness.
High-entropy alloys (HEAs) have emerged as promising HER catalysts[2,3]. HEAs offer unprecedented tunability through multi-elemental synergy, structural diversity, and exceptional chemical stability[2,3]. Their compositionally complex surfaces provide diverse active sites and electronic environments, potentially breaking traditional activity-stability trade-offs. Building on this foundation, strain engineering further amplifies this potential by enabling precise modulation of d-band centers and atomic arrangements, thereby optimizing adsorption energies and reaction pathways[4,5]. This dual approach - compositional complexity combined with mechanical tuning - provides new opportunities for rational catalyst design and enhanced HER performance.
Despite significant advances in predicting adsorption energies on HEA surfaces[6,7], accurate modeling of transition states (TSs) and activation barriers remains a critical challenge. As first-order saddle points on the potential energy surface (PES), TSs dictate reaction kinetics and pathway selectivity[8,9]. The molecular trajectory across the entire energy landscape, rather than any single static configuration, fundamentally governs chemical reactivity[10]. Consequently, precise TS identification is essential for understanding reaction mechanisms, quantifying activation barriers, and optimizing catalytic performance.
While density functional theory (DFT) excels at modeling ordered intermetallic surfaces with limited active sites[11], HEAs present formidable challenges. Their intrinsic atomic-level disorder creates highly heterogeneous surfaces with exponentially expanding numbers of possible adsorption and reaction sites. Strain engineering compounds this complexity, as different local environments respond distinctively to applied deformation[12], necessitating extensive configurational sampling. The vast compositional space of HEAs - with element combinations growing exponentially - far exceeds first-principles computational capacity[13,14], creating an urgent need for more efficient modeling approaches.
Recent advances in graph neural networks (GNNs) for catalysis - including Crystal Hamiltonian GNN (CHGNet)[15], geometric message passing GNN (GemNet)[16], directional message passing GNN (DimeNet)++[5,17], and Equiformer, an SE(3)/E(3)-equivariant GNN that integrates 3D-aware irreducible-representation features with a Transformer-style attention mechanism[11] - highlight their remarkable potential for accelerating predictions of energy and forces. These models, pretrained on large DFT databases[18] such as Materials Project[19], Open Catalyst 2020 (OC20)[20], and Open Catalyst 2022 (OC22)[21], show promising transferability across different catalytic systems. However, critical gaps remain for HEA applications: (1) extreme surface heterogeneity exceeds original training distributions; (2) strain-induced structural sensitivity amplifies prediction challenges; and (3) most methods focus on unstrained state or static adsorption configurations, lacking robust strategies for TS discovery and barrier prediction in chemical reactions. Particularly for strain-engineered HEA surfaces, no existing approach offers satisfactory balance among accuracy, efficiency, and generalization.
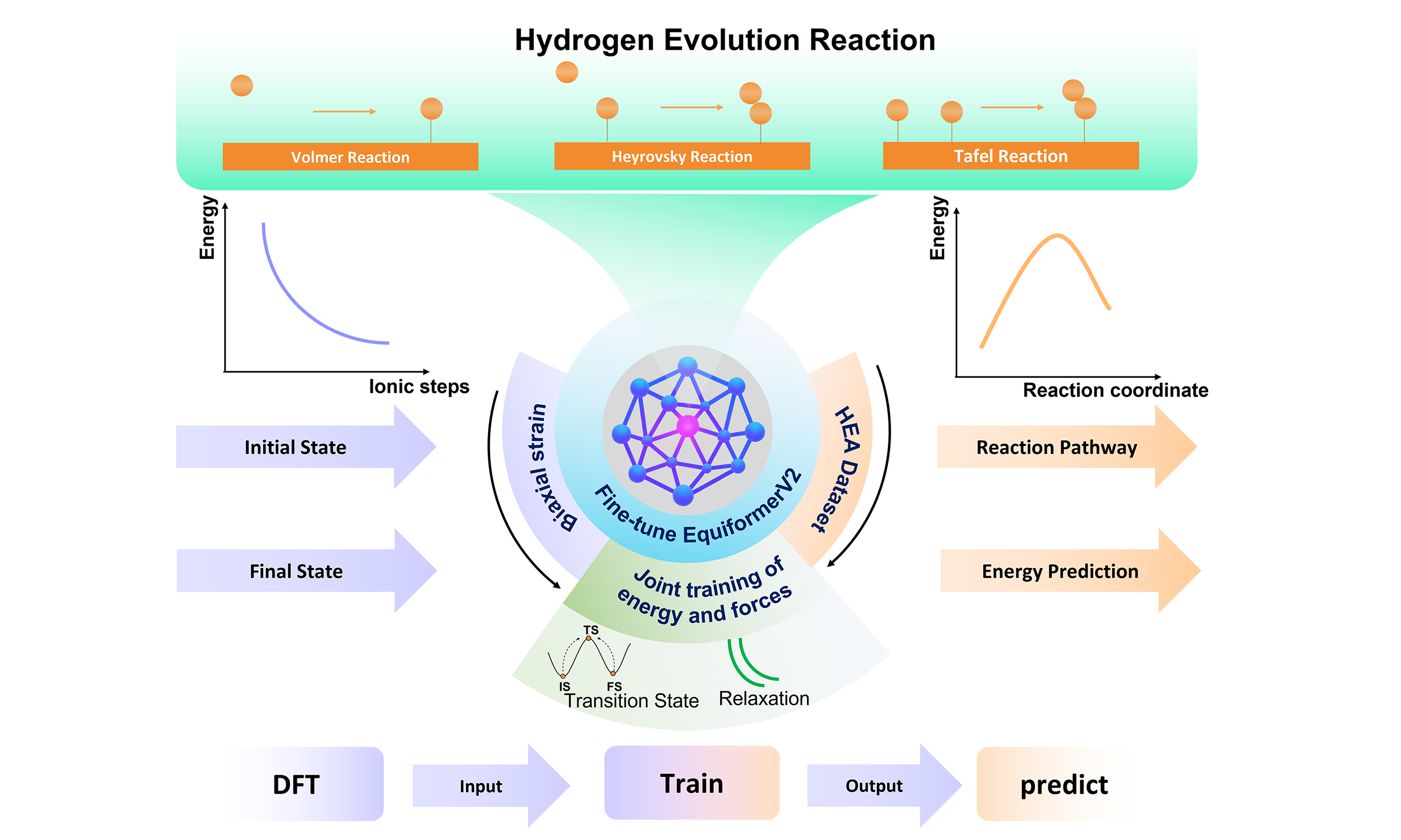
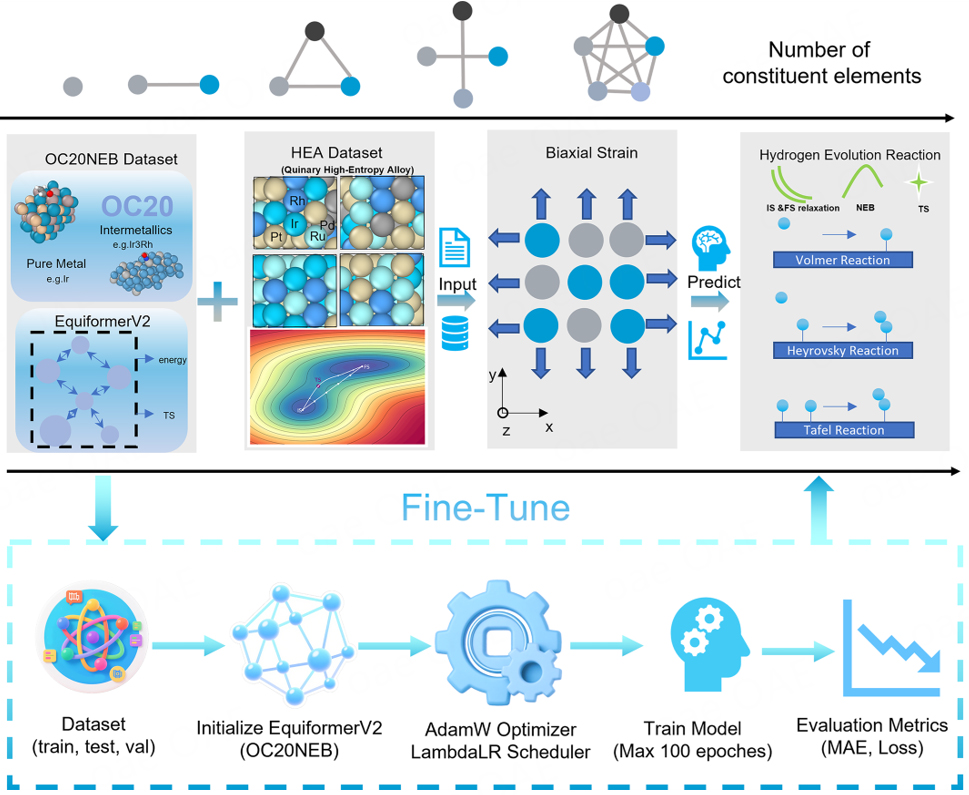
To address these fundamental challenges, we introduce a fine-tuned EquiformerV2[22] (eqV2) framework specifically designed for HER pathway prediction in strain-engineered HEAs. Figure 1 illustrates our comprehensive approach to modeling Volmer, Heyrovsky, and Tafel pathways across the compositionally complex Ir-Pt-Rh-Pd-Ru system under systematic biaxial strain conditions. By leveraging transfer learning from the OC20 dataset within the CatTSunami framework [a framework that transfers OC20-pretrained GNNs to NEB tasks and uses the OC20 Nudged Elastic Band (OC20NEB) dataset][11], our model converts computationally prohibitive TS searches into rapid, second-scale predictions while maintaining high accuracy.
Figure 1. Predicted reaction pathways of HEAs under unstrained state and biaxial strain conditions using the fine-tuned EquiformerV2 model. HEA: High-entropy alloy; OC20: Open Catalyst 2020; NEB: Nudged Elastic Band; MAE: mean absolute error.
Our lightweight eqV2-31M model, with only 31 million parameters, achieves mean absolute errors (MAEs) below 0.1 eV for HER pathway energies and correctly predicts over 88.8% of structures within 0.1 Å root mean square deviation (RMSD), representing more than a 100-fold computational speed-up compared with conventional DFT. Crucially, the model successfully captures strain-dependent electronic structure modulation and energy barrier variations, enabling systematic exploration of the composition-strain design space. This work establishes a scalable computational framework that overcomes traditional bottlenecks in high-dimensional material screening and provides a practical roadmap for strain-engineered catalyst optimization. Beyond HER, our approach offers a generalizable strategy for extending rapid TS prediction to other electrocatalytic pathways, positioning machine learning as a transformative tool for next-generation catalyst discovery.
MATERIALS AND METHODS
High-entropy alloy surface construction
In this study, we strategically selected the Ir-Pt-Rh-Pd-Ru quinary HEA system as our model catalyst, taking advantage of its outstanding HER performance and the computational complexity that challenges conventional modeling approaches. This five-element noble metal system forms a thermodynamically stable face-centered cubic (FCC) solid solution with negative formation enthalpy, effectively suppressing elemental segregation[23]. The system offers unique advantages for our study: (1) multi-elemental synergistic effects enable significant electronic structure tunability; (2) highly heterogeneous local environments provide diverse HER reaction pathways; and (3) pronounced strain-responsive behavior makes it an ideal testbed for investigating structure-property relationships under mechanical perturbation.
Surface models were constructed systematically to capture the full complexity of HEA catalysis. The surface models comprised 4-layer 3 × 4 FCC (111) slabs with randomly distributed Ir, Pt, Rh, Pd, and Ru atoms on lattice sites to reproduce the inherent chemical disorder of HEAs. The bottom two layers were constrained to simulate the bulk environment, while the top two layers underwent full structural relaxation to account for surface reconstruction and adsorption effects. Based on crystallographic symmetry considerations, we selected high-symmetry adsorption sites - including top and hollow positions - to construct comprehensive adsorption models for both atomic hydrogen (H) and molecular hydrogen (H2). This systematic approach ensures representative sampling of the diverse catalytic environments inherent to HEA surfaces while maintaining computational tractability for model training. To examine the impact of lattice strain on catalytic performance, biaxial strain was applied to the optimized surface structures using the deformation gradient method, where the strain tensor ε scales the lattice vectors according to A' = (I + ε)·A, with A′ representing the strained lattice matrix, I the identity matrix, and A the original lattice matrix[24]. Biaxial strain ranging from 0.0 to 0.1, with an increment of 0.01, was systematically applied along both the x and y directions.
First-principle DFT calculations
All DFT calculations were conducted using the Vienna Ab initio Simulation Package (VASP)[25]. The interactions between core and valence electrons were described using the projector augmented wave (PAW) method[26]. Meanwhile, exchange-correlation effects were treated within the generalized gradient approximation (GGA) using the Perdew-Burke-Ernzerhof (PBE) functional[27]. To ensure consistency with the OC20NEB dataset, we adopted standardized computational parameters: A plane-wave basis set with an energy cutoff of 350 eV, the convergence thresholds were set to 10-4 eV for total energy and 0.05 eV/Å for forces[11]. Brillouin zone sampling was performed using Monkhorst-Pack k-point grids with densities optimized for each unit cell geometry. Structural optimizations and TS searches employed 4 × 3 × 1 k-point meshes. The unstrained lattice parameters were set to approximately a = 8.2956Å, b = 9.5790 Å, and c = 21.7734 Å[23], based on a weighted average of constituent metals following Vegard’s law[28]. Following the approach of Batchelor et al.[23], this averaged value was used to represent the zero-strain state, since the lattice parameter is determined on a longer length scale than the local atomic environment. Biaxial strain was subsequently applied relative to this reference state. To avoid spurious periodic interactions between surface slabs, a vacuum spacing of 15 Å was applied along the z-direction.
Transition state discovery protocol
TS searches were performed using the climbing image nudged elastic band (CI-NEB) method[29]. CI-NEB calculations were initialized with a reaction path generated using the Image Dependent Pair Potential (IDPP) method[30], which produces a geometrically smoother and energetically more reasonable initial guess by minimizing deviations in atomic pairwise distances between adjacent images. The primary objective of NEB is to determine the minimum energy path (MEP) on the PES connecting two local minima. In the TS search with five images, three intermediate images were generated by interpolation between the endpoints. The climbing image identifies the saddle point, while the remaining images trace the reaction pathway. Upon convergence, the climbing image accurately locates the saddle point without additional computational cost, as all images relax simultaneously. Convergence thresholds for transition-state calculations were set equal to those used for structural optimizations, consistent with the OC20NEB dataset, ensuring reliable and reproducible determination of reaction pathways under both unstrained and strained conditions.
Our comprehensive TS search protocol encompasses all fundamental HER mechanisms: Volmer (H+ + e- + * → H*), Heyrovsky (
Machine learning model development
Data generation and curation
Our training dataset comprises extensive DFT-calculated TS trajectories for the Ir-Pt-Rh-Pd-Ru HEA system, strategically designed to capture both unstrained and strain-engineered surface chemistry. The dataset includes 229 unique reaction trajectories (103 unstrained paths and 126 biaxial-strain paths), containing a total of 1,145 energy and force data points. An 80:10:10 train/validation/test split ensures unbiased performance evaluation, with each subset maintaining balanced representation across all three HER pathways and strain conditions. These 229 trajectories encompass top and hollow adsorption sites under biaxial strains of 0.01-0.10, using 48-atom FCC slabs with stochastically sampled Ir-Pt-Rh-Pd-Ru ratios. Each trajectory comprises five configurations - two endpoints and three interpolated intermediate images - providing comprehensive characterization of reaction pathways. The dataset’s extensive coverage of composition, adsorption site, and strain parameters, together with joint training on energies and forces across complete trajectories, enables robust extrapolation to unexplored composition-strain regimes.
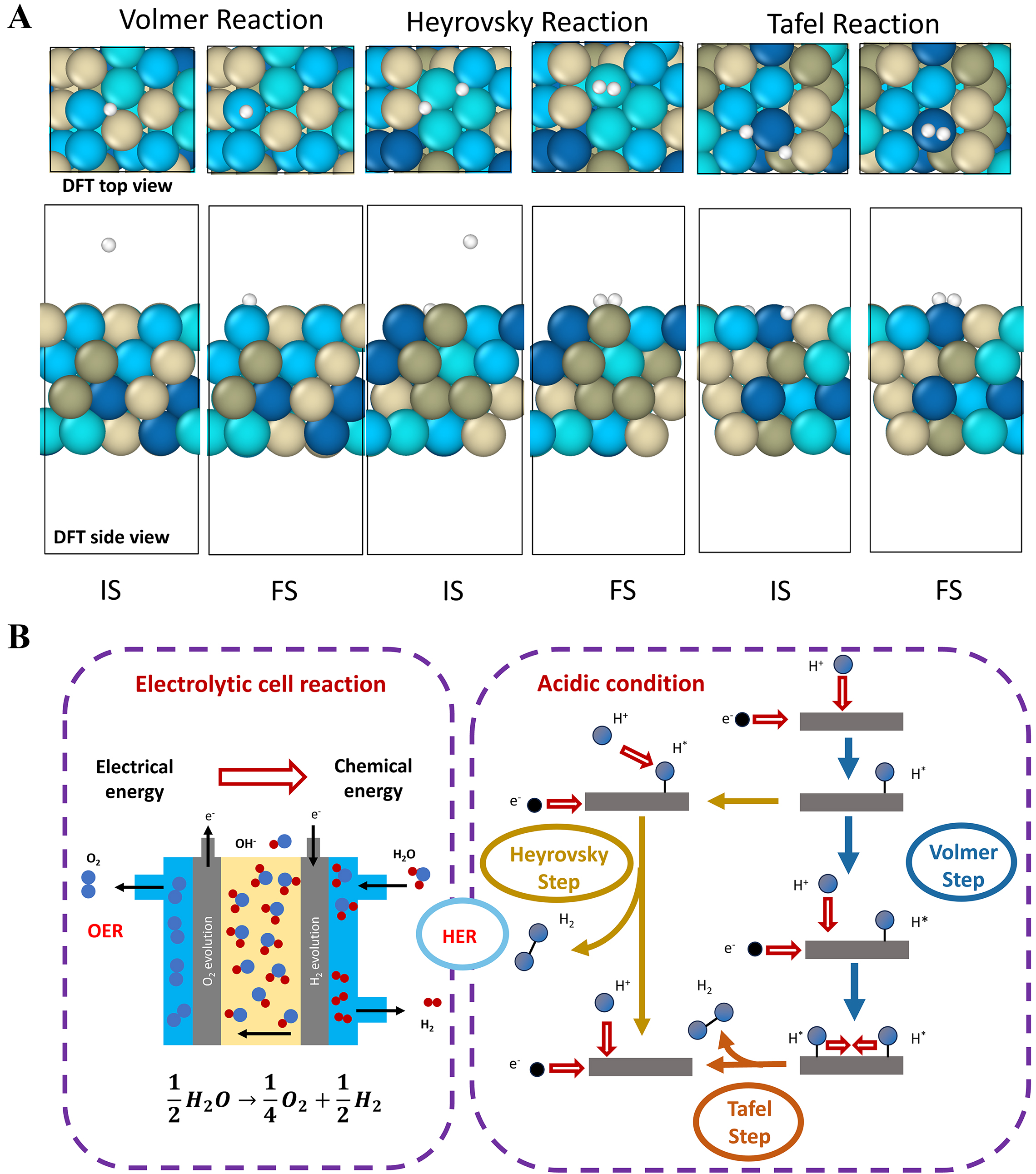
Initial (IS) and final states (FS) for each reaction were constructed on fully relaxed HEA surfaces to ensure realistic starting configurations. Volmer pathways describe the transition of hydrogen atoms from vacuum to surface-adsorbed states at top or FCC hollow sites. Heyrovsky mechanisms involve concurrent proton-electron transfer to pre-adsorbed surface hydrogen. Tafel reactions model the combination of two surface-bound hydrogen atoms into molecular H2 [Figure 2A]. Bridge sites were excluded due to their limited ability to stably adsorb H or H2; DFT studies show that hydrogen initially placed at bridge sites tends to migrate to more stable top or hollow positions during geometry optimization, reflecting the energetic instability of bridge-site adsorption[31-33]. This approach captures the full mechanistic diversity of HER on complex alloy surfaces.
Figure 2. Electrochemical cell reactions and HER under acidic conditions. (A) Initial and final configurations of the Volmer, Heyrovsky, and Tafel steps in the HER. (B) Reaction pathway of the HER. DFT: Density functional theory; IS: initial states; FS: final states; OER: oxygen evolution reaction; HER: hydrogen evolution reaction.
EquiformerV2 architecture and fine-tuning
eqV2 is a TS-pretrained model developed by Meta (Menlo Park, CA, USA) within the CatTSunami framework using the OC20-NEB dataset[11], which demonstrates exceptional capabilities in energy pathways prediction. The model employs an equivariant graph attention Transformer architecture, using graph attention mechanisms to ensure consistent physical property predictions under spatial rotations and translations - a critical requirement for accurately modeling structurally diverse TS configurations with significant atomic displacements.
To improve the model’s adaptability and generalization in predicting catalytic reaction pathways on strain-engineered HEA surfaces, we fine-tuned pretrained eqV2-31M model. The architecture comprises eight GNN layers (num_layers = 8), eight attention heads (num_heads = 8), and 128-dimensional channels for atoms, edges, and spherical harmonics (sphere_channels = 128, edge_channels = 128). The Sigmoid-weighted Linear Units (SiLU) activation function and on-the-fly graph construction enable dynamic adaptation to varying atomic environments characteristic of HEA surfaces.
The model was trained using the Adam with decoupled weight decay (AdamW) optimizer[34] with carefully tuned hyperparameters: 4 × 10-5 initial learning rate and 0.01 weight decay, 100 training epochs. A cosine learning rate scheduler[35] (PyTorch LambdaLR) with a linear warm-up during the first five epochs (warm-up factor: 0.05) was employed. To enhance training stability, gradient clipping (clip_grad_norm = 100) and an exponential moving average (EMA, decay rate: 0.999) were applied. All training and evaluation were performed on an NVIDIA RTX 4090 GPU (NVIDIA Corporation, Santa Clara, CA, USA).
The model was trained with a joint regression objective for energy and force, using a loss function defined as:
where
for scalar quantities. For vector quantities such as atomic forces, the L2_MAE is defined as:
where
RESULTS AND DISCUSSION
HER pathway characterization
Under acidic conditions, the HER generally proceeds via a classical three-step mechanism comprising the Volmer, Heyrovsky, and Tafel steps[36,37], as illustrated in Figure 2B. HER serves as the key cathodic process in water electrolysis and, together with the oxygen evolution reaction (OER) at the anode, completes the electrocatalytic splitting of water molecules, thereby enabling the efficient conversion of electrical energy into chemical energy.
The first step of the HER is the Volmer step (H⁺ + e- + * → H*), in which a proton (H+) combines with an electron and adsorbs onto the catalyst’s active site to form adsorbed hydrogen (H*). This electrochemical reduction step governs the initial electron transfer efficiency of the reaction. As indicated by the blue arrow in Figure 2B, the Volmer process is strongly influenced by the catalyst’s proton affinity and electron transport capability. Subsequently, HER can proceed through one of two pathways. The first is the Heyrovsky step (
Overall, precise modulation of the energy barriers and intermediate stability across the three elementary steps allows for effective control of the HER rate, providing the fundamental scientific basis for the rational design of high-performance electrocatalysts.
Unstrained reaction energetics
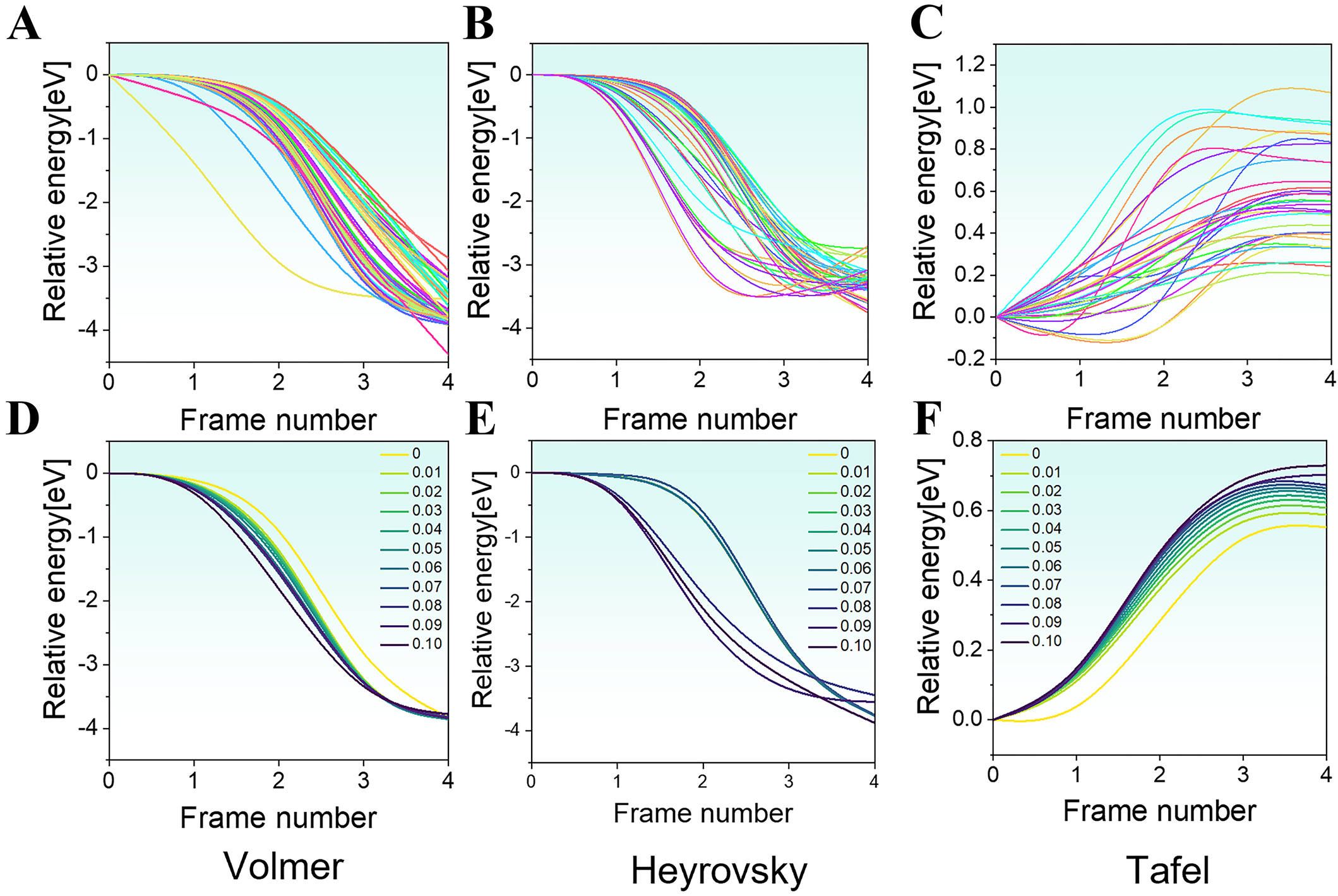
Under unstrained conditions, the Volmer reaction pathway describes the transition from the IS, where a free hydrogen atom approaches the catalyst surface, to the FS, where it becomes adsorbed. During this process, the total energy decreases significantly. This indicates that the process is thermodynamically favorable and exothermic, occurring without a significant activation barrier [Figure 3A].
Figure 3. DFT-calculated HER pathways under unstrained state and biaxial strain conditions: (A) Volmer pathway under unstrained state conditions; (B) Heyrovsky pathway under unstrained state conditions; (C) Tafel pathway under unstrained state conditions; (D) Volmer pathway under biaxial strain (0.01-0.1); (E) Heyrovsky pathway under biaxial strain (0.01-0.1); (F) Tafel pathway under biaxial strain ranging from (0.01-0.1). DFT: Density functional theory; HER: hydrogen evolution reaction.
Similarly, the Heyrovsky reaction also displays a barrierless energy profile. In this step, the initial configuration consists of a surface-adsorbed hydrogen atom and a free proton-electron pair. As the system transitions to the FS, its energy continuously decreases, ultimately forming a stable H₂ molecule adsorbed at the top site of catalytically active atoms such as Ru, Rh, or Pd [Figure 3B]. This indicates that, similar to the Volmer step, the Heyrovsky reaction proceeds spontaneously without extra energy input.
In contrast, the Tafel pathway in the HER involves a significant energy barrier. In this step, two adsorbed hydrogen atoms recombine on the catalyst surface to form an H₂ molecule, which remains stably adsorbed. Along the reaction coordinate, the system’s energy reaches a distinct maximum, corresponding to the activation barrier [Figure 3C]. This barrier represents the energy required for the recombination of the two surface-bound hydrogen atoms and is a critical factor influencing the reaction kinetics.
Strain-induced catalytic modulation
Furthermore, we examined the influence of lattice strain on the HER pathways. By applying biaxial strain in the range of 0.01 to 0.1 within the model, we found that the energies associated with the Volmer and Heyrovsky steps decreased with increasing strain, accompanied by accelerated reaction rates, indicating that these processes become more favorable under strain [Figure 3D and E]. In contrast, the Tafel pathway showed an increase in the activation barrier under biaxial strain, likely due to strain-induced structural distortions that hinder the cooperative migration of hydrogen atoms and consequently raise the energy barrier for H2 formation [Figure 3F].
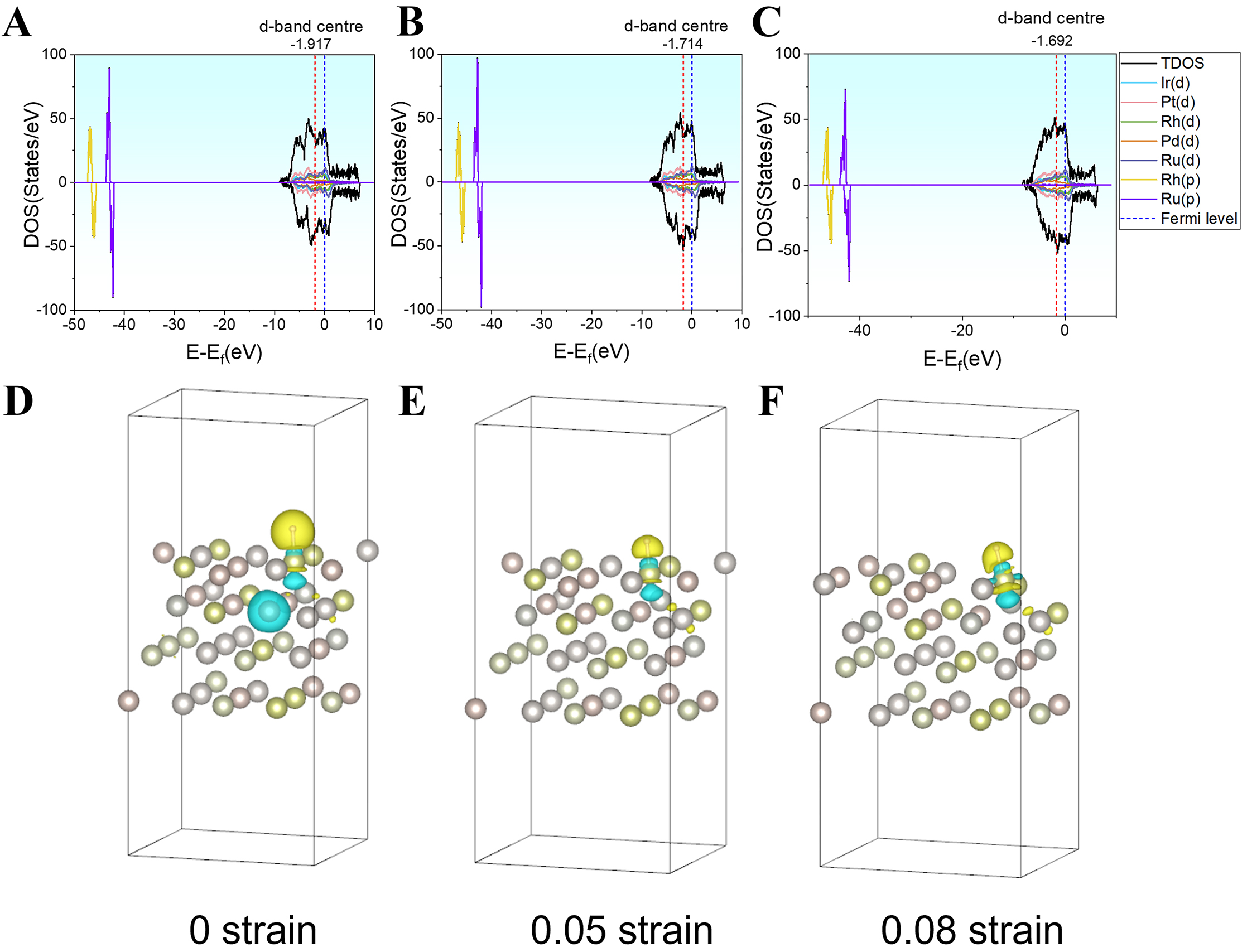
Under biaxial tensile strain, the d-band center of the system shifts upward toward the Fermi level [Figure 4A-C], indicating an increased participation of d-electrons from the metal surface. According to the d-band center theory, an upward shift of the d-band center results in fewer occupied anti-bonding states, thereby enhancing the adsorption strength of intermediates such as H. Conversely, a downward shift leads to increased anti-bonding state occupancy, weakening the adsorbate-surface interaction. Thus, the strain-induced upward shift of the d-band suggests an enhanced adsorption capability of the catalyst[4,38]. However, simply increasing adsorption strength does not necessarily improve catalytic performance. Based on the Sabatier principle, an ideal catalyst must balance adsorption and desorption: weak adsorption leads to unstable intermediates, whereas overly strong adsorption hinders product desorption, ultimately reducing the reaction rate. A moderate upward shift of the d-band can therefore adjust the adsorption energy into an optimal range, enhancing overall catalytic activity and improving the energy landscape along the reaction pathway.
Figure 4. Electronic structure changes under biaxial strain: (A-C) d-band center positions, total density of states (DOS), and projected density of states (PDOS) under biaxial strain; (D-F) charge density difference under biaxial strain (isovalue = 0.006 e Å-3), where yellow regions indicate electron accumulation and green regions indicate electron depletion. TDOS: total density of states.
Further insights from differential charge density analysis [Figure 4D-F] show that as the strain increases from 0 to 0.08, charge redistribution becomes increasingly localized at the metal surface and adsorption sites. Notably, in Figure 4E and F, regions of electron accumulation (yellow) and depletion (cyan) concentrate at active surface sites, indicating that strain significantly modulates electronic localization and the charge environment around the adsorption region[39]. This modulation not only strengthens electronic coupling between the metal and the adsorbate[40] but may also affect the stability of reaction intermediates and the activation barriers of TSs, thereby substantially altering the energy profile of the reaction pathway[41,42]. Consequently, biaxial tensile strain, by elevating the d-band center and restructuring charge density distributions, enables multiscale regulation of the surface electronic structure and local electronic environment at catalytic sites, potentially optimizing both the reaction pathway and the kinetics of the HER.
Strain has a pronounced regulatory effect on both the electronic structure and reaction pathways, thereby modulating catalytic performance. However, this modulation also introduces substantial complexity into reaction modeling, particularly for systems with high surface heterogeneity such as HEAs. In these materials, the results highlight that reaction pathways under strain are strongly dependent on the local atomic environment, making TS predictions significantly more challenging. While DFT remains a reliable tool for accurate calculations on limited configuration sets, its application to TS searches typically requires several hours of computation per reaction pathway, thereby rendering large-scale catalyst screening computationally prohibitive. As the dimensionality of external strain control increases, the number of relevant configurations and associated computational costs grow exponentially, further compounding the modeling challenge. Thus, we fine-tune a pretrained GNN model using a small set of DFT-calculated reaction pathways. This approach enables rapid prediction of energy variations in HER pathways under complex strain conditions, drastically reducing computational cost and time while maintaining high accuracy and strong physical fidelity. It provides an efficient and practical solution for modeling TSs and performing high-throughput screening of strain-engineered HEA catalysts.
Fine-tuned equiformerV2 model
The OC20NEB model, pretrained with the eqV2 architecture within the CatTSunami framework[11], has shown high accuracy in predicting reaction pathways for material systems with up to three elements. However, its predictive performance declines significantly when applied to HEA systems with complex elemental compositions and disordered surface structures. To overcome this limitation, we fine-tuned the eqV2 model using surface data from HEAs composed of Ir, Pt, Rh, Pd, and Ru. This fine-tuning improves the model’s adaptability and accuracy in predicting reaction pathways within complex surface environments, providing a practical solution for the efficient screening of advanced catalytic materials.
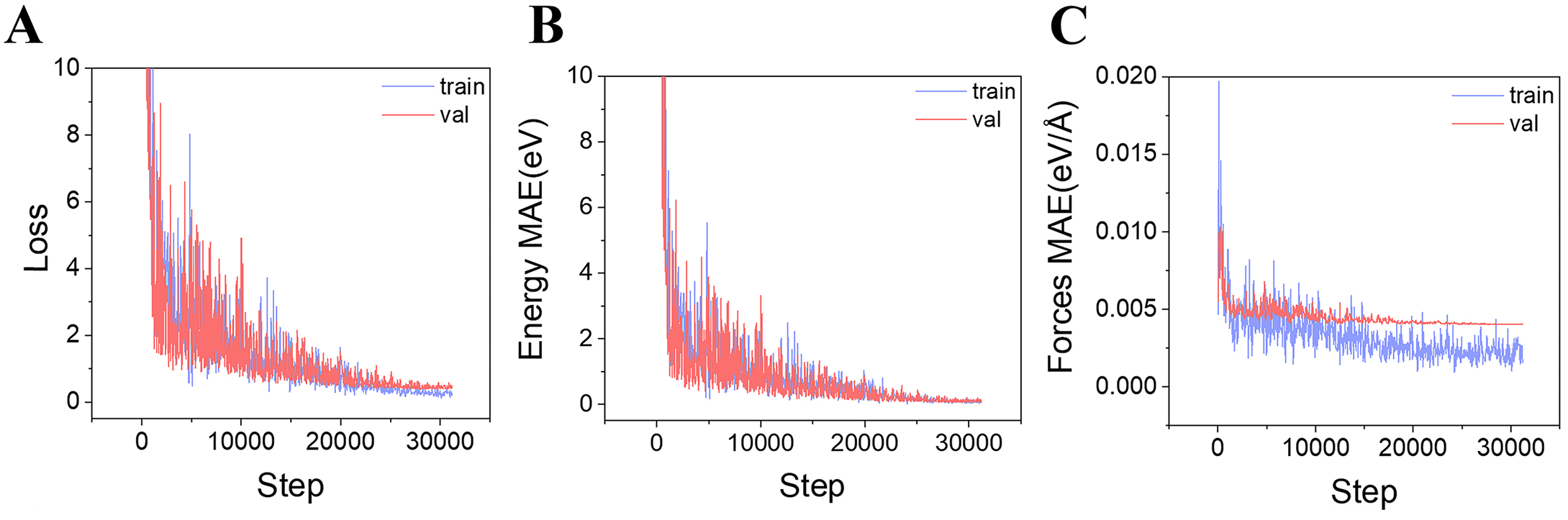
During fine-tuning, the loss function exhibited a consistent downward trend for both the training and validation sets [Figure 5A], reflecting stable learning and progressive model convergence. Meanwhile, the MAEs for both energy and force predictions decreased steadily with training steps [Figure 5B and C], eventually reaching a plateau, indicating that the model effectively learned to jointly predict these two physical quantities. The maximum number of training epochs was selected as the early stopping criterion, as no signs of overfitting were observed and the validation loss showed no rebound. The evolution of the loss function closely mirrored the MAE trends, confirming that the fine-tuned eqV2 model achieved accurate modeling of complex reaction pathways, demonstrated effective generalization, and maintained training stability.
Figure 5. MAE and loss curves for the training and validation sets: (A) Loss function curve; (B) MAE of energies; (C) MAE of forces. MAE: Mean absolute error.
Unstrained reaction prediction
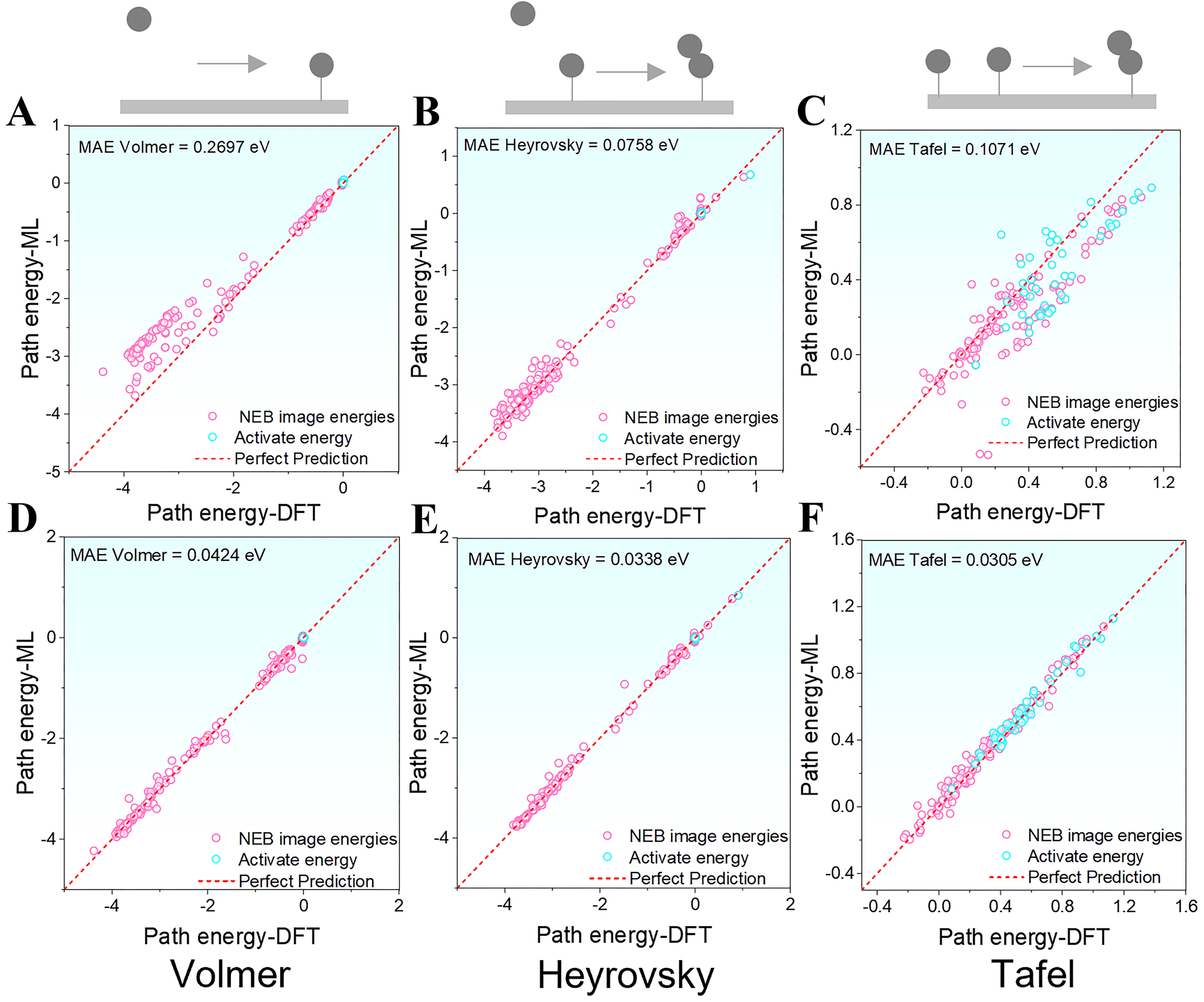
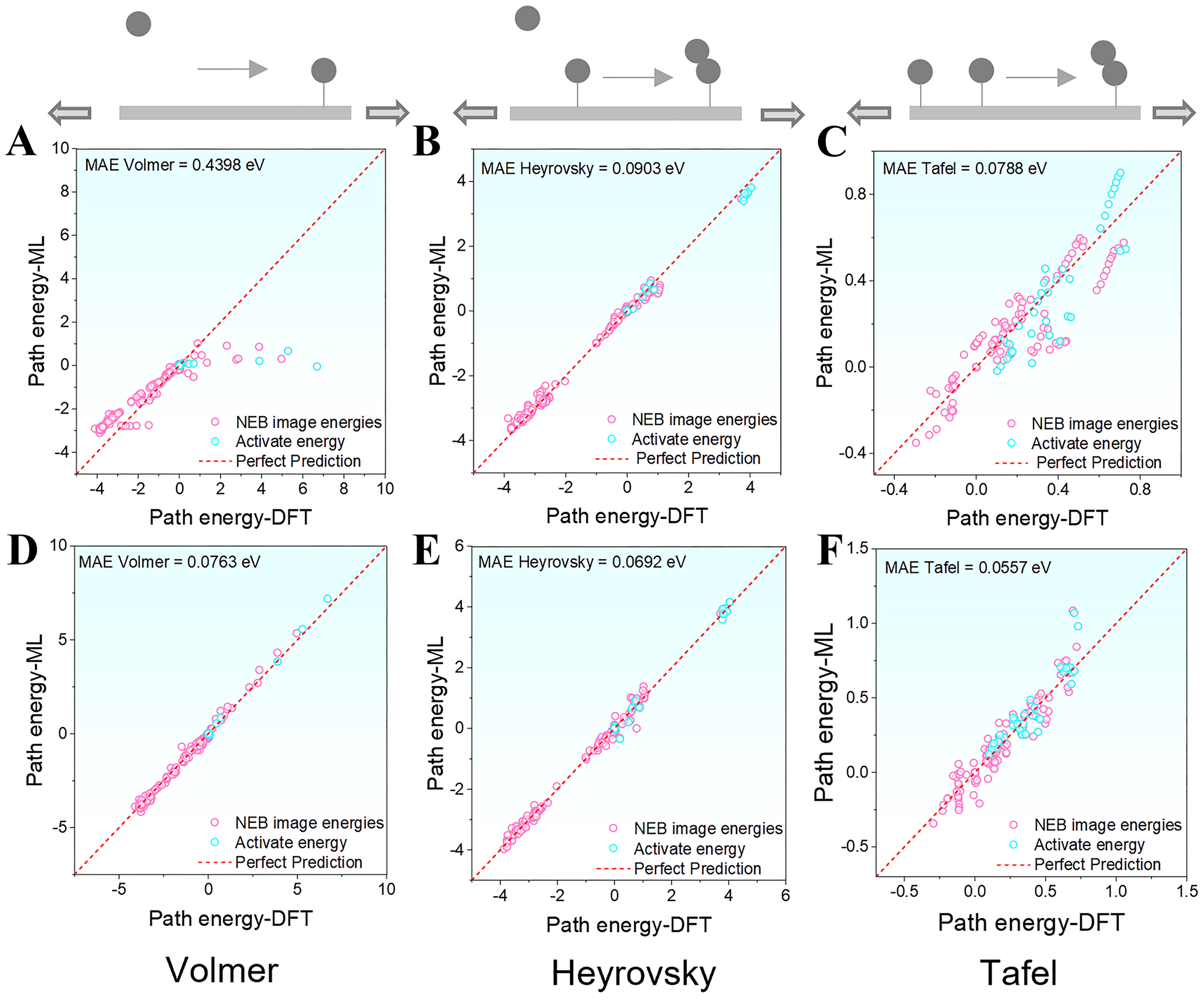
When using the pretrained eqV2-31M model to predict HER energy pathways, the model outputs relative energy values by subtracting the energy of the IS from that of each intermediate configuration along the reaction pathway. Although the overall predictions are relatively well aligned with the “Perfect Prediction” reference line, notable errors remain across the three representative reaction pathways. The Volmer step shows the largest deviation, with a maximum MAE of 0.2697 eV [Figure 6A], indicating limited accuracy for this reaction type. Predictions for the Heyrovsky step (0.05 eV) and Tafel step (0.1071 eV) are comparatively more stable, but the energies of TSs and intermediate configurations still exhibit significant scatter, compromising the continuity and physical consistency of the pathway [Figure 6B and C]. After fine-tuning the eqV2-31M model with a small dataset of Volmer, Heyrovsky, and Tafel pathways specific to HEA systems, its predictive performance improved significantly. The model achieved markedly more accurate relative energy predictions across all configurations, with reduced MAEs of 0.0424 eV for Volmer, 0.0338 eV for Heyrovsky, and 0.0305 eV for Tafel [Figure 6D-F]. These results demonstrate that fine-tuning with HEA data substantially enhances the model’s accuracy and generalization capability for complex multi-element catalytic systems.
Figure 6. Relative energy prediction errors of HER pathways under unstrained state conditions before and after fine-tuning (referenced to the first frame of each pathway): (A-C) Energy prediction errors of the pretrained model for the Volmer, Heyrovsky, and Tafel steps, respectively; (D-F) Energy prediction errors of the fine-tuned model for the Volmer, Heyrovsky, and Tafel steps, respectively. ML: Machine learning; MAE: mean absolute error; NEB: Nudged Elastic Band; DFT: density functional theory.
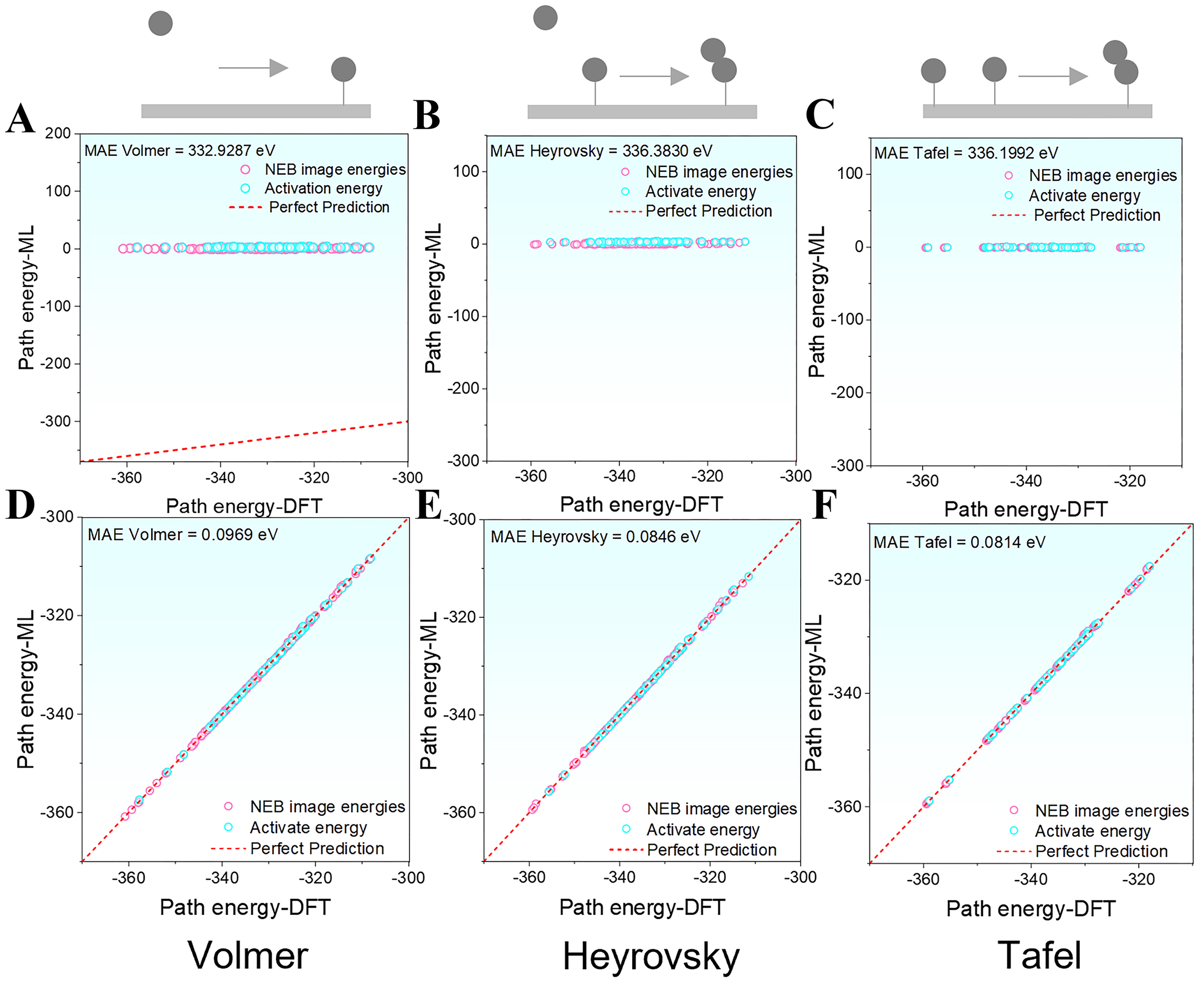
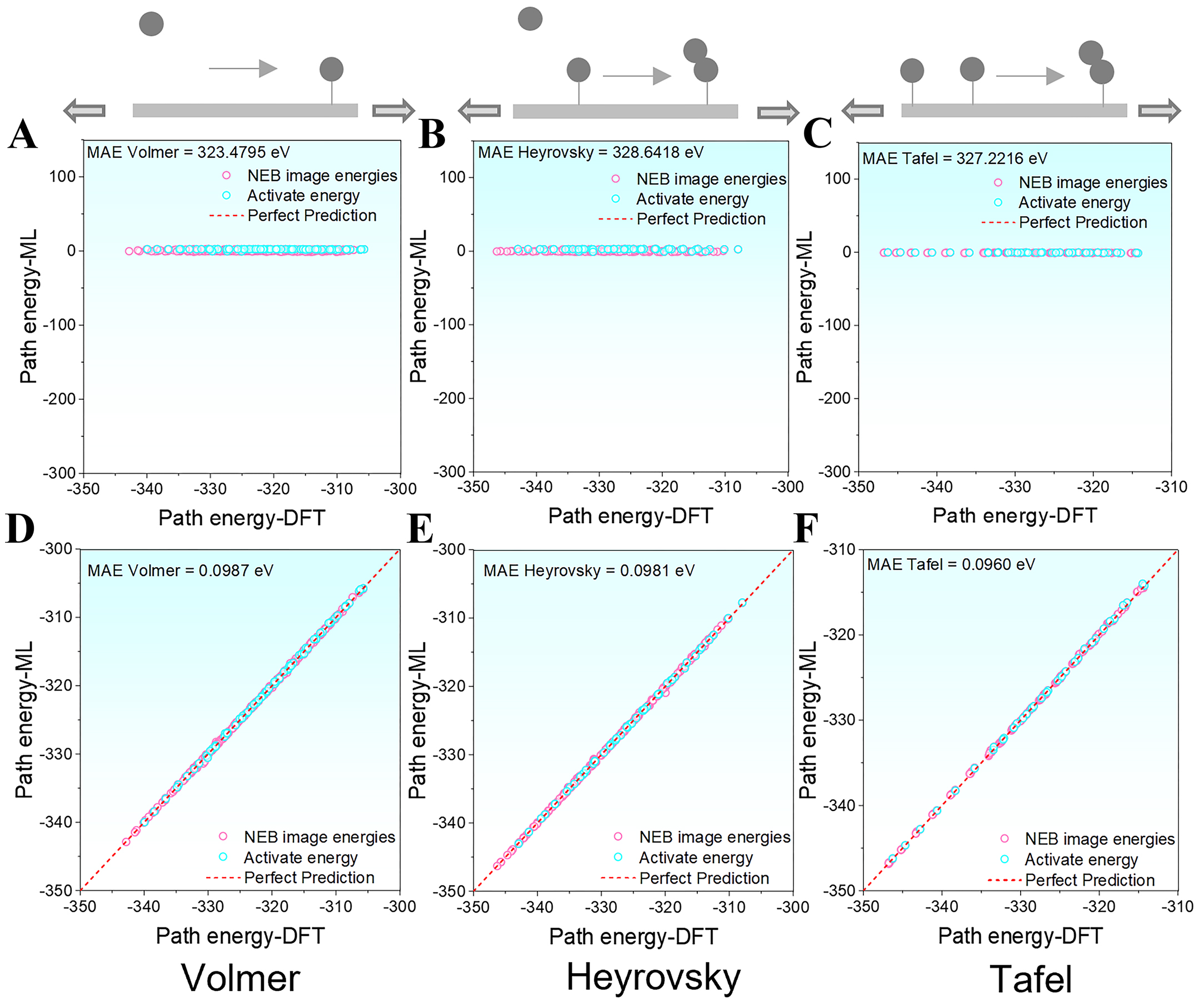
The OC20NEB-pretrained model achieves moderate accuracy for relative energy predictions, with its low error margins largely resulting from referencing each configuration to the IS, which cancels systematic errors. However, absolute energy prediction, which provides more direct physical insight for catalytic analysis, presents significant challenges, with errors exceeding 330 eV for the Volmer, Heyrovsky, and Tafel pathways [Figure 7A-C]. These deviations arise from the pretraining dataset’s bias toward low-energy structures, small systems, and few-component materials, as well as its emphasis on adsorption energies rather than total energies, the latter being more consistent with DFT calculations[22]. Consequently, the model exhibits limited transferability to high-energy configurations and multi-component surfaces, leading to reduced accuracy for complex HEA systems.
Figure 7. Absolute energy prediction errors for the HER pathways in the ground state: (A-C) Energy prediction errors of the pretrained model for the Volmer, Heyrovsky, and Tafel reactions, respectively; (D-F) Energy prediction errors of the fine-tuned model for the Volmer, Heyrovsky, and Tafel reactions, respectively. ML: Machine learning; MAE: mean absolute error; NEB: Nudged Elastic Band; DFT: density functional theory; HER: hydrogen evolution reaction.
After fine-tuning the model with HEA data encompassing the Volmer, Heyrovsky, and Tafel reaction pathways, its performance in absolute energy prediction improved markedly. The prediction errors were significantly reduced, with MAEs of 0.0969 eV for Volmer, 0.0846 eV for Heyrovsky, and 0.0814 eV for Tafel [Figure 7D-F], all within the 0.1 eV threshold. These results demonstrate that the proposed fine-tuning strategy not only enhances the model’s adaptability to complex high-entropy catalytic systems but also enables accurate pointwise prediction of absolute energies along the reaction pathways. This advancement provides a practical and efficient approach for substantially reducing the computational cost of DFT calculations and accelerating the high-throughput screening and rational design of HEA catalysts.
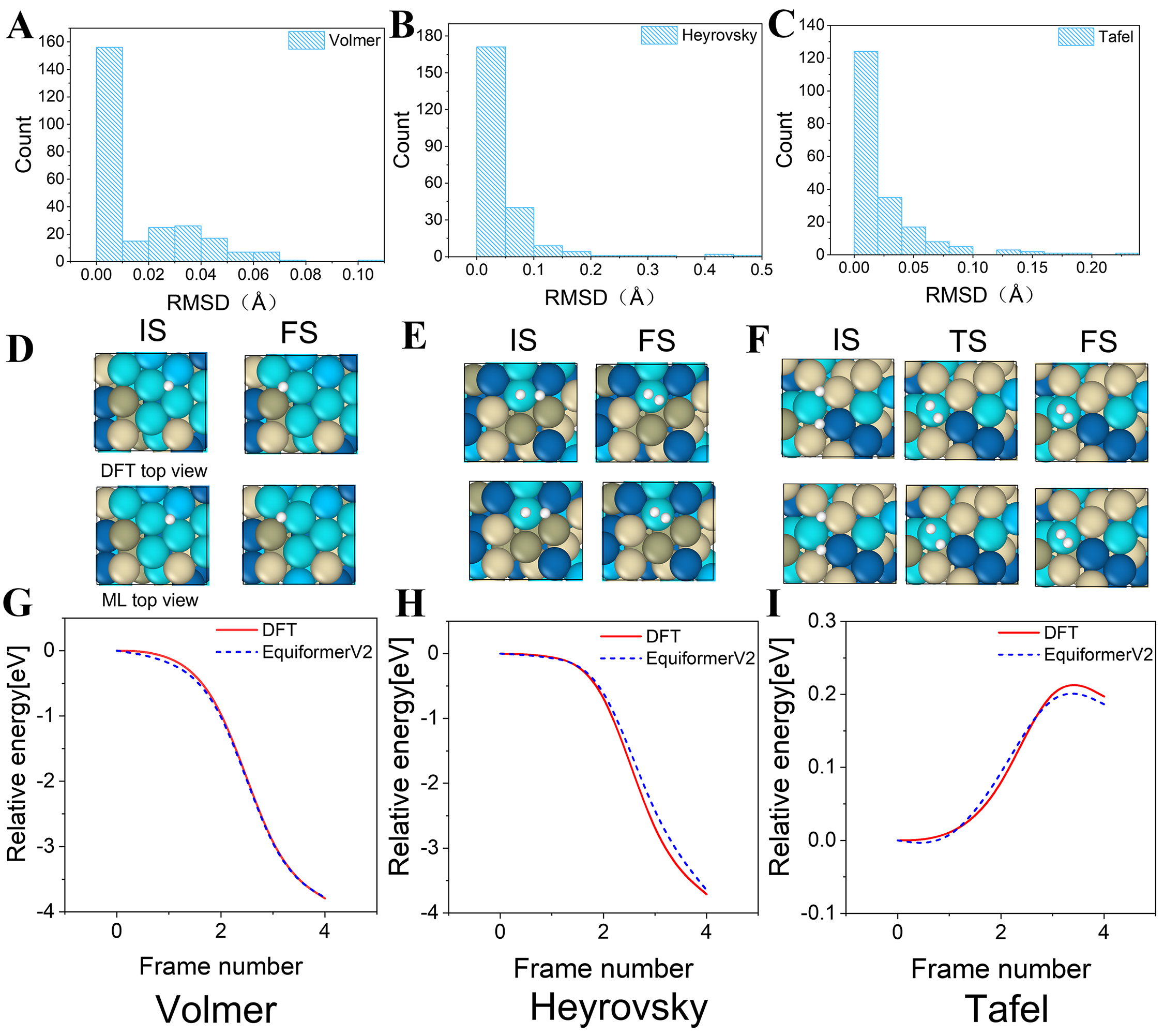
Using the fine-tuned eqV2 model, we accurately predicted the structural configurations and energy evolution profiles of three representative HER pathways: Volmer, Heyrovsky, and Tafel. The model exhibited excellent structural accuracy, with RMSD values below 0.1 Å for 91.7% of the predicted configurations across Volmer, Heyrovsky, and Tafel steps under unstrained conditions [Figure 8A-C]. As shown in Figure 8D-F, both IS and FS were reconstructed with exceptional accuracy, achieving structural errors below 0.01 Å for all three reactions. For the Tafel reaction, the model also demonstrated high accuracy in predicting the TS structure, with a RMSD of only 0.26 Å, a precision level acceptable when compared to typical lattice constants [Figure 8F]. Moreover, the prediction process was completed within seconds, representing a substantial reduction in computational cost compared to conventional DFT calculations. For example, the Tafel reaction required approximately 19,016 ~ 28,136 s (≈ 5.3 ~ 7.8 h) using DFT, whereas our fine-tuned eqV2 model completed the prediction in approximately 6 ~ 20 s on an RTX 4090 GPU. These results highlight the model’s strong capability to capture key configurations along complex reaction pathways, ensuring both physical consistency of energy estimates and a robust geometric foundation for subsequent pathway analysis.
Figure 8. Machine learning-predicted HER pathways under unstrained state conditions: (A-C) Configuration errors under unstrained state conditions; (D-F) Initial and final configurations of the Volmer, Heyrovsky, and Tafel steps, along with the transition-state configuration of the Tafel step; (G-I) Energy profiles of the Volmer, Heyrovsky, and Tafel reactions. RMSD: Root mean square deviation; IS: initial states; FS: final states; DFT: density functional theory; HER: hydrogen evolution reaction.
HEA surfaces inherently exhibit heterogeneous adsorption energies arising from diverse local atomic environments, yielding both strongly and weakly binding sites[23,43,44]. This heterogeneity was explicitly captured in our dataset through systematic sampling of multiple adsorption sites across varied local configurations. We evaluated hydrogen adsorption energies at several representative adsorption sites using both DFT and the eqV2-31M model. The resulting site-to-site variations, with the eqV2-31M model accurately reproducing DFT-predicted binding strengths with MAEs below 0.1 eV. This confirms the model's ability to distinguish between overbinding and underbinding regimes across heterogeneous HEA surfaces. Additionally, the CI-NEB trajectories implicitly capture short-range hydrogen migration between neighboring sites[45-47]; aggregating these local steps across different sites provides a coherent picture of surface-wide diffusion behavior.
Regarding reaction energy pathway prediction, the model’s relative energy profiles show good overall agreement with DFT results. For the Volmer and Heyrovsky pathways, only minor deviations are observed during the energy-decreasing stages [Figure 8G and H], indicating that the model provides consistent energy predictions even for barrierless pathways. Although the Tafel reaction features a distinct activation barrier, the model accurately captures both the upward energy trend and the position of the energy peak, with the largest deviation occurring near the TS [Figure 8I]. This slight discrepancy is primarily due to the inherent instability of the TS and small structural deviations in the predicted configuration, which can introduce fluctuations in energy estimation.
Overall, the fine-tuned model not only significantly improves prediction efficiency but also achieves structural and energy pathway accuracies comparable to those of DFT calculations. These results highlight its potential as an efficient and reliable alternative for high-throughput modeling of catalytic reaction pathways.
Strain-engineered prediction
Strain-induced modulation of the electronic structure can significantly alter catalytic reaction pathways, thereby increasing the complexity of reaction modeling and posing greater challenges for machine learning-based pathway prediction. Under biaxial strain, the pretrained eqV2-31M model showed significant deficiencies in predicting the energy profile of the Volmer reaction. The MAE for Volmer reached 0.4398 eV. This value was substantially higher than the errors for the Heyrovsky reaction (0.0903 eV) and the Tafel reaction (0.0788 eV), as shown in Figure 9A-C. This trend was consistent with the model’s performance under unstrained conditions. After fine-tuning with HEA data, the prediction errors for all three HER pathways were significantly reduced to below 0.1 eV, with MAEs of 0.0763 eV for Volmer, 0.0692 eV for Heyrovsky, and 0.0557 eV for Tafel [Figure 9D-F]. The improvement for the Volmer pathway was particularly pronounced, with predicted points closely aligning with the “Perfect Prediction” reference line, indicating a substantial enhancement in model precision.
Figure 9. Relative energy prediction errors of HER pathways under biaxial strain before and after fine-tuning (referenced to the first frame of each pathway): (A-C) Pretrained model errors for the Volmer, Heyrovsky, and Tafel steps, respectively; (D-F) Fine-tuned model errors for the Volmer, Heyrovsky, and Tafel steps, respectively. ML: Machine learning; MAE: mean absolute error; NEB: Nudged Elastic Band; DFT: density functional theory; HER: hydrogen evolution reaction.
It is worth noting that biaxial strain can markedly influence the pathway characteristics of certain Volmer configurations. Under strain-free conditions, adsorbed hydrogen atoms (H*) can stably embed into the surface, resulting in a downward energy trend. However, when strain is applied, changes in the electronic structure of surface metal atoms, such as shifts in the d-band center and local density of states, alter the energy landscape. These subtle yet critical energy variations were accurately captured by the fine-tuned model, further demonstrating its robustness and physical adaptability under complex external perturbations, and providing strong support for strain-engineered catalyst performance prediction.
In modeling HER pathways, accurate absolute energy predictions are crucial for evaluating reaction thermodynamics and activation barriers. As shown in Figure 10A-C, the OC20NEB-pretrained model exhibits systematic deviations under biaxial strain, with predicted energies for the Volmer, Heyrovsky, and Tafel pathways consistently diverging from the ideal “Perfect Prediction” reference line. As a result, the MAEs for these pathways exceed 320 eV. This overall shift, similar to the model’s behavior under unstrained conditions, highlights its limited applicability to HEA systems with large, multi-component surfaces. The limitation stems from the absence of high-energy and compositionally complex structures in the training dataset, indicating that the pretrained model lacks generalizability to large-scale HEA surfaces.
Figure 10. Absolute energy prediction errors of HER pathways under biaxial strain before and after fine-tuning. (A-C) Pretrained model errors for the Volmer, Heyrovsky, and Tafel steps, respectively; (D-F) Fine-tuned model errors for the Volmer, Heyrovsky, and Tafel steps, respectively. ML: Machine learning; MAE: mean absolute error; NEB: Nudged Elastic Band; DFT: density functional theory; HER: hydrogen evolution reaction.
After fine-tuning, the model’s absolute energy predictions improved markedly. As shown in Figure 10D-F, the MAEs for the Volmer, Heyrovsky, and Tafel pathways were reduced to 0.0987 eV, 0.0981 eV, and 0.0960 eV, respectively, all within the 0.1 eV threshold. Although achieving MAEs below 0.05 eV remains challenging for systems spanning a large energy range (-350 eV to -300 eV), the attained accuracy is sufficient to support practical high-throughput screening of catalytic materials.
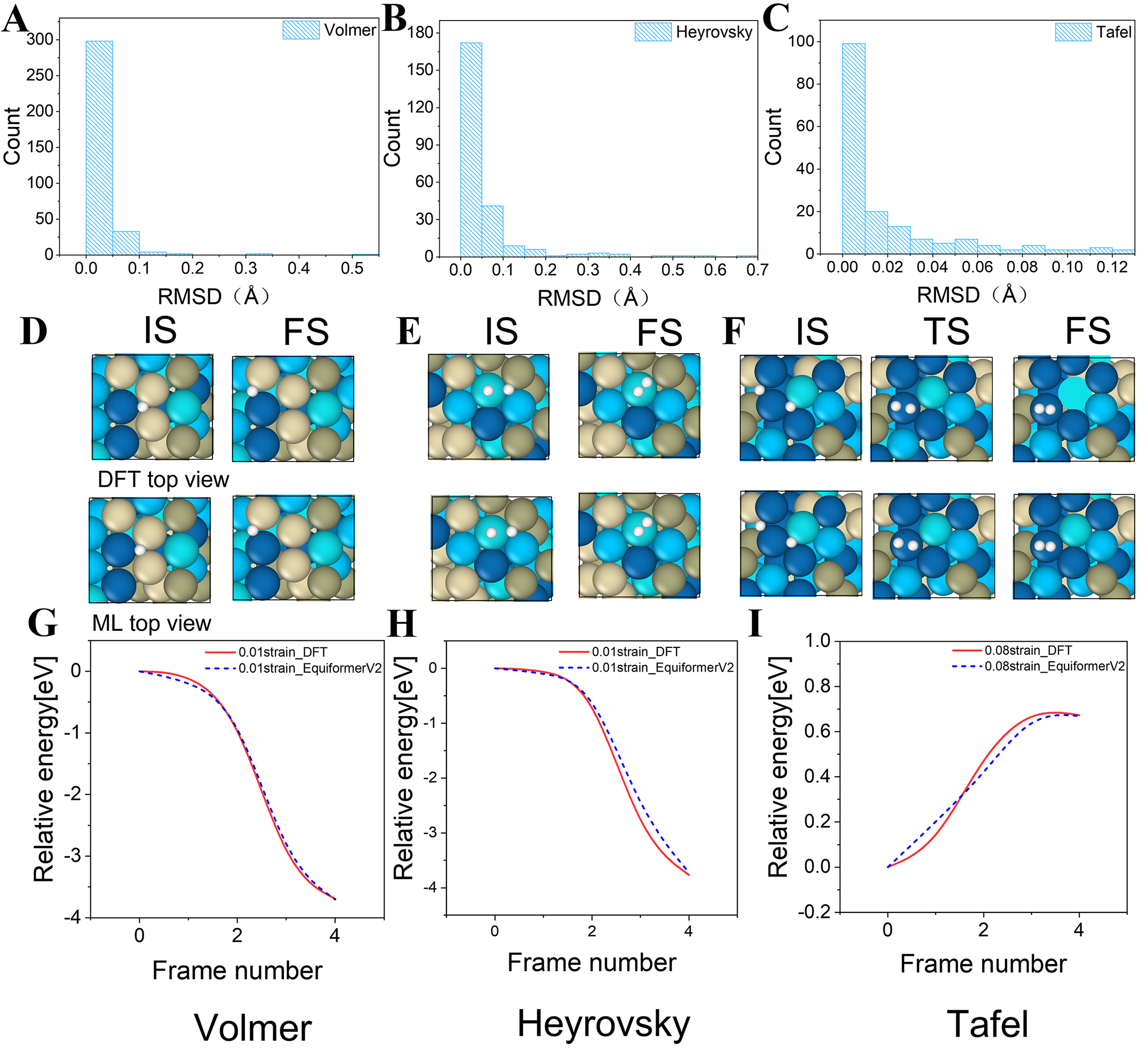
Using the fine-tuned eqV2 model, we incorporated HER pathway data for HEAs under various biaxial strain conditions, enabling highly accurate predictions of reaction pathways in strained environments. Under biaxial strain, the model also exhibited excellent structural accuracy, with RMSD values below 0.1 Å for 88.8% of the predicted configurations across Volmer, Heyrovsky, and Tafel steps [Figure 11A-C]. Leveraging its comprehensive training on unstrained configurations and energies, the model demonstrated effective transferability and rapid convergence upon the introduction of strain. In terms of structural prediction, the model consistently maintained exceptional accuracy for both IS and FS, achieving errors below 0.01 Å for all three reactions [Figure 11D-F]. Notably, for the Tafel reaction, the predicted TS configuration achieved an exceptionally low error of only 0.01 Å [Figure 11F]. These results underscore the model’s outstanding capability to accurately predict complex non-equilibrium structures under varying strain conditions.
Figure 11. Machine learning-predicted HER pathways under biaxial strain: (A-C) Configuration errors under biaxial strain; (D-F) Initial and final configurations of the Volmer, Heyrovsky, and Tafel steps, including the transition-state configuration for the Tafel step; (G-I) Energy profiles of the Volmer, Heyrovsky, and Tafel reactions. RMSD: root mean square deviation; IS: initial states; FS: final states; DFT: density functional theory; HER: hydrogen evolution reaction; ML:
In terms of energy prediction, the model accurately reproduced the energy variation trends of the Volmer and Heyrovsky pathways, closely aligning with DFT-calculated results and exhibiting the expected monotonic decrease along the reaction coordinate [Figure 11G and H]. For the Tafel reaction, which features a pronounced activation barrier, the model effectively captured both the position and magnitude of the energy peak. The prediction errors were primarily localized around the TS [Figure 11I], with the maximum deviation remaining below 0.1 eV, well within an acceptable range.
In catalytic materials, lattice strain - typically induced by surface defects, alloying, or heterogeneous interfaces - plays a pivotal role in regulating adsorption energies and reaction barriers. Although moderate strain is often intentionally applied to optimize catalytic activity[48], it simultaneously increases the configurational complexity of reaction pathways, leading to prohibitively high computational costs for conventional DFT-based investigations. In this study, the fine-tuned model demonstrated the ability to accurately predict reaction pathways under biaxial strain, capturing both energy profiles and transition-state features with high precision. These findings confirm that the proposed fine-tuning strategy preserves strong generalization capability and accuracy under strain-engineered conditions, significantly enhancing the efficiency of structural and energy predictions while providing a robust computational framework for high-throughput screening and the mechanistic exploration of strain effects in HEA catalysts.
Although this study focuses on the Ir-Pt-Rh-Pd-Ru HEA (111) surface under biaxial strain, nanocrystal catalysts commonly expose multiple facets including (100), (110), and stepped surfaces with distinct coordination and electronic environments that modulate hydrogen adsorption and HER barriers[49,50]. We focus on the (111) facet as it represents the close-packed, thermodynamically most stable FCC surface frequently expressed in nanoparticle morphologies[51,52]. Additionally, (111) surfaces offer well-characterized adsorption sites with extensive theoretical and experimental benchmarks, facilitating reliable cross-validation[53-55]. Accordingly, we systematically constructed adsorption models on (111) surfaces and applied biaxial strain to capture the interplay between local chemistry and lattice deformation effects on transition-state energetics. Notably, this framework extends beyond (111) facets - with appropriate CI-NEB training data, the fine-tuned eqV2 approach can be extended to other crystallographic orientations, enabling comprehensive facet-dependent exploration in future work.
CONCLUSIONS
In this study, we fine-tuned the eqV2 GNN model to predict HER pathways in strain-engineered Ir-Pt-Rh-Pd-Ru HEA catalysts. The lightweight eqV2-31M model achieved exceptional accuracy with a MAE below 0.1 eV for pathway energy predictions and over 88.8% of structural predictions within 0.1 Å RMSD, while reducing computational time from hours to seconds compared to conventional DFT calculations. The model demonstrates robust performance across Volmer, Heyrovsky, and Tafel reaction pathways under biaxial strain conditions (0.01-0.10), accurately capturing strain-induced electronic structure modulation and energy barrier variations. In future work, incorporating solvent effects, either through implicit solvation models or explicit water layers, would further improve the realism of the simulations and enhance the model’s applicability to electrochemical environments. In particular, the VASPsol implicit solvation model, with a dielectric constant of 78.4 to represent water, could be employed to account for solvent effects in a computationally efficient manner[56]. Hydrogen adsorption Gibbs free energy (ΔGH*) serves as a widely adopted descriptor for HER activity evaluation[57-59]. In this work, however, our primary contribution is methodological: establishing a framework for accurate reaction-path prediction in strain-engineered systems. While this architecture can be extended to free-energy calculations through standard thermodynamic corrections within the computational hydrogen electrode (CHE) framework[60-65], we focus on total energy predictions to efficiently validate our core methodology. This approach maintains computational efficiency while providing actionable insights for HER catalyst screening and design.
This approach addresses the computational bottlenecks of traditional DFT methods for HEA systems, enabling practical high-throughput screening of strain-engineered catalysts. Although the present work focuses on acidic HER pathways, the modeling framework exhibits strong extensibility to alkaline media and other electrocatalytic reactions. By incorporating appropriate training data for alkaline HER mechanisms or alternative reaction pathways such as CO2 reduction and oxygen reduction, the fine-tuned eqV2 model can effectively capture distinct reaction energetics and pathway characteristics. Furthermore, the fine-tuning strategy demonstrated here is readily extensible to other electrocatalytic reactions such as CO₂ reduction and oxygen reduction. Future work will integrate active learning algorithms[66] to efficiently explore optimal HEA configurations and couple the framework with generative models for inverse catalyst design[67]. This work establishes machine learning as a powerful tool for accelerating the discovery and rational design of next-generation electrocatalysts.
DECLARATIONS
Authors’ contributions
Investigation, formal analysis, visualization, writing - original draft: Wang, L.
Investigation, formal analysis, validation: Zhou, F.; Ying, P.
Supervision, resources, funding acquisition: Liu, Y.; Chen, Y.
All authors read and approved the final version of the manuscript.
Availability of data and materials
The pre-trained model weights are available at the OCP GitHub repository. Parity plots for all reported results, along with configuration files and trajectories, are publicly accessible at: https://github.com/LeiWang25/TS_Prediction
Financial support and sponsorship
The authors acknowledge financial support from the National Key Research and Development Program (2024YFA1209801), the National Natural Science Foundation of China (12302140, 12325204), the China Postdoctoral Science Foundation (2023M732794, 2025T180517), the Fundamental Research Funds for the Central Universities of China (sxzy012023213), the Scientific Research Program of Shaanxi Province (2023JC-XJ-02), the Young Talent Support Program of Xi’an Science and Technology Association (959202413069), and the Postdoctoral Fellowship Program (Grade B) of the China Postdoctoral Science Foundation (GZB20230575).
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2026.
REFERENCES
1. Gao, D.; Xu, Y.; Liu, Z.; et al. Understanding of strain effect on Mo-based MXenes for electrocatalytic CO2 reduction. Appl. Surf. Sci. 2024, 654, 159501.
2. Löffler, T.; Savan, A.; Garzón-manjón, A.; et al. Toward a paradigm shift in electrocatalysis using complex solid solution nanoparticles. ACS. Energy. Lett. 2019, 4, 1206-14.
3. Lu, Z.; Chen, Z. W.; Singh, C. V. Neural network-assisted development of high-entropy alloy catalysts: decoupling ligand and coordination effects. Matter 2020, 3, 1318-33.
4. Li, G.; Yang, Q.; Rao, J.; et al. In situ induction of strain in iron phosphide (FeP2) catalyst for enhanced hydroxide adsorption and water oxidation. Adv. Funct. Mater. 2020, 30, 1907791.
5. Price, C. C.; Singh, A.; Frey, N. C.; Shenoy, V. B. Efficient catalyst screening using graph neural networks to predict strain effects on adsorption energy. Sci. Adv. 2022, 8, eabq5944.
6. Gariepy, Z.; Chen, Z.; Tamblyn, I.; Singh, C. V.; Tetsassi Feugmo, C. G. Automatic graph representation algorithm for heterogeneous catalysis. APL. Mach. Learn. 2023, 1, 036103.
7. Clausen, C. M.; Rossmeisl, J.; Ulissi, Z. W. Adapting OC20-trained equiformerV2 models for high-entropy materials. J. Phys. Chem. C. 2024, 128, 11190-5.
8. Dewyer, A. L.; Argüelles, A. J.; Zimmerman, P. M. Methods for exploring reaction space in molecular systems. WIREs. Comput. Mol. Sci. 2017, 8, e1354.
9. Choi, S. Prediction of transition state structures of gas-phase chemical reactions via machine learning. Nat. Commun. 2023, 14, 1168.
10. Kim, J.; Kang, M.; Yoon, J. H.; Kim, S. K. Tracking the structural change of the predissociating molecule near the transition state. Nat. Commun. 2025, 16, 210.
11. Wander, B.; Shuaibi, M.; Kitchin, J. R.; Ulissi, Z. W.; Zitnick, C. L. CatTSunami: accelerating transition state energy calculations with pretrained graph neural networks. ACS. Catal. 2025, 15, 5283-94.
12. Sun, Y.; Dai, S. High-entropy materials for catalysis: a new frontier. Sci. Adv. 2021, 7, eabg1600.
13. Butler, K. T.; Davies, D. W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547-55.
14. Jinnouchi, R.; Karsai, F.; Kresse, G. On-the-fly machine learning force field generation: application to melting points. Phys. Rev. B. 2019, 100, 014105.
15. Jingchen, L.; Xiao, F.; Xuhe, G.; Ruijuan, X.; Hong, L. High-throughput NEB for Li-ion conductor discovery via fine-tuned CHGNet potential. arXiv 2025, arXiv:2507.02334. Available online: https://doi.org/10.48550/arXiv.2507.02334. (accessed 10 July 2025).
16. Wander, B.; Broderick, K.; Ulissi, Z. W. Catlas: an automated framework for catalyst discovery demonstrated for direct syngas conversion. Catal. Sci. Technol. 2022, 12, 6256-67.
17. Lan, J.; Palizhati, A.; Shuaibi, M.; et al. AdsorbML: a leap in efficiency for adsorption energy calculations using generalizable machine learning potentials. NPJ. Comput. Mater. 2023, 9, 172.
18. Hu, Y.; Chen, J.; Wei, Z.; He, Q.; Zhao, Y. Recent advances and applications of machine learning in electrocatalysis. J. Mater. Inf. 2023, 3, 18.
19. Jain, A.; Ong, S. P.; Hautier, G.; et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL. Mater. 2013, 1, 011002.
20. Chanussot, L.; Das, A.; Goyal, S.; et al. Open Catalyst 2020 (OC20) Dataset and community challenges. ACS. Catal. 2021, 11, 6059-72.
21. Tran, R.; Lan, J.; Shuaibi, M.; et al. The Open Catalyst 2022 (OC22) Dataset and challenges for oxide electrocatalysts. ACS. Catal. 2023, 13, 3066-84.
22. Liao, Y. -L.; Wood, B.; Das, A.; Smidt, T. EquiformerV2: improved equivariant transformer for scaling to higher-degree representations. arXiv 2024, arXiv:2306.12059. Available online: https://doi.org/10.48550/arXiv.2306.12059 (accessed 10 July 2025).
23. Batchelor, T. A.; Pedersen, J. K.; Winther, S. H.; Castelli, I. E.; Jacobsen, K. W.; Rossmeisl, J. High-entropy alloys as a discovery platform for electrocatalysis. Joule 2019, 3, 834-45.
24. Yang, X.; Wang, Y.; Tong, X.; Yang, N. Strain engineering in electrocatalysts: fundamentals, progress, and perspectives. Adv. Energy. Mater. 2021, 12, 2102261.
25. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. Condens. Matter. 1996, 54, 11169-86.
26. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 1999, 59, 1758-75.
27. Perdew, J. P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865-8.
29. Henkelman, G.; Uberuaga, B. P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901-4.
30. Smidstrup, S.; Pedersen, A.; Stokbro, K.; Jónsson, H. Improved initial guess for minimum energy path calculations. J. Chem. Phys. 2014, 140, 214106.
31. Boda, A.; Chandorkar, N.; Ali, S. M. Density functional theoretical assessment of titanium metal for adsorption of hydrogen, deuterium and tritium isotopes. Theor. Chem. Acc. 2023, 142, 46.
32. Montoya, A.; Schlunke, A.; Haynes, B. S. Reaction of hydrogen with Ag(111): binding states, minimum energy paths, and kinetics. J. Phys. Chem. B. 2006, 110, 17145-54.
33. Ignatov, S. K.; Okhapkin, A. I.; Gadzhiev, O. B.; Razuvaev, A. G.; Kunz, S.; Bäumer, M. Adsorption and diffusion of hydrogen on the surface of the Pt24 subnanoparticle. A DFT Study. J. Phys. Chem. C. 2016, 120, 18570-87.
34. Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2019, arXiv:1711.05101. Available online: https://doi.org/10.48550/arXiv.1711.05101 (accessed 10 July 2025).
35. Loshchilov, I.; Hutter, F. SGDR: stochastic gradient descent with warm restarts. arXiv 2017, arXiv:1608.03983. Available online: https://doi.org/10.48550/arXiv.1608.03983. (accessed 10 July 2025).
36. Wang, Z.; Hu, S.; Wang, D.; et al. A HER-inhibiting layer based on M‐H bond regulation for achieving stable zinc anodes in aqueous zinc-ion batteries. Adv. Funct. Mater. 2025, 35, 2502186.
37. Wei, J.; Zhou, M.; Long, A.; et al. Heterostructured electrocatalysts for hydrogen evolution reaction under alkaline conditions. Nanomicro. Lett. 2018, 10, 75.
38. Li, Q.; Zou, X.; Ai, X.; Chen, H.; Sun, L.; Zou, X. Revealing activity trends of metal diborides toward pH-universal hydrogen evolution electrocatalysts with Pt-like activity. Adv. Energy. Mater. 2018, 9, 1803369.
39. Tang, S.; Xu, L.; Dong, K.; et al. Curvature effect on graphene-based Co/Ni single-atom catalysts. Appl. Surf. Sci. 2023, 615, 156357.
40. Liu, G.; Shih, A. J.; Deng, H.; et al. Site-specific reactivity of stepped Pt surfaces driven by stress release. Nature 2024, 626, 1005-10.
41. Khorshidi, A.; Violet, J.; Hashemi, J.; Peterson, A. A. How strain can break the scaling relations of catalysis. Nat. Catal. 2018, 1, 263-8.
42. Wang, L.; Zhou, X.; Luo, Z.; et al. Review of external field effects on electrocatalysis: machine learning guided design. Adv. Funct. Mater. 2024, 34, 2408870.
43. Plenge, M. K.; Pedersen, J. K.; Bagger, A.; Rossmeisl, J. Catalysis of C-N coupling on high-entropy alloys. J. Catal. 2024, 430, 115322.
44. Cao, G.; Yang, S.; Ren, J. C.; Liu, W. Electronic descriptors for designing high-entropy alloy electrocatalysts by leveraging local chemical environments. Nat. Commun. 2025, 16, 1251.
45. Yan, L.; Yamamoto, Y.; Shiga, M.; Sugino, O. Nuclear quantum effect for hydrogen adsorption on Pt(111). Phys. Rev. B. 2020, 101, 165414.
46. Henkelman, G.; Jónsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978-85.
47. Bhatia, B.; Sholl, D. S. Chemisorption and diffusion of hydrogen on surface and subsurface sites of flat and stepped nickel surfaces. J. Chem. Phys. 2005, 122, 204707.
48. Wang, L.; Zeng, Z.; Gao, W.; et al. Tunable intrinsic strain in two-dimensional transition metal electrocatalysts. Science 2019, 363, 870-4.
49. Hsiao, Y. C.; Wu, C. Y.; Lee, C. H.; et al. A library of seed@high-entropy-alloy core-shell nanocrystals with controlled facets for catalysis. Adv. Mater. 2025, 37, e2411464.
50. Wang, C.; Huang, Z.; Ding, Y.; Xie, M.; Chi, M.; Xia, Y. Facet-controlled synthesis of platinum-group-metal quaternary alloys: the case of nanocubes and {100} facets. J. Am. Chem. Soc. 2023, 145, 2553-60.
51. Altantzis, T.; Lobato, I.; De Backer, A.; et al. Three-dimensional quantification of the facet evolution of Pt nanoparticles in a variable gaseous environment. Nano. Lett. 2019, 19, 477-81.
52. Boukouvala, C.; Daniel, J.; Ringe, E. Approaches to modelling the shape of nanocrystals. Nano. Converg. 2021, 8, 26.
53. Karlberg, G. S.; Jaramillo, T. F.; Skúlason, E.; Rossmeisl, J.; Bligaard, T.; Nørskov, J. K. Cyclic voltammograms for H on Pt(111) and Pt(100) from first principles. Phys. Rev. Lett. 2007, 99, 126101.
54. Miller, D. J.; Öberg, H.; Kaya, S.; et al. Oxidation of Pt(111) under near-ambient conditions. Phys. Rev. Lett. 2011, 107, 195502.
55. Kormányos, A.; Dong, Q.; Xiao, B.; et al. Stability of high-entropy alloys under electrocatalytic conditions. iScience 2023, 26, 107775.
56. Lu, S.; Cao, J.; Zhang, Y.; Lou, F.; Yu, Z. Transition metal single-atom supported on PC3 monolayer for highly efficient hydrogen evolution reaction by combined density functional theory and machine learning study. Appl. Surf. Sci. 2022, 606, 154945.
57. Yang, Y.; Qian, Y.; Li, H.; et al. O-coordinated W-Mo dual-atom catalyst for pH-universal electrocatalytic hydrogen evolution. Sci. Adv. 2020, 6, eaba6586.
58. Fung, V.; Hu, G.; Wu, Z.; Jiang, D. Descriptors for hydrogen evolution on single atom catalysts in nitrogen-doped graphene. J. Phys. Chem. C. 2020, 124, 19571-8.
59. Wang, Y.; Qiu, W.; Song, E.; et al. Adsorption-energy-based activity descriptors for electrocatalysts in energy storage applications. Natl. Sci. Rev. 2018, 5, 327-41.
60. Oh, N. K.; Seo, J.; Lee, S.; et al. Highly efficient and robust noble-metal free bifunctional water electrolysis catalyst achieved via complementary charge transfer. Nat. Commun. 2021, 12, 4606.
61. Di Liberto, G.; Cipriano, L. A.; Pacchioni, G. Universal principles for the rational design of single atom electrocatalysts? Handle with care. ACS. Catal. 2022, 12, 5846-56.
62. Wu, T.; Stone, M. L.; Shearer, M. J.; et al. Crystallographic facet dependence of the hydrogen evolution reaction on CoPS: theory and experiments. ACS. Catal. 2018, 8, 1143-52.
63. Zhang, Y.; Lee, S.; Jeong, S.; et al. Phase-bridged hierarchical catalysts for efficient and stable water electrolysis. Adv. Funct. Mater. 2023, 34, 2309250.
64. Nazari, S.; Najmi, A.; Kumar, P.; et al. Configuring a liquid state high-entropy metal alloy electrocatalyst. Small 2025, 21, e2504087.
65. Chang, C.; Ting, Y.; Yen, F.; Li, G.; Lin, K.; Lu, S. High performance anion exchange membrane water electrolysis driven by atomic scale synergy of non-precious high entropy catalysts. Energy. Mater. 2025, 5, 500117.
66. Moon, J.; Beker, W.; Siek, M.; et al. Active learning guides discovery of a champion four-metal perovskite oxide for oxygen evolution electrocatalysis. Nat. Mater. 2024, 23, 108-15.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data

















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].