Stacked machine learning for accurate and interpretable prediction of MXenes’ work function
Abstract
MXenes, with tunable compositions and rich surface chemistry, enable precise control of electronic, optical, and mechanical properties, making them promising materials in electronics and energy-related applications. In particular, the work function plays a critical role in determining their physicochemical properties. However, the accurate prediction of the work function of MXenes with machine learning (ML) remains challenging due to the lack of robust models with high accuracy and interpretability. To this end, we propose a stacked model and introduce high-quality descriptors constructed via Sure Independence Screening and Sparsifying Operator method to improve the prediction accuracy of the work function of MXenes in this work. The stacked model initially generates predictions from multiple base models, and then employs these predictions as inputs to a meta-model for secondary learning, thereby enhancing both predictive performance and generalization capability. The results show that by integrating the high-quality descriptors, the model’s performance improves significantly, yielding a coefficient of determination of 0.95 and mean absolute error of 0.2, respectively. Last but not least, we demonstrate that MXenes’ work functions are predominantly governed by their surface functional groups, where SHapley Additive exPlanations value analysis quantitatively resolves the structure–property relationship between surface functional groups and the work function of MXenes. Specifically, O terminations can lead to the highest work functions, while OH terminations result in the lowest value (over 50% reduction), and transition metals or C/N elements have a relatively smaller effect. This work achieves an optimal balance between accuracy and interpretability in ML predictions of MXenes’ work functions, providing both fundamental insights and practical tools for materials discovery.
Keywords
INTRODUCTION
Two-dimensional (2D) carbides and nitrides, MXenes, are an emerging class of low-dimensional materials that have received considerable interest over the last decade[1,2], which exhibit tunable compositions and rich surface chemistry[3-5]. The tunability of MXenes allows for the optimization of their electrical conductivity, mechanical robustness, and chemical stability, making them indispensable in widespread applications[6-8]. In particular, their work function can be tuned over a wide range from 1.3 to 7.2 eV, making MXenes highly promising candidates in the fields of optoelectronics, catalysis, sensing, etc.[9-12]. In photonic devices, the work function is a critical parameter that influences the device’s performance. However, performing density functional theory (DFT) calculations for each candidate material is impractical because of the enormous computational and time costs, which renders traditional trial-and-error approaches less feasible.
The rapid advancements of machine learning (ML) have established it as a transformative tool for accelerating material science research[13-16]. Leveraging large-scale datasets, ML has emerged as a crucial enabler in predicting material properties and uncovering insights into complex systems. For example, ML models have been used not only to evaluate the stability of 2D materials[17], but also to facilitate swift assessments of novel compounds with potential applications in photocatalysis and energy storage devices[18]. Expanding upon these capabilities, AI-driven frameworks have successfully addressed complex challenges in material design, and achieved significant achievements. For example, the development of ML models, including gradient boosting and symbolic regression, with DFT to accelerate the design of MXene and MN4-graphene bifunctional oxygen electrocatalysts[19], the creation of the CrabNet neural network architecture to predict material properties from compositions, enhancing regression performance through attention mechanisms and element embeddings[20], and the discovery of stable AA0MH6 semiconductors via generative adversarial networks (GAN) coupled with DFT validations, etc.[21]. Therefore, ML can provide an efficient strategy for screening and predicting materials with desired work functions.
However, although Roy et al. have employed ML methods to predict the work function of MXenes and reduced the mean absolute error (MAE) to approximately 0.26 eV[22], there are still some limitations. First, further improving the predictive accuracy of the models remains a challenge, limited by the diversity of available algorithms and the size of valid data[23]. Secondly, further enhancing the interpretability of ML models remains a challenge, limited by their “black box” character, making it difficult to understand the intrinsic relationship between material features and target performance[24]. Therefore, there is an urgent need to develop a ML model integrated with advanced algorithms that not only enhances the prediction accuracy of the work function of MXenes but also improves the model’s interpretability, thereby elucidating the intrinsic connection between material characteristics and the work function.
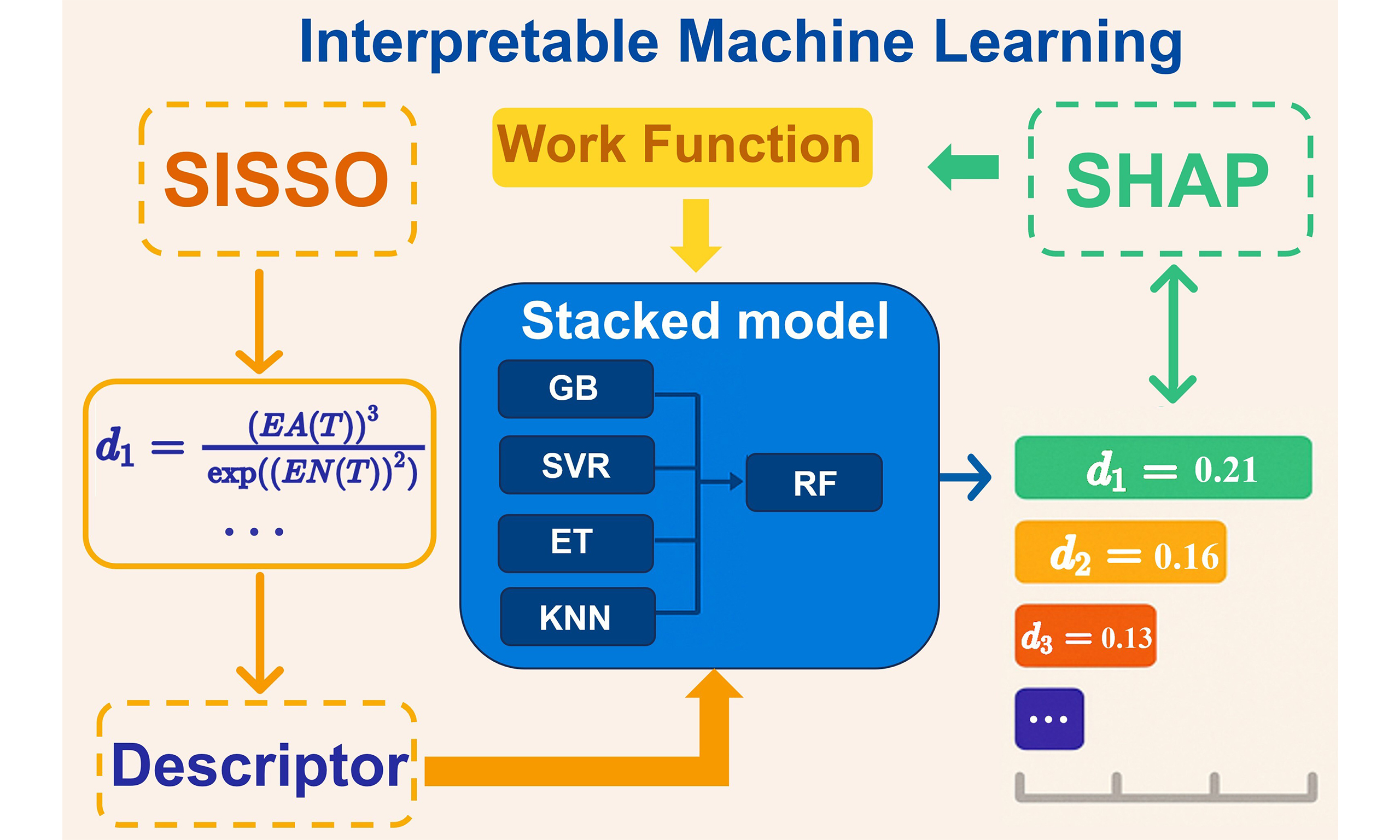
In this study, we integrate the Sure Independence Screening and Sparsifying Operator (SISSO) method with the stacked model approach to improve the prediction accuracy of the work function of MXenes. The SISSO method generates highly correlated descriptors of the target features, which provide a transparent and intuitive overview of the relationship between the target features and the physical properties. The stacked model further improves the model performance by integrating the prediction results from multiple base models and using them as inputs for secondary learning. By interpreting the ML model using the SHapley Additive exPlanations (SHAP) method, we provide an in-depth analysis of the key factors that lead to a wide range of values for the work function of MXenes, thereby transforming the traditional “black box” model into a transparent “glass box” model. Our approach not only provides valuable insights into the determinants of the work function but also offers a scalable strategy applicable to a broader range of material categories.
MATERIALS AND METHODS
The data containing 4,034 materials was extracted from Computational 2D Materials Database (C2DB)[25,26]. Ninety-eight characteristics were recorded for each material, including properties such as Fermi energy level, elastic modulus, material ID, volume, and relative molecular mass. To validate the feasibility of our stacking model approach, we conducted tests using various models, including random forest (RF)[27], gradient boosting decision tree (GBDT)[28], and lightGBM (LGB)[29], as meta-models. To enhance the model’s predictive capability, we generated additional effective features using the SISSO[30] method and incorporated them into the training process. Furthermore, we employed SHAP[31] values to analyze the importance of each feature, thereby gaining deeper insights into the model’s decision-making mechanism. All data processing and ML tasks were conducted in Python, with data processing handled by the Pandas library and ML algorithms implemented using the Scikit-learn library. The performance of the models was evaluated by using MAE and coefficient of determination (R2). These metrics are mathematically defined in the Supplementary Equations (1) and (2).
RESULTS AND DISCUSSION
Workflow
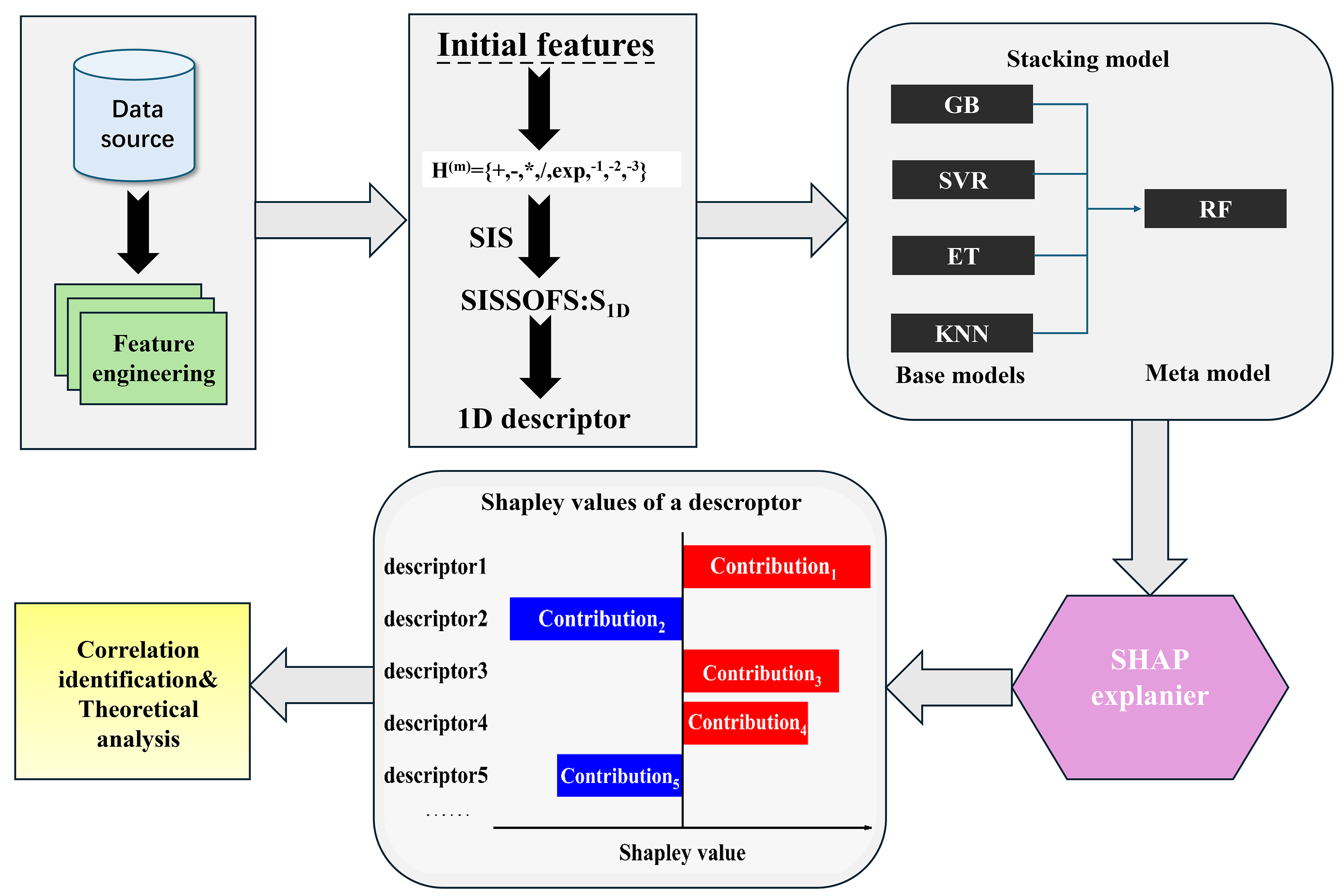
As illustrated in Figure 1, the workflow begins with rigorous data selection and cleaning for model training and validation. Herein, the raw data of the work function of MXenes were curated from the recently created C2DB. Then, the SISSO algorithm was utilized to construct the descriptors with enriched physics insights between features and target properties, which will effectively improve the accuracy and interpretability of ML. Meanwhile, a stacked model that combines predictions from various base models into a refined meta-model was constructed, which was confirmed to possess not only enhanced generalization but also effectively reduced errors, overfitting, and biases. Additionally, SHAP was leveraged to determine feature importance, providing nuanced insights into the role of atomic-layer compositions and feature interdependencies in governing work function behavior. Ultimately, ML, combined with material science knowledge, provides a deeper understanding of the factors influencing the work function of MXenes.
Data preparation and feature screening
Our study focused on a subset of 275 MXenes that were screened from 4,034 candidate materials, particularly the work function values obtained through DFT calculations[32,33]. For the purpose of model development, 80% of the MXene data were allocated to the training set, while the remaining 20% were reserved for testing. This dataset provides a solid foundation for in-depth analysis and predictive modeling due to its richness. However, the 98 features contained in the dataset also pose challenges for modeling, prompting us to pay attention to feature engineering. Feature engineering, as an important aspect of ML, directly affects the performance of ML models. For instance, the excessive feature set will lead to the well-known dimensionality curse[34], which not only amplifies the computational demands and resource usage of the model but also exacerbates the risk of overfitting. Overfitting is a common phenomenon during the training of ML models. It refers to the model excessively learning the details and noise of the training data, to the extent that it fails to capture underlying patterns. This leads to a significant decline in the model’s performance on new data[24,35]. Therefore, it is crucial to control overfitting and ensure the model has good generalization ability. Here, we proposed a new metric to quantify the degree of model overfitting; that is, the relative overfitting index (ROI). ROI is defined as the difference between the MAE of the test set and the MAE of the training set, normalized by the MAE of the test set as[36]:
Then, we identified the key features with physical significance to reduce the risk of overfitting ML models. Herein, the feature screening was initiated by computing the Pearson correlation coefficients (R) among the various variables with[36]
where xi and yi represent the true values of two different features, while
Construction of SISSO descriptors
After completing feature engineering, we implemented SISSO to systematically identify optimal descriptors demonstrating strong correlations with work function. SISSO is a “glass-box” ML model that is designed to address the challenges of high-dimensional data and feature selection[30]. In this context, it identifies both linear and nonlinear relationships between input features and target properties, offering insights into the mechanisms influencing the work function of MXenes.
During the discovery of descriptors, the mathematical operators H = {“−, *, /, ^-1, ^2, ^3, sqrt, exp,” etc.} were used in constructing the descriptors. Herein, the parameter “fcomplexity”, representing the number of operators, was typically set between 0 and 7. With these settings, the descriptor sets including 35,822, 630,070, 78,025,280, 2,033,702,714, 36,517,309,938, and 287,772,622,033 descriptors were generated in fcomplexity of 2, 3, 4, 5, 6, and 7, respectively. They represent the number of descriptors generated by SISSO models in different complexity, whose accuracy increases with increasing complexity. To evaluate the performance across different model complexities (fcomplexity), we conducted a systematic analysis of the SISSO-generated features by comparing the average correlation of the top 20 features (with respect to the work function) against the computational time. Specifically, as fcomplexity increased from 1 to 7, the average correlation progressively improved (0.300 at fcomplexity = 1, 0.816 at fcomplexity = 5, and 0.848 at fcomplexity = 7, respectively), indicating that higher complexities produce more relevant descriptors. However, the computational consumption increased almost exponentially, from 0.8 seconds at fcomplexity = 1, escalating to 966 seconds at fcomplexity = 5, and surging to about 17.2 kiloseconds at fcomplexity = 6 and 37.9 kiloseconds at fcomplexity = 7 (details in Supplementary Figure 1), respectively. Given that the correlation gains plateau after fcomplexity = 5 while the computational overhead intensifies sharply, we selected fcomplexity = 5 as the optimal descriptor, thereby achieving an effective balance between feature relevance and computational efficiency[30]. Therefore, it is reasonable that the descriptor at fcomplexity = 5 is selected as the optimal descriptor[38]. At a fcomplexity of 5 (see Supplementary Table 2 for additional parameters), 1,000 candidate descriptors were successfully generated. These descriptors are derived from the original features based on predefined mathematical operators, thereby ensuring complete transparency.
ML model design
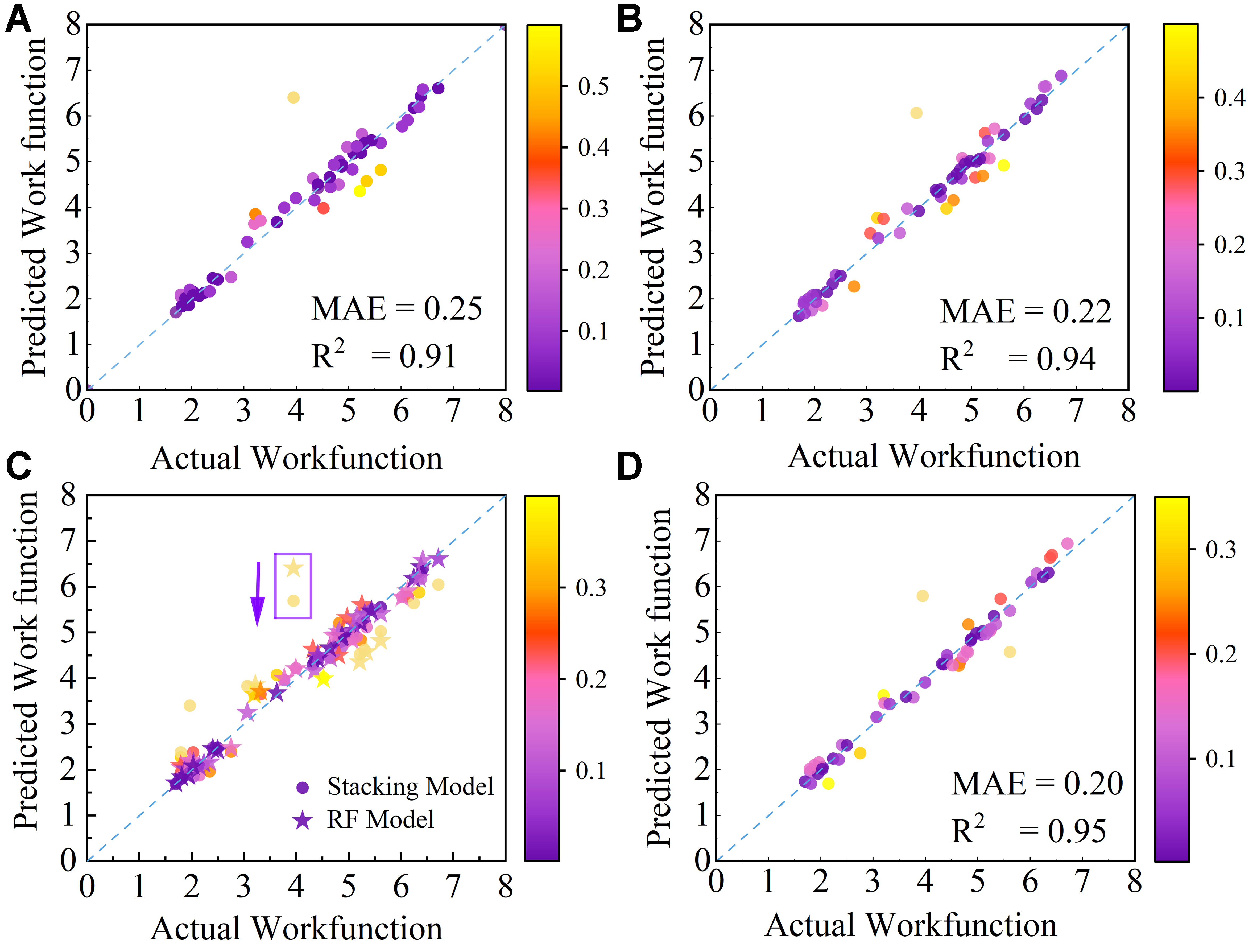
In this section, we constructed a stacked model using the RF[27] model as the meta-model, while the gradient boosting tree (GB)[39], support vector regression (SVR)[40], extreme gradient boosting tree (ET)[41], and K nearest neighbor regression (KNR)[42] were selected as the base models. Stacked models, built using a stacking architecture, endow meta-models with the ability to integrate the predictive outputs of the base models, incorporating multiple patterns and insights that may be difficult for a single algorithm to achieve on its own[43]. As shown in Figure 2A, the general RF model exhibits an MAE of 0.25 with a R2 of 0.91 after optimizing the parameters through grid search and 5-fold cross-validation[44,45]. Comparably, the stacked model possesses a lower MAE (0.22) and higher R2 (0.94) under the same parameter tuning conditions [Figure 2B], demonstrating that the layering strategy can achieve significantly improved performance. Furthermore, we have further combined the prediction data of the general RF model and the stacked model in Figure 2C. Upon comparison, it is evident that the prediction points of the general RF model within the purple box deviate significantly from the prediction line, indicating these points are potential outliers or in areas of reduced prediction accuracy. While after the integration of base models, the prediction points noticeably move closer to the prediction line. In order to further demonstrate the superior capability of stacked model in handling outliers, we have evaluated an alternative meta-model, GBDT, through five-fold cross-validation. The results are shown in Supplementary Figure 2, indicating that in Supplementary Figure 2A, B, D, and E, the predictions (blue circles) of stacked model for the same data points are markedly closer to the perfect prediction line than those of the general GBDT model (red triangles), which can be evidenced by reduced scatter and lower MAE values (e.g., 0.2026 vs. 0.2468 in fold 1). Even in Supplementary Figure 2C (fold 3), a modest decrease in error dispersion is also observed. This clearly illustrates the stacked model’s capacity to enhance prediction accuracy for the work function of MXenes by leveraging the advantages of multiple base models.
Figure 2. Scatter plots comparing predicted and actual work function values. (A) General RF model; (B) Stacked model with RF as the meta-model; (C) Stacked model with RF as the meta-model and General RF model; and (D) Stacked model with RF as the meta-model and incorporating SISSO descriptors. The color bar represents the deviation z between calculated and predicted values. RF: Random forest; SISSO: Sure Independence Screening and Sparsifying Operator.
To establish a crucial foundation for subsequent interpretable ML analysis, we integrated the aforementioned SISSO descriptors into the dataset. Considering the model complexity arising from an excessive number of features and the difficulty of improving model accuracy and interpretability without significantly increasing complexity, we moderately selected three SISSO descriptors that exhibit optimal correlation with the work function, as detailed in Table 1.
The three optimal one-dimensional SISSO descriptors with the highest correlation to the work function
| Rank | Descriptor |
| 1 | |
| 2 | |
| 3 |
After incorporating key effective descriptors, these SISSO descriptors significantly improved the model’s interpretability, enabling it to capture subtle yet influential data patterns. Consequently, the MAE of the improved stacked model decreases from 0.22 to 0.20, and the R2 increases from 0.91 to 0.95 as shown in Figure 2D. Moreover, z is used as a variable and color mapping to deviation, with lighter data points indicating greater bias, which is expressed as follows:
where ytest represents the calculated value derived from the DFT calculation, and ypre indicates the predicted value of the ML model. It is clear that the stacked model with RF as the meta-model and incorporating SISSO descriptors exhibits a stronger generalization ability on the testing set than the General RF model in Figure 2. Furthermore, the enhanced generalization performance translates into a significant reduction in overfitting; specifically, the ROI decreases by 48.3% when transitioning from the General RF model to the stacked model with SISSO descriptors, indicating that overfitting has been effectively suppressed.
To verify the generality of the prediction performance improvement after stacking approaches and adding SISSO descriptors, we constructed additional stacked models using GBDT and LGB as meta-models, respectively. As summarized in Figure 3 and Supplementary Figure 3 (which shows the results of five-fold cross-validation), using GBDT as the meta-model in the stacked architecture reduces the MAE from 0.27 to 0.23, representing a 14.8% improvement, and lowers the ROI from 0.75 to 0.54, corresponding to a 28% decrease. With the incorporation of SISSO descriptors, the MAE further declines to 0.20 (25.9% reduction), and the ROI decreases significantly to 0.35 (53.3% reduction). Similarly, employing LGB as the meta-model yields a decrease in MAE from 0.26 to 0.23 (11.5%) and a slight reduction in ROI from 0.42 to 0.41 (2.4%). After introducing SISSO descriptors, the MAE further drops to 0.21 (19.2%), while the ROI is reduced to 0.25 (40.5%) (detailed MXene work function data in Supplementary Tables 3 and 4, and model parameters in Supplementary Table 5). These consistent improvements observed across both GBDT and LGB meta-models confirm the robustness of the stacked learning framework and underscore the effectiveness of SISSO-derived descriptors in enhancing predictive performance.
Figure 3. Performance comparison of different ML models. (A) MAE bar chart for three model types: RF, GBDT, and LGB; (B) ROI bar chart for three model types: RF, GBDT, and LGB. ML: Machine learning; MAE: mean absolute error; RF: random forest; GBDT: gradient boosting decision tree; LGB: lightGBM; ROI: relative overfitting index.
Explanations of ML models
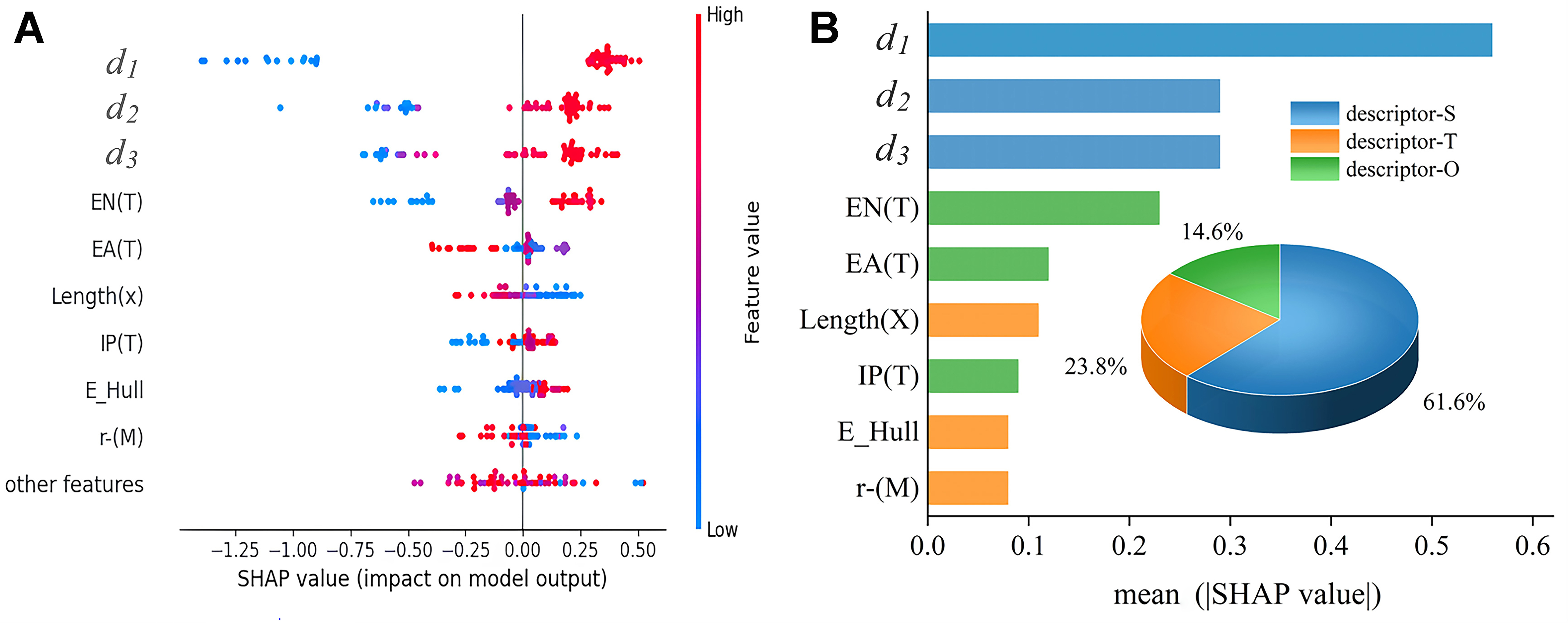
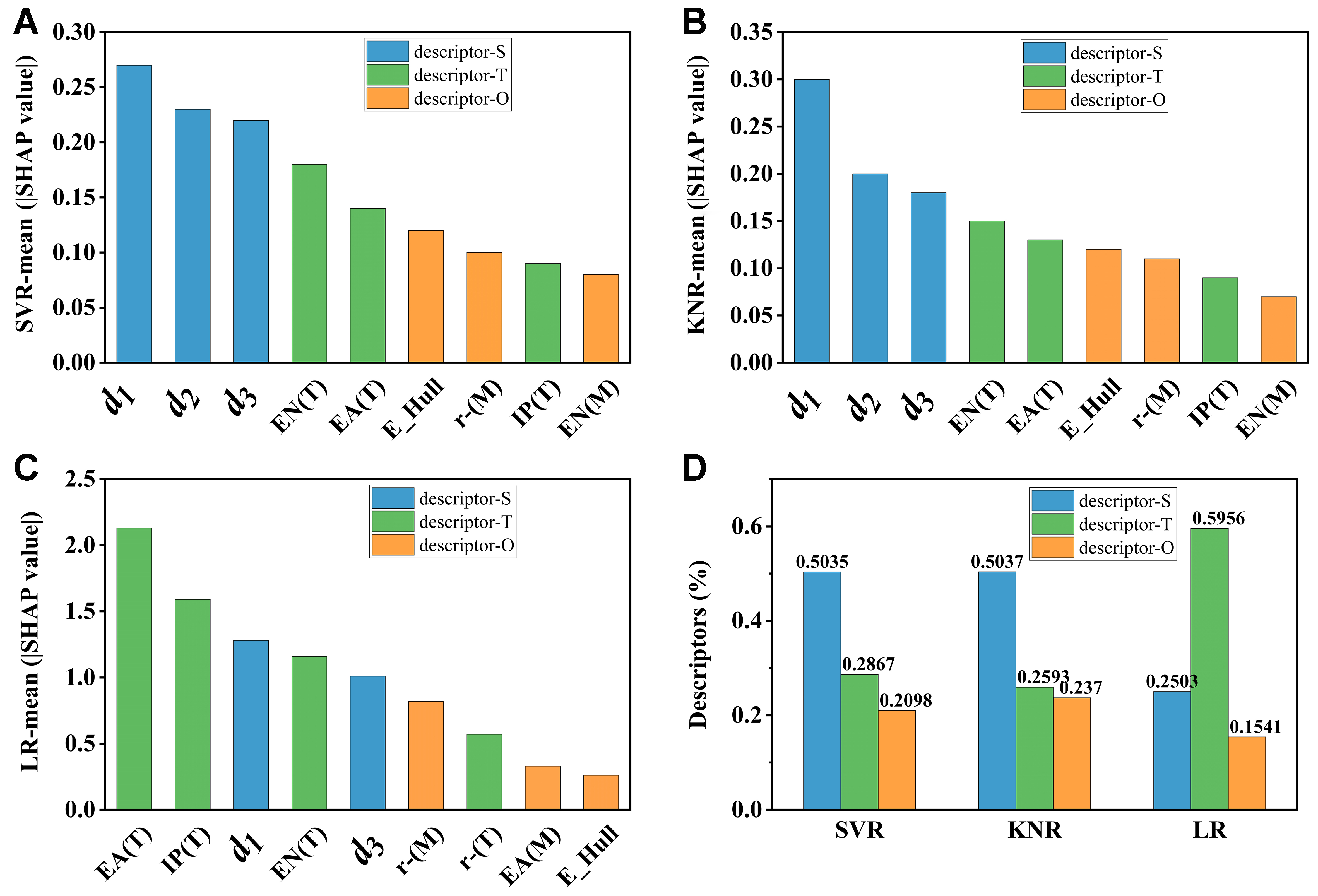
With the ML model established, we utilized the SHAP method to conduct a thorough explainability analysis. Figure 4A presents the SHAP summary plot for the best performing RF stacked model in the aforementioned ML study. Shapley values can measure the degree of change in the target variable (work function in this study) when a specific descriptor is included or excluded. Positive values indicate the increase in work function, while negative values indicate a decrease case. The color of the points changed from blue to red represents the change of descriptor values from low to high[46]. As shown in Figure 4A, the Shapley value for the most important descriptor, “d1” increased with the descriptor value, where the point color shifted from blue to red, indicating a positive correlation between the descriptor and work function. Conversely, the color change from red to blue indicates a negative correlation between the descriptor and work function. Additionally, we employed the permutation feature importance method to evaluate the stacked model, determining the approximate importance ranking of the nine most significant features. Permutation feature importance assesses the significance of each feature by randomly shuffling the feature values and observing the impact on model performance. In Figure 4B, descriptors-S refers to the SISSO descriptor, descriptors-T encompasses descriptors associated with functional groups, and descriptors-O comprises additional descriptor types. The feature importance analysis demonstrates that SISSO descriptors hold the top three positions, contributing a significant 61.6% to the model’s performance, thereby acting as a crucial component for enhancing overall model performance. It is worth noting that three out of the four most important features immediately following the SISSO descriptors are associated with the functional groups of MXenes. Moreover, the three selected SISSO descriptors that exhibit the highest correlation with the work function were also centered around the properties of these functional groups. Consequently, the SISSO approach proves effective in identifying key features that not only enhance the reliability and stability of the model, but also reveal a strong correlation between the work function of MXenes and their surface functional groups.
Figure 4. Feature importance analysis using SHAP values. (A) SHAP value plot showing the impact of various features on the model output; (B) Bar chart of mean SHAP values for different features, with a pie chart illustrating the proportion of descriptor categories: SISSO descriptors (S), functional group descriptors (T), and other descriptors (O). SHAP: SHapley Additive exPlanations; SISSO: Sure Independence Screening and Sparsifying Operator.
To validate the previous conclusion that SISSO descriptors and functional group descriptors consistently play a crucial role across all models, we verified their interpretability by comparing them with other models. To ensure the fairness of the comparison, three representative simple non-ensemble models were selected and trained, including SVR, KNR, and linear regression (LR)[47]. Subsequently, we employed the permutation feature importance method to evaluate the feature importance of the stacked model. As shown in Figure 5, the Shapley value analysis revealed that SISSO descriptors and functional group descriptors consistently ranked within the top five positions in feature importance across all models, with proportions of 79.02%, 76.3%, and 84.6%, respectively. The strong agreement between the analysis results from the ensemble models and the non-ensemble model powerfully corroborates the reliability of our conclusion.
Figure 5. SHAP value analysis of feature importance. (A) SVR model; (B) KNR model; (C) LR model; and (D) Proportional contributions of descriptor categories across models. SHAP: SHapley Additive exPlanations; SVR: support vector regression; KNR: k-nearest neighbors regression; LR: linear regression.
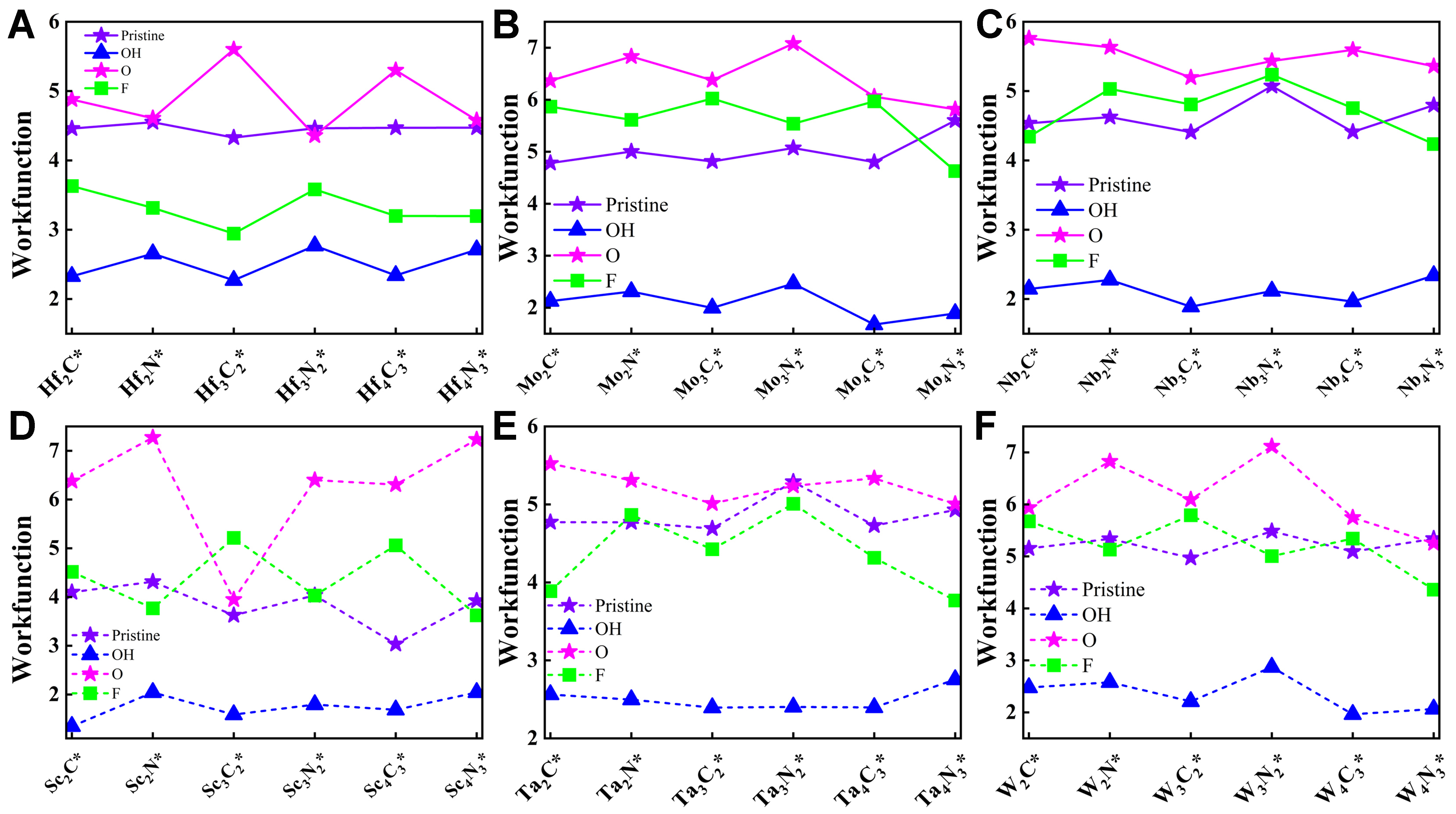
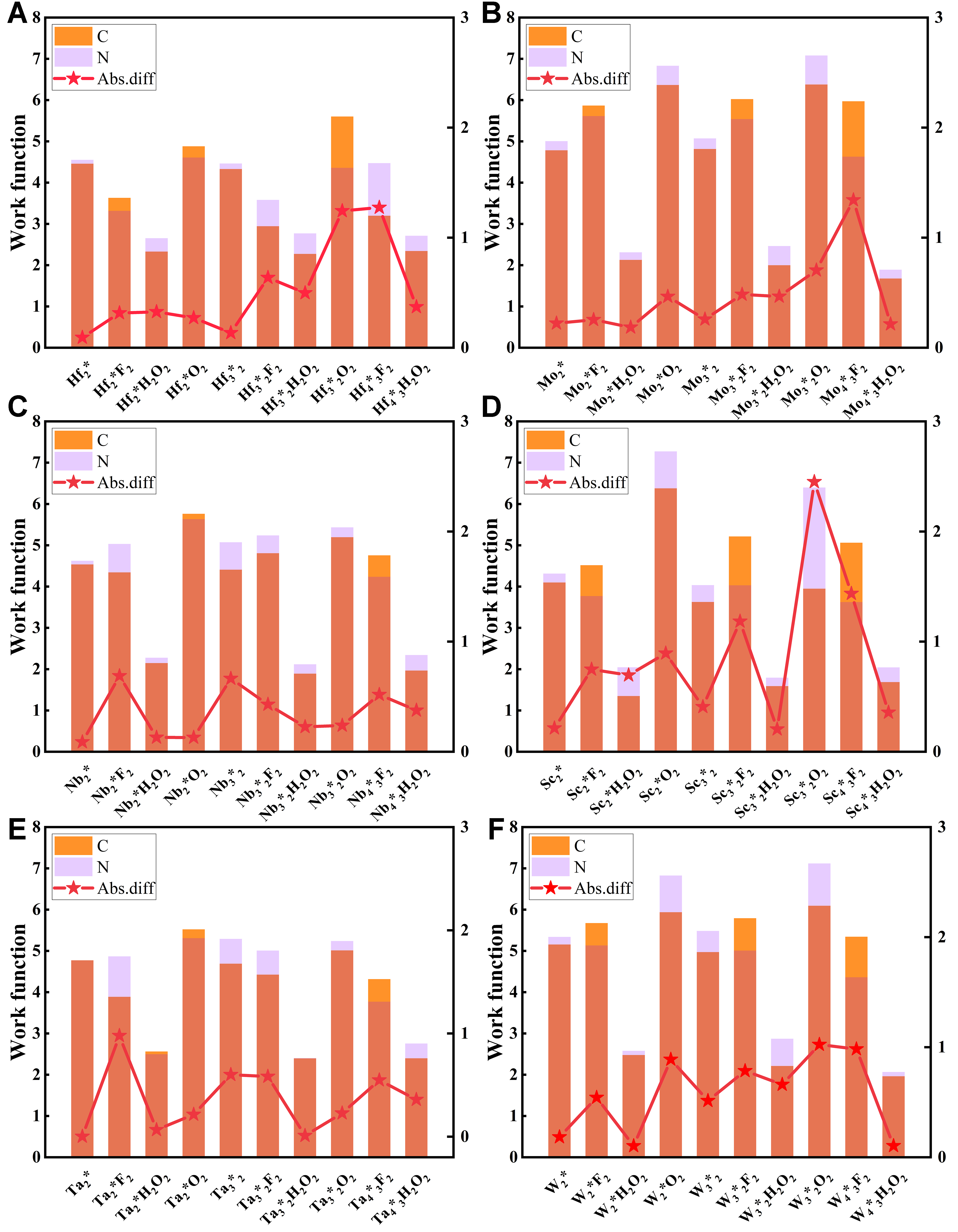
The ML results demonstrate a strong correlation between the work function of MXenes and their functional groups. To elucidate the underlying mechanism of this phenomenon, we first plotted the work function curves of a series of bare and functionalized MXenes with varied surface terminations (T = OH*, F*, O*), as illustrated in Figure 6 (bar chart shown in Supplementary Figure 4, with box plots of distributions shown in Supplementary Figure 5). Comparisons among MXenes with different transition metals indicate that the work function is moderately influenced by the metal type, yet the overall values remain relatively consistent. For MXenes sharing the same transition metal M, the layer number exerts minimal impact, resulting in only slight variations in work function. Under identical layer counts, O-terminated MXenes typically exhibit the highest work functions, while F-terminated or bare MXenes occupy an intermediate range with minor fluctuations; in contrast, OH-terminated MXenes consistently display the lowest values, reduced by at least 50% relative to their bare counterparts. To investigate the influence of C and N atoms on work function variations, we further analyzed the work function of MXenes classified as carbides (X = C) and nitrides (X = N) as shown in Figure 7. In the figure, the yellow-orange and pink bars represent carbides and nitrides, respectively, with the overlapping orange area indicating their common range. The red lines further highlight that the absolute differences in work function between the two types are generally small, typically around 1 eV. As shown in Figure 7, bare MXenes or those with OH as the functional group exhibit essentially negligible differences in work function between carbide and nitride forms. MXenes with F or O as the functional group show certain variations in work function between carbide and nitride forms, but these differences are relatively small, approximately around 1 eV. Based on the above analysis, it can be concluded that the work function of MXenes is primarily determined by the surface functional groups, with a relatively minor dependence on whether their chemical compositions are carbides or nitrides. This research also offers valuable guidance for practical applications, enabling materials to be tailored to specific requirements. For applications requiring high work functions, such as advanced sensors that rely on stable surface potential for accurate detection or photodetectors benefiting from efficient charge separation with minimal recombination, O-terminated MXenes are preferable. Conversely, in scenarios demanding low work functions, including vacuum ion plating processes that depend on facile electron emission for uniform coating or field emission displays requiring low-threshold electron sources for high-brightness imaging, OH-terminated MXenes are preferred.
Figure 6. Work function comparison under different surface conditions for various compounds. (A) Hf compounds; (B) Mo compounds; (C) Nb compounds; (D) Sc compounds; (E) Ta compounds; and (F) W compounds. Each panel shows the work function for bare surfaces as well as for surfaces terminated by OH, O, and F groups.
Figure 7. Work function comparisons for different Mn+1Xn compounds (X = C or N). (A) Hf compounds; (B) Mo compounds; (C) Nb compounds; (D) Sc compounds; (E) Ta compounds; and (F) W compounds. Each panel presents the work function results for both the carbide (C) and nitride (N) variants.
To further elucidate this rule, we refer to the Langmuir-Gettys theorem, which defines the work function
According to Khazaei et al., the change in ρ(z), denoted as ΔP, can be decomposed into three distinct contributions[48], as determined by the relationship in Supplementary Equation (4): Δp, pa and (ps - po). Here, Δp denotes the induced dipole moment arising from charge transfer between the substrate and the functional group. For instance, in the case of the OH group, electrons transfer from the substrate to the OH group, generating a negative dipole moment. The term pa represents the intrinsic dipole moment of the functional group, oriented from the hydrogen atom toward the oxygen atom in OH. The terms ps and po correspond to the dipole moments of the MXene surface atomic layers after and before functionalization, respectively, with their difference (ps - po) capturing the dipole moment shift due to surface relaxation. Typically, surface relaxation induces a negative dipole moment. Substituting these components into the equation yields[48]:
Next, we examine the contributions of each term to ΔΦ for different functional groups, when Δp + ps - po > 0, ΔΦ < 0, leading to a decrease in the work function. Conversely, when Δp + ps - po < 0, ΔΦ > 0, resulting in an increase in the work function. For F/O functional groups, since fluorine (F) and oxygen (O) are non-polar groups, pa = 0. In contrast, for the OH functional group, which is a polar, pa is a large positive value, directed outward from the surface. Although Δp and (ps - po) are generally negative, the substantial positive contribution from pa ensures that Δp + pa + ps - po > 0. Consequently, ΔΦ becomes significantly negative value, resulting in a notable reduction in the work function[48]. An experimental correlation between dipole moment and functional group electronegativity has been established by Lang et al.[49].
Based on the above analysis, we conclude that functional groups modulate the surface dipole moment (ΔP) through their polarity, electronegativity, and interactions with the substrate, thereby influencing the increase or decrease in the work function of MXenes. This effect is primarily governed by differences in electronegativity and is reflected in the variation of vacuum energy levels (ΔEVac). In the ML analysis, SHAP interpretation identified EN(T) as the most critical factor in determining the work function, consistent with the theoretical understanding. These findings demonstrate that interpretable ML approaches can reveal the underlying physical mechanisms of material behavior, helping to demystify ML as a “black box” and offering new opportunities for data-driven materials discovery.
CONCLUSIONS
Through this research, we have developed a high-precision and interpretable ML model for predicting the work function of MXenes. Initially, a stacked model was constructed using a RF as the meta-model. This approach reduces MAE by 12% and achieves an R2 of 0.94. Upon incorporating a transparent SISSO-derived descriptor, which is strongly correlated with the work function, into the stacked model, the predictive performance further improved, with a 20% reduction in MAE, an increase in R2 to 0.95, and a 48.3% decrease in ROI. To demonstrate the general applicability of the methodology, we employed various meta-models under the same predictive framework, consistently obtaining similar results that confirm its robustness. Furthermore, SHAP analysis revealed that descriptors such as functional group energy are strongly associated with the work function of MXenes. In OH-terminated MXenes, the difference in electronegativity between oxygen, which is closer to the surface and carries a partial negative charge, and hydrogen, which points toward the vacuum and carries a partial positive charge, creates an outward dipole layer that reduces the electrostatic potential barrier, vacuum level, and work function. These findings align with the interpretable ML results, confirming the essential role of functional groups in governing the work function of MXenes. Our work achieves a balance of high accuracy and interpretability in ML predictions of the work function of MXenes, providing valuable insights and tools for materials science.
DECLARATIONS
Authors’ contributions
Investigation, formal analysis, writing - original draft: Shang, L.
Analyzed the data, contributed analysis tools: Yang, Y.
Provide professional guidance on data processing, machine learning: Yu, Y.
Supervision: Xiang, P.
Provide support in material expertise: Ma, L.
Validation, funding acquisition, software: Guo, Z.
Validation, supervision: Dai, M.
Availability of data and materials
The data and code supporting the findings of this study are available at: https://github.com/Moneshanghai/MXeneStackedML. Further inquiries can be directed to the corresponding author(s).
Financial support and sponsorship
This work was supported by the National Natural Science Foundation of China (No. 52403306) and the Hebei Natural Science Foundation (No. B2024202047).
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
Supplementary Materials
REFERENCES
1. Gogotsi, Y.; Huang, Q. MXenes: two-dimensional building blocks for future materials and devices. ACS. Nano. 2021, 15, 5775-80.
2. Wu, Y.; Sun, M. Recent progress of MXene as an energy storage material. Nanoscale. Horiz. 2024, 9, 215-32.
3. Björk, J.; Rosen, J. Functionalizing MXenes by tailoring surface terminations in different chemical environments. Chem. Mater. 2021, 33, 9108-18.
4. Ayodhya, D. A review of recent progress in 2D MXenes: synthesis, properties, and applications. Diam. Relat. Mater. 2023, 132, 109634.
5. Gouveia, J. D.; Galvão, T. L. P.; Iben Nassar, K.; Gomes, J. R. B. First-principles and machine-learning approaches for interpreting and predicting the properties of MXenes. npj. 2D. Mater. Appl. 2025, 9, 529.
6. Bhat, M. Y.; Adeosun, W. A.; Prenger, K.; et al. Frontiers of MXenes-based hybrid materials for energy storage and conversion applications. Adv. Compos. Hybrid. Mater. 2025, 8, 1121.
7. Gokul Eswaran, S.; Rashad, M.; Santhana Krishna Kumar, A.; El-Mahdy, A. F. M. A comprehensive review of Mxene-based emerging materials for energy storage applications and future perspectives. Chem. Asian. J. 2025, 20, e202401181.
8. Worku, A. K.; Alemu, M. A.; Ayele, D. W.; Getie, M. Z.; Teshager, M. A. Recent advances in MXene-based materials for high-performance metal-air batteries. Green. Chem. Lett. Rev. 2024, 17, 2325983.
9. Ko, T. Y.; Ye, H.; Murali, G.; et al. Functionalized MXene ink enables environmentally stable printed electronics. Nat. Commun. 2024, 15, 3459.
10. Yan, J.; Cao, D.; Li, M.; et al. High-throughput computational screening of all-MXene metal-semiconductor junctions for Schottky-Barrier-Free contacts with weak fermi-level pinning. Small 2023, 19, e2303675.
11. Chen, J.; Liu, X.; Li, Z.; Cao, F.; Lu, X.; Fang, X. Work-function-tunable MXenes electrodes to optimize p-CsCu2I3/n-Ca2Nb3-xTaxO10 junction photodetectors for image sensing and logic electronics. Adv. Funct. Mater. 2022, 32, 2201066.
12. Ahn, S.; Han, T. H.; Maleski, K.; et al. A 2D titanium carbide MXene flexible electrode for high-efficiency light-emitting diodes. Adv. Mater. 2020, 32, e2000919.
13. Gregoire, J. M.; Zhou, L.; Haber, J. A. Combinatorial synthesis for AI-driven materials discovery. Nat. Synth. 2023, 2, 493-504.
14. Ghalati, M. K.; Zhang, J.; El-Fallah, G. M. A. M.; Nenchev, B.; Dong, H. Toward learning steelmaking - a review on machine learning for basic oxygen furnace process. Mater. Genome. Eng. Adv. 2023, 1, e6.
15. Lombardo, T.; Duquesnoy, M.; El-Bouysidy, H.; et al. Artificial intelligence applied to battery research: hype or reality? Chem. Rev. 2022, 122, 10899-969.
16. Shi, Y.; Zhang, Y.; Wen, J.; et al. Interpretable machine learning for stability and electronic structure prediction of Janus III-VI van der Waals heterostructures. Mater. Genome. Eng. Adv. 2024, 2, e76.
17. Schleder, G. R.; Acosta, C. M.; Fazzio, A. Exploring two-dimensional materials thermodynamic stability via machine learning. ACS. Appl. Mater. Interfaces. 2020, 12, 20149-57.
18. Huang, M.; Wang, S.; Zhu, H. A comprehensive machine learning strategy for designing high-performance photoanode catalysts. J. Mater. Chem. A. 2023, 11, 21619-27.
19. Bai, X.; Lu, S.; Song, P.; et al. Heterojunction of MXenes and MN4-graphene: machine learning to accelerate the design of bifunctional oxygen electrocatalysts. J. Colloid. Interface. Sci. 2024, 664, 716-25.
20. Tao, Q.; Xu, P.; Li, M.; Lu, W. Machine learning for perovskite materials design and discovery. npj. Comput. Mater. 2021, 7, 23.
21. Siriwardane, E. M. D.; Zhao, Y.; Perera, I.; Hu, J. Generative design of stable semiconductor materials using deep learning and density functional theory. npj. Comput. Mater. 2022, 8, 164.
22. Roy, P.; Rekhi, L.; Koh, S. W.; Li, H.; Choksi, T. S. Predicting the work function of 2D MXenes using machine-learning methods. J. Phys. Energy. 2023, 5, 034005.
23. Prasad Raju, N. V. D. S. S. V.; Devi, P. N. A comparative analysis of machine learning algorithms for big data applications in predictive analytics. Int. J. Sci. Res. Manag. 2024, 12, 1608-30.
24. Zhong, X.; Gallagher, B.; Liu, S.; Kailkhura, B.; Hiszpanski, A.; Han, T. Y. Explainable machine learning in materials science. npj. Comput. Mater. 2022, 8, 204.
25. Gjerding, M. N.; Taghizadeh, A.; Rasmussen, A.; et al. Recent progress of the Computational 2D Materials Database (C2DB). 2D. Mater. 2021, 8, 044002.
26. Haastrup, S.; Strange, M.; Pandey, M.; et al. The Computational 2D Materials Database: high-throughput modeling and discovery of atomically thin crystals. 2D. Mater. 2018, 5, 042002.
27. Li, H.; Deng, C.; Li, F.; Ma, M.; Tang, Q. Investigation of dual atom doped single-layer MoS2 for electrochemical reduction of carbon dioxide by first-principle calculations and machine-learning. J. Mater. Inf. 2023, 3, 25.
28. Abdullah, G. M. S.; Ahmad, M.; Babur, M.; et al. Boosting-based ensemble machine learning models for predicting unconfined compressive strength of geopolymer stabilized clayey soil. Sci. Rep. 2024, 14, 2323.
29. Alzamzami, F.; Hoda, M.; El Saddik, A. Light gradient boosting machine for general sentiment classification on short texts: a comparative evaluation. IEEE. Access. 2020, 8, 101840-58.
30. Ouyang, R.; Curtarolo, S.; Ahmetcik, E.; Scheffler, M.; Ghiringhelli, L. M. SISSO: a compressed-sensing method for identifying the best low-dimensional descriptor in an immensity of offered candidates. Phys. Rev. Mater. 2018, 2, 083802.
31. Lundberg, S.; Lee, S. I. A unified approach to interpreting model predictions. arXiv 2017, arXiv:1705.07874. https://doi.org/10.48550/arXiv.1705.07874. (accessed 1 Aug 2025).
32. Sun, T.; Wang, Z.; Zeng, L.; Feng, G. Identifying MOFs for electrochemical energy storage via density functional theory and machine learning. npj. Comput. Mater. 2025, 11, 90.
33. Li, S. Density functional theory for catalyst development and mechanistic insights. Nat. Rev. Clean. Technol. 2025, 1, 602.
34. Chen, L.; Chen, Z.; Yao, X.; et al. High-entropy alloy catalysts: high-throughput and machine learning-driven design. J. Mater. Inf. 2022, 2, 19.
35. Xu, M.; Xu, M.; Miao, X. Deep machine learning unravels the structural origin of mid-gap states in chalcogenide glass for high-density memory integration. InfoMat 2022, 4, e12315.
36. Pearson, K. VII. Mathematical contributions to the theory of evolution. - III. Regression, heredity, and panmixia. Philos. Trans. R. Soc. Lond. A. 1896, 187, 253-318.
37. Ma, B.; Wu, X.; Zhao, C.; et al. An interpretable machine learning strategy for pursuing high piezoelectric coefficients in (K0.5Na0.5)NbO3-based ceramics. npj. Comput. Mater. 2023, 9, 229.
38. Wang, T.; Hu, J.; Ouyang, R.; et al. Nature of metal-support interaction for metal catalysts on oxide supports. Science 2024, 386, 915-20.
39. Friedman, J. H. Greedy function approximation: a gradient boosting machine. Ann. Statist. 2001, 29, 1189-232. https://www.jstor.org/stable/2699986. (accessed 1 Aug 2025).
40. Roy, A.; Chakraborty, S. Support vector machine in structural reliability analysis: a review. Reliab. Eng. Syst. Saf. 2023, 233, 109126.
42. Xu, L.; Kong, Z.; Zhu, B.; et al. Mn-atomic-layered antiphase boundary enhanced ferroelectricity in KNN-based lead-free films. Nat. Commun. 2025, 16, 5907.
43. Naimi, A. I.; Balzer, L. B. Stacked generalization: an introduction to super learning. Eur. J. Epidemiol. 2018, 33, 459-64.
44. King, R. D.; Orhobor, O. I.; Taylor, C. C. Cross-validation is safe to use. Nat. Mach. Intell. 2021, 3, 276.
45. Hanifi, S.; Cammarono, A.; Zare-Behtash, H. Advanced hyperparameter optimization of deep learning models for wind power prediction. Renew. Energy. 2024, 221, 119700.
46. Yang, Z.; Sheng, Y.; Zhu, C.; et al. Accurate and explainable machine learning for the power factors of diamond-like thermoelectric materials. J. Materiomics. 2022, 8, 633-9.
48. Khazaei, M.; Arai, M.; Sasaki, T.; Ranjbar, A.; Liang, Y.; Yunoki, S. OH-terminated two-dimensional transition metal carbides and nitrides as ultralow work function materials. Phys. Rev. B. 2015, 92, 075411.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Special Topic
Copyright
Data & Comments
Data

















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].