Neuroevolution potential for thermal transport in silicon carbide
Abstract
Silicon carbide (SiC) is a representative high-thermal-conductivity semiconductor for applications in power electronics and quantum devices. In these applications, thermal management becomes critical for stable functioning. Meanwhile, SiC crystallizes into hundreds of polytypes with various stacking orders and small energy difference. Such a characteristic also leads to the formation of stacking faults. To understand the thermal transport property of SiC in the presence of polytypism and crystallographic defects, we have developed a neuroevolution potential for SiC. The model is trained on a diverse dataset with stoichiometric and off-stoichiometric SixCy configurations. The dataset is strategically sampled using graph network encoding and clustering in the feature space. The potential achieves high accuracy with energy error of 4.1 meV/atom and force error of 0.22 eV/Å in the test set. And the dataset diversity is found to be critical to the model robustness. The application of this model is demonstrated by simulating the thermal transport property of SiC polytypes and stacking faults using homogeneous nonequilibrium molecular dynamics. The thermal resistance of stacking faults can reach substantial values up to 10-10 K·m2·W-1, which may create hot spots and impede heat dissipation in devices. The thermal resistance varies considerably among different fault types, with those exhibiting consecutive cubic k stacking configurations demonstrating remarkably lower resistance. This work provides an accurate and efficient machine-learning interatomic potential for simulations of thermal and phonon properties of SiC and understanding of its thermal management in the presence of polytypism and crystallographic defects.
Keywords
INTRODUCTION
Silicon carbide (SiC) is deemed the representative wide-bandgap semiconductor[1] for power electronics[2] and quantum information[3,4] applications. The applications are endowed by its wide bandgap, high breakdown field, abundance of color centers in communication band, and compatibility with silicon-based fabrication techniques[3,5-7]. More importantly, the outstanding high thermal conductivity and stability ensure the stable functionality in harsh conditions including high power density and extreme temperature, where heat dissipation and thermal management becomes a critical issue. SiC has a room-temperature thermal conductivity over 400 W·m-1·K-1, much higher than that of Si. This allows an efficient heat removal from the hot spot and maintain a stable working temperature. However, the SiC crystallizes into more than 200 polytypes which differ only in the stacking order of the hexagonal SiC layer, and the energy differences between different stacking orders are very small. Therefore, the presence of different stacking sequences is a common but undesired phenomenon in its crystal growth which leads to polytypes and stacking faults. Different polytypes are known to exhibit distinct thermal conductivities and anisotropies according to theoretical[8-10] and experimental[11-18] investigations. However, whether the general observations in simple polytypes still hold in complex polytypes remains elusive. As demonstrated by Boteler et al., for semiconductor materials with thermal conductivity between 150 and 400 W·m-1·K-1, the contribution from the device constitutes a significant fraction of the overall temperature rise in the power electronic module[19]. Additionally, if the semiconductor’s thermal conductivity is improved beyond 400 W·m-1·K-1, the thermal management will be limited mainly by the packaging and heat sink. While single-crystal SiC has an ideal thermal conductivity of up to 500 W·m-1·K-1, a high density of defects such as stacking faults can drastically reduce it to 327 W·m-1·K-1[20], potentially causing undesirable temperature rise. In color-center-based SiC quantum devices, large thermal shift of signal can be observed[21]. So their functionality is also sensitive to temperature stability. Therefore, defect control becomes essential in the thermal management of SiC devices. Although there are some ways to recognize the stacking faults[22-24] and the presence of isolated stacking faults is known to cause carrier localization, shortened carrier lifetime, and device degradation[25], understanding of its impact on the heat transport is still limited.
Heat transport calculations based on various techniques have advanced significantly in the past decades. The Boltzmann transport theory has been efficiently implemented in numerous software with various levels of approximation[26-32], allowing accurate prediction of thermal conductivity with phonon-phonon, phonon-electron, and phonon-defect scattering in the perturbative region[27,28,32]. However, the computational complexity increases drastically when the unit cell becomes more complex. Alternatively, molecular-dynamics-based techniques are capable of dealing with more complex structures. Nonequilibrium molecular dynamics (NEMD) based on temperature-difference-induced heat current simulation and equilibrium molecular dynamics (EMD) based on current autocorrelation within Green-Kubo formula are well developed, efficiently implemented and widely employed[33-44]. More recently, homogeneous NEMD (HNEMD) method[45] is significantly advanced in terms of theory and efficiency thanks to the development of GPUMD, a molecular dynamics (MD) software running on graphic processing units (GPU). These techniques have been employed for materials with large unit cells[46], amorphous[47] and liquid[48] systems, and metamaterials[49], achieving accurate prediction and in-depth understanding of heat transport phenomena[50]. However, all these methods require a large simulation cell and long equilibration and simulation time, which necessitates accurate and highly efficient interatomic potentials. In recent years, machine-learning interatomic potentials (MLIP) have been developed based on first principles datasets and have achieved successful application in many crystal materials[51-63]. MLIPs with a wide range of accuracy and speed have been developed. MLIPs based on complex and deep neural networks exhibit high accuracy, generalization ability, and learning efficiency[64-74]. A deep potential (DP) trained on simple SiC polytypes has been employed to investigate their thermal conductivities with NEMD[43,75]. Meanwhile, highly efficient MLIPs such as momentum tensor potential (MTP)[69] and neuroevolution potential (NEP)[72-74] have been developed and proved suitable for thermal transport property calculations[58,60,61,76]. Therefore, the development of MLIP for SiC becomes a feasible approach to overcome the difficulty in simulating heat transport in complex SiC polytypes and defects.
In this study, we develop a SiC dataset covering SiC polytypes and off-stoichiometry SixCy structures to ensure general and robust applicability. The structures are first generated by deforming the supercells along all Voigt directions and performing MD simulations using empirical interatomic potentials. The trajectory collection consisting of millions of structures is sampled by combining featurization, dimensionality reduction, and clustering to arrive at a representative sampled collection consisting of 1,868 structures. The structures are then labeled using density functional theory (DFT) calculations, and the resulting dataset is used to train a NEP. The NEP exhibits comparable accuracy for both SiC polytypes and off-stoichiometry SixCy and outstanding efficiency as compared to other MLIPs trained on the same dataset. We then apply the NEP to investigate the thermal transport properties of common SiC polytypes and stacking faults using HNEMD. The results agree with experimental results for all known polytypes. Moreover, we found that stacking faults have a high thermal resistance of around 0.1 Km2/GW, equivalent to the thermal resistance of hundreds of SiC layers. These findings highlight the importance of defect control in the application of SiC as high-thermal-conductivity materials for power electronics and thermal management.
MATERIALS AND METHODS
Dataset generation
In earlier works, SiC datasets for MLIP training were constructed in various ways. Reliable phonon calculations require accurate potential energy surface around equilibrium structure. For the evaluation of phonon and heat transport, where the structures are not far away from ground-state structure during simulation, datasets were constructed mainly using major polytypes as prototypical structures[63]. Based on these prototypes, perturbed structures were generated through MD and distortions and then sampled based on prediction uncertainty among coarse MLIP models as implemented in Deep Potential GENerator (DP-GEN)[77,78]. For the simulations of crystallization and defect formation, structures far from equilibrium are needed to describe the more complex local structures. Therefore, amorphous and defective structures are also included in those datasets for diversity and robustness[79,80].
In this work, we investigate the thermal transport of both polytypes and defective structures containing stacking faults. Therefore, to achieve data diversity and model robustness, we construct a dataset including both polytypes and off-stoichiometric structures near and far away from equilibrium, as illustrated in Figure 1. In total, 28 SiC polytypes and four off-stoichiometry SixCy structures obtained from the Materials Project[81] are used as the initial prototypical structures. In addition, lattice deformation along 6 Voigt components is performed on the six most common polytypes (3C, 2H, 4H, 6H, 15R, and B1) to generate heavily deformed structures with strain from -10% to 10%. MD simulations in canonical (NVT) ensemble are then performed with a large-scale atomic/molecular massively parallel simulator (LAMMPS)[36,82] starting from these structures using classical Tersoff potential[83]. The time step was set to 0.5 fs, and the temperature was maintained at 300 K through a Nose-Hoover thermostat where the damping time is 50 fs. Each MD run extends for 2 × 104 steps and configurations are sampled every 10 steps, resulting in more than 3 × 106 configurations in total. Five percent of these configurations are picked out with equal spacing to avoid close correlation. These configurations are then encoded into feature vectors using M3GNet[84]. Using the DImensionality-Reduced Encoded Clusters with sTratified (DIRECT) sampling method[85], representative configurations are sampled from the generated configurations in the feature space with principal component transformation. In the DIRECT sampling method, the MD trajectories are first encoded using M3GNet to obtain feature vectors for all configurations. Then a principal component analysis is applied to the feature vectors for all the configurations and the feature vectors are transformed into the principal component space. Finally, the configurations are clustered in the principal component space and one configuration was selected from each cluster such that this configuration is closest to the cluster centroid. A total of 1,868 configurations are sampled and then labeled using energies, forces, and stresses from DFT calculations.
The DFT calculations were carried out using Vienna ab initio simulation package (VASP)[86-89]. The electron-ion interactions are described using projector-augmented wave (PAW) method[90,91] and the Kohn-Sham wave functions are expanded in plane waves with a cutoff energy of 800 eV. The exchange-correlation function in generalized gradient approximation (GGA) proposed by Perdew, Burke, and Ernzerhof for solids (PBESol) is used. The Brillouin zone is sampled using uniform k-mesh with a constant k-point spacing of 0.1 Å-1 across all configurations for consistency. The final dataset consists of 1,868 energies, 1.5 × 105 force components, and 1.2 × 104 stress components.
Model training
With the first-principles dataset, the NEP was trained with a random 4:1 train-test splitting. The NEP3 version[72,74] was used with a cutoff radius of 6 Å. The number of radial (nmaxR) and angular descriptor components (nmaxA) is set to 8, and number of basis functions is also 8 for both radial and angular descriptors. The maximum angular expansion order is 4 for three-body and 2 for four-body terms. The hidden layer contains 30 neurons. A full-batch training was carried out for 3 × 105 generations to reach convergence. Detailed training hyperparameters are given in Supplementary Table 1.
In order to dive deeper into the role of dataset diversity and choice of models, we trained three NEP models using different training sets. The first model was trained on the undeformed polytype structures in the training set. The second model is trained using both undeformed polytypes and off-stoichiometric SixCy structures. The final model was trained on the whole training set. Additionally, we trained a DP and a MTP using the whole training set and the same cutoff radius for comparison. The computational efficiency and accuracy are compared among all models, as detailed in Supplementary Figures 1 and 2.
Heat transport calculations
The thermal conductivity of all systems, including the SiC polytype single crystals and stacking faults in 4H-SiC, is calculated using HNEMD implemented in GPUMD. All models for simulations are orthogonalized and replicated to a sufficiently large size where all edges are around 40 Å which contain about 7 × 103 atoms. For each production run, the model was first equilibrated for 1 ns in NVT ensemble with Nose-Hoover chain thermostat. After equilibration, HNEMD calculation was performed for 20 ns which is long enough to reach convergence. The driving force magnitude was around 2 × 10-5 Å, and the time step length was 1 fs. Detailed computational parameters are given in Supplementary Table 2.
After obtaining the thermal conductivity of single crystals and supercells containing stacking faults, the thermal resistance is computed using the obtained thermal conductivity in the following way. With κSC and
where L is the length of the stacking-fault-containing supercell along the transport direction.
Here in this work, we focus on major stacking fault types in the 4H-SiC, which is the most technologically relevant polytype in power electronics and quantum applications. The stacking fault is a crystallographic defect where the stacking order of a few neighboring atomic layers is different from the order of the host polytype. In 4H-SiC, the single-crystal stacking order is periodic hkhk, where h and k refer to the wurtzite-like hexagonal stacking and zincblende-like cubic stacking between adjacent layers. The Shockley-type stacking faults (SSSFs) emerge due to the gliding of atomic layers. When shear motion induces one gliding, the single SSSF emerges. And with an additional gliding, the double Shockley-type stacking fault (DSSF) is generated. The Frank-type stacking faults, on the other hand, involve the insertion or removal of atomic layers. Here we investigate three kinds of Frank-type stacking faults labeled as Frank-1 to Frank-3. The stacking sequences of SSSF, DSSF and Frank-1 to Frank-3 are visualized in Figure 2.
RESULTS AND DISCUSSION
Model performance
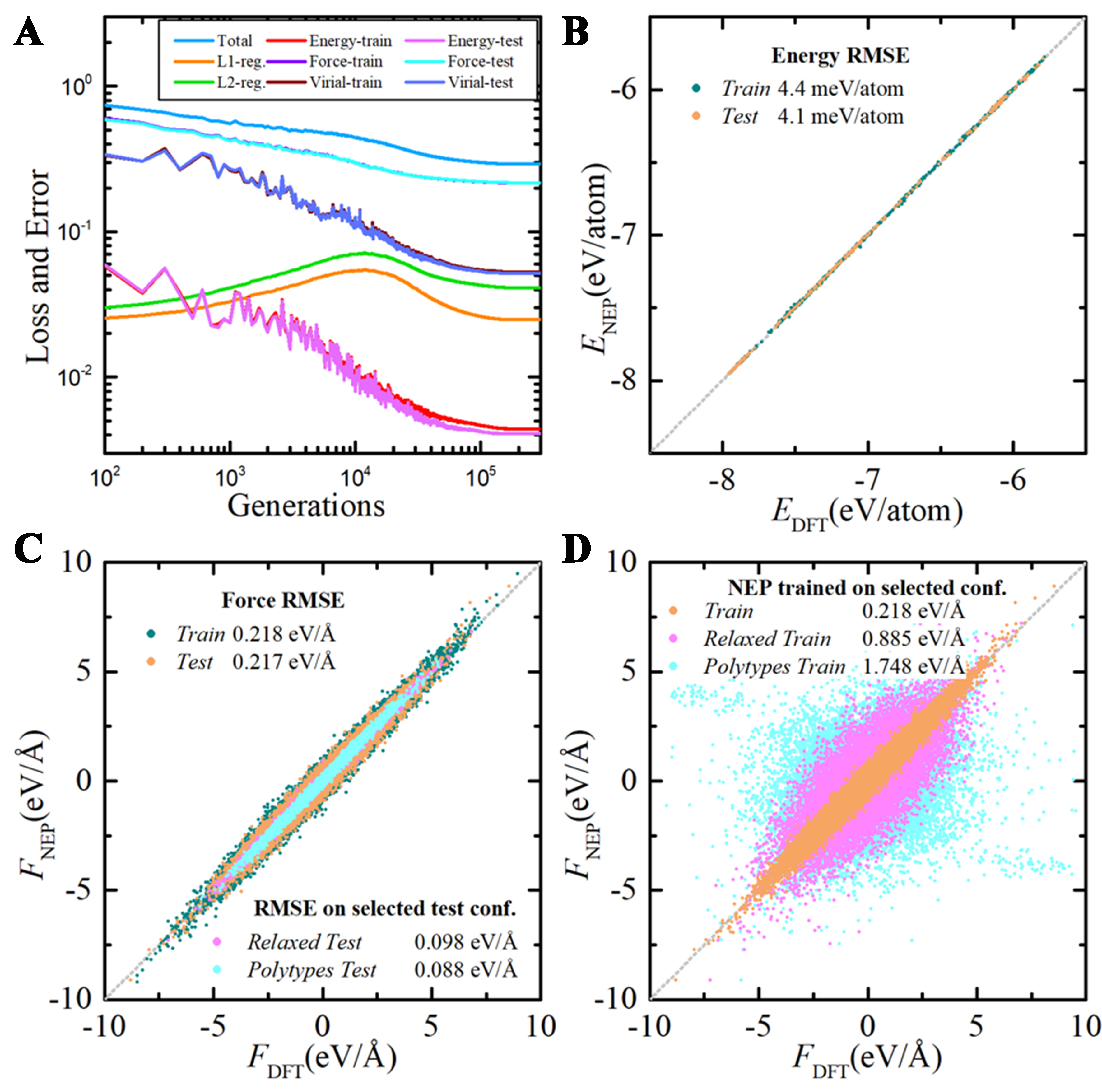
The first evaluation of the obtained NEPs is performed by comparing their predicted energies, forces, and stresses with those from DFT calculations, as shown in Figure 3. Despite the inclusion of heavily deformed and off-stoichiometry structures that are far from equilibrium, the energy root mean square error (RMSE) is only 4.4 meV/atom for the training set and 4.1 meV/atom for the testing set. The force RMSE is 0.218 eV/Å for training set and 0.217 eV/Å for testing set. The stress RMSE is 0.86 and 0.83 GPa for the training and testing sets, respectively. This accuracy is comparable to the performance of DP trained on a dataset containing only polytype structures with smaller deformation which are closer to equilibrium[63]. The deformation significantly changes the bond lengths and bond angles, thus making the chemical environment more complex to describe. Therefore, a smaller prediction error is naturally expected for configurations with smaller lattice deformation. To demonstrate this point, we test the NEP model performance on the subset of the testing set, as shown in Figure 1B. The test RMSE on the subset without lattice deformation (Relaxed) becomes even smaller (0.098 eV/Å). If the off-stoichiometric structures are excluded to further simplify the chemical environment in a relaxed polytype-only subset (Polytypes), the test RMSE is further reduced to 0.088 eV/Å. The origin of this difference is that the Relaxed test set contains off-stoichiometric SixCy structures, in addition to the polytype structures contained in the Polytypes set. Therefore, the Relaxed test set has a more complex chemical and bonding environment than the Polytypes set. Therefore, it is naturally expected that errors are larger for the Relaxed test set. This result suggests that the NEP model trained on the diverse training set can perform very well for structures around equilibrium.
Figure 3. The training loss and accuracy of NEP models. (A) The loss function evolution during model training; The (B) energy and (C) force RMSE between DFT results and NEP results on the training set (Train) and testing set (Test); (D) The Test set performance of different NEP models trained on different training subsets. NEP: Neuroevolution potential; RMSE: root mean square error; DFT: density functional theory.
While the test error on the Polytypes set is still non-negligible, its origin can be understood as follows. First of all, although both silicon and carbon are group IV elements, SiC is still a polar semiconductor with large Born and quadrupolar effective charges and resulting long-ranged dipolar interactions. This long-ranged interaction may not be accurately captured by NEP without explicit inclusion of Coulombic interactions, as evidenced by the absence of LO-TO splitting in the phonon dispersion from NEP calculation. Secondly, the NEP model in this work is designed and trained on a diverse SiC structure set. Therefore, the chemical environment of the whole training set is more complex than the polytypes. This could result in a trade-off between general applicability and accuracy for specific systems. A similarly increased error was also observed for general-purpose silicon NEP as compared to NEP trained specifically for silicene. Finally, compared with PbTe[73], another typical system with long-ranged interaction, SiC is a harder material where the atomic forces induced by certain displacements are larger. The hardness, in conjunction with the structure diversity, leads to a wider span of atomic forces in the training set from approximately -6 to
For a better understanding of how the dataset diversity affects the model accuracy and robustness, we trained three different NEP models using varying training sets. The first set only contains MD snapshots for polytypes with relaxed lattice constant (Polytypes Train); the second set contains both undeformed polytypes and off-stoichiometric SixCy (Relaxed Train); the last one is the whole training set (Train). Then the three models are tested on the whole test set containing all types of structures. Compared to the model trained on the whole training set (0.217 eV/Å), the model trained on the Relaxed Train set has a much larger RMSE of around 0.885 eV/Å. This suggests that configurations with lattice deformation are necessary for accurate force prediction. Furthermore, if the off-stoichiometric SixCy are excluded and the models are trained only on polytypes with relaxed lattice constants, the force RMSE can be as large as 1.748 eV/Å. Such a drastic difference in force RMSE is an important indication for the MLIP reliability, considering the similar range of force distribution over 10 eV/Å. Therefore, both lattice deformation and chemical diversity are necessary for the training dataset in order to obtain an accurate and robust MLIP. This is naturally expected since the lattice deformation and chemical diversity are further away from the equilibrium structure, and act as a regularization that prevents the model from overfitting the close-to-equilibrium results. The overfitting would cause large deviation when extrapolating to configurations with greater atomic displacement and bond distortion. Therefore, the NEP model trained on polytype structures with relaxed lattice parameters fails to describe those configurations with lattice deformation and chemical diversity.
To further validate the NEP model, we performed elastic constant and phonon dispersion calculations using both NEP and DFT. The elastic constants computed using NEP and DFT are compared in Table 1. As shown in Table 1, most elastic constants computed from NEP and DFT generally agree with each other with an error of less than 10%. The largest difference appears for the C13 component for 6H, which may arise from its relatively small value compared to the axial component. The phonon dispersions are also computed using NEP and DFT, respectively. Alamode is used for the DFT phonon dispersion calculation, where nonanalytical corrections due to Born effective charges are included. As shown in Supplementary Figure 3, the phonon NEP phonon dispersion agrees well with DFT phonon dispersion, with a significant difference only in optical phonons. The most prominent difference is due to the splitting between longitudinal (LO) and transverse optical (TO) phonons. The NEP model is short-ranged in nature, so the long-ranged interactions described by Born effective charges are not accurately captured by NEP. While these long-ranged interactions lead to the LO-TO splitting in SiC, they only affect high-frequency phonons, which have a relatively small contribution to the thermal conductivity. Therefore, the NEP is reliable in phonon and thermal transport property calculations.
The elastic constants computed using NEP and DFT
| C11 (GPa) | C12 (GPa) | C33 (GPa) | C44 (GPa) | C13 (GPa) | C66 (GPa) | |||||||
| DFT | NEP | DFT | NEP | DFT | NEP | DFT | NEP | DFT | NEP | DFT | NEP | |
| 3C | 389 | 380 | 137 | 154 | 389 | 380 | 244 | 235 | - | - | - | - |
| 2H | 503 | 489 | 110 | 128 | 544 | 630 | 150 | 152 | 57 | 64 | 196 | 181 |
| 4H | 496 | 486 | 113 | 126 | 546 | 596 | 157 | 151 | 58 | 66 | 192 | 180 |
| 6H | 499 | 484 | 119 | 126 | 575 | 574 | 160 | 151 | 46 | 67 | 190 | 179 |
| 15R | 496 | 486 | 114 | 125 | 546 | 583 | 159 | 151 | 58 | 66 | 191 | 180 |
The NEP model accuracy is further compared with DP[70] and MTP[54,69,92] models trained on the same training set. To make comparison on equal footing, we employ the same cutoff radius of 6 Å for all models. The energy and force weights in the loss function are all set to 1 for the training of all models. After achieving reasonable convergence for the loss function, we further test the obtained DP and MTP models on the same test set used for NEP. The DP model obtained an outstanding energy RMSE of 2.24 meV/atom and force RMSE of 0.141 eV/Å. And the MTP model has a slightly larger error with energy RMSE of
Thermal conductivity of polytypes
Using the trained NEP model, we proceed to evaluate the thermal conductivity of various SiC polytypes. Among the over 200 polytypes, 2H, 3C, 4H, 6H, and 15R are major polytypes that may appear in crystal growth[2]. Among these polytypes, 3C is in cubic crystal class and therefore isotropic, while others are in hexagonal or trigonal class which are anisotropic[2]. To investigate the lattice thermal conductivity, we employ the HNEMD simulation where the atoms are subject to an external driving force that depends on the atomic energy and virial[45]. The instantaneous heat current is computed from the atomic virial, and the time-averaged heat current is used to compute the thermal conductivity.
When employing the HNEMD method to predict thermal conductivity, it is essential to investigate the system size effect since the calculated thermal conductivity is inherently dependent on the simulation cell length. In this study, we systematically examined the convergence of 3C-SiC thermal conductivity with respect to supercell model dimensions (6 × 6 × 6, 8 × 8 × 8, 10 × 10 × 10, and 12 × 12 × 12) through 20 ns HNEMD simulations. The time-averaged thermal conductivity values extracted from the last 5 ns revealed that when increasing the supercell size from 6 × 6 × 6 to 10 × 10 × 10, the thermal conductivity decreased from 718 to 470 to 399 W·m-1·K-1, showing a significant 34.5% and 15.1% variation, which indicates strong size dependence in this range. However, for further enlarged supercells from 10 × 10 × 10 to 12 × 12 × 12, the thermal conductivity exhibited only minor change between 399 and 412 W·m-1·K-1, with a small deviation of 3.2%. Therefore, in the subsequent investigations, we perform all HNEMD calculations for polytypes and stacking faults using models equivalent to a 10 × 10 × 10 3C-SiC supercell in terms of number of atoms and cell dimensions.
We first compare the lattice thermal conductivity at 300 K among all polytypes. The predicted lattice thermal conductivity of 3C-SiC is 403 W·m-1·K-1, which is lower than the time-domain thermoreflectance (TDTR) measurements around 500 W·m-1·K-1. The 4H-SiC has a lattice thermal conductivity of 296 W·m-1·K-1 along axial and 347 W·m-1·K-1 along planar directions. This can be compared with the TDTR results[11] which are around 324 and 471 W·m-1·K-1. The values for 6H-SiC are 237 and 347 W·m-1·K-1 along axial and planar directions, respectively. They are also slightly lower than the TDTR results of 273 and
Figure 4. The temperature dependent lattice thermal conductivity of SiC polytypes along (A) planar and (B) axial directions. SiC: Silicon carbide.
It can be seen that there is a slight underestimating trend of single-crystal lattice thermal conductivities from HNEMD prediction, as compared to the TDTR experiments. There are several possible sources of discrepancy as we will discuss as follows. First, we confirm whether it is the size effect due to finite MD cell by performing additional simulations with models containing different numbers of unit cells and atoms. In this work, the HNEMD simulations are carried out using a finite model consisting of single-crystal or defect-containing supercells. Such model corresponds to a Born-von-Karman boundary condition where only momentums compatible with the supercell are active. Therefore, it is similar to a uniform k-point sampling grid where discrete k points are allowed. In this case, however, some long-wavelength phonons are effectively frozen by the Born-von-Karman boundary condition and thus not contributing to the heat transport. However, by comparing the results of different model sizes, it can be seen that the difference between a model containing around 2 × 103 and 7 × 103 atoms is only around 10 W·m-1·K-1 for these polytypes, suggesting that the 7 × 103 atom models employed here are large enough. Therefore, its impact is much smaller than the difference between TDTR and HNEMD results. Another possible origin of underestimation is the error in NEP force prediction, which was shown to lead to underestimated thermal conductivity especially for high-conductivity materials[95,96]. Such effect is consistently present in both single-crystal and stacking-fault containing system. Therefore, we expect it to have minor impact on the thermal resistance of stacking faults.
When we compare the thermal conductivity of 3C-SiC at 300 K with the literature, we find that the HNEMD result agrees well with that obtained using Boltzmann transport equation combined with PBE functional[63]. Meanwhile, the PBE result in the literature is generally lower than that of the local density approximation (LDA)[63]. Although the LDA result coincides with the TDTR thermal conductivity at
Thermal resistance of stacking faults
With the obtained NEP potential, we also proceed to simulate the thermal transport properties in the presence of stacking faults. Different stacking fault types, including single and double SSSFs (SSSP, DSSP) and three Frank-type stacking faults (Frank-1, Frank-2, Frank-3), are simulated. The corresponding stacking orders have been illustrated in Figure 2. We first computed the phonon density of states (PDOS) at 300 K for 4H-SiC crystal model with and without stacking faults. As shown in Figure 5, there is no frequency shift in the overall PDOS, and we have not observed emerging peaks that could hint at the presence of highly localized vibrational modes. Therefore, it may be inferred that stacking faults, despite being defects, may not introduce highly localized defect vibrational modes or strain-induced phonon shifts. This is the expected behavior considering the previous observations where polytypes having different stacking orders generally share a common trend and folded phonon dispersion[93,99]. The high-frequency PDOS remains largely unchanged, suggesting that stacking faults have limited impact on the optical phonons. However, there are some fluctuations in the low-frequency PDOS, which may be related to additional scattering of acoustic phonons.
Figure 5. The PDOS of perfect 4H-SiC crystal model and models with various stacking faults. PDOS: Phonon density of states; SiC: silicon carbide.
To assess the stacking faults’ impact on the thermal transport, we evaluated the lattice thermal conductivity of 4H-SiC with a stacking fault introduced into the models. Such insertion of stacking faults changes the stacking order of Si-C atomic layers as visualized in Figure 2. Therefore, it may be considered as a scattering center along the axial direction because it breaks the translational symmetry along the axial direction. However, the translational symmetry remains unchanged in the planar direction. Therefore, one would expect that the impact on axial thermal conductivity will be greater than that on the planar thermal conductivity. Indeed, this is what was observed in our calculations. As shown in Figure 6A, the planar thermal conductivity is almost unchanged across a wide temperature range from 300 to 1,500 K. However, the room-temperature axial thermal conductivity is drastically reduced along the axial direction, as shown in Figure 6B. And at elevated temperatures where phonon-phonon scattering becomes stronger due to enhanced phonon population, the stacking-fault-induced thermal conductivity change becomes less significant along axial direction.
Figure 6. The computed thermal conductivity of 4H-SiC models containing various stacking faults along the (A) planar and (B) axial directions; (C) The thermal resistance induced by stacking faults evaluated using Equation (1) along the axial direction. SiC: Silicon carbide.
The thermal resistance induced by stacking fault is understood as the consequence of stacking-dependent phonon frequency. As we have shown recently through first principles calculations, different polytypes have distinctive phonon dispersion after being unfolded into a common extended Brillouin zone. This stacking-dependent phonon dispersion arises from the change of symmetry which causes phonon hybridization and avoided crossing. Therefore, it is expected that the sudden change of stacking order around stacking fault also gives rise to a local shift of phonon frequency, despite the absence of local phonon modes. This is confirmed by the small but evident change in PDOS in Figure 5. The change in frequency around stacking fault can effectively act as a barrier that scatters the phonons propagating across the defect. Therefore, an apparent thermal resistance is observed in the axial direction while it has little effect on the thermal transport along basal planes.
The impact of stacking faults is further quantified by computing the thermal resistance of stacking faults according to Equation (1), similar to the interfacial thermal resistance[100]. The computed thermal resistance along the axial direction is shown in Figure 6C. Interestingly, two stacking fault types, SSSF and Frank-2, have much larger thermal resistance than the other three. Looking into the stacking sequence of these stacking faults in Figure 2, it is noticed that the low-thermal-resistance stacking faults share a common feature where a consecutive k stacking emerges around the stacking faults. Combining this observation with the fact that 3C-SiC has an apparently higher thermal conductivity than 2H-SiC despite the same number of atoms per primitive unit cell, there is a possible correlation where consecutive cubic (k) stacking could be beneficial for phonon transport. The variation of thermal resistance across different stacking fault types can also be understood through the stacking-dependent phonon dispersion and thermal transport. In general, all stacking faults break the symmetry and act as a scattering center for phonons propagating along the axial direction. Meanwhile, the consecutive k-stacking layers emerging in DSSF, Frank-1, and Frank-3 type stacking faults create a 3C-like region within the stacking faults. As we have shown through both HNEMD simulation in this work and first-principles Boltzmann transport calculations in an earlier work, 3C-SiC has a significantly higher thermal conductivity than other hexagonal polytypes. Therefore, the consecutive k-stacking in DSSF, Frank-1, and Frank-3 effectively reduces the thermal resistance within the stacking faults, partially cancelling the stacking-fault-induced scattering effect. Meanwhile, SSSF and Frank-2 stacking faults only create hexagonal local stacking order, which has a lower thermal conductivity than the 3C-like region. Therefore, their thermal resistances remain high which mainly arise from the defect scattering effect.
As demonstrated in this work, the stacking faults have a large thermal resistance of up to 10-10 K·m2·W-1. For comparison, the Al/sapphire interfacial thermal resistance is as low as 10-9 K·m2·W-1[100]. Considering the fact that sapphire has a thermal conductivity of 30 W·m-1·K-1, which is lower than that of SiC by one order of magnitude, the thermal resistance of stacking faults in SiC is very significant. The presence of high-thermal-resistance region around the stacking faults may introduce heat accumulation and hot spots in the high-power SiC devices and cause local failure due to high temperature. Moreover, as the substrate for 4H-SiC devices are mainly <0001> substrate with a small offcut, the high axial thermal conductivity is essential to the heat dissipation from the device region to the substrate and thereafter the heat sink. An increased number of stacking faults in the substrate and devices may significantly deteriorate the heat dissipation capability of SiC and hinder the efficient thermal management of power electronics and quantum devices.
CONCLUSIONS
In summary, we strategically developed a diverse SiC dataset with energies and forces from DFT calculations. A NEP was trained using this dataset and achieved high accuracy on SiC polytypes and off-stoichiometric SixCy structures with energy error of 4.1 meV/atom and force error of 0.217 eV/Å in the test set. We demonstrated that the diversity of training dataset is fundamental to the accuracy and transferability of the interatomic potential. Its even higher accuracy on SiC polytypes, with force error less than 0.1 eV/Å, allows MD simulations of phonon and thermal transport properties in SiC materials. The potential is employed to investigate the SiC polytype thermal conductivities which achieves good agreement with the literature. The thermal transport properties of stacking faults are also investigated which reveals a high thermal resistance up to 10-10 K·m2·W-1 that can affect the heat dissipation efficiency, suggesting an important role of defect control in thermal management. The machine learning potential obtained in this study holds promising applications in large-scale MD simulations towards understanding of thermal and phonon properties of SiC.
DECLARATIONS
Authors’ contributions
Made substantial contributions to conception and design of the study and performed data analysis and interpretation: Zhang, H.; Pi, X.; Yang, D.; Deng, T.
Performed administrative, technical, and material support: Cheng, M.; Jiang, X.; Zhang, H.
Availability of data and materials
The data supporting the findings can be obtained from the corresponding author upon reasonable request.
Financial support and sponsorship
This work was supported by the “Pioneer” and “Leading Goose” R&D Program of Zhejiang Province (2022C01021 and 2023C01010), the National Natural Science Foundation of China (62204218), Leading Innovative and Entrepreneur Team Introduction Program of Hangzhou (TD2022012), and the Program of Qianjiang Distinguished Experts of Hangzhou. The computational resources are supported by the National Supercomputer Center in Tianjin.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
Supplementary Materials
REFERENCES
1. Morkoç, H.; Strite, S.; Gao, G. B.; Lin, M. E.; Sverdlov, B.; Burns, M. Large-band-gap SiC, III-V nitride, and II-VI ZnSe-based semiconductor device technologies. J. Appl. Phys. 1994, 76, 1363-98.
2. Kimoto, T.; Cooper, J. A. Fundamentals of silicon carbide technology: growth, characterization, devices and applications. John Wiley & Sons, 2014.
3. Wellmann, P.; Ohtani, N.; Rupp, R. Wide bandgap semiconductors for power electronics: materials, devices, applications. Wiley Online Library, 2021.
4. Koehl, W. F.; Buckley, B. B.; Heremans, F. J.; Calusine, G.; Awschalom, D. D. Room temperature coherent control of defect spin qubits in silicon carbide. Nature 2011, 479, 84-7.
5. Castelletto, S.; Johnson, B. C.; Ivády, V.; et al. A silicon carbide room-temperature single-photon source. Nat. Mater. 2014, 13, 151-6.
6. Schöner, A.; Krieger, M.; Pensl, G.; Abe, M.; Nagasawa, H. Fabrication and characterization of 3C-SiC-based MOSFETs. Chem. Vap. Depos. 2006, 12, 523-30.
7. Aldalbahi, A.; Li, E.; Rivera, M.; et al. A new approach for fabrications of SiC based photodetectors. Sci. Rep. 2016, 6, 23457.
8. Protik, N. H.; Katre, A.; Lindsay, L.; Carrete, J.; Mingo, N.; Broido, D. Phonon thermal transport in 2H, 4H and 6H silicon carbide from first principles. Mater. Today. Phys. 2017, 1, 31-8.
9. Kawamura, T.; Hori, D.; Kangawa, Y.; Kakimoto, K.; Yoshimura, M.; Mori, Y. Thermal conductivity of SiC calculated by molecular dynamics. Jpn. J. Appl. Phys. 2008, 47, 8898.
10. Zywietz, A.; Karch, K.; Bechstedt, F. Influence of polytypism on thermal properties of silicon carbide. Phys. Rev. B. Condens. Matter. 1996, 54, 1791-8.
11. Qian, X.; Jiang, P.; Yang, R. Anisotropic thermal conductivity of 4H and 6H silicon carbide measured using time-domain thermoreflectance. Mater. Today. Phys. 2017, 3, 70-5.
12. Burgemeister, E. A.; von Muench, W.; Pettenpaul, E. Thermal conductivity and electrical properties of 6H silicon carbide. J. Appl. Phys. 1979, 50, 5790-4.
13. Cheng, Z.; Liang, J.; Kawamura, K.; et al. High thermal conductivity in wafer-scale cubic silicon carbide crystals. Nat. Commun. 2022, 13, 7201.
14. Wei, R.; Song, S.; Yang, K.; et al. Thermal conductivity of 4H-SiC single crystals. J. Appl. Phys. 2013, 113, 053503.
15. Zheng, Q.; Li, C.; Rai, A.; Leach, J. H.; Broido, D. A.; Cahill, D. G. Thermal conductivity of GaN, 71GaN, and SiC from 150 K to 850 K. Phys. Rev. Mater. 2019, 3, 014601.
16. Slack, G. A. Thermal conductivity of pure and impure silicon, silicon carbide, and diamond. J. Appl. Phys. 1964, 35, 3460-6.
17. Morelli, D. T.; Heremans, J. P.; Beetz, C. P.; Yoo, W. S.; Matsunami, H. Phonon-electron scattering in single crystal silicon carbide. Appl. Phys. Lett. 1993, 63, 3143-5.
18. Nilsson, O.; Mehling, H.; Horn, R.; et al. Determination of the thermal diffusivity and conductivity of monocrystalline silicon carbide (300-2300 K). High. Temp. High. Press. 1997, 29, 73-9.
19. Boteler, L.; Lelis, A.; Berman, M.; Fish, M. Thermal conductivity of power semiconductors - when does it matter? In 2019 IEEE 7th Workshop on Wide Bandgap Power Devices and Applications (WIPDA), Raleigh, USA. Oct 29-31, 2019. IEEE; 2019. pp. 270-6.
20. Goela, J. S.; Brese, N. E.; Pickering, M. A.; Graebner, J. E. Chemical-vapor-deposited materials for high thermal conductivity applications. MRS. Bull. 2001, 26, 458-63.
21. Hoang, T. M.; Ishiwata, H.; Masuyama, Y.; et al. Thermometric quantum sensor using excited state of silicon vacancy centers in 4H-SiC devices. Appl. Phys. Lett. 2021, 118, 044001.
22. Yang, G.; Luo, H.; Li, J.; et al. Discrimination of dislocations in 4H-SiC by inclination angles of molten-alkali etched pits. J. Semicond. 2022, 43, 122801.
23. Kawahara, C.; Suda, J.; Kimoto, T. Identification of dislocations in 4H-SiC epitaxial layers and substrates using photoluminescence imaging. Jpn. J. Appl. Phys. 2014, 53, 020304.
24. Yang, G.; Xu, L.; Cui, C.; Pi, X.; Yang, D.; Wang, R. Anisotropic etching mechanisms of 4H-SiC: experimental and first-principles insights. J. Semicond. 2024, 45, 012502.
25. Wang, P.; Cheng, W.; Li, Y.; et al. Stacking faults in 4H-SiC epilayers and IGBTs. Mater. Sci. Semicond. Process. 2024, 177, 108369.
26. Harris, S. An introduction to the theory of the Boltzmann equation. Courier Corporation, 2004. https://books.google.com/books?id=KfYK1lyq3VYC&printsec=frontcover#v=onepage&q&f=false. (accessed 14 May 2025).
27. Tadano, T.; Gohda, Y.; Tsuneyuki, S. Anharmonic force constants extracted from first-principles molecular dynamics: applications to heat transfer simulations. J. Phys. Condens. Matter. 2014, 26, 225402.
28. Li, W.; Carrete, J.; A,
29. Madsen, G. K.; Carrete, J.; Verstraete, M. J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 2018, 231, 140-5.
30. Carrete, J.; Vermeersch, B.; Katre, A.; et al. almaBTE: a solver of the space–time dependent Boltzmann transport equation for phonons in structured materials. Comput. Phys. Commun. 2017, 220, 351-62.
31. Zhou, J.; Park, J.; Lu, I.; Maliyov, I.; Tong, X.; Bernardi, M. PERTURBO: a software package for ab initio electron–phonon interactions, charge transport and ultrafast dynamics. Comput. Phys. Commun. 2021, 264, 107970.
32. Cepellotti, A.; Coulter, J.; Johansson, A.; Fedorova, N. S.; Kozinsky, B. Phoebe: a high-performance framework for solving phonon and electron Boltzmann transport equations. J. Phys. Mater. 2022, 5, 035003.
33. Bi, K.; Chen, Y.; Yang, J.; Wang, Y.; Chen, M. Molecular dynamics simulation of thermal conductivity of single-wall carbon nanotubes. Phys. Lett. A. 2006, 350, 150-3.
34. Kannam, S. K.; Todd, B. D.; Hansen, J. S.; Daivis, P. J. Slip length of water on graphene: limitations of non-equilibrium molecular dynamics simulations. J. Chem. Phys. 2012, 136, 024705.
35. Yu, J.; Wang, H. A molecular dynamics investigation on evaporation of thin liquid films. Int. J. Heat. Mass. Transf. 2012, 55, 1218-25.
36. Thompson, A. P.; Aktulga, H. M.; Berger, R.; et al. LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171.
37. Haile, J. M. Molecular dynamics simulation: elementary methods. John Wiley & Sons, Inc., 1992. https://dl.acm.org/doi/10.5555/531139. (accessed 14 May 2025).
38. Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 1957, 12, 570-86.
39. Müller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082-5.
40. Ikeshoji, T.; Hafskjold, B. Non-equilibrium molecular dynamics calculation of heat conduction in liquid and through liquid-gas interface. Mol. Phys. 1994, 81, 251-61.
41. Jund, P.; Jullien, R. Molecular-dynamics calculation of the thermal conductivity of vitreous silica. Phys. Rev. B. 1999, 59, 13707-11.
42. Sarman, S. S.; Evans, D. J.; Cummings, P. T. Recent developments in non-Newtonian molecular dynamics. Phys. Rep. 1998, 305, 1-92.
43. Cummings, P. T.; Evans, D. J. Nonequilibrium molecular dynamics approaches to transport properties and non-Newtonian fluid rheology. Ind. Eng. Chem. Res. 1992, 31, 1237-52.
44. Salaway, R. N.; Zhigilei, L. V. Molecular dynamics simulations of thermal conductivity of carbon nanotubes: resolving the effects of computational parameters. Int. J. Heat. Mass. Transf. 2014, 70, 954-64.
45. Fan, Z.; Dong, H.; Harju, A.; Ala-Nissila, T. Homogeneous nonequilibrium molecular dynamics method for heat transport and spectral decomposition with many-body potentials. Phys. Rev. B. 2019, 99, 064308.
46. Ying, P.; Liang, T.; Xu, K.; et al. Sub-micrometer phonon mean free paths in metal-organic frameworks revealed by machine learning molecular dynamics simulations. ACS. Appl. Mater. Interfaces. 2023, 15, 36412-22.
47. Wang, Y.; Fan, Z.; Qian, P.; Caro, M. A.; Ala-Nissila, T. Quantum-corrected thickness-dependent thermal conductivity in amorphous silicon predicted by machine learning molecular dynamics simulations. Phys. Rev. B. 2023, 107, 054303.
48. Xu, K.; Hao, Y.; Liang, T.; et al. Accurate prediction of heat conductivity of water by a neuroevolution potential. J. Chem. Phys. 2023, 158, 204114.
49. de Araujo Oliveira, H.; Fan, Z.; Harju, A.; Pereira, L. F. C. Tuning the thermal conductivity of silicon phononic crystals via defect motifs: implications for thermoelectric devices and photovoltaics. ACS. Appl. Nano. Mater. 2025, 8, 4364-72.
50. Mortazavi, B. Recent advances in machine learning-assisted multiscale design of energy materials. Adv. Energy. Mater. 2025, 15, 2403876.
51. Shimamura, K.; Takeshita, Y.; Fukushima, S.; Koura, A.; Shimojo, F. Computational and training requirements for interatomic potential based on artificial neural network for estimating low thermal conductivity of silver chalcogenides. J. Chem. Phys. 2020, 153, 234301.
52. Qian, X.; Peng, S.; Li, X.; Wei, Y.; Yang, R. Thermal conductivity modeling using machine learning potentials: application to crystalline and amorphous silicon. Mater. Today. Phys. 2019, 10, 100140.
53. Zeng, Z.; Zhang, C.; Xia, Y.; Fan, Z.; Wolverton, C.; Chen, Y. Nonperturbative phonon scatterings and the two-channel thermal transport in Tl3VSe4. Phys. Rev. B. 2021, 103, 224307.
54. Korotaev, P.; Novoselov, I.; Yanilkin, A.; Shapeev, A. Accessing thermal conductivity of complex compounds by machine learning interatomic potentials. Phys. Rev. B. 2019, 100, 144308.
55. Ouyang, Y.; Yu, C.; He, J.; Jiang, P.; Ren, W.; Chen, J. Accurate description of high-order phonon anharmonicity and lattice thermal conductivity from molecular dynamics simulations with machine learning potential. Phys. Rev. B. 2022, 105, 115202.
56. Li, R.; Lee, E.; Luo, T. A unified deep neural network potential capable of predicting thermal conductivity of silicon in different phases. Mater. Today. Phys. 2020, 12, 100181.
57. Zhao, C. Y.; Tao, Y. B.; He, Y. Microstructure and thermophysical property prediction for chloride composite phase change materials: a deep potential molecular dynamics study. J. Phys. Chem. C. 2023, 127, 6852-60.
58. Sun, Z.; Qi, Z.; Liang, K.; et al. A neuroevolution potential for predicting the thermal conductivity of α, β, and ε-Ga2O3. Appl. Phys. Lett. 2023, 123, 192202.
59. Zhang, P.; Zhang, Z.; Liu, Y.; Wang, Z.; Lu, Z.; Xiong, R. Phonon thermal transport in Bi2Te3 from a deep-neural-network interatomic potential. Phys. Rev. Appl. 2022, 18, 054022.
60. Ouyang, N.; Wang, C.; Chen, Y. Temperature- and pressure-dependent phonon transport properties of SnS across phase transition from machine-learning interatomic potential. Int. J. Heat. Mass. Transf. 2022, 192, 122859.
61. Wieser, S.; Zojer, E. Machine learned force-fields for an Ab-initio quality description of metal-organic frameworks. npj. Comput. Mater. 2024, 10, 1205.
62. Zhang, P.; Liao, W.; Zhu, Z.; et al. Tuning the lattice thermal conductivity of Sb2Te3 by Cr doping: a deep potential molecular dynamics study. Phys. Chem. Chem. Phys. 2023, 25, 15422-32.
63. Fu, B.; Sun, Y.; Jiang, W.; et al. Determining the thermal conductivity and phonon behavior of SiC materials with quantum accuracy via deep learning interatomic potential model. J. Nucl. Mater. 2024, 591, 154897.
64. Behler, J.; Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 2007, 98, 146401.
65. Bartók, A. P.; Payne, M. C.; Kondor, R.; Csányi, G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 2010, 104, 136403.
66. Caro, M. A. Optimizing many-body atomic descriptors for enhanced computational performance of machine learning based interatomic potentials. Phys. Rev. B. 2019, 100, 024112.
67. Byggmästar, J.; Nordlund, K.; Djurabekova, F. Simple machine-learned interatomic potentials for complex alloys. Phys. Rev. Mater. 2022, 6, 083801.
68. Thompson, A.; Swiler, L.; Trott, C.; Foiles, S.; Tucker, G. Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials. J. Comput. Phys. 2015, 285, 316-30.
69. Novikov, I. S.; Gubaev, K.; Podryabinkin, E. V.; Shapeev, A. V. The MLIP package: moment tensor potentials with MPI and active learning. Mach. Learn. Sci. Technol. 2021, 2, 025002.
70. Wang, H.; Zhang, L.; Han, J.; E, W. DeePMD-kit: a deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 2018, 228, 178-84.
71. Drautz, R. Atomic cluster expansion for accurate and transferable interatomic potentials. Phys. Rev. B. 2019, 99, 014104.
72. Fan, Z.; Zeng, Z.; Zhang, C.; et al. Neuroevolution machine learning potentials: combining high accuracy and low cost in atomistic simulations and application to heat transport. Phys. Rev. B. 2021, 104, 104309.
73. Fan, Z. Improving the accuracy of the neuroevolution machine learning potential for multi-component systems. J. Phys. Condens. Matter. 2022, 34, 125902.
74. Fan, Z.; Wang, Y.; Ying, P.; et al. GPUMD: a package for constructing accurate machine-learned potentials and performing highly efficient atomistic simulations. J. Chem. Phys. 2022, 157, 114801.
75. Evans, D. J.; Morriss, G. Statistical mechanics of nonequilbrium liquids, 2nd ed.; ANU Press, 2007.
76. Cheng, R.; Shen, X.; Klotz, S.; et al. Lattice dynamics and thermal transport of PbTe under high pressure. Phys. Rev. B. 2023, 108, 104306.
77. Zhang, L.; Lin, D.; Wang, H.; Car, R.; E, W. Active learning of uniformly accurate interatomic potentials for materials simulation. Phys. Rev. Mater. 2019, 3, 023804.
78. Zhang, Y.; Wang, H.; Chen, W.; et al. DP-GEN: a concurrent learning platform for the generation of reliable deep learning based potential energy models. Comput. Phys. Commun. 2020, 253, 107206.
79. Liu, Y.; Wang, H.; Guo, L.; et al. Deep learning inter-atomic potential for irradiation damage in 3C-SiC. Comput. Mater. Sci. 2024, 233, 112693.
80. Lim, J.; Shim, Y.; Park, J.; et al. Molecular dynamics study of silicon carbide using an ab initio-based neural network potential: effect of composition and temperature on crystallization behavior. J. Phys. Chem. C. 2023, 127, 22692-703.
81. Jain, A.; Ong, S. P.; Hautier, G.; et al. Commentary: The Materials Project: a materials genome approach to accelerating materials innovation. APL. Mater. 2013, 1, 011002.
82. Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1-19.
83. Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B. Condens. Matter. 1989, 39, 5566-8.
84. Chen, C.; Ong, S. P. A universal graph deep learning interatomic potential for the periodic table. Nat. Comput. Sci. 2022, 2, 718-28.
85. Qi, J.; Ko, T. W.; Wood, B. C.; Pham, T. A.; Ong, S. P. Robust training of machine learning interatomic potentials with dimensionality reduction and stratified sampling. npj. Comput. Mater. 2024, 10, 1227.
86. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B. Condens. Matter. 1993, 47, 558-61.
87. Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B. Condens. Matter. 1994, 49, 14251-69.
88. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15-50.
89. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. Condens. Matter. 1996, 54, 11169-86.
90. Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B. Condens. Matter. 1994, 50, 17953-79.
91. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 1999, 59, 1758-75.
92. Shapeev, A. V. Moment tensor potentials: a class of systematically improvable interatomic potentials. Multiscale. Model. Simul. 2016, 14, 1153-73.
93. Feldman, D. W.; Parker, J. H.; Choyke, W. J.; Patrick, L. Phonon dispersion curves by Raman scattering in SiC, polytypes 3C, 4H, 6H, 15R, and 21R. Phys. Rev. 1968, 173, 787-93.
94. Zhang, H.; Jiang, X.; Zhang, H.; Pi, X.; Yang, D.; Deng, T. Phonon folding and transport in SiC polytypes from first principles. Appl. Phys. Lett. 2025, 126, 142202.
95. Zhou, W.; Liang, N.; Wu, X.; Xiong, S.; Fan, Z.; Song, B. Insight into the effect of force error on the thermal conductivity from machine-learned potentials. Mater. Today. Phys. 2025, 50, 101638.
96. Wu, X.; Zhou, W.; Dong, H.; et al. Correcting force error-induced underestimation of lattice thermal conductivity in machine learning molecular dynamics. J. Chem. Phys. 2024, 161, 014103.
97. Petretto, G.; Dwaraknath, S.; Miranda, H. P. C.; et al. High-throughput density-functional perturbation theory phonons for inorganic materials. Sci. Data. 2018, 5, 180065.
98. Zhou, H.; Zhou, S.; Hua, Z.; Bawane, K.; Feng, T. Extreme sensitivity of higher-order interatomic force constants and thermal conductivity to the energy surface roughness of exchange-correlation functionals. Appl. Phys. Lett. 2023, 123, 192201.
99. Karch, K.; Pavone, P.; Windl, W.; Schütt, O.; Strauch, D. Ab initio calculation of structural and lattice-dynamical properties of silicon carbide. Phys. Rev. B. Condens. Matter. 1994, 50, 17054-63.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Special Issue
Copyright
Data & Comments
Data





















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].