An effective index for high-performance piezoelectrics

Piezoelectric materials, capable of interconverting mechanical energy and electrical energy, are vital components in modern electromechanical devices and have been attracting significant interest in both technological applications and fundamental research^[1,2]. Since the discovery of the perovskite Pb(Zr,Ti)O₃ (PZT) system in the 1950s, various perovskite solid-solution systems with high piezoelectricity have been developed. These include Pb-based systems, such as PZT-derived ternary systems and Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃ (PMN-PT)-based system^[3,4], as well as Pb-free alternatives, notably (K,Na)NbO₃ (KNN)-based^[5-7] and BaTiO₃ (BT)-based systems^[8]. Meanwhile, the mechanism underlying high piezoelectricity has long been a core focus of research. During the past decades, various mechanisms from different perspectives have been proposed to explain the high piezoelectricity. One frequently-discussed mechanism involves the coexistence of multiple ferroelectric phases (e.g., rhombohedral, tetragonal, and orthorhombic) at morphotropic or polymorphic phase boundaries (MPBs/PPBs), which enhances the piezoelectricity by providing richer polarization variants and enabling facile domain switching^[9,10]. The low-symmetry monoclinic phase is recognized to enable smooth and continuous polarization rotation, thereby generating large lattice contributions to piezoelectric response^[11-13]. Nanodomains, characterized by high-density domain walls with improved mobility, act as extrinsic contributions that further increase piezoelectricity^[14]. Furthermore, local structural heterogeneity, macroscopically manifested as a frequency-dependent diffusive phase transition, has been elucidated to play an important role in enhancing both dielectric and piezoelectricity^[2,15,16]. Although current theories and observed phenomena can explain high piezoelectricity in specific systems, a unified framework applicable across diverse perovskite piezoelectric materials elusive.

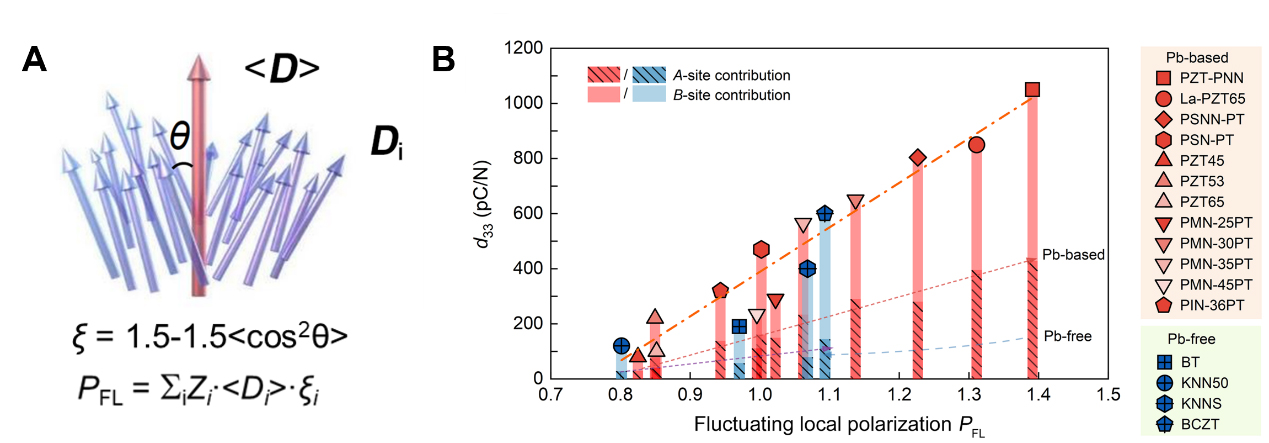
Recently, Yao et al.^[1] introduced the concept of fluctuating local polarization (FLP) as an effective index for high piezoelectricity in perovskite ferroelectrics. FLP is defined as a metric integrating two key factors: the magnitude of local electric dipoles and their orientations. In practice, FLP is calculated by summing the nominal charge-weighted average polar displacement (charge × <D>, where <D> denotes the average displacement vector) of each A-site and B-site ion, multiplied by a disorder parameter (ξ) that quantifies the spread of polarization direction [Figure 1A]. A high FLP value thus indicates a ferroelectric material with both large local dipole moments and a broad distribution of dipole orientations. Yao et al.^[1] determined FLP for 16 representative perovskite compositions, including classical Pb-based and Pb-free ceramics, by performing neutron total scattering experiments combined with reverse Monte Carlo modeling, which captured atom-associated local polar displacement vectors. This approach provides a statistical picture of polarization directions across the entire material, rather than focusing on isolated microdomains. They found a strong positive correlation between FLP and the macroscopic piezoelectric coefficient d₃₃^[1]. Higher FLP corresponds to higher d₃₃ values [Figure 1B]. Increasing FLP involves introducing greater diversity in local polarization states with various orientations while preserving substantial dipole magnitudes. First-principles calculations further corroborated this relationship. For example, high-FLP compositions, such as La-doped PZT and Sb-doped KNN, were found to have a “flatter” local polarization energy landscape (lower polarization anisotropy and stiffness) compared to low-FLP counterparts^[1]. This flattened energy landscape allows polarization to vary more easily under an electric field, resulting in a larger d₃₃. The FLP concept not only rationalizes the composition-dependent piezoelectric performance in individual solid solutions but also explains high piezoelectricity across distinct systems, serving as an effective index for high-performance perovskite piezoelectrics. In general, obtaining the FLP value for a new material requires integrating experimental measurements of local polar structure with computational analysis. Techniques such as high-resolution transmission electron microscopy or X-ray and neutron scattering can reveal local displacement vectors of ions. The FLP can then be calculated following the method of Yao et al. once the local dipole magnitudes and orientation spread are determined, and this value can be used to predict the material’s approximate macroscopic piezoelectric coefficient d₃₃^[1].

Figure 1. (A) Illustration of the method for quantifying orientation disorder and fluctuating local polarization P_FL. <D> denotes the average displacement vector, and represents the angular deviation of each individual vector D_i from the average direction; (B) Relationship between piezoelectric coefficient d₃₃ and fluctuating local polarization P_FL. Reproduced from Ref.^[1] under the CC BY 4.0 license. PZT: Pb(Zr,Ti)O₃; PMN: Pb(Mg_1/3Nb_2/3)O₃; BT: BaTiO₃; KNNS: K_0.48Na_0.52Nb_0.955Sb_0.045O₃; KNN50: (K_0.5Na_0.5)NbO₃; BCZT: 0.5(Ba_0.7Ca_0.3)TiO₃-0.5Ba(Zr_0.2Ti_0.8)O₃; PSNN-PT: 0.14Pb(Sc_0.5Nb_0.5)O₃-0.52Pb(Ni_1/3Nb_2/3)O₃-0.34PbTiO₃; PSN: Pb(Sc_0.5Nb_0.5)O₃; PNN: Pb(Ni_1/3Nb_2/3)O₃.

Beyond individual cases, the FLP concept provides a broader mechanistic framework that can reconcile previously proposed mechanisms. For instance, compositions at MPBs/PPBs with mixed ferroelectric phases inherently contain multiple permissible polarization directions, broadening the distribution of local polarization vectors. This diversity in polarization states corresponds to a higher FLP, yielding an elevated d₃₃. Similarly, the monoclinic phase - with polarization oriented within its monoclinic plane and featuring 24 polarization variants - also increases the diversity of local polarization vectors. Nanoscale polarization disorder in relaxor ferroelectrics and the higher fraction of domain walls in soft ferroelectrics, enabled by nanodomains, contribute extrinsic flexibility to the polarization configuration, further increasing FLP. On the other hand, the FLP concept helps explain why Pb-free alternatives generally exhibit lower piezoelectricity than Pb-based counterparts. In BT- and KNN-based Pb-free systems, relatively lower atomic-scale polar displacements - attributed to the absence of strong A-O hybridization - limit the enhancement of FLP. Notably, the FLP concept does not supersede these traditional viewpoints; rather, it rationalizes them under a common microscopic index: local polarization flexibility. In summary, these diverse phenomena - phase coexistence, polarization rotation, nanoscale domain engineering, and local structural disorder - can all be viewed as strategies to increase a material’s local polarization flexibility, thereby boosting the macroscopic piezoelectric response.

While FLP is a powerful atomic-scale index, it is important to recognize its limitations. The macroscopic piezoelectric properties of a ceramic are not determined solely by atomic-scale polarization; they are also influenced by microstructural factors spanning the nano- to macro-scale. The current FLP model primarily characterizes intrinsic, atomic-level polarization fluctuations. Consequently, materials with identical FLP values may still exhibit different measured d₃₃ if their microstructures differ. A high FLP is therefore a strongly favorable factor for achieving high piezoelectricity, but it is not the sole determinant. Caution is advised in over-interpreting FLP in isolation, and future refinements could integrate FLP with microstructural descriptors, such as grain and domain structure parameters, to develop a more comprehensive predictive framework for piezoelectric performance.

The FLP concept proposed by Yao et al.^[1], as an effective descriptor, underpins enhanced piezoelectricity in both Pb-based and Pb-free ferroelectrics. By correlating the orientation disorder and magnitude of local electric dipole moments with macroscopic piezoelectric performance, FLP provides a deeper understanding of high piezoelectricity. This concept also explains other enhancement strategies, ranging from phase-boundary engineering to relaxor behavior. Maximizing FLP can serve as a clear target in the quest to improve piezoelectricity. Thus, FLP can be used as a figure-of-merit descriptor in computational screening, including machine-learning-driven searches, to accelerate advances in piezoelectrics. In this light, FLP is not merely an explanatory fingerprint of high piezoelectricity - it is a practical reference for engineering the next generation of ferroelectric materials.