Magnetic-field driven domain wall evolution in rhombohedral magnetostrictive single crystals: a phase-field simulation
Abstract
Single crystal of Tb0.3Dy0.7Fe2 (Terfenol-D) with a composition close to the pre-transitional rhombohedral side of the ferromagnetic morphotropic phase boundary has demonstrated remarkable magnetostrictive properties, stimulating intensive research interest in the field of magneto-mechanical transducers and actuators. The enhanced magnetoelastic response of (Tb-Dy)Fe2 single crystals has been extensively linked to the structural phase transition and magnetic domain evolution. This research utilized the micromagnetic microelastic phase-field technique to examine the evolution of domain walls in rhombohedral ferromagnetic single crystals of (Tb-Dy)Fe2, which is essential for understanding the magnetostriction “jump” effect. The study involved simulating the creation and development of domains and domain boundaries under a periodic boundary condition that allows for non-zero strain. It was found that the two typical distinct types of domain walls (i.e., 71° and 109°) exhibited disparate responses to the applied magnetic fields. At magnetic field magnitudes below the coercive field, a domain wall broadening mechanism was detected within the 71° domain wall. However, upon surpassing the coercive field, a process of homogeneous magnetization switching ensued, devoid of evident displacement of the 71° domain walls. The magnetization switching effectively elucidated the magnetostriction “jump” effect of the rhombohedral single crystals. The act of sweeping the 109° domain walls resulted in the occurrence of heterogeneous magnetization switching. This study elucidates the evolutionary mechanism of two typical rhombohedral domain walls in response to applied magnetic fields, potentially offering valuable insights into the future design of excellent magnetostrictive materials through domain engineering.
Keywords
INTRODUCTION
Giant magnetostrictive materials, i.e., quasi-binary (Tb-Dy)Fe2 alloys, have attracted considerable attention due to their potential applications as energy conversion components in magneto-mechanical transducers and actuators[1-6]. During the past decades, efforts have been made to develop an anisotropy compensation system that minimizes magnetic anisotropy in order to take advantage of the giant magnetostriction at low fields[7-10]. Newnham[11] firstly credits the spin reorientation boundary of (Tb-Dy)Fe2 as a magnetic equivalent to the morphotropic phase boundary (MPB) of a quasi-binary ferroelectric solid solution, i.e., the ferromagnetic MPB, which has been confirmed by Yang et al.[12] and Bergstrom et al.[13]. While the ferromagnetic MPB has demonstrated utility as a design approach for achieving highly sensitive magnetoelastic responses, the predominant focus in current research has been on materials exhibiting a rhombohedral structure, exemplified by Tb0.3Dy0.7Fe2 (Terfenol-D)[13,14]. This is because of the highly anisotropic magnetostriction λ111 in the pre-transitional rhombohedral side of ferromagnetic MPB, in which giant magnetostriction could be induced by movement of non-180° domain walls or rotation of magnetic moments[1,14-16].
As is well known, the magnetization of the rhombohedral (Tb-Dy)Fe2 domains is expected to distribute equally along one of the eight <111> easy axes, as shown in Figure 1. The magnetostriction “jump” effect is primarily attributed to the motions of 109° and 71° domain walls under applied magnetic fields[17-19], although the underlying internal mechanism remains unclear. Several phenomenological approximations, such as domain wall motion and magnetization rotation models, have been proposed to elucidate the magneto-mechanical behaviors of Terfenol-D[8,20-23]. However, the prevailing mechanisms largely overlook the presence of internal magnetic (stress) fields and assume that each domain evolves independently, which means no magnetic and elastic long-range interactions among domains are considered. Furthermore, the inherent stress resulting from elastic incompatibility in domain walls is of considerable significance, particularly in the case of giant magnetostrictive materials with large intrinsic strain. Since Khachaturyan’s microelasticity theory[24] was introduced into the phase-field method, it has emerged as a robust technique for simulating the mesoscale microstructural evolution of ferroelectric systems[25-28]. Zhang et al. have proposed a phase-field model that integrates the Khachaturyan microelasticity theory with micromagnetic simulation, enabling the prediction of domain structure stability and temporal evolution[29]. Subsequently, comparable micromagnetic microelastic phase-field models have been developed to explore domain evolution and magnetoelastic response in proximity to the ferromagnetic MPB[15,16,30,31].
In this work, the micromagnetic microelastic phase-field method was employed to study the formation and evolution of domains in (Tb-Dy)Fe2 single crystals within the rhombohedral phase region of the ferromagnetic MPB. Particular emphasis was placed on the two distinct categories of domain walls, namely 71° and 109° domain walls. In the case of the 71° domain wall, the application of an external magnetic field below the coercive field leads to the observation of a domain wall broadening effect, while exceeding the coercive field results in domain switching. Additionally, the applied external magnetic field in the [100] direction leads to 109° domain walls sweeping, which results in heterogeneous magnetization switching.
MATERIALS AND METHODS
The phase-field model employs the local magnetization vector M (m1, m2, m3) as the primary order parameter, with its spatial distribution representing the magnetic domain microstructure. Therefore, the domain structure can be derived from the time evolution of the local magnetization configuration as governed by the Landau-Lifshitz-Gilbert (LLG) equation, denoted as
where Ms represents the saturation magnetization, and α and γ0 denote the damping constant and gyromagnetic ratio, respectively.
The effective magnetic field, denoted as Heff, is calculated by Heff = -(μ0Ms)-1(δEtot/δm) with the vacuum permeability μ0 and the total free energy Etot. The total free energy, expressed as[1]
is composed of the magnetocrystalline anisotropy (Eani), exchange (Eexc), magnetostatic (Ems), elastic (Eel), and external energy (Eext).
The magnetocrystalline anisotropy energy can be defined as[20,32]
where K1 and K2 represent the magnetocrystalline anisotropy coefficients, and V indicates the total volume of the system.
The exchange energy is determined solely by the spatial variation of the magnetization direction and can be written as[29]
where spatial differentiation is denoted by a comma and A is the exchange stiffness constant.
The magnetostatic energy of a system can be denoted as[29,33]
where Hd represents the stray field resulting from the long-range interaction between magnetic moments within the system. In the context of a periodic boundary condition, the simulation system is conceptualized as a repetitive building block within 3-D space, and the stray field can be expressed as
where ND is the demagnetizing factor dependent solely on the sample’s shape. Additionally,
The elastic energy resulting from local deformation can be given as[20,24,34]
where cijkl represents the elastic stiffness tensor, eij denotes the elastic strain, εij signifies the total strain, and
Where λ100 and λ111 are the magnetostrictive constants. Khachaturyan’s elastic theory[24] posits that the total strain εij can be expressed as the sum of homogeneous strain
where the stress component σij is calculated using
Given the assumption of elastic equilibrium at each evolutionary step, the strain and stress values are determined by solving the mechanical equilibrium equation
The external energy resulting from the influence of an externally applied magnetic field, denoted as Hex, can be established as[36]
The LLG equation is employed to elucidate the progression of domain microstructure, and its numerical solution is achieved through the Gauss-Seidel projection method[37]. The simulation focuses on the representative rhombohedral ferromagnetic single system, utilizing material parameters derived from a combination of experimental data and theoretical computations conducted previously[1,38-41], as outlined comprehensively in Table 1. Figure 1 provides a schematic illustration of the unit cell of (Tb-Dy)Fe2, which is cubic. The process of domain formation was simulated using the phase-field method, with a dimension of 512Δx × 512Δx × 1Δx. (The 3D phase-field simulation of the domain formation process can be seen in Supplementary Figure 1 in Supplementary Materials) The simulation grid Δx is 2 nm, smaller than the exchange length
The material parameters of (Tb-Dy)Fe2 in the work
| Parameters | Value | Units |
| Saturation magnetization Ms | 8 × 105 | A/m |
| First-order anisotropy coefficient K1 | -6 × 104 | J/m3 |
| Second-order anisotropy coefficient K2 | -2 × 105 | J/m3 |
| Exchange constant A | 9 × 10-12 | J/m |
| Elastic stiffness c11 | 1.41 × 1011 | N/m2 |
| Elastic stiffness c12 | 6.48 × 1010 | N/m2 |
| Elastic stiffness c44 | 4.87 × 1010 | N/m2 |
| Magnetostrictive constant λ111 | 1,640 | ppm |
| Magnetostrictive constant λ100 | 100 | ppm |
RESULTS AND DISCUSSION
Figure 2 illustrates the evolution of domain formation within a representative volume element of the rhombohedral ferromagnetic single crystal, guided by energy minimization towards equilibrium. The initial state is characterized by a random distribution of magnetization, devoid of any predetermined assumptions. The local energy minimum, in conjunction with the presence of inhomogeneous internal stress, serves as the driving force for the initiation nucleation and subsequent growth of various domains. (The distribution of stress during the domain formation process can be seen in Supplementary Figure 2 in
Figure 2. Domain formation process of the rhombohedral (Tb-Dy)Fe2 single crystal. The colors correspond to the intensity of magnetization along the z direction, while the black arrows indicate the orientations of magnetization.
We first study the evolution of the 71° domain wall below the coercive field. As shown in Figure 3, the initial configuration of the simulation is a domain structure containing four 71° domain walls, which consist of [111] and
Figure 3. The broadening effect of the 71° domain walls occurs when the applied magnetic field is below the coercive field. The domain wall is magnified to illustrate the fluctuations in its thickness.
Magnetization switching is observed upon surpassing the coercive field, as depicted in Figure 4. When the applied magnetic field in the
Figure 4. Magnetization switching occurs upon surpassing the coercive field. The domains before and after switching are depicted on the left.
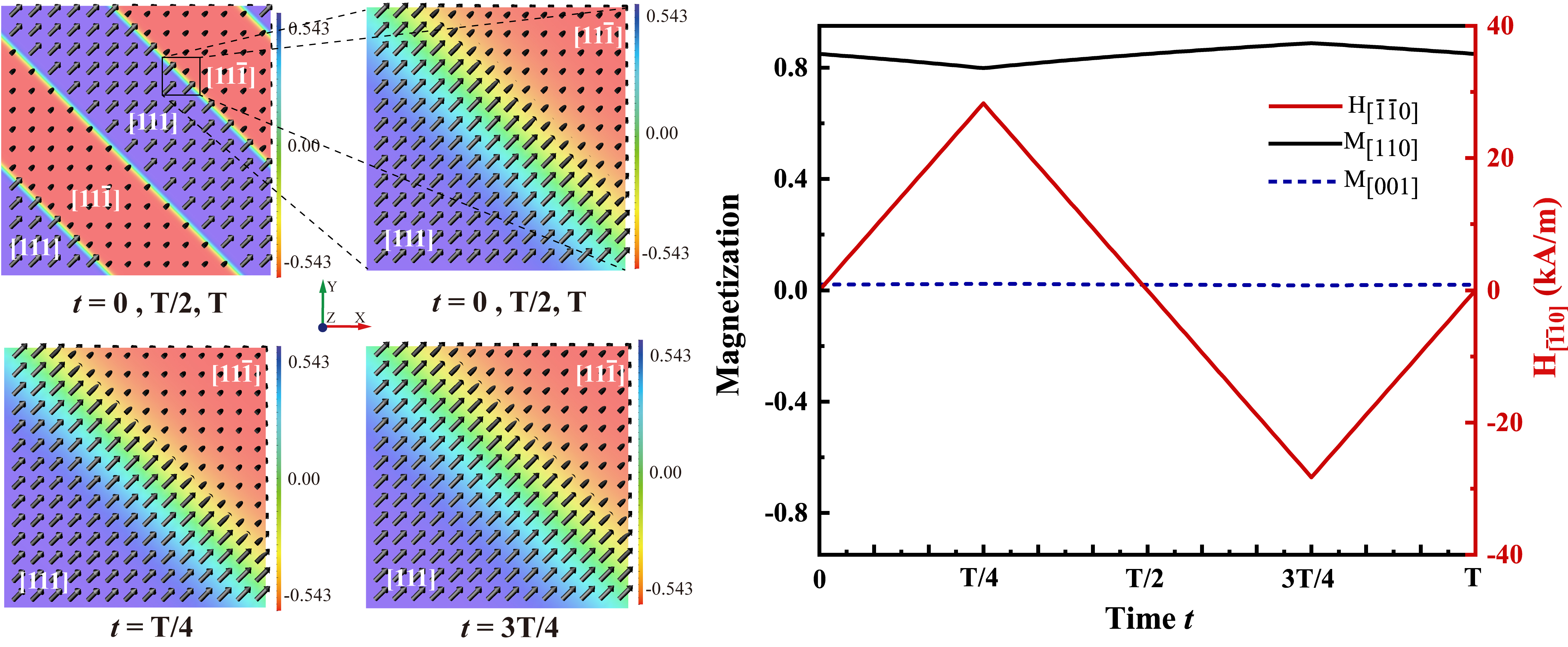
Figure 5 shows magnetic field dependence of the 109° domain wall, which consists of
CONCLUSIONS
This study utilized micromagnetic microelastic modeling through the phase-field method to investigate the process of domain formation and the evolution of domain walls in (Tb-Dy)Fe2 single crystals situated in the vicinity of the rhombohedral region of the ferromagnetic MPB. Particular emphasis was placed on the 71° and 109° domain walls, as their alterations in domain structure under applied magnetic field are crucial to the magnetelastic response of giant magnetostrictive materials. In the case of low applied magnetic field, a phenomenon of domain wall broadening was noted on the 71° domain walls, whereas in the case of high applied magnetic field, homogeneous magnetization switching took place without any observable movement of domain walls. The magnetization switching also helps understand the magnetostriction "jump" effect of the rhombohedral single crystal. The act of sweeping the 109° domain walls resulted in the occurrence of heterogeneous magnetization switching through the movement of domain walls. The detailed analysis of the two domain evolution mechanisms provided insightful understanding into the engineered domain structures of rhombohedral (Tb-Dy)Fe2 single crystals. Furthermore, these findings offer valuable guidance for the future design of magnetostrictive materials through domain engineering.
DECLARATIONS
Authors’ contributions
Conception and design of the study: Hu CC, Zhang Z, Xu YX
Data analysis and interpretation: Xu YX, Hu CC, Dong SZ, Huang HH, Li W
Manuscript writing and revising: Xu YX, Cai TT, Hu CC, Zhang Z, Li W
Simulation guide: Huang HB, Rao WF, Chen LQ
Supervision: Hu CC, Zhang Z, Rao WF
Availability of data and materials
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Financial support and sponsorship
This work was financially supported by the National Natural Science Foundation of China (No. 52301088), the Science Foundation of Shandong Province, China (No. ZR2022ME030 and No. ZR2020QE028), the National Natural Science Foundation of China (No. 12204215 and No. 12174210), the Research Foundation of Liaocheng University (No. 318012119). Chen LQ is the owner of Mu-PRO LLC, which licensed the computer codes for generating the phase-field results from the Penn State Research Foundation.
Conflicts of interest
Chen LQ is the owner of Mu-PRO LLC, which licensed the computer codes for generating the phase-field results from the Penn State Research Foundation, while the other authors have declared that they have no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2024.
Supplementary Materials
REFERENCES
1. Clark AE. Handbook of ferromagnetic materials. In: Wohlfarth EP, editor. Magnetostrictive rare earth-Fe2 compounds. Amsterdam: North-Holland; 1980. pp. 531-89.
3. Zhou SZ, Gao XX. Magnetostrictive materials. Beijing: Metallurgical Industry Press; 2017.
4. Yu C, Niu R, Peng Z, et al. A current sensor based on capillary microresonator filled with terfenol-D nanoparticles. IEEE Photon Technol Lett 2021;33:239-42.
5. Liu C, Shen T, Feng Y, Liu H, Han W. First-principles calculations to investigate electronic, magnetism, elastic properties of
6. Tu S, Mai Y, Tong Y, Liu T, Dong M, Wang Q. Enhancement of magnetostrictive performance of Tb0.27Dy0.73Fe1.95 by solidification in high magnetic field gradient. J Alloys Compd 2018;741:1006-11.
7. Liu J, Ren W, Li D, et al. Magnetic transitions and magnetostrictive properties of TbxDy1-x(Fe0.8Co0.2)2(0.20 ≤ x ≤ 0.40). Phys Rev B 2007;75:064429.
8. Hu CC, Shi YG, Shi DN, Tang SL, Fan JY, Du YW. Anisotropy compensation and magnetostrictive properties in
9. Zhou Z, Li J, Bao X, Liu M, Gao X. Improvement of mechanical properties of magnetostrictive Tb-Dy-Fe alloys via preparing sintered material with low-melting Dy-Cu alloy binder. J Alloys Compd 2022;895:162572.
10. Dong M, Liu T, Guo X, Liu Y, Dong S, Wang Q. Enhancement of mechanical properties of Tb0.27Dy0.73Fe1.95 alloy by directional solidification in high magnetic field. Mater Sci Eng A 2020;785:139377.
12. Yang S, Bao H, Zhou C, et al. Large magnetostriction from morphotropic phase boundary in ferromagnets. Phys Rev Lett 2010;104:197201.
13. Bergstrom R Jr, Wuttig M, Cullen J, et al. Morphotropic phase boundaries in ferromagnets: Tb1-xDyxFe2 alloys. Phys Rev Lett 2013;111:017203.
14. Hu C, Zhang Z, Cheng X, Huang H, Shi Y, Chen L. Ultrasensitive magnetostrictive responses at the pre-transitional rhombohedral side of ferromagnetic morphotropic phase boundary. J Mater Sci 2021;56:1713-29.
15. Ke X, Zhou C, Tian B, et al. Direct evidence of magnetization rotation at the ferromagnetic morphotropic phase boundary in
16. Xu Y, Wu Y, Hu C, et al. Domain engineering in ferromagnetic morphotropic phase boundary with enhanced and non-hysteretic magnetostriction: a phase-field simulation. Scr Mater 2024;242:115916.
17. Wang B, Busbridge S, Li Y, Wu G, Piercy A. Magnetostriction and magnetization process of Tb0.27Dy0.73Fe2 single crystal. J Magn Magn Mater 2000;218:198-202.
18. Galloway N, Schulze MP, Greenough RD, Jiles DC. Enhanced differential magnetostrictive response in annealed Terfenol-D. Appl Phys Lett 1993;63:842-4.
19. Zhao Y, Jiang C, Zhang H, Xu H. Magnetostriction of <110> oriented crystals in the TbDyFe alloy. J Alloys Compd 2003;354:263-8.
20. Jiles D, Thoelke J. Theoretical modelling of the effects of anisotropy and stress on the magnetization and magnetostriction of
21. Desimone A, James RD. A theory of magnetostriction oriented towards applications. J Appl Phys 1997;81:5706-8.
22. Zhao X, Lord D. Effect of demagnetization fields on the magnetization processes in Terfenol-D. J Magn Magn Mater 1999;195:699-707.
23. Armstrong WD. An incremental theory of magneto-elastic hysteresis in pseudo-cubic ferro-magnetostrictive alloys. J Magn Magn Mater 2003;263:208-18.
24. Khachaturyan AG. Theory of structural transformation in solids. New York: Wiley; 1983.
25. Choudhury S, Li Y, Krilliii C, Chen L. Phase-field simulation of polarization switching and domain evolution in ferroelectric polycrystals. Acta Mater 2005;53:5313-21.
26. Ke X, Wang D, Ren X, Wang Y. Polarization spinodal at ferroelectric morphotropic phase boundary. Phys Rev Lett 2020;125:127602.
27. Rao W, Wang YU. Domain wall broadening mechanism for domain size effect of enhanced piezoelectricity in crystallographically engineered ferroelectric single crystals. Appl Phys Lett 2007;90:041915.
28. Guo C, Huang H. Design of super-elastic freestanding ferroelectric thin films guided by phase-field simulations. Microstructures 2022;2:2022021.
29. Zhang J, Chen L. Phase-field microelasticity theory and micromagnetic simulations of domain structures in giant magnetostrictive materials. Acta Mater 2005;53:2845-55.
30. Huang YY, Jin YM. Phase field modeling of magnetization processes in growth twinned Terfenol-D crystals. Appl Phys Lett 2008;93:142504.
31. Hu C, Yang T, Huang H, et al. Phase-field simulation of domain structures and magnetostrictive response in Tb1-xDyxFe2 alloys near morphotropic phase boundary. Appl Phys Lett 2016;108:141908.
32. Yang YV, Huang YY, Jin YM. Effects of magnetocrystalline anisotropy constant K2 on magnetization and magnetostriction of Terfenol-D. Appl Phys Lett 2011;98:012503.
33. Hu J, Nan CW. Electric-field-induced magnetic easy-axis reorientation in ferromagnetic/ferroelectric layered heterostructures. Phys Rev B 2009;80:224416.
35. Sun Z, Li L, Yang G, Wang L. Micromagnetic simulation of Nd-Fe-B demagnetization behavior in complex environments. J Magn Magn Mater 2024;589:171555.
37. Wang XP, Garcı́a-Cervera CJ, E W. A gauss-seidel projection method for micromagnetics simulations. J Comput Phys 2001;171:357-72.
38. Clark A, Savage H, Spano M. Effect of stress on the magnetostriction and magnetization of single crystal Tb0.27Dy0.73Fe2. IEEE Trans Magn 1984;20:1443-5.
39. Wang BL, Jin YM. Magnetization and magnetostriction of Terfenol-D near spin reorientation boundary. J Appl Phys 2012;111:103908.
40. Martin KN, de Groot PAJ, Rainford BD, et al. Magnetic anisotropy in the cubic Laves REFe2 intermetallic compounds. J Phys Condens Matter 2006;18:5861-71.
41. Shu Y, Lin M, Wu K. Micromagnetic modeling of magnetostrictive materials under intrinsic stress. Mech Mater 2004;36:975-97.
42. Abo GS, Hong Y, Park J, Lee J, Lee W, Choi B. Definition of magnetic exchange length. IEEE Trans Magn 2013;49:4937-9.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.























Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].