Ultralow thermal conductivity via weak interactions in PbSe/PbTe monolayer heterostructure for thermoelectric design

Crystal structure, chemical bonding, and stability

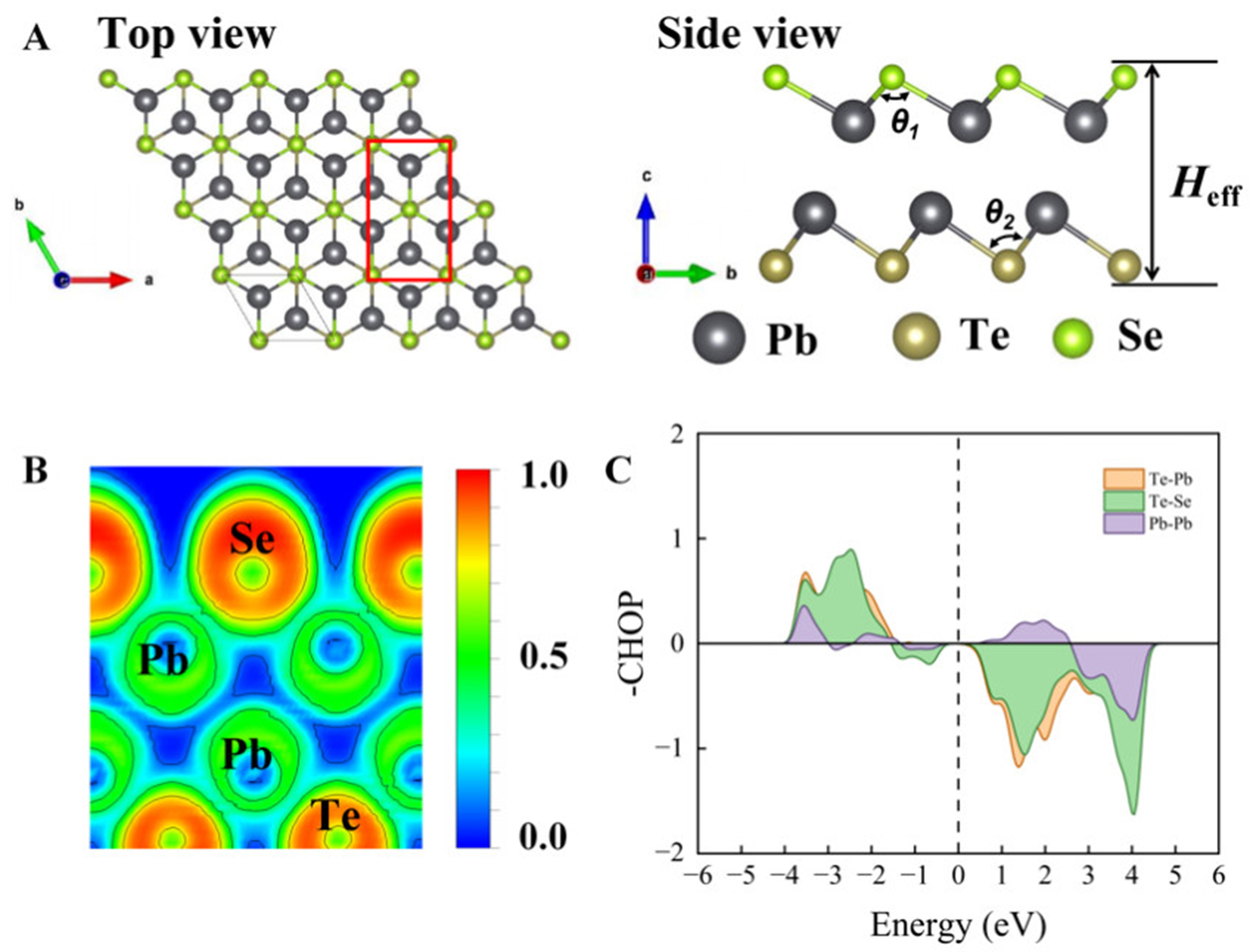
As illustrated in Figure 1A, the monolayer PbSe/PbTe monolayer heterostructure exhibits a pronounced wrinkled morphology. The crystal structure consists of two Pb atomic layers sandwiched by alternately arranged Se and Te atoms, and belongs to the $$ P3m1 $$ (No. 156) space group. According to the structural parameters listed in Table 1, the in-plane lattice constant of the heterostructure is 4.30 Å, which lies between those of monolayer PbSe (4.091 Å) and PbTe (4.364 Å). The atomic size mismatch between Te (atomic radius: 2.07 Å) and Se (1.90 Å) leads to noticeable asymmetry in the bond lengths and bond angles of the Pb–Te and Pb–Se bonds, resulting in local structural distortion at the heterointerface and the formation of a complex wrinkled configuration. This asymmetric wrinkled architecture not only imparts distinctive geometric characteristics to the material, but also enhances interfacial phonon scattering, effectively suppressing the $$ {\kappa_{{\rm{L}}}} $$. To define the transport directions and standardize the simulation domain, a standard unit cell containing eight atoms, as highlighted by the red rectangle in Figure 1A, is chosen for all analyses in this work.

Figure 1. Supercell structure of the PbSe/PbTe monolayer heterostructure: (A) Top view and side view; (B) ELF; (C) -COHP analysis. ELF: Electron localization function.

Bonding characteristics play a crucial role in determining the performance of thermoelectric materials. To gain deeper insight into the bonding behavior in the PbSe/PbTe monolayer heterostructure and its impact on $$ {\kappa_{{\rm{L}}}} $$, we further computed the electron localization function (ELF)^[51], Bader charge and COHP^[38]. The ELF was first proposed by Becke and Edgecombe^[52], and then was further interpreted by Savin et al. in terms of the Pauli kinetic energy density ($$ t_p $$) corrected by the homogeneous electron gas kinetic energy density ($$ t_{\mathrm{HEG}} $$)^[51]: $$ \mathrm{ELF} = \dfrac{1}{1 + \chi^2} $$, in which $$ \chi = \dfrac{1}{1 + \left( t_p / t_{\mathrm{HEG}} \right)^2} $$. Therefore, ELF lies in the range from 0 to 1 by definition. An ELF value of 1.0 corresponds to perfect electron localization, while an ELF value of 0.5 indicates a homogeneous electron gas (i.e., complete delocalization^[53]). The ELF is an effective tool to visualize lone-pair electrons^[54] and to understand bonding^[55]. COHP analysis is a theoretical method for quantitatively characterizing chemical bonding in solid-state systems^[38,56]. It partitions the band-structure energy into orbital-pair interactions between adjacent atoms, yielding a bond-weighted density of states (DOS) that distinguishes between bonding and antibonding contributions. The energy integration of the COHP curve provides the energetic contribution of a specific atom pair ("bond") to the total energy of the system, typically expressed in eV or kJ · mol$$^{-1}$$, thus enabling a quantitative assessment of bond strength. As shown in Figure 1B, the ELF values for both Pb-Se and Pb-Te bonds are relatively low, indicating a weak degree of electron localization. This suggests that the bonding nature is not purely covalent but contains weakly ionic characteristics. To further analyze the bonding characteristics, the Bader charges of the atoms were calculated. The results show that the Bader charges of Pb, Te, and Se are +0.54e, –0.43e, and –0.64e, respectively. These values are far smaller than the corresponding nominal charges (Pb²⁺: +2e, Te^2-: –2e, Se^2-: –2e). The large differences between the nominal oxidation states and the Bader charges indicate that the Pb-Te and Pb-Se bonds show significant covalent character. These observations are consistent with the ELF analysis results. Overall, the combination of partial electron transfer and relatively low ELF values suggests that the Pb-Se and Pb-Te bonds are polar covalent, characterized by partial electron sharing alongside minor ionic contributions. Furthermore, COHP projection analysis [Figure 1C] reveals significantly negative -COHP values for Pb-Se and Pb-Te bonds in the energy range of about -2 to -3 eV below the Fermi level, indicating the presence of dominant antibonding states. These antibonding states weaken the bond strength and lead to pronounced repulsive interactions. The reduction in bond strength and uneven distribution of bond energies disrupt lattice periodicity and phonon propagation, enhancing phonon scattering and further reducing $$ \kappa_{L} $$. In summary, the Pb-Se and Pb-Te bonds in the PbSe/PbTe monolayer heterostructure are mainly polar covalent with weak ionic character. Partial charge transfer, low ELF values, and the occupation of antibonding states collectively contribute to weakened bond strength and enhanced lattice anharmonicity, which are key electronic structure origins for achieving low $$ {\kappa_{{\rm{L}}}} $$ in this system.

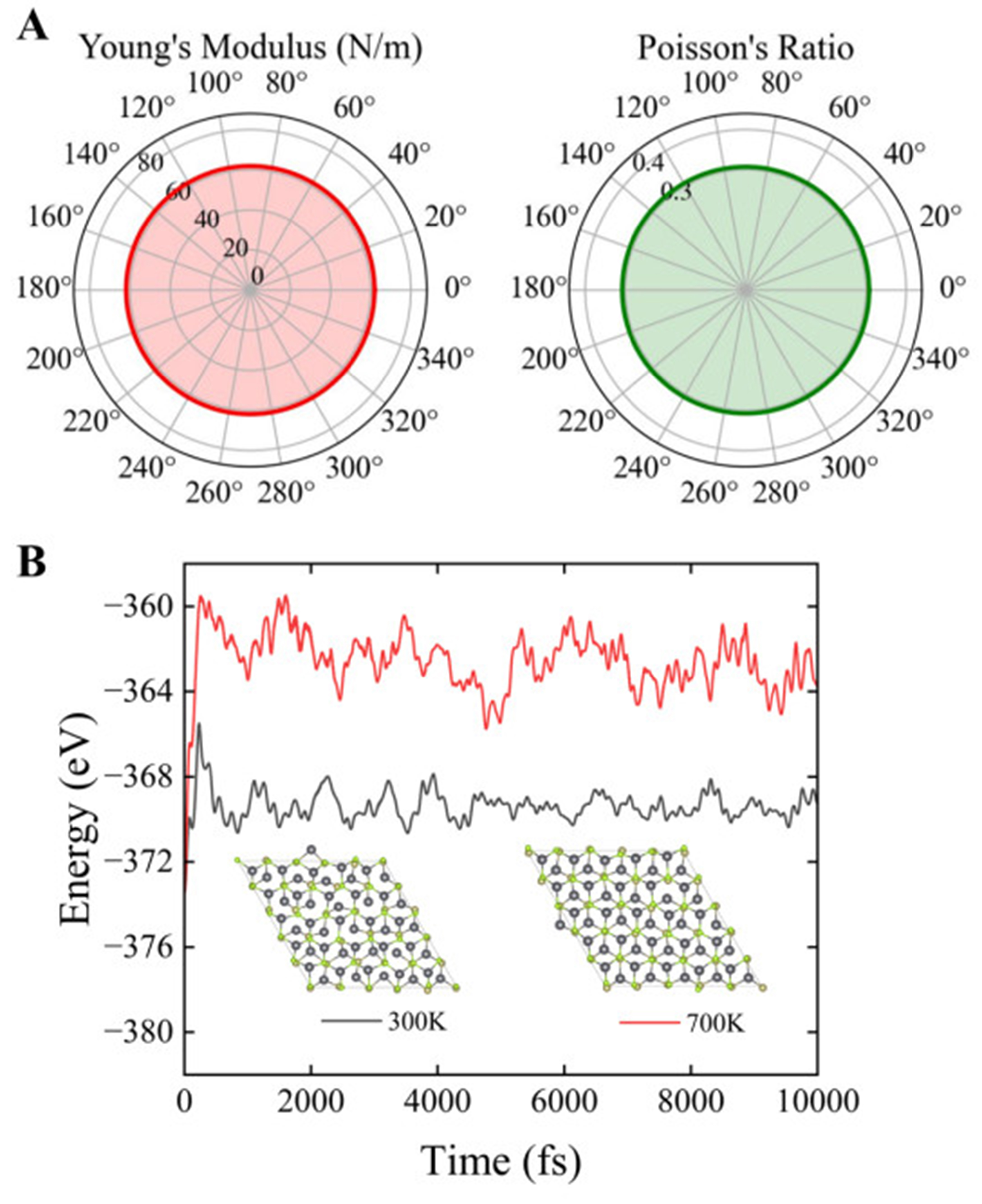
Good stability is essential for thermoelectric materials. Firstly, the elastic constants matrix of the PbSe/PbTe monolayer heterostructure was calculated, as shown in Table 2. The PbSe/PbTe monolayer heterostructure satisfies the Born-Huang criteria for mechanical stability, namely: $$ C_{11} > 0 $$; $$ C_{66}> 0 $$; $$ C_{11}C_{22} - C_{12}^2 > 0 $$. Therefore, the PbSe/PbTe monolayer is mechanically stable. Furthermore, the relationship among Young's modulus (Y), Poisson's ratio (ν), and elastic constants is given by^[57]:

where $$ A = (C_{11}C_{22} - C_{12}^2)/C_{66} - 2C_{12} $$, $$ B = C_{11} + C_{22} - (C_{11}C_{22} - C_{12}^2)/C_{66} $$, $$ C_{66} = (C_{11} - C_{12})/2 $$, and θ denotes the polar angle measured from the x-axis. Based on the polar coordinate representation shown in Figure 2A, the Young's modulus of the PbSe/PbTe monolayer heterostructure is 61.94N · m⁻¹, significantly lower than common 2D materials such as h-BN (270N · m⁻¹) and graphene ($$ 350 \pm 3.15 $$ N · m⁻¹)^[58,59]. The Poisson's ratio of the PbSe/PbTe heterostructure is 0.307, higher than that of h-BN (0.211) and graphene (0.175)^[58,59]. This indicates that the PbSe/PbTe monolayer exhibits lower stiffness and greater flexibility compared to other common 2D materials. Additionally, the Debye temperature of the PbSe/PbTe monolayer was calculated to be 43.9 K. Compared with the Debye temperatures of BP (500 K)^[60] and h-MoSi₂ (600 K)^[61], the lower Debye temperature of PbSe/PbTe suggests a correspondingly low $$ {\kappa_{{\rm{L}}}} $$.

Figure 2. (A) Young's modulus and Poisson's ratio of the PbSe/PbTe monolayer heterostructure;(B) AIMD results of the 4 × 4 × 1 supercell of PbSe/PbTe monolayer heterostructure at 300 and 700 K. AIMD: Ab initio molecular dynamics.

To further assess the thermal stability of the PbSe/PbTe monolayer heterostructure, AIMD simulations were performed in the NVT ensemble using a 4 × 4 × 1 supercell at 300 and 700 K, with a total simulation time of 10 ps and a time step of 1 fs. The results are presented in Figure 2B, indicating that the total energy remained relatively constant throughout the simulations, and the supercell crystal structure exhibited no distortion or disintegration. These findings confirm the structural stability of the PbSe/PbTe monolayer heterostructure at both room temperature (300 K) and elevated temperature (700 K).

Phonon transport properties

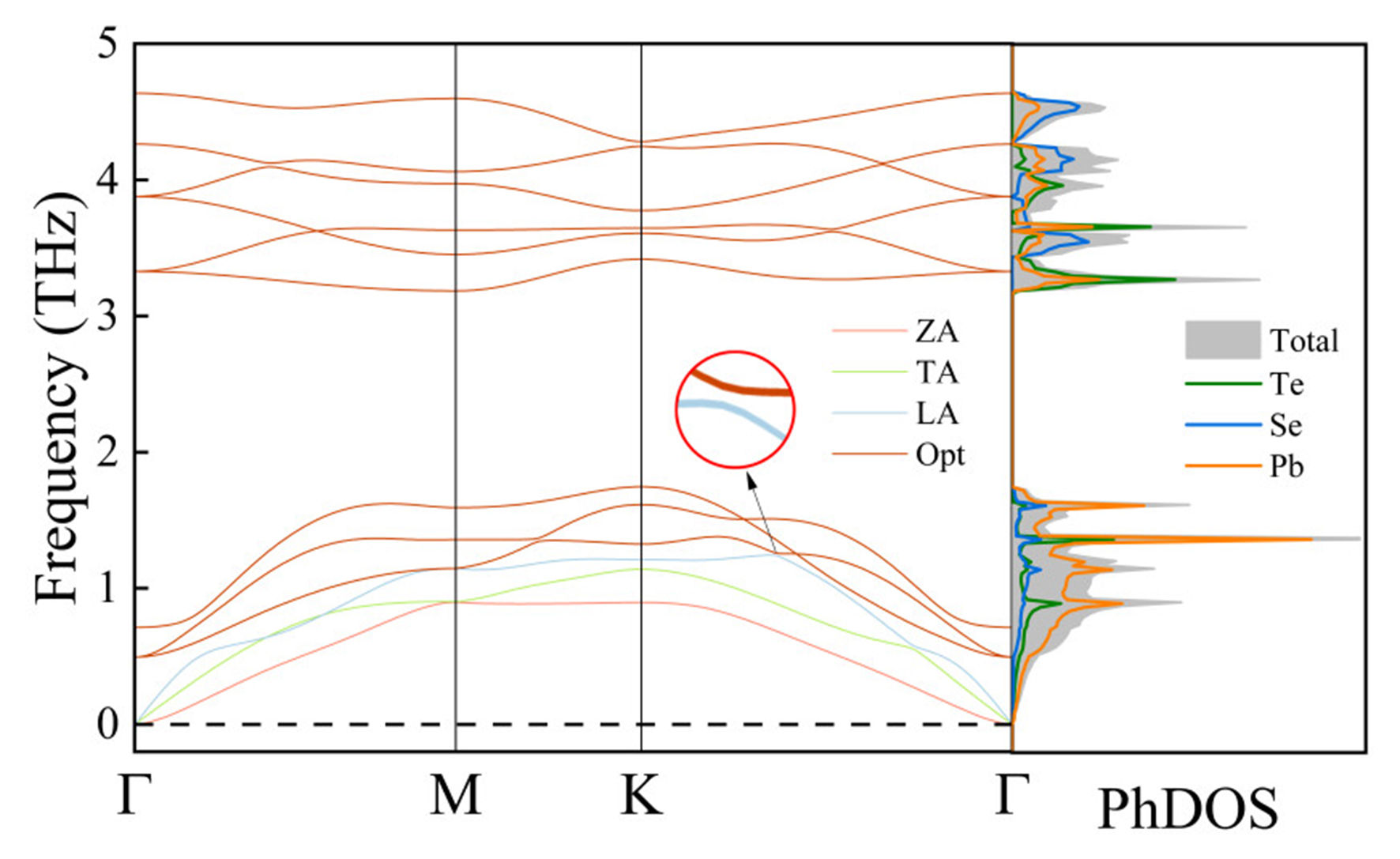
Based on the machine learning MTP method, we systematically evaluated the phonon dispersion characteristics of the PbSe/PbTe monolayer heterostructure. This method achieves a favorable balance between computational accuracy and efficiency, and its effectiveness in thermoelectric materials research has been extensively validated by numerous studies. Moreover, our previous work has confirmed its applicability to similar systems^[50,62]. Furthermore, as shown in Supplementary Figure 4, the phonon dispersion curves of the PbSe/PbTe monolayer heterostructure unit cell calculated using the finite displacement method and the MTP potential exhibit excellent agreement, which fully validates the reliability of the MTP approach employed in predicting the phonon transport properties of the PbSe/PbTe monolayer heterostructure. Figure 3 shows the phonon dispersion relations and corresponding phonon density of states (PhDOS) of the PbSe/PbTe monolayer heterostructure along the high-symmetry path Γ-M-K-Γ. The system comprises three acoustic phonon branches, corresponding to the out-of-plane (ZA), transverse (TA), and longitudinal (LA) vibrational modes, while the remaining nine branches represent optical modes. No imaginary frequencies appear throughout the Brillouin zone, indicating dynamical stability of the structure. Further analysis of the phonon spectrum reveals that the highest phonon frequency of the material is 4.72 THz, significantly lower than typical thermoelectric materials such as ZnSe (~8 THz) and MoS2 (~14 THz)^[63,64]. This low-frequency characteristic typically indicates a reduced $$ {\kappa_{{\rm{L}}}} $$. The acoustic branches are concentrated within the 0-1.2 THz range, whereas the optical branches mainly lie between 1.2 and 4.7 THz, exhibiting a distinct acoustic–optical phonon gap. Notably, the acoustic modes in the phonon dispersion curves show pronounced flatness, especially the ZA branch, whose dispersion is the flattest, implying an extremely low phonon group velocity. It is well known that lower phonon group velocities suppress $$ {\kappa_{{\rm{L}}}} $$. Therefore, the synergistic effects of frequency range, mode coupling, and phonon transport characteristics in the PbSe/PbTe monolayer heterostructure collectively contribute to the effective reduction of $$ {\kappa_{{\rm{L}}}} $$.

Figure 3. Phonon dispersion curves and PhDOS of the PbSe/PbTe monolayer heterostructure. "Opt" represents the optical phonon modes. PhDOS: Phonon density of states.

In the phonon dispersion relations, we clearly observe an avoided crossing between the longitudinal acoustic (LA) branch and the low-energy optical branch along the $$ K−\Gamma $$ path. As shown in Figure 3, the two dispersion curves that would otherwise intersect repel each other and form a small gap, accompanied by a significant reduction in group velocity. This behavior reflects strong coupling and hybridization between the phonon modes. The avoided crossing originates from the interaction between propagating acoustic phonons and low-frequency flat optical modes^[65]. In addition, Pb atoms exhibit dominant vibrational contributions in the low-frequency acoustic region (~0 to 1.7 THz), and their contributions in the mid- to high-frequency optical region (~3.2 to 4.8 THz) are also non-negligible. This phenomenon may originate from the complex vibrational coupling induced by weak Pb–Pb bonds between the top and bottom Pb layers, which enhances both phonon–phonon and acoustic–optical phonon scattering mechanisms, further suppressing $$ {\kappa_{{\rm{L}}}} $$.

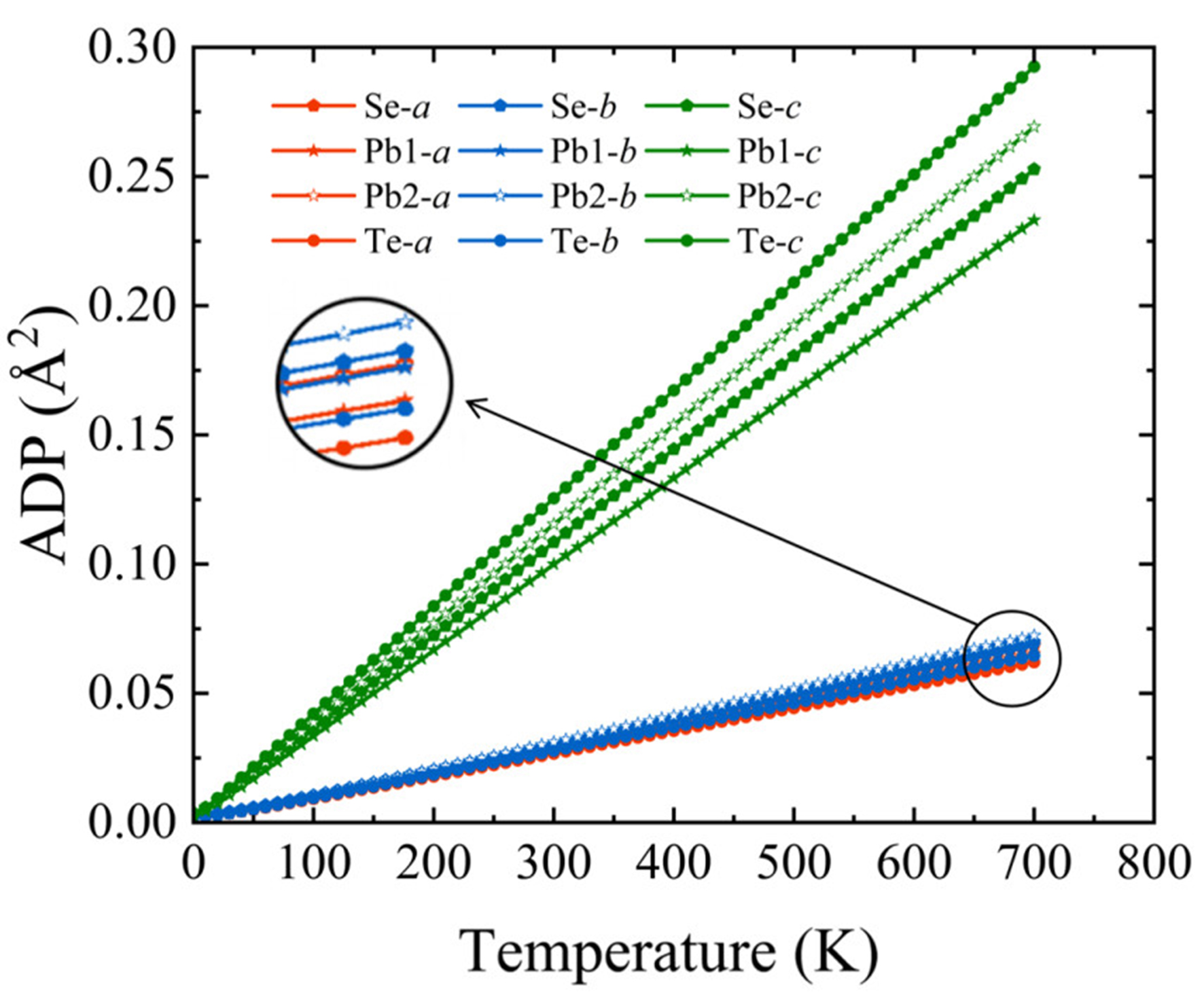
Intense atomic thermal vibrations are often closely related to strong anharmonicity in the crystal structure. To further quantify the degree of anharmonicity and characterize atomic vibrations in the PbSe/PbTe monolayer heterostructure, we computed the anisotropic displacement parameters (ADPs) of atoms along different crystallographic axes. The ADP not only reflects the intensity of atomic vibrations but also indirectly indicates the strength of atomic bonds. When the chemical bonds between atoms are stronger, the amplitude of atomic vibrations is smaller, leading to a lower ADP value. Conversely, when the bonds are weaker, the atomic vibrations are larger, resulting in a higher ADP value. The detailed calculation method of ADPs is provided in the Supplementary Materials. As shown in Figure 4. It is clearly observed that the ADPs along the c-axis are significantly larger than those along the a- and b-axes, indicating more intense thermal vibrations perpendicular to the plane. Specifically, Pb atoms in the top and bottom layers exhibit relatively smaller ADP than Te atoms, which is mainly attributed to their larger atomic mass^[66], whereas the higher ADP values of Te atoms can be ascribed to the weaker bonding strength with surrounding atoms. This finding is consistent with the previous conclusions from ELF and –COHP analyses, indicating weak chemical bonding interactions between Pb and Te, which allows freer atomic thermal motion and thereby enhances the structural anharmonicity.

Figure 4. ADP of different atoms along various directions in the PbSe/PbTe monolayer heterostructure. ADP: Anisotropic displacement parameter.

Overall, the pronounced atomic vibration amplitudes along the c-axis, the local bonding strength heterogeneity, and the large ADP values in the PbSe/PbTe monolayer heterostructure collectively indicate strong anharmonicity of the system, which effectively enhances phonon scattering and consequently significantly reduces the $$ {\kappa_{{\rm{L}}}} $$.

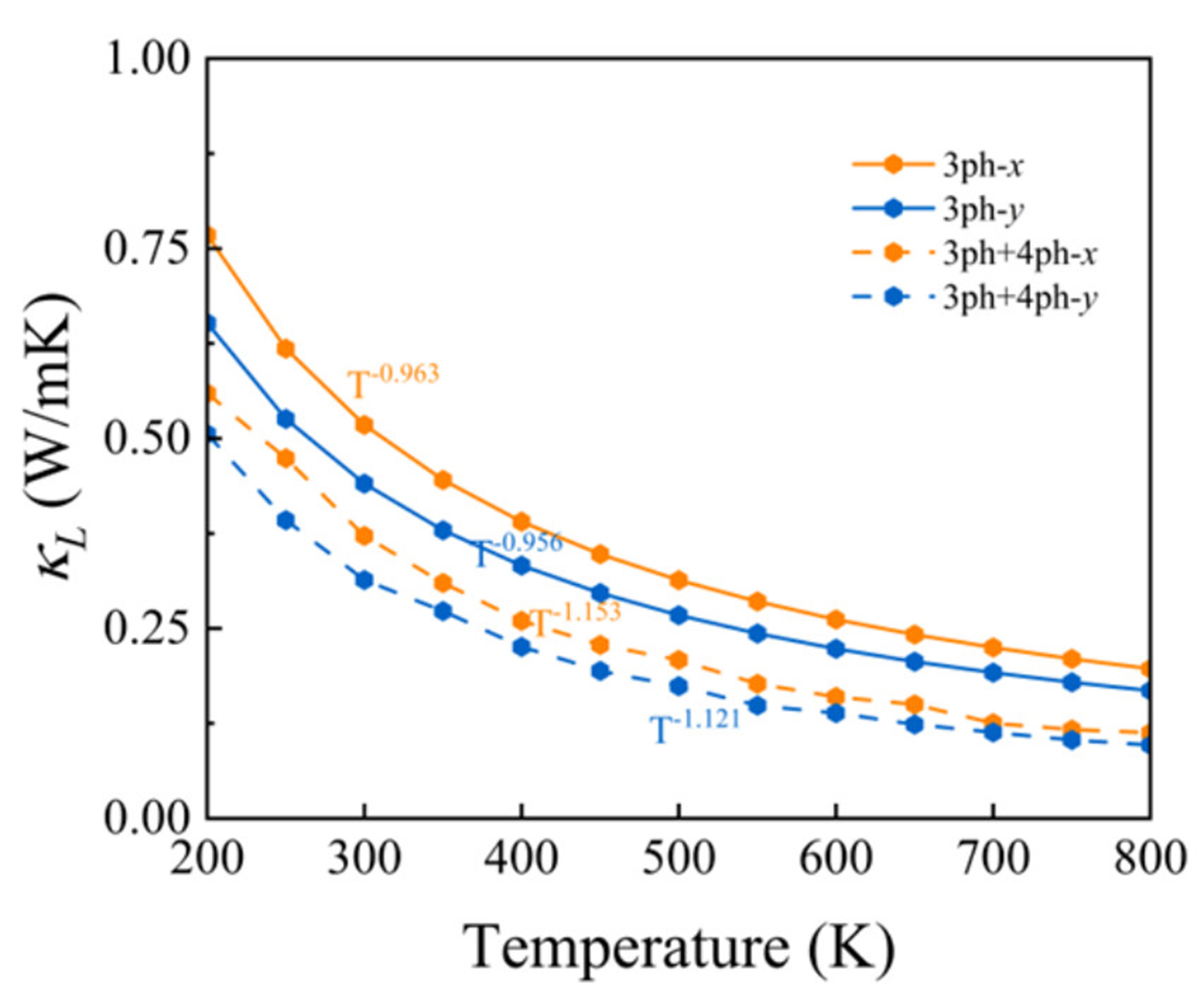
From the previous analyses, it is evident that the PbSe/PbTe monolayer heterostructure exhibits considerable anharmonicity, and we therefore predict that the PbSe/PbTe monolayer heterostructure will possess a low $$ {\kappa_{{\rm{L}}}} $$. To more accurately evaluate the thermal transport properties of the PbSe/PbTe monolayer heterostructure, we introduced a four-phonon scattering model in addition to the three-phonon scattering processes, thereby enabling a comprehensive assessment of phonon-mediated thermal transport. Based on the phonon BTE, the $$ {\kappa_{{\rm{L}}}} $$ can be expressed as^[67]:

Here, $$ C_{kq} $$, $$ v_{kq} $$ and $$ \tau_{kq} $$ denote the mode-specific heat capacity, phonon group velocity, and phonon relaxation time of the k-th phonon branch, respectively. As shown in Figure 5, the temperature dependence of the $$ {\kappa_{{\rm{L}}}} $$ of the monolayer PbSe/PbTe monolayer heterostructure was systematically analyzed under different scattering mechanisms, where the solid lines represent results considering only three-phonon scattering processes, and the dashed lines include the four-phonon scattering mechanism as well. Overall, $$ {\kappa_{{\rm{L}}}} $$ gradually decreases with increasing temperature, which is primarily attributed to the enhanced phonon-phonon scattering strength at elevated temperatures. In particular, the approximately inverse-temperature trend observed here is a well-known signature of resistive phonon–phonon Umklapp scattering, where momentum-relaxing processes increasingly dominate at high temperatures, leading to a phonon mean free path (MFP) that scales roughly as $$ 1/T $$. Such behavior is a typical outcome in ShengBTE calculations when Umklapp scattering is the primary heat-resistance mechanism^[46,68,69]. Due to the pronounced anisotropy of the heterostructure, the $$ {\kappa_{{\rm{L}}}} $$ along the y-direction remains consistently lower than that along the x-direction, reflecting the directional dependence of its lattice dynamical properties. At 300 K, When the three- and four-phonon scattering processes are considered, the thermal conductivities of the lattice $$ \kappa_{\rm L} $$ along the x and y directions are as low as 0.37 and 0.31 W · m⁻¹ · K⁻¹, respectively, representing decreases of approximately 29 % and 10 % compared to 0.52 and 0.44 W · m⁻¹ · K⁻¹ obtained with only three-phonon scattering. This significant reduction is attributed to the introduction of additional energy dissipation channels by four-phonon scattering processes, which further enhance phonon scattering intensity and effectively suppress the increase in thermal conductivity. To further understand the influence of four-phonon scattering, we fitted the temperature dependence of $$ \kappa_{\rm L} $$ using a power-law relationship ($$ \kappa_{\rm L} \sim T^{-\alpha} $$), as shown in Figure 5. In the three-phonon-only case, the extracted exponents are $$ \alpha_{x} = 0.963 $$ and $$ \alpha_{y} = 0.956 $$, which are close to the well-established $$ T^{-1} $$ scaling predicted by the conventional phonon gas model and consistent with Umklapp-limited transport^[70]. This agreement indicates that under three-phonon scattering, the system exhibits relatively weak anharmonicity and maintains well-defined phonon quasiparticles. However, upon including four-phonon scattering, the temperature dependence becomes noticeably stronger, with $$ \alpha_{x} = 1.153 $$ and $$ \alpha_{y} = 1.121 $$. This enhancement reflects the increased phonon-phonon scattering rates at elevated temperatures due to additional anharmonic channels. While the behavior remains consistent with a phonon-mediated transport picture, the stronger temperature sensitivity highlights the importance of higher-order anharmonic interactions. These results underscore the need to include four-phonon processes for accurate thermal conductivity predictions, especially under high-temperature conditions. Therefore, four-phonon scattering plays a crucial role in the thermal transport behavior of the material studied in this work and must be thoroughly considered when accurately evaluating the $$ \kappa_{\rm L} $$. To further elucidate the effect of higher-order scattering processes on $$ {\kappa_{{\rm{L}}}} $$, we analyzed the variation of phonon lifetime (τ), group velocity ($$ v_{g} $$), and specific heat ($$ C_{v} $$) upon inclusion of four-phonon scattering, as presented in Supplementary Figure 5. The results reveal that the introduction of four-phonon processes markedly decreases the phonon lifetime compared to the case with only three-phonon scattering, particularly in the low-frequency region, indicating a substantial increase in scattering rates. In contrast, the phonon group velocity remains nearly unchanged under both scattering conditions, suggesting that it is primarily dictated by phonon dispersion rather than scattering mechanisms. Similarly, the specific heat exhibits negligible variation between the two cases, indicating that the heat capacity is unaffected by the additional scattering channels. These findings demonstrate that the reduction in $$ {\kappa_{{\rm{L}}}} $$ upon inclusion of four-phonon processes mainly stems from the significant shortening of phonon lifetime, while the contributions of group velocity and specific heat remain nearly constant.

Figure 5. Temperature dependence of $$ {\kappa_{{\rm{L}}}} $$ of the PbSe/PbTe monolayer heterostructure along the x and y directions considering three-phonon and four-phonon scattering mechanisms.

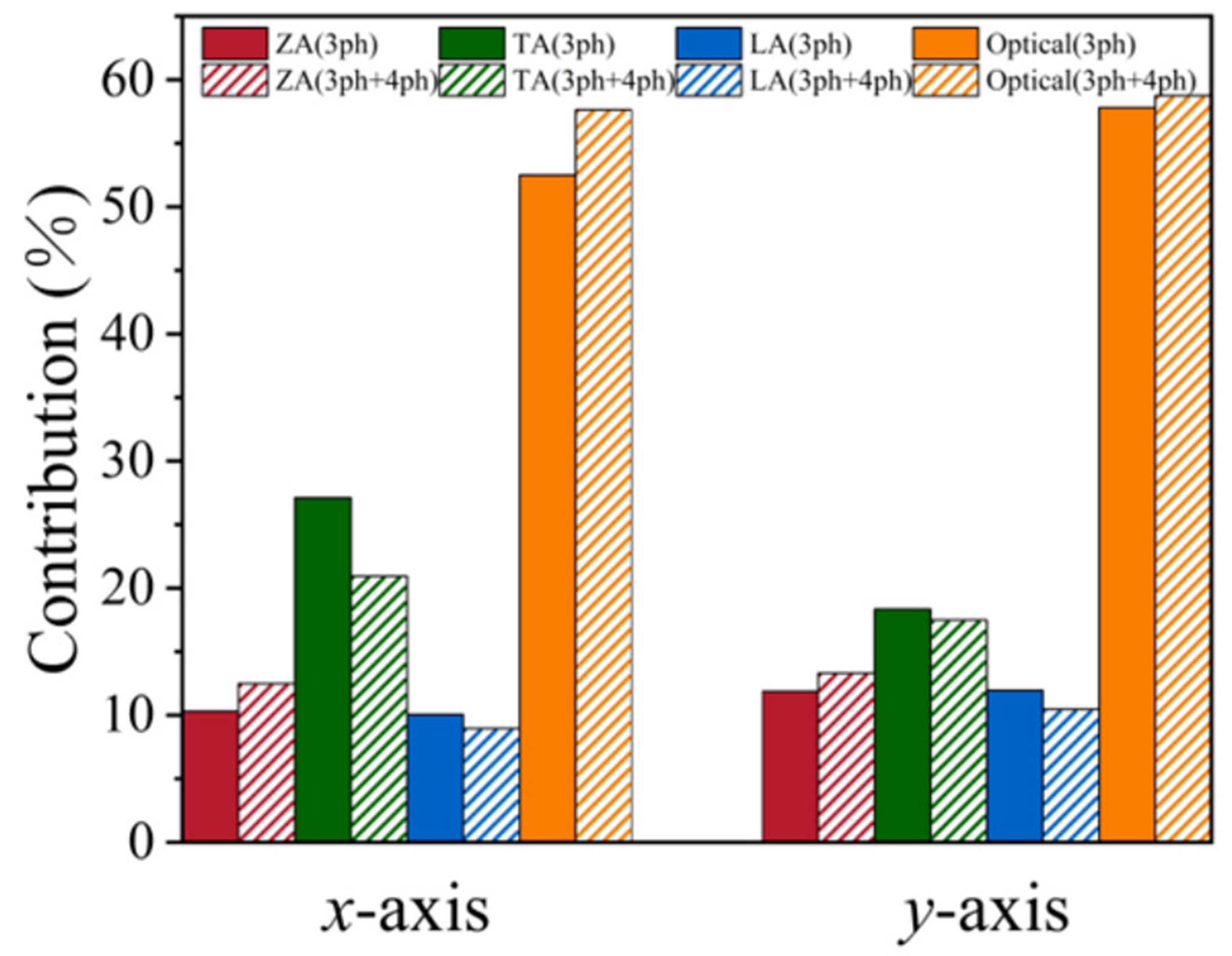
To further elucidate the phonon transport mechanisms in the monolayer PbSe/PbTe monolayer heterostructure, we performed a detailed analysis of the contributions of different acoustic modes (ZA, TA, LA) and optical modes to the total $$ {\kappa_{{\rm{L}}}} $$. As shown in Figure 6, at 300 K, the contributions of each phonon branch to $$ \kappa_{ \rm{L}} $$ were evaluated under both three-phonon scattering only, and the combination of three- and four-phonon scattering models. The results indicate that regardless of the phonon scattering model employed, the contribution of optical branches to the $$ \kappa_{ \rm{L}} $$ consistently exceeds 50 %. Generally, acoustic phonon modes are the primary contributors to $$ \kappa_{ \rm{L}} $$^[71]; however, it is noteworthy that in the PbSe/PbTe monolayer heterostructure, the optical modes play a dominant role. Specifically, under the four-phonon scattering model, the contribution of optical modes along the y-direction can reach up to 58 %. This can be attributed to our subsequent analysis of group velocity and Grüneisen parameters, which reveals that certain optical modes exhibit exceptionally high group velocities exceeding 1.5 km · s⁻¹, even surpassing those of the ZA and TA acoustic modes. This finding challenges the conventional assumption that optical phonons make a minor contribution due to their typically low group velocities. Moreover, the Grüneisen parameters of the optical phonons are moderate and smoothly distributed, indicating limited anharmonicity and relatively weak scattering strength. Although their scattering rates are comparatively high [Supplementary Figure 6], the combination of a high modal density, large group velocities, and controllable anharmonicity renders optical phonons the primary heat carriers in this system.

Figure 6. Contributions of different phonon modes (ZA, TA, LA, and Optical) to $$ {\kappa_{{\rm{L}}}} $$ of the PbSe/PbTe monolayer heterostructure, including four-phonon scattering in both the x and y directions. Solid-filled bars represent results obtained using the three-phonon scattering model, while hatched-filled bars denote results considering four-phonon scattering. ZA: Out-of-plane; TA: transverse; LA: longitudinal.

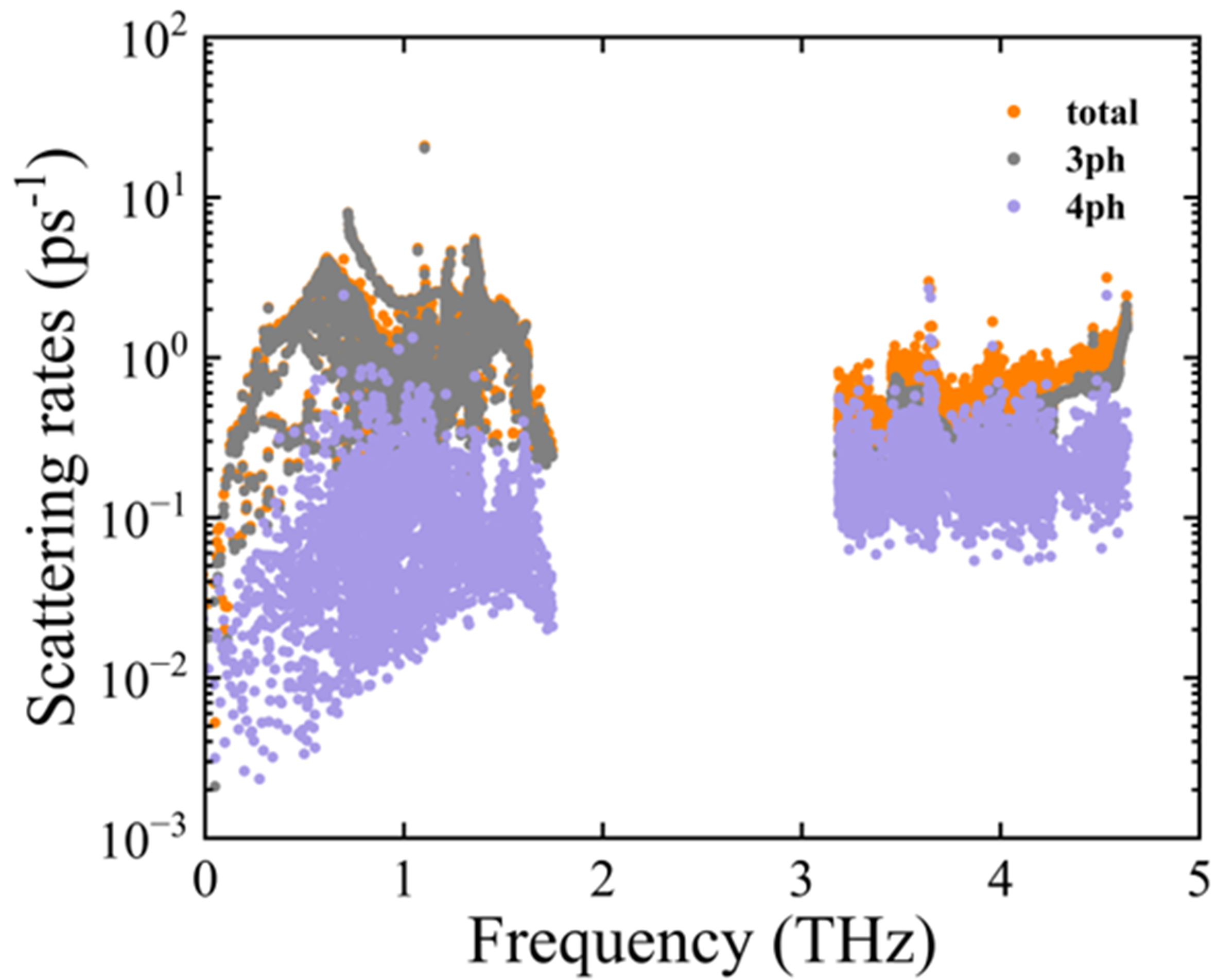
To verify the validity of the phonon quasiparticle picture, we plotted the total phonon scattering rates from 400 to 800 K under the four-phonon scattering model, and included a reference red line corresponding to the breakdown threshold of the quasiparticle picture, defined as $$ 1/\tau_{\rm ph} = \omega_{\rm ph}/2\pi $$. When the total scattering rate exceeds this curve, the phonon lifetime is shorter than its vibrational period, and the quasiparticle description fails^[72]. As shown in Supplementary Figure 7, although a few low-frequency modes exceed this threshold at higher temperatures, the majority of phonon modes remain within an acceptable range, confirming the validity of using the BTE in this study. Next, to gain deeper insight into the low thermal conductivity exhibited by the PbSe/PbTe monolayer heterostructure, we further analyzed its anharmonic phonon-phonon scattering behavior. As shown in Figure 7, the frequency-dependent three-phonon and four-phonon scattering rates of the PbSe/PbTe heterostructure at 300 K are presented. Overall, the anharmonic scattering rates of this material span the range from $$ 10^{-2} $$ to $$ 10^{1} $$ ps⁻¹. Compared to some reported highly anharmonic thermoelectric materials, the scattering rates are significantly higher than those of materials with relatively low anharmonic scattering levels such as GeS^[73], KBaBi^[74] and Na$$ _2 $$TiSb^[75] (which typically exhibit rates below 1 ps⁻¹), indicating the pronounced anharmonicity of the PbSe/PbTe heterostructure.

Figure 7. Frequency-dependent three-phonon and four-phonon scattering rates of PbSe/PbTe monolayer heterostructure.

As the frequency increases, both three-phonon and four-phonon scattering rates exhibit a gradually increasing trend, reaching peaks in certain frequency ranges before stabilizing, with two distinct scattering peaks observed near approximately 0.5 and 1.5 THz, respectively. Based on PhDOS analysis, as shown in Figure 3, the scattering peak around 0.5 THz is primarily attributed to the low-frequency vibrational modes of Pb atoms, where strong coupling occurs between the lowest optical branch and acoustic branches, thereby facilitating enhanced phonon-phonon scattering processes. Although the magnitudes of three- and four-phonon scattering rates are comparable, the latter exhibits significant influence across multiple frequency ranges, indicating that four-phonon scattering is also a critical mechanism governing $$ {\kappa_{{\rm{L}}}} $$ in the anharmonic thermal transport of the PbSe/PbTe monolayer heterostructure. Figure 8A illustrates the scattering channel behavior under three-phonon scattering mechanisms, distinguishing between absorption processes ($$ \lambda+\lambda^{\prime}\rightarrow \lambda^{\prime\prime} $$) and emission processes ($$ \lambda\rightarrow \lambda^{\prime}+\lambda^{\prime\prime} $$). With increasing frequency, the scattering rate of the emission process significantly increases, whereas that of the absorption process exhibits a decreasing trend. This behavior indicates that the large optical phonon gap effectively suppresses the activation of absorption-type three-phonon scattering channels, thereby revealing the complexity of dynamic equilibrium in phonon interactions and energy transfer^[76].

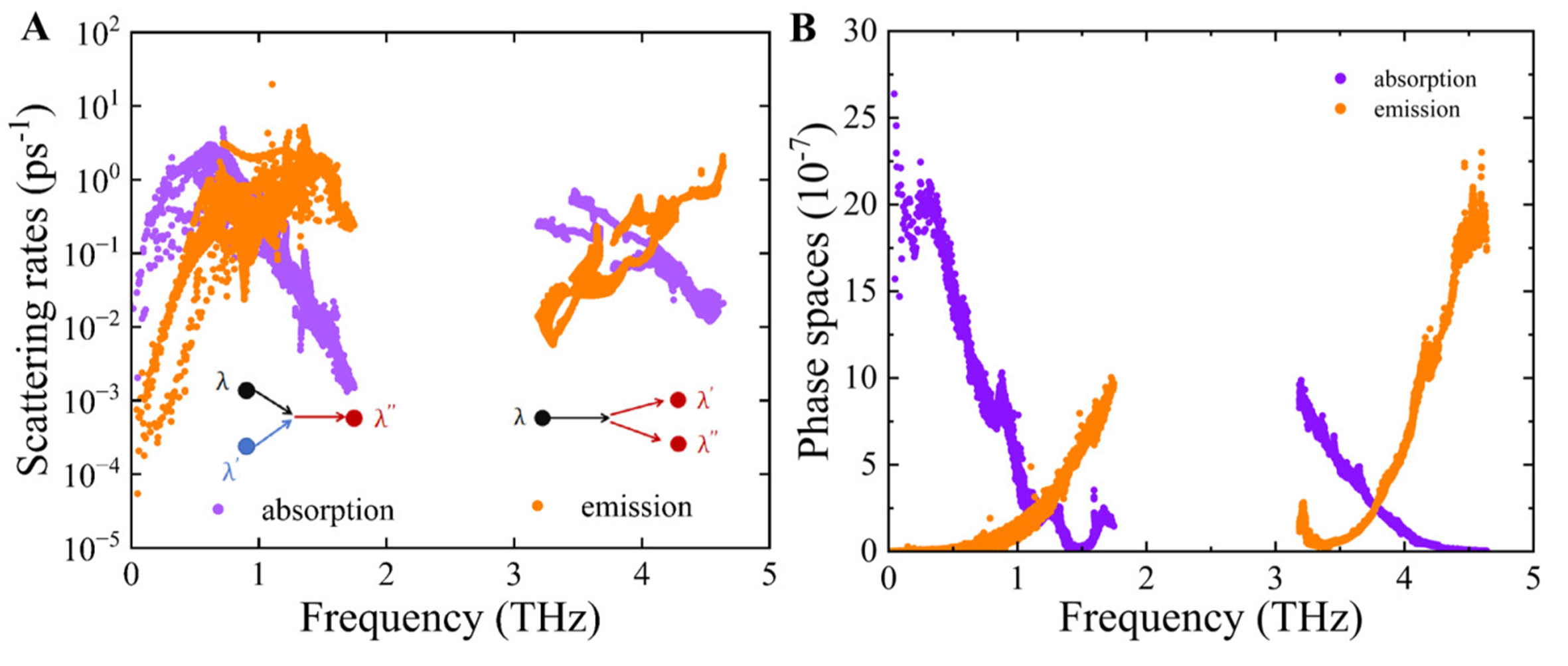
Figure 8. Absorption and emission processes under three-phonon scattering of PbSe/PbTe monolayer heterostructure: (A) scattering rates; (B) phase space as a function of frequency.

To further understand the frequency dependence of these scattering channels, the three-phonon scattering phase space was computed and is presented in Figure 8B, separately for absorption and emission processes. It is evident that in the low-frequency range (0 to 1 THz), the absorption process possesses a broad scattering phase space, while a relatively large emission phase space exists in the high-frequency range (approximately 4 to 4.8 THz). As shown in Figure 3, PhDOS analysis indicates that the low-frequency region is mainly contributed by acoustic modes of Pb atoms, whereas the high-frequency region is dominated by optical vibrations primarily involving Pb and Se atoms. These results suggest that the optical branches involving Pb and Se atoms provide abundant three-phonon scattering channels at high frequencies, which enhances the density of scattering events and plays a critical role in reducing the thermal conductivity.

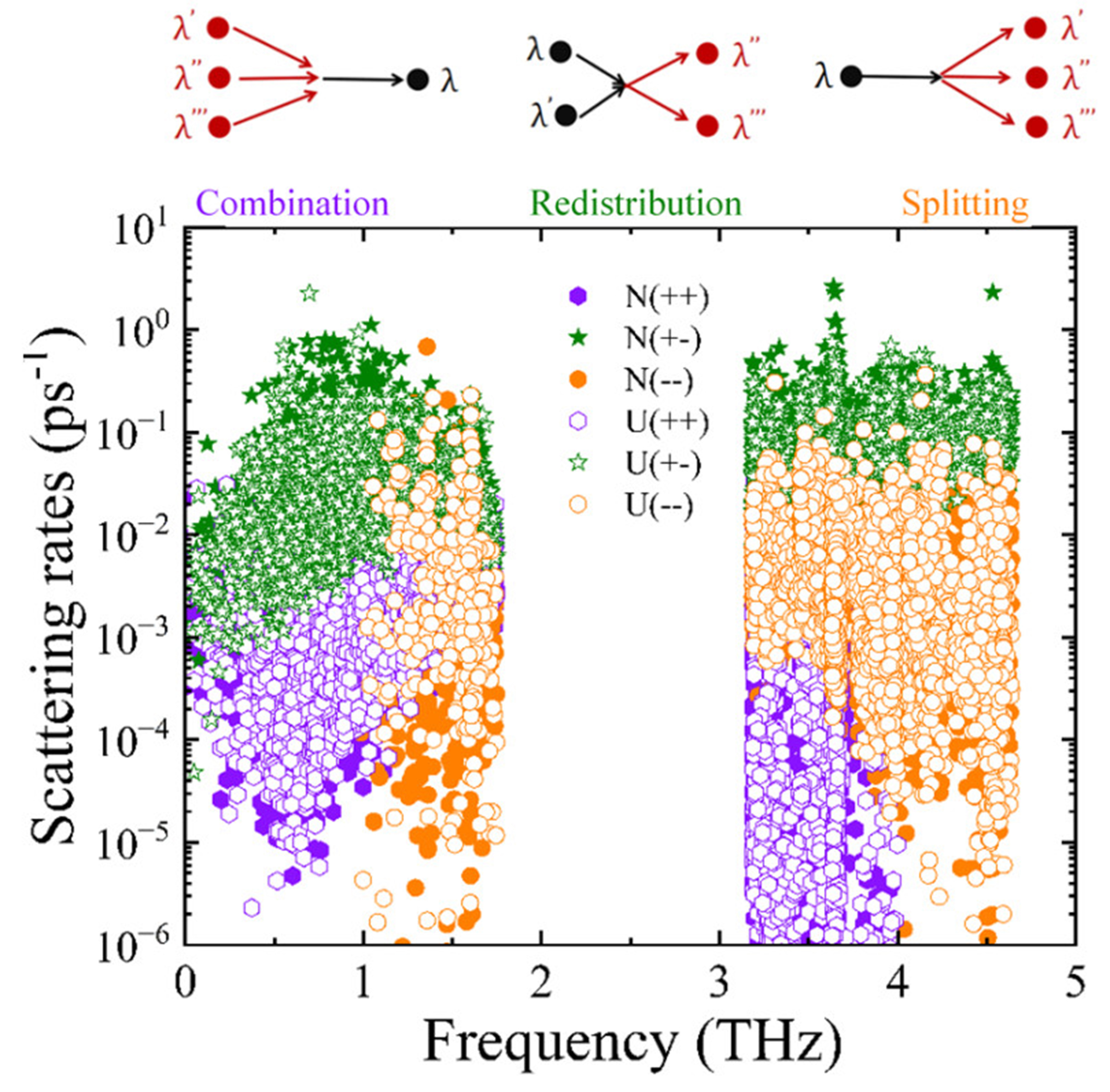
To gain deeper insight into four-phonon scattering mechanisms, we further investigated all possible scattering channels in the monolayer PbSe/PbTe heterostructure. As shown in Figure 9, the four-phonon scattering processes in the PbSe/PbTe monolayer heterostructure include both Umklapp and Normal types. These processes can be classified into three main scattering channels: combination (++ process, $$ \lambda'+\lambda''+\lambda'''\rightarrow \lambda $$), redistribution (+– process, $$ \lambda+\lambda^{\prime}\rightarrow \lambda''+\lambda''' $$) and splitting (—process, $$ \lambda\rightarrow \lambda^{\prime}+\lambda''+\lambda''' $$), where λ represents a phonon mode. It can be observed that the Umklapp and Normal processes contribute comparably. Although normal processes do not directly resist heat flow, they influence thermal conductivity via phonon-momentum redistribution. In contrast, Umklapp processes introduce direct thermal resistance and reduce the $$ {\kappa_{{\rm{L}}}} $$. The Umklapp process clearly dominates the four-phonon scattering contribution in the PbSe/PbTe heterostructure. More importantly, among these scattering events, the redistribution process plays the most significant role. This dominant channel contributes substantially to the ultralow $$ {\kappa_{{\rm{L}}}} $$ observed in the PbSe/PbTe monolayer heterostructure^[77].

Figure 9. Calculated four-phonon scattering rates of PbSe/PbTe heterostructure monolayer as a function of phonon frequency, including three scattering channels: combination (++), redistribution (+-), and splitting (- -). "U" denotes Umklapp processes, while "N" refers to the normal processes.

Moreover, in the PbSe/PbTe monolayer heterostructure, the strong four-phonon scattering is intrinsically associated with the presence of an acoustic-optical phonon band gap, as shown in Figure 3. In the vicinity of the pronounced gap between the acoustic and optical branches (1.7 to 3.2 THz), the available phase space for three-phonon scattering processes is significantly reduced. As illustrated in Figure 8A and B, this leads to a notable suppression of both the three-phonon phase space and the corresponding scattering rates. Specifically, absorption-type three-phonon processes are largely prohibited due to the strict energy conservation constraints imposed by the gap. In contrast, four-phonon processes particularly redistribution and splitting channels remain active near the gap region, as demonstrated in Figure 9. These higher-order interactions are less constrained by energy selection rules and are capable of bridging the phonon band gap, thereby introducing additional anharmonic scattering pathways that are forbidden in the three-phonon regime. This mechanism is further supported by Figure 7, which shows that while the contribution of four-phonon processes is generally lower than that of three-phonon processes in the low-frequency region, a noticeable increase in four-phonon scattering occurs near the gap where three-phonon scattering is substantially weakened. This results in a comparable contribution from both scattering mechanisms in the gap region. These findings highlight the dual role of the phonon band gap: it suppresses conventional three-phonon scattering while simultaneously enhancing the importance of four-phonon interactions. Therefore, the increased activity of four-phonon processes plays a critical role in reducing the $$ {\kappa_{{\rm{L}}}} $$ of the PbSe/PbTe monolayer system.

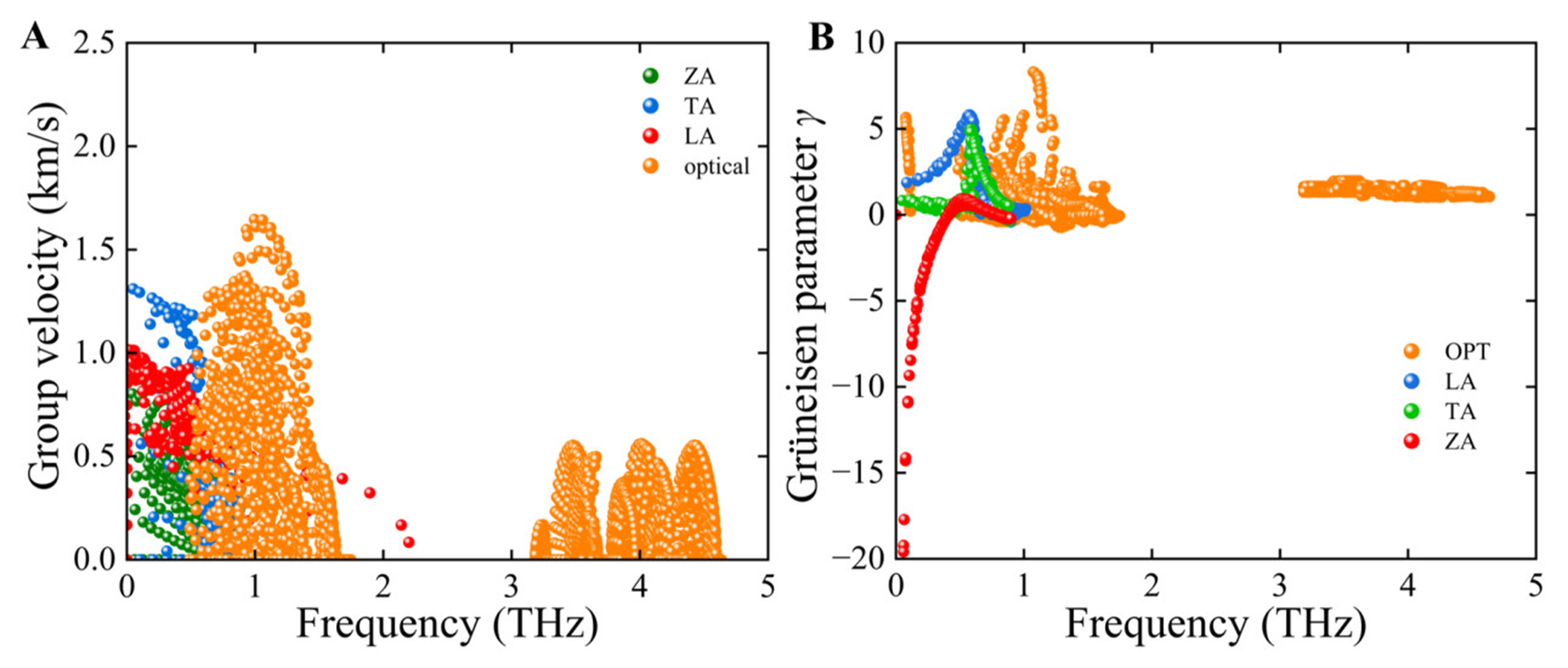
We further calculated the phonon group velocity of the PbSe/PbTe monolayer heterostructure at 300 K based on the standard group velocity expression^[67]:

where $$ \omega_{k}(q) $$ and q denote the phonon frequency and wave vector of the k-th mode, respectively. The calculated results are illustrated in Figure 10A. It is observed that the group velocity of optical modes is significantly larger than that of the acoustic modes. Among the acoustic branches, the ZA mode exhibits the lowest group velocity, which is consistent with our earlier analysis of the phonon dispersion curves. Interestingly, the group velocity of optical phonons near 0.8 THz is comparable to that of acoustic phonons. This phenomenon can be attributed to the presence of weak interatomic bonding and harmonic mixing between optical and acoustic branches. From the mode-resolved thermal conductivity contribution analysis, it is evident that the $$ {\kappa_{{\rm{L}}}} $$ of the PbSe/PbTe heterostructure monolayer is predominantly determined by the optical phonons. Therefore, the group velocity of optical modes plays a crucial role in shaping $$ {\kappa_{{\rm{L}}}} $$. Further analysis reveals that the peak group velocity of the PbSe/PbTe monolayer heterostructure reaches only 1.64 km · s⁻¹, which is significantly lower than that of well-known thermoelectric materials such as PbTe (~1.80 km · s⁻¹) and As₂Ge (~4.5 km · s⁻¹)^[28,78]. Such a low group velocity peak is a typical indicator of low $$ {\kappa_{{\rm{L}}}} $$. The Grüneisen parameter (γ), which quantifies the degree of anharmonicity in a material, can be expressed as^[76]:

Figure 10. (A) Phonon group velocity ($$ v_g $$) and (B) Grüneisen parameter (γ) as functions of phonon frequency for PbSe/PbTe monolayer heterostructure.

Here, $$ \omega_{k} $$ represents the phonon frequency of the k-th mode at the equilibrium volume $$ V_{0} $$. A larger absolute value of the Grüneisen parameter $$ |\gamma| $$ indicates stronger anharmonicity, which typically correlates with lower $$ \kappa_{L} $$. As shown in Figure 10B, the absolute Grüneisen parameter $$ |\gamma| $$ of the PbSe/PbTe monolayer heterostructure at 300 K exhibits relatively high values for both acoustic and optical phonon modes, with a maximum reaching up to 20. This clearly indicates a strong anharmonic phonon scattering behavior in the structure, which is consistent with the previous analyses. Moreover, materials with such pronounced anharmonicity necessitate the inclusion of four-phonon scattering mechanisms in thermal transport evaluations, as their contributions to phonon-phonon scattering and the suppression of $$ {\kappa_{{\rm{L}}}} $$ become non-negligible.

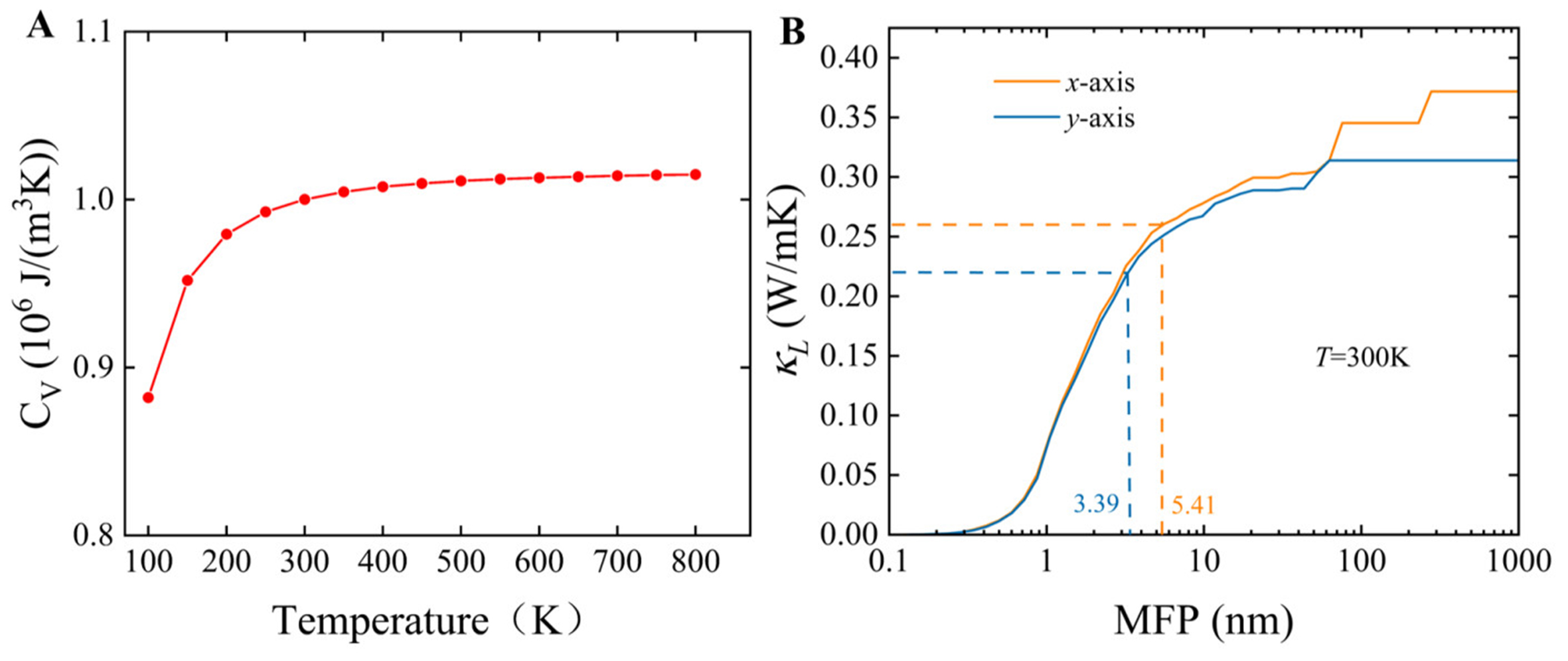
In addition, we evaluated the specific heat capacity $$ C_v $$, another critical parameter influencing the $$ \kappa_{L} $$. As shown in Figure 11A, $$ C_v $$ of the PbSe/PbTe monolayer heterostructure increases gradually with temperature and eventually approaches saturation at high temperatures. Notably, the maximum value of $$ C_v $$ reaches only 1.01×10⁶ J · m⁻³ · K⁻¹, and such a low heat capacity also contributes to the ultralow $$ \kappa_{L} $$ observed in this system. Furthermore, we calculated the phonon MFP of the PbSe/PbTe heterostructure monolayer.

Figure 11. (A) Calculated volumetric heat capacity of PbSe/PbTe heterostructure monolayer as a function of temperature; (B) $$ {\kappa_{{\rm{L}}}} $$ at 300 K vs. phonon MFP. MFP: Mean free path.

As depicted in Figure 11B, the relationship between $$ \kappa_{L} $$ and phonon MFP is illustrated. The critical MFP corresponding to 50 % of the total $$ {\kappa_{{\rm{L}}}} $$ is highlighted. Typically, nanostructures exhibit phonon MFPs under 100 nm^[67]; however, the values of MFP along the x and y directions for the PbSe/PbTe monolayer heterostructure are as small as 5.41 and 3.39 nm, respectively. This indicates that the thermal conductivity in this system is relatively insensitive to dimensional scaling. Therefore, conventional structural engineering strategies such as nanostructuring or polycrystallization may have limited effectiveness in reducing $$ \kappa_{L} $$.

Electronic transport properties

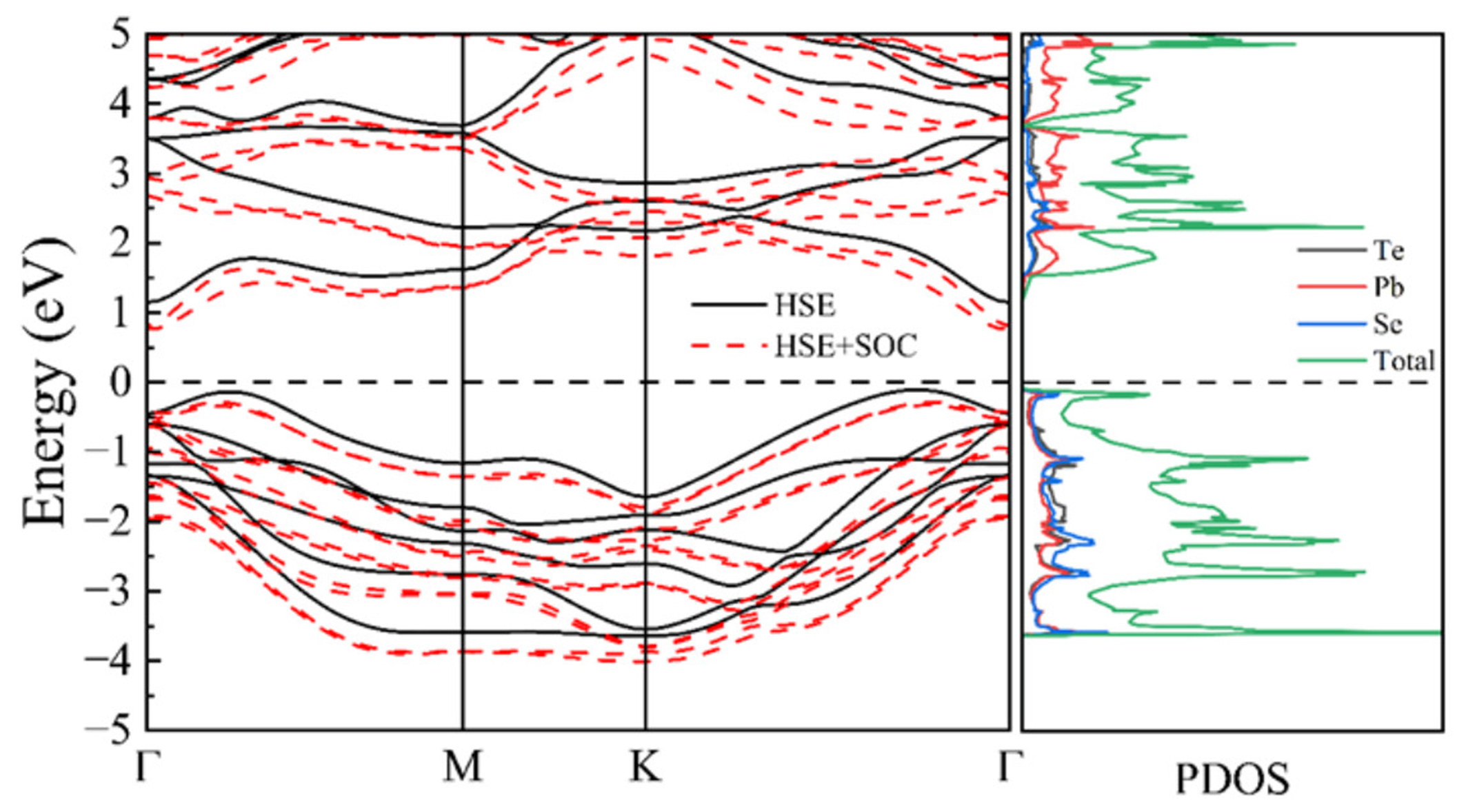
We next analyzed the electronic transport properties of the PbSe/PbTe monolayer heterostructure. Initially, the electronic band structure was calculated using the PBE functional. As shown in Supplementary Table 1 and Supplementary Figure 8, the PbSe/PbTe monolayer heterostructure exhibits a band gap of 0.77 eV, indicating its semiconducting nature. However, it is well known that the PBE functional tends to significantly underestimate band gaps. To obtain more accurate electronic band characteristics, we further performed calculations using the hybrid HSE06 functional. The resulting band structure and DOS are presented in Figure 12. The PbSe/PbTe monolayer heterostructure exhibits an indirect band gap, with the band gap value increasing to 1.25 eV, as listed in Supplementary Table 1. This increase is primarily attributed to the upward shift of the conduction band upon applying the HSE06 method.

Figure 12. Band structures and PDOS calculated using HSE and HSE + SOC methods. PDOS: Projected density of states; HSE: Heyd–Scuseria–Ernzerhof; SOC: spin-orbit coupling.

Moreover, the electronic states near the valence band maximum (VBM) are relatively flat, resulting in a large effective mass that contributes to a high Seebeck coefficient. In contrast, the sharp and highly dispersive nature of the conduction band minimum (CBM) favors high carrier mobility. These intrinsic band characteristics are beneficial for achieving excellent thermoelectric (TE) performance. The projected density of states (PDOS) analysis shows that the CBM is primarily contributed by Pb atoms, while the VBM originates mainly from Se atoms. Additionally, the sharp increase in the DOS near the Fermi level is indicative of a potentially enhanced Seebeck coefficient.

Given the heavy atomic mass of Pb in the PbSe/PbTe heterostructure monolayer, we also considered the influence of spin-orbit coupling (SOC). Upon including SOC in HSE06 calculations, we observed an overall downward shift in the band structure shown in Figure 12. However, the bandgap remains at approximately 1.05 eV, showing no significant deviation from the value without SOC. Therefore, SOC effects can be reasonably neglected in subsequent calculations.

Based on the analysis of the band structure, we predict that the PbSe/PbTe monolayer heterostructure possesses promising electronic transport properties. To quantitatively evaluate this, we calculated the Seebeck coefficient (S) and electrical conductivity (σ) of the PbSe/PbTe heterojunction in the temperature range of 300 to 800 K using the semiclassical BTE as implemented in the BoltzTraP code^[48].

In addition, the rigid band approximation (RBA) was employed to simulate the effect of carrier doping on the electronic performance. The RBA assumes that the overall band structure remains unchanged upon doping, while only the position of the Fermi level shifts accordingly to represent different doping concentrations. These electronic transport properties can be expressed as^[48]:

Here, μ represents the chemical potential, e is the elementary charge of an electron, and f denotes the Fermi-Dirac distribution function of charge carriers. The function $$ \Sigma(\epsilon) $$ refers to the transport distribution function, which is defined as^[48]:

Here, v represents the electron group velocity. The temperature-dependent relaxation time τ is determined based on the deformation potential theory. Considering the dominant role of acoustic phonon scattering, the 2D carrier mobility $$ \mu_{\text{2D}} $$ and the electron relaxation time τ can be determined by^[79]:

Here, $$ C^{\text{2D}} $$ denotes the elastic modulus of the 2D material, defined as:

where ρ is the uniaxial strain applied along the corresponding direction, and S is the cross-sectional area projected along the z-axis. The effective mass $$ m^* $$ along the transport direction is defined as: The effective mass $$ m^* $$ along the transport direction is defined as:

Here, ε denotes the energy of the electronic band, $$ \hbar $$ is the reduced Planck constant, and k represents the electron wavevector. The deformation potential constant E is defined as E = d$$ E_e $$/dρ, where $$ E_e $$ denotes the energy at the band edge, corresponding to the VBM and CBM. The elementary charge is denoted as e, and the geometric mean of the effective masses along the x- and y-directions is given as $$ \sqrt{m_x^* m_y^*} $$. $$ k_B $$ stands for the Boltzmann constant. It should be noted that carrier relaxation times in this study were calculated using the deformation potential theory, which primarily accounts for phonon scattering while neglecting other electronic scattering mechanisms, such as polar phonon and impurity scattering^[80]. Although this may slightly overestimate relaxation times, the error is generally acceptable. The deformation potential approach is widely used due to its computational efficiency and physical relevance, particularly for 2D materials. Given the high computational cost of first-principles electron–phonon coupling calculations including polar optical phonons, the deformation potential approximation offers a practical balance between accuracy and efficiency. Many previous studies have successfully applied deformation potential theory to analyze carrier transport and thermoelectric performance in 2D systems^[50,57,67], making it a reliable tool for preliminary evaluation of carrier mobility and thermoelectric properties^[81]. As summarized in Table 3, a significant difference in carrier mobility is observed between electrons and holes. This trend is consistent with the band structure analysis, indicating that the effective mass of holes is larger than that of electrons. Notably, the high electron mobility in the PbSe/PbTe heterostructure monolayer is comparable to that of MoS2. Furthermore, at 300 K, the relaxation time of electrons is noticeably longer than that of holes, leading to superior electronic transport properties under n-type doping. Both the high electron mobility and the relatively long relaxation time are beneficial for enhanced electrical transport performance.

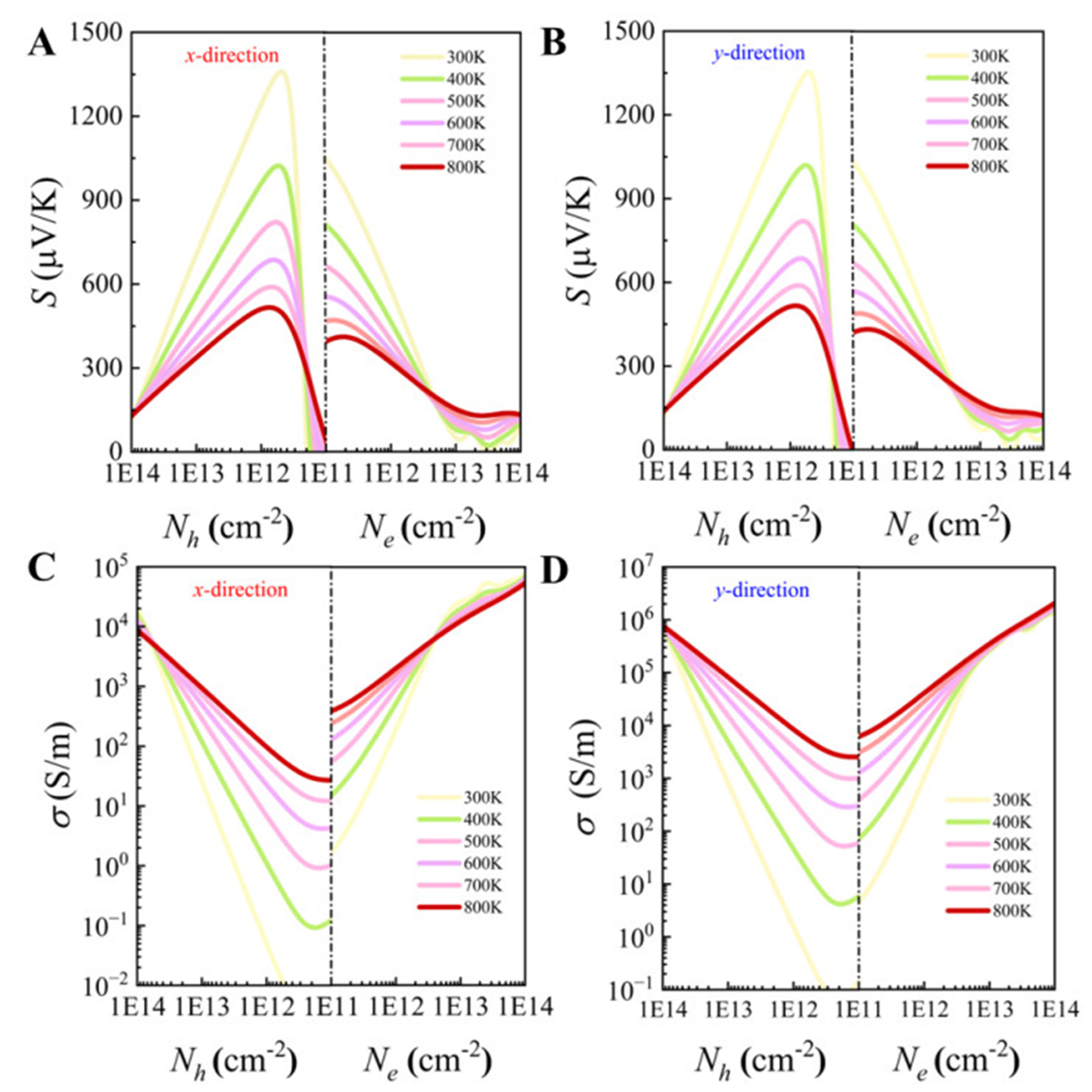
The Seebeck coefficients (S) of p-type and n-type PbSe/PbTe monolayer heterostructures are shown in Figure 13A and B. Clearly, S increases with rising temperature, and the S values for n-type doping are significantly lower than those for p-type doping, which is consistent with our previous analysis of the effective masses at the VBM and CBM. At 300 K, the maximum S values for p-type (n-type) doping along the x and y directions reach $$ 1, 358.6 \, \mu\text{V} \cdot \text{K}^{-1} $$ ($$ 1, 039.1 \, \mu\text{V} \cdot \text{K}^{-1} $$) and $$ 1, 353.6 \, \mu\text{V} \cdot \text{K}^{-1} $$ ($$ 1, 013.2 \, \mu\text{V} \cdot \text{K}^{-1} $$), respectively. To investigate the origin of the extremely large $$S$$, we performed an additional analysis using the 2D degenerate Fermi gas approximation combined with Mott's relation. The results indicate that the extremely high $$S$$ primarily arises from strong energy-selective transport (or energy filtering) under low-doping conditions. Specifically: (1) At extremely low carrier concentrations, the Fermi level lies very close to the band edge, making transport strongly dependent on the energy distribution; (2) A relatively large effective mass increases the DOS near the band edge, enhancing the energy gradient of the DOS; (3) The steep DOS results in a pronounced energy dependence of $$\sigma(E)$$, which, under the Mott relation, greatly enhances $$S$$. The detailed inverse calculation procedure is provided in the Supplementary Materials. Due to the trade-off relationship between S, the concentration-dependent behavior of σ shown in Figure 13C and D exhibits a contrasted trend with that of S. Furthermore, the electrical conductivity of the p-type material is significantly lower than that of the n-type, which aligns with the analysis of carrier concentration. Additionally, σ increases gradually with temperature. The large S leads to relatively low σ in the PbSe/PbTe heterostructure monolayer, with values around 1×10⁵ S · m⁻¹ at optimal doping concentrations.

Figure 13. Seebeck coefficient (S) vs. carrier concentration of PbSe/PbTe monolayer heterostructure along x and y directions in the temperature range 300 to 800 K: (A) p-type; (B) n-type. Electrical conductivity (σ) vs. carrier concentration: (C) p-type; (D) n-type.

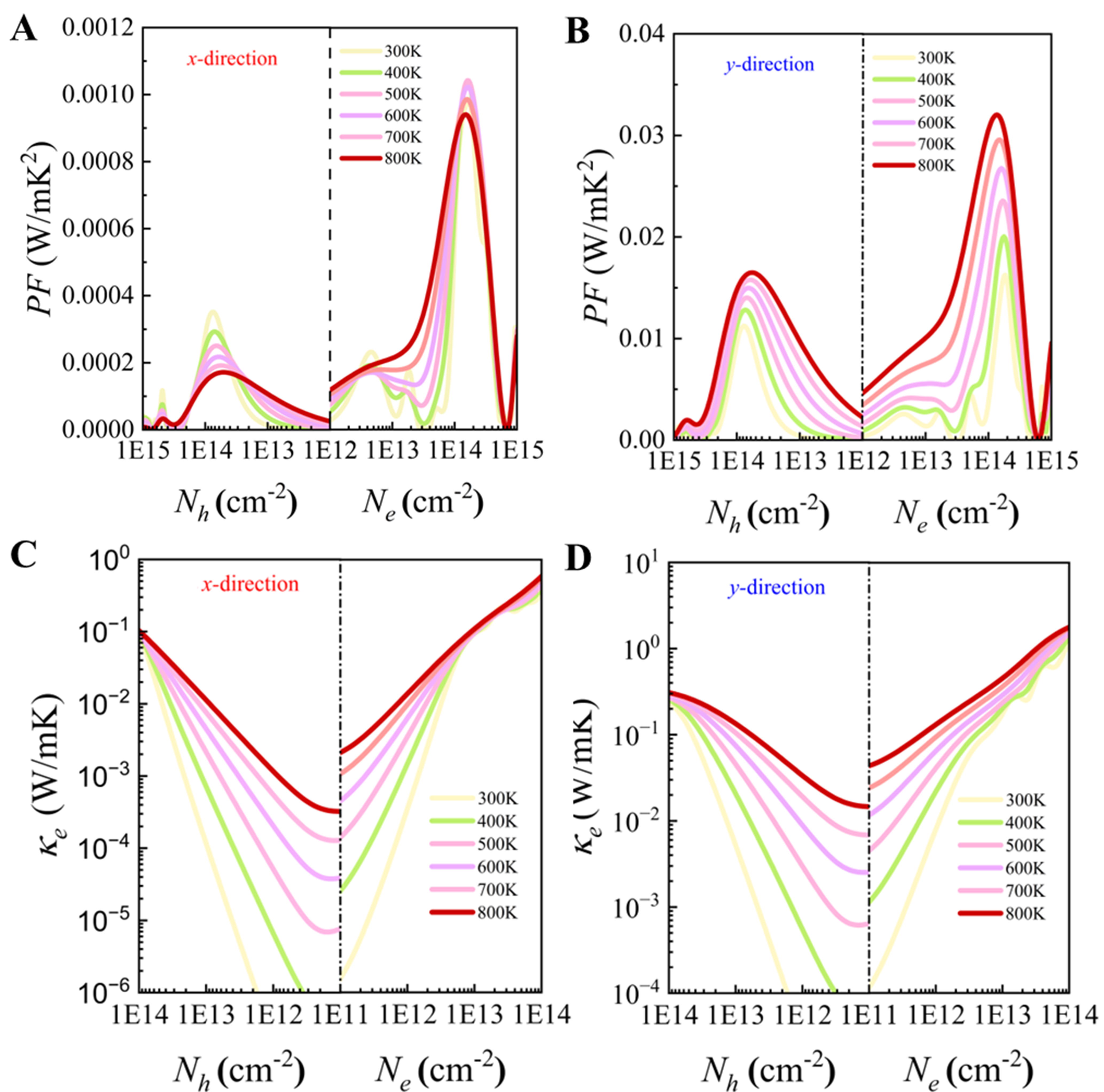
Next, the electronic transport performance of the PbSe/PbTe monolayer heterostructure is evaluated using the power factor. As shown in Figure 14A and B, the values of power factors under n-type doping are significantly higher than those under p-type doping. Moreover, the power factors along the y-direction are evidently greater than those along the x-direction. Specifically, under n-type doping, the power factor in the y-direction reaches a maximum of 0.035 W · m⁻¹ · K⁻², which is much higher than that of common 2D thermoelectric materials such as ZrSn₂N₄ (3.13 mW · m⁻¹ · K⁻²)^[82] and PbTe (~5.861 mW · m⁻¹ · K⁻²)^[83], indicating the superior electronic transport properties of the PbSe/PbTe heterostructure monolayer along the y-direction. The observed asymmetry in power factor enhancement between n-type and p-type doping can be attributed to their distinct electronic structures, as previously discussed. The VBM exhibits a relatively flat dispersion, resulting in a larger effective mass for holes, which is favorable for achieving a high Seebeck coefficient. In contrast, the CBM is more dispersive and sharper, leading to a smaller effective mass for electrons and, consequently, higher carrier mobility. This fundamental difference in band curvature underlies the disparity in power factor between n-type and p-type doping. Moreover, the transport parameters listed in Table 3 quantitatively support this interpretation. The effective mass of n-type carriers is only 0.122 m₀ in both directions, significantly lower than that of p-type carriers, which ranges from 0.531 m₀ to 0.627 m₀. As a result, the mobility of n-type carriers reaches 1,126.8 and 1,243.0 cm² · V⁻¹ · s⁻¹ along the x and y directions, respectively - substantially exceeding the mobilities of p-type carriers (118.87 and 240.95 cm² · V⁻¹ · s⁻¹). Additionally, the relaxation time (τ) of n-type carriers is generally longer, further enhancing their transport properties. Although the deformation potential constant (E) of n-type carriers is slightly higher, the advantages in effective mass and relaxation time compensate for this, yielding superior overall mobility. In summary, the lower effective mass, enhanced mobility, and longer relaxation time of n-type carriers collectively account for the more pronounced power factor enhancement observed under n-type doping.

Figure 14. Power factor vs. carrier concentration of PbSe/PbTe monolayer heterostructure along x and y directions in the temperature range 300 to 800 K: (A) p-type; (B) n-type. Electronic thermal conductivity ($$ \kappa_e $$) vs. carrier concentration: (C) p-type; (D) n-type.

The electronic thermal conductivity ($$ \kappa_e $$) is calculated according to the Wiedemann-Franz law^[84]:

where L is the Lorenz number, σ is the electrical conductivity, and T is the temperature. As an important component of the total thermal conductivity, $$ \kappa_e $$ cannot be neglected at high carrier concentrations and may even dominate the heat transport. Figure 14C and D shows that the variation trend of $$ \kappa_e $$ with carrier concentration is consistent with that of σ, and $$ \kappa_e $$ increases with rising temperature. Additionally, the electronic thermal conductivity under n-type doping is significantly higher than that under p-type doping, which may result in lower ZT values for p-type materials. However, due to the overall low electrical conductivity of the PbSe/PbTe monolayer heterostructure, its electronic thermal conductivity remains relatively small, below 10 W · m⁻¹ · K⁻¹, which helps enhance the thermoelectric performance of the material.

Thermoelectric figure of merit

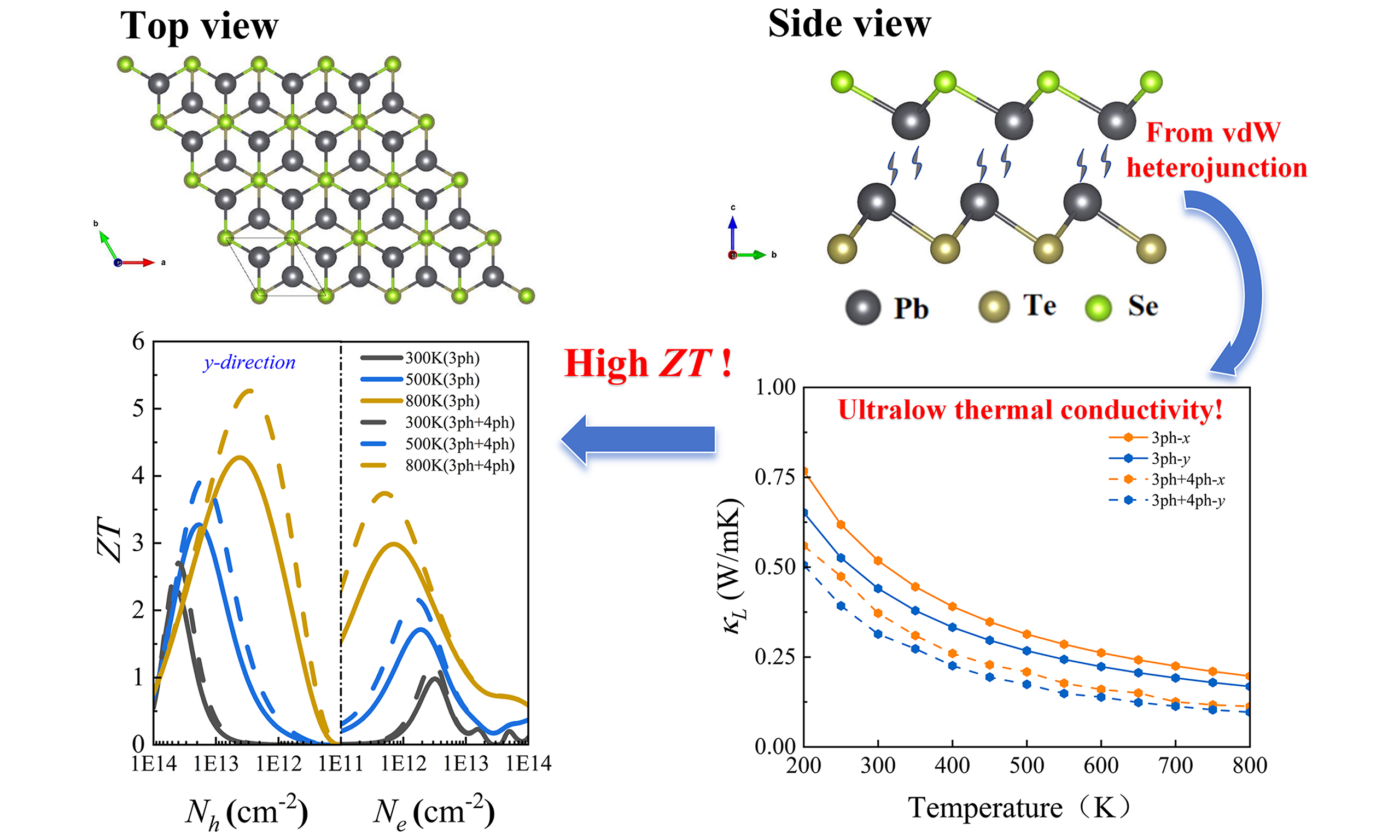
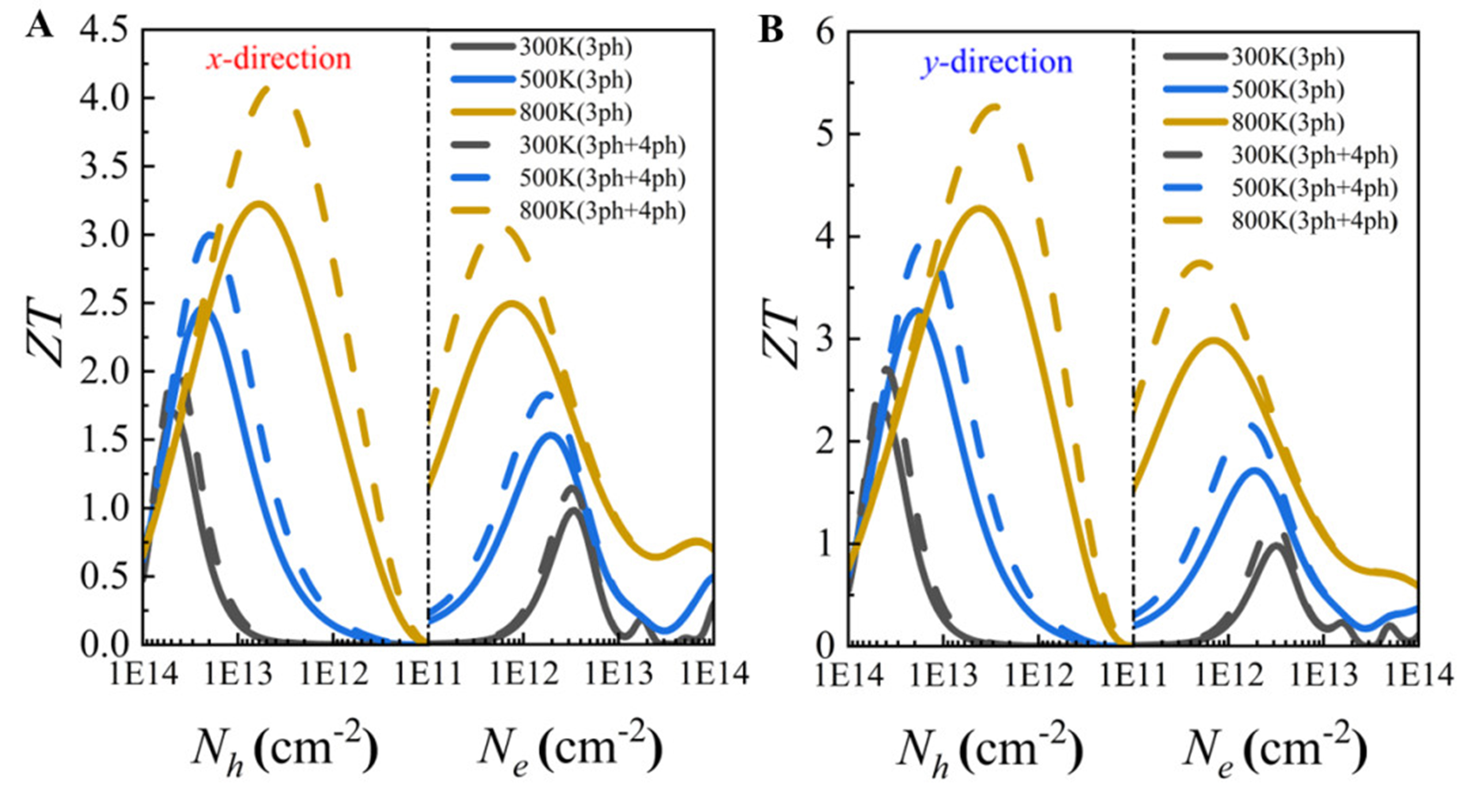
Combining its ultralow $$ {\kappa_{{\rm{L}}}} $$, moderate electronic thermal conductivity, and excellent power factor, we further evaluated the thermoelectric ZT of the PbSe/PbTe monolayer heterostructure. As shown in Figure 15, the variation of ZT with carrier concentration at 300, 500, and 800 K is presented considering both three-phonon (solid lines) and four-phonon (dashed lines) scattering mechanisms.

Figure 15. Thermoelectric figure of merit ($$ ZT $$) of PbSe/PbTe monolayer heterostructure as a function of carrier concentration along (A) x and (B) y directions at 300, 500, and 800 K. Solid lines represent results with only three-phonon scattering; dashed lines include four-phonon scattering.

The results reveal pronounced anisotropic thermoelectric transport behavior, with the ZT values under p-type doping significantly higher than those under n-type doping. This is primarily attributed to the increased electronic thermal conductivity under n-type conditions, which suppresses the enhancement of ZT. Moreover, the inclusion of four-phonon scattering mechanisms improves the accuracy of the calculated thermoelectric performance. At 800 K, the maximum ZT values along the x and y directions under p-type doping reach 4.1 and 5.3, respectively - an increase of approximately 23 % compared to the values considering only three-phonon scattering (3.2 and 4.3). For n-type doping, the ZT values also increase from 2.5 (x direction) and 2.9 (y direction) to 3.1 and 3.7, respectively, further confirming the critical role of four-phonon scattering in accurately evaluating thermoelectric performance.

Notably, the optimal ZT value of the PbSe/PbTe monolayer heterostructure is 5.3, occurring at 800 K under p-type doping along the y-direction, which is significantly higher than the corresponding values for pure monolayer PbTe (1.55) and PbSe (1.3), highlighting the effectiveness of heterostructure design in substantially enhancing thermoelectric performance. Overall, the PbSe/PbTe heterostructure monolayer exhibits outstanding thermoelectric properties at high temperatures, achieving the maximum ZT within the carrier concentration range of 10¹² cm⁻² to 10¹³ cm⁻², demonstrating good experimental feasibility and practical application potential.

Moreover, due to the weak interlayer interactions in the PbSe/PbTe monolayer vdW heterostructure, previous studies have indicated the potential for tuning its electronic structure via cross-plane compressive strain. It has been reported that such strain may modify the band structure and band alignment, thereby influencing carrier effective masses and transport properties^[85,86]. Although this work does not directly investigate the effects of cross-plane compressive strain, based on these studies, we believe this tuning mechanism holds promise for optimizing the electronic performance of PbSe/PbTe heterostructures and warrants further exploration in future research.