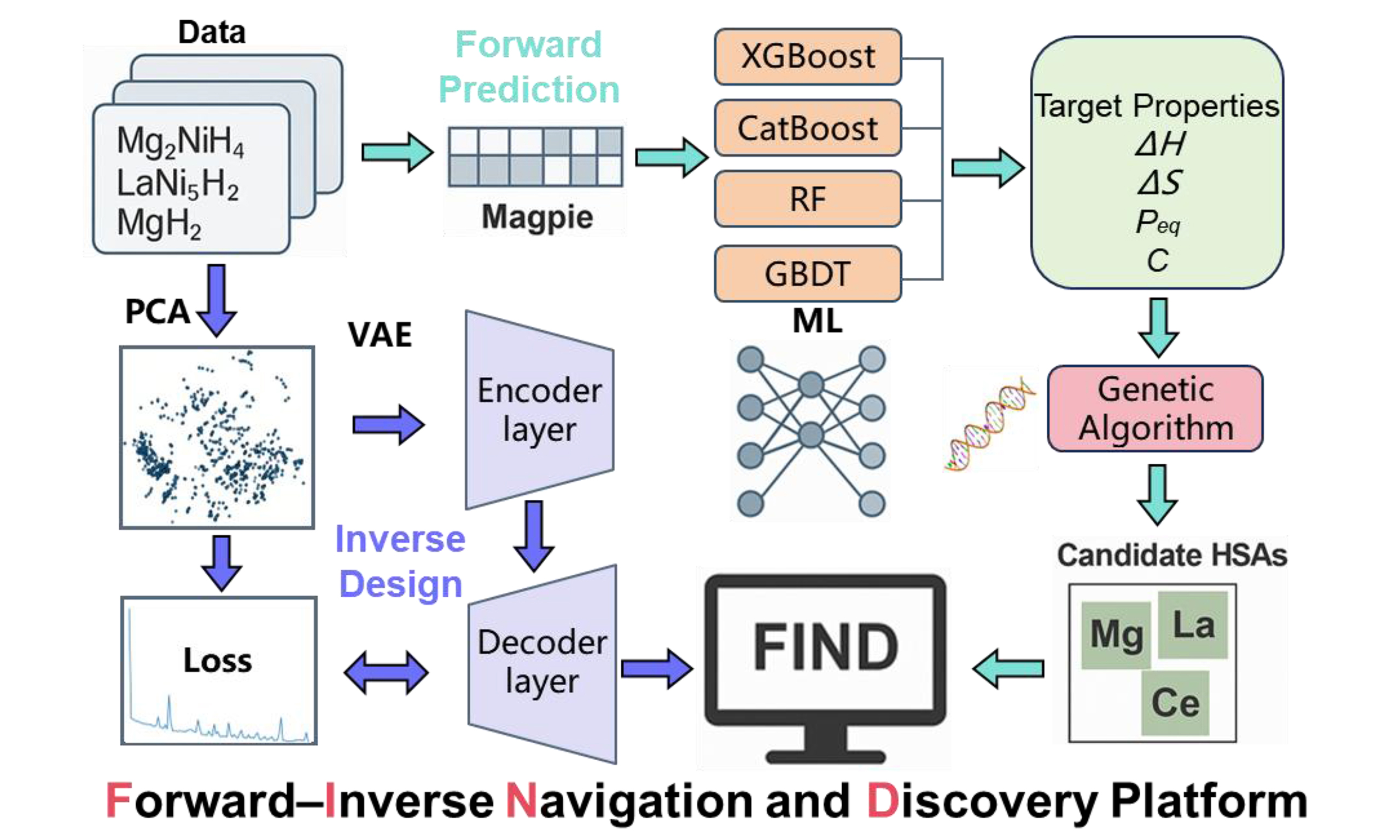
FIND: a forward–inverse navigation and discovery platform for hydrogen storage alloys powered by data-driven machine learning
Abstract
High-performance solid-state hydrogen storage alloys are among the key factors enabling the widespread application of hydrogen energy. However, current materials still face challenges such as limited hydrogen storage capacity and excessive thermodynamic stability, which urgently need to be addressed. In this work, we constructed a large-scale solid-state hydride database, encompassing over 1,000 alloy systems and more than 6,000 valid data records. By integrating alloying strategies with machine learning (ML) techniques, the Magpie tool was utilized for feature generation, and a multi-objective regression model was developed to simultaneously predict absorption/desorption plateau pressure, enthalpy change, entropy change, and maximum hydrogen storage capacity using various ML algorithms. Furthermore, we achieved the inverse design of solid-state hydrogen storage materials using a variational autoencoder. By integrating the forward prediction and inverse design models, we developed a forward–inverse navigation and discovery platform for hydrogen storage alloys powered by data-driven ML: FIND. The forward module enables rapid prediction of absorption and desorption properties based on alloy composition and testing temperature. Building upon this, an advanced function allows fast prediction for multicomponent systems with flexible molar ratios. Subsequently, the inverse module facilitates the screening of potential alloy candidates based on user-defined target properties. Finally, the predictive models were integrated with a genetic algorithm to optimize alloy compositions within the Mg–Ni–La–Ce and Mg–Ni–La systems. Multiple novel high-performance alloy candidates were identified, providing a powerful tool and methodological foundation for high-throughput screening and intelligent development of hydrogen storage materials.
Keywords
INTRODUCTION
To enable large-scale application of hydrogen energy, the development of efficient and safe hydrogen storage materials remains one of the critical bottlenecks. Research in this area is of great significance for promoting the transition to clean energy[1-3]. Consequently, the development of high-performance hydrogen storage materials has become a research hotspot in the field of energy materials. Over the past decades, the study of hydrogen storage materials has primarily relied on traditional approaches, such as empirical experimental screening[4-8], thermodynamic modeling[9-11], and density functional theory (DFT) calculations[12-17], all of which have played crucial roles in advancing the understanding and development of hydrogen storage systems[18]. Regarding the ideal properties of hydrogen storage materials, the U.S. Department of Energy (DOE) has proposed specific requirements for onboard hydrogen storage systems in commercial vehicles, including a hydrogen content of 6.5 wt%, operating pressure of 5-12 bar, temperature around 85 °C, and the material must be able to withstand multiple cycles without degradation (> 1,000 cycles)[19].
Liu et al. employed alloying experiments to enhance the hydrogen storage performance of Ti-Fe-Zr-Mn-
In recent years, informatics approaches have been increasingly applied in the field of materials science[20]. Machine learning (ML) algorithms enable rapid prediction by learning from previously untapped historical data. Announced in 2011, the Materials Genome Initiative (MGI) aims to integrate data science into the research, synthesis, and innovation of materials. As a discipline that applies informatics methods to address materials science problems, materials informatics has emerged as the fourth paradigm of materials research[21]. In the development of solid-state hydrogen storage alloys, researchers have already made substantial progress using ML models. For example, Lu et al. combined ML with DFT to predict and investigate the dehydrogenation enthalpy of V-Ti-Cr-Fe alloys[22]. They developed an extreme gradient boosting (XGBoost) model with feature selection, achieving relative prediction errors below 15% for most of the data. Suwarno et al. applied ML techniques to study the performance of AB2-type hydrogen storage alloys[23]. Their results indicated that the elements Ni, Cr, and Mn significantly affect hydrogen storage performance: Ni governs the formation enthalpy of hydrides, Cr is a key determinant of the C14 Laves phase fraction, and Mn influences hydrogen storage capacity. Dong et al. constructed a database of Mg-based alloys and their hydrogen storage properties, which was used to train various ML regression models predicting maximum absorption capacity and maximum desorption capacity[24]. These models achieved high predictive accuracy, with coefficient of determination (R2) values of 0.947 and 0.922 on the test sets, respectively. In addition, researchers have investigated the relationships between structural and chemical parameters and hydrogen storage performance[25-28]. In addition, other researchers have conducted extensive investigations at the intersection of materials informatics and hydrogen storage materials[29-34]. These studies investigate material systems, data, and modeling to reveal relationships among composition, structure, and thermodynamic properties. They demonstrate the feasibility of ML in solid-state hydrogen storage and guide our model development and evaluation.
Data is at the core of ML, and in many cases, simple models trained on large datasets outperform complex models trained on limited data[35]. The HydPARK dataset, released by the U.S. DOE, is a well-known and widely recognized database of metal hydrides, which has served as a foundation for numerous studies[20,36,37]. For instance, Wilson et al. expanded the HydPARK dataset by extracting data from research articles and patents, adding 462 new compositions along with their H2 wt% values at specific absorption temperatures[36]. This enhancement reduced the mean absolute error (MAE) of their model from 0.31 to 0.29 and improved the R2 score from 0.77 to 0.79. Rahnama et al. used ML to investigate the publicly available HydPARK dataset, finding that magnesium-based hydrides exhibited the highest potential hydrogen weight percentages[20]. Hattrick-Simpers et al. developed regression models to predict hydrogenation enthalpy based on the existing HydPARK alloy data, achieving a MAE of 8.56 kJ/mol and a mean relative error of 28%[37]. Their work preliminarily identified 6,110 candidate alloys that meet hydrogen compressor standards. It is worth noting that the HydPARK dataset encompasses a wide range of intermetallic and complex hydride materials and has served as an important resource for hydrogen storage research. In 2019, Witman et al. developed a ML–ready version of the HydPARK database by cleaning and standardizing the original dataset, thereby significantly improving its quality[38]. More recently, the database has been further updated to include additional data on a broader set of alloy compositions (https://zenodo.org/records/10680097). These efforts have greatly enhanced the accessibility and reliability of HydPARK for ML applications. More importantly, although numerous researchers have developed high-performance ML models based on datasets such as HydPARK, a publicly accessible and integrated materials design platform incorporating these models has yet to be established. As a result, most studies have focused on enhancing model performance itself, while systematic tool support for scientific and industrial applications remains insufficient. In addition, a major challenge in materials design - the inverse design problem - remains unresolved. While most research focuses on forward prediction (predicting properties from compositions), deducing compositions from target properties lacks general, accurate, and scalable methods. Building a stable, practical inverse design framework is a key scientific challenge. To advance intelligent design of solid-state hydrogen storage materials, a publicly accessible platform integrating predictive and optimization capabilities for both forward and inverse design is urgently needed, with dynamic model updates from new data.
In this study, we compiled and curated authoritative data published from 2001 to 2024, encompassing a comprehensive dataset of solid-state hydrogen storage alloys developed via alloying strategies. The resulting database is characterized by improved completeness and high reliability. Based on this dataset, we utilized the Magpie tool[16] for feature generation and integrated ML models to construct a multi-objective prediction framework. For the first time, this framework simultaneously investigates both hydrogen absorption and desorption properties of solid-state hydrogen storage alloys, including plateau pressure, enthalpy change, entropy change, and maximum hydrogen storage capacity. In addition, the variational autoencoder (VAE) model was employed in this study for the inverse design of hydrogen storage materials. Therefore, we developed a forward–inverse navigation and discovery platform for hydrogen storage alloys powered by data-driven ML: FIND. Based on this powerful FIND platform and genetic algorithm (GA), we discovered 27 unreported alloy compositions with the dehydrogenation temperature range of 533.5 to
MATERIALS AND METHODS
Thermodynamic data collection and processing
To systematically collect experimental data closely related to the thermodynamic properties of solid-state hydrogen storage materials, this study utilized authoritative literature databases such as Web of Science. Keywords including “solid-state hydrogen storage”, “thermodynamic properties”, “AB5”, “AB2”, “V-based”, and “Mg-based” were employed to retrieve relevant publications. Through a rigorous manual screening process, approximately 400 publications highly relevant to the thermodynamic characteristics of solid-state hydrogen storage alloys were identified. The full-text PDFs and supporting information of these publications were downloaded for subsequent data extraction and database construction. The DOIs of all references included in the FIND database are provided in Supplementary Table 1. The collected data span representative systems such as rare-earth-based alloys, TiFe/TiMn-based alloys, V-based alloys, and Mg-based hydrogen storage alloys.
In this study, we focused on collecting several core parameters closely related to the thermodynamic performance of solid-state hydrogen storage alloys. These parameters include the material chemical composition, experimental temperature, plateau pressures for both hydrogen absorption and desorption, enthalpy change (ΔH), entropy change (ΔS), and maximum hydrogen storage capacity. For numerical values explicitly reported in the literature, we directly extracted and compiled the data. For incomplete data entries, mean imputation based on unsupervised clustering was employed. Additionally, unknown enthalpy and entropy values were estimated using the van’t Hoff equation[39]:
where K is the equilibrium constant, ΔH represents the standard enthalpy change (J/mol), ΔS indicates the standard entropy change [J/(mol·K)], R stands for the gas constant [8.314 J/(mol·K)], and T signifies the temperature (K).
Feature generation
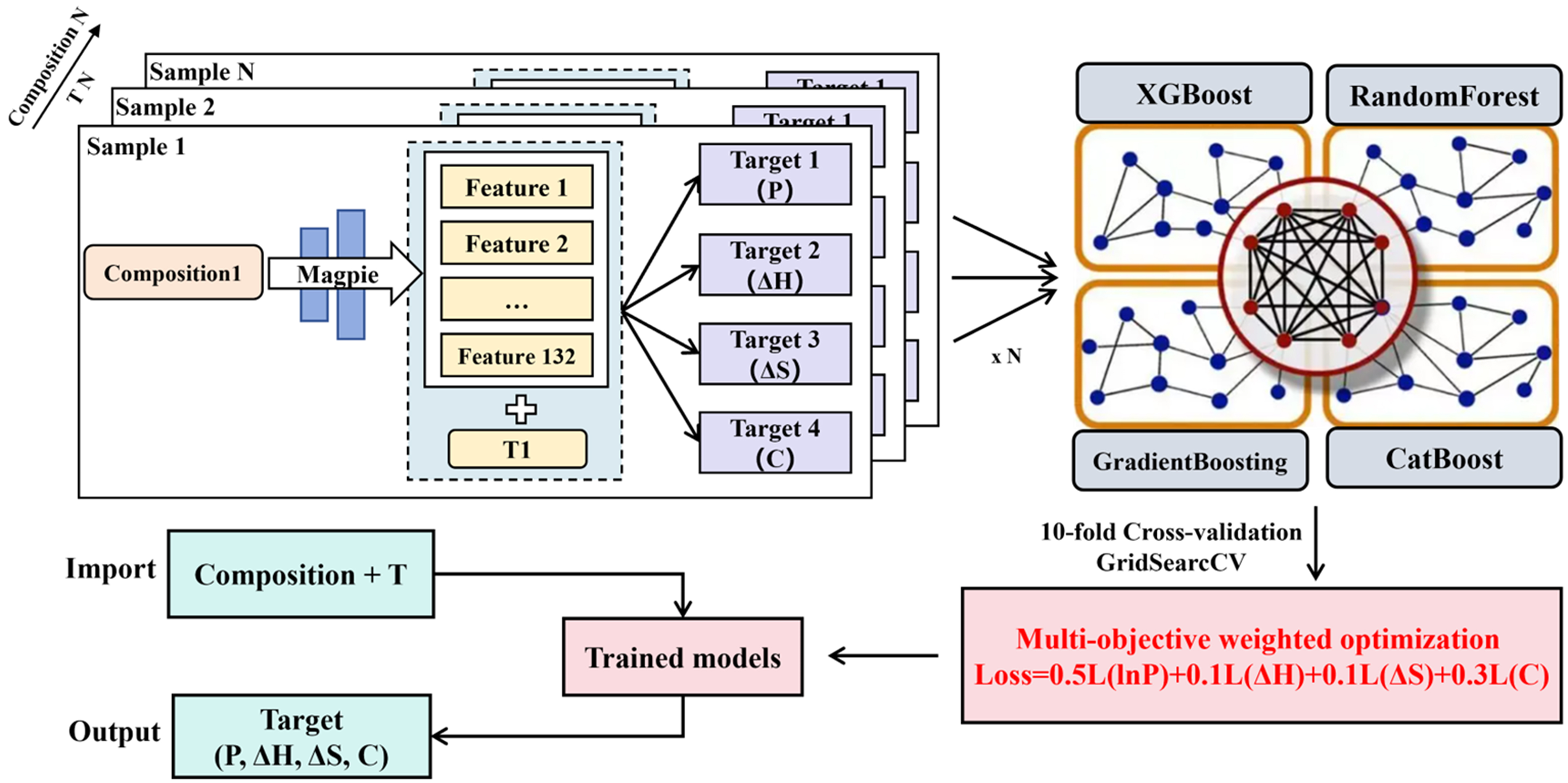
In this study, the input features used in the training model were generated based on the Magpie tool. Magpie is a feature engineering tool widely used in the interdisciplinary research field of materials science and ML. It can automatically extract a series of statistical and physical features based on chemical formulas, thereby showing good versatility and scientificity in material property prediction tasks. Especially in the process of data-driven material design, the composition-derived descriptors provided by Magpie, based on elemental properties, have been shown to be highly valuable in predicting and correlating material compositions with their macroscopic properties. For example, Witman et al. constructed a gradient boosting regression model based on the 145 material descriptors generated by Magpie to predict thermodynamic parameters such as equilibrium plateau pressure, enthalpy change and entropy change of hydrides[38]; Ward et al. also used the 145 features generated by Magpie and combined them with the random subspace method to train a random forest classifier set to achieve effective discrimination of material categories[16]. Inspired by previous studies, we adopt a feature set consisting of 132 material descriptors generated by Magpie and the temperature, yielding 133 input dimensions for the predictive model.
ML models
For the forward model, this study adopts a multi-objective regression framework and unified training to simultaneously predict four key thermodynamic property indicators: plateau pressure, enthalpy, entropy and maximum hydrogen storage capacity. Since the numerical magnitude of the plateau pressure is significantly lower than that of other target variables, it was logarithmically transformed before training to avoid being ignored in the loss function. In addition, in order to further improve the prediction performance of the overall model for each target, a weighted strategy was introduced in the design of the multi-objective loss function. The specific weights were set to 0.5 for the logarithmic plateau pressure, 0.1 for enthalpy, 0.1 for entropy, and 0.3 for capacity to achieve a balance between prediction accuracy and the importance of each performance indicator. The training set ratio is divided into 0.8 and the test set ratio is divided into 0.2. We built a variety of ensemble learning models, including XGBoost, categorical boosting (CatBoost), random forest, and gradient boosting regressor, to improve the predictive generalization ability of the model. These models were implemented within a MultiOutputRegressor framework from the scikit-learn package (version 1.5.2) in Python 3.9.19. At the same time, in order to enhance the robustness and prediction accuracy of the model, Bayesian optimization and grid search hyperparameter tuning methods were applied during training, and 10-fold cross-validation was employed for model evaluation and selection.
For composition optimization, traditional methods rely on enumeration and grid search to exhaustively explore all possible alloy compositions. Although feasible, these approaches are associated with prohibitive time and computational costs. Once a reliable forward model with low prediction error is established, there is an urgent need to identify the optimal chemical composition that yields the best hydrogen storage performance within a given material system. This is of great significance for accelerating the discovery of new materials. GAs provide an efficient and effective means of searching within a predefined space to rapidly identify high-performing candidates.
Inverse design of alloys based on material properties is a performance-driven materials design strategy. Compared with traditional trial-and-error approaches or forward design methods, it starts from the target properties and explores potential material combinations, thereby enabling more efficient and targeted materials development. However, due to the large variety of elements and the continuous variation of compositional ratios, the design space grows exponentially, leading to the “Curse of Dimensionality”. Exhaustive search becomes impractical, making it essential to employ optimization algorithms for efficient exploration. In this study, a VAE[40] model is employed for the inverse design of hydrogen storage materials. VAE is a probabilistic generative model trained by maximizing the variational lower bound, which balances reconstruction accuracy and latent space regularization[40]. It has been widely applied in inverse design tasks, such as the generation and optimization of materials and molecules[41,42]. The VAE not only learns a compressed representation (latent representation) of the data, but also generates new samples similar to the original data by sampling from the learned latent space. Therefore, it is well-suited for the inverse design of hydrogen storage materials.
The VAE consists of two main components: the encoder and the decoder. The encoder maps the input data x to a probabilistic latent space distribution qϕ(z|x), outputting the mean μ and standard deviation σ of a Gaussian distribution. The decoder reconstructs the data by decoding the latent variable z back to the original data space, yielding a reconstructed sample x = pθ(x|z). Unlike traditional autoencoders that perform deterministic compression, VAE introduces probabilistic encoding by modeling the distribution of latent variables.
Maximizing the marginal likelihood[40]:
Since the integral is intractable, variational inference is employed by introducing an approximate posterior
Eq(z|x)[logp(x|z)] represents the reconstruction loss, while DKL[q(z|x)||P(z)] is the Kullback–Leibler (KL) divergence, which regularizes the latent variable distribution to be close to a standard normal distribution.
The total loss function is:
Model evaluation metrics
In order to systematically evaluate the performance of the model, a variety of regression indicators are used, including mean absolute error (MAE), root mean square error (RMSE), mean absolute percentage error (MAPE), and decision coefficient (R2). These metrics are defined as follows:
where yi denotes the true value, yi indicates the predicted value, y stands for the mean of the true values, and n signifies the number of samples.
RESULTS AND DISCUSSION
FIND database
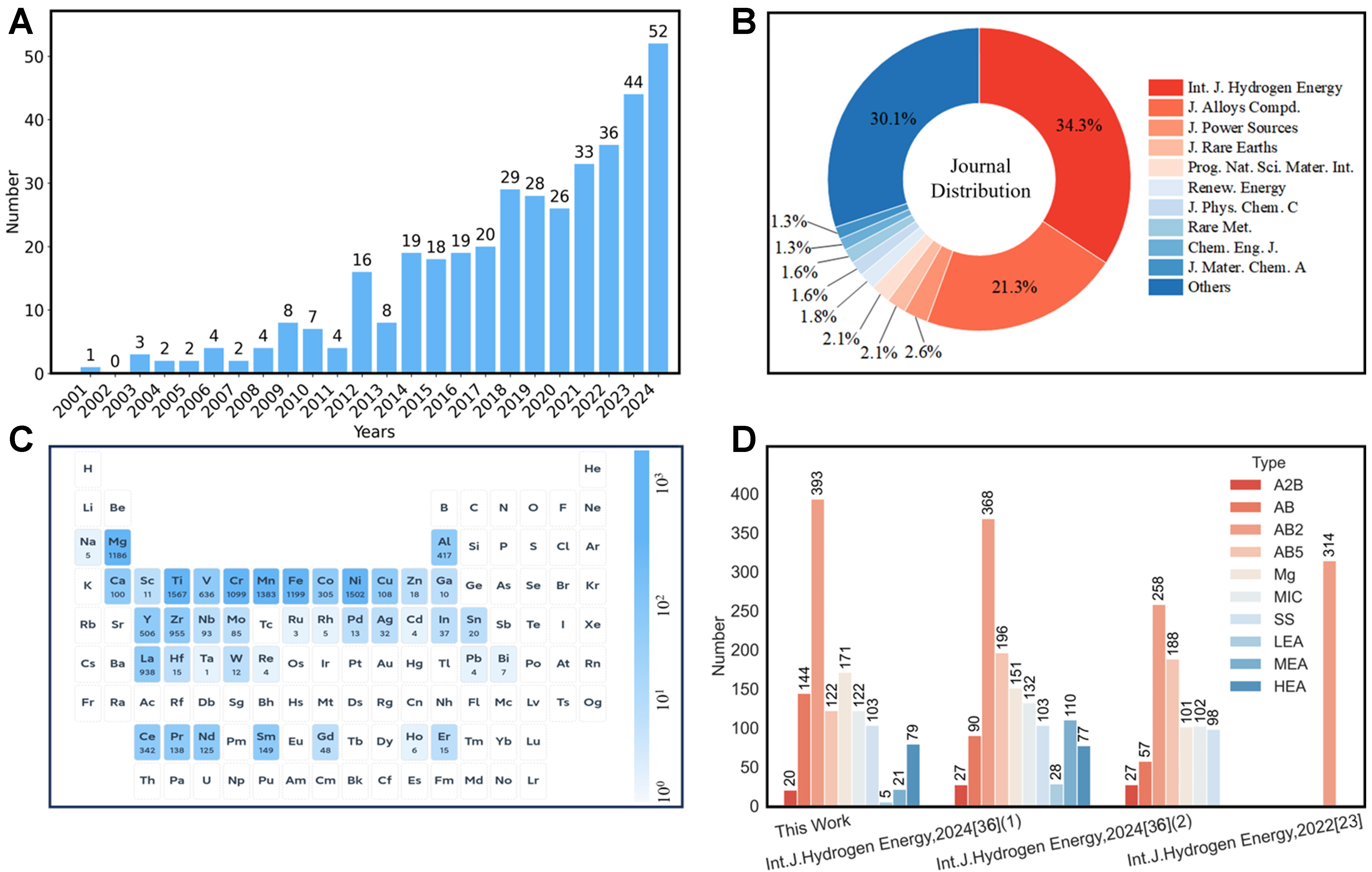
Based on previous literature, we successfully built a large-scale solid hydride database covering more than 1,000 alloys and 6,000 valid data records. All Data were uploaded in the Digital Hydrogen-S (https://s-hydrogendataplatform.nas.cpolar.cn/index-white.html). This new database mainly includes literature data published between 2001 and 2024, as shown in Figure 1A. Obviously, there has been an explosive growth of publication numbers since 2014. At the same time, we also classified and counted the sources of journal publications, as shown in Figure 1B. The most common source is International Journal of Hydrogen Energy, followed by Journal of Alloys and Compounds and Journal of Power Sources. In addition, the statistical results of elemental occurrence frequencies in the database are presented in the periodic table, as shown in Figure 1C. The frequency of each element is visualized by the color intensity according to the color bar, while the detailed value is labeled at the bottom of each cell. The database covers a total of 40 metal elements, which basically covers the main group elements, transition metals and rare earth elements commonly used in hydrogen storage alloy research, suggesting this database exhibits substantial material diversity. To further validate the diversity of the database, we compared the types of alloys with those reported in the literature[23,24,36,38,43], as shown in Figure 1D. The alloy types are rich, covering A2B, AB, AB2, AB5, Mg system, MIC (intermetallic compound), SS (solid solution), LEA (low entropy alloy), MEA (medium entropy alloy) and HEA (high entropy alloy). Beyond the extensive variety of alloy types, our database exhibits clear advantages in terms of the coverage ranges for hydrogen storage capacity (0.33-
Unsupervised learning of data
To gain an initial understanding of the constructed database and to explore potential relationships among thermodynamic performance parameters, we employed unsupervised learning methods to conduct a clustering analysis on key performance indicators. Three representative thermodynamic features - (temperature, plateau pressure, and hydrogen storage capacity) - were selected to construct a three-dimensional feature space. These thermodynamic data were taken from the same PCT curve for each sample, with conditions from the original literature that vary across samples. Although temperature-dependent, these properties were used to explore overall distribution patterns rather than compare values at a fixed temperature. Based on this space, clustering modeling was performed using the K-Means algorithm. To achieve optimal clustering performance, we conducted a systematic grid search for the number of clusters k, and evaluated the clustering results using two standard metrics: the Silhouette Score[44] and the Davies–Bouldin Index (DBI)[45]. Specifically, the Silhouette Score measures how well each data point fits within its cluster compared to other clusters, with values closer to 1 indicating better clustering. The DBI evaluates the average similarity between clusters, where lower values represent more distinct and compact clusters. The search results indicated that the optimal performance was achieved at k = 3, where the Silhouette Score reached 0.6546 and the DBI was 0.5461 [Supplementary Figure 2]. As shown in Figure 2A, the clustering results clearly divide the samples into three distinct types of materials, each exhibiting significantly different thermodynamic behaviors [Table 1]. To further visualize the distribution characteristics of these three material types in the feature space, we rendered three directional views of the 3D clustering results from different perspectives [Figure 2B-D], which enhanced the clarity of cluster boundaries and feature distinctions.
Figure 2. Unsupervised clustering of data. (A) 3D K-Means clustering using the features “Temperature”, “Plateau pressure”, and “Capacity”; (B) Side view of 3D clustering, features “Capacity” and “Temperature”; (C) Front view of 3D clustering, features “Plateau pressure” and “Capacity”; (D) Top view of 3D clustering, features “Plateau pressure” and “Temperature”.
Some characteristics of each cluster
| Cluster | Feature | Element system | Alloy examples |
| 0 | Moderate temperature Low plateau pressure Moderate capacity | V–Ti-based alloys | V65Ti15Cr2 V70Ti10Cr20 Ti36V26Cr9Mn29 |
| 1 | Higher temperature Low plateau pressure Large capacity | Mg–RE-based alloys | Mg85Ni10La4Y Mg85Nd5Al10 Mg94Al5Y |
| 2 | Moderate temperature High plateau pressure Low capacity | Ti–Fe and Ti–Mn-based alloys | TiCr1.1Mn0.3Fe0.6 Ti1.02Cr1.1Mn0.3Fe0.6 |
From the clustering visualization results, it can be observed that although the materials in Cluster 0 do not exhibit the highest hydrogen storage capacity, they demonstrate relatively low values in both temperature and plateau pressure. Notably, some samples within this cluster achieve hydrogen capacities exceeding
Cluster 1 also exhibits distinct thermodynamic characteristics. Materials within this cluster generally possess high hydrogen storage capacities, with some samples exceeding 7 wt%, indicating strong hydrogen storage potential. Additionally, their plateau pressures are relatively low, mostly below 2 MPa. However, the hydrogen absorption/desorption temperatures for this cluster are typically high (> 500 K), which imposes certain limitations on their direct application in low- to moderate-temperature environments. Nevertheless, the combination of high capacity and relatively low plateau pressure suggests that, with appropriate materials design strategies to adjust the hydrogenation/dehydrogenation temperature, Cluster 1 materials have great potential to become high-performance hydrogen storage candidates. In particular, they hold promise for industrial applications that demand high hydrogen capacity and can tolerate medium-to-high operating temperatures, such as metal hydride heat pumps[47].To further elucidate the compositional characteristics of this cluster, we extracted several representative chemical compositions of Cluster 1 from the database [Supplementary Table 2]. The compositional analysis reveals that these materials are primarily composed of Mg, rare-earth elements (e.g., La, Ce, Pr, Nd, Sm, Y), and Ni, with minor additions of elements such as Al, Zn, and Cu. These compositional trends are consistent with prior reports showing that the incorporation of rare-earth elements and small amounts of Al, Zn, or Cu into Mg–Ni-based alloys can effectively enhance hydrogen storage performance, including increasing hydrogen capacity, improving hydrogenation/dehydrogenation kinetics, and reducing operating temperatures[48].
In contrast to the previous two clusters, materials belonging to Cluster 2 generally exhibit inferior thermodynamic performance. This group is characterized by low hydrogen storage capacities and significantly elevated plateau pressures. Such attributes deviate markedly from the ideal property profile desired for practical hydrogen storage alloys, which typically includes high capacity, low plateau pressure, and moderate hydrogenation/dehydrogenation temperatures. As a result, materials in Cluster 2 face considerable challenges in meeting the demands of real-world hydrogen storage applications. Nevertheless, an in-depth analysis of the compositional features of this cluster remains of significant value, as it can help identify elemental combinations that may negatively impact hydrogen storage performance. Representative chemical compositions of Cluster 2 materials were extracted from the database [Supplementary Table 2], revealing that these materials commonly possess complex multi-element alloy formulations. The dominant elements include Ti, Cr, Mn, and Fe, with some samples also containing other transition metals such as V and Zr. Although the thermodynamic performance of Cluster 2 materials is not outstanding, this cluster serves as a representative of the non-optimal performance region.
Therefore, the above unsupervised clustering is of great help to our search for new alloy compositions that can balance low plateau pressure, high capacity and moderate temperature, and can help us clarify our goals and directions. These alloys are roughly located at the position of “Target” in Figure 2A and B.
In summary, the thermodynamic properties of hydrogen storage alloys are closely related to their elemental composition and the molar ratio of each element. These factors largely determine the key performance indicators of the alloy, such as the hydrogen absorption and desorption temperature, plateau pressure, and hydrogen storage capacity.
Forward prediction model
Model training
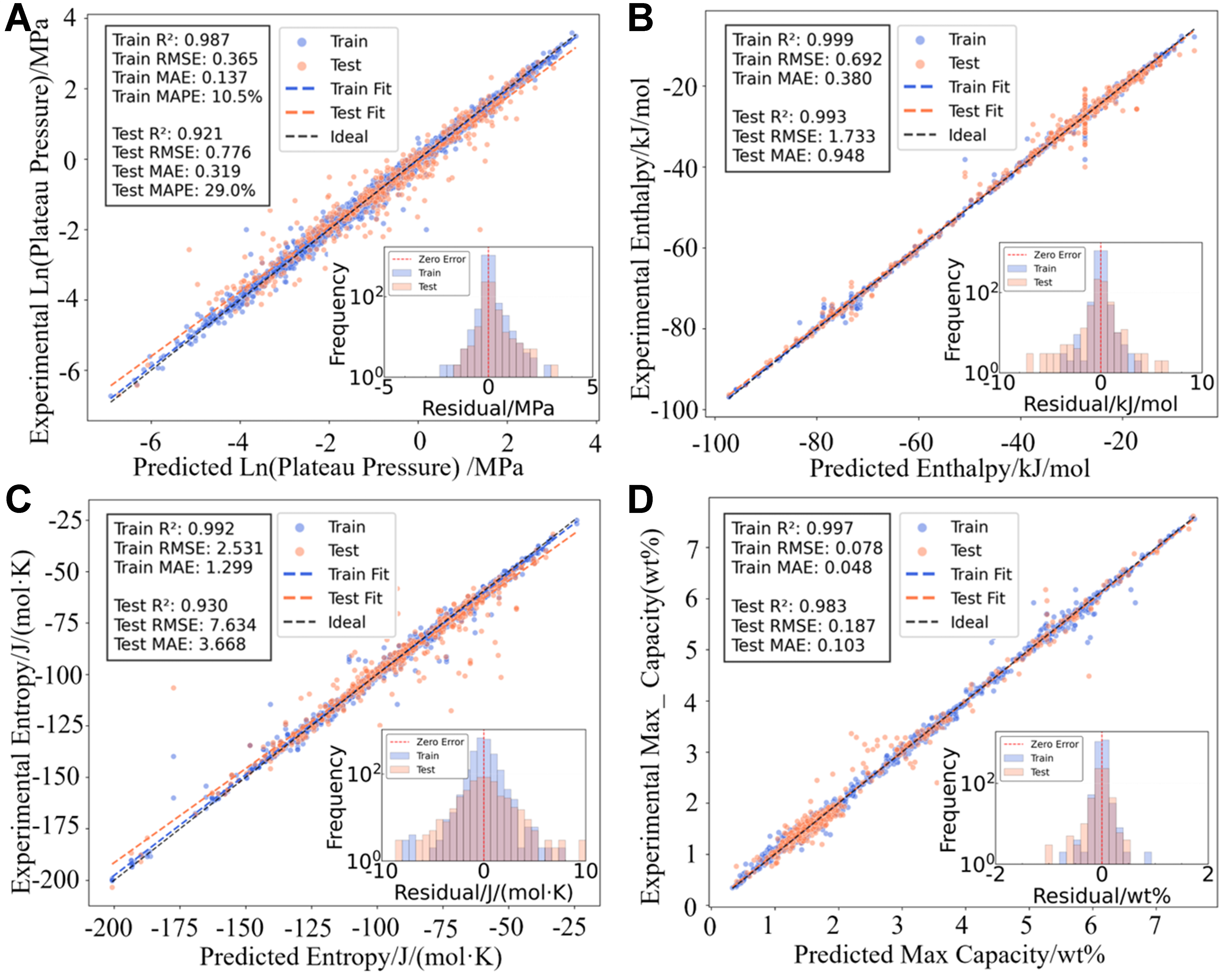
Figure 3 is a framework flow chart of the forward model. After the model training is completed, the target value can be predicted by inputting new components and temperatures. This study expanded the number of training targets and successfully achieved multi-objective joint prediction of four key indicators, namely plateau pressure, enthalpy, entropy, and maximum hydrogen storage capacity, thereby demonstrating a strong comprehensive modeling capability. Table 2 summarizes the training performance of the XGBoost, CatBoost, Random Forest, and Gradient Boosting models for hydrogen absorption, along with a systematic comparison to representative models from the literature. From the perspective of various evaluation indicators (including MAE, RMSE, MAPE and R2), the model constructed in this paper is significantly better than previous studies in terms of prediction accuracy, especially in the task of simultaneously predicting multiple thermodynamic performance indicators. The training results on the dehydrogenation side are listed in Supplementary Table 3, which also shows good model performance. However, it is important to note that datasets used in different studies are often inconsistent in size, composition, and diversity of material categories, which can significantly affect training accuracy and generalization. The dataset used in this work consists of multi-category hydrogen storage materials, and the model training accuracy is based on this dataset. In addition, to further demonstrate the fitting effect of the model, Figure 4 presents a scatter plot of the experimental value and predicted value based on the XGBoost model on the hydrogen absorption side, and its data point height is close to the diagonal, indicating that the model has good prediction accuracy. The corresponding scatter plot on the dehydrogenation side is shown in Supplementary Figure 3, which also reflects the high consistency and robustness of the model in modeling the dehydrogenation process. The training hyperparameters for hydrogen absorption and desorption of the four ML models are listed in Supplementary Table 4.
Figure 4. Scatter plots and residual histograms of the XGBoost model for hydrogen absorption. (A) ln(Plateau pressure/MPa; (B) Enthalpy/kJ/mol; (C) Entropy/J/(mol·K); (D) Max Capacity/wt%. XGBoost: Extreme gradient boosting.
Comparison of predicted hydrogen absorption properties between this study and literature models
| Target | ML model | MAE | RMSE | MAPE | R2 |
| ln(Peq) | GBR[38] | 1.52 | - | - | - |
| ln(Peq) | GBR[49] | 1.44 | - | - | - |
| ln(Peq) | SVM[33] | 0.226 | 0.339 | - | 0.951 |
| ln(Peq) | XGBoost | 0.319 | 0.776 | 29% | 0.921 |
| ln(Peq) | RF | 0.487 | 1.142 | 49.55% | 0.829 |
| ln(Peq) | GradientBoosting | 0.300 | 0.697 | 28.47% | 0.936 |
| ln(Peq) | CatBoost | 0.286 | 0.676 | 26.02% | 0.940 |
| ΔH | GBR[38] | 6.1 | - | - | - |
| ΔH | GBR[49] | 5.51 | - | - | - |
| ΔH | RF[37] | 8.56 | - | 22% | - |
| ΔH | RF[23] | 4.36 | 5.75 | - | 0.647 |
| ΔH | ETR[50] | 5.76 | - | - | 0.89 |
| ΔH | XGBoost | 0.948 | 1.733 | 3.53% | 0.993 |
| ΔH | RF | 1.599 | 2.853 | 6.10% | 0.980 |
| ΔH | GradientBoosting | 0.892 | 1.846 | 3.29% | 0.992 |
| ΔH | CatBoost | 0.844 | 1.735 | 3.16% | 0.993 |
| ΔS | GBR[49] | 13.66 | - | - | - |
| ΔS | XGBoost | 3.688 | 7.634 | 4.54% | 0.930 |
| ΔS | RF | 5.283 | 9.165 | 6.70% | 0.900 |
| ΔS | GradientBoosting | 3.153 | 7.259 | 3.90% | 0.937 |
| ΔS | CatBoost | 3.168 | 7.128 | 3.88% | 0.939 |
| H2wt% | NN[20] | 0.0030 | - | - | 0.83 |
| H2wt% | RF[23] | 0.101 | 0.126 | - | 0.688 |
| H2wt% | Ada_Stacking[43] | 0.187 | 0.4324 | - | 0.783 |
| H2wt% | ETR[50] | 0.31 | - | - | 0.81 |
| H2wt% | GBDT[33] | 0.075 | 0.100 | - | 0.644 |
| H2wt% | XGBoost | 0.103 | 0.187 | 5.39% | 0.983 |
| H2wt% | RF | 0.125 | 0.229 | 6.53% | 0.975 |
| H2wt% | GradientBoosting | 0.104 | 0.194 | 5.36% | 0.982 |
| H2wt% | CatBoost | 0.100 | 0.181 | 5.15% | 0.984 |
To evaluate the predictive performance of the model, the CatBoost algorithm was selected as a representative example for residual analysis, where residuals are defined as the differences between predicted and actual values. The red dashed line in Figure 4 indicates the ideal zero-error reference, serving as a visual aid for assessing the deviation of model predictions. As shown in the figure, the residual histograms of the four target variables on the hydrogen absorption side exhibit approximately normal distributions centered around zero for both the training and testing sets, suggesting that the model does not exhibit significant systematic bias. However, larger prediction errors are observed in regions with lower training data frequency, reflecting the impact of data distribution imbalance, as the model has fewer samples to learn from in these ranges. Furthermore, the mean and standard deviation of residuals were calculated for each target across both datasets, as shown in Supplementary Table 5. For instance, in the training set, the mean and standard deviation of residuals for plateau pressure are 0.03 and 0.30 MPa, respectively, reflecting high predictive accuracy and consistency. In the testing set, these values are 0.14 and 0.66 MPa, respectively, indicating good generalization performance without notable bias. The residual analysis of the CatBoost model on the hydrogen desorption side is presented in Supplementary Figure 3.
Model validation
To further validate the generalization capability and predictive accuracy of the developed forward prediction model, we employed experimental data not included in the training database as an external test set. Based on the data reported in reference[51], we first evaluated the predictive performance of the model on the La0.6MgxNi3.45Nd0.1 alloy system (x = 0.2, 0.25, 0.3, 0.35, 0.4) under a constant temperature of 298 K. Specifically, we predicted the plateau pressures and maximum hydrogen storage capacities during both hydrogen absorption and desorption processes. As shown in Figure 5A-C, the model demonstrates excellent predictive performance for this alloy system. The predicted values exhibit high consistency with the experimental results, accurately capturing the trends associated with varying Mg contents.
Figure 5. Comparison between experimental and predicted values for the alloys La0.6MgxNi3.45Nd0.1 (x = 0.2, 0.25, 0.3, 0.35, 0.4) at
Furthermore, to assess the model’s adaptability to temperature variations, we selected a fixed-composition alloy, La0.6Mg0.2Ni3.45Nd0.1, and conducted predictions of plateau pressures and maximum hydrogen storage capacities at different temperatures (T = 298, 308, 318, 333 K). The predicted results were then compared with experimental data. As shown in Figure 5D-F, the predicted values are in good agreement with the experimental measurements, further confirming the model’s robustness and applicability across a range of temperatures.
In summary, the results indicate that the forward prediction model developed in this study is capable of accurately capturing the thermodynamic behavior of hydrogen storage materials across different compositions and temperatures. Moreover, the model demonstrates strong generalization performance when applied to previously unseen samples, highlighting its potential utility in practical material design and screening applications.
To further evaluate the overall performance of the proposed model in multi-objective prediction tasks, a systematic comparative analysis was conducted against a representative model from existing literature. Specifically, we selected the predictive model developed by Zhou et al. as a benchmark, and the comparison results are presented in Table 3[33]. This comparison involved six groups of real material data that were not included in the training set. Each group comprises experimental values, predictions from the model by Zhou et al., and predictions from the present study[33]. The assessed thermodynamic and hydrogen storage performance parameters include hydrogen absorption plateau pressure (Pa/MPa), hydrogen desorption plateau pressure (Pd/MPa), reaction enthalpy change (ΔHd, kJ/mol), and maximum hydrogen storage capacity (Capacity, wt%). Both the experimental data and benchmark model results were obtained from the study by Zhou et al. The comparison results demonstrate that, for the six representative Ti-Mn-Cr-(VFe)-(Zr) alloys, the model proposed in this study can accurately reproduce the values of Pa, Pd, ΔHd, and Capacity. The proposed model exhibits high accuracy and robustness in predicting multiple key performance indicators and generally outperforms the model developed by Zhou et al.[33]. Overall, the present model not only achieves superior prediction accuracy for individual parameters but also demonstrates strong capability in simultaneous multi-objective prediction, offering a clear advantage in maintaining consistency across multiple output variables.
Comparison of multi-property predictions for out-of-training hydrogen storage alloys between this study and previous works
| Alloy | Properties statement | T/°C | Pa/MPa | Pd/MPa | ΔHd/kJ/mol | Capacity/wt% |
| Ti1.02Mn1.5Cr0.05(VFe)0.45 | Experimental value | 20 | 2.29 | 1.42 | 24.88 | 1.96 |
| Literature model | 20 | 1.43 | 0.98 | 25.61 | 2.03 | |
| This study | 20 | 1.860 | 1.439 | 26.553 | 1.955 | |
| Ti1.02Mn1.45Cr0.1(VFe)0.45 | Experimental value | 20 | 2.20 | 1.40 | 25.04 | 1.94 |
| Literature model | 20 | 1.45 | 1.00 | 25.61 | 1.98 | |
| This study | 20 | 2.063 | 1.500 | 26.494 | 1.934 | |
| Ti1.02Mn1.4Cr0.2(VFe)0.4 | Experimental value | 20 | 2.58 | 1.90 | 23.06 | 1.96 |
| Literature model | 20 | 2.00 | 1.35 | 22.74 | 1.97 | |
| This study | 20 | 2.542 | 2.098 | 26.581 | 1.917 | |
| Ti0.9Zr0.12Mn1.2Cr0.55(VFe)0.25 | Experimental value | 20 | 1.35 | 0.80 | 26.99 | 1.90 |
| Literature model | 20 | 1.18 | 0.71 | 25.21 | 1.86 | |
| This study | 20 | 1.388 | 0.765 | 25.555 | 1.898 | |
| Ti0.9Zr0.12Mn1.2Cr0.6(VFe)0.2 | Experimental value | 20 | 1.76 | 0.99 | 26.57 | 1.89 |
| Literature model | 20 | 1.62 | 0.93 | 25.21 | 1.86 | |
| This study | 20 | 1.620 | 0.944 | 25.785 | 1.844 | |
| Ti0.9Zr0.12Mn1.15Cr0.7(VFe)0.15 | Experimental value | 20 | 2.10 | 1.17 | 26.13 | 1.88 |
| Literature model | 20 | 2.10 | 1.20 | 24.98 | 1.85 | |
| This study | 20 | 2.091 | 1.310 | 25.087 | 1.818 |
Ingredient optimization
Mg-based hydrogen storage materials offer a high hydrogen capacity, reaching up to 7.6 wt%[19]. However, their hydrogen absorption/desorption temperatures and enthalpy changes are relatively high. Alloying has proven to be a promising strategy to mitigate these issues. We selected the Mg–Ni–La–Ce system due to its prominence in hydrogen storage research and the abundance of related data in our database, making it ideal for compositional optimization. The target temperature of 450 K was selected based on the operating temperature of high-temperature proton exchange membrane fuel cells[52]. Meanwhile, according to our database statistics, this temperature also represents a challenging target for Mg-based hydrogen storage materials.
The optimization problem is formulated as follows:
where H = reaction enthalpy change (kJ/mol), T = Temperature (K), Mg, Ni, La, Ce = mole fraction of each element in the alloy, dimensionless.
Within the defined elemental range, the goal is to identify alloy compositions that satisfy the constraints of a hydrogen storage capacity greater than 6 wt%, entropy below 140 J/(mol·K), and plateau pressure under
Based on these optimization objectives, we constructed a GA-based parameter optimization framework to explore the optimal alloy composition and corresponding operating temperature. Each individual in the GA population is represented as a vector: [Mg, La, Ni, Ce, T]. The initial population size is set to 200. To enhance diversity and ensure effective coverage of the search space, a hybrid initialization strategy is employed. Molar fraction combinations are generated using the Dirichlet distribution to satisfy the normalization constraint, while Gaussian perturbation sampling is introduced to strengthen local exploration in promising regions. The crossover rate is set to 0.8, and the mutation rate starts at 0.3 and decreases over generations to facilitate convergence. The temperature parameter (T) is sampled uniformly from the range of 450 to 750 K. During the selection phase, we adopt the tournament selection strategy, where several subsets of the current population are randomly selected and the individual with the highest fitness in each subset is chosen as a parent. This ensures that individuals with higher fitness have a greater probability of propagating to the next generation. The new generation is produced through a combination of elitism and genetic operations. Specifically, the top 10% of individuals with the highest fitness in the current population are directly carried over to the next generation to preserve superior genetic information. The remaining 90% are generated via crossover and mutation. Crossover recombines parental traits, while mutation introduces moderate stochastic variations to maintain population diversity. After each generation, the molar fractions are renormalized to meet compositional constraints. This iterative process continues until convergence criteria are met, either by reaching the maximum number of generations or observing minimal improvement in fitness over consecutive generations.
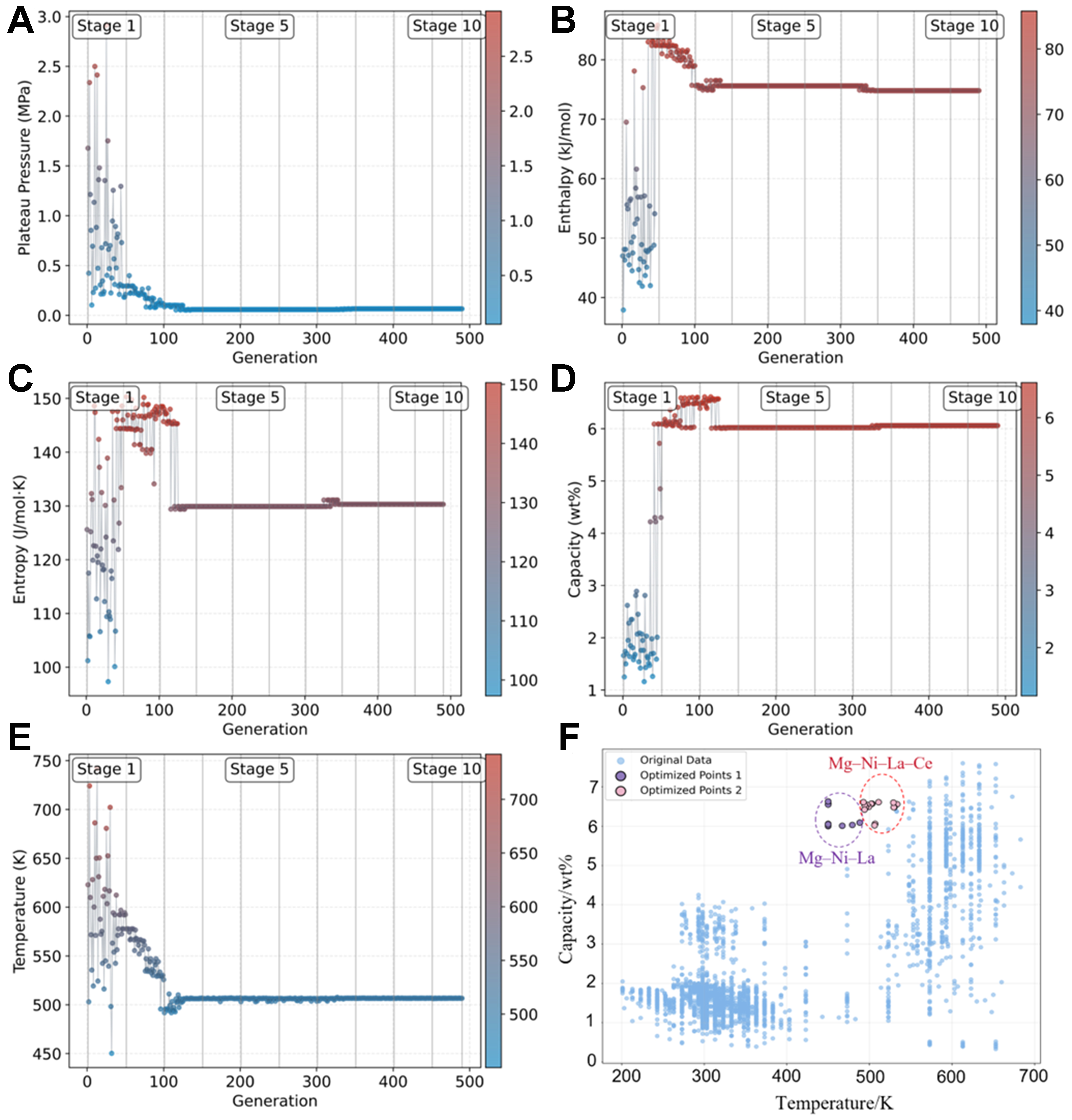
The optimization process is illustrated in Figure 6A-E, where the evolution of all five parameters is tracked. During the first 125 generations, substantial population variation is observed, facilitating exploration of the optimal regions. Ultimately, 15 potential optimal alloy–temperature combinations were identified [Table 4]. These candidates were compared against existing database materials, with the results shown as red points in Figure 6F.
Figure 6. GA optimization of alloys in the Mg–Ni–La–Ce system. (A) Evolution of plateau pressure over generations; (B) Evolution of enthalpy over generations; (C) Evolution of entropy over generations; (D) Evolution of hydrogen storage capacity over generations; (E) Evolution of temperature over generations; (F) Distribution of the potential optimal alloys in the original database.
Fifteen potential optimal Mg–Ni–La–Ce alloy–temperature combinations identified by the GA
| Number | Components | Temperature/K | Plateau pressure/MPa | Enthalpy/ kJ/mol | Entropy/ J/(mol·K) | Max capacity/wt% |
| 1 | Mg0.975La0.001Ni0.022Ce0.001 | 533.5 | 0.154 | 79.8 | 146.2 | 6.56 |
| 2 | Mg0.979La0.001Ni0.019Ce0.001 | 530.1 | 0.119 | 78.9 | 147 | 6.48 |
| 3 | Mg0.981La0.001Ni0.017Ce0.001 | 529.5 | 0.116 | 79.4 | 148 | 6.48 |
| 4 | Mg0.978La0.001Ni0.020Ce0.001 | 529.1 | 0.118 | 78.9 | 147.5 | 6.6 |
| 5 | Mg0.978La0.001Ni0.020Ce0.001 | 511 | 0.101 | 75.5 | 148 | 6.61 |
| 6 | Mg0.961La0.009Ni0.022Ce0.007 | 506.8 | 0.066 | 74.8 | 130.3 | 6.06 |
| 7 | Mg0.957La0.019Ni0.023Ce0.001 | 506.2 | 0.059 | 75.6 | 129.9 | 6.02 |
| 8 | Mg0.976La0.001Ni0.022Ce0.001 | 503.3 | 0.101 | 74.9 | 145.3 | 6.57 |
| 9 | Mg0.976La0.001Ni0.022Ce0.001 | 502.2 | 0.101 | 74.9 | 145.3 | 6.57 |
| 10 | Mg0.979La0.001Ni0.019Ce0.001 | 499.2 | 0.104 | 75.3 | 147.5 | 6.49 |
| 11 | Mg0.975La0.001Ni0.023Ce0.001 | 497.2 | 0.101 | 75.2 | 145.7 | 6.54 |
| 12 | Mg0.981La0.001Ni0.017Ce0.001 | 495.6 | 0.101 | 75.7 | 148.5 | 6.49 |
| 13 | Mg0.975La0.001Ni0.023Ce0.001 | 494.1 | 0.100 | 75.2 | 145.7 | 6.54 |
| 14 | Mg0.972La0.001Ni0.026Ce0.001 | 494.1 | 0.086 | 75.5 | 147.1 | 6.42 |
| 15 | Mg0.978La0.001Ni0.020Ce0.001 | 492.7 | 0.103 | 75.2 | 148 | 6.61 |
In addition, a GA optimization was performed for the Mg-Ni-La system. Apart from representing each individual in the GA as [Mg, La, Ni, T], the optimization problem was defined in the same way as described above. The optimization process is illustrated in Supplementary Figure 4A-E, which shows the evolution of five key parameters. During the first 50 generations, the population underwent significant variation to ensure effective exploration of the optimal parameter space. Ultimately, 12 potential optimal combinations of alloy compositions and operating temperatures were identified [Supplementary Table 6]. These 12 candidate materials were then compared with existing materials in the database, as indicated by the purple dots in Figure 6F and Supplementary Figure 4F.
Inverse model
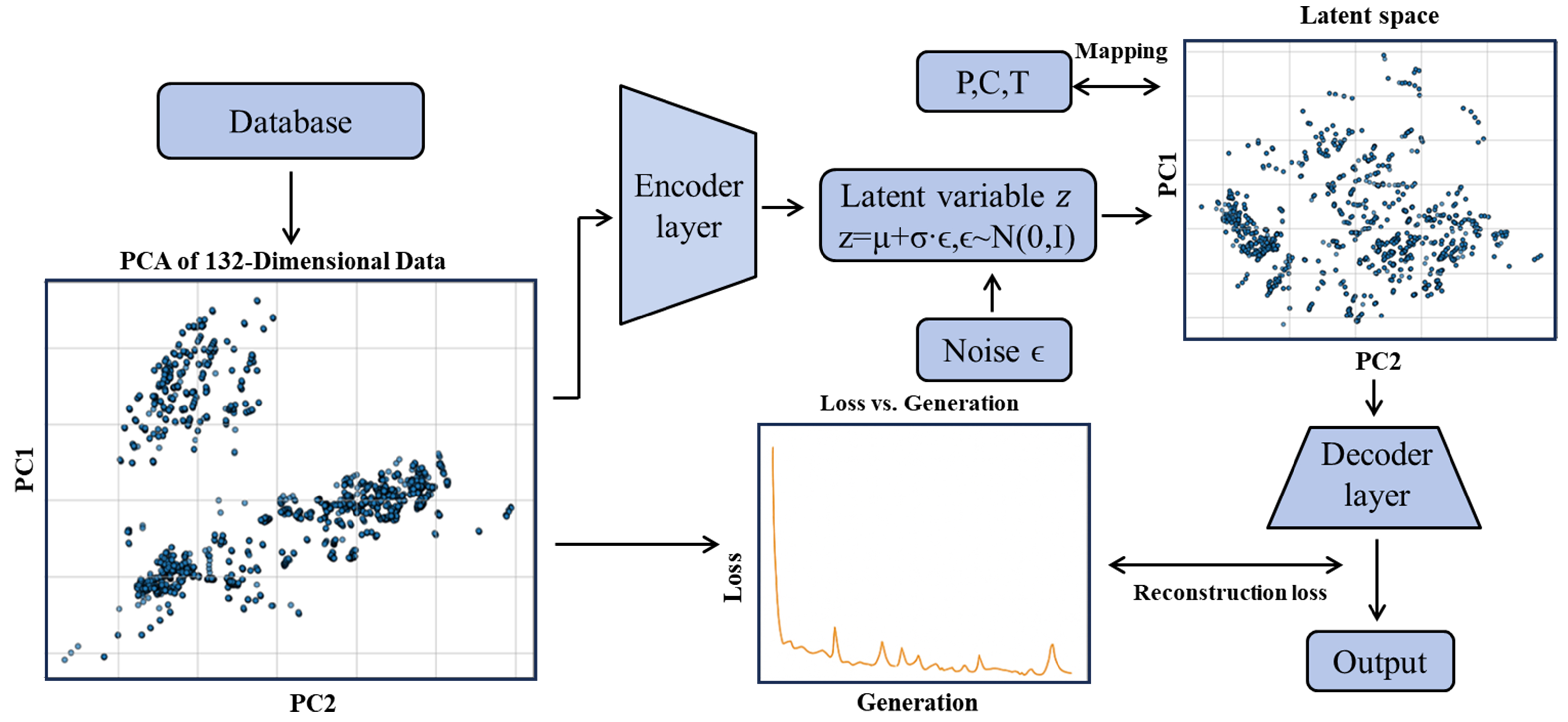
Figure 7 shows the process framework. The encoder compresses and transforms complex input data into latent space vectors by extracting key features. By approximating prior and posterior distributions, the latent space distribution is regularized to be close to a standard normal distribution through the introduction of Gaussian noise N(0,1). This noise adds flexibility, allowing the model to learn data diversity instead of memorizing rigidly. The decoder then reconstructs latent vectors back into raw data form. The reconstruction loss measures the difference between input and output, which the model minimizes during training to ensure outputs closely match inputs.
In this article, we adopt a conditional VAE architecture to process 133-dimensional Magpie material features combined with 1-dimensional temperature input. The encoder maps the 134-dimensional input data to a 3-dimensional latent space (outputting mean μ and variance σ). Using the reparameterization trick, random sampling is performed as z = μ + ε·σ. The decoder reconstructs the original feature dimension from the latent space. Training employs standardized preprocessing and the Adam optimizer (learning rate = 0.001). The loss function combines reconstruction mean squared error and KL divergence:
where β = 0.5 controls the regularization strength of the latent space. This latent space serves as the material “genomic map”, supporting temperature-constrained conditional generation, latent vector interpolation, and noise-injected sampling (Gaussian noise with standard deviation σ = 0.1). Together with downstream networks, it enables end-to-end material design from processing parameters (T, P, C) to chemical formulas. The alloy design space is restricted to the 40 metal elements mentioned earlier in the manuscript.
After constructing and training the VAE inverse design model, we evaluated its effectiveness in practical material inverse design tasks by specifying a representative set of target performance parameters. Specifically, we selected a plateau pressure of 0.2 MPa, a maximum hydrogen storage capacity of 5 wt%, and a temperature of 573 K as the target conditions. The inverse model was then used to generate alloy compositions that potentially meet these requirements. After removing duplicates, a total of eight candidate alloys were obtained, as listed in Table 5. To further validate the reliability of the inverse design results, the compositions of the eight candidate alloys were input into the forward prediction model to estimate key properties such as plateau pressure and hydrogen storage capacity. The predicted results are also presented in Table 5. It can be observed that most of the inversely generated alloys satisfactorily met the preset target in terms of hydrogen capacity, demonstrating the model’s strong capability in capacity control. However, for plateau pressure, some predicted values were slightly below the target, indicating that the model still exhibits certain deviations in specific performance dimensions. Overall, the proposed inverse design framework exhibits good generative capability and practical feasibility under multi-objective performance constraints.
Inverse-designed alloy compositions targeting 0.2 MPa, 5 wt%, and 573 K, and their forward-predicted hydrogen storage properties
| Number | Inverse discovery materials | Forward prediction properties (573 K) | |
| Plateau pressure/MPa | Capacity/wt% | ||
| 1 | Ni20Mg76La3Pr2 | 0.122 | 4.353 |
| 2 | Ni15Mg81 | 0.253 | 4.869 |
| 3 | Ni18Mg78Pr2 | 0.136 | 4.994 |
| 4 | Ni19Mg77La2Pr2 | 0.130 | 4.825 |
| 5 | Ni16Mg80Pr2 | 0.124 | 5.062 |
| 6 | Ni17Mg79Pr2 | 0.131 | 4.908 |
| 7 | Ni18Mg79Pr2 | 0.139 | 5.005 |
| 8 | Ni19Mg78La2Pr2 | 0.126 | 4.860 |
However, it should be noted that while the VAE can generate compositions differing from the training data in element ratios and combinations, the degree of novelty is constrained by the latent space learned from the dataset. Moreover, the current framework does not assess the experimental formability of generated alloys, and some may phase-separate rather than form homogeneous structures. Future work will integrate computational formability evaluation to enhance the practical utility of the FIND platform.
FIND platform
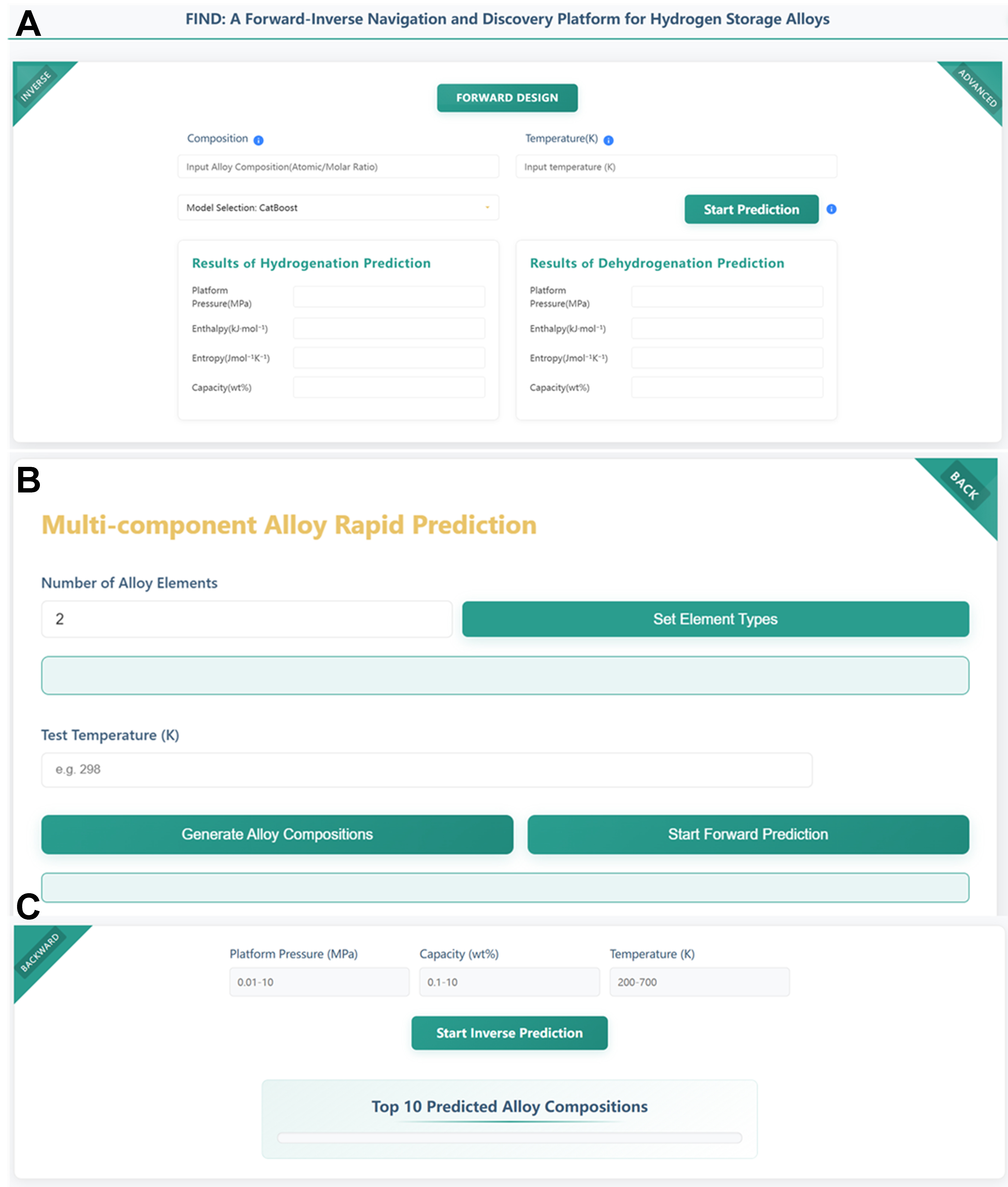
FIND is a bilingual (Chinese–English) platform that supports the bidirectional design of hydrogen storage alloy materials. We developed the FIND platform based on Python’s Flask framework, a lightweight WSGI web application framework. For data storage and management, the platform utilizes an SQLite database. The front-end interface is built using HTML, CSS, and JavaScript, incorporating modern web development technologies to enable efficient data interaction and an enhanced user experience. In the forward design mode, users can predict both absorption and desorption plateau pressures, enthalpy, entropy, and hydrogen storage capacity based on the chemical formula and testing temperature. The advanced forward function extends this capability by enabling rapid prediction of multicomponent alloy compositions with arbitrary elemental molar ratios. In the inverse design mode, the platform allows users to back-calculate possible alloy compositions based on target plateau pressure, temperature, and hydrogen capacity. FIND platform connection: https://find4hyalloy.zicp.fun.
Based on the forward modeling framework presented in Section “Based on the forward prediction model”, the FIND Forward Design Platform was developed, as shown in Figure 8A. Upon entering the FIND homepage, users are presented with the forward prediction interface. By inputting the chemical formula under “Composition” and the test temperature under “Temperature (K)”, users can initiate predictions. The platform offers four predictive models, selectable via the “Model Selection” menu. After completing the input settings, clicking “Start Prediction” will trigger the prediction process. Upon completion, the results will be displayed, showing the predicted plateau pressure, enthalpy, entropy, and capacity for both hydrogen absorption and desorption.
Figure 8. FIND platform. (A) Forward design platform; (B) Advanced function platform; (C) Inverse discovery platform.
Building upon this forward platform, an advanced function has been developed, as shown in Figure 8B. By clicking the “ADVANCED” button in the top-right corner of the homepage, users are redirected to the Multicomponent Alloy Rapid Prediction interface. This module supports flexible input of multicomponent alloys with variable elemental molar ratios (e.g., Mg0.6NixLayCez). It automatically enumerates all possible compositions and predicts their thermodynamic performance. Taking a ternary alloy as an example, users first specify the alloying elements and click “Set”. Then, they input the individual elements under “element1”, “element2”, and “element3”, and define the “Initial Value” and “Step Size” for their molar ratios. After entering the test temperature in “Test Temperature (K)”, clicking “Generate Alloy Compositions” initiates the enumeration of all possible chemical formulas. Once composition generation is complete, clicking “Start Forward Prediction” launches the prediction process. The platform then provides the predicted plateau pressure, enthalpy, entropy, and hydrogen storage capacity for both absorption and desorption sides. The results are visualized as categorized line plots.
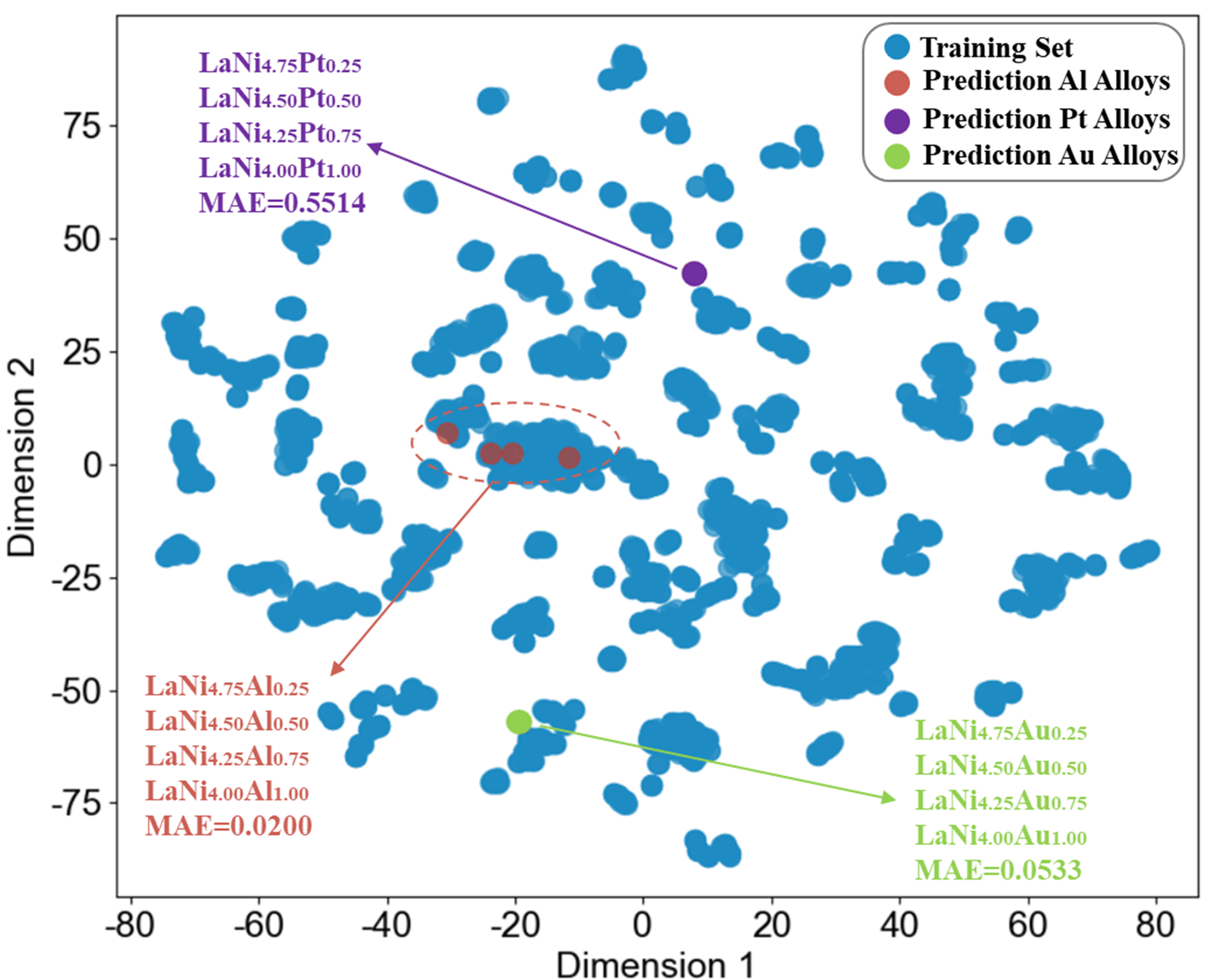
In addition, to further evaluate the reliability of the Prediction results, the predicted alloy compositions were projected onto the low-dimensional feature space of the original database. By comparing the relative positions of the new data and the training data in this space, one can preliminarily assess whether the predicted results fall within the distribution learned by the model, thereby indirectly reflecting their reasonableness and reliability. Taking the LaNi(5-x)Mx (M = Al, Pt, Au, x = 0.25, 0.50, 0.75, 1.00) alloy series at 298 K as an example, each element corresponds to 4 alloys with different doping ratios. Pt and Au are elements outside the training database, and their corresponding alloy series can be used as external reference samples to evaluate the generalization ability of the model. The projection of all samples in the t-SNE dimensionality reduction space of the original database is shown in Figure 9. As can be seen from the figure, all Al-doped samples are distributed in the training data clustering area (MAE = 0.0200), indicating that their predictions fall within the knowledge domain learned by the model and have high credibility. In contrast, Pt-doped (MAE = 0.5514) and Au-doped samples (MAE = 0.0533) deviate significantly from the training data distribution in the dimensionality reduction space, and their respective doped samples overlap with each other to form independent outlier clusters, showing low model confidence.
Figure 9. t-SNE dimensionality reduction distribution of LaNi(5-x)Mx (M = Al, Pt, Au, x = 0.25, 0.50, 0.75, 1.00) alloys in the original database at 298 K.
Based on the inverse modeling approach introduced in Section “Based on the inverse model”, the FIND Inverse Design Platform was developed, as shown in Figure 8C. By clicking the “INVERSE” button in the top-left corner of the homepage, users can access the inverse design interface. Here, users specify the target performance by entering the desired “Plateau pressure (MPa)”, “Capacity (wt%)”, and “Temperature (K)”. Clicking “Start Inverse Prediction” initiates the reverse prediction process, which outputs the top ten candidate alloy compositions most likely to meet the specified targets.
CONCLUSIONS
In this study, a large-scale solid-state hydride database was constructed based on authoritative literature sources, encompassing over 1,000 alloy systems and more than 6,000 valid data records. On this basis, material features were extracted using the Magpie tool, and a series of ML methods were employed to develop a multi-target regression model capable of simultaneously predicting plateau pressure, enthalpy change, entropy change, and maximum hydrogen storage capacity for both hydrogen absorption and desorption processes. Furthermore, a VAE was implemented to enable the inverse design of solid-state hydrogen storage materials. By integrating forward prediction and inverse design models, we developed a forward–inverse navigation and discovery platform for hydrogen storage alloys powered by data-driven ML. This platform allows users to input alloy compositions and testing temperatures to rapidly predict hydrogen storage performance in both absorption and desorption. Its advanced mode extends the basic prediction capability to support multicomponent composition prediction with arbitrary molar ratios. Additionally, it enables inverse screening of potential alloy candidates based on user-defined target performance criteria. Finally, GA-based optimization was applied to the Mg-Ni-La-Ce and Mg-Ni-La alloy systems, resulting in the identification of multiple promising high-performance alloy compositions. This work provides an effective tool and methodological foundation for high-throughput screening and intelligent development of hydrogen storage materials.
DECLARATIONS
Acknowledgments
During the preparation of this work, the authors used ChatGPT in order to improve language expression and check grammar. After using this tool, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.
Authors’ contributions
Conceived and guided the work: Yang, W.
Dataset construction, training and evaluation of models: Lu, X.; Luo, S.; Chen, M.; Yao, T.
Provide technical and material support: Li, J. (Jiongyang Li); Xu, Z.; Yan, Y.; Li, J. (Jun Li); Shao, X.; Gao, Z.
All authors discussed the results and commented on the manuscript.
Availability of data and materials
All data used in this study have been uploaded to the Digital Hydrogen-S platform (https://s-hydrogendataplatform.nas.npolar.cn/index-white.html). The forward–inverse navigation and discovery of hydrogen storage alloys can be achieved through the FIND platform (https://find4hyalloy.zicp.fun).
Financial support and sponsorship
The authors gratefully acknowledge financial support for this work from the Natural Science Foundation of Hebei (Grant No. E2023502006), the Fundamental Research Fund for the Central Universities (2025MS131) and the Fundamental Research Funds for the Central Universities (Grant No. 2025JC008).
Conflicts of interest
Yang, W. is a Guest Editor of the journal Journal of Materials Informatics, but was not involved in any steps of editorial processing, notably including reviewer selection, manuscript handling, and decision making, while the other authors have declared that they have no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
Supplementary Materials
REFERENCES
1. Sakintuna, B.; Lamaridarkrim, F.; Hirscher, M. Metal hydride materials for solid hydrogen storage: a review. Int. J. Hydrogen. Energy. 2007, 32, 1121-40.
2. Schlapbach, L.; Züttel, A. Hydrogen-storage materials for mobile applications. Nature 2001, 414, 353-8.
3. Zhang, J.; Liu, M.; Qi, J.; et al. Advanced Mg-based materials for energy storage: fundamental, progresses, challenges and perspectives. Prog. Mater. Sci. 2025, 148, 101381.
4. Liu, H.; Zhang, J.; Zhou, C.; Sun, P.; Liu, Y.; Fang, Z. Z. Hydrogen storage properties of Ti-Fe-Zr-Mn-Nb alloys. J. Alloys. Compd. 2023, 938, 168466.
5. Zhang, Y.; Shang, H.; Gao, J.; Zhang, W.; Wei, X.; Yuan, Z. Effect of Sm content on activation capability and hydrogen storage performances of TiFe alloy. Int. J. Hydrogen. Energy. 2021, 46, 24517-30.
6. Dematteis, E. M.; Dreistadt, D. M.; Capurso, G.; Jepsen, J.; Cuevas, F.; Latroche, M. Fundamental hydrogen storage properties of TiFe-alloy with partial substitution of Fe by Ti and Mn. J. Alloys. Compd. 2021, 874, 159925.
7. Ali, W.; Hao, Z.; Li, Z.; et al. Effects of Cu and Y substitution on hydrogen storage performance of TiFe0.86Mn0.1Y0.1-xCux. Int. J. Hydrogen. Energy. 2017, 42, 16620-31.
8. Chen, Z.; Xiao, X.; Chen, L.; et al. Development of Ti–Cr–Mn–Fe based alloys with high hydrogen desorption pressures for hybrid hydrogen storage vessel application. Int. J. Hydrogen. Energy. 2013, 38, 12803-10.
9. Zepon, G.; Silva, B. H.; Zlotea, C.; Botta, W. J.; Champion, Y. Thermodynamic modelling of hydrogen-multicomponent alloy systems: calculating pressure-composition-temperature diagrams. Acta. Mater. 2021, 215, 117070.
10. Lototsky, M.; Yartys, V.; Marinin, V.; Lototsky, N. Modelling of phase equilibria in metal–hydrogen systems. J. Alloys. Compd. 2003, 356-7, 27-31.
11. Zhou, Z.; Zhang, J.; Ge, J.; Feng, F.; Dai, Z. Mathematical modeling of the PCT curve of hydrogen storage alloys. Int. J. Hydrogen. Energy. 1994, 19, 269-73.
12. Loh, S. M.; Grant, D. M.; Walker, G. S.; Ling, S. Substitutional effect of Ti-based AB2 hydrogen storage alloys: a density functional theory study. Int. J. Hydrogen. Energy. 2023, 48, 13227-35.
13. Xie, X.; Hou, C.; Chen, C.; et al. First-principles studies in Mg-based hydrogen storage Materials: a review. Energy 2020, 211, 118959.
14. Sun, H.; Gao, X.; Zhao, F.; Li, Y.; Zhang, Y.; Ren, H. Interactions of Y and Cu on Mg2Ni type hydrogen storage alloys: a study based on experiments and density functional theory calculation. Int. J. Hydrogen. Energy. 2020, 45, 28974-84.
15. Hu, J.; Shen, H.; Jiang, M.; et al. A DFT study of hydrogen storage in high-entropy alloy TiZrHfScMo. Nanomaterials 2019, 9, 461.
16. Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj. Comput. Mater. 2016, 2, 16028.
17. Batalović, K.; Koteski, V.; Stojić, D. Hydrogen storage in martensite Ti–Zr–Ni alloy: a density functional theory study. J. Phys. Chem. C. 2013, 117, 26914-20.
18. Yang, H.; Ding, Z.; Li, Y.; et al. Recent advances in kinetic and thermodynamic regulation of magnesium hydride for hydrogen storage. Rare. Met. 2023, 42, 2906-27.
19. Yadav, S.; Oberoi, A. S.; Mittal, M. K. Electrochemical hydrogen storage: achievements, emerging trends, and perspectives. Int. J. Energy. Res. 2022, 46, 16316-35.
20. Rahnama, A.; Zepon, G.; Sridhar, S. Machine learning based prediction of metal hydrides for hydrogen storage, part I: Prediction of hydrogen weight percent. Int. J. Hydrogen. Energy. 2019, 44, 7337-44.
21. Zhou, P.; Zhou, Q.; Xiao, X.; et al. Machine learning in solid-state hydrogen storage materials: challenges and perspectives. Adv. Mater. 2025, 37, e2413430.
22. Lu, Z.; Wang, J.; Wu, Y.; Guo, X.; Ma, T.; Xiao, W. Prediction and theoretical investigation of dehydrogenation enthalpy of V–Ti–Cr–Fe alloy using machine learning and density functional theory. Int. J. Hydrogen. Energy. 2024, 50, 379-89.
23. Suwarno, S.; Dicky, G.; Suyuthi, A.; et al. Machine learning analysis of alloying element effects on hydrogen storage properties of AB2 metal hydrides. Int. J. Hydrogen. Energy. 2022, 47, 11938-47.
24. Dong, S.; Wang, Y.; Li, J.; Li, Y.; Wang, L.; Zhang, J. Exploration and design of Mg alloys for hydrogen storage with supervised machine learning. Int. J. Hydrogen. Energy. 2023, 48, 38412-24.
25. Kanti, P. K.; Shrivastav, A. P.; Sharma, P.; Maiya, M. Thermal performance enhancement of metal hydride reactor for hydrogen storage with graphene oxide nanofluid: model prediction with machine learning. Int. J. Hydrogen. Energy. 2024, 52, 470-84.
26. Salehi, K.; Rahmani, M.; Atashrouz, S. Machine learning assisted predictions for hydrogen storage in metal-organic frameworks. Int. J. Hydrogen. Energy. 2023, 48, 33260-75.
27. Jiang, H.; Ding, Z.; Li, Y.; et al. Hierarchical interface engineering for advanced magnesium-based hydrogen storage: synergistic effects of structural design and compositional modification. Chem. Sci. 2025, 16, 7610-36.
28. Ding, Z.; Li, Y.; Yang, H.; et al. Tailoring MgH2 for hydrogen storage through nanoengineering and catalysis. J. Magnes. Alloys. 2022, 10, 2946-67.
29. Athul, A. S.; Muthachikavil, A. V.; Buddhiraju, V. S.; Premraj, K.; Runkana, V. Identification of stable intermetallic compounds for hydrogen storage via machine learning. Energy. Storage. 2025, 7, e70115.
30. Radhika, N.; Niketh, M. S.; Akhil, U.; Adediran, A. A.; Jen, T. High entropy alloys for hydrogen storage applications: a machine learning-based approach. Results. Eng. 2024, 23, 102780.
31. Halpren, E.; Yao, X.; Chen, Z. W.; Singh, C. V. Machine learning assisted design of BCC high entropy alloys for room temperature hydrogen storage. Acta. Mater. 2024, 270, 119841.
32. Dangwal, S.; Ikeda, Y.; Grabowski, B.; Edalati, K. Machine learning to explore high-entropy alloys with desired enthalpy for room-temperature hydrogen storage: prediction of density functional theory and experimental data. Chem. Eng. J. 2024, 493, 152606.
33. Zhou, P.; Xiao, X.; Zhu, X.; et al. Machine learning enabled customization of performance-oriented hydrogen storage materials for fuel cell systems. Energy. Storage. Mater. 2023, 63, 102964.
34. Ahmed, A.; Siegel, D. J. Predicting hydrogen storage in MOFs via machine learning. Patterns 2021, 2, 100291.
35. Halevy, A.; Norvig, P.; Pereira, F. The unreasonable effectiveness of data. IEEE. Intell. Syst. 2009, 24, 8-12.
36. Wilson, N.; Verma, A.; Maharana, P. R.; Sahoo, A. B.; Joshi, K. HyStor: an experimental database of hydrogen storage properties for various metal alloy classes. Int. J. Hydrogen. Energy. 2024, 90, 460-9.
37. Hattrick-simpers, J. R.; Choudhary, K.; Corgnale, C. A simple constrained machine learning model for predicting high-pressure-hydrogen-compressor materials. Mol. Syst. Des. Eng. 2018, 3, 509-17.
38. Witman, M.; Ling, S.; Grant, D. M.; et al. Extracting an empirical intermetallic hydride design principle from limited data via interpretable machine learning. J. Phys. Chem. Lett. 2020, 11, 40-7.
39. Van’t Hoff JH. Studies in chemical dynamics (in French). 1884. https://www.google.com/books?id=A_VoAAAAcAAJ. (accessed 26 Aug 2025).
40. Kingma, D. P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. https://doi.org/10.48550/arXiv.1312.6114. (accessed 26 Aug 2025).
41. Sanchez-Lengeling, B.; Aspuru-Guzik, A. Inverse molecular design using machine learning: generative models for matter engineering. Science 2018, 361, 360-5.
42. Gómez-Bombarelli, R.; Wei, J. N.; Duvenaud, D.; et al. Automatic chemical design using a data-driven continuous representation of molecules. ACS. Cent. Sci. 2018, 4, 268-76.
43. Lu, Z.; Wang, J.; Wu, Y.; Guo, X.; Xiao, W. Predicting hydrogen storage capacity of V–Ti–Cr–Fe alloy via ensemble machine learning. Int. J. Hydrogen. Energy. 2022, 47, 34583-93.
44. Rousseeuw, P. J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53-65.
45. Davies, D. L.; Bouldin, D. W. A cluster separation measure. IEEE. Trans. Pattern. Anal. Mach. Intell. 1979, 1, 224-7.
46. Tsukahara, M. Hydrogenation properties of vanadium-based alloys with large hydrogen storage capacity. Mater. Trans. 2011, 52, 68-72.
47. Ge, Y.; Lang, P. Alloy selections in high-temperature metal hydride heat pump systems for industrial waste heat recovery. Energy. Rep. 2022, 8, 3649-60.
48. Li, Y. L.; Li, P.; Zhai, F. Q.; Zhang, W. N.; Qu, X. H. Hydrogen storage properties of Mg1.7M0.3Ni (M = Mg, La, Ce, Nd) hydrogen storage alloys. Adv. Mater. Res. 2012, 512-5, 1503-8.
49. Witman, M.; Ek, G.; Ling, S.; et al. Data-driven discovery and synthesis of high entropy alloy hydrides with targeted thermodynamic stability. Chem. Mater. 2021, 33, 4067-76.
50. Verma, A.; Wilson, N.; Joshi, K. Solid state hydrogen storage: decoding the path through machine learning. Int. J. Hydrogen. Energy. 2024, 50, 1518-28.
51. Wang, X.; Zhu, F.; Xue, X.; et al. Suction-cast strategy to enhance hydrogen storage performance of rare earth-based alloys. Int. J. Hydrogen. Energy. 2025, 104, 220-7.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Special Issue
Copyright
Data & Comments
Data



















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].