Active learning-based generative design of halogen-free flame-retardant polymeric composites
Abstract
It is of significant importance to design flame-retardant polymeric composites (FRPCs) with superior flame retardancy and appropriate mechanical properties. However, discovering such materials is often reliant on serendipity, as the conventional “trial-and-error” approach is inadequate for navigating the vast virtual space. To overcome this challenge, we propose an active generative design framework to accelerate the development of FRPCs within the expansive virtual space. This framework operates as a closed-loop system, integrating machine learning, knowledge-embedded generative model, and experimental exploration. Through this approach, we derived two interpretable linear expressions and identified a key composition threshold that when the mass fraction of zinc stannate is below 2.5% and that of piperazine pyrophosphate exceeds 12.5%, the flame retardancy of polypropylene (PP)-based FRPCs is significantly enhanced. By processing and characterizing 10 FRPCs, we successfully designed two composites with flame retardancy improved by 1% compared to the top-performing reference FRPC in the initial dataset - without compromising mechanical properties. This work effectively resolves the trade-off between flame retardancy and mechanical performance at a low cost, demonstrating a promising pathway for the accelerated discovery of PP-based FRPCs with balanced properties.
Keywords
INTRODUCTION
Recently, functional polymeric materials have been developed to meet diverse needs across various fields[1,2]. Due to exceptional mechanical properties, excellent chemical stability, outstanding cost-performance ratio, and facilitated processing properties[3,4], polypropylene (PP) has been widely utilized in the electronics[5,6], automobile[7,8], packaging[9,10], architecture[11,12], textile[13,14], environmental protection[15], and medical industries[16,17]. However, its inherently low flame-retardancy poses a significant fire hazard, limiting its broader application[18,19]. Consequently, it is of paramount importance to enhance the flame-retardancy of PP.
Since the 1970s[20], halogenated flame retardants have been extensively employed to improve the flame resistance of PP-based composites[21,22]. These retardants release halogen free radicals during combustion, which scavenge active hydrogen and hydroxyl radicals, thereby terminating further flaming. However, the emission of toxic gases during this process has raised serious environmental concerns, leading to regulatory restrictions and bans on halogenated flame retardants[23]. As a result, halogen-free flame retardants have emerged as effective and environmentally friendly alternatives. These retardants form a dense carbonized layer upon flaming, insulating oxygen and preventing further combustion. They have enhanced flame-retardancy of PP-based flame-retardant polymeric composites (FRPCs)[24,25], with the highest reported limited oxygen index (LOI) reaching 39.9%[26]. However, the large filler loadings required for enhanced flame retardancy often compromise the mechanical properties of PP-based FRPCs, restricting their practical applications. Therefore, it is urgent to propose a solution to enhancing the flame-retardancy of FRPCs without compromising mechanical properties. Given the vast virtual space and the high cost and time investment associated with conventional “trial-and-error” approaches[27], it is challenging to design PP-based FRPCs with balanced flame-retardancy and mechanical properties.
Machine learning (ML) uncovers the hidden correlations within existing data, predicts uncharted territories, and identifies novel materials, thereby accelerating the development of copolymer materials[28,29], thermal conductive polymer materials[30,31], organic solar cells polymeric materials[32,33], perovskite optoelectronic materials[34,35], perovskite solar cells[36,37], high entropy alloys[38,39], amorphous alloys[40,41], metal-organic frameworks (MOFs) catalyst[42,43], and organic semiconductor materials[44,45]. In the field of PP-based FRPC design, ML has demonstrated considerable potential. For example, Chen et al. successfully combined ML with experimental validation on small datasets to design optimized PP-based FRPCs[46,47]. However, the PP composites contain multiple fillers, which may cause data sparsity in the high-dimensional small-sample PP composites dataset. Sparse data is unable to depict the complete relation between features and properties, leading to big challenges for material design[48,49]; thus, the direct recipe-property prediction is still elusive because of the comparably small databases[50], because small database may cause the model over-fitting or under-fitting[51,52], affecting the prediction accuracy of the model and complicating the exploration of recipe-property relation[53,54]. Active learning strategy can explore the accurate insights for further design, thereby accelerating the discovery of novel materials with reduced costs, ensuring a more reliable and accurate design process[55,56].
Here, we proposed an active generative design framework to discover the halogen-free PP-based FRPCs with enhanced LOI and appropriate tensile strength (TS). The framework integrates ML, generative model (GM) and experimental exploration in a closed-loop process. First, the data collected from literature and experiments was preprocessed. Then, five algorithms were considered to select the optimal algorithm for further optimized models for both properties. Next, a knowledge-embedded generative design approach was applied to generate virtual FRPC candidates within the prior distribution space. The optimal models were then used to screen these candidates, selecting those with superior LOI and appropriate TS for experimental validation. The experimental results were subsequently fed back into the dataset to refine the models, and the iterative process continued until the desired FRPCs were successfully identified. After two iterations, two FRPCs with exceptional LOI and appropriate TS were designed, with 1% improvement of LOI and comparable TS to the reference FRPC. Our framework not only offers a rational method to accelerate the design of FRPCs, but also elucidates the relationship between mass fraction and properties through interpretable linear functions. Moreover, it addresses the contradiction between flame retardancy and mechanical properties of FRPCs.
MATERIALS AND METHODS
Here, we proposed an active generative design framework to design PP-based FRPCs with desired LOI and appropriate TS. The workflow of the framework can be represented as Figure 1. It encompassed four parts. (A) Data collection and preprocessing, which involved data collection and data preprocessing to ensure data quality and usability; (B) Model establishment and selection. The appropriate models were established for further FRPCS design; (C) Generative design. The optimal models and GM were combined to design virtual FRPCs with desired properties; (D) Experimental exploration. The obtained novel experimental FRPCs are fed back to the original dataset to improve the performance of model and design new FRPCs in next iteration.
Figure 1. The workflow of the active generative design framework for FRPCs. FRPCs: Flame-retardant polymeric composites.
Data collection and preprocessing
The original 227 LOI data and 233 TS data were collected from our previous work[46,47] and additional experiments. Each data point contains the mass fraction of PP matrix and fillers, with corresponding properties (LOI or TS), and the data are stored at https://github.com/WYDCXHJLMWB/Data-and-Software-sharing. To ensure data quality, an outlier detection and removal process was executed to mitigate the impact of outliers on the subsequent ML models. For this purpose, isolation forest, one-class support vector machine (SVM), and local outlier factor (LOF) were employed; these algorithms labeled each data point with a 0 (normal) or 1 (anomaly). A data point was considered as an outlier and subsequently removed if at least two of the three algorithms flagged it as such. After outlier deletion, the preprocessed data were randomly split as training set and test set according to the ratio 4:1. To neutralize the effects of varying data scales, standardization was performed on the dataset using the scikit-learn 1.5.1.
Model establishment and selection
The mass fractions of fillers and matrix of the composites were extracted as key features for model construction. A comparative analysis was then conducted among five ML algorithms: support vector regression (SVR), ridge regression (Ridge), gradient boosting regression (GBR), robust extremely gradient boosting regression (XGBoost), and random forest regression (RF). This goal was to identify the optimal models for two properties. In model selection, the interpretability and model performance were comprehensively considered. Pearson correlation coefficients (r), coefficient of determination (R2) and root mean squared error (RMSE) were set as the estimating indicators of the models. Higher values of r and R2, and lower RMSE values, indicate better model performance. To assess the robustness of each model, leave-one-out cross-validation (LOOCV) was employed on the training set. Meanwhile, the test set was utilized to gauge the generalization capabilities of models; notably, the test set is applied after hyperparameter optimization. When selecting the optimal algorithm, model interpretability was prioritized when the performance of different algorithms was comparable. Linear models, such as Ridge regression, offer high interpretability by representing the relationship between features and target properties through explicit linear equations. For instance, as depicted in Supplementary Figure 1, in the prediction of LOI, the nonlinear models SVR, XGBoost, GBR, and RF achieved LOOCV R2 values of 0.907, 0.942, 0.958, and 0.956, r of 0.955, 0.971, 0.979, and 0.978, and RMSE values of 2.393, 1.893, 1.612, and 1.642, respectively. In comparison, the linear Ridge model achieved an R2 of 0.944, r of 0.971, and RMSE of 1.857 under LOOCV. Given the similar performance between the nonlinear models and Ridge, the Ridge model was selected as the optimal one due to its inherent interpretability. Then, the optimal models for two properties were optimized via grid search method, the optimization was aimed at searching for the appropriate hyperparameter sets resulting the best model performance. The process of model construction is depicted in Supplementary Figure 2. After gaining the optimized model, the stability of the optimized models was evaluated by randomly splitting the training set and test set based on the ratio 4:1 repeatedly 100 times, and the average results of the repetition were considered to validate the stability of the models.
Generative design
The design of the FRPCs was conducted based on GM. In this process, GM, ML models, and sampling were combined to perform a large-scale search of desired FRPCs. Initially, Wasserstein autoencoder (WAE)[57] was applied to learn the low-dimensional latent distribution of the original dataset. The essence of WAE is to minimize the maximum mean discrepancy (MMD)[58] between latent distribution of original dataset and Gaussian prior. The MMD quantifies the difference in moments between two distributions, with a smaller MMD indicating greater similarity between the distributions. Then, the Gaussian mixture model (GMM) was applied to describe the distribution of the optimal latent space. Finally, virtual materials were generated using Metropolis-Hastings Markov chain Monte Carlo (MCMC) sampling in the latent space. The MCMC sampling starts with the initial point in the low dimension, and the next sampling will be based on the prior distribution - Gaussian distribution. The GMM was applied to calculate the acceptance probability of the candidate. The acceptance probability is the measurement of the distance between the sampling points and prior distribution. The candidates were sampled by minimizing the acceptance probability, thus approaching the prior distribution. When decoding, the rules gained from the ML models were embedded to the GM as constraints of reconstructing the data. Then, the constructed ML models were applied to select FRPCs with excellent LOI and appropriate TS for further experimental exploration.
Experimental exploration
The synthesis steps were as follows. First, PP, piperazine pyrophosphate (PAPP), melamine polyphosphate (MPP), zinc stannate (ZS), and anti-drip-agent (ADA) were dried in the 105 °C-oven for 8 h to prevent the formation of bubbles when processing which would influence the property of materials. Second, measuring the mass of each component of FRPCs. Then, the components were mixed in the high-speed mixer to form symmetrical mixture. Then, the mixture was put into the Twin-screw extruder (TSE-20 type) for melt blending, setting the temperature of the melt blending process as 195 °C. After air cooling, the master batch of PP flame retardant composites was prepared by the pelletizer. In order to meet the needs of property tests, the standard specimens of the PP-based FRPCs were prepared by putting the dried master batch into the injection molding machine. Here, the master batch were dried in the same condition mentioned above.
After synthesis of the standard specimens of the FRPCs, the LOI and TS tests were conducted. The LOI values of the designed FRPCs were tested by Oxygen index tester (Model 5801A). According to the GB/T2406.2-2009, the minimized oxygen concentration to maintain the combustion of samples in the nitrogen and oxygen mixture was recorded as the LOI of the samples. The TS of the FRPCs was tested by a universal testing machine (UTM). According to ASTM d638 standard, the sample for tests was fixed, and the rate of tensile was set as 50 mm/min; in the process, the Stress-Strain Curves of materials were recorded to gain the TS. In order to remove experimental error, each sample was tested twice parallelly during the TS test.
Then, the novel experiments fed back to the original dataset to improve the performance of models and accelerate the process of designing desired FRPCs. There are five FRPCs with highest LOI (43%) in the original dataset, and the FRPC with the best TS among them was considered as reference FRPC. If the designed FRPCs show enhanced LOI and comparable TS to the reference FRPC, the active iteration stops.
RESULTS AND DISCUSSION
Interpretable Ridge models construction
The distribution of the LOI and TS values in original data is depicted in Supplementary Figure 3A. It is evident that the LOI values span from a minimum of 19 to a maximum of 43, while the TS values range from 10.434 to 22.35. A clear negative correlation between LOI and TS is observed in Supplementary Figure 3B, which can be attributed to the incorporation of substantial amounts of flame retardants. After outlier deletion, the LOI data reduced from 227 to 217, and the TS data reduced from 233 to 228. This curation of the dataset is essential for enhancing the reliability of subsequent models.
The mass fractions of fillers and matrix of the FRPCs were leveraged to construct models using five ML algorithms. As depicted in Figure 2A, in the initial iteration of the active framework, nonlinear and linear algorithms exhibit notably high R2 and r values for LOOCV, with values all exceeding 0.9 for the LOI model. These results underscore the exceptional robustness of these models. Notably, the linear model shows almost the same model performance as the nonlinear models, illustrating commendable robustness (R2 of 0.944, r of 0.971, and RMSE of 1.857 under LOOCV), coupled with its inherent interpretability. Adhering to the principle of “Ockham’s Razor”[59], which advocates for simplicity and practicality in model selection, the Ridge algorithm was chosen for further application. Although the linear model is unable to express the inherent nonlinear relation in electric conductive polymer composites[60,61], the Ridge model illustrates excellent robustness for this dataset. To further optimize the Ridge model, a grid search method was employed to identify the optimal regularization parameter (alpha). As illustrated in Figure 2B, when alpha was set to 0.1, the model shows outstanding robustness (R2 of 0.945 for LOOCV) and commendable generalization ability (R2 of 0.919 for the test set).
Figure 2. (A) The comparison of the five algorithms in the first iteration for LOI and TS models; (B) The functions between the experimental and predicted values of LOI and TS models; (C) The average results of repetition of 100 times of random splitting in the first iteration for LOI and TS models. LOI: Limited oxygen index; TS: tensile strength.
Subsequently, the training set and test set were randomly split 100 times to assess the model’s stability. The average r, R2, and RMSE were calculated from these repetitions. As presented in Figure 2C, the average results closely resemble those of the optimized model, with the deviation of results remaining within a narrow range, thereby confirming the stability of the LOI-Ridge model.
For the TS model, the Ridge model stands out for its excellent interpretability, coupled with strong robustness, as evidenced in Figure 2A. As a result, the Ridge model was chosen as the optimal model for TS. The TS model was further refined using the grid search method. As shown in Figure 2B, when the alpha is set to 16, the robustness of model improves, with the R2 of LOOCV increasing from 0.717 to 0.722. And it represents commendable generalization ability. Chen et al. constructed a TS Screening and Sparsifying Operator (SISSO) model for FRPCs with the results that the R2 of test results is lower than 0.5[46]. Joo et al. constructed a TS deep neural network model with the RMSE of 4.9358[62]. Our constructed TS model illustrates better R2 of 0.752 and RMSE of 1.246 for test set. We consider improving the LOI prior to improving the TS, thus in spite of the medium-level model performance of TS, it can meet application requirements. To confirm the stability of the TS model, the random splitting process was repeated 100 times, and the average model results were used for stability verification. As depicted in Figure 2C, the average outcomes of these repetitions closely match those of the optimized model, with the deviation of results remaining within a narrow range, thereby confirming the stability of the TS model. The function between the experimental and predicted values of LOI and TS is shown in Figure 2B. The scatter plots, which cluster closely around the diagonal line, affirm the remarkable robustness and generalization capabilities of models. Notably, the Ridge models elucidate the relationship between the features and the properties through interpretable linear functions, offering greater transparency compared to those constructed by Chen et al.[46]. The models established accurate, interpretable and concise equations with physical insights, facilitating the proposal of general scientific laws. Notably, since the types of matrix and fillers are consistent across all samples, and the processing parameters are also identical, it is unnecessary to consider molecular structural parameters and processing conditions in this dataset. However, this may also imply a potential limitation of the current models.
Knowledge discovery
The optimized LOI-Ridge model in the first iteration can be expressed as:
And the optimized TS Ridge model in the first iteration can be expressed as:
where each coefficient depicts the impact of the feature. It is evident that the PAPP is the most important feature for the LOI model with the largest coefficient. The addition of PAPP, ADA, and wollastonite improves LOI, while the ZS, Mg(OH)2, 9,10-dihydro-9-oxa-10-phosphaphenanthrene-10-oxide-phosphonamidate (DOPO), and MPP are detrimental to the LOI. Moreover, it is obvious that the addition of ZS is positive to the TS, while the addition of DOPO is detrimental to the TS. The coefficient of FP-250S is 0, indicating the slight impact of the feature. This is because only one FRPC contains the FP-250S in the original dataset, the model was unable to find any rules of the FP-250S. In order to research the synergistic effects of different features, the linear equation was extended by adding interaction term. Here, the interaction term was created by multiplying PAPP and MPP. According to the extended LOI equation in the Supplementary Materials, the positive coefficient of the interaction term indicates the positive synergistic effects of PAPP and MPP for the LOI, which can be explained by the synergistic effect between PAPP and MPP in the gas phase and the condensed phase[26]. Similarly, the interaction term in the extended TS model is positive, signifying a beneficial synergistic effect on TS.
According to the statistical analysis of original data of LOI [Figure 3A], when the addition of ZS is below 2.5% and the addition of PAPP is above 12.5%, the FRPCs tend to exhibit a higher LOI, as shown in Figure 3B, the TS tends to be higher when the content of PAPP is smaller.
Figure 3. (A) The statistical analysis of the effect of ZS and PAPP on LOI original data; (B) The statistical analysis of the effect of ZS and PAPP on TS original data. ZS: Zinc stannate; PAPP: piperazine pyrophosphate; LOI: limited oxygen index; TS: tensile strength.
While the linear equations highlight the importance of each filler and correlation between each filler and properties, they are unable to provide insight into the optimal filler range for addition. Therefore, the SHapley Additive exPlanations (SHAP) method was employed to better understand the relationship between features and properties, allowing for the identification of the optimal ranges for each feature. The feature importance reduces from top to bottom in Figure 4A. The PAPP is the most important feature for the LOI, which is consistent with the rule concluded by coefficient of the LOI-Ridge equation. The global impact of SHAP is depicted in Figure 4B; the abscissa is the SHAP values; higher SHAP values with higher feature values reveal the positive impact of the feature on the target property. It is evident to find that the PAPP is positive to the LOI and the Mg(OH)2 is negative to LOI. According to the SHAP impact of each feature [Figure 4C], it is evident that when the addition of ZS is lower than 2.5%, and addition of PAPP is beyond 12.5%, the FRPCs tend to show increased LOI. It is transparent that the coexistence of PAPP and MPP is positive to the LOI when the PAPP is upper than 12.5% [Figure 4C], which is consistent with the rule found by the LOI-Ridge equation.
Figure 4. (A) The feature importance and SHAP global impact of the LOI model in the first iteration; (B) The SHAP global impact of the LOI model in the first iteration; (C) The SHAP local impact of the LOI and the interaction of PAPP and MPP on LOI. SHAP: SHapley Additive exPlanations; LOI: limited oxygen index; PAPP: piperazine pyrophosphate; MPP: melamine polyphosphate.
From the analysis, it is concluded that PAPP positively influences LOI, attributable to the synergistic effects of phosphorus and nitrogen. During combustion, nitrogen-containing compounds release non-flammable gases such as ammonia, which dilute the oxygen concentration and reduce fire intensity. Additionally, phosphorus and nitrogen together contribute to forming a thicker, more effective foaming carbon barrier, thereby improving flame-retardancy[63]. Moreover, Mg(OH)2 is found to have a detrimental effect on LOI, and the finding aligns with the patterns observed by Chen et al.[46]. This phenomenon can be attributed to the uneven dispersing performance of Mg(OH)2 in the PP matrix[64]. Additionally, the DOPO exerts a negative impact on TS, consistent with the observations made by Chen et al.[46].
Knowledge-embedded generative design
Drawing from the insights gleaned by the LOI and TS models, we identified PAPP and ZS as crucial fillers in the new FRPCs. The mass fraction of PAPP is mandated to exceed 12.5% due to its positive influence on LOI, while ZS should be limited to less than 2.5% to maximize its beneficial effect on TS while minimizing its negative influence on LOI. Additionally, recognizing the synergistic effects of PAPP and MPP, MPP is also designated as an essential filler in the new FRPCs. Considering the beneficial effects on the LOI, ADA is considered as a necessary filler as well; moreover, the addition of ADA can prevent the potential secondary fires during combustion caused by the dripping of PP. Furthermore, considering the positive impact of the addition of wollastonite on the LOI, it is another essential filler in new FRPCs.
Although considering the knowledge, the possible space contains C699, namely 75287520 kinds of FRPCs, according to the “Stars and Bars” combinatorial method, which is enormous for enumeration method. As shown in Figure 5A, based on the distribution of the original dataset, the WAE could generate new FRPCs according to the insights of models. Here, WAE was applied to learn the latent space of the original dataset, and the GMM was applied to depict the latent space. As shown in Supplementary Figure 4, different colors of points represent different clusters in the latent space. The MCMC sampling was conducted in the latent space to sample virtual points. Then, during the decoding phase, we reconstructed the dataset based on the constraints of the insights gleaned from ML models to ensure viable FRPCs. The process of designing virtual samples includes a sampling process and a decoding process. In sampling process, the Metropolis Acceptance Criterion was applied to ensure that the distribution of generated samples is similar to the prior distribution. In decoding process, the insights gleaned from the models limit the decoding process strictly. This process maintains a trade-off between the exploration of new formulation spaces and conformity to knowledge-based constraints. The ML models were applied to predict the LOI and TS values of the virtual FRPCs. Ultimately, we have designed virtual novel FRPCs with predicted exceptional LOI and appropriate TS. As shown in Supplementary Figure 5 and Supplementary Table 1, none of the experimental LOI surpasses that of reference FRPC; however, the costs of all these materials are comparatively low, confirming the cost-effectiveness of the strategy.
Figure 5. (A) Using GM and Ridge models to explore the virtual space; (B) The conceptual workflow of the tensile test of designed FRPCs. GM: Generative model; FRPCs: flame-retardant polymeric composites.
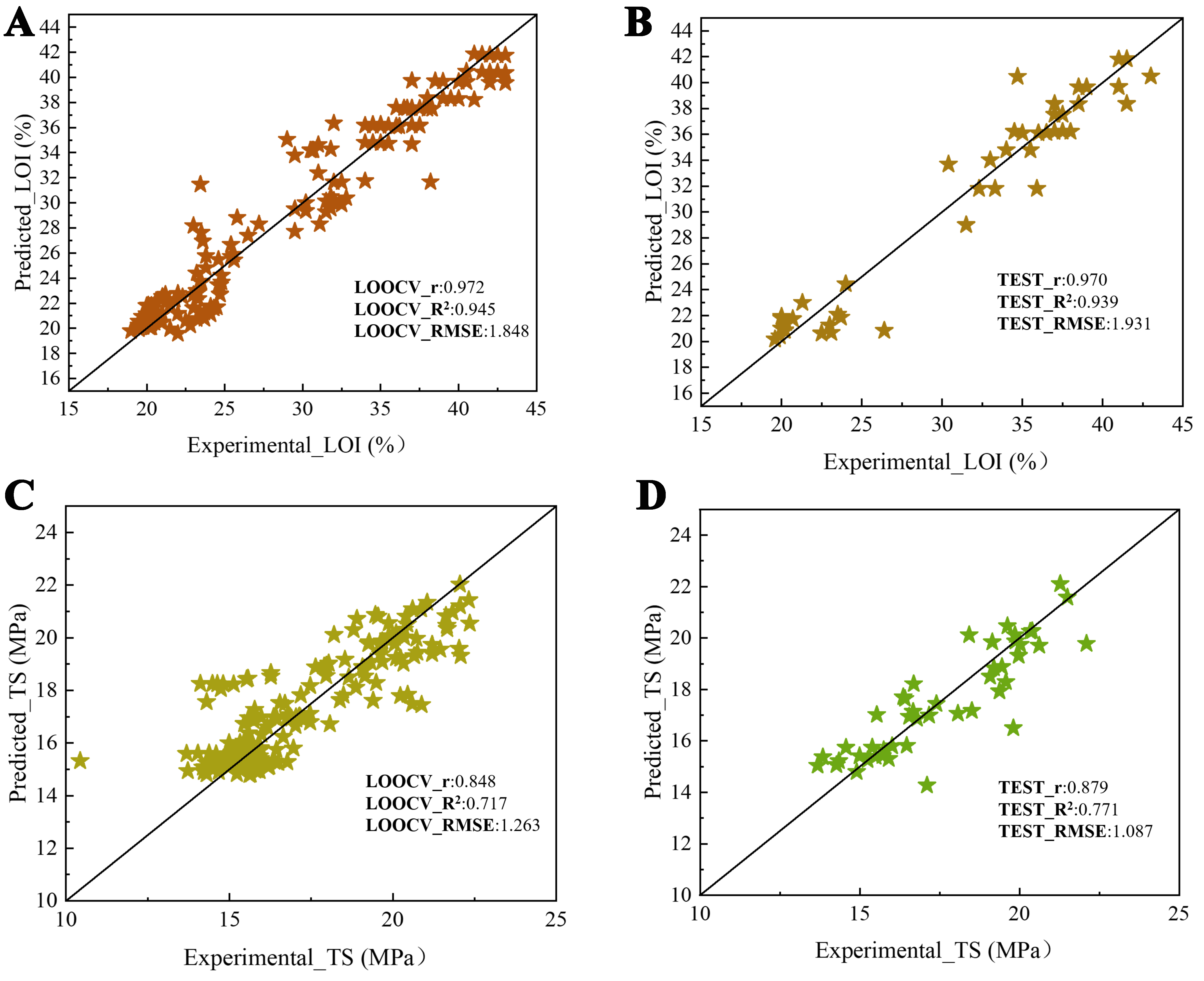
In order to design FRPCs with enhanced LOI and appropriate TS, the new experimental values are fed back to the framework to implement next iteration of the active framework. As shown in Supplementary Figure 6, the Ridge model was selected again due to interpretability and consistent model results compared to nonlinear models. As shown in Figure 6, the R2 of Ridge LOI model for test set increases to 0.939, and the R2 for the test set of the Ridge TS model rises to 0.771, reflecting improved generalization ability for both models. The stability of models is confirmed through the average results of repeated splitting with minimal deviations for the LOI and TS models [Supplementary Figure 7].
Figure 6. The functions between the experimental and predicted values of (A) LOOCV of LOI model, (B) Test set of LOI model, (C) LOOCV of TS model, (D) Test set of TS model in the second iteration. LOOCV: Leave-one-out cross-validation; LOI: limited oxygen index; TS: tensile strength.
The equations for the LOI and TS Ridge models in the second iteration are detailed in the Supplementary Materials. The coefficients of the equations in the second iteration reveal that ZS and PAPP have positive effects on TS and LOI, respectively. Although ZS appears to be negatively correlated with LOI, SHAP analysis [Supplementary Figure 8] indicates that when ZS is below 3.5%, it has a positive impact on LOI, and when the PAPP is upper than 12.5%, the LOI tends to be higher. In this iteration, the insights regarding ZS and PAPP were updated by combining the rules derived from both the current and the previous iteration. Additionally, the chemists specialized in experiments could predict the LOI and TS of new PP-based FRPCs on https://github.com/WYDCXHJLMWB/Online-prediction-of-LOI-and-TS, which could be convenient for the material design of PP-based FRPCs. The insights were embedded to generative design again. The TS of the designed FRPCs was calculated according to the stress-strain curves [Figure 5B and Supplementary Figure 9]. The TS was obtained from:
Here, the unit of stress is Newton. The maximum stress is obtained from the highest point of the curves, and the size of the specimen is 10 millimeters (mm) × 4 mm; thus, the cross-sectional area of the specimen is 40 square millimeters (mm2). The average TS of parallel test was recorded as the TS of designed FRPCs.
As shown in Table 1, two of the novel FRPCs exhibit superior LOI (with improvement of 1%) and comparable TS to the reference FRPC. The relative error (RE) between the predicted and experimental values is within the RMSE of ML models, validating the reliability of the constructed models. Furthermore, the costs of the designed materials are deemed acceptable; thus, they are promising for practical applications.
The experimental valuesa and predicted valuesb, and the RE of designed materials in the second iteration
| No. | PP | PAPP | ZS | MPP | ADA | W | LOI | TS | LOI RE | TS RE | Cost (RMB/kg) |
| FRPC-1 | 63.2 | 23 | 1.5 | 9 | 0.3 | 3 | 43.500a 40.500b | 15.845a 15.553b | -6.91% | -1.84% | 16.203 |
| FRPC-2 | 65.2 | 23 | 1.5 | 7 | 0.3 | 3 | 43.000a 40.499b | 16.940a 15.716b | -5.82% | -7.23% | 15.863 |
| FRPC-3 | 59.2 | 23 | 1.5 | 11 | 0.3 | 5 | 42.500a 41.814b | 16.146a 14.961b | -1.61% | -7.34% | 16.523 |
| FRPC-4 | 58.2 | 23 | 0.5 | 13 | 0.3 | 5 | 43.500a 41.796b | 15.303a 14.820b | -3.92% | -3.16% | 16.403 |
| FRPC-5 | 62.7 | 20 | 1 | 13 | 0.3 | 3 | 37.5a 38.344b | 17.208a 15.330b | 2.25% | -10.91% | 16.023 |
| FRPC-6 | 61.7 | 23 | 1 | 9 | 0.3 | 5 | 43.000a 41.809b | 15.832a 15.135b | -2.77% | -4.40% | 15.953 |
CONCLUSIONS
In summary, we have proposed an active generative framework aimed at designing PP-based FRPCs with superior LOI and appropriate TS. We have constructed two Ridge models for LOI and TS. These models provided valuable insights that guided our generative design. Integrating generative design with the optimal models for LOI and TS, we conceived novel FRPCs for further experimental exploration. After two iterations of the active generative framework, two of the designed FRPCs show enhanced LOI (improvement of 1%) with comparable TS to the reference FRPC. Additionally, the costs of all designed materials were relatively low, underscoring their practical potential for application. Our models revealed that when the mass fraction of ZS is below 2.5% and the mass fraction of PAPP exceeds 12.5%, the LOI tends to be higher. These insights offer valuable guidance for future experimental design. Overall, our framework merges active learning, knowledge-embedded generative design and experiments exploration to engineer FRPCs, proposing a solution to trade-off flame retardancy and mechanical properties of the PP-based FRPCs. With the continuous development of experimental exploration, the accumulation of data in the future will enhance the model’s performance, accelerate material design, and deepen the understanding of the relationship between high-dimensional features and properties. This will not only help to reduce uncertainties but also pave the way for more reliable real-world applications.
DECLARATIONS
Authors’ contributions
Writing - original draft, conceptualization, software, formal analysis: Ma, W.
Methodology, validation, investigation: Li, L.
Investigation, visualization: Zhang, Y.
Writing - review and editing, conceptualization: Li, M.
Writing - review and editing, data curation: Song, N.
Writing - review and editing, conceptualization, funding acquisition: Ding, P.
Availability of data and materials
The data underlying this study are openly available at https://github.com/WYDCXHJLMWB/Data-and-Software-sharing.
Financial support and sponsorship
This work was supported by the Key Program of Science and Technology of Yunnan Province (202302AB080022) and Suzhou Key Technology Research Project (SYG2024017).
Conflicts of interest
Ding, P. is the Guest Editor of the Special Issue “Design of Polymer and Its Composites Driven by Data and Domain Knowledge”. Ding, P. was not involved in any steps of editorial processing, notably including reviewers’ selection, manuscript handling and decision-making. The other authors declare that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
Supplementary Materials
REFERENCES
1. Li, Q.; Yang, X.; Li, X.; et al. Cross-scale optimization of interfacial adhesion and thermal-mechanical performance in carbon fiber-reinforced polyimide composites through sizing agent evolution. Compos. Sci. Technol. 2025, 266, 111174.
2. Wang, N.; Li, X.; Cao, W.; et al. Lightweight polyimide nanocomposites with 3D cocarbonized MXene/carbon fiber networks for electromagnetic interference shielding and high-temperature stability. ACS. Appl. Nano. Mater. 2025, 8, 7347-59.
3. Yuan, H.; Hu, S.; Zhou, Y.; et al. Enhanced electrical properties of styrene-grafted polypropylene insulation for bulk power transmission HVDC cables. CSEE. J. Power. Energy. Syst. 2024, 10, 361-70.
4. Wang, K.; Wang, Q.; Wang, L.; Chen, D.; Ma, Y.; Yang, W. Sustainable furfuryl alcohol-based flame retardants with regular spherical morphology: endow polypropylene with excellent flame retardancy, smoke suppression, and mechanical properties. Chem. Eng. J. 2024, 496, 153848.
5. Sui, H.; Wu, K.; Zhao, G.; Yang, K.; Dong, J.; Li, J. Greatly enhanced temperature stability of eco-friendly polypropylene for cable insulation by multifold long-chain branched structures. Chem. Eng. J. 2024, 485, 149811.
6. Zhou, G.; Li, L.; Wang, D. W.; et al. A flexible sulfur-graphene-polypropylene separator integrated electrode for advanced Li-S batteries. Adv. Mater. 2015, 27, 641-7.
7. Reale Batista, M. D.; Drzal, L. T.; Kiziltas, A.; Mielewski, D. Hybrid cellulose-inorganic reinforcement polypropylene composites: lightweight materials for automotive applications. Polym. Compos. 2020, 41, 1074-89.
8. Wu, G.; Lei, L.; Wu, Y.; Yu, F.; Li, J.; He, H. Preparation and characterization of polypropylene/sepiolite nanocomposites for potential application in automotive lightweight materials. Polymers 2023, 15, 802.
9. Antosik, A. K.; Kowalska, U.; Stobińska, M.; et al. Development and characterization of bioactive polypropylene films for food packaging applications. Polymers 2021, 13, 3478.
10. Dixit, S.; Yadav, V. L. Optimization of polyethylene/polypropylene/alkali modified wheat straw composites for packaging application using RSM. J. Clean. Prod. 2019, 240, 118228.
11. Echeverria, C. A.; Pahlevani, F.; Sahajwalla, V. Valorisation of discarded nonwoven polypropylene as potential matrix-phase for thermoplastic-lignocellulose hybrid material engineered for building applications. J. Clean. Prod. 2020, 258, 120730.
12. Blazy, J.; Blazy, R. Polypropylene fiber reinforced concrete and its application in creating architectural forms of public spaces. Case. Stud. Constr. Mater. 2021, 14, e00549.
13. Frankenbach, L. A.; Lukoschek, S.; Kruppke, I.; Cherif, C. Multifilament spinning of mechanically recycled polypropylene from post-consumer sources for a circular economy in textile applications. Sci. Rep. 2025, 15, 14047.
14. Karaduman, Y.; Onal, L. Flexural behavior of commingled jute/polypropylene nonwoven fabric reinforced sandwich composites. Compos. B. Eng. 2016, 93, 12-25.
15. Raee, E.; Kaffashi, B. Biodegradable polypropylene/thermoplastic starch nanocomposites incorporating halloysite nanotubes. J. Appl. Polym. Sci. 2018, 135, 45740.
16. Zhang, X.; Yu, N.; Ren, Q.; et al. Janus nanofiber membranes with photothermal-enhanced biofluid drainage and sterilization for diabetic wounds. Adv. Funct. Mater. 2024, 34, 2315020.
17. Ludwicka, K.; Kolodziejczyk, M.; Gendaszewska-Darmach, E.; et al. Stable composite of bacterial nanocellulose and perforated polypropylene mesh for biomedical applications. J. Biomed. Mater. Res. B. Appl. Biomater. 2019, 107, 978-87.
18. Xu, S.; Li, S. Y.; Zhang, M.; et al. Fabrication of green alginate-based and layered double hydroxides flame retardant for enhancing the fire retardancy properties of polypropylene. Carbohydr. Polym. 2020, 234, 115891.
19. He, S.; Deng, C.; Zhao, Z.; Chen, Z.; Wang, Y. Hyperbranched polyamide-amine based phosphorous-containing flame retardant for simultaneous flame retardancy and high performance of polypropylene. Compos. B. Eng. 2023, 250, 110431.
20. Shaw, S. D.; Blum, A.; Weber, R.; et al. Halogenated flame retardants: do the fire safety benefits justify the risks?. Rev. Environ. Health. 2010, 25, 261-305.
21. Ferry, L.; Lopez Cuesta, J.; Chivas, C.; Mac Way Hoy, G.; Dvir, H. Incorporation of a grafted brominated monomer in glass fiber reinforced polypropylene to improve the fire resistance. Polym. Degrad. Stab. 2001, 74, 449-56.
22. Chen, X.; Xu, G.; Zhang, S.; et al. Improving the flame retardancy of the polypropylene/aramid fiber composites by the introduction of decabromodiphenyl ethane and antimony trioxide. J. Appl. Polym. Sci. 2013, 127, 1446-53.
23. He, W.; Song, P.; Yu, B.; Fang, Z.; Wang, H. Flame retardant polymeric nanocomposites through the combination of nanomaterials and conventional flame retardants. Prog. Mater. Sci. 2020, 114, 100687.
24. Tang, W.; Qian, L.; Prolongo, S. G.; Qiu, Y.; Wang, D. Macromolecular piperazine/aluminum phosphate hybrid and its efficient intumescent flame retardant/thermal conductive polypropylene. Chem. Eng. J. 2024, 495, 153162.
25. Zheng, Z.; Liu, Y.; Dai, B.; Meng, C.; Guo, Z. Fabrication of cellulose-based halogen-free flame retardant and its synergistic effect with expandable graphite in polypropylene. Carbohydr. Polym. 2019, 213, 257-65.
26. Yuan, Z.; Wen, H.; Liu, Y.; Wang, Q. Synergistic effect between piperazine pyrophosphate and melamine polyphosphate in flame retarded glass fiber reinforced polypropylene. Polym. Degrad. Stab. 2021, 184, 109477.
27. Wang, Y.; Guo, R.; Zhang, J.; Wang, H.; Niu, B.; Yan, H. P/N/Si-rich and flexible coating imparting polypropylene excellent flame retardancy without compromising its inherent mechanical properties. Chem. Eng. J. 2024, 487, 150519.
28. Tamasi, M. J.; Patel, R. A.; Borca, C. H.; et al. Machine learning on a robotic platform for the design of polymer-protein hybrids. Adv. Mater. 2022, 34, 2201809.
29. Reis, M.; Gusev, F.; Taylor, N. G.; et al. Machine-learning-guided discovery of 19F MRI agents enabled by automated copolymer synthesis. J. Am. Chem. Soc. 2021, 143, 17677-89.
30. Zhu, M.; Song, H.; Yu, Q.; Chen, J.; Zhang, H. Machine-learning-driven discovery of polymers molecular structures with high thermal conductivity. Int. J. Heat. Mass. Transf. 2020, 162, 120381.
31. Ma, R.; Zhang, H.; Xu, J.; et al. Machine learning-assisted exploration of thermally conductive polymers based on high-throughput molecular dynamics simulations. Mater. Today. Phys. 2022, 28, 100850.
32. Tahir, M. H.; Farrukh, A.; Alqahtany, F. Z.; Badshah, A.; Shaaban, I. A.; Assiri, M. A. Accelerated discovery of polymer donors for organic solar cells through machine learning: from library creation to performance forecasting. Spectrochim. Acta. A. Mol. Biomol. Spectrosc. 2025, 326, 125298.
33. Alzahrani, F. M. A.; Saqib, M.; Arooj, M.; et al. Virtual screening of efficient building blocks and designing of new polymers for organic solar cells. J. Phys. Chem. Solids. 2023, 178, 111340.
34. Luo, W.; Xian, X.; Zhu, J.; et al. Highly efficient screening of halide double perovskite optoelectronic materials based on machine learning. ACS. Appl. Mater. Interfaces. 2025, 17, 18609-22.
35. Harth, M.; Vesce, L.; Kouroudis, I.; Stefanelli, M.; Di Carlo, A.; Gagliardi, A. Optoelectronic perovskite film characterization via machine vision. Sol. Energy. 2023, 262, 111840.
36. Wang, J.; Qi, Y.; Zheng, H.; et al. Advancing vapor-deposited perovskite solar cells via machine learning. J. Mater. Chem. A. 2023, 11, 13201-8.
37. Im, J.; Lee, S.; Ko, T.; Kim, H. W.; Hyon, Y.; Chang, H. Identifying Pb-free perovskites for solar cells by machine learning. npj. Comput. Mater. 2019, 5, 177.
38. Zeng, Y.; Man, M.; Ng, C. K.; et al. Machine learning-based inverse design for single-phase high entropy alloys. APL. Mater. 2022, 10, 101104.
39. Ren, W.; Zhang, Y.; Wang, W.; Ding, S.; Li, N. Prediction and design of high hardness high entropy alloy through machine learning. Mater. Design. 2023, 235, 112454.
40. Li, Z.; Long, Z.; Lei, S.; Tang, Y. Machine learning driven rationally design of amorphous alloy with improved elastic models. Mater. Design. 2022, 220, 110881.
41. Tang, Y.; Wan, Y.; Wang, Z.; et al. Machine learning and Python assisted design and verification of Fe–based amorphous/nanocrystalline alloy. Mater. Design. 2022, 219, 110726.
42. Bai, X.; Li, Y.; Xie, Y.; Chen, Q.; Zhang, X.; Li, J. High-throughput screening of CO2 cycloaddition MOF catalyst with an explainable machine learning model. Green. Energy. Environ. 2025, 10, 132-8.
43. Liu, Y.; Sun, J.; Chai, Y.; Yang, Y.; Yang, Z. Screening of two-dimensional conductive MOFs as OER catalysts assisted by machine learning. J. Mater. Sci. 2025, 60, 2863-77.
44. Johnson, H. M.; Gusev, F.; Dull, J. T.; et al. Discovery of crystallizable organic semiconductors with machine learning. J. Am. Chem. Soc. 2024, 146, 21583-90.
45. Katubi, K. M.; Saqib, M.; Maryam, M.; et al. Machine learning assisted designing of organic semiconductors for organic solar cells: high-throughput screening and reorganization energy prediction. Inorg. Chem. Commun. 2023, 151, 110610.
46. Chen, F.; Guo, Z.; Wang, J.; et al. Accelerated feasible screening of flame-retardant polymeric composites using data-driven multi-objective optimization. Comput. Mater. Sci. 2023, 230, 112479.
47. Chen, F.; Weng, L.; Wang, J.; et al. An adaptive framework to accelerate optimization of high flame retardant composites using machine learning. Compos. Sci. Technol. 2023, 231, 109818.
48. Zhang, J.; Lu, W. Sparse data machine learning for battery health estimation and optimal design incorporating material characteristics. Appl. Energy. 2022, 307, 118165.
49. Conrad, F.; Wiemer, H.; Ihlenfeldt, S. Leveraging multi-task learning regressor chains for small and sparse tabular data in materials design. Mach. Learn. Sci. Technol. 2025, 6, 015045.
50. Rao, Z.; Tung, P. Y.; Xie, R.; et al. Machine learning-enabled high-entropy alloy discovery. Science 2022, 378, 78-85.
51. Achar, S. K.; Keith, J. A. Small data machine learning approaches in molecular and materials science. Chem. Rev. 2024, 124, 13571-3.
52. Dou, B.; Zhu, Z.; Merkurjev, E.; et al. Machine learning methods for small data challenges in molecular science. Chem. Rev. 2023, 123, 8736-80.
53. Wu, S.; Kondo, Y.; Kakimoto, M.; et al. Machine-learning-assisted discovery of polymers with high thermal conductivity using a molecular design algorithm. npj. Comput. Mater. 2019, 5, 203.
54. Chen, C.; Ong, S. P. AtomSets as a hierarchical transfer learning framework for small and large materials datasets. npj. Comput. Mater. 2021, 7, 639.
55. Xue, D.; Balachandran, P. V.; Hogden, J.; Theiler, J.; Xue, D.; Lookman, T. Accelerated search for materials with targeted properties by adaptive design. Nat. Commun. 2016, 7, 11241.
56. Chen, S.; Cao, H.; Ouyang, Q.; Wu, X.; Qian, Q. ALDS: an active learning method for multi-source materials data screening and materials design. Materi. Design. 2022, 223, 111092.
57. Tolstikhin, I.; Bousquet, O.; Gelly, S.; Schölkopf, B. Wasserstein auto-encoders. arXiv 2017; arXiv:1711.01558. Available online: https://doi.org/10.48550/arXiv.1711.01558. (accessed 12 May 2025).
58. Gretton, A.; Borgwardt, K. M.; Rasch, M. J.; Scholkopf, B.; Smola, A. J. A kernel method for the two-sample-problem. arXiv 2008; arXiv:0805.2368. Available online: https://doi.org/10.48550/arXiv.0805.2368. (accessed 12 May 2025).
59. Bargagli Stoffi, F. J.; Cevolani, G.; Gnecco, G. Simple models in complex worlds: Occam’s Razor and Statistical Learning Theory. Minds. Mach. 2022, 32, 13-42.
60. Elaskalany, M.; Behdinan, K. Stochastic multiscale modeling of electrical conductivity of carbon nanotube polymer nanocomposites: an interpretable machine learning approach. Adv. Eng. Mater. 2024, 26, 2401233.
61. Razavi, S. M.; Sadollah, A.; Al-Shamiri, A. K. Prediction and optimization of electrical conductivity for polymer-based composites using design of experiment and artificial neural networks. Neural. Comput. Appl. 2022, 34, 7653-71.
62. Joo, C.; Park, H.; Kwon, H.; et al. Machine learning approach to predict physical properties of polypropylene composites: application of MLR, DNN, and random forest to industrial data. Polymers 2022, 14, 3500.
63. Sun, Z.; Hou, Y.; Hu, Y.; Hu, W. Effect of additive phosphorus-nitrogen containing flame retardant on char formation and flame retardancy of epoxy resin. Mater. Chem. Phys. 2018, 214, 154-64.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Special Issue
Copyright
Data & Comments
Data





















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].