Machine learning assisted crystal structure prediction made simple

Chuan-Nan Li; Han-Pu Liang; Bai-Qing Zhao; Su-Huai Wei; Xie Zhang

doi:10.20517/jmi.2024.18

Download PDF

Review | Open Access | 29 Sep 2024

Machine learning assisted crystal structure prediction made simple

Views: 111 | Downloads: 18 | Cited:

0

Chuan-Nan Li^1,2,3

,

Han-Pu Liang²

, ...

Xie Zhang^1,*

J Mater Inf 2024;4:15.

10.20517/jmi.2024.18 | © The Author(s) 2024.

Author Information

Article Notes

Cite This Article

Abstract

Crystal structure prediction (CSP) plays a crucial role in condensed matter physics and materials science, with its importance evident not only in theoretical research but also in the discovery of new materials and the advancement of novel technologies. However, due to the diversity and complexity of crystal structures, trial-and-error experimental synthesis is time-consuming, labor-intensive, and insufficient to meet the increasing demand for new materials. In recent years, machine learning (ML) methods have significantly boosted CSP. In this review, we present a comprehensive review of the ML models applied in CSP. We first introduce the general steps for CSP and highlight the bottlenecks in conventional CSP methods. We further discuss the representation of crystal structures and illustrate how ML-assisted CSP works. In particular, we review the applications of graph neural networks (GNNs) and ML force fields in CSP, which have been demonstrated to significantly speed up structure search and optimization. In addition, we provide an overview of advanced generative models in CSP, including variational autoencoders (VAEs), generative adversarial networks (GANs), and diffusion models. Finally, we discuss the remaining challenges in ML-assisted CSP.

Graphical Abstract

Keywords

Crystal structure prediction, machine learning, structure representation, graph neural network, machine learning force field, generative model

Download PDF 0 1

INTRODUCTION

With the rapid development of artificial intelligence, we are now in the so-called Big Data Era, a time when vast amounts of data are generated and collected from various sources at an unprecedented pace^[1,2]. In this context, the data-driven research paradigm has become mainstream in modern materials science^[3–7]. This paradigm leverages big data and machine learning (ML) technologies to accelerate the discovery and design of new materials, marking a shift from traditional research methods that rely on experiments and theory to more efficient and automated methodologies. The data-driven research paradigm focuses on extracting features and patterns from a large database to guide the design and property prediction of new materials^[8,9]. The typical workflow of data-driven materials science research includes: (ⅰ) collecting data; (ⅱ) building ML models; and (ⅲ) using ML models for rapid computation and data analysis^[10]. Obviously, data collection constitutes the basis of this workflow^[11,12], with materials science data originating from two primary sources: experimental results and theoretical predictions.

Crystal structure prediction (CSP) serves as a vital data source for modern data-driven materials science research, providing structural information crucial for understanding the electronic, optical, and magnetic properties of materials^[13,14]. The goal of CSP is to determine the most stable arrangement of atoms solely based on chemical composition^[15,16]. CSP also explores metastable states that might possess unique properties^[12,17] and examines all possible compositions to discover new compounds^[18,19]. When the temperature drops to 0 K, the free energy transforms into enthalpy, consistent with the total energies calculated by most first-principle calculation software [e.g., the Vienna Ab-initio Simulation Package (VASP)^[20–22]]. Therefore, in most cases, we are looking for the global minimum on the potential energy surface.

As illustrated in Figure 1, ML-based CSP can continuously supply structural data for databases or practical applications. This ML-driven materials design process is highly efficient and facilitates the discovery of new materials through high-throughput CSP. Additionally, CSP involves exploring potential material structures under extreme conditions and environments, and identifying materials that may emerge from experiments but are costly to synthesize or require numerous attempts^[23–26]. In short, compared to data collection that solely relies on trial-and-error experimental synthesis - which is time-consuming and labor-intensive - CSP is more economical, environmentally friendly, and safer^[27–29]. CSP can be transformed into a combinatorial problem, with general steps including^[30]: (ⅰ) space gridding; (ⅱ) atom arrangement; and (ⅲ) energy evaluation. By extensively repeating the last two steps, we can find the low-energy arrangements of atoms. However, this exhaustive structure search method is suitable when the number of structures is small, but faces significant challenges when the number of structures explodes.

Machine learning assisted crystal structure prediction made simple

Figure 1. ML-driven materials design. First, researchers use ML-based CSP methods to explore low-energy structures of target compositions in a short time. Then, the low-energy structures can be added to databases or used in quantum mechanical calculations. Finally, the potential candidates can be synthesized in experiment. ML: Machine learning; CSP: crystal structure prediction.

The main difficulty in CSP is that the number of possible structures increases explosively as the number of atoms in a unit cell increases^[14,31]. If we use the general steps mentioned above, the number of possible structures can be estimated using^[14]:

(1)

$$ C = \frac{1}{(V/\delta^3)} \frac{(V/\delta^3)!}{[(V/\delta^3)-N]!N!}, $$

where $$ \delta $$ is the grid resolution (e.g., $$ \delta=1\; \mathrm{\mathring{A}} $$), $$ V $$ is the volume of the unit cell, and $$ N $$ is the number of atoms in the unit cell. The number of possible crystal structures grows exponentially with increasing the degrees of freedom ($$ d = 3N + 3 $$): $$ C \approx \exp(a \cdot d) $$, where $$ a $$ is a constant. Clearly, it is impractical to exhaustively enumerate all possible atomic arrangements, making it necessary to design algorithms or methods for the problem of CSP. Here, we summarize the challenges faced in CSP as follows:

● High-dimensional potential energy surfaces^[32,33]: A large number of atoms in the unit cell leads to very high-dimensional potential energy surfaces. The number of possible structures on the potential energy surface increases exponentially with the number of atoms, making it extremely difficult to search for the global minimum in high-dimensional spaces. Simple exhaustive methods are not suitable for CSP.

● Computational cost^[13,34]: Determining the accurate energies of crystal structures typically requires first-principles calculations based on density functional theory (DFT). However, the computational complexity of DFT increases rapidly with the number of electrons, limiting the size of systems where DFT can be applied.

● Limitations of empirical force fields^[35,36]: Empirical force fields can be used for energy calculations and structure optimization because they are faster. However, due to their reliance on empirical parameters, they often fail to accurately describe the entire potential energy surface.

● Local minima^[37,38]: The potential energy surface contains numerous local minima corresponding to metastable structures. Without appropriate global search methods, structure searches can easily become trapped in local minima.

To overcome these challenges, various algorithms have been adopted in conventional CSP methods, including particle swarm optimization^[39,40], genetic algorithm (GA)^[41,42], Bayesian optimization^[43,44], and simulated annealing^[45,46]. Nowadays, ML methods have been applied to CSP, greatly improving the efficiency of structure searches. These include the graph neural network (GNN)^[47,48], ML force field^[49,50], and generative model^[51,52].

CONVENTIONAL CSP METHODS

Conventional CSP methods mainly refer to those that do not use ML techniques. In this section, we briefly discuss these methods to convey their basic ideas, progress, and bottlenecks.

As shown in Figure 2, conventional CSP methods mainly include three parts: (ⅰ) structure generation; (ⅱ) structure optimization; and (ⅲ) structure search. The initial structures are always generated randomly with symmetry and distance constraints, and then DFT and global search algorithms are combined to explore low-energy structures on the potential energy surface. The main difference between different CSP methods lies in the global optimization algorithms. Therefore, we classify conventional CSP methods based on these algorithms as follows.

Figure 2. General steps in CSP. (A) Initial structures generated randomly with physical constraints; (B) Structure optimization by DFT or classical force fields; (C) New structures generated by global optimization algorithms. CSP: Crystal structure prediction; DFT: density functional theory.

Random search

The random search algorithm is the most basic method in CSP^[53,54]. This method searches for the lowest-energy structures through extensive random exploration. For instance, ab initio random structure searching (AIRSS)^[55] is a typical implementation of the random search algorithm. AIRSS first generates a large number of structures randomly and then uses first-principles calculations to relax these structures. Using random search methods, novel structures have been discovered for defect clusters of various sizes^[56], high-pressure phases of solid hydrogen^[57], nitrogen^[58], and lithium^[59]. Combining random search with a set of correlation functions as the objective, the well-known special quasirandom structures (SQS)^[60,61] approach has been developed for modeling the chemically disordered state within a fixed lattice for alloys with variable compositions. By using SQS, it is also possible to investigate order-disorder phase transitions^[60,61], such as phase transitions in Fe-C alloys^[62], BeZnO₂ alloys^[63], and Cs₂AgBiBr₆ perovskite^[64]. Despite the accomplishments, random search algorithms face challenges due to the giant configurational space. To improve search efficiency, several strategies can be applied: using geometric constraints to reduce the search space^[65,66], adopting ML models for rapid screening and energy calculations^[67], and utilizing parallel computing to accelerate the search process^[68]. These strategies have made random search algorithms reasonably practical in the field of CSP, especially in the generation of initial structures.

Particle swarm optimization

The particle swarm optimization^[69,70] is based on swarm intelligence, inspired by the collective behavior of birds or fishes in nature. In particle swarm optimization, particles move through the solution space, updating their positions and velocities based on their own experiences and the experiences of other particles in the swarm. For instance, crystal structure analysis by particle swarm optimization (CALYPSO)^[69] is a CSP package based on the particle swarm optimization. The general workflow of CALYPSO includes the following steps: First, initial structures are randomly generated with physical constraints, including minimum interatomic distances and crystal symmetry. Then, structures are characterized using crystal fingerprints to eliminate duplicate or similar structures. After removing duplicate structures, local optimization is applied to candidate structures to reach the local minima. Finally, the particle swarm optimization is used for structural evolution, generating initial structures for the next iteration. These steps are repeated until the convergence conditions are met. To date, a large number of functional materials have been discovered by CALYPSO, covering wide applications in lithium batteries^[71,72], superconductors^[73], photovoltaics^[74], and electronics^[75]. The particle swarm optimization is simple to implement, with relatively few parameters that are easy to adjust. However, it may get trapped in local optima, especially in complex high-dimensional spaces or non-convex optimization problems.

GA

The GA^[17,76,77] mimics the mechanism of natural selection, choosing individuals with the highest adaptability for reproduction. In CSP, each individual represents a potential crystal structure, and the fitness of the configuration is primarily determined by its energy, with lower energy indicating higher fitness. For instance, Universal Structure Predictor: Evolutionary Xtallography (USPEX)^[17] is a GA-based CSP software widely used for discovering new materials, optimizing existing ones, and understanding the underlying principles of crystal formation. The core steps include: First, selecting two or more parent crystal structures from the existing population based on the fitness function. Then, a crossover operation is performed, where parts of the parent chromosomes are exchanged to generate new offspring crystal structures. Subsequently, with a certain probability, mutation is introduced in the offspring chromosomes, randomly altering some genes (e.g., unit cell parameters) to introduce genetic diversity. The new generation population includes high-fitness individuals inherited from the parents and high-fitness offspring. This process iterates until the convergence conditions are met. USPEX has been widely utilized to identify various functional materials^[78–81], such as novel electride materials Sr₅P₃^[82], hard metallic phase TiN₂^[83], high $$ T_{c} $$ superconductor H₃S^[84], and transparent high-pressure phase of sodium^[85]. The GA demonstrates significant capability in handling complex, nonlinear optimization problems, effectively avoiding entrapment in local optima. However, GA-based methods for CSP sometimes require numerous evaluations of potential solutions to evolve optimal candidate structures. When combined with computationally intensive calculations such as DFT, the overall computational cost can become substantial, particularly in systems with large numbers of atoms where DFT calculations are especially time-consuming^[86]. Fortunately, recent advancements, such as the integration of ML models in USPEX, have helped to alleviate some of these challenges^[87].

Bayesian optimization

Making use of the Bayesian theory and Gaussian process regression, Bayesian optimization^[88] can significantly reduce the computational time and accelerate the structure search process by constructing surrogate models. It mainly consists of two parts: the surrogate model based on Gaussian process regression, and the acquisition function, which guides the search process. Bayesian optimization has been widely applied to search for clusters, such as Cu₁₅^[89], CuNi^[90], and C₂₄^[91] clusters. Bayesian optimization exhibits great potential in CSP but still faces several challenges^[92–94]. First, updating the surrogate model and calculating the acquisition function can be very time-consuming. In addition, the noise and uncertainty in actual calculations can affect the accuracy of the model and the stability of the optimization process.

Simulated annealing

The simulated annealing^[95–97] is a random search method inspired by the natural phenomenon of atomic rearrangement in solid-state materials that achieve the lowest-energy state through slow cooling after heating. The core principle is to temporarily allow the system to enter higher energy states during the search process, which helps to avoid premature convergence to local optima. Simulated annealing has been successfully used to predict the crystal structures of LiF^[97], GeF₂^[98] and BN^[99] and to investigate the properties of IrO₂ and RuO₂ surfaces^[100]. Simulated annealing is favored in optimization problems mainly due to its simplicity and effectiveness in avoiding trapping by local minima, thereby increasing the likelihood of finding the global minimum. However, the performance of the algorithm heavily depends on parameter settings, such as initial temperature, cooling rate, and termination temperature. Determining the optimal values for these parameters often requires extensive experience and numerous tests.

Template-based method

Besides these ab initio methods, another widely used CSP approach is the template-based method. A well-known example of this approach is ion substitution^[101]. Traditionally, this method involves replacing an ion in the crystal structure of a known compound with a chemically similar ion, guided by empirical rules such as the Goldschmidt rules^[102]. This process has been further enhanced by a probabilistic model, which quantitatively predicts the likelihood of successful ionic substitution by analyzing a vast database of crystal structures^[103]. This data-driven model not only improves the accuracy of predicting new compounds, but also accelerates the materials discovery process by efficiently identifying novel structures with reduced computational resources. For instance, using this method, a comprehensive stability map of inorganic ternary metal nitrides has been constructed, leading to the synthesis of several new Zn- and Mg-based ternary nitrides^[104].

Although conventional CSP methods have achieved remarkable accomplishments, most of them still suffer from low computational efficiencies, in addition to the limitations of each global optimization algorithm mentioned above. The main time cost lies in the optimization of structures, as there is rarely a guarantee that the structures are near the local minima on the potential energy surface, leading to tens of thousands of DFT calculations or time-consuming optimizations. Fortunately, advanced ML techniques have shed new light on tackling these challenges, opening up new possibilities in this direction.

APPLICATIONS OF ML IN CSP

In recent years, ML has achieved a better balance between speed and accuracy by embedding physical knowledge into neural networks^[105], such as energies, forces, stresses, and magnetic moments, and training on large-scale data^[106]. By leveraging the advantages of ML models, they can usually be combined with CSP in the following four aspects.

● Crystal Structure Representation: ML-based structure representation methods can accurately capture the geometric and topological features of crystals [Figure 3A-C]^[107–111], converting complex structural information into high-dimensional crystal feature vectors^[109,112]. These feature vectors not only contain sufficient structural information, but also exhibit rotational invariance, translational invariance, and index permutation invariance^[107]. Most importantly, these feature vectors can reveal intrinsic connections and differences between structures, greatly enhancing the effectiveness of structure clustering during the search process.

Figure 3. Application of machine-learning models in CSP. (A) Representation of atoms in machine-learning models. Reproduced with permission^[107]. Copyright 2018, American Physical Society; (B) Neighbor search using Voronoi tessellation and construction of a global periodic graph. Reproduced from Ref.^[108]. CC BY 4.0; (C) Representation of bonding between atoms in machine-learning models. Reproduced from Ref.^[109]. CC BY 4.0; (D) Architecture of crystal graph convolutional neural network. Reproduced with permission^[107]. Copyright 2018, American Physical Society; (E) Architecture of the neural network used in machine-learning force fields. Reproduced from Ref.^[110]. CC BY-NC 4.0; (F) VAE for stable structure generation. Reproduced from Ref.^[111]. CC BY-NC 4.0. CSP: Crystal structure prediction; VAE: variational autoencoder.

● Property Prediction and Rapid Screening: ML models, especially the GNN shown in Figure 3D, can quickly predict the physical properties of candidate materials^[113–115], such as energy, band gap, and performance for different applications. Moreover, by combining ML models with global optimization algorithms such as simulated annealing, GAs, and particle swarm optimization, low-energy crystal structures can be efficiently identified^[116].

● Machine-Learning Force Field: ML force fields [Figure 3E] can be used for structure optimization. Compared to classical force fields, ML-based force fields maintain near first-principles calculation accuracy while significantly reducing the computational cost, making the simulation of large-scale complex systems feasible^[117,118]. Also, they enable high-throughput material screening and the construction of material databases^[119,120].

● Generative Model: Generative models [Figure 3F] learn the distribution of data and sample new data instances from this learned distribution^[111], enabling the exploration of a more diverse range of crystal structures. Some advanced generative models provide better compositional and structural diversity than substitution-based enumeration in high-throughput calculations and better structural generation efficiency^[121,122] than conventional CSP techniques.

In this section, we review applications of crystal structure characterization, property prediction, and ML force fields in structure generation, global structure search, and local structure optimization, respectively. Finally, we will discuss the generative model, which differs from the typical CSP workflow.

Structure generation

In the ML-based CSP, once the initial structures are generated, suitable descriptors are needed to capture the geometric and topological information of the crystal structure. By converting crystal structures into a readable format using ML models, we can effectively represent structures and learn the relationship between structure and properties. The descriptors used to construct ML models should meet the following three basic criteria^[107,123]:

1. Physical Consistency: The descriptors should maintain physical invariance, meaning that their values should not change with the rotation and translation of the structure.

2. Index Invariance: The descriptors should be insensitive to the indexing order of the atoms. Even if the order or numbering of the atoms changes, the descriptor values should remain unchanged, ensuring model consistency and stability.

3. Discrimination: The descriptors should be able to distinguish different atomic environments. Similar local chemical environments should yield similar descriptors, while different local chemical environments should result in significantly different descriptors.

There are currently two main approaches to structure representation: continuous 3D voxel representation and matrix representation. In the continuous 3D voxel representation^[124], encoders and decoders are employed to prepare 2D crystal graphs and to reconstruct 3D voxel images. In the matrix representation^[125–127], crystal structure features such as lattice parameters, atomic occupation coordinates, and elemental properties are separated into different matrix rows and columns. Since widely used GNN and ML force fields mainly adopt the matrix representation, we will focus on the matrix representation, including the atom features and bonding features.

Atom features

Atom features are used to describe different atoms in ML models^{[107,126,128]}. As illustrated in Table 1^{[107,129–132]}, the initial atomic feature vectors contain various elemental properties. These descriptors can uniquely determine each element and include their main physical properties. In advanced GNNs, such as message passing neural network (MPNN)^[128], crystal graph convolutional neural network (CGCNN)^[107], materials graph network (MEGNet)^[126], and atomistic line graph neural network (ALIGNN)^[133], the initial atomic features are processed through fully connected layers to construct atomic representations that are more strongly correlated with the target properties.

Table 1

Atom features used in CGCNN

Descriptor	Unit	Range	Number of categories
Group number	-	1,2,…,18	18
Period number	-	1,2,…,9	9
Electronegativity^[129,130]	-	0.5-4.0	10
Covalent radius^[131]	pm	25-250	10
Valence electrons	-	1,2,…,12	12
First ionization energy	eV	1.3-3.3	10
Electron affinity^[132]	eV	-3-3.7	10
Block	-	s,p,d,f	4
Atomic volume	cm³/mol	1.5-4.3	10

Bonding features

Bonding features are used to describe the local environment of each atom. In GNNs, the bonding features are directly used as input to the ML model. In ML force fields, the input is the atom positions, and the bonding features are obtained via symmetry functions. The Behler-Parrinello and smooth overlap of atomic positions (SOAP) descriptors are two commonly used bonding features, and we introduce them as follows.

The Behler-Parrinello descriptor^[32,134] uses a set of symmetry functions to characterize the local chemical environment of each atom. It consists of two types of symmetry functions: radial and angular symmetry functions, which capture distance and angle information between atoms, respectively.

SOAP is another descriptor used to characterize the local environment of atoms^[135]. The SOAP descriptor represents the environment of each atom as a continuous density field, capturing the geometric properties of the atomic environment by calculating the overlap of density fields.

The calculation process of the SOAP descriptor for the local environment of atom $$ i $$ can be expressed by

(2)

$$ \rho_i({\mathbf r}) = \sum\limits_{j \neq i} \exp\left(-\frac{|{\mathbf r} - {\mathbf r}_{ij}|^2}{2\sigma^2}\right), $$

where $$ {\mathbf r}_{ij} $$ is the position vector of atom $$ j $$ relative to atom $$ i $$, and $$ \sigma $$ is the width of the Gaussian function.

To incorporate angular information, the atomic density $$ \rho_i({\mathbf r}) $$ is expanded using spherical harmonics $$ Y_{lm}(\theta, \phi) $$ and radial basis functions $$ g_n(r) $$:

(3)

$$ \rho({\mathbf r}) = \sum\limits_{n, l, m} c_{nlm} g_n(r) Y_{lm}(\theta, \phi). $$

The expansion coefficients are calculated by inner product:

(4)

$$ c_{nlm} = \int \rho_i({\mathbf r}) g_n(r) Y_{lm}(\theta, \phi) d{\mathbf r}, $$

where $$ r = |{\mathbf r}| $$, and $$ \theta $$ and $$ \phi $$ are the polar and azimuthal angles in the spherical coordinate system, respectively.

To ensure the rotational invariance of the descriptor, the SOAP descriptor calculates the power spectrum of the expansion coefficients:

(5)

$$ p_{nn'l} = \sqrt{\frac{4\pi}{2l+1}} \sum\limits_{m=-l}^{l} c_{nlm} c_{n'lm}^*. $$

The vector composed of the power spectrum $$ p_{nn'l} $$ constitutes the SOAP descriptor. It not only captures the local environmental characteristics of atom $$ i $$, but also ensures invariance to translation and rotation. Therefore, the SOAP descriptor can accurately characterize the distances and directions between an atom and its neighbors.

When constructing ML models, atoms can be encoded by property-based one-hot vectors. The Behler-Parrinello or SOAP descriptors generate a high-dimensional bonding feature vector for each atom. These vectors serve as input for the ML models, and the output is the total energy, enabling the ML model to map the local atomic environment to energy.

Global structure search

With the increasing size of open material databases^{[18,120,136–138]} and the development of ML models^[139–141], it has become a common practice to screen hundreds of thousands of materials to identify potential candidates^[19,142,143]. A typical workflow for applying an ML model to screen structures in CSP is shown in Figure 4A^{[107,126,128,133,144]}. The ML model is pretrained using databases [Figure 4B] and then takes the generated structures as input, predicting their energies. In this way, the ML model can identify low-energy candidates from a vast number of initial structures, allowing the low-energy areas on the potential energy surface to be quickly located. In this section, we introduce the commonly used GNNs for property prediction in CSP and GNN-based CSP methods.

Figure 4. GNNs applied in CSP. (A) Prediction pipeline; (B) Examples of structures stored in database. Reproduced from Ref.^[144]. CC BY 4.0; (C) MPNN predicts the quantum properties of an organic molecule. Reproduced from Ref.^[128]. CC BY-NC 4.0; (D) Illustration of the CGCNN, including construction of the crystal graph and then building the structure of the convolutional neural network on top of the crystal graph. Reproduced with permission^[107]. Copyright 2018, American Physical Society; (E) Overview of MEGNet. The initial graph is represented by the set of atomic attributes $$ V = \{v_i\}_{i=1}^{N_v} $$, bond attributes $$ E = \{(e_k, r_k, s_k)\}_{k=1}^{N_e} $$, and global state attributes $$ u $$. Reproduced with permission^[126]. Copyright 2019, American Chemical Society; (F) ALIGNN convolution layer alternates between message passing on the bond graph and its line graph. Reproduced from Ref.^[133]. CC BY 4.0. GNNs: Graph neural networks; CSP: crystal structure prediction; MPNN: message passing neural network; CGCNN: crystal graph convolutional neural network; MEGNet: materials graph network; ALIGNN: atomistic line graph neural network.

The MPNN^[128] provides a general framework for GNN [Figure 4C]. It includes three stages: message generation, message passing, and message readout. Messages generated at adjacent vertices are collected by the central vertex to update its representation. By repeating this process, the GNN captures higher-order abstract features. Last, through the message readout process, the global graph features are mapped to the target properties.

Specifically, MPNN updates the representation of each vertex in the graph through the following steps:

1. Message Passing: Each vertex $$ v $$ collects messages from its neighbors $$ w \in N(v) $$ and updates its state based on these messages:

(6)

$$ {\mathbf m}_{v}^{t+1} = \sum\limits_{w \in N(v)} M_{t}({\mathbf h}_{v}^{t}, {\mathbf h}_{w}^{t}, {\mathbf e}_{vw}), $$

(7)

$$ {\mathbf h}^{t+1}_{v} = U_{t}({\mathbf h}_{v}^{t}, {\mathbf m}_{v}^{t+1}), $$

where $$ {\mathbf h}_v^{t} $$ is the feature vector of vertex $$ v $$ at the $$ t $$-th iteration, $$ M_{t} $$ is used to aggregate messages from neighbors, and $$ U_{t} $$ is used to update the vertex features.

2. Message Readout: After $$ T $$ rounds of message passing, the global representation of the graph can be obtained by aggregating the feature vectors of all vertices:

(8)

$$ \hat{y} = R(\{{\mathbf h}_{v}^{T} \mid v \in \mathcal{V}\}), $$

where $$ R $$ is the readout function, which can be a simple summation or a more complex pooling operation.

Most GNNs can be represented using the MPNN framework, including the Molecular Fingerprint Convolution Network^[145], the Gated Graph Neural Network^[146], Interaction Networks^[147], Molecular Graph Convolutional Networks^[148], Deep Tensor Networks^[127], and Graph Laplacian Matrix Networks^[149]. Here, we concentrate on three GNNs suitable for crystal property prediction: CGCNN^[107], MEGNet^[126], and ALIGNN^[133], which can also be built using the MPNN framework.

CGCNN is a well-known GNN model designed for predicting crystal properties [Figure 4D]. It effectively transforms periodic crystal structures into undirected multigraph representations and introduces a crystal graph convolution operator as a message aggregation function. Specifically, the graph convolution operator is defined as

(9)

$$ {\mathbf v}_{i}^{(t+1)}={\mathbf v}_{i}^{(t)}+\sum\limits_{j, k}\sigma({\mathbf z}_{(i, j)_{k}}^{(t)}{\mathbf W}_{f}^{(t)}+{\mathbf b}_{f}^{(t)})\odot g({\mathbf z}_{(i, j)_{k}}^{(t)}{\mathbf W}_{s}^{(t)}+{\mathbf b}_{s}^{(t)}), $$

where $$ \sigma $$ is the Sigmoid function, $$ {\mathbf W}_{f}^{(t)} $$ and $$ {\mathbf W}_{s}^{(t)} $$ are the shared weights for the $$ t $$-th aggregation, and $$ {\mathbf b}_{f}^{(t)} $$ and $$ {\mathbf b}_{s}^{(t)} $$ are the shared biases for the $$ t $$-th aggregation. The interaction feature is defined as $$ {\mathbf z}_{(i, j)_{k}}^{(t)}={\mathbf v}_{i}^{(t)}\oplus{\mathbf v}_{j}^{(t)}\oplus{\mathbf u}_{(i, j)_{k}}. $$

Thus, the graph convolution operator effectively represents atomic interactions using $$ \sigma(\cdot) $$ for weights and $$ g(\cdot) $$ for bonding features. By repeatedly aggregating the atomic feature vectors $$ {\mathbf v}_{i}^{(t)} $$ using the graph convolution operator, we obtain the feature representation of atoms in the crystal $$ {\mathbf v}_{N}^{(R)} $$. The crystal feature vector is obtained by a pooling layer $$ {\mathbf v}_{c}=\mathrm{Pool}\bigg({\mathbf v}_{0}^{(0)}, {\mathbf v}_{1}^{(0)}, ..., {\mathbf v}_{N}^{(0)}, ..., {\mathbf v}_{N}^{(R)}\bigg). $$ Finally, a fully connected network associates the crystal feature vector with material properties to predict properties.

MEGNet is a universal property prediction model for molecules and crystals. Compared to CGCNN, MEGNet encodes the macroscopic properties of the system (such as temperature, pressure, entropy, etc.) into feature vectors, enhancing the ability to predict material properties. As shown in Figure 4E, the feature encoding and aggregation process in MEGNet includes the atomic feature vector $$ {\mathbf v}_{i} $$, the bond feature vector $$ {\mathbf e}_{k} $$, and the system feature vector $$ {\mathbf u} $$, which contains information about the macroscopic properties of the system.

ALIGNN is a GNN model designed for predicting crystal properties [Figure 4F]. Its key innovation is the construction of a line graph that includes angular information, allowing messages to be passed between the bond graph and its corresponding line graph. Compared to CGCNN, ALIGNN explicitly incorporates angular information, enhancing the ability to distinguish between different structures.

Combining GNN and CSP, Cheng et al. have developed an accelerated CSP framework^[67]. It mainly includes three parts: (ⅰ) pre-training of ML models; (ⅱ) structure generation with physical constraints; and (ⅲ) structure search and optimization based on ML. In the framework, GNNs such as CGCNN, MEGNet, ALIGNN, and CHGNet can be potentially used as prediction models, while algorithms such as random search, simulated annealing, GAs, or particle swarm optimization can be employed.

Recently, the symmetry-based combinatorial crystal optimization program (SCCOP)^[150,151] has been developed for 2D materials. The workflow of SCCOP is shown in Figure 5. SCCOP first converts the structures generated from 17 plane space groups to crystal vectors using a direct asymmetry space-based GNN and predicts their energies. Then, Bayesian optimization is performed to explore the structure located at the minimum of the potential energy surface.

Figure 5. Workflow of SCCOP for the search of two-dimensional materials. Step 1: generating structures by symmetry. Step 2: characterizing structures into crystal vectors and exploring the potential energy surface by Bayesian optimization. Step 3: updating the energy prediction model. Step 4: optimizing structures to obtain the lowest-energy configuration by ML and DFT. The whole program runs in a closed loop. Reproduced from Ref.^[150]. CC BY 4.0. SCCOP: Symmetry-based combinatorial crystal optimization program; ML: machine learning; DFT: density functional theory.

For the desired structures, SCCOP optimizes them with ML-accelerated simulated annealing, in conjunction with a limited number of DFT calculations, to obtain the lowest-energy structure.

To evaluate the effectiveness of SCCOP, it was applied to a total of 35 representative 2D materials. Figure 6A provides a comparison between the lowest-energy structure in the 2D material database and the structures discovered by SCCOP. The results demonstrated that SCCOP successfully reaches the lowest energy level for 30 compounds within only a few minutes. Additionally, Figure 6B shows the three lowest-energy structures for eight compounds. For example, in the case of AgI, the lowest-energy structure in the database corresponds to a honeycomb structure (-2.308 eV/atom), while SCCOP identifies an energetically more favorable puckered structure with space group $$ P2_{1}/m $$ (-2.37 eV/atom). Furthermore, MgCl₂ is recorded as having a four-fold coordination (-3.509 eV/atom) in the database, but SCCOP discovers that a structure with six-fold coordination exhibits lower energy (-3.591 eV/atom). SCCOP has been further applied to validate the stability of Cu- and Ag-based ternary compounds in the chalcopyrite structure prototype^[152]. It has also been successfully utilized to investigate the mixed-coordination structures of IB-VA-VIA2 compounds, which have the lowest free energy at low temperatures compared to the octahedrally coordinated structure in experiments^[153]. These applications highlight the wide-range applicability of SCCOP and demonstrate the feasibility of using GNNs to accelerate CSP.

Figure 6. Performance of SCCOP on 35 representative compounds. (A) Time cost and lowest energy for each compound, with all energy calculations evaluated with DFT; (B) Three lowest-energy structures identified by SCCOP. Each compound has been explored five times by SCCOP, with up to ten atoms in the unit cell. Reproduced from Ref.^[150]. CC BY 4.0. SCCOP: Symmetry-based combinatorial crystal optimization program; DFT: density functional theory.

Local structure optimization

Although ML models can identify potential candidates in a short time, high-accuracy structure optimization is still needed to fully relax structures to their local minima on the potential energy surface. In conventional CSP methods, structures are optimized by DFT or classical force fields. While DFT has high accuracy, it is time-consuming. Classical force fields are much faster than DFT, but often lack sufficient precision when dealing with complex systems, such as metal-organic frameworks and biological macromolecules, especially in scenarios involving intricate electronic effects and chemical reactions^[154,155].

Currently, ML force fields exhibit the potential to speed up the structure optimization. ML force fields can maintain the speed advantage of classical force fields while significantly improving prediction accuracy for complex systems, particularly in cases where classical force fields perform poorly. Through collective efforts of the field, many ML force fields have been developed, e.g., MEGNet^[126], CHGNet^[105], NequIP^[156], and MACE^[157]. ML force fields are commonly applied in studying the properties of new materials^[158], the mechanisms of drug molecules^[159], and the protein folding process^[160]. Thus, using ML force fields to replace time-consuming structural relaxation is a feasible way to speed up conventional CSP. In this section, we will discuss ML force fields and their applications in CSP.

While constructing ML force fields [Figure 7], the total energy is usually expressed as follows^[32]:

(10)

$$ E_{\text{tot}} = \sum\limits_{i}^{N} E_{i}({\mathbf G}_{i}), $$

Figure 7. Neural network of ML force fields. This feedforward neural network consists of an input layer, two hidden layers, and an output layer. The input is a coordination matrix. The hidden layers transform the inputs to the local environment of each atom, mapping it to local energy, and finally summing them to get the total energy. Reproduced from Ref.^[110]. CC BY-NC 4.0. ML: Machine learning.

where $$ N $$ is the number of atoms in the unit cell, and $$ {\mathbf G}_{i} $$ is the feature vector of the $$ i $$-th atom, representing the local chemical environment. $$ E_{i} $$ is the energy contribution of the $$ i $$-th atom.

To train the ML force field, the simplest loss function only fits the energy:

(11)

$$ \mathcal{L} = \sum\limits_{i=1}^{M} (E_i^{\text{ref}} - E_i^{\text{pred}})^2, $$

where $$ M $$ represents the number of samples in the training set. More generally, by calculating the gradient of the energy with respect to the coordinates (i.e., atomic forces), we can derive a loss function commonly used for model training^[161]:

(12)

$$ \mathcal{L} = \sum\limits_{k=1}^{M} \left[ \alpha \left( \frac{E_{k}^{\text{ref}}}{N_{k}} - \frac{E_{k}^{\text{pred}}}{N_{k}} \right)^2 + \frac{\beta}{3N_{k}} \sum\limits_{l=1}^{3} \sum\limits_{i=1}^{N_{j}} ({\mathbf F}_{il}^{\text{ref}} - {\mathbf F}_{il}^{\text{pred}})^2 \right], $$

where $$ N_{j} $$ is the number of atoms in sample $$ k $$, $$ l $$ denotes the $$ x $$, $$ y $$, or $$ z $$ direction in the Cartesian coordinate system, and $$ \alpha $$ and $$ \beta $$ are the weighting coefficients for energy and force, respectively. Some ML force fields add stress to the loss function during training^[162,163], thereby improving the efficiency of data utilization.

As shown in Figure 8A, ML force fields have been tested on the TiO₂ system^[110], which contains three different polymorphs: Anatase, Brookite, and Rutile. They have been demonstrated for other crystal systems such as Al₂O₃, Cu, Ge, and Si, as well as on MoS₂ slabs and small molecular systems. These results demonstrate that the trained ML force fields can adapt to various types of systems, and the energy is fitted with high precision, indicating its strong capability in force calculations.

Figure 8. Validity and time cost of machine-learning force fields. (A) Comparison of the DFT energies and the DeepPot-SE predicted energies on the testing snapshots. Reproduced from Ref.^[110]. Copyright 2018, Curran Associates Inc.; (B) Phonon band structure and DOS of fcc Al using DFT (blue dashed lines), and optimized (red solid lines) and original (green dashed lines) ML interatomic potentials. Reproduced with permission^[162]. Copyright 2019, AIP Publishing; (C) Correlation functions of liquid water from DPMD and PI-AIMD. Reproduced with permission^[164]. Copyright 2018, Elsevier; (D) Computational cost of MD steps versus system size with DPMD, TIP3P, PBE + TS, and PBE0 + TS. Reproduced with permission^[164]. Copyright 2018, Elsevier. DFT: Density functional theory; DOS: density of states; ML: machine learning; DPMD: deep potential molecular dynamics; PI-AIMD: path-integral Ab initio molecular dynamics; MD: molecular dynamics; TIP3P: transferable intermolecular potential with 3 points; PBE: Perdew-Burke-Ernzerhof functional; TS: Tkatchenko-Scheffler functional.

In addition to energy prediction, ML force fields can be used for more complex tasks, including phonon spectra and solid-liquid phase transitions. Figure 8B shows the phonon spectrum of fcc Al calculated using both DFT and ML force fields. The ML results are consistent with the DFT ones, demonstrating that ML force fields can accurately describe the vibrational behavior of materials^[162]. In the case of water and ice, ML force fields and DFT were used to simulate different thermodynamic conditions^[164]. The average energy, density, radial distribution functions [Figure 8C], and a representative angular distribution function (i.e., a three-body correlation function) have been reproduced with high accuracy. These results indicated that ML force fields can maintain the accuracy of DFT by model training. As shown in Figure 8D, the computational cost of ML force fields scales linearly with the number of atoms. Since all the physical quantities in an ML force field are sums of local contributions, this also means that after training on a relatively small system, the ML force field can be directly applied to much larger systems.

To alleviate the bottleneck in CSP, ML force fields have been employed to replace the time-consuming DFT optimization. For example, a ML and graph theory assisted universal structure searcher (MAGUS) combines ML force fields with global optimization algorithms for structure search [Figure 9A]^[165]. Specifically, the initial population is first generated by seeding and random generation. In each generation, the structures in the population are optimized using DFT or other force fields. Next, duplicate structures are removed from the population to maintain diversity. The remaining structures are then selected for crossover and mutation to create offspring. Generally, structures with higher fitness are more likely to be chosen as parents for crossover and mutation. The selection process can also incorporate the confidence level of the fitness with Bayesian optimization methods. As illustrated in Figure 9B, MAGUS trains an on-the-fly ML model during structure search, and uses this model to select and relax candidate structures to accelerate global searches. Using MAGUS, a stable superhard tungsten nitride (WN₆) has been discovered, which can be quenched to ambient pressure after high-pressure synthesis^[166]. Two different stable stoichiometries for helium-water compounds have also been predicted^[167], both of which exhibit a superionic state at high pressures and temperatures.

Figure 9. Workflow of MAGUS. (A) Classical evolutionary algorithm; (B) Machine-learning CSP. Reproduced from Ref.^[165]. Copyright 2023, Oxford University Press. MAGUS: Machine learning and graph theory assisted universal structure searcher; CSP: crystal structure prediction.

Many conventional CSP methods have adopted ML force fields to accelerate the optimization process. To integrate ML force fields with CSP, a sampling strategy using disordered structures to train ML models has been developed^[168]. By combining ML force fields and CALYPSO, the putative global minimum structure for the B₈₄ cluster has been uncovered, and the computational cost was substantially reduced by 1-2 orders of magnitude compared to full DFT-based structure searches^[169,170]. In the ML-based USPEX, the methodology was first tested on the prediction of crystal structures of carbon, high-pressure phases of sodium, and boron allotropes. For the test cases, the main allotropes have been reproduced, and a previously unknown 54-atom structure of boron has been predicted with very moderate computational effort^[87]. Additionally, by integrating ML force fields with GAs, the structure prediction of inorganic crystals using neural network potentials with evolutionary and random searches (SPINNER) method has been presented, which identified experimentally known or theoretically more stable phases with a success rate of 80% for 60 ternary compounds^[171], and high-throughput discovery of oxide materials using SPINNER has been conducted^[172]. Furthermore, the $$ \beta $$-rhombohedral boron structure has been studied^[173] by ML-based AIRSS.

Despite these achievements, the implementation of ML force fields for structure optimization faces several challenges, including data requirements, model complexity, transferability, and computational efficiency. Solutions to these challenges include using data augmentation and transfer learning to enlarge datasets^[174,175], applying explainable tools for better model interpretability^[176], developing domain-specific and hybrid models to improve generalization^[32], and employing model compression and efficient algorithms to enhance computational efficiency^[177,178]. These strategies assist researchers in effectively utilizing ML force fields for accurate and efficient structure optimization.

Generative model

Combining ML models with the general CSP steps has achieved significant progress in CSP, but it still struggles with the vast search space of feasible materials. Nowadays, thanks to breakthroughs in image generation^[179,180], video generation^[181,182], and realistic text generation^[183], generative models in materials science show an unprecedented ability to learn the mapping between the structure and property spaces [Figure 10A]. Thus, generative models such as variational autoencoders (VAEs), generative adversarial networks (GANs), and diffusion models offer a powerful approach for predicting material properties and discovering new materials, significantly reducing the computational cost and enabling rapid screening of target systems.

Figure 10. Material property prediction and inverse design by generative models. (A) Schematic showing material property prediction from the structure space to the property space (downward arrow), and inverse material design from the property space back to the structure space (upward arrow). Reproduced from Ref.^[111]. CC BY-NC 4.0; (B) VAE. The VAE consists of an encoder that transforms the input sample feature vector to a latent distribution space, and a decoder that reconstructs the sample given the hidden distribution. The VAE also models the latent space vector $$ z $$ from a normal distribution $$ N(\mu, \sigma) $$ with a mean $$ \mu $$ and a standard deviation $$ \sigma $$. Reproduced from Ref.^[111]. CC BY-NC 4.0; (C) GAN. GAN uses a generator to transform a random noise variable into the generated sample, and a discriminator to distinguish whether a sample is real or generated. Reproduced from Ref.^[111]. CC BY-NC 4.0; (D) Inorganic materials design with MatterGen. It generates stable materials by reversing a corruption process by iteratively denoising an initially random structure. Reproduced from Ref.^[121]. CC BY-NC 4.0. VAE: Variational autoencoder; GAN: generative adversarial network.

Among the generative models, VAEs, composed of an encoder and a decoder, minimize the reconstruction error between the decoded and input data [Figure 10B]. Representative VAE structure predictors include image-based materials generators (iMatGen)^[184] and the Fourier-transformed crystal properties (FTCP) framework^[185]. Specifically, iMatGen uses an invertible image-based representation to encode solid-state materials, leading to the generation of synthesizable V-O compounds. FTCP adds a target-learning branch to map latent points to target properties, resulting in the generation of 142 new crystals with desired ground- and excited-state properties. VAEs are relatively easy to train and provide more diversified structures that better cover the distribution compared to other generative models. These models generate diversified structures, but may have a lower output validity rate.

GANs use a minimax game theory approach, with a generator transforming a random latent variable into a sample and a discriminator distinguishing real from generated samples [Figure 10C]. Many GAN-based CSP methods have been developed, such as the composition-conditioned srystal GAN^[186], crystalGAN^[187], the zeolite GAN (ZeoGAN)^[188], and the constrained crystals deep convolutional generative adversarial network (CCDCGAN)^[189]. For instance, the composition-conditioned crystal GAN allows the extension of the latent variable $$ z $$ with desired conditions, such as user-defined composition, leading to the discovery of 23 novel Mg-Mn-O potential photoanode materials. CrystalGAN utilizes a cross-domain GAN to generate complex ternary Pd–H–Ni structures from simpler binary Pd–H and Ni–H structures. CCDCGAN employs a VAE to learn a reverse map from a latent 2D crystal representation back to crystal structures, which is then used to train a GAN to generate new crystal structures. Long et al. applied CCDCGAN to explore the binary Bi-Se system, revealing distinct crystal structures that cover the entire composition range. While GANs produce realistic structures, they are more challenging to train, requiring a balance between the generator and discriminator to prevent issues such as non-convergence and mode collapse.

The diffusion model generates samples by learning a score network to reverse a fixed destruction process^[190]. In image generation, the diffusion process typically adds Gaussian noises. However, crystals have unique periodic structures and symmetries that require a customized diffusion process. In MatterGen, Zeni et al. introduced a novel diffusion process tailored for crystal structures^[121]. As shown in Figure 10D, they defined a destruction process for each component that fits its geometry and has a physically meaningful noise distribution. Specifically, the coordinate diffusion adopts a wrapped normal distribution to obey periodic boundaries, approaching a uniform distribution at the noise limit. The lattice diffusion uses a symmetric form, approaching a cubic lattice distribution with an average value corresponding to the average atomic density in the training data. Atom diffusion is defined in a categorical space, where individual atoms are damaged to a masked state. Based on the destroyed structure, a score network is learned, which outputs equivariant scores for atom types, coordinates, and lattice, respectively, eliminating the need to learn symmetry from the data. Compared to prior generative models, e.g., crystal diffusion variational autoencoders (CDVAE), structures produced by MatterGen were more than twice as likely to be novel and stable, and more than 15 times closer to the local energy minimum.

From the introduction of advanced generative models applied in CSP, we can see that the biggest difference between generative models and the applications of ML in general CSP steps is that generative models, such as VAE, GAN, and diffusion models, are end-to-end systems. This means that the structure generation, structure search, and structure optimization are all done by neural networks, making it difficult to control each step. Interestingly, this is also the biggest advantage of current advanced ML models: they reduce human intervention. Parameters are determined by algorithms and training data, giving ML models the potential to extract better features and design better workflows than humans. However, there is still a long way to go, and more efforts are needed to fully control these advanced ML models.

At the end of this section, to help the readers quickly learn about the progress of CSP method development or to apply CSP codes in their research, we summarize the conventional CSP and ML-based CSP methods in Tables 2 and 3.

Table 2

Summary of CSP algorithm categories with their advantages and disadvantages

Category	Advantages	Disadvantages/limitations
Conventional Methods	Effective for complex search spaces Fast convergence	Computationally expensive Can get trapped in local minima
ML-based Methods	Efficient with large datasets Captures structural properties well	Requires extensive training data Complexity in integration
Generative Models	Good for exploring novel structures Generates diverse structures	Computationally intensive Complex model training

CSP: Crystal structure prediction.

Table 3

Some conventional and ML-based CSP codes, along with their applications

Software	Methods	Part of applications
USPEX (2006)^[66]	Evolutionary algorithm	NaCl (2013)^[191], W-B (2018)^[192]
XtalOPT (2010)^[193]	Evolutionary algorithm	NaH_n (2011)^[194], H₂O (2012)^[195]
AIRSS (2011)^[53,196]	Random search	SiH₄ (2006)^[196], NH_3±x (2008)^[197]
CALYPSO (2012)^[69,70]	Particle swarm optimization	Li (2011)^[198], LaH₁₀ (2017)^[199], P (2024)^[200]
GASP (2013)^[201]	Evolutionary algorithm	Li-Be (2008)^[202], Li-Si (2013)^[203]
AGA (2013)^[86]	Adaptive GA	Zr-Co (2014)^[204], MgO-SiO₂ (2017)^[205]
MUSE (2014)^[206]	Evolutionary algorithm	IrB₄ (2016)^[207], NbSe₂ (2017)^[208]
IM²ODE (2015)^[209]	Differential evolution	TiO₂ (2014)^[210], 2D SiS (2016)^[211]
SYDSS (2018)^[54]	Random search	H₂O-NaCl (2018)^[54], Cl-F (2020)^[212]
MAISE (2021)^[213]	Evolutionary algorithm	Fe-B (2010)^[214], NaSn₂ (2016)^[215]
GOFEE (2020)^[216]	Bayesian optimization & GA	C₂₄ (2022)^[91], Carbon clusters (2022)^[91]
BEACON (2021)^[89,90]	Bayesian optimization	Cu₁₅ (2021)^[89], CuNi clusters (2021)^[90]
CrySPY (2021)^[217]	Bayesian optimization & GA	Y₂Co₁₇ (2018)^[218], Al₂O₃ (2018)^[218]
FTCP (2022)^[185]	VAE	Au₂Sc₂O₃ (2022)^[185], Y₂Zn₂As₂O₃ (2022)^[185]
GN-OA (2022)^[67]	GNN & Optimization algorithms	Tested on typical compounds (2022)^[67]
MAGUS (2023)^[165,219]	GA & Bayesian optimization	WN₆ (2018)^[166], HeH₂O (2019)^[167]
SCCOP (2023)^[150]	GNN & Simulated annealing	B-C-N (2023)^[150], AgBiS₂ (2024)^[152,153]
iMatGen (2019)^[184]	VAE	V-O (2019)^[184]
CrystalGAN (2019)^[187]	GAN	Pd-Ni-H (2019)^[187], Mg-Ti-H (2019)^[187]
CCDCGAN (2021)^[189]	GAN	MoSe₂ (2021)^[189]
MatterGen (2024)^[121]	Diffusion model	V-Sr-O (2024)^[121]
UniMat (2024)^[220]	Diffusion model	Tested on typical compounds (2024)^[220]
DiffCSP (2024)^[221]	Diffusion model	Tested on typical compounds (2024)^[221]
LLaMA-2 (2024)^[222]	Large language-based model	Tested on typical compounds (2024)^[222]

When selecting CSP methods, it is important to consider the system's complexity and specific needs. GAs, such as those in USPEX, are effective for exploring large search spaces, making them ideal for complex, multi-modal problems. Random search methods in AIRSS provide a straightforward, computationally inexpensive option for initial explorations. Particle swarm optimization, as used in CALYPSO, is suitable for systems requiring quick convergence. For versatile applications, evolutionary algorithms in genetic algorithm for structure and phase predictions (GASP) and module for ab initio structure evolution (MAISE) are recommended. Bayesian optimization in global optimization with first-principles energy expressions (GOFEE) and BEACON excels in optimizing expensive functions with fewer evaluations, which is ideal for computationally intensive problems. Generative models, such as those in iMatGen and CrystalGAN, are excellent for innovative materials design and exploring unknown structures by learning complex distributions. For systems requiring relevant property modeling, GNNs in SCCOP and graph network-optimization algorithm (GN-OA) are powerful tools. Finally, to leverage large datasets, consider language-based models such as LLaMA-2. For beginners, starting with USPEX or AIRSS is recommended, while CALYPSO and MAGUS are better suited for complex systems. MatterGen and iMatGen are ideal for innovative designs, while IM$$ ^{2} $$ODE is great for constrained problems. SCCOP can greatly shorten the time while maintaining the DFT accuracy.

In general, conventional CSP methods remain successful due to their proven reliability and ability to handle complex systems^{[14,73,191,192,198]}. These methods are grounded in fundamental physical and chemical principles, making them robust and trustworthy for a wide range of materials. They also benefit from incorporating geometric constraints and prior knowledge. Despite being computationally intensive, ongoing improvements and the integration of ML techniques have further solidified their status in modern materials science. For the ML-based CSP methods, they can significantly reduce computational time compared to conventional methods such as DFT. Traditional CSP approaches can take days to weeks to predict a structure on a small server containing dozens to hundreds of CPU cores, while ML models, once trained, can predict structures in seconds to minutes using the same computational resources^[87,150,170]. This efficiency is achieved because ML approaches learn from existing data, facilitating effective feature extraction, rapid structure screening, and optimization, thereby offering a more cost-effective alternative to conventional methods.

SUMMARY

In this review, we discussed the current progress in CSP, particularly focusing on the applications of ML in CSP. To help the readers understand the basic concepts, progress, and challenges in this field, we first introduced the basics of conventional CSP methods. Next, we reviewed ML models combined with general CSP steps, including descriptors in structure generation, GNNs in structure search, and ML force fields in structure optimization. The application of ML models has significantly reduced the time required for CSP, and ML-based CSP methods have helped to find more low-energy structures for desired compositions^[113–115]. We further discussed generative models, which differ greatly from ML models combined with general CSP steps. Generative models for CSP are entirely based on neural networks without DFT calculations; thus, they can be applied to very large systems.

Although ML models have made significant progress in solving CSP, they still face several challenges: (ⅰ) Overfitting and data collapse: ML models may overfit the database, preventing them from identifying low-energy structures in CSP, or may cause data collapse in generative models. To mitigate overfitting, techniques such as data augmentation^[223], dropout regularization^[224], and ensemble learning can be employed^[225]. Additionally, employing early stopping and cross-validation methods can help prevent overfitting by ensuring the model is generalizing well on unseen data; (ⅱ) Limited training data: ML models are often trained on stable or metastable structures stored in databases, which represent only a small part of the complex potential energy surface; thus, the generalization of ML models cannot be guaranteed. To address this, transfer learning^[175] and active learning can be used to enhance model performance by incrementally expanding the training dataset with more diverse structures; (ⅲ) Mismatch between local fitting models and global optimization algorithms: in CSP, ML models lack a theoretical guarantee of global generalization, which may cause global optimization algorithms to fail while converging to the correct results. This issue can be tackled by techniques such as multi-fidelity modeling^[226], which combine high-fidelity simulations with ML predictions to improve the reliability of global optimization. Despite these challenges, we remain optimistic that ML models will ultimately solve the challenging task of CSP, similar to the advancements seen in protein structure prediction^[227], thereby boosting materials science research and the discovery and design of new materials.

DECLARATIONS

Authors' contributions

Writing-original draft preparation: Li CN

Proposed the conception and design: Li CN, Liang HP, Zhang X

References collection: Li CN, Liang HP, Zhao BQ

Writing-review and editing: Zhang X, Wei SH

Supervision: Zhang X, Wei SH

Availability of data and materials

Not applicable.

Financial support and sponsorship

We acknowledge financial support from the National Natural Science Foundation of China (Nos. 52172136, 11774416, 11991060, 12088101, and U2230402).

Conflicts of interest

All authors declared that there are no conflicts of interest.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Copyright

REFERENCES

1. Eisenstein M. Big data: the power of petabytes. Nature 2015;527:S2-4.

2. Ghiringhelli LM, Baldauf C, Bereau T, et al. Shared metadata for data-centric materials science. Sci Data 2023;10:626.

3. Tolle KM, Tansley DSW, Hey AJG. The fourth paradigm: data-intensive scientific discovery [point of view]. Proc IEEE 2011;99:1334-7.

4. Agrawal A, Choudhary A. Perspective: materials informatics and big data: Realization of the “fourth paradigm” of science in materials science. APL Mater 2016;4:053208.

5. Rajan K. Materials informatics: the materials “gene” and big data. Annu Rev Mater Sci 2015;45:153-69.

6. Liu Y, Zhao T, Ju W, Shi S. Materials discovery and design using machine learning. J Materiomics 2017;3:159-77.

7. Zdeborová L. New tool in the box. Nat Phys 2017;13:420-1.

8. Rupp M. Machine learning for quantum mechanics in a nutshell. Int J Quantum Chem 2015;115:1058-73.

9. Ramprasad R, Batra R, Pilania G, Mannodi-Kanakkithodi A, Kim C. Machine learning in materials informatics: recent applications and prospects. NPJ Comput Mater 2017;3:54.

10. Himanen L, Geurts A, Foster AS, Rinke P. Data-driven materials science: status, challenges, and perspectives. Adv Sci 2019;6:1900808.

11. Lin Y, Wang H, Li J, Gao H. Data source selection for information integration in big data era. Inf Sci 2019;479:197.

12. Needs RJ, Pickard CJ. Perspective: role of structure prediction in materials discovery and design. APL Mater 2016;4:053210.

13. Jain A, Shin Y, Persson KA. Computational predictions of energy materials using density functional theory. Nat Rev Mater 2016;1:15004.

14. Oganov AR, Pickard CJ, Zhu Q, Needs RJ. Structure prediction drives materials discovery. Nat Rev Mater 2019;4:331-48.

15. Oganov AR. Modern methods of crystal structure prediction Weinheim: Wiley-VCH; 2011.

16. Oganov AR, Lyakhov AO, Valle M. How evolutionary crystal structure prediction works - and why. Acc Chem Res 2011;44:227-37.

17. Oganov AR, Glass CW. Crystal structure prediction using ab initio evolutionary techniques: principles and applications. J Chem Phys 2006;124:244704.

18. Saal JE, Kirklin S, Aykol M, Meredig B, Wolverton C. Materials design and discovery with high-throughput density functional theory: the open quantum materials database (OQMD). JOM 2013;65:1501-9.

19. Rosen AS, Fung V, Huck P, et al. High-throughput predictions of metal–organic framework electronic properties: theoretical challenges, graph neural networks, and data exploration. NPJ Comput Mater 2022;8:112.

20. Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys Rev B 1993;47:558-61.

21. Kresse G, Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal - amorphous-semiconductor transition in germanium. Phys Rev B 1994;49:14251-69.

22. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B 1996;54:11169-86.

23. Zunger A. Inverse design in search of materials with target functionalities. Nat Rev Chem 2018;2:0121.

24. Butler KT, Davies DW, Cartwright H, Isayev O, Walsh A. Machine learning for molecular and materials science. Nature 2018;559:547-55.

25. Gubernatis JE, Lookman T. Machine learning in materials design and discovery: examples from the present and suggestions for the future. Phys Rev Mater 2018;2:120301.

26. Goldsmith BR, Esterhuizen J, Liu JX, Bartel CJ, Sutton C. Machine learning for heterogeneous catalyst design and discovery. AIChE J 2018;64:2311-23.

27. Woodley SM, Catlow R. Crystal structure prediction from first principles. Nat Mater 2008;7:937-46.

28. Gražulis S, Chateigner D, Downs RT, et al. Crystallography open database - an open-access collection of crystal structures. J Appl Cryst 2009;42:726-9.

29. Curtarolo S, Setyawan W, Hart GLW, et al. AFLOW: An automatic framework for high-throughput materials discovery. Comput Mater Sci 2012;58:218-26.

30. Gusev VV, Adamson D, Deligkas A, et al. Optimality guarantees for crystal structure prediction. Nature 2023;619:68-72.

31. Gavezzotti A. Are crystal structures predictable? Acc Chem Res 1994;27:309-14.

32. Behler J, Parrinello M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys Rev Lett 2007;98:146401.

33. Lorenz S, Groß A, Scheffler M. Representing high-dimensional potential-energy surfaces for reactions at surfaces by neural networks. Chem Phys Lett 2004;395:210-5.

34. Wu X, Kang F, Duan W, Li J. Density functional theory calculations: a powerful tool to simulate and design high-performance energy storage and conversion materials. Prog Nat Sci 2019;29:247-55.

35. Monticelli L, Tieleman DP. Force fields for classical molecular dynamics. In: Monticelli L, Salonen E. editors. Biomolecular simulations. Methods in molecular biology. Humana Press; 2013. pp. 197-213.

36. Röcken S, Zavadlav J. Accurate machine learning force fields via experimental and simulation data fusion. NPJ Comput Mater 2024;10:69.

37. Pietrucci F. Strategies for the exploration of free energy landscapes: unity in diversity and challenges ahead. Rev Phys 2017;2:32-45.

38. Wales DJ, Bogdan TV. Potential energy and free energy landscapes. J Phys Chem B 2006;110:20765-76.

39. Bonyadi MR, Michalewicz Z. Particle swarm optimization for single objective continuous space problems: a review. Evol Comput 2017;25:1-54.

40. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN'95 - International Conference on Neural Networks; 1995 Nov 27 - Dec 01; Perth, Australia. IEEE; 1995. pp. 1942-8.

41. Gerges F, Zouein G, Azar D. Genetic algorithms with local optima handling to solve sudoku puzzles. In: Proceedings of the 2018 International Conference on Computing and Artificial Intelligence. Association for Computing Machinery; 2018. pp. 19-22.

42. Katoch S, Chauhan SS, Kumar V. A review on genetic algorithm: past, present, and future. Multimed Tools Appl 2021;80:8091-126.

43. Mockus J. The Bayesian approach to global optimization. In: Drenick RF, Kozin F, editors. System modeling and optimization. 1982. p. 473-81.

44. Močkus J. On Bayesian methods for seeking the extremum. In: Optimization Techniques IFIP Technical Conference Novosibirsk; 1974 Jul 1-7. 1975. pp. 400-4.

45. Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. J Chem Phys 1953;21:1087-92.

46. Khachaturyan A, Semenovsovskaya S, Vainshtein B. The thermodynamic approach to the structure analysis of crystals. Acta Cryst 1981;37:742-54.

47. Corso G, Stark H, Jegelka S, Jaakkola T, Barzilay R. Graph neural networks. Nat Rev Methods Primers 2024;4:17.

48. Zhou J, Cui G, Hu S, et al. Graph neural networks: a review of methods and applications. AI Open 2020;1:57-81.

49. Botu V, Batra R, Chapman J, Ramprasad R. Machine learning force fields: construction, validation, and outlook. J Phys Chem C 2017;121:511-22.

50. Unke OT, Chmiela S, Sauceda HE, et al. Machine learning force fields. Chem Rev 2021;121:10142-86.

51. Kingma DP, Welling M. Auto-encoding variational bayes. arXiv. [Preprint.] Dec 10, 2022 [accessed on 2024 Sep 23]. Available from: https://arxiv.org/abs/1312.6114.

52. Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial networks. arXiv. [Preprint.] Jun 10, 2014 [accessed on 2024 Sep 23]. Available from: https://arxiv.org/abs/1406.2661.

53. Pickard CJ, Needs RJ. Ab initio random structure searching. J Phys Condens Matter 2011;23:053201.

54. Domingos R, Shaik KM, Militzer B. Prediction of novel high-pressure H₂O-NaCl and carbon oxide compounds with a symmetry-driven structure search algorithm. Phys Rev B 2018;98:174107.

55. Lu Z, Zhu B, Shires BWB, Scanlon DO, Pickard CJ. Ab initio random structure searching for battery cathode materials. J Chem Phys 2021;154:174111.

56. Morris AJ, Pickard CJ, Needs RJ. Hydrogen/nitrogen/oxygen defect complexes in silicon from computational searches. Phys Rev B 2009;80:144112.

57. Pickard CJ, Needs RJ. Structure of phase Ⅲ of solid hydrogen. Nat Phys 2007;3:473-6.

58. Pickard CJ, Needs RJ. High-pressure phases of nitrogen. Phys Rev Lett 2009;102:125702.

59. Pickard CJ, Needs RJ. Dense low-coordination phases of lithium. Phys Rev Lett 2009;102:146401.

60. Wei SH, Ferreira LG, Bernard JE, Zunger A. Electronic properties of random alloys: special quasirandom structures. Phys Rev B 1990;42:9622-49.

61. Zunger A, Wei SH, Ferreira LG, Bernard JE. Special quasirandom structures. Phys Rev Lett 1990;65:353-6.

62. Zhang X, Wang H, Hickel T, Rogal J, Li Y, Neugebauer J. Mechanism of collective interstitial ordering in Fe–C alloys. Nat Mater 2020;19:849-54.

63. Qin LX, Liang HP, Jiang RL. Structural transition from ordered to disordered of BeZnO₂ alloy. Chinese Phys Lett 2020;37:057101.

64. Yang J, Zhang P, Wei SH. Band structure engineering of Cs₂AgBiBr₆ perovskite through order–disordered transition: a first-principle study. J Phys Chem Lett 2018;9:31-5.

65. Falls Z, Avery P, Wang X, Hilleke KP, Zurek E. The XtalOpt evolutionary algorithm for crystal structure prediction. J Phys Chem C 2021;125:1601-20.

66. Glass CW, Oganov AR, Hansen N. USPEX - evolutionary crystal structure prediction. Comput Phys Commun 2006;175:713-20.

67. Cheng G, Gong XG, Yin WJ. Crystal structure prediction by combining graph network and optimization algorithm. Nat Commun 2022;13:1492.

68. Florence AJ, Johnston A, Price SL, Nowell H, Kennedy AR, Shankland N. An automated parallel crystallisation search for predicted crystal structures and packing motifs of carbamazepine. J Pharm Sci 2006;95:1918-30.

69. Wang Y, Lv J, Zhu L, Ma Y. Crystal structure prediction via particle-swarm optimization. Phys Rev B 2010;82:094116.

70. Wang Y, Lv J, Zhu L, Ma Y. CALYPSO: a method for crystal structure prediction. Comput Phys Commun 2012;183:2063-70.

71. Yang G, Shi S, Yang J, Ma Y. Insight into the role of Li₂S₂ in Li–S batteries: a first-principles study. J Mater Chem A 2015;3:8865-9.

72. Li D, Tian F, Lv Y, et al. Stability of sulfur nitrides: a first-principles study. J Phys Chem C 2017;121:1515-20.

73. Feng X, Lu S, Pickard CJ, Liu H, Redfern SAT, Ma Y. Carbon network evolution from dimers to sheets in superconducting ytrrium dicarbide under pressure. Commun Chem 2018;1:85.

74. Lv J, Xu M, Lin S, et al. Direct-gap semiconducting tri-layer silicene with 29 efficiency. Nano Energy 2018;51:489-95.

75. Zhang C, Kuang X, Jin Y, et al. Prediction of stable ruthenium silicides from first-principles calculations: stoichiometries, crystal structures, and physical properties. ACS Appl Mater Interfaces 2015;7:26776-82.

76. Deaven DM, Ho KM. Molecular geometry optimization with a genetic algorithm. Phys Rev Lett 1995;75:288-91.

77. Lyakhov AO, Oganov AR, Stokes HT, Zhu Q. New developments in evolutionary structure prediction algorithm USPEX. Comput Phys Commun 2013;184:1172-82.

78. Liu W, Liang H, Duan Y, Wu Z. Predicting copper gallium diselenide and band structure engineering through order-disordered transition. Phys Rev Mater 2019;3:125405.

79. Lv F, Liang H, Duan Y. Funnel-shaped electronic structure and enhanced thermoelectric performance in ultralight C_x(BN)_1−x biphenylene networks. Phys Rev B 2023;107:045422.

80. Liang H, Zhong H, Huang S, Duan Y. 3-X structural model and common characteristics of anomalous thermal transport: the case of two-dimensional boron carbides. J Phys Chem Lett 2021;12:10975-80.

81. Liang H, Duan Y. Structural reconstruction and visible-light absorption versus internal electrostatic field in two-dimensional GaN–ZnO alloys. Nanoscale 2021;13:11994.

82. Wang J, Hanzawa K, Hiramatsu H, et al. Exploration of stable strontium phosphide-based electrides: theoretical structure prediction and experimental validation. J Am Chem Soc 2017;139:15668-80.

83. Yu S, Zeng Q, Oganov AR, Frapper G, Zhang L. Phase stability, chemical bonding and mechanical properties of titanium nitrides: a first-principles study. Phys Chem Chem Phys 2015;17:11763-9.

84. Duan D, Liu Y, Tian F, et al. Pressure-induced metallization of dense (H₂S)₂H₂ with high-T_c superconductivity. Sci Rep 2014;4:6968.

85. Ma Y, Eremets M, Oganov AR, et al. Transparent dense sodium. Nature 2009;458:182-5.

86. Wu SQ, Ji M, Wang CZ, et al. An adaptive genetic algorithm for crystal structure prediction. J Phys Condens Matter 2013;26:035402.

87. Podryabinkin EV, Tikhonov EV, Shapeev AV, Oganov AR. Accelerating crystal structure prediction by machine-learning interatomic potentials with active learning. Phys Rev B 2019;99:064114.

88. Shahriari B, Swersky K, Wang Z, Adams RP, de Freitas N. Taking the human out of the loop: a review of Bayesian optimization. Proc IEEE 2016;104:148-75.

89. Kaappa S, del Río EG, Jacobsen KW. Global optimization of atomic structures with gradient-enhanced Gaussian process regression. Phys Rev B 2021;103:174114.

90. Kaappa S, Larsen C, Jacobsen KW. Atomic structure optimization with machine-learning enabled interpolation between chemical elements. Phys Rev Lett 2021;127:166001.

91. Bisbo MK, Hammer B. Global optimization of atomic structure enhanced by machine learning. Phys Rev B 2022;105:245404.

92. Regis RG. Trust regions in Kriging-based optimization with expected improvement. Eng Optim 2016;48:1037-59.

93. Titsias M. Variational learning of Inducing variables in sparse Gaussian processes. In: Proceedings of the Twelfth International Conference on Artificial Intelligence and Statistics. 2009. pp. 567-74. Available from: https://proceedings.mlr.press/v5/titsias09a.html. [Last accessed on 23 Sep 2024].

94. Siemenn AE, Ren Z, Li Q, Buonassisi T. Fast Bayesian optimization of Needle-in-a-Haystack problems using zooming memory-based initialization (ZoMBI). NPJ Comput Mater 2023;9:79.

95. Kirkpatrick S, Gelatt CD Jr, Vecchi MP. Optimization by simulated annealing. Science 1983;220:671-80.

96. Wille LT. Searching potential energy surfaces by simulated annealing. Nature 1987;325:374.

97. Doll K, Schön JC, Jansen M. Global exploration of the energy landscape of solids on the ab initio level. Phys Chem Chem Phys 2007;9:6128-33.

98. Doll K, Jansen M. Ab initio energy landscape of GeF₂: a system featuring lone pair structure candidates. Angew Chem Int Ed 2011;50:4627-32.

99. Doll K, Schön JC, Jansen M. Structure prediction based on ab initio simulated annealing for boron nitride. Phys Rev B 2008;78:144110.

100. Timmermann J, Lee Y, Staacke CG, Margraf JT, Scheurer C, Reuter K. Data-efficient iterative training of Gaussian approximation potentials: Application to surface structure determination of rutile IrO₂ and RuO₂. J Chem Phys 2021;155:244107.

101. Fischer CC, Tibbetts KJ, Morgan D, Ceder G. Predicting crystal structure by merging data mining with quantum mechanics. Nat Mater 2006;5:641-6.

102. Goldschmidt VM. Die gesetze der krystallochemie. Naturwissenschaften 1926;14:477-85.

103. Hautier G, Fischer C, Ehrlacher V, Jain A, Ceder G. Data mined ionic substitutions for the discovery of new compounds. Inorg Chem 2011;50:656-63.

104. Sun W, Bartel CJ, Arca E, et al. A map of the inorganic ternary metal nitrides. Nat Mater 2019;18:732-9.

105. Deng B, Zhong P, Jun K, et al. CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling. Nat Mach Intell 2023;5:1031-41.

106. Merchant A, Batzner S, Schoenholz SS, et al. Scaling deep learning for materials discovery. Nature 2023;624:80-5.

107. Xie T, Grossman JC. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys Rev Lett 2018;120:145301.

108. Isayev O, Oses C, Toher C, Gossett E, Curtarolo S, Tropsha A. Universal fragment descriptors for predicting properties of inorganic crystals. Nat Commun 2017;8:15679.

109. Deringer VL, Bartók AP, Bernstein N, Wilkins DM, Ceriotti M, Csányi G. Gaussian process regression for materials and molecules. Chem Rev 2021;121:10073-141.

110. Zhang L, Han J, Wang H, Saidi WA, Car R, E W. End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems. In: Proceedings of the 32nd International Conference on Neural Information Processing Systems; Montréal, Canada. 2018. Available from: https://proceedings.neurips.cc/paper_files/paper/2018/file/e2ad76f2326fbc6b56a45a56c59fafdb-Paper.pdf. [Last accessed on 23 Sep 2024].

111. Noh J, Gu GH, Kim S, Jung Y. Machine-enabled inverse design of inorganic solid materials: promises and challenges. Chem Sci 2020;11:4871-81.

112. Damewood J, Karaguesian J, Lunger JR, et al. Representations of materials for machine learning. Annu Rev Mater Sci 2023;53:399-426.

113. Greeley J, Jaramillo TF, Bonde J, Chorkendorff I, Nørskov JK. Computational high-throughput screening of electrocatalytic materials for hydrogen evolution. Nat Mater 2006;5:909-13.

114. Yeo BC, Nam H, Nam H, et al. High-throughput computational-experimental screening protocol for the discovery of bimetallic catalysts. NPJ Comput Mater 2021;7:137.

115. Rittiruam M, Noppakhun J, Setasuban S, et al. High-throughput materials screening algorithm based on first-principles density functional theory and artificial neural network for high-entropy alloys. Sci Rep 2022;12:16653.

116. Szymanski NJ, Rendy B, Fei Y, et al. An autonomous laboratory for the accelerated synthesis of novel materials. Nature 2023;624:86-91.

117. Chmiela S, Vassilev-Galindo V, Unke OT, et al. Accurate global machine learning force fields for molecules with hundreds of atoms. Sci Adv 2023;9:eadf0873.

118. Sauceda HE, Gálvez-González LE, Chmiela S, Paz-Borbón LO, Müller KR, Tkatchenko A. BIGDML - towards accurate quantum machine learning force fields for materials. Nat Commun 2022;13:3733.

119. Jain A, Ong SP, Hautier G, et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Mater 2013;1:011002.

120. Choudhary K, Garrity KF, Reid ACE, et al. The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design. NPJ Comput Mater 2020;6:173.

121. Zeni C, Pinsler R, Zügner D, et al. MatterGen: a generative model for inorganic materials design. arXiv. [Preprint.] Jan 29, 2024 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2312.03687.

122. Xie T, Fu X, Ganea OE, Barzilay R, Jaakkola T. Crystal diffusion variational autoencoder for periodic material generation. arXiv. [Preprint.] Mar 14, 2022 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2110.06197.

123. Behler J. Constructing high-dimensional neural network potentials: a tutorial review. Int J Quantum Chem 2015;115:1032-50.

124. Hoffmann J, Maestrati L, Sawada Y, Tang J, Sellier JM, Bengio Y. Data-driven approach to encoding and decoding 3-D crystal structures. arXiv. [Preprint.] Sep 3, 2019 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.1909.00949.

125. Schütt KT, Sauceda HE, Kindermans PJ, Tkatchenko A, Müller KR. SchNet - a deep learning architecture for molecules and materials. J Chem Phys 2018;148:241722.

126. Chen C, Ye W, Zuo Y, Zheng C, Ong SP. Graph networks as a universal machine learning framework for molecules and crystals. Chem Mater 2019;31:3564-72.

127. Schütt KT, Arbabzadah F, Chmiela S, Müller KR, Tkatchenko A. Quantum-chemical insights from deep tensor neural networks. Nat Commun 2017;8:13890.

128. Gilmer J, Schoenholz SS, Riley PF, Vinyals O, Dahl GE. Neural message passing for quantum chemistry. arXiv. [Preprint.] Jun 12, 2017 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.1704.01212.

129. Sanderson RT. An interpretation of bond lengths and a classification of bonds. Science 1951;114:670-2.

130. Sanderson RT. An explanation of chemical variations within periodic major groups. J Am Chem Soc 1952;74:4792-4.

131. Cordero B, Gómez V, Platero-Prats AE, et al. Covalent radii revisited. Dalton Trans 2008:2832-8.

132. Haynes WM. CRC handbook of chemistry and physics. CRC Press; 2014. Available from: https://doi.org/10.1201/b17118. [Last accessed on Sep 23 2024].

133. Choudhary K, DeCost B. Atomistic line graph neural network for improved materials property predictions. NPJ Comput Mater 2021;7:185.

134. Behler J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J Chem Phys 2011;134:074106.

135. Bartók AP, De S, Poelking C, et al. Machine learning unifies the modeling of materials and molecules. Sci Adv 2017;3:e1701816.

136. Irwin JJ, Tang KG, Young J, et al. ZINC20 - a free ultralarge-scale chemical database for ligand discovery. J Chem Inf Model 2020;60:6065-73.

137. Haastrup S, Strange M, Pandey M, et al. The computational 2D materials database: high-throughput modeling and discovery of atomically thin crystals. 2D Mater 2018;5:042002.

138. Zhou J, Shen L, Costa MD, et al. 2DMatPedia, an open computational database of two-dimensional materials from top-down and bottom-up approaches. Sci Data 2019;6:86.

139. Alizamir M, Kisi O, Ahmed AN, et al. Advanced machine learning model for better prediction accuracy of soil temperature at different depths. PLoS One 2020;15:e0231055.

140. Salehin I, Islam MS, Saha P, et al. AutoML: a systematic review on automated machine learning with neural architecture search. J Inf Intell 2024;2:52-81.

141. Ali Y, Hussain F, Haque MM. Advances, challenges, and future research needs in machine learning-based crash prediction models: a systematic review. Accid Anal Prev 2024;194:107378.

142. Jun K, Sun Y, Xiao Y, et al. Lithium superionic conductors with corner-sharing frameworks. Nat Mater 2022;21:924-31.

143. Zhong M, Tran K, Min Y, et al. Accelerated discovery of CO₂ electrocatalysts using active machine learning. Nature 2020;581:178-83.

144. Leitherer A, Ziletti A, Ghiringhelli LM. Robust recognition and exploratory analysis of crystal structures via Bayesian deep learning. Nat Commun 2021;12:6234.

145. Duvenaud DK, Maclaurin D, Iparraguirre J, et al. Convolutional networks on graphs for learning molecular fingerprints. arXiv. [Preprint.] Nov 3, 2015 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.1509.09292.

146. Li Y, Tarlow D, Brockschmidt M, Zemel R. Gated graph sequence neural networks. arXiv. [Preprint.] Sep 22, 2017 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.1511.05493.

147. Battaglia PW, Pascanu R, Lai M, Rezende D, Kavukcuoglu K. Interaction networks for learning about objects, relations and physics. arXiv. [Preprint.] Dec 1, 2016 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.1612.00222.

148. Kearnes S, McCloskey K, Berndl M, Pande V, Riley P. Molecular graph convolutions: moving beyond fingerprints. J Comput Aided Mol Des 2016;30:595-608.

149. Bruna J, Zaremba W, Szlam A, LeCun Y. Spectral networks and locally connected networks on graphs. arXiv. [Preprint.] May 21, 2014 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.1312.6203.

150. Li CN, Liang HP, Zhang X, Lin Z, Wei SH. Graph deep learning accelerated efficient crystal structure search and feature extraction. NPJ Comput Mater 2023;9:176.

151. Li C, Liang H, Duan Y, Lin Z. Machine-learning accelerated annealing with fitting-search style for multicomponent alloy structure predictions. Phys Rev Mater 2023;7:033802.

152. Liang HP, Geng S, Jia T, et al. Unveiling disparities and promises of Cu and Ag chalcopyrites for thermoelectrics. Phys Rev B 2024;109:035205.

153. Liang HP, Li CN, Zhou R, et al. Critical role of configurational disorder in stabilizing chemically unfavorable coordination in complex compounds. J Am Chem Soc 2024;146:16222-8.

154. Harrison JA, Schall JD, Maskey S, Mikulski PT, Knippenberg MT, Morrow BH. Review of force fields and intermolecular potentials used in atomistic computational materials research. Appl Phys Rev 2018;5:031104.

155. Senftle TP, Hong S, Islam MM, et al. The ReaxFF reactive force-field: development, applications and future directions. NPJ Comput Mater 2016;2:15011.

156. Batzner S, Musaelian A, Sun L, et al. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nat Commun 2022;13:2453.

157. Batatia I, Kovács DP, Simm GNC, Ortner C, Csányi G. MACE: higher order equivariant message passing neural networks for fast and accurate force fields. arXiv. [Preprint.] Jan 26, 2023 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2206.07697.

158. Gale JD, LeBlanc LM, Spackman PR, Silvestri A, Raiteri P. A universal force field for materials, periodic GFN-FF: implementation and examination. J Chem Theory Comput 2021;17:7827-49.

159. Cole DJ, Horton JT, Nelson L, Kurdekar V. The future of force fields in computer-aided drug design. Future Med Chem 2019;11:2359-63.

160. Robustelli P, Piana S, Shaw DE. Developing a molecular dynamics force field for both folded and disordered protein states. Proc Natl Acad Sci 2018;115:E4758-66.

161. Deringer VL, Caro MA, Csányi G. Machine learning interatomic potentials as emerging tools for materials science. Adv Mater 2019;31:1902765.

162. Gao H, Wang J, Sun J. Improve the performance of machine-learning potentials by optimizing descriptors. J Chem Phys 2019;150:244110.

163. Liu P, Verdi C, Karsai F, Kresse G. Phase transitions of zirconia: machine-learned force fields beyond density functional theory. Phys Rev B 2022;105:L060102.

164. Zhang L, Han J, Wang H, Car R, EW. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics. Phys Rev Lett 2018;120:143001.

165. Wang J, Gao H, Han Y, et al. MAGUS: machine learning and graph theory assisted universal structure searcher. Natl Sci Rev 2023;10:nwad128.

166. Xia K, Gao H, Liu C, et al. A novel superhard tungsten nitride predicted by machine-learning accelerated crystal structure search. Sci Bull 2018;63:817-24.

167. Liu C, Gao H, Wang Y, et al. Multiple superionic states in helium-water compounds. Nat Phys 2019;15:1065-70.

168. Hong C, Choi JM, Jeong W, et al. Training machine-learning potentials for crystal structure prediction using disordered structures. Phys Rev B 2020;102:224104.

169. Tong Q, Xue L, Lv J, Wang Y, Ma Y. Accelerating CALYPSO structure prediction by data-driven learning of a potential energy surface. Faraday Discuss 2018;211:31-43.

170. Tong Q, Gao P, Liu H, et al. Combining machine learning potential and structure prediction for accelerated materials design and discovery. J Phys Chem Lett 2020;11:8710-20.

171. Kang S, Jeong W, Hong C, Hwang S, Yoon Y, Han S. Accelerated identification of equilibrium structures of multicomponent inorganic crystals using machine learning potentials. npj Comput Mater 2022;8:108.

172. Hwang S, Jung J, Hong C, Jeong W, Kang S, Han S. Stability and equilibrium structures of unknown ternary metal oxides explored by machine-learned potentials. J Am Chem Soc 2023;145:19378-86.

173. Deringer VL, Pickard CJ, Csányi G. Data-driven learning of total and local energies in elemental boron. Phys Rev Lett 2018;120:156001.

174. Smith JS, Isayev O, Roitberg AE. ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost. Chem Sci 2017;8:3192-203.

175. Zhuang F, Qi Z, Duan K, et al. A comprehensive survey on transfer learning. Proc IEEE 2021;109:43-76.

176. Zhang Q, Zhu S. Visual interpretability for deep learning: a survey. Frontiers Inf Technol Electronic Eng 2018;19:27-39.

177. Han S, Pool J, Tran J, Dally WJ. Learning both weights and connections for efficient neural networks. arXiv. [Preprint.] Oct 30, 2015 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.1506.02626.

178. Cheng Y, Wang D, Zhou P, Zhang T. Model compression and acceleration for deep neural networks: the principles, progress, and challenges. IEEE Signal Process Mag 2018;35:126-36.

179. Ramesh A, Pavlov M, Goh G, et al. Zero-shot text-to-image generation. arXiv. [Preprint.] Feb 26, 2021 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2102.12092.

180. Yu J, Xu Y, Koh JY, et al. Scaling autoregressive models for content-rich rext-to-image generation. arXiv. [Preprint.] Jun 22, 2022 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2206.10789.

181. Ho J, Chan W, Saharia C, et al. Imagen video: high definition video generation with diffusion models. arXiv. [Preprint.] Oct 5, 2022 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2210.02303.

182. Singer U, Polyak A, Hayes T, et al. Make-a-video: text-to-video generation without text-video data. arXiv. [Preprint.] Sep 29, 2022 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2209.14792.

183. Anil R, Dai AM, Firat O, et al. PaLM 2 technical report. arXiv. [Preprint.] Sep 13, 2023 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2305.10403.

184. Noh J, Kim J, Stein HS, et al. Inverse design of solid-state materials via a continuous representation. Matter 2019;1:1370-84.

185. Ren Z, Tian SIP, Noh J, et al. An invertible crystallographic representation for general inverse design of inorganic crystals with targeted properties. Matter 2022;5:314-35.

186. Kim S, Noh J, Gu GH, Aspuru-Guzik A, Jung Y. Generative adversarial networks for crystal structure prediction. ACS Cent Sci 2020;6:1412-20.

187. Nouira A, Sokolovska N, Crivello JC. CrystalGAN: learning to discover crystallographic structures with generative adversarial networks. arXiv. [Preprint.] May 25, 2019 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.1810.11203.

188. Kim B, Lee S, Kim J. Inverse design of porous materials using artificial neural networks. Sci Adv 2020;6:eaax9324.

189. Fung V, Zhang J, Hu G, Ganesh P, Sumpter BG. Inverse design of two-dimensional materials with invertible neural networks. NPJ Comput Mater 2021;7:200.

190. Ho J, Jain A, Abbeel P. Denoising diffusion probabilistic models. arXiv. [Preprint.] Dec 16, 2020 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2006.11239.

191. Zhang W, Oganov AR, Goncharov AF, et al. Unexpected stable stoichiometries of sodium chlorides. Science 2013;342:1502.

192. Zhao C, Duan Y, Gao J, et al. Unexpected stable phases of tungsten borides. Phys Chem Chem Phys 2018;20:24665.

193. Lonie DC, Zurek E. XtalOpt: an open-source evolutionary algorithm for crystal structure prediction. Comput Phys Commun 2011;182:372-87.

194. Baettig P, Zurek E. Pressure-stabilized sodium polyhydrides: NaH_n (n > 1). Phys Rev Lett 2011;106:237002.

195. Hermann A, Ashcroft NW, Hoffmann R. High pressure ices. Proc Natl Acad Sci 2012;109:745-50.

196. Pickard CJ, Needs RJ. High-pressure phases of silane. Phys Rev Lett 2006;97:045504.

197. Pickard CJ, Needs RJ. Highly compressed ammonia forms an ionic crystal. Nat Mater 2008;7:775-9.

198. Lv J, Wang Y, Zhu L, Ma Y. Predicted novel high-pressure phases of lithium. Phys Rev Lett 2011;106:015503.

199. Liu H, Naumov II, Hoffmann R, Ashcroft NW, Hemley RJ. Potential high-T_C superconducting lanthanum and yttrium hydrides at high pressure. Proc Natl Acad Sci USA 2017;114:6990.

200. Wang H, Song Y, Huang G, et al. Seeded growth of single-crystal black phosphorus nanoribbons. Nat Mater 2024;23:470-8.

201. Tipton WW, Hennig RG. A grand canonical genetic algorithm for the prediction of multi-component phase diagrams and testing of empirical potentials. J Phys Condens Matter 2013;25:495401.

202. Feng J, Hennig RG, Ashcroft NW, Hoffmann R. Emergent reduction of electronic state dimensionality in dense ordered Li-Be alloys. Nature 2008;451:445-8.

203. Tipton WW, Bealing CR, Mathew K, Hennig RG. Structures, phase stabilities, and electrical potentials of Li-Si battery anode materials. Phys Rev B 2013;87:184114.

204. Zhao X, Nguyen MC, Zhang WY, et al. Exploring the structural complexity of intermetallic compounds by an adaptive genetic algorithm. Phys Rev Lett 2014;112:045502.

205. Umemoto K, Wentzcovitch RM, Wu S, Ji M, Wang CZ, Ho KM. Phase transitions in MgSiO₃ post-perovskite in super-Earth mantles. Earth Planet Sci Lett 2017;478:40-5.

206. Liu ZL. M_use: multi-algorithm collaborative crystal structure prediction. Comput Phys Commun 2014;185:1893-900.

207. Li X, Wang H, Lv J, Liu Z. Phase diagram and physical properties of iridium tetraboride from first principles. Phys Chem Chem Phys 2016;18:12569.

208. Liu ZL, Jia H, Li R, Zhang XL, Cai LC. Unexpected coordination number and phase diagram of niobium diselenide under compression. Phys Chem Chem Phys 2017;19:13219.

209. Zhang YY, Gao W, Chen S, Xiang H, Gong XG. Inverse design of materials by multi-objective differential evolution. Comput Mater Sci 2015;98:51.

210. Chen HZ, Zhang YY, Gong X, Xiang H. Predicting new TiO₂ phases with low band gaps by a multiobjective global optimization approach. J Phys Chem C 2014;118:2333-7.

211. Yang JH, Zhang Y, Yin WJ, Gong XG, Yakobson BI, Wei SH. Two-dimensional SiS layers with promising electronic and optoelectronic properties: theoretical prediction. Nano Lett 2016;16:1110-7.

212. Olson MA, Bhatia S, Larson P, Militzer B. Prediction of chlorine and fluorine crystal structures at high pressure using symmetry driven structure search with geometric constraints. J Chem Phys 2020;153:094111.

213. Hajinazar S, Thorn A, Sandoval ED, Kharabadze S, Kolmogorov AN. MAISE: Construction of neural network interatomic models and evolutionary structure optimization. Comput Phys Commun 2021;259:107679.

214. Kolmogorov AN, Shah S, Margine ER, Bialon AF, Hammerschmidt T, Drautz R. New superconducting and semiconducting Fe-B compounds predicted with an ab initio evolutionary search. Phys Rev Lett 2010;105:217003.

215. Shao J, Beaufils C, Kolmogorov AN. Ab initio engineering of materials with stacked hexagonal tin frameworks. Sci Rep 2016;6:28369.

216. Bisbo MK, Hammer B. Efficient global structure optimization with a machine-learned surrogate model. Phys Rev Lett 2020;124:086102.

217. Yamashita T, Kanehira S, Sato N, et al. CrySPY: a crystal structure prediction tool accelerated by machine learning. Science Technol Adv Mater 2021;1:87-97.

218. Terayama K, Yamashita T, Oguchi T, Tsuda K. Fine-grained optimization method for crystal structure prediction. npj Comput Mater 2018;4:32.

219. Gao H, Wang J, Guo Z, Sun J. Determining dimensionalities and multiplicities of crystal nets. NPJ Comput Mater 2020;6:143.

220. Yang S, Cho K, Merchant A, et al. Scalable diffusion for materials generation. arXiv. [Preprint.] Jun 3, 2024 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2311.09235.

221. Jiao R, Huang W, Lin P, et al. Crystal structure prediction by joint equivariant diffusion. arXiv. [Preprint.] Mar 7, 2024 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2309.04475.

222. Gruver N, Sriram A, Madotto A, Wilson AG, Zitnick CL, Ulissi Z. Fine-tuned language models generate stable inorganic materials as text. arXiv. [Preprint.] Feb 6, 2024 [accessed on 2024 Sep 23]. Available from: https://doi.org/10.48550/arXiv.2402.04379.

223. Shorten C, Khoshgoftaar TM. A survey on image data augmentation for deep learning. J Big Data 2019;6:60.

224. Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. J Mach Learn Res 2014;15:1929-58. Available from: https://www.jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf?utm_content=buffer79b43&utm_medium=social&utm_source=twitter.com&utm_campaign=buffer. [Last accessed on 23 Sep 2024].

225. Dietterich TG. Ensemble methods in machine learning. In: Multiple classifier systems. Springer Berlin Heidelberg; 2000. pp. 1-15.

226. Peherstorfer B, Willcox K, Gunzburger M. Survey of multifidelity methods in uncertainty propagation, inference, and optimization. SIAM Review 2018;60:550.

227. Jumper J, Evans R, Pritzel A, et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021;596:583-9.

Cite This Article

Review

Open Access

Machine learning assisted crystal structure prediction made simple

Chuan-Nan Li

, ... Xie Zhang

How to Cite

Li, C. N.; Liang H. P.; Zhao B. Q.; Wei S. H.; Zhang X. Machine learning assisted crystal structure prediction made simple. J. Mater. Inf. 2024, 4, 15. http://dx.doi.org/10.20517/jmi.2024.18

Download Citation

If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click on download.

Export Citation File:

RIS BibTeX EndNote

Type of Import

Direct Import Indirect Import

Tips on Downloading Citation

This feature enables you to download the bibliographic information (also called citation data, header data, or metadata) for the articles on our site.

Citation Manager File Format

Use the radio buttons to choose how to format the bibliographic data you're harvesting. Several citation manager formats are available, including EndNote and BibTex.

Type of Import

If you have citation management software installed on your computer your Web browser should be able to import metadata directly into your reference database.

Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.

Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.

About This Article

Special Issue

This article belongs to the Special Issue Application of Machine Learning to Crystal Structure Prediction

Copyright

© The Author(s) 2024. Open Access This article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Data & Comments

Data

Views

111

Downloads

18

Citations

0

Comments

0

1

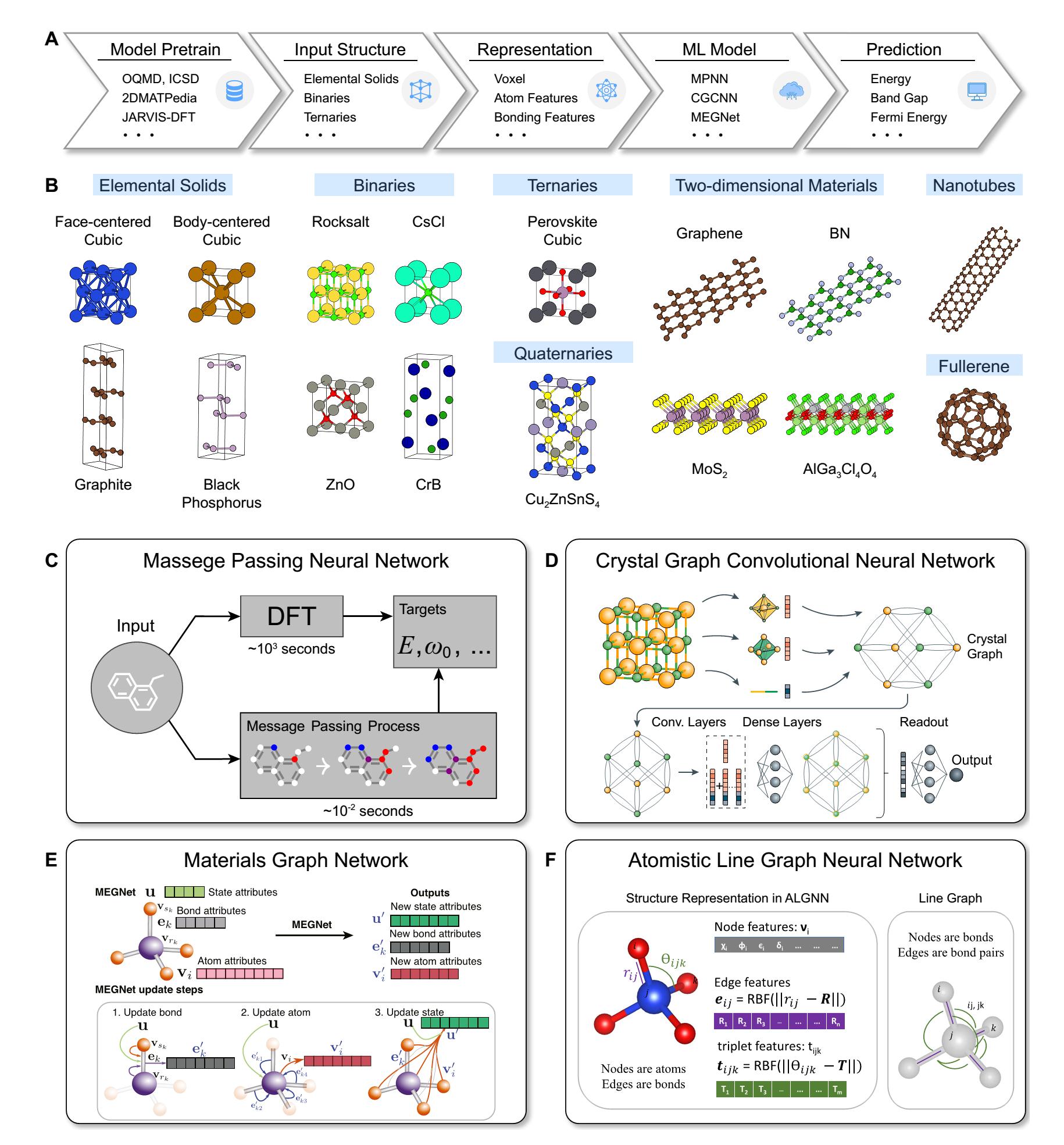
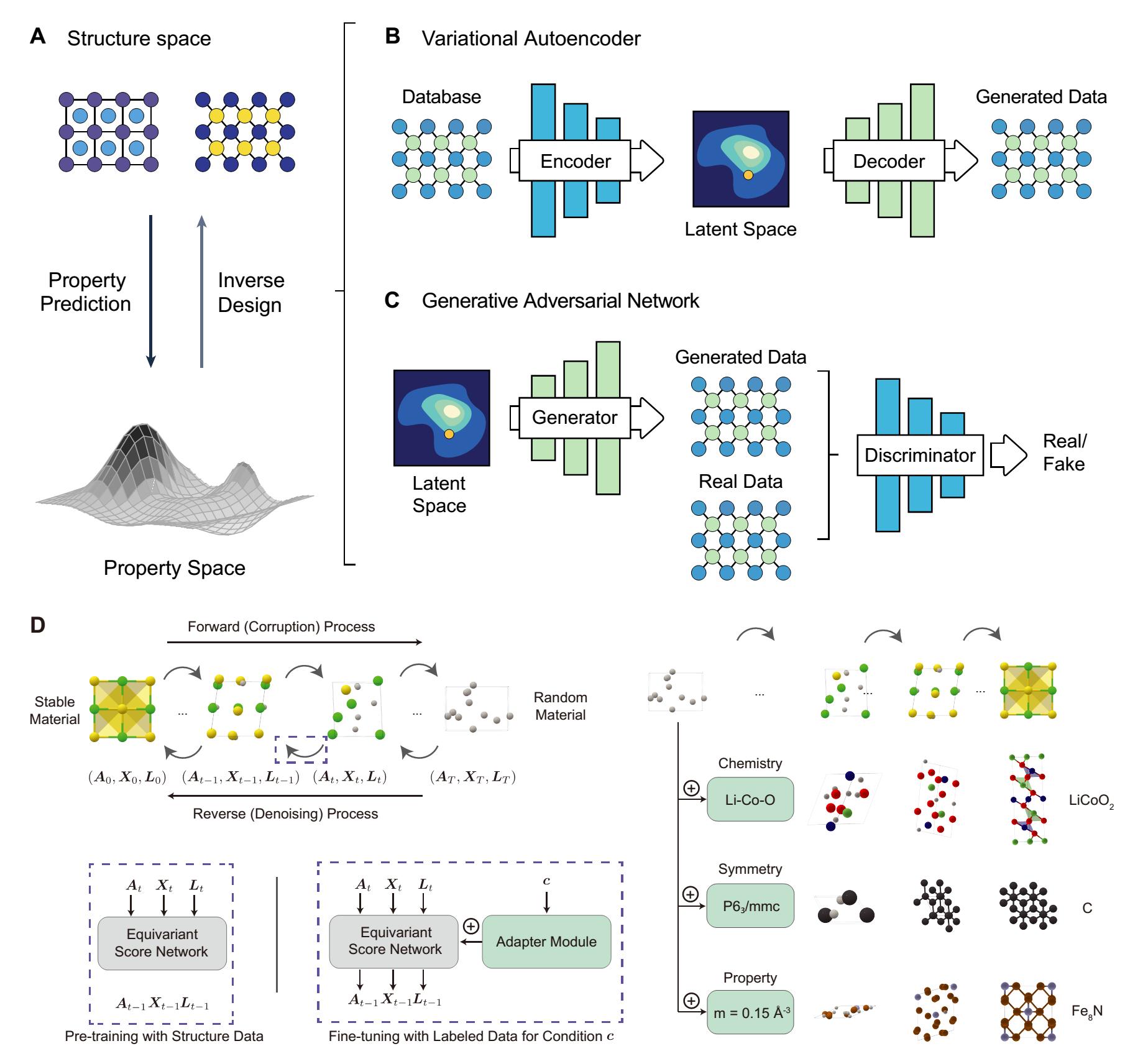
Comments

Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.

⁰

Download PDF

Download XML 1 downloads

Cite This Article 0 clicks

Export Citation 0 clicks

Like This Article 1 likes

Share This Article

https://www.oaepublish.com/articles/jmi.2024.18

Scan the QR code for reading!

See Updates

Contents

Figures

Machine learning assisted crystal structure prediction made simple

Abstract

Graphical Abstract

Keywords

INTRODUCTION

CONVENTIONAL CSP METHODS

Random search

Particle swarm optimization

GA

Bayesian optimization

Simulated annealing

Template-based method

APPLICATIONS OF ML IN CSP

Structure generation

Atom features

Bonding features

Global structure search

Local structure optimization

Generative model

SUMMARY

DECLARATIONS

Authors' contributions

Availability of data and materials

Financial support and sponsorship

Conflicts of interest

Ethical approval and consent to participate

Consent for publication

Copyright

REFERENCES

Cite This Article

How to Cite

Download Citation

Export Citation File:

Type of Import

Tips on Downloading Citation

Citation Manager File Format

Type of Import

About This Article

Special Issue

Copyright

Data & Comments

Data

Comments

Share This Article

See Updates

Committee on Publication Ethics

Portico

Committee on Publication Ethics

Portico