Graph neural networks for molecular and materials representation
Abstract
Material molecular representation (MMR) plays an important role in material property or chemical reaction prediction. However, traditional expert-designed MMR methods face challenges in dealing with high dimensionality and heterogeneity of material data, leading to limited generalization capabilities and insufficient information representation. In recent years, graph neural networks (GNNs), a deep learning algorithm specifically designed for graph structures, have made inroads into the field of MMR. It will be instructive and inspiring to conduct a survey on various GNNs used for MMR. To achieve this objective, we compare GNNs with conventional MMR methods and illustrate the advantages of GNNs, such as their expressiveness and adaptability. In addition, we systematically classify and summarize the methods and applications of GNNs. Finally, we provide our insights into future research directions, taking into account the characteristics of molecular data and the inherent drawbacks of GNNs. This comprehensive survey is intended to present a holistic view of GNNs for MMR, focusing on the core concepts, the main techniques, and the future trends in this area.
Keywords
INTRODUCTION
Material molecular representation (MMR) is a hot topic of research in materials informatics[1,2] and an essential basis for the studying of various properties of materials. The quantitative structure-activity relationship (QSAR)[3,4] studies have shown that accurate predictions depend on the quality of representation. In addition, MMR also plays a vital role in the investigation of the quantum chemistry and physicochemical properties of materials[5]. The purpose of MMR is to encode the molecular and atomic composition of materials to obtain important properties. However, traditional methods of MMR suffer from human influence and incomplete information. Recent studies have found that MMR based on graph neural networks (GNNs) has shown powerful capabilities[6-9]. In this paper, we compare the advantages and disadvantages of GNNs over traditional methods and provide a systematic review of recent advances in MMR. Figure 1 shows the proportion of GNN publications to molecular property prediction publications and the intersection of publications included in this survey.
Figure 1. Shows the proportion of GNN publications to molecular property prediction publications and the intersection of publications included in this survey. The keywords were retrieved from Google Scholar up to 2022.12. GNN: Graph neural network.
Motivation 1: MMR based on GNNs is a trend
As computational resources and data availability increase, deep learning gradually replaces traditional methods in various fields. Convolutional neural networks extract multi-scale local spatial features and are widely used in computer vision[10-12]. Recurrent neural networks (RNNs) are deep learning algorithms that use sequential data as input and are making a splash in speech recognition and natural language processing[13-15]. In addition to these, GNNs are algorithms explicitly designed for graph-structured data[16,17]. GNNs have shown excellent performance in processing unstructured data and have a wide range of applications, such as recommendation systems and social network analysis. Unlike traditional MMR based on feature engineering, GNNs can automatically extract node relationships and topology structure information, reducing the cost of manually designing features and eliminating human influence. The increasing availability of computational resources and data will further promote the trend of using GNNs in practical applications.
Motivation 2: GNNs have advantages over traditional methods
With the development of GNNs, the shortcomings of the traditional MMR methods are becoming more apparent. Traditional MMR is based on molecular fingerprints[18] or strings[19]. While the molecular fingerprints-based method is simple to use, it tends to produce sparse results for small molecule materials[20]. With the increasing advancement of natural language processing, string-based methods have been explored; however, it is difficult to express complex molecular structures in a single linear sequence. In contrast, the GNN approach directly encodes the material topology, capturing richer information than the string-based approach. Moreover, the end-to-end learning approach of GNNs makes the MMR denser and smoother, which benefits the learning of downstream tasks. A comprehensive comparison between GNNs and traditional methods is described in the section titled “REQUIREMENTS FOR GOOD MMR”.
Contributions
The main contributions of this work are summarized as follows:
• We set out some requirements for good MMR and then compare GNNs with traditional methods.
• We systematically review MMR methods based on GNNs and classify and summarize these methods and corresponding datasets.
• In response to some problems with GNNs in the field of MMR, we share our thoughts on future research directions to provide a reference for the community.
REQUIREMENTS FOR GOOD MMR
As shown in Figure 2, research on MMR has gone through three phases in the last few decades, from molecular fingerprints to string-based methods to GNNs. During the earlier stages, specific rules were devised to extract features of material molecules, and these hand-crafted features were used in machine learning (ML) to predict the properties of materials. For example, Ding et al. successfully predicted the properties of ionic liquids by combining molecular fingerprints and XGBoost[21]. Molecular fingerprints have also been widely used in the studying of material similarities[22]. Extended-Connectivity Fingerprints (ECFP)[23] are typical molecular fingerprints. They first assign a unique identifier to each atom, then update the identifier through its neighbors, and finally compress it into a 2048-dimensional vector. In addition, the Rapid Overlay of Chemical Structures (ROCS)[24] and Molecular ACCess System (MACCS)[25] are also critical molecular fingerprints. However, these methods require extensive feature engineering and are unsuitable for all downstream tasks. To avoid these issues, string-based MMR has been proposed, and the main idea of such an approach is to encode a string containing material molecular information using a sequence model-like RNN[26,27]. Widely used strings are the simplified molecular input line entry specification (SMILES)[28] and the international chemical identifier(InChI)[29], which store material molecular information compactly in a standardized format. Lin et al.[30] combines SMILES and BiGRU to successfully learn a low-dimensional representation of molecules, achieving state-of-the-art performance on some datasets. However, string-based MMR compresses the two-dimensional (2D) spatial information of material molecules. The distance between neighboring atoms in the sequence dimension is stretched, which poses an obstacle to the aggregation of atoms. Recently, MMR based on GNNs has become popular, which treats material molecules as graphs, atoms or groups as nodes, and chemical bonds as edges[31]. Compared with molecular fingerprints, GNNs do not need to construct features manually, and the representation of molecules is dense. Unlike string-based methods, GNNs directly aggregate atoms on 2D molecular graphs with less information loss. In order to compare the three methods mentioned above more systematically, we put forward four requirements for good MMR, as shown below.
Figure 2. The annual trend of research literature on the MMR included by Google Scholar. GAT: graph attention networks; GCN: graph convolutional network; InChI: international chemical identifier; MACCS: molecular ACCess system; MMR: Material molecular representation; ROCS: rapid overlay of chemical structures; SMILES: simplified molecular input line entry specification; UGRNN: undirected graph recursive neural networks.
Expressive: The expressiveness of MMR[32] is required to be rich and fine-grained. Rich means that it contains extensive information and describes the physical and chemical properties of material molecules in a multi-layered and multi-faceted manner. Fine-grained means that molecules, atoms, and chemical bonds can be described. Specifically, the expressiveness of MMR necessitates the ability to capture information about atoms, chemical bonds, multi-order adjacencies, and topologies.
Adaptive: Adaptive[33,34] MMR adjusts itself to different downstream tasks. A frozen representation will only be helpful for some tasks that are highly relevant to that representation. Correspondingly, the adaptive representation will actively generate representation relevant to the downstream task based on the characteristics of that task, which is the most significant difference between adaptive and frozen MMR. In addition, the most crucial part of MRR is the mining of adjacent atomic information. A dynamic approach will make the representation more flexible.
Multipurpose: Multipurpose[35,36] means that MMR can be competent for various downstream tasks, reflecting the breadth of applications. Specifically, downstream tasks can be divided into four categories: node classification, graph classification, connection prediction, and node clustering.
Invariant[37,38]: The MMR must be stable, and the same material molecule should have the exact representation. String-based MMR contains a massive pitfall in this requirement because completely different SMILES sequences can represent the same molecule. For example, the SMILES sequences “CC1=CC(CCC1)Br” and “CC1=CC(Br)CCC1” represent the same molecule, which would introduce risk in the sequence model.
Table 1 shows the specific relationships between the aforementioned methods and requirements. It can be observed that the molecular fingerprint-based MMR does not meet the requirements of being adaptive and multipurpose. String-based MRR, while somewhat less expressive, also fails to meet the requirement of invariance. In contrast, the GNN meets all the requirements. However, there are still problems, such as poor interpretability of GNN, which will be discussed in the “OUTLOOK” section.
The relationship between the methods and the requirements
| Requirements\Methods | Molecular fingerprints | String- based | GNNs | |
| Expressive | Atoms, chemical bonds | √ | √ | √ |
| Multi-order adjacencies | √ | × | √ | |
| topologies | √ | × | √ | |
| Representation of atoms and chemical bonds | × | √ | √ | |
| Adaptive | Generate representation relevant to the downstream task | × | √ | √ |
| Dynamic mining of adjacent atomic information | × | × | √ | |
| Multipurpose | Node classification | × | √ | √ |
| Graph classification | √ | √ | √ | |
| Connection prediction | × | × | √ | |
| Node clustering | × | √ | √ | |
| Invariant | / | √ | × | √ |
Influenced by the new generation of artificial intelligence techniques, the method of materials science research is transforming into a data-centered drive[39,40]. One of the goals pursued by the industry is to combine the latest GNN with massive material information[41,42]. In recent years, significant progress has been made in GNN research, especially in its localization application in the field of materials[43-47], which plays a vital role in promoting the realization of the value of GNNs.
This paper discusses the task scenarios of these excellent benchmarking GNNs in the background of material data. They were classified according to basic graph elements, granularity, and scale of different material tasks. In addition, classic application cases were listed to analyze the differences between these tasks in detail and show the specific coping and solving details of the GNN model. Figure 3 shows the different application scenarios of GNNs for MMR.
METHODOLOGY
There are many types of GNNs that are commonly applied to MMR. Material molecules are generally considered as undirected graphs, with atoms as nodes and chemical bonds as edges. Each node and edge in the graph have its own set of features. The main concept behind MMR based on GNNs is to develop a propagation method that enables the aggregation of the attributes and topological information of the atoms. GNNs can be divided into convolution-based GNNs and recurrence-based GNNs, depending on the propagation method. The convolution-based GNN is effective in extracting local features of material topology, while the recurrence-based GNN is more adept at extracting features over long distances. Specifically, convolution can be further subdivided into spectral convolution and spatial convolution. In addition, skip connection and subgraph embedding are also essential components of GNNs. Skip connection is intended to address the problem of “over-smoothing”, characterized by node-level representations of materials that become too similar and difficult to differentiate. Subgraph embedding introduces subgraph-level representation that enhances specific semantic and structural information, performing well in heterogeneous graphs. This section presents various methods and typical examples of GNNs for MMR. Figure 4 shows the different types of GNNs used in MMR.
Figure 4. The GNNs with different methods. (A) spectral convolution; (B) spatial convolution; (C) recurrence; (D) skip connection; (E) subgraph embedding. GNNs: graph neural networks.
Convolution
Convolution-based GNNs are the most common, and their main idea is to extend the convolution operator from convolution neural networks (CNNs) to the graph domain. Research in this area has evolved from spectral to spatial convolution. Spectral convolution draws on traditional signal processing methods and performs convolution operations in the spectral domain. In contrast, spatial convolution draws on the CNN method to weigh adjacent nodes.
Spectral convolution
The graph structure is not as stable as the 2D grid structure, with each node having different neighboring nodes. Therefore, it is impractical to use the same convolution kernel directly for all nodes. To address this challenge, researchers propose that convolution can be defined in the spectral domain. As shown in Figure 4A, the graph-domain signal is first converted into a spectral-domain signal by the Fourier transform. The convolution operation is then performed on the spectral-domain signal, and finally, the spectral-domain signal is converted back into a graph-domain signal by the inverse Fourier transform. Spectral convolution is defined as follows:
Here, x is the graph signal input, g is the convolution operator in the graph domain, F is the Fourier transform, F-1 is the inverse Fourier transform, U is the matrix of eigenvectors of the normalized graph Laplacian
Defferrard[48]et al. used a graph convolutional network (GCN) for convolutional operations and carried out research related to material molecular graph classification. The GCN replaces the spectral convolution operator with a first-order Chebyshev polynomial, avoiding the time loss associated with eigenvalue decomposition and changing the computation from global to local. In addition, GCN reduces the risk of overfitting compared to multi-order Chebyshev polynomials[49]. The convolution operator of the GCN is defined as follows:
Here, w is learnable parameters, and parameters, parameters, and à = A + IN,
GCN-like spectral convolutions are designed for graphs with fixed or shared structures. However, the sizes of molecules and the connectivity of atoms are different for material molecular graph data. Li[50]et al. proposed adaptive graph convolutional neural networks (AGCN) and designed two learnable adjacency matrices, B and C, to learn the underlying relationships of the data. B is used to learn the typical patterns of molecular graphs, while C is used to learn the unique patterns of each molecular graph. AGCN has proven effective in multi-task prediction on material molecular datasets.
Spectral convolution has a rigorous theoretical foundation that provides the basis for generalizing convolution operators to the graph domain. However, most spectral convolution methods heavily rely on the adjacency matrix of the graph. While this explicit information aid is effective in the training set, it can be less accurate in the test set due to the low level of generalization.
Spatial convolution
Spatial convolution-based GNNs perform convolutional operations directly in the graph domain, updating the state of the current node by assigning different weights to neighboring nodes. The general steps are divided into three parts: (a) initialize the node features, (b) for each node, aggregate the neighborhood information by weighted summation of the features of neighboring nodes, and then obtain new node features by a non-linear transformation of the aggregated information, and (c) repeat the operation of (b) until the number of repetitions reaches a predefined number.
As shown in Figure 4B, some researchers have used various methods, such as summation and averaging, to allocate weights. Neural FPs[20] are an ECFP-like neural network that uses summation to aggregate features of neighboring nodes to ensure the order invariance of neighboring atoms. Monti et al.[51] considers the importance of each neighbor to be different and uses the degree of a node to measure the importance of neighboring nodes. The greater the degree of a neighbor node, the less significant it is. Diffusion-convolutional neural networks (DCNN)[52] use an averaging operation to aggregate neighborhood features, but the neighborhood nodes selected differ for each aggregation. For the first aggregation, the selected neighbor nodes are nodes with a distance of 1 from the current node, while nodes with a length of 2 are selected for the second aggregation. These methods are computationally simple and exhibit some scalability, but the predefined methods consider limited information and are difficult to validate in complex MMR scenarios.
Regarding the success of attention mechanisms in machine translation[53], some researchers adaptively calculate the weights of neighboring nodes by attention mechanisms. This approach is less affected by outliers and has better generalization capabilities. Graph attention networks (GAT)[54] successfully applied the attention mechanism to feature propagation of nodes and the weights of node i and node j were calculated as follows:
Here, W is a shared parameter that enables data augmentation by performing a linear transformation of node features. [∙||∙] is a splicing operation, a is an N × 1 parameter matrix that maps the high-dimensional features to an actual number, and LeakyReLU is the activation function that normalizes the weights. In addition, GAT follows the multi-head attention mechanism, using multiple attention operators to calculate and weigh multiple sets of weights. Compared with the predefined weights, GAT better integrates the correlation between nodes into the model. In MMR, the spatial convolution-based approach is more commonly used than spectral convolution because it aligns with human intuition.
Recurrence
Another trend in GNNs is the combination of RNN models for information propagation, an approach known as recurrence-based GNNs, which improves the effectiveness of information propagation over long distances. In contrast to the convolution-based approach, recurrence-based GNNs share weights between each layer of the network, enabling the parameters to converge quickly. While this method has some drawbacks in extracting local topological information, it proves advantageous when dealing with slender material molecules. The following section describes commonly used recurrence-based GNNs.
Lusci[55]et al. used undirected graph recursive neural networks (UGRNN) to predict the water solubility of molecules. Molecules are usually described by undirected recurrent graphs, whereas recurrence-based GNNs are usually applied to directed acyclic graphs. To address this discrepancy, the authors propose to build directed acyclic graphs centered on heavy atoms. As shown in Figure 4C, a heavy atom is selected, and the other atoms generate the shortest path with that heavy atom as the target, thus obtaining a directed acyclic graph. If a molecule has multiple heavy atoms, multiple directed acyclic graphs can be generated. Each directed acyclic graph is then characterized using RNN. Finally, the representations of all the directed acyclic graphs are aggregated to obtain a representation of the molecule. Although this approach performs effectively on several benchmark datasets, it suffers from high complexity and is unsuitable for small datasets.
Altae-Tran[56]et al. combined a variant of LSTM with MMR to develop iterative refinement long short-term memory networks (Iterative LSTMs) based on one-shot learning, which significantly improved the learning of meaningful distance metrics for small molecules. The method has also been shown to have a strong generalization capability and maintain accuracy in predictions for unseen material molecules. Recurrence-based GNNs have not only made their mark in the field of one-shot learning but also in the field of material molecular generation. Segler[57]et al. applied recurrence-based GNNs to generate material molecular structures, similar to text generation in natural language processing. Overall, recurrence-based GNNs have been developed rapidly with the help of sequence models, which often lead to unexpected results in specially shaped material molecules.
Skip connection
Some experts have pointed out that deeper networks abstract features to a higher degree and greatly outperform shallower networks, for the same time, complexity. Therefore, attempts have been made to deepen the GNN and enhance the aggregation ability of each node to neighboring nodes to obtain better results. However, many experiments have demonstrated that the performance does not improve as the GNN deepens. The reason is that as the network gets deep, similar representations are created between nodes, a problem known as “over-smoothing”. To solve this problem, some experts have taken inspiration from residual networks in computer vision and added “skip connection” to GNNs. As shown in Figure 4D, “skip connection” allows the model to directly connect between two non-adjacent layers during information transmission, enabling the model to better combine low-level information with high-level information. In this section, two examples of “skip connection” are presented.
Rahimi[58]et al. proposed the highway GCN model, where a gating mechanism is added to each layer of the network to achieve a skip connection. Specifically, the input is multiplied by the weights obtained from the gating mechanism and then added to the output to obtain the final output. The gating mechanism is designed to balance the old inputs with the new outputs, and in the worst case, the original inputs can be used as outputs, thus allowing the network to become deeper. However, the experimental results found that the number of layers of the network still cannot be deepened indefinitely and that the best performance is achieved when the number of layers equals four.
Li[59]et al. combined residual connection in Resnet and dense connection in Densenet and used hole convolution to implement skip connection. The hole convolution picks k*d neighboring nodes for each node and samples the neighboring nodes in steps of d to obtain k neighboring nodes. The hole convolution uses different contextual information and increases the diversity of neighboring nodes. A 56-layer GCN was constructed in this approach, and better results were obtained.
The introduction of skip connection provides a viable solution for deepening GNNs. Skip connection avoids overlap in the neighborhood of each node and allows for a more diverse representation of nodes. However, the problems that come with deepening the network have not been completely resolved.
Subgraph embedding
Spatial convolution is popular with researchers because of its locality (only neighboring nodes need to be considered) and linear complexity. However, some studies[60] have shown that this method is comparable to the one-dimensional Weisfeiler-Leman graph isomorphism heuristic (1-WL) and has limited ability to distinguish non-isomorphic graphs. 1-WL is a classical method for determining whether two graphs are structurally isomorphic. A small perturbation of the graphs that fail the 1-WL test allows them to pass it. This idea has led to research related to subgraph embedding. As shown in Figure 4E, the original graph is partitioned into multiple subgraphs, and higher-quality graph embeddings can be obtained by performing convolution operations and aggregation on each subgraph.
Papp[61]et al. proposed dropout GNNs, where multiple subgraphs are generated by performing a dropout on the input graph (each node has a probability p of being deleted. Embeddings are obtained for each subgraph, and eventually, these embeddings are combined to obtain graph representation. In multiple subgraphs, the neighborhood information seen by each node is different, which enhances the ability of the model to discriminate between non-isomorphic graphs. DropEdge[62], which generates subgraphs by removing a certain number of edges from the input graph, also shows strong competitiveness.
Sun[63]et al. proposed SUGAR, which enhances the generalization ability of the model by selecting significant subgraphs through reinforcement learning without prior knowledge. A mechanism based on self-supervised mutual information maximization is proposed to enrich the diversity of subgraphs. In addition, the authors analyzed the relationship between model and subgraph size and found that larger size subgraphs can significantly improve performance.
Bevilacqua[64]et al. considered subgraphs as the key information to distinguish non-isomorphic graphs and thus proposed equivariant subgraph aggregation networks (ESAN). ESAN represents each graph as a set of subgraphs via a predefined policy, then uses the same encoder for each subgraph and finally aggregates the representation of the subgraphs. In addition, a subgraph sampling algorithm is proposed that not only solves the time complexity problem caused by multiple subgraphs but also improves the expressiveness of the model by increasing the randomness of the network. ESAN can even distinguish isomorphic graphs that are indistinguishable from 3-WL, which is challenging with other methods.
Subgraph embedding can be understood as a data augmentation method. It effectively improves the representation of the model to the graph by adding sub-graph level representations but also increases the computational burden.
Recently, there has been widespread attention to new GNN architectures in fields such as materials and molecules, which aim to model and predict chemical molecules at specific spatial structures. Gasteiger[65]et al. proposed a direction message passing method called DimeNet for molecular graphs. This method transforms the dependency between atoms and chemical bonds into directed edges and nodes for directional message passing. Experimental results show that this model can achieve better performance in physical and chemical tasks. Liu[66]et al. proposed a spherical message-passing method called SphereNet for modeling and predicting features of 3D molecule graphs. This method embeds atoms in a sphere and uses convolutional neural networks for statistical information extraction, which can be applied in drug design and materials science. GemNet[67] is also a generic directional GNN used for classification, regression, and generation tasks of chemical molecules. The method contains two components: the edge-attribute network, which encodes geometric information such as distances and angles of neighboring chemical bonds around each atom, and the internal energy network, which explicitly models the overall atomic features. In summary, these graph-based neural network methods demonstrate unparalleled potential in material and molecular fields and can help material researchers better understand the structure and properties of matter.
MATERIAL SIMULATION AND DESIGN
High throughput computation and experiments generate material data, which brings challenges and opportunities to material design and discovery[68]. Fast and accurate screening of structure, chemistry, and property spaces of material molecules and shortening the development cycle of new materials are the goals of current efforts[69,70]. Material space search techniques based on GNNs can efficiently explore and visualize the space of the materials to help identify underlying patterns. The general idea of material space search is to embed the high dimensional material representation into the low dimensional manifolds, which requires the model to have strong material feature representation ability. Recently, node-level feature embeddings can efficiently map the properties of high-dimensional materials. Xie et al. used the powerful feature representation capability of the crystal graph convolutional neural network (CGCNN) for material molecules. They extracted the learned vector representation of the local environments at the atomic scale from different layers of the model and then used comprehensive distance metrics to describe the similarities between materials at different scales, including elemental similarities, local environment similarities, and local energies[71]. This work can provide richer hierarchical feature representations than graph-level embedding-based material space search tasks; however, since the graph-level embedding considers the overall material feature map, a more continuous space can be obtained compared to the discrete material space output based on the node level, which facilitates the subsequent introduction of optimization algorithms such as gradient descent. They applied the proposed method to perovskites, elemental boron, and inorganic compounds, showing promising applications in automated materials design. In exploring peroxides, CGCNN achieved a mean absolute error of 0.042 on 2,000 test data points, and such high prediction performance can steadily increase with an increase in training data amount. The representation vectors learned through CGCNN can improve accuracy by at least 60% compared to random representations and were proven in experiments predicting properties such as block type for each element. In addition, Gómez-Bombarelli[72]et al. proposed a graph autoencoder VAE that consists of an encoder, a decoder, and a predictor to provide a continuous space for representing material molecular features. Although VAE is independent of chemical properties and only generated through training using SMILES strings, it can indeed generate molecules that conform to the inherent distribution of the training set. Furthermore, the molecules generated by VAE were closer to the training dataset compared to those generated by the genetic algorithm. The authors concluded that this approach performs better when the training samples have a larger combinatorial space. In contrast, genetic algorithms tend to produce molecules with higher chemical complexity but lower drug similarity.
Zhao[73]et al. proposed a framework for synthesizing inorganic Colloidal Nanocrystals (NCs), which includes data-driven robotic synthesis, robot-assisted controllable synthesis, and morphology-oriented inverse design. In the process of data-driven robotic synthesis, synthesis parameters were initially determined by mining existing literature and applied to the concentrations of known surfactants for gold NCs and the types of unknown surfactants for lead-free double-perovskite NCs. Then, by building experimental databases and training ML models, the controllable synthesis of morphology-tunable NCs was achieved. Additionally, the morphology-oriented inverse design was successfully used in the reverse design of gold nanotubes and double perovskite nanotubes. The proposal of this framework aims to reduce the dependence on manual tasks and can achieve results on par with or even surpass experienced scientists in certain fields.
Material generation and design is a critical topic for materials science and has attracted growing attention[74-76]. Based on the deep neural network model, Zhao[77]et al. proposed a generative adversarial network (GAN) for creating hypothetical materials with new compositions and structures and identified several exploitive special property crystal structures. Current work for material molecular structure generation is usually handled with deep generative models, which are essentially different from discriminative models in GNNs to introduce node-level and graph-level tasks. In a molecular graph generative model, the edge generation decision strongly impacts the overall task. You et al. extended the original graph RNN generation model GraphRNN[78] and introduced it into molecular structure generation to realize the generation of effective molecules[79]. However, generalizing this problem to an edge-level task is challenging due to diverse decision sequences resulting from different orders of edges for the same molecular graph. Moreover, the generation of edge cases is a critical consideration in this task. At last, it is important to combine node-level and graph-level information to increase the diversity of subgraph generation. Therefore, in material molecular graph generation, multiple-scale information is usually interdependent and mutually influenced.
Material design
Xie[71]et al. present a unified framework for visualizing the similarity between materials using the GNN. The GNN framework enables efficient exploration and visualization of materials data generated by high-throughput computations and ML methods in novel materials design. As the typical application, such a framework was demonstrated on three classes of materials: perovskites, elemental boron, and general inorganic crystals, and it showed that patterns automatically emerge that reflect similarities at different scales. As shown in Figure 5A, several representative elemental boron patterns were successfully identified. The method could help in the transition to a data-centered exploration of material space in automated materials design. In 2018, Gómez-Bombarelli[72]et al. described a method for transforming between discrete and continuous representations of molecules, which enables the generation of new molecules through exploration and optimization in chemical compounds, as shown in Figure 5B. A deep neural network trained on hundreds of thousands of existing chemical structures was used to create three functions: an encoder, a decoder, and a predictor. The encoder converts discrete molecular representations into continuous vectors, the decoder converts the continuous vectors back into discrete representations, and the predictor predicts chemical properties from the latent continuous vector representation of the molecule. The continuous representation of molecules allows the automatic generation of novel chemical structures and efficient optimization with gradient-based methods.
Figure 5. (A) Visualization of the local environment representations learned from the elemental boron dataset. The color of each plot is coded with learned local energy. Reproduced with permission[71]. Copyright 2018, AIP Publishing; (B) A diagram of the autoencoder used for molecular design, including the joint property prediction model; (C) Different types of molecular representations applied to one molecule. Reproduced with permission[80]. Copyright 2018, American Association for the Advancement of Science; (D) A scheme of how TS-MGCN works; (E) Model Structure of molecular distance matrix prediction mode. Reproduced with permission[81]. Copyright 2022, Elsevier; (F) Overview of a MEGNet module. Reproduced with permission[41]. Copyright 2019, American Chemical Society. MEGNet: matErials graph network; MLP: multilayer perceptron; SMILES: simplified molecular input line entry specification.
The large space of potential materials is computationally difficult to fully explore; therefore, inverse designs aim to discover materials that satisfy a particular desired feature. Advances in ML, particularly in the field of GNN, have led to the rapid development of methods for inverse molecular design. These methods[80-82] have been applied to a wide range of materials, including drugs, organic compounds, photovoltaics, redox flow batteries, and solid-state materials [Figure 5C-E]. As a pioneering work, Jain et al. present MatErials Graph Network (MEGNet), a framework for predicting the relationship between structure, state, and properties in both molecules and crystals. MEGNet models, as shown in Figure 5F, based on graph networks, are a generalization of previous graph-based models and outperform previous ML models in predicting properties on the QM9 and Materials Project datasets[83]. The authors also propose a new strategy for unifying multiple free energy MEGNet models into a single model by incorporating state variables as global inputs, resulting in a multi-fold increase in training data size with minimal increase in model parameters. The authors also show how interpretable chemical trends can be extracted from elemental embeddings and used in transfer learning to improve the performance of models with smaller datasets.
Due to the difficulty in obtaining strain energy density functions for hyperelastic materials with complex hexagonal and tetragonal crystal structures, Im[84]et al. bypassed the assumption of strain energy density functions and constructed neural network constitutive models (NNCMs) to obtain data for a wide range of materials under different deformations. Performance prediction is significant in modern materials design; as previously mentioned, graph-level embeddings can handle multiple task scenarios, and graph-level classification task in materials science is perfect for applying material properties prediction[45,85-87]. Since Xie et al. proposed CGCNN, the convolution GNN has become a general paradigm and one of the most competitive models for material molecular modeling. Only using the distance information between atoms to aggregate and fit the properties of molecules has certain defects, especially the over-smoothing issue also hinders the efficiency of the model. The subsequent introduction of the attention mechanism and skip-connection can continue to exploit the potential of the convolutional GNN, and the priority rules or experience that can improve predictions successfully push the predictive performance of such models to the extreme[88]. Based on GNNs, Li[89]et al. proposed a deep learning algorithm with general applicability to extract useful interactions between target atoms and their neighboring clusters for bioactivity prediction and other tasks related to drug discovery and material design, achieving a minimum mean absolute error.
Optimization in the material design process can be achieved through pre-training and database creation:
(i) Pre-training is a technique used by GNNs to achieve high performance through the use of a large amount of labeled data, similar to most neural networks. However, when it comes to material molecules, there is a finite amount of labeled data available, and most labeling tasks are expensive and time-consuming. To address this problem, an approach similar to self-supervised pre-training in natural language processing[90-92] can be employed. Specifically, GNNs can enhance the representation of molecules by pre-training on large amounts of unlabeled data. Wang[93]et al. proposed a self-supervised learning framework to implement pre-training of GNNs using contrast learning. This approach enriches intrinsic molecular representation by widening the distance between positive and negative samples. Positive samples are obtained by data enhancement of the molecular graph, such as atomic masking, bond deletion, and subgraph deletion. Undoubtedly, pre-training of GNNs is a hot research area for the future, as it allows the efficient use of unlabeled data and reduces the cost of data annotation. Ding[94]et al. proposed an ensemble of ensemble technology for ML to predict the ability of hydrogen release of LiBH4 compounds and rank each influence factor based on importance. Their work provides a valuable reference for future material design.
(ii) Datasets applied to MMR cover multiple material properties levels, which we describe mainly at the quantum mechanical and physicochemical levels:
Quantum mechanics provides insights into the microscopic level and expresses the internal properties of molecules. QM7[95], QM8[96], and QM9[97] are datasets commonly used in quantum mechanics studies and contain properties such as coulomb matrix representation of molecules and atomization energies. Traditional methods use density functional theory to model these properties[98,99], much slower than methods based on GNNs. Liao[100]et al. constructed a low-rank approximation to the graph Laplacian using the Lanczos algorithm for graph convolution. The method achieves promising results on the QM8 quantum dataset. Louis[101]et al. combined the GATGNN based on spatial convolution with the atomic composition and coordinates in 3D space to study electrode properties. In addition, Omee[102]et al. constructed a deeperGATGNN with more than 30 layers based on spatial convolution and skip connection to achieve state-of-the-art results in energy and band gap[103] prediction for high-performance materials.
The study of physical chemistry includes molecular interactions with solvents and inherent thermodynamic properties of molecules. The former includes the free energy of hydration[104], permeability[105], and water solubility[106], while the latter includes properties such as boiling point[107] and melting point[108]. Meng[109]et al. designed ExGCN by combining the attention mechanism and skip connection, achieving better performance in lipophilicity and solubility datasets. In addition, the properties of polycrystals also belong to the Physical Chemistry level. Dai[110]et al. designed PolycrystalGraph around the three factors of grain size, orientation, and interactions between neighboring grains and used it for embedding polysilicon microstructures. Datasets about quantum mechanics and physical chemistry are often used to predict material molecular properties. The quality of the MMR is reflected in the accuracy of the prediction, with more accurate predictions representing a higher quality of MMR.
In addition, we have sorted out the commonly used datasets and the corresponding methods. Table 2 contains the commonly used datasets for quantum mechanics and physical chemistry levels and the description of each dataset. Table 3 contains the classical methods on each level dataset.
Common datasets at different levels
| Level | Datasets | Description |
| Quantum mechanics | QM7[95], QM8[96], QM9[97] | Computer-generated quantum mechanical properties |
| CSD[111], COD[112] | Coordinates | |
| OPV[113] | Molecular properties and equilibrium coordinates | |
| ISO17[114] | Atomic forces | |
| Physical Chemistry | FreeSolv[104] | Hydration free energy |
| Lipophilicity[105], Az-logD[115] | Permeability | |
| Huuskonen[106], ESOL[116], Abraham[108], Delaney[108], OCHEM[105], Intrinsic Solubility[117] | Aqueous solubility | |
| Alkanes[107], Bradley[108] | Boiling Point, Melting Point | |
| Others | PoLyInfo[118] | A polymer database with polymer properties, chemical structures, etc. |
Classic GNNs in MMR
| Methodologies\Levels | Spectral convolution | Spatial convolution | Recurrence | Skip connection | Subgraph embedding |
| Quantum mechanics | LanczosNet[100], HANet[119] | MV-GNN[120], GATGNN[98,101], DeeperGATGNN[102], DGGNN[121], MEGNet[122] | RNN[123], PotentialNet[124], EMNN[125], DGGNN[121] | DeeperGATGNN[102], InfoGraph[126] | DropGNNs[61] |
| Physical Chemistry | AGCN[50], PolycrystalGraph[110] | MV-GNN[120], ExGCN[109], SAMPN[105], SkipGNN[127], C-SGEN[128] | EMNN[125], PotentialNet[124], UGRNN[55] | C-SGEN[128], ExGCN[109] | FraGAT[129] |
PREDICTION OF MATERIAL PROPERTIES USING GNN
Next, we focus on advances in ML-based methods for material property prediction. While the aforementioned ML methods mainly focus on the study of configurations, ML methods based on targeted material properties can be effective in the reverse design of materials. These methods enable the design of new materials with specific applications. For example, Choi[130]et al. present a computational workflow that uses the HydraGNN library to perform Distributed Data-Parallel (DDP) training to predict the HOMO-LUMO gap of molecules, which can be trained on both CPUs and GPUs. The proposed workflow is shown in Figure 6A. The accuracy and convergence behavior of distributed training with an increasing number of GPUs was also demonstrated. The authors state that HydraGNN provides an effective surrogate model for accurate and rapid screening of large chemical spaces for molecular design. Similarly, Pablo-García[135]et al. introduced the GNN GAME-Net, which is six orders of magnitude faster than density functional theory in evaluating adsorption energy tasks. The authors highlighted that this framework represents a useful tool for rapidly screening catalytic materials, especially for cases that cannot be simulated by traditional methods. In addition to molecular systems, much more relevant research has progressed in periodic systems. For CO2 adsorption in metal-organic frameworks (MOFs), the Atomistic Line GNN (ALIGNN) method was proposed to predict CO2 adsorption in MOFs. The method is trained on a database of 137953 hypothetical MOFs with CO2 adsorption data obtained from grand canonical Monte Carlo simulations, as shown in the linear shape in Figure 6B. The ALIGNN model is then applied to the CoREMOF database to rank MOFs for experimental synthesis, showing the strengths and limitations of such GNN models, with a few selected MOFs evaluated using additional simulations to validate the ML predictions. In addition to these studies, the GNN approach for the study of functional materials with targeted properties has been applied to other areas, such as the data-driven theoretical design of novel 2D materials[132], the properties of polycrystalline materials[110], the design of doped transition metal compounds with good stability, and suitable electrical conductivity[133], as shown in Figure 6C-E. Very recently, a new approach for predicting the methane adsorption of MOFs using a GNN algorithm has been proposed[134]. The method (MOF-CGCNN, as shown in Figure 6F) takes into account key physical properties of MOFs and information on secondary building blocks. The new force field for CH4 was refined specifically for MOFs containing open metal sites. Analyses show that the new algorithm has a high Pearson correlation coefficient and a low mean error. The model uses the adsorption volume as the embedding representation, allowing transfer learning. The method can predict the methane adsorption volumes of all MOFs in a large database within hours and is expected to be a useful tool in the early stages of virtual screening for novel porous materials for gas adsorption or separation.
Figure 6. Selected examples of investigations based on ml-method predictions for targeted functional material design. (A) A computational workflow to predict the HOMO-LUMO gap. This workflow pits the conventional method against two alternative approaches: density functional-based tight binding (DFTB) calculations and a GCNN model. The latter leverages molecular structure as its input to estimate the HOMO-LUMO gap. Reproduced with permission[130]. Copyright 2022, BioMed Central; (B) GNN predictions and grand canonical Monte Carlo (GCMC) actual value comparisons of void fraction and adsorption at 2.5 bar using the Atomistic Line Graph Neural Network method. Reproduced with permission[130]. Copyright 2022, BioMed Central; (C) Schematic of the workflow of deep transfer learning for predicting 2D host material properties and identifying promising hosts (for example, 2D BN and 2D MoS2). Reproduced with permission[132]. Copyright 2020, American Chemical Society; (D) A graphical representation of a polycrystalline microstructure composed of N grains. Reproduced with permission[110]. Copyright 2021, Springer Nature Limited; (E) The proposed workflow diagram of a visual interactive software (DeepTMC) to targeted design doped transition metal compounds. Reproduced with permission[133]. Copyright 2022, Elsevier; (F) Proposed crystal graph convolutional neural network (CGCNN) method for CH4 adsorption in MOFs. Reproduced with permission[134]. Copyright 2022, Elsevier.
The uncertainty characterization/quantification in material property prediction is of great significance for the success and reliability of artificial intelligence in materials science. If the uncertainty of predicted values is unknown, it will be questioned. In many works, the confidence interval of the prediction model is reported. Typically, the smaller the confidence interval, the more reliable the prediction results of the model, and the lower the confidence interval, the less reliable the prediction results. Tavazza[136]et al. compared three methods, namely quantile loss function, ML, and Gaussian processes, for obtaining uncertainty on 12 physical properties. The authors found that Gaussian processes have a better estimation of uncertainty, which is influenced by hyperparameters, but this method is time-consuming. The quantile loss function needs to fit three models, and its effect is slightly lower than that of Gaussian processes. One of the greatest advantages of ML is that it adapts to any loss function. Kwon[137]et al. used GNNs to predict the uncertainty of chemical reaction yield. They represented a chemical reaction as a set of graphs, with the output being the mean and variance of the reaction yield, i.e., the uncertainty. In the Buchwald-Hartwig and Suzuki-Miyaura datasets, they demonstrated the effectiveness of the proposed method and showed that greater uncertainty leads to higher prediction errors and may result in rejecting predictions. Often, error estimation can provide a quantitative assessment of uncertainty, which can be more reliable than applying only the root mean square error (RMSE) of the predictor. Gaussian process regression and random forest decision trees are powerful error assessment models that can provide a more comprehensive understanding of model errors. Therefore, when assessing real ML models, these approaches should be considered for improved reliability.
THE ATOMIC FORCE FIELD DEVELOPMENT USING ML
In this section, we focus on ML force field (MLFF)-based materials research toolkits that can extend the computational simulation system across time and length scales, eventually facilitating the rational design of novel materials and their performance prediction. To construct a high-precision MLFF for a specific task, a number of modeling steps are required [Figure 7A]. First, the general approach is to use the general approach is to use Discrete Fourier Transform (DFT) calculations in the data preparation stage to obtain sufficient first-principles data. It is ideal to consider the limitations of the chosen level of the theory itself (e.g., different functionals and long-range interactions, etc.). So far, numerous models have been developed, typically such as Behler-Parrinello neural network potentials[138], moment tensor potentials[139], aenet[140], DeePMD[141], etc. Although all of these methods can be used to construct MLFFs for any given chemical system, for some tasks, a particular method may be more promising than others. As a result, it is difficult to give a general recommendation for method selection. However, some key general rules should be followed to ensure transferability, compatibility, and computational efficiency[142-145]: (1) The training model should be able to describe molecules and periodic crystals, covering multiple dimensions of conformation. (2) Scalability of physical quantities in real space needs to be ensured. (3) Invariants such as translations and rotations in the structure should be preserved. (4) Human intervention should be avoided as far as possible.
Figure 7. Development and typical application of the MLFF. (A) The MLFF constructed by beginning with an initial dataset (AIMD simulation generally). Subsequently, the MLFF is validated through a multistep process (i.e., force root mean square error (RMSE), radial distribution functions (RDFs) of the selected structures randomly). If the potential quality is deemed insufficient, problematic structures are identified and included in the training set until the final potential is achieved. Reproduced with permission[148]. Copyright 2021, American Chemical Society; (B) The MLFF fitting database for elemental phosphorus by using the many-body Smooth Overlap of Atomic Positions (SOAP) model. Reproduced with permission[148]. Copyright 2021, American Chemical Society; (C) The application of active learning molecular dynamics approach for the perovskite. The black curve represents the actual error, while the red curve represents the estimated error from MLFF. When the estimated error exceeds a certain threshold, it triggers DFT calculations to generate new data, which is then used to retrain the MLFF. The top structures highlight the hydrogen atom with the highest error in red for two different snapshots. Reproduced with permission[148]. Copyright 2021, American Chemical Society; (D)The figure on the left shows the performance assessment of the committee NNP (c-NNP) for six different systems. The figure on the right is a bar plot that summarizes the accuracy of the RDFs, VDOS, and force predictions for each system. Reproduced with permission[153]. Copyright 2021, National Academy of Science; (E) (Left) Slab model of amorphous carbon from MLFF-based simulation. (Right) Crystal structures and electron localization function (ELF) of (a) B4C and (b) Al-doped boron carbide (labeled as B12 -CAlC), and models of the B12-CAlC sliding system along different (c, d) slip directions. The blue, orange, and yellow spheres represent B, C, and Al atoms, respectively. Reproduced with permission[155]. Copyright 2018, American Physical Society. Reproduced with permission[156]. Copyright 2023, American Physical Society.
The next step is model training, where the parameters of the model are tuned to minimize the loss function, which measures the difference between the training data and the model predictions. The literature has increasingly emphasized the importance of validating MLFFs not only on the basis of numerical error levels but also on the basis of the predicted physical behavior[146,147]. The main motivation for the final training of MLFF was to use it for specific production applications, i.e., performing MD simulations. Once the transferability and accuracy of the force field have been fully tested, it can be used for large-scale molecular dynamics simulations. Due to the performance advantages of MLFFs, it is possible to extend the time scale of computational simulations beyond nanoseconds while maintaining first-principles accuracy, which is a significant advance in the theoretical study of materials[148]. We will then show this with some typical applications.
A first typical example is the development of an MLFF for elemental phosphorus by Deringer et al.[149]. As shown in Figure 7B, using the newly developed GAP+R6 model for MLFF training, they have been able to account for the effects of many-body dispersion in layered phosphorus. The calculated results show that this MLFF can accurately represent the exfoliation process of black and violet phosphorus with the accurate prediction compared to the traditional empirical potential force field. The model was also applied to larger-scale nanoribbon systems, demonstrating the power of accurate and flexible ML-driven force fields for modeling next generation materials. Another pioneering work comes from the VASP development group, which has developed an on-the-fly MLFF method and applied it to molecular dynamics simulations of hybrid perovskite, as shown in Figure 7C[150]. They found a strong correlation between the uncertainty estimate and the actual error in the MLFF, demonstrating that the method can effectively use data from DFT calculations. This results in a 99% reduction in the computational effort required for the corresponding ab initio trajectory, allowing the potential to be used to study complex phase transitions[151]. This feature is already supported in the latest version of VASP and is expected to provide even more valuable theoretical support for multi-scale studies of materials. Compared to solid or molecular systems, materials with solid-liquid interfaces, such as water on the surface or water under solidification, are important systems to examine[152]. However, current theoretical tools for calculating these systems of responsibility are challenging. Recently, Schran[153]et al. Figure 7D have shown how these limitations can be overcome in an automated ML procedure. For several different solution systems, MLFFs were obtained with an accuracy range close to that of DFT, showing that MLFFs can be used as effective tools to accelerate theoretical studies of complex systems. Another important application of MLFF is the simulation of nucleation processes in crystal structure and the simulation of mechanical properties of large-scale systems. Since the simulation of nucleation processes is not considered to be feasible with conventional DFT calculations [too many atoms for ab initio molecular dYnamics (AIMD) simulations], the traditional approach is to simulate them using the empirical force field method, but the accuracy of the simulation is highly dependent on the force field[154]. The development of MLFF overcomes this limitation and allows the simulation of nucleation processes and mechanical deformation of crystals with first-principles accuracy, typically for the simulation of amorphous carbon and the simulation of the mechanical properties of superhard materials as shown in Figure 7E.
OUTLOOK
MMR based on GNNs has evolved over the years, gradually replacing traditional methods with the mainstream and achieving better results in different levels of research. However, there are still some unresolved challenges. This section discusses some issues in GNNs for MMR and provides future research directions for reference.
Interpretability
The black box problem of deep learning has been criticized for a long time; therefore, interpretability[157,158] studies of GNNs can help researchers gain insight into which features influence representation. It can be helpful when designing new approaches for MMR, such as enhancing the portrayal of important features. Ma[120]et al. visualized the attention weights learned by GNNs and found that most of the carbon atoms responsible for building the topology of the molecule had zero weight. At the same time, the trifluoromethyl and cyanide of toxic functional groups showed highly high weights. It can then be surmised that in the study of toxicity, researchers will enhance the portrayal of functional groups known to be toxic. To this end, the interpretable study of MMR based on GNNs is a potential future direction. Although the propagation mechanism of GNNs is more explanatory than traditional neural networks, it is not enough for MMR.
Dynamic molecular graphs
Understanding the relationship between time and space is an important research topic in network science, and in the MMR field, this topic focuses on dynamic molecular graphs. Dynamic molecular graphs are widely referred to in studies such as protein folding and molecular reactions, where nodes and edges of molecules evolve over time. Indeed, dynamic graph-based GNNs have been well studied in applications such as communication and transport networks[159,160], recommender systems[161,162], and epidemiology[163,164] but have not been generalized in dynamic molecular graphs. Compared to other dynamic graphs, dynamic molecular graphs present two significant difficulties. Firstly, the space is microscopic, and descriptions of nodes in molecular graphs are not as detailed as those of macroscopic objects and cannot be effectively distinguished in the time dimension. Secondly, time is fleeting, and changes in the molecular graph over time are rapid and less detectable than in transport networks. Research in this direction is bound to become an essential element of GNNs in the field of molecular representation.
CONCLUSIONS
In this work, we present neural graph networks for MMR, compare them with traditional methods, and present ideas for the future direction of the subject. Firstly, compared to traditional methods, GNNs are superior in all four requirements: Expressive, Adaptive, Multipurpose, and Invariant. Secondly, we believe that spatial convolution-based GNNs are the most versatile approach and are competent for studying material molecular properties at multiple levels. Skip connection and subgraph embedding methods are outstanding in solving specific problems. Thirdly, we discuss in detail the different application scenarios of the GNN in the field of material information and the classical processing cases based on the GNN according to the types and granularity of the applicable tasks. Finally, we provide ideas for two future directions: interpretability and dynamic molecular graphs.
DECLARATIONS
AcknowledgmentsWe appreciate the support of the High Performance Computing Center of Shanghai University, and Shanghai Engineering Research Center of Intelligent Computing System.
Authors’ contributionsConceptualization: Wu X, Li Q
Data curation: Qian Q
Methodology: Wu X
Writing-original draft preparation: Wang H
Writing-review and editing: Wu X, Qian Q, Li Q, Wang H, Fan D, Gong Y, Ding P
Supervision: Wu X
All authors have read and agreed to the published version of the manuscript.
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was sponsored by the National Key Research and Development Program of China (2022YFB3707800), National Natural Science Foundation of China (No. U2102212), Key Program of Science and Technology of Yunnan Province (No. 202102AB080019-3, 202002AB080001-2), Key Research Project of Zhejiang Laboratory (No.2021PE0AC02), Key Project of Shanghai Zhangjiang National Independent Innovation Demonstration Zone (No. ZJ2021-ZD-006).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2023.
REFERENCES
2. Hara K, Yamada S, Kurotani A, Chikayama E, Kikuchi J. Materials informatics approach using domain modelling for exploring structure-property relationships of polymers. Sci Rep 2022;12:10558.
3. Kuz’min V, Artemenko A, Ognichenko L, et al. Simplex representation of molecular structure as universal QSAR/QSPR tool. Struct Chem 2021;32:1365-92.
4. Keyvanpour MR, Shirzad MB. An analysis of QSAR research based on machine learning concepts. Curr Drug Discov Technol 2021;18:17-30.
5. Poulson BG, Alsulami QA, Sharfalddin A, et al. Cyclodextrins: structural, chemical, and physical properties, and applications. Polysaccharides 2022;3:1-31.
7. Lee JB, Rossi R, Kong X. Graph classification using structural attention. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; London, United Kingdom; 2018. pp. 1666-74.
8. Gilmer J, Schoenholz SS, Riley PF, Vinyals O, Dahl GE. Neural message passing for quantum chemistry. Proceedings of the 34th International Conference on Machine Learning; Sydney, NSW, Australia; 2017. pp. 1263-72. Available from: https://proceedings.mlr.press/v70/gilmer17a [Last accessed on 7 Jun 2023]
9. Wei X, Wang C, Jia Z, Xu W. High-cycle fatigue S-N curve prediction of steels based on a transfer learning-guided convolutional neural network. J Mater Inf 2022;2:9.
10. Luo H, Xiong C, Fang W, Love PED, Zhang B, Ouyang X. Convolutional neural networks: computer vision-based workforce activity assessment in construction. Autom Constr 2018;94:282-9.
11. Zhang J, Zhang J, Wu X, Shi Z, Hwang J. Coarse-to-fine multiscale fusion network for single image deraining. J Electron Imag 2022;31:043003.
12. Wu X, Zhang Y, Li Q, Qi Y, Wang J, Guo Y. Face aging with pixel-level alignment GAN. Appl Intell 2022;52:14665-78.
13. Khurana D, Koli A, Khatter K, Singh S. Natural language processing: state of the art, current trends and challenges. Multimed Tools Appl 2023;82:3713-44.
14. Wu X, Jin Y, Wang J, Qian Q, Guo Y. MKD: Mixup-based knowledge distillation for mandarin end-to-end speech recognition. Algorithms 2022;15:160.
15. Wu X, Tang B, Zhao M, Wang J, Guo Y. STR transformer: a cross-domain transformer for scene text recognition. Appl Intell 2023;53:3444-58.
16. Zhou J, Cui G, Hu S, et al. Graph neural networks: a review of methods and applications. AI Open 2020;1:57-81.
17. Wu Z, Pan S, Chen F, Long G, Zhang C, Yu PS. A comprehensive survey on graph neural networks. IEEE Trans Neural Netw Learn Syst 2021;32:4-24.
18. Zagidullin B, Wang Z, Guan Y, Pitkänen E, Tang J. Comparative analysis of molecular fingerprints in prediction of drug combination effects. Brief Bioinform 2021;22:bbab291.
20. Duvenaud D, Maclaurin D, Aguilera-Iparraguirre J, et al. Convolutional networks on graphs for learning molecular fingerprints. Proceedings of the 28th International Conference on Neural Information Processing Systems; Montreal, Canada; 2015. pp. 2224-32. Available from: https://dl.acm.org/doi/10.5555/2969442.2969488 [Last accessed on 8 Jun 2023]
21. Ding Y, Chen M, Guo C, Zhang P, Wang J. Molecular fingerprint-based machine learning assisted QSAR model development for prediction of ionic liquid properties. J Mol Liq 2021;326:115212.
22. Maggiora G, Vogt M, Stumpfe D, Bajorath J. Molecular similarity in medicinal chemistry. J Med Chem 2014;57:3186-204.
24. Rush TS 3rd, Grant JA, Mosyak L, Nicholls A. A shape-based 3-D scaffold hopping method and its application to a bacterial protein-protein interaction. J Med Chem 2005;48:1489-95.
25. Durant JL, Leland BA, Henry DR, Nourse JG. Reoptimization of MDL keys for use in drug discovery. J Chem Inf Comput Sci 2002;42:1273-80.
26. Liu X, Liu C, Huang R, et al. Long short-term memory recurrent neural network for pharmacokinetic-pharmacodynamic modeling. Int J Clin Pharmacol Ther 2021;59:138-46.
27. Goulas A, Damicelli F, Hilgetag CC. Bio-instantiated recurrent neural networks: Integrating neurobiology-based network topology in artificial networks. Neural Netw 2021;142:608-18.
28. Weininger D. SMILES, a chemical language and information system. 1. introduction to methodology and encoding rules. J Chem Inf Comput Sci 1988;28:31-6.
29. Heller SR, McNaught A, Pletnev I, Stein S, Tchekhovskoi D. InChI, the IUPAC international chemical identifier. J Cheminform 2015;7:23.
30. Lin X, Quan Z, Wang ZJ, Huang H, Zeng X. A novel molecular representation with BiGRU neural networks for learning atom. Brief Bioinform 2020;21:2099-111.
31. Feng YH, Zhang SW. Prediction of drug-drug interaction using an attention-based graph neural network on drug molecular graphs. Molecules 2022;27:3004.
32. Chuang KV, Gunsalus LM, Keiser MJ. Learning molecular representations for medicinal chemistry. J Med Chem 2020;63:8705-22.
33. Bengio Y, Courville A, Vincent P. Representation learning: a review and new perspectives. IEEE Trans Pattern Anal Mach Intell 2013;35:1798-828.
34. Zhang Z, Shao L, Xu Y, Liu L, Yang J. Marginal representation learning with graph structure self-adaptation. IEEE Trans Neural Netw Learn Syst 2018;29:4645-59.
35. Xie Y, Jin P, Gong M, Zhang C, Yu B. Multi-task network representation learning. Front Neurosci 2020;14:1.
36. Wang S, Wang Q, Gong M. Multi-task learning based network embedding. Front Neurosci 2019;13:1387.
37. Khasanova R, Frossard P. Graph-based isometry invariant representation learning. Proceedings of the 34th International Conference on Machine Learning; Sydney, NSW, Australia; 2017. pp. 1847-56. Available from: http://proceedings.mlr.press/v70/khasanova17a.html?ref=https://githubhelp.com [Last accessed on 8 Jun 2023]
39. Batra R, Song L, Ramprasad R. Emerging materials intelligence ecosystems propelled by machine learning. Nat Rev Mater 2021;6:655-78.
40. Agrawal A, Choudhary A. Deep materials informatics: applications of deep learning in materials science. MRS Commun 2019;9:779-92.
41. Chen C, Ye W, Zuo Y, Zheng C, Ong SP. Graph networks as a universal machine learning framework for molecules and crystals. Chem Mater 2019;31:3564-72.
42. Park CW, Wolverton C. Developing an improved crystal graph convolutional neural network framework for accelerated materials discovery. Phys Rev Materials 2020;4:063801.
43. Sumpter BG, Noid DW. Neural networks and graph theory as computational tools for predicting polymer properties. Macromol Theory Simul ;3:363-78.
44. Xie T, Grossman JC. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys Rev Lett 2018;120:145301.
45. Coley CW, Jin W, Rogers L, et al. A graph-convolutional neural network model for the prediction of chemical reactivity. Chem Sci 2019;10:370-7.
46. Wu Z, Ramsundar B, Feinberg EN, et al. MoleculeNet: a benchmark for molecular machine learning. Chem Sci 2018;9:513-30.
47. Schmidt J, Marques MRG, Botti S, Marques MAL. Recent advances and applications of machine learning in solid-state materials science. npj Comput Mater 2019;5:83.
48. Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering. Available from: https://arxiv.org/abs/1606.09375 [Last accessed on 8 Jun 2023].
49. Hammond DK, Vandergheynst P, Gribonval R. Wavelets on graphs via spectral graph theory. Appl Comput Harmon A 2011;30:129-50.
51. Monti F, Boscaini D, Masci J, Rodolà E, Svoboda J, M. Bronstein MM. Geometric deep learning on graphs and manifolds using mixture model CNNs. Available from: https://ieeexplore.ieee.org/document/8100059 [Last accessed on 8 Jun 2023].
52. Atwood J, Towsley D. Diffusion-convolutional neural networks. Available from: https://proceedings.neurips.cc/paper_files/paper/2016/hash/390e982518a50e280d8e2b535462ec1f-Abstract.html [Last accessed on 8 Jun 2023]
53. Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Available from: https://proceedings.neurips.cc/paper_files/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html [Last accessed on 8 Jun 2023]
54. Veličković P, Cucurull G, Casanova A, Romero A, Liò P, Bengio Y. Graph attention networks. Available from: https://arxiv.org/abs/1710.10903 [Last accessed on 8 Jun 2023].
55. Lusci A, Pollastri G, Baldi P. Deep architectures and deep learning in chemoinformatics: the prediction of aqueous solubility for drug-like molecules. J Chem Inf Model 2013;53:1563-75.
56. Altae-Tran H, Ramsundar B, Pappu AS, Pande V. Low data drug discovery with one-shot learning. ACS Cent Sci 2017;3:283-93.
57. Segler MHS, Kogej T, Tyrchan C, Waller MP. Generating focused molecule libraries for drug discovery with recurrent neural networks. ACS Cent Sci 2018;4:120-31.
58. Rahimi A, Cohn T, Baldwin T. Semi-supervised user geolocation via graph convolutional networks. Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); Melbourne, Australia; 2018. pp. 2009-19.
59. Li G, Müller M, Thabet A, Ghanem B. DeepGCNs: can GCNs go as deep as CNNs? 2019 IEEE/CVF International Conference on Computer Vision (ICCV); Seoul, Korea (South); 2019. pp. 9266-76. Available from: https://openaccess.thecvf.com/content_ICCV_2019/html/Li_DeepGCNs_Can_GCNs_Go_As_Deep_As_CNNs_ICCV_2019_paper.html [Last accessed on 8 Jun 2023]
60. Morris C, Ritzert M, Fey M, et al. Weisfeiler and leman go neural: higher-order graph neural networks. AAAI 2019;33:4602-9.
61. Papp PA, Martinkus K, Faber L, Wattenhofer R. DropGNN: random dropouts increase the expressiveness of graph neural networks. Available from: https://proceedings.neurips.cc/paper/2021/hash/b8b2926bd27d4307569ad119b6025f94-Abstract.html [Last accessed on 8 Jun 2023]
62. Rong Y, Huang W, Xu T, Huang J. DropEdge: towards deep graph convolutional networks on node classification. Available from: https://openreview.net/forum?id=Hkx1qkrKPr [Last accessed on 8 Jun 2023].
63. Sun Q, Li J, Peng H, et al. SUGAR: subgraph neural network with reinforcement pooling and self-supervised mutual information mechanism. Available from: https://arxiv.org/abs/2101.08170 [Last accessed on 8 Jun 2023].
64. Bevilacqua B, Frasca F, Lim D, et al. Equivariant subgraph aggregation networks. Available from: https://openreview.net/forum?id=dFbKQaRk15w [Last accessed on 8 Jun 2023].
65. Gasteiger J, Yeshwanth C, Günnemann S. Directional message passing on molecular graphs via synthetic coordinates. Available from: https://proceedings.neurips.cc/paper/2021/hash/82489c9737cc245530c7a6ebef3753ec-Abstract.html [Last accessed on 8 Jun 2023]
66. Liu Y, Wang L, Liu M, et al. Spherical message passing for 3D molecular graphs. Available from: https://par.nsf.gov/servlets/purl/10353844 [Last accessed on 8 Jun 2023].
67. Gasteiger J, Becker F, Günnemann S. Gemnet: universal directional graph neural networks for molecules. Available from: https://proceedings.neurips.cc/paper/2021/hash/35cf8659cfcb13224cbd47863a34fc58-Abstract.html [Last accessed on 8 Jun 2023]
68. Vasudevan RK, Choudhary K, Mehta A, et al. Materials science in the AI age: high-throughput library generation, machine learning and a pathway from correlations to the underpinning physics. MRS Commun 2019;9:10.1557/mrc.2019.95.
69. Lu S, Zhou Q, Ouyang Y, Guo Y, Li Q, Wang J. Accelerated discovery of stable lead-free hybrid organic-inorganic perovskites via machine learning. Nat Commun 2018;9:3405.
70. Xie T, France-Lanord A, Wang Y, et al. Accelerating amorphous polymer electrolyte screening by learning to reduce errors in molecular dynamics simulated properties. Nat Commun 2022;13:3415.
71. Xie T, Grossman JC. Hierarchical visualization of materials space with graph convolutional neural networks. J Chem Phys 2018;149:174111.
72. Gómez-Bombarelli R, Wei JN, Duvenaud D, et al. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent Sci 2018;4:268-76.
73. Zhao H, Chen W, Huang H, et al. A robotic platform for the synthesis of colloidal nanocrystals. Nat Synth 2023;2:505-14.
74. Lee YJ, Kahng H, Kim SB. Generative adversarial networks for de novo molecular design. Mol Inform 2021;40:e2100045.
75. Patel RA, Borca CH, Webb MA. Featurization strategies for polymer sequence or composition design by machine learning. Mol Syst Des Eng 2022;7:661-76.
76. Putin E, Asadulaev A, Ivanenkov Y, et al. Reinforced adversarial neural computer for de novo molecular design. J Chem Inf Model 2018;58:1194-204.
77. Zhao Y, Al-Fahdi M, Hu M, et al. High-throughput discovery of novel cubic crystal materials using deep generative neural networks. Adv Sci 2021;8:e2100566.
78. You J, Ying R, Ren X, Hamilton W, Leskovec J. GraphRNN: generating realistic graphs with deep auto-regressive models. Proceedings of the 35th International Conference on Machine Learning; 2018. pp. 5708-17. Available from: http://proceedings.mlr.press/v80/you18a.html?ref=https://githubhelp.com [Last accessed on 8 Jun 2023]
79. Lai X, Yang P, Wang K, Yang Q, Yu D. MGRNN: structure generation of molecules based on graph recurrent neural networks. Mol Inform 2021;40:e2100091.
80. Sanchez-Lengeling B, Aspuru-Guzik A. Inverse molecular design using machine learning: generative models for matter engineering. Science 2018;361:360-5.
81. Lin X, Jiang Y, Yang Y. Molecular distance matrix prediction based on graph convolutional networks. J Mol Struct 2022;1257:132540.
82. Gong S, Wang Y, Tian Y, Wang L, Liu G. Rapid enthalpy prediction of transition states using molecular graph convolutional network. AIChE Journal 2023:69.
83. Jain A, Ong SP, Hautier G, et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Materials 2013;1:011002.
84. Im S, Kim H, Kim W, Cho M. Neural network constitutive model for crystal structures. Comput Mech 2021;67:185-206.
85. Dunn A, Wang Q, Ganose A, Dopp D, Jain A. Benchmarking materials property prediction methods: the matbench test set and automatminer reference algorithm. npj Comput Mater 2020;6:138.
86. Fung V, Zhang J, Juarez E, Sumpter BG. Benchmarking graph neural networks for materials chemistry. npj Comput Mater 2021;7:84.
87. Choudhary K, Decost B. Atomistic line graph neural network for improved materials property predictions. npj Comput Mater 2021;7:185.
88. Louis SY, Zhao Y, Nasiri A, et al. Graph convolutional neural networks with global attention for improved materials property prediction. Phys Chem Chem Phys 2020;22:18141-8.
89. Li Y, Li P, Yang X, et al. Introducing block design in graph neural networks for molecular properties prediction. Chem Eng J 2021;414:128817.
90. Trieu HL, Miwa M, Ananiadou S. BioVAE: a pre-trained latent variable language model for biomedical text mining. Bioinformatics 2022;38:872-4.
91. Zhang ZC, Zhang MY, Zhou T, Qiu YL. Pre-trained language model augmented adversarial training network for Chinese clinical event detection. Math Biosci Eng 2020;17:2825-41.
92. Lee J, Yoon W, Kim S, et al. BioBERT: a pre-trained biomedical language representation model for biomedical text mining. Bioinformatics 2020;36:1234-40.
93. Wang Y, Wang J, Cao Z, Barati Farimani A. Molecular contrastive learning of representations via graph neural networks. Nat Mach Intell 2022;4:279-87.
94. Ding Z, Chen Z, Ma T, Lu CT, Ma W, Shaw L. Predicting the hydrogen release ability of LiBH4 -based mixtures by ensemble machine learning. Energy Stor Mater 2020;27:466-77.
95. Blum LC, Reymond JL. 970 million druglike small molecules for virtual screening in the chemical universe database GDB-13. J Am Chem Soc 2009;131:8732-3.
96. Ruddigkeit L, van Deursen R, Blum LC, Reymond JL. Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17. J Chem Inf Model 2012;52:2864-75.
97. Ramakrishnan R, Dral PO, Rupp M, von Lilienfeld OA. Quantum chemistry structures and properties of 134 kilo molecules. Sci Data 2014;1:140022.
98. Gan Y, Zhou J, Sun Z. Prediction of the atomic structure and thermoelectric performance for semiconducting Ge1Sb6Te10 from DFT calculations. J Mater Inf 2021;1:2.
99. Elegbeleye IF, Maluta NE, Maphanga RR. Density functional theory study of optical and electronic properties of (TiO2)n=5,8,68 clusters for application in solar cells. Molecules 2021;26:955.
100. Liao R, Zhao Z, Urtasun R, Zemel R. LanczosNet: multi-scale deep graph convolutional networks. Available from: https://openreview.net/forum?id=BkedznAqKQ [Last accessed on 8 Jun 2023].
101. Louis SY, Siriwardane EMD, Joshi RP, Omee SS, Kumar N, Hu J. Accurate prediction of voltage of battery electrode materials using attention-based graph neural networks. ACS Appl Mater Interfaces 2022;14:26587-94.
102. Omee SS, Louis SY, Fu N, et al. Scalable deeper graph neural networks for high-performance materials property prediction. Patterns 2022;3:100491.
103. Breuck P, Heymans G, Rignanese G. Accurate experimental band gap predictions with multifidelity correction learning. J Mater Inf 2022;2:10.
104. Shang C, Liu Q, Tong Q, Sun J, Song M, Bi J. Multi-view spectral graph convolution with consistent edge attention for molecular modeling. Neurocomputing 2021;445:12-25.
105. Tang B, Kramer ST, Fang M, Qiu Y, Wu Z, Xu D. A self-attention based message passing neural network for predicting molecular lipophilicity and aqueous solubility. J Cheminform 2020;12:15.
106. Huuskonen J. Estimation of aqueous solubility for a diverse set of organic compounds based on molecular topology. J Chem Inf Comput Sci 2000;40:773-7.
107. Micheli A. Neural network for graphs: a contextual constructive approach. IEEE Trans Neural Netw 2009;20:498-511.
108. Coley CW, Barzilay R, Green WH, Jaakkola TS, Jensen KF. Convolutional embedding of attributed molecular graphs for physical property prediction. J Chem Inf Model 2017;57:1757-72.
109. Meng M, Wei Z, Li Z, Jiang M, Bian Y. Property prediction of molecules in graph convolutional neural network expansion. 2019 IEEE 10th International Conference on Software Engineering and Service Science (ICSESS); Beijing, China.
110. Dai M, Demirel MF, Liang Y, Hu J. Graph neural networks for an accurate and interpretable prediction of the properties of polycrystalline materials. npj Comput Mater 2021;7:103.
111. Groom CR, Bruno IJ, Lightfoot MP, Ward SC. The cambridge structural database. Acta Crystallogr B Struct Sci Cryst Eng Mater 2016;72:171-9.
112. Gražulis S, Daškevič A, Merkys A, et al. Crystallography open database (COD): an open-access collection of crystal structures and platform for world-wide collaboration. Nucleic Acids Res 2012;40:D420-7.
113. Hao Z, Lu C, Huang Z, et al. ASGN: An active semi-supervised graph neural network for molecular property prediction. Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; Virtual Event, CA, USA; 2020. pp. 731-52.
114. Park CW, Kornbluth M, Vandermause J, Wolverton C, Kozinsky B, Mailoa JP. Accurate and scalable graph neural network force field and molecular dynamics with direct force architecture. npj Comput Mater 2021;7:73.
115. Vugmeyster Y, Harrold J, Xu X. Absorption, distribution, metabolism, and excretion (ADME) studies of biotherapeutics for autoimmune and inflammatory conditions. AAPS J 2012;14:714-27.
116. Delaney JS. ESOL: estimating aqueous solubility directly from molecular structure. J Chem Inf Comput Sci 2004;44:1000-5.
117. Bergström CA, Strafford M, Lazorova L, Avdeef A, Luthman K, Artursson P. Absorption classification of oral drugs based on molecular surface properties. J Med Chem 2003;46:558-70.
118. Otsuka S, Kuwajima I, Hosoya J, Xu Y, Yamazaki M. PoLyInfo: polymer database for polymeric materials design. 2011 International Conference on Emerging Intelligent Data and Web Technologies; Tirana, Albania; 2011. pp. 22-9.
119. Li M, Ma Z, Wang YG, Zhuang X. Fast haar transforms for graph neural networks. Neural Netw 2020;128:188-98.
120. Ma H, Bian Y, Rong Y, et al. Cross-dependent graph neural networks for molecular property prediction. Bioinformatics 2022;38:2003-9.
121. Mansimov E, Mahmood O, Kang S, Cho K. Molecular geometry prediction using a deep generative graph neural network. Sci Rep 2019;9:20381.
122. Allotey J, Butler KT, Thiyagalingam J. Entropy-based active learning of graph neural network surrogate models for materials properties. J Chem Phys 2021;155:174116.
123. Bertinetto C, Duce C, Micheli A, Solaro R, Starita A, Tiné MR. Evaluation of hierarchical structured representations for QSPR studies of small molecules and polymers by recursive neural networks. J Mol Graph Model 2009;27:797-802.
124. Feinberg EN, Sur D, Wu Z, et al. PotentialNet for molecular property prediction. ACS Cent Sci 2018;4:1520-30.
125. Withnall M, Lindelöf E, Engkvist O, Chen H. Building attention and edge message passing neural networks for bioactivity and physical-chemical property prediction. J Cheminform 2020;12:1.
126. Sun FY, Hoffman J, Verma V, Tang J. InfoGraph: Unsupervised and semi-supervised graph-level representation learning via mutual information maximization. International Conference on Learning Representations; Addis Ababa, Ethiopia; 2020. pp. 1-16. Available from: https://research.aalto.fi/en/publications/infograph-unsupervised-and-semi-supervised-graph-level-representa [Last accessed on 8 Jun 2023]
127. Huang K, Xiao C, Glass LM, Zitnik M, Sun J. SkipGNN: predicting molecular interactions with skip-graph networks. Sci Rep 2020;10:21092.
128. Wang X, Li Z, Jiang M, Wang S, Zhang S, Wei Z. Molecule property prediction based on spatial graph embedding. J Chem Inf Model 2019;59:3817-28.
129. Zhang Z, Guan J, Zhou S. FraGAT: a fragment-oriented multi-scale graph attention model for molecular property prediction. Bioinformatics 2021;37:2981-7.
130. Choi JY, Zhang P, Mehta K, Blanchard A, Lupo Pasini M. Scalable training of graph convolutional neural networks for fast and accurate predictions of HOMO-LUMO gap in molecules. J Cheminform 2022;14:70.
131. Choudhary K, Yildirim T, Siderius DW, Kusne AG, Mcdannald A, Ortiz-montalvo DL. Graph neural network predictions of metal organic framework CO2 adsorption properties. Comput Mater Sci 2022;210:111388.
132. Frey NC, Akinwande D, Jariwala D, Shenoy VB. Machine learning-enabled design of point defects in 2D materials for quantum and neuromorphic information processing. ACS Nano 2020;14:13406-17.
133. Wang Z, Han Y, Cai J, Wu S, Li J. DeepTMC: A deep learning platform to targeted design doped transition metal compounds. Energy Stor Mater 2022;45:1201-11.
134. Wang R, Zou Y, Zhang C, Wang X, Yang M, Xu D. Combining crystal graphs and domain knowledge in machine learning to predict metal-organic frameworks performance in methane adsorption. Micropor Mesopor Mat 2022;331:111666.
135. Pablo-García S, Morandi S, Vargas-Hernández RA, et al. Fast evaluation of the adsorption energy of organic molecules on metals via graph neural networks. Nat Comput Sci 2023;3:433-42.
136. Tavazza F, DeCost B, Choudhary K. Uncertainty prediction for machine learning models of material properties. ACS Omega 2021;6:32431-40.
137. Kwon Y, Lee D, Choi YS, Kang S. Uncertainty-aware prediction of chemical reaction yields with graph neural networks. J Cheminform 2022;14:2.
138. Behler J, Parrinello M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys Rev Lett 2007;98:146401.
139. Shapeev AV. Moment tensor potentials: a class of systematically improvable interatomic potentials. Multiscale Model Simul 2016;14:1153-73.
140. Artrith N, Urban A. An implementation of artificial neural-network potentials for atomistic materials simulations: Performance for TiO2. Comput Mater Sci 2016;114:135-50.
141. Wang H, Zhang L, Han J, E W. DeePMD-kit: a deep learning package for many-body potential energy representation and molecular dynamics. Comput Phys Commun 2018;228:178-84.
142. Unke OT, Chmiela S, Sauceda HE, et al. Machine learning force fields. Chem Rev 2021;121:10142-86.
144. Yao N, Chen X, Fu ZH, Zhang Q. Applying classical, ab initio, and machine-learning molecular dynamics simulations to the liquid electrolyte for rechargeable batteries. Chem Rev 2022;122:10970-1021.
145. Mai H, Le TC, Chen D, Winkler DA, Caruso RA. Machine learning for electrocatalyst and photocatalyst design and discovery. Chem Rev 2022;122:13478-515.
146. Kovács DP, Oord CV, Kucera J, et al. Linear atomic cluster expansion force fields for organic molecules: beyond RMSE. J Chem Theory Comput 2021;17:7696-711.
147. Morrow JD, Gardner JLA, Deringer VL. How to validate machine-learned interatomic potentials. J Chem Phys 2023;158:121501.
148. Behler J. Four generations of high-dimensional neural network potentials. Chem Rev 2021;121:10037-72.
149. Deringer VL, Caro MA, Csányi G. A general-purpose machine-learning force field for bulk and nanostructured phosphorus. Nat Commun 2020;11:5461.
150. Jinnouchi R, Lahnsteiner J, Karsai F, Kresse G, Bokdam M. Phase transitions of hybrid perovskites simulated by machine-learning force fields trained on the fly with bayesian inference. Phys Rev Lett 2019;122:225701.
151. Margraf JT. Science-driven atomistic machine learning. Angew Chem Int Ed Engl 2023;26:e202219170.
152. Freitas R, Reed EJ. Uncovering the effects of interface-induced ordering of liquid on crystal growth using machine learning. Nat Commun 2020;11:3260.
153. Schran C, Thiemann FL, Rowe P, Müller EA, Marsalek O, Michaelides A. Machine learning potentials for complex aqueous systems made simple. Proc Natl Acad Sci U S A 2021;118:e2110077118.
154. Anwar J, Zahn D. Uncovering molecular processes in crystal nucleation and growth by using molecular simulation. Angew Chem Int Ed Engl 2011;50:1996-2013.
155. Caro MA, Deringer VL, Koskinen J, Laurila T, Csányi G. Growth mechanism and origin of high sp^{3} content in tetrahedral amorphous carbon. Phys Rev Lett 2018;120:166101.
156. Li J, Luo K, An Q. Activating mobile dislocation in boron carbide at room temperature via al doping. Phys Rev Lett 2023;130:116104.
157. Cao B, Yang S, Sun A, Dong Z, Zhang T. Domain knowledge-guided interpretive machine learning: formula discovery for the oxidation behavior of ferritic-martensitic steels in supercritical water. J Mater Inf 2022;2:4.
158. Li X, Zhou Y, Dvornek N, et al. BrainGNN: interpretable brain graph neural network for fMRI analysis. Med Image Anal 2021;74:102233.
159. Ali A, Zhu Y, Zakarya M. Exploiting dynamic spatio-temporal graph convolutional neural networks for citywide traffic flows prediction. Neural Netw 2022;145:233-47.
160. Yang L, Jiang S, Zhang F. Multitask learning with graph neural network for travel time estimation. Comput Intell Neurosci 2022;2022:6622734.
161. Wu X, Li Y, Wang J, Qian Q, Guo Y. UBAR: user behavior-aware recommendation with knowledge graph. Knowl-Based Syst 2022;254:109661.
162. Zhu J, Yaseen A. A recommender for research collaborators using graph neural networks. Front Artif Intell 2022;5:881704.
163. Gatta V, Moscato V, Postiglione M, Sperli G. An epidemiological neural network exploiting dynamic graph structured data applied to the COVID-19 outbreak. IEEE Trans Big Data 2021;7:45-55.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.










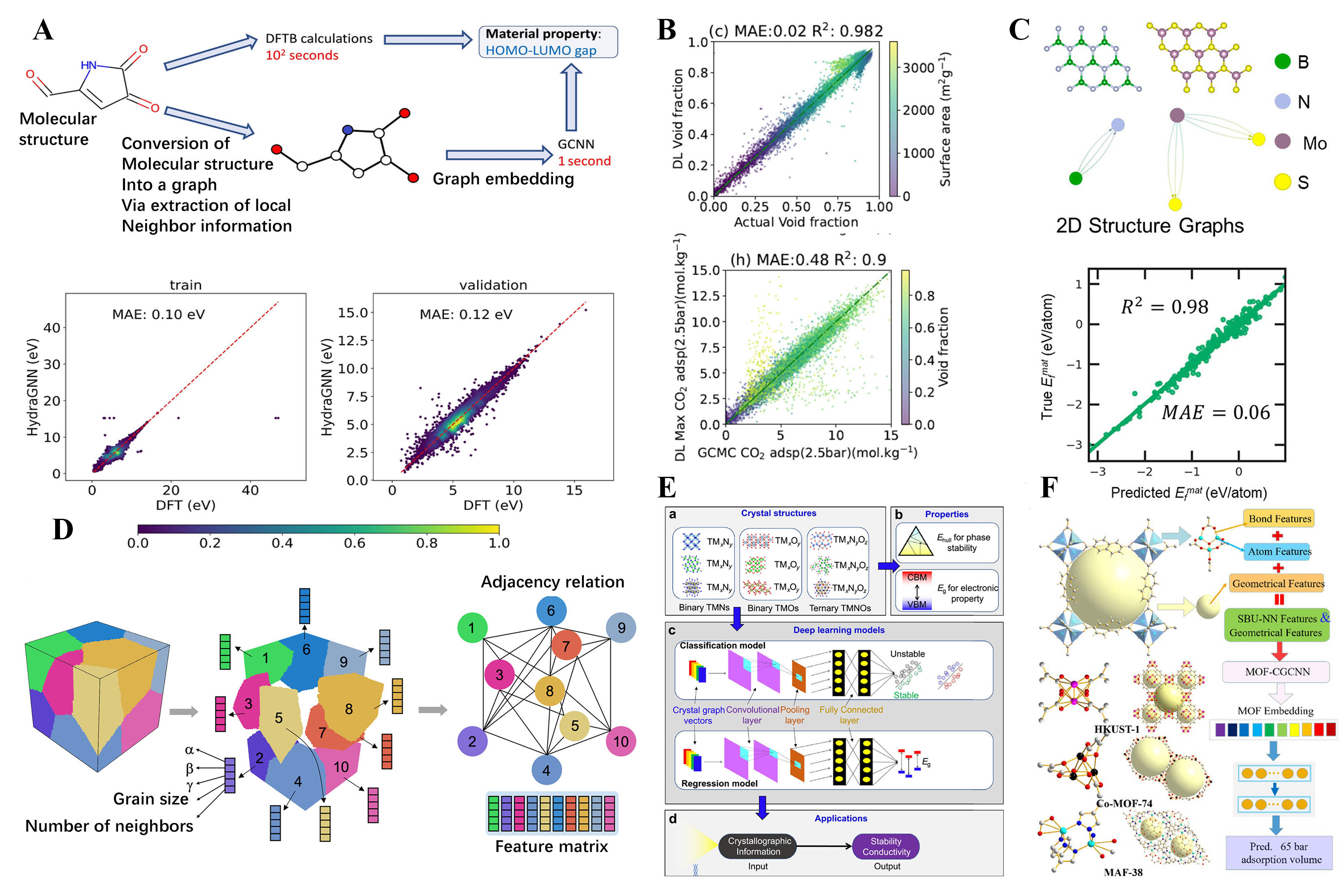
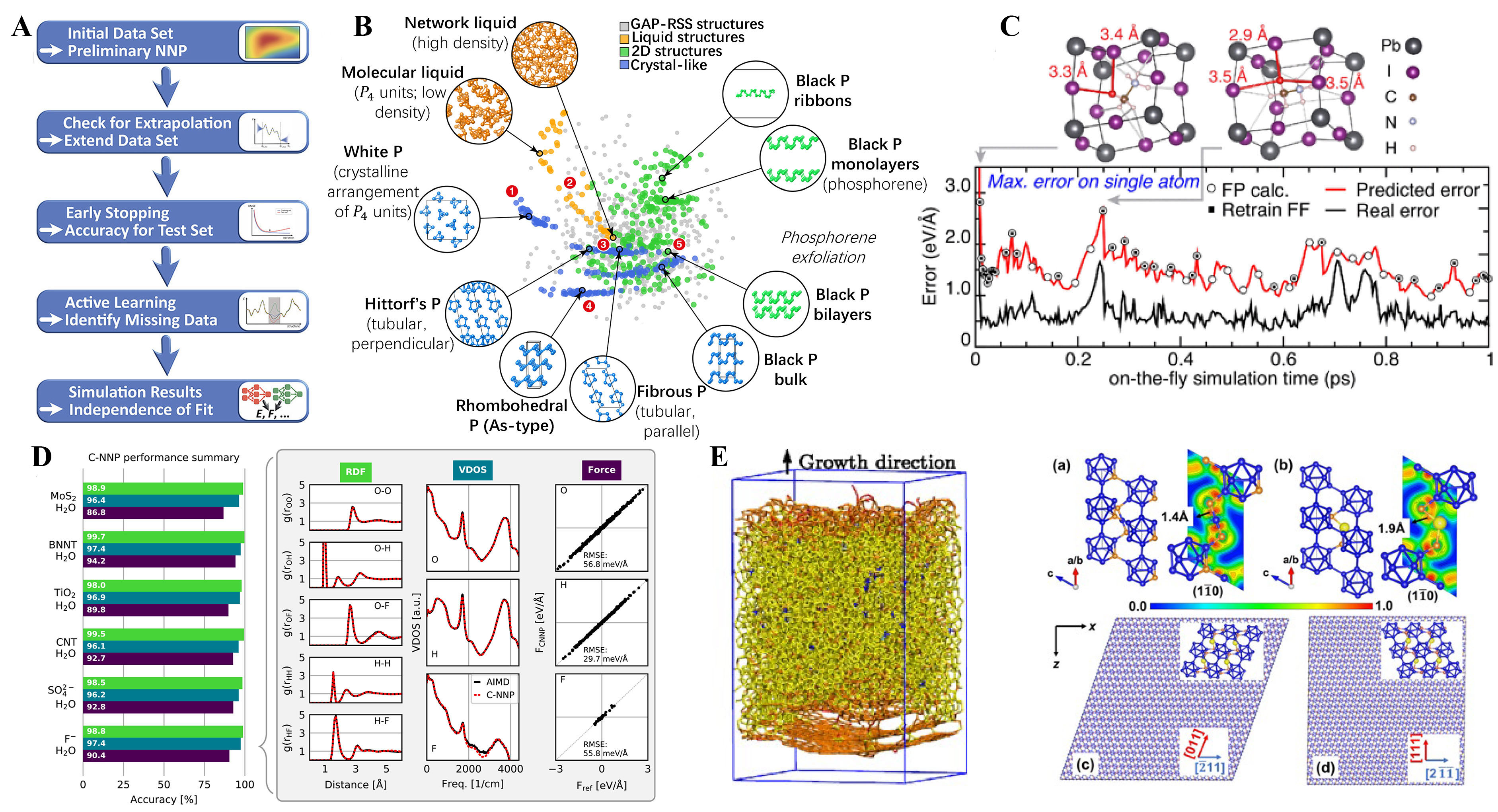













Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].