A review on high-throughput development of high-entropy alloys by combinatorial methods
Abstract
High-entropy alloys (HEAs) are an emerging class of alloys with multi-principal elements that greatly expands the compositional space for advanced alloy design. Besides chemistry, processing history can also affect the phase and microstructure formation in HEAs. The number of possible alloy compositions and processing paths gives rise to enormous material design space, which makes it challenging to explore by traditional trial-and-error approaches. This review highlights the progress in combinatorial high-throughput studies towards rapid prediction, manufacturing, and characterization of promising HEA compositions. This review begins with an introduction to HEAs and their unique properties. Then, this review describes high-throughput computational methods such as machine learning that can predict desired alloy compositions from hundreds or even thousands of candidates. The next section presents advances in combinatorial synthesis of material libraries by additive manufacturing for efficient development of high-performance HEAs at bulk scale. The final section discusses the high-throughput characterization techniques used to accelerate the material property measurements for systematic understanding of the composition-processing-structure-property relationships in combinatorial HEA libraries.
Keywords
INTRODUCTION AND MOTIVATION
Throughout history, metallurgists have altered the properties and compositions of alloys to achieve higher-performance materials. Traditional alloy design strategies involved microalloying trace elements into a primary base element, resulting in the discovery of many valuable alloys such as Cu-based bronze, Fe-based steels, and Ni-based superalloys. Over time the increasing demand for high-performance materials has led to increasingly complex alloys[1]. This trend has peaked in the past 20 years with the introduction of multi-principal element alloys or high-entropy alloys (HEAs)[2]. Unlike traditional alloys, HEAs do not contain a single primary element; instead, multiple elements in the alloy are mixed in relatively similar (almost equiatomic) concentrations. Cantor and Yeh first popularized this new alloying strategy concept in 2004 when they independently published works describing the manufacture and design philosophy of this new class of alloys[3,4]. Since the publication of these two works, the field of HEAs has exploded as such a new alloy design paradigm opens up a vast compositional space that was previously unexplored[5]. Although some fundamental questions such as phase selection and diffusion kinetics in HEAs remain elusive, many HEAs have shown high strength[6-8], large ductility[9], exceptional hardness and wear resistance[10-12], and superior corrosion resistance[13].
Despite the great potential that HEAs present for researchers, some crucial challenges must be overcome to increase their viability for future applications. While HEAs open up an uncharted multicomponent compositional space for material design, the vast compositional space makes it impractical to explore via traditional metallurgical techniques[14]. Additionally, the cost of HEAs can vary wildly due to the variety of possible elemental combinations. Some alloy systems only contain cheap transition metals (Fe, Ni, Cr)[15] that may be easy to scale, while other systems contain refractory elements (W, Nb, Ta)[16], which can significantly raise the cost of material. Finally, processing history significantly affects the microstructure and material properties even for a given nominal alloy composition. Many processing conditions including temperature, cooling rate, mechanical deformation, and irradiation can play a significant role in the formation of constituent phases and microstructures in HEAs[17-20]. Hence, processing imposes an additional and orthogonal dimension that multiplies with the huge compositional dimension and makes it more difficult to efficiently identify high-performance alloys using conventional alloy development strategies[21-23]. Thus, it is paramount for researchers to utilize efficient workflow to minimize the cost and experimental trials to study HEAs.
Over the past decade, many high-throughput material development techniques have emerged to tackle the combinatorial nature of HEAs. These techniques include magnetron sputtering, diffusion multiples, and additive manufacturing. Magnetron sputtering uses a magnetically confined plasma to accelerate positively charged ions toward a target material, leading to the sputtering of the target atoms onto a substrate to form a thin film with a thickness ranging from a few nanometers to a few microns[24]. A combinatorial materials library can be built by sputtering multiple elemental targets onto a single substrate[24-29]. The diffusion multiples method involves arranging different metals such that they are physically touching. Then this configuration is heated to an elevated temperature that enables atomic diffusion across the interfaces between the different metals. This process leads to a compositional gradient near the interface that serves as a compositional library[30-34]. Despite the large compositional space that diffusion multiples and magnetron sputtering can achieve, these approaches encounter some difficult issues. Both techniques involve samples of microscopic length scales, and thus, the microstructures and material properties observed from these libraries may not be representative of these materials at bulk scales. In addition, magnetron sputtering involves extremely high cooling rates on the order of 1010 K/s, which are substantially higher than those involved in routine metal manufacturing[35,36]. As such, the phases and microstructures in sputtered thin films are almost exclusively polymorphic or even amorphous and thus do not represent the microstructures of bulk materials for most practical applications.
Additive manufacturing (AM), also called 3D printing, is a technology to make objects from 3D digital data, usually layer upon layer, as opposed to subtractive manufacturing technologies[37]. There exist several types of AM systems that can be used to produce metal alloys: powder bed systems, powder feed systems, thermal spray systems, and wire feed systems. In the case of a powder bed system, the feedstock powders are spread over a flatbed, and a 2D pattern is selectively melted over the bed using either a laser or electron beam as a heat source[38,39]. Powder feed systems flow powders through a delivery nozzle using a carrier gas and then melt the powders onto the substrate as it impacts the substrate using heat from a laser[40,41]. Thermal spray 3D printing (TS3DP) systems spray heated powders at high velocities onto a substrate leading to bonding between powder particles as they impact the substrate surface. This allows parts to be built layer by layer without the large heating and cooling rates of laser-based techniques[42]. Finally, wire feed systems use metal wires as feedstock and can use either electric- or plasma-based welding arcs to melt the wire and build a part layer by layer[43-46]. AM of multiple elemental feedstock powders or wires offers the capability to build large compositional libraries at bulk length scales. Furthermore, careful control of the printing parameters during AM, such as laser power and scan speed, allows for tailoring the cooling rates and resulting solidification microstructures to expand the material development space.
In order to rapidly discover new HEAs with desirable properties, researchers need to utilize an efficient workflow to leverage the strengths of various design and characterization techniques. Figure 1 illustrates a typical protocol for high-throughput development of HEAs. First, the elements of interest are selected based on their fundamental properties and interactions, which are fed into a high-throughput computational method like machine learning, molecular dynamics, CALculation of PHAse Diagram (CALPHAD), or first-principles calculations. These computational methods can then predict the bulk materials’ phase formation, microstructure, and properties for initial screening of potential compositions of interest. Subsequently, high-throughput manufacturing can be used to fabricate the vast material library and high-throughput materials characterization enables rapid measurements of the material properties. This review focuses on high-throughput computational techniques, synthesis methods, and characterization studies that produce and analyze alloys with reasonable cooling rates at bulk scale. First, this review explores the high-throughput computational methods that can easily identify the potential compositions that show promising properties for structural or functional applications. Then, it discusses the high-throughput manufacturing of bulk compositional libraries encompassing a wide range of potentially interesting alloys by AM. The final section of this review describes some high-throughput characterization techniques to accelerate screening of multicomponent metal alloys. This combination of high-throughput methods offers a guideline for researchers to discover new alloys rapidly and efficiently.
Figure 1. Schematic illustration of a typical protocol for high-throughput development of HEAs. (A) Selection of elements for a prospective alloy system; (B) high-throughput computational methods are used to select a range of promising compositions that can be explored experimentally; (C) high-throughput manufacturing and characterization of the promising compositions selected via computation to determine the target composition. The lower illustration in (C) is quoted with permission from Borkar et al.[47], copyright 2016, Elsevier. HEA: High-entropy alloy.
OVERVIEW OF HEAS
Definition of HEAs
There currently exist two well-accepted definitions of HEAs. The first one, referred to as the “compositional definition”, states that HEAs are alloys with multiple principal elements (at least 5) where each principal element makes up 5 at. % to 35 at. % of the overall composition[4,48]. The most commonly studied HEA is the Cantor alloy system which contains equiatomic CoCrFeNiMn, a prime example of this definition[2,3]. Figure 2A illustrates this high-entropy region within a ternary phase diagram, with the center of the phase diagram covered by the high-entropy region[49]. It should be noted that the edges of the phase diagram in Figure 2A may contain two or more elements to match the composition definition. Additionally, minor elements can be added to a base HEA system to tune its properties further[50].
Figure 2. (A) Schematic illustration of the composition space of conventional alloys, equiatomic HEAs, and non-equiatomic HEAs. This figure is quoted with permission from Li et al.[49]; (B) ashby chart of the yield strength vs. fracture toughness of many material groups showing high/medium entropy alloys have excellent damage tolerance, adapted from George et al.[5], copyright 2019, Springer Nature. HEA: High-entropy alloy.
The second widely accepted definition is based on the mixing entropy of an alloy system, assuming an ideal random solution state. The mixing entropy is calculated as 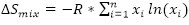 where R is the ideal gas constant, n is the number of principal elements, and xi is the atomic fraction of the ith element[48]. Yeh et al. separated the alloy design space into three regimes where a low entropy alloy has ΔSmix < 0.69R, a medium entropy alloy has 0.69R < ΔSmix < 1.61R and a HEA has 1.61R < ΔSmix[51]. It should be noted that the definition of mixing entropy above includes the assumption that the random solution state is defined as the liquid state or a high-temperature solid solution state such that the atoms have enough energy to maintain completely random configurations[51]. However, it has been pointed out by Miracle et al. that the above threshold for HEAs would exclude certain non-equiatomic alloys with five principal elements, as calculations show that such alloys exhibit ΔSmix < 1.61R[48]. Miracle et al. also pointed out that others have suggested using a threshold of 1.36R < ΔSmix which would include the alloys that were excluded by the threshold proposed by Yeh et al., making the entropy definition more consistent with the principal element definition[48].
where R is the ideal gas constant, n is the number of principal elements, and xi is the atomic fraction of the ith element[48]. Yeh et al. separated the alloy design space into three regimes where a low entropy alloy has ΔSmix < 0.69R, a medium entropy alloy has 0.69R < ΔSmix < 1.61R and a HEA has 1.61R < ΔSmix[51]. It should be noted that the definition of mixing entropy above includes the assumption that the random solution state is defined as the liquid state or a high-temperature solid solution state such that the atoms have enough energy to maintain completely random configurations[51]. However, it has been pointed out by Miracle et al. that the above threshold for HEAs would exclude certain non-equiatomic alloys with five principal elements, as calculations show that such alloys exhibit ΔSmix < 1.61R[48]. Miracle et al. also pointed out that others have suggested using a threshold of 1.36R < ΔSmix which would include the alloys that were excluded by the threshold proposed by Yeh et al., making the entropy definition more consistent with the principal element definition[48].
Four core effects
Despite their relatively short history, HEAs have already shown great potential for practical applications. Their properties are already competitive with and even exceed those of state-of-the-art materials. This potential is highlighted in Figure 2B, which illustrates the exceptional combination of high toughness and yield strength of HEAs compared to traditional structural materials[5]. The origin of these outstanding properties is often attributed to four core effects associated with HEAs: the high entropy effect, severe lattice distortion, sluggish diffusion, and cocktail effect[48]. Figure 3 presents a schematic illustration of the four core effects associated with HEAs. Each of these effects contributes to the unique properties observed in HEAs, and these contributions will be discussed below.
Figure 3. Schematic illustration of properties of HEAs. This figure is quoted with permission from Li et al.[52], copyright 2021, John Wiley and Sons. HEA: High-entropy alloy.
High entropy effect
Traditional alloying strategies suggest that alloys with multi-principal elements form multi-phase, brittle intermetallic systems[51]. However, many works on HEAs show they could achieve metastable and stable single-phase solid solutions[53-55]. Even in HEAs that show multiple phases, the number of phases is much lower than the maximum number predicted by the Gibbs phase rule[56-58]. These results suggest that the high mixing entropy leads to increased mutual solubility of elements in HEA systems. The effect of high mixing entropy is described by the equation for Gibbs free energy of formation, which implies that phases with high entropy will have a lower Gibbs free energy and thus be more stable[59]. Thus, the high mixing entropy aids in stabilizing single-phase solid solutions as long as this contribution overcomes the enthalpy of formation of possible intermetallic phases, especially at elevated temperatures. Additionally, this relationship also implies that the contribution of the mixing entropy to the Gibbs free energy decreases at lower temperatures and suggests that HEAs in the form of solid solutions at high temperatures may become metastable and decompose at low temperatures. For example, Stepanov et al. showed that Cantor alloy exhibits a typical single-phase face-centered cubic (FCC) structure upon quenching; however, it can decompose with the precipitation of a secondary Cr-rich σ-phase after prolonged annealing at 600 °C[60]. This representative finding again underscores the importance of processing history in the phase selection of HEAs, which will be discussed in later sections.
Sever lattice distortion
In HEA systems, various atoms with different atomic sizes lead to varying bond configurations and local lattice energies. These bond configurations create a high lattice distortion within the crystal structure[61,62]. The severe lattice distortion has been experimentally confirmed in many HEA systems via X-ray diffraction (XRD), neutron diffraction, and TEM[62-66]. Such severe lattice distortion leads to more diffuse scattering through the lattice and causes the broadening of diffraction peaks with a decrease in the peak intensities compared to traditional dilute alloy systems. The increase in lattice distortion also impedes the motion of dislocations through the matrix, which leads to solid solution strengthening. Traditional solid solution strengthening models typically involve the contributions of solute atoms to a matrix of solvent atoms. Still, these models are challenging to apply to HEAs as the solvent and solute atoms cannot be clearly distinguished[59]. To that end, new solid solution hardening models have been developed by accounting for the lattice and shear modulus distortion in the local environment near each constituent atom[61,67]. The lattice distortion within HEA systems has also been shown to correlate strongly with the stability of various phases. For example, single-phase solid solutions tend to be more stable in systems with low lattice distortions. In contrast, intermetallic and multi-phase structures are more likely to form in systems with high lattice distortions. This effect can sometimes outweigh the effect of high configurational entropy in phase selection[55,68,69].
Sluggish diffusion
Diffusion through HEAs can be much slower than diffusion in conventional alloys. Many researchers have investigated the elemental diffusion in HEA systems and have found that the diffusivities are often much lower than those in binary or dilute alloy systems[70-72]. This sluggish diffusion can improve the stability of solid solution phases as harmful intermetallic phases can be largely suppressed. Intermetallic phases can only form under non-polymorphic solidification conditions, which require long-range diffusion. Additionally, metastable solid solutions form under polymorphic crystallization conditions, which only require topological atomic rearrangements on the atomic length scale[23]. Thus, the sluggish diffusion in HEAs suppresses the long-range diffusion that would lead to the formation of brittle intermetallic phases and instead promotes polymorphic crystallization to form solid solutions. Additionally, the coarsening of grains can be inhibited due to sluggish diffusion, leading to improved thermal stability and thermomechanical performance at elevated temperatures[73-75].
Cocktail effect
Dr. Ranganathan first proposed the cocktail effect to describe the synergistic nature of compositionally complex alloys[76]. This effect describes the unexpected properties observed in HEAs, bulk metallic glasses, and super-elastic and super-plastic metals (also called “gum” metals)[48]. Unlike the other effects described earlier, the cocktail effect does not predict the expected properties of HEAs. Still, it serves as a reminder that certain elemental combinations can achieve synergistic effects that are not predicted from the base constituent elements.
HIGH-THROUGHPUT COMPUTATIONAL METHODS TO DESIGN HEAS
As previously mentioned, the compositional space opened by the concept of HEAs is vast. This design space is too large to explore through traditional trial-and-error means. Thus, it is of significant interest to identify promising compositions and phases via high-throughput computational methods[77]. These computational methods include machine learning, first-principles calculations, molecular dynamics, and CALPHAD. The field of high-throughput computational studies is extremely wide and covers too many topics to discuss succinctly. As such, the discussion of computational methods is limited to studies focused on phase formation and mechanical properties of HEAs to illustrate the potential advantages and disadvantages of the previously mentioned methods.
Machine learning
Machine learning (ML) is a powerful computational tool to rapidly explore vast design space through statistical methods[78]. These methods include artificial neural networks (ANN), support vector machines (SVM), and decision trees, which can often be used to quantitatively predict material properties such as hardness[79] or to predict qualitative factors such as the expected phases of a given alloy composition[80]. Over the past decade, as computational power has continued to increase, there has been an explosion in the topics of machine learning and big data[81]. Machine learning methods have an extremely high potential to handle large databases due to their statistical nature. This section includes examples from literature of various ML techniques and methods that are representative of the state-of-the-art results achieved in the field.
ML techniques are capable of predicting the structure and properties of various alloys in reasonably short periods. However, this predictive capability is largely dependent on the size and quality of the training data, a thorough consideration of appropriate input variables (also known as feature engineering), and the choice of ML model[82]. Typically robust databases of training data only exist for materials that have been well studied, such as the Ni-Ti-Hf shape memory alloy (SMA) systems[83]. For example, Liu et al. developed Gaussian process regression (GPR) models to estimate thermal parameters related to the martensite and austenite finish temperatures in a Ni-Ti-Hf alloy system to design a SMA[83]. The predicted parameters were described as 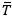 = (Af + Mf)/2, and ΔT = Af - Mf, where Af and Mf are the austenite finish and martensite finish temperatures, respectively. The value of
= (Af + Mf)/2, and ΔT = Af - Mf, where Af and Mf are the austenite finish and martensite finish temperatures, respectively. The value of 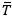 represents the average of the austenite finish and martensite finish temperatures and thus illustrates the temperature region where an SMA is expected to transform. Tuning this range can be useful in aerospace applications where autonomous actuation can be induced due to the temperature difference of the surroundings at take-off (typically 275 K) and cruising (usually
represents the average of the austenite finish and martensite finish temperatures and thus illustrates the temperature region where an SMA is expected to transform. Tuning this range can be useful in aerospace applications where autonomous actuation can be induced due to the temperature difference of the surroundings at take-off (typically 275 K) and cruising (usually
As previously mentioned, an essential aspect of building an ML model is the determination of the input variables that will most accurately predict the output variables. Typically, adding more input variables can improve the model’s accuracy, as variables that do not correlate strongly with the output variables will have to be emphasized less through training sets. However, using too many input variables increases the dimensionality of the model, making it computationally expensive to execute. Additionally, the solution space formed by many input variables can often contain local minima that require many iterations to escape. For this reason, Liu et al. initially started with 48 input variables based on the relevance of those variables to the physical processes involved in martensitic and austenitic phase transformations[83]. These chosen features included fundamental atomic properties (e.g., atomic radius, atomic number, relative atomic mass, etc.), thermal properties (e.g., melting point, boiling point, the heat of fusion, thermal conductivity, etc.), overall alloy compositions, electronic configurations, and process conditions (e.g., solution temperature, aging temperature, etc.). This variable space was refined via mutual information (MI) and Pearson correlation (PC). MI indicates the dependency of the output variable on the input variables, which ensures that only the most impactful variables are used. In contrast, the PC between the two variables illustrates their correlations. Input variables strongly correlated to each other produce redundant information and can thus be disregarded. Using this method, Liu et al. built a model that explored a 4500-point compositional space in which seven compositions were identified that exhibit 230 < 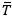 < 260 and the lowest ΔT values. These results illustrate ML models’ capabilities to selectively tune a material system’s properties using robust training datasets from previous studies and carefully selected input variables.
< 260 and the lowest ΔT values. These results illustrate ML models’ capabilities to selectively tune a material system’s properties using robust training datasets from previous studies and carefully selected input variables.
Most ML techniques are black-box ML with limited interpretability, which can hinder the development of chemical insight into the origin of preferable properties. Recently, a new method to implement ML described as a ML-based alloy design system (MADS) has been developed to predict alloys and maximize the hardness within an Al-Co-Cr-Cu-Fe-Ni-V alloy system[79]. This method is schematically illustrated in Figure 4A and consists of four steps. First, a database containing alloy compositions within the selected system and their measured hardness is established. Then a set of 142 features to model the hardness is established and refined to remove all except the five most crucial factors. This refinement step is important to reduce the computational cost and redundancy of information within the ML model. A model utilizing the most critical parameters is constructed and then executed to optimize the composition toward maximum hardness. Finally, the designed alloy compositions are experimentally fabricated and tested to verify the predicted properties. The five features selected were the average deviation of the atomic weight, the average deviation of the period column in the periodic table, the average deviation of the specific volume, the valance electron concentration, and the mean melting point for the alloy. After exploring the presented alloy system, the optimized composition was determined to be Co18Cr7Fe35Ni5V35 which was predicted to have a hardness of 1,002 HV and was experimentally verified to show a hardness of 1,148 HV, showing the prediction is in good agreement with the experimental value. This new HEA exhibits about 25% greater hardness than the maximum hardness in the original training dataset. The hardness improvement illustrates ML methods’ ability to take previous experimental data and extrapolate it to discover new compositions with better properties than previously achieved.
Figure 4. (A) Schematic diagram of machine learning-based approach to design new HEAs. This figure is quoted with permission from Yang et al.[79], copyright 2022, Elsevier; (B) schematic illustration of artificial neural network method, adapted from Risal et al.[87], copyright 2021, Elsevier; (C) actual versus predicted misfit and yield strength for 10-fold cross-validation of machine learning models, insets show the error distribution around the mean. This figure is quoted with permission from Vazquez[90], copyright 2022, Elsevier; (D) elemental content distribution of predicted eutectic HEAs, adapted from Wu et al.[6], copyright 2020, Elsevier. HEA: High-entropy alloy.
Artificial neural networks (ANNs) are common ML methods that use a layered architecture of input, hidden, and output nodes trained to predict useful material properties such as phase formation, hardness, and yield strength. The input layer consists of multiple nodes which hold values of the parameters that are known either a priori or from databases. Then each node in the 1st hidden layer is calculated by a weighted sum of the nodes from the input layer. Nodes in subsequent hidden layers are calculated by a weighted sum of the nodes from the previous layer. Finally, the output layer consists of the target/output parameters calculated from a weighted sum of the nodes from the hidden layer immediately preceding the output layer. These parameters can include the predicted properties of the studied alloys, such as the hardness of a material, the elastic properties, phase prediction classifier etc. The weights for every calculated sum are initialized as a best guess and then adjusted to minimize the error between the predicted and experimental values for training data. Once the error is minimized, the adjusted weights can then be used in conjunction with input data for new alloy systems outside of the training set to predict properties of interest[81,84,85].
Notably, Nassar et al. used two different ANNs (NN1 and NN2) to predict the phase formation with 37 possible elements in the alloy composition[86]. NN1 had only composition data as its inputs and, thus, only 37 input nodes. NN2 used composition data and some calculated thermodynamic properties of each composition, such as the entropy of mixing, enthalpy of mixing, valence electron concentration (VEC), atomic radius difference, and Pauling electronegativity difference. The output node values were a binary of 0 or 1, where 1 indicates the formation of a single-phase solid solution (SS) or a solid solution plus intermetallic (SS + IM). At the same time, 0 predicts a primary IM phase or IM + amorphous phase structure. After training, the neural networks could accurately predict the type of microstructure given an arbitrary composition with 92% and 90% accuracy for NN1 and NN2, respectively. The improved accuracy of NN1 is surprising, given that it only used the elemental composition as input, while NN2 included features related to thermodynamic properties.
Another work that shows consistent results with NN2 is that of Risal et al., where 598 alloy compositions extracted from the literature were used as the training set, and the input parameters included the VEC, melting temperature of the alloy, enthalpy of fusion and variance of atomic radius[87]. The basic structure of the neural network used in their work is illustrated in Figure 4B. Interestingly, they achieved a prediction accuracy of 90.66%, slightly lower than that of NN1 and almost the same as NN2 in Nassar et al.’s work[86]. This result can be rationalized by the fact that NN typically only elucidates the correlation between parameters and thus may not always reveal the underlying physical connection between the input and output variables. Many examples exist in the literature on NNs, providing valuable predictions for HEAs’ microstructure type and material properties. However, further study is needed to understand the mechanisms that lead to these valuable properties.
A common criticism of ML models is that they often lack interpretability despite their high predictive accuracy[88,89]. Sure-independence screening and sparsifying operator (SISSO) is an example of an ML method that can produce easy-to-understand relationships between the input and output variables. SISSO can output these relationships as analytical equations such that the dependence of the output variables on each input variable can be easily understood. Vazquez et al. recently used SISSO to predict the mechanical properties of alloys within a Ta-W-Nb-Mo-V refractory HEA (RHEA) system[90]. This method functions very differently from other ML algorithms as most methods attempt to filter the possible valuable features to build an input space that is computationally efficient to analyze, as shown in previous examples. In the case of SISSO, the features are compiled as mathematical functions (descriptors) by applying mathematical operators to arbitrary groupings of the features. The descriptor space is then narrowed using sure independence screening (SIS) to identify descriptors that most strongly correlate to the target properties. Then, the sparsifying operator (SO) produces a linear model of the descriptors that best predicts the target property[91]. In this way, SISSO can produce models which converge even if the initial feature space is larger than the data set. Additionally, Vazquez et al. point out that SISSO is computationally inexpensive compared to typical ab-initio calculation methods like DFT[90]. Figure 4C shows the prediction of misfit volume and yield strength vs. the actual values calculated by DFT. The accuracy of the prediction of the misfit volume suggests that SISSO can reliably predict the mechanical properties of RHEA systems while remaining computationally much cheaper than DFT calculations. While the yield strength prediction overall shows a very low root mean squared error (RMSE), the R2 value is quite large, which arises due to limited experimental data and a lack of documentation of the processing conditions related to many compositions in the yield strength database. This result highlights the need for larger, more robust, and more detailed databases of experimental HEA data to improve the training quality of future ML models.
As previously mentioned, ML models can predict phase formation using solely composition information. This concept is taken even further by Wu et al., who used a NN to study the effect of each element in a HEA system on the phase to predict the primary phase fraction after casting[6]. With this technique, they could design near-eutectic compositions within the Al-Co-Cr-Fe-Ni system[6]. The database[6] to train the model was prepared using experimental data from the literature, and CALPHAD calculations were performed using the nickel-based superalloy database TTNI8. Wu et al. chose to only use the elemental compositions as the input nodes and the primary phase fraction as the output node. The primary phase fraction was defined as 0 for eutectic compositions. In contrast, hyper- and hypo-eutectic compositions showed a positive value when FCC was predicted as the primary phase and a negative value when body-centered cubic (BCC) was predicted as the primary. After training and executing the NN, the authors identified 400 near-eutectic compositions and correlated them with the atomic fraction of each element. This plot is shown in Figure 4D, where it can be seen that the majority of the near-eutectic compositions fall into the region when Al content (at. %) is between 15% and 20% and the Cr content is below 25%. The other elements do not seem to significantly affect the formation of eutectic structures, which suggests that the Al and Cr contents are most crucial for eutectic structure formation in this alloy system. Thus, the NN was first used to predict the amount of Al that needed to be added to an equiatomic CoFeNi alloy to form a eutectic microstructure and how much Cr could be added to maintain that microstructure. Finally, the ratios of the other elements were further adjusted to predict a near-eutectic microstructure. The best composition based on the criteria of stable eutectic microstructure was Ni32Co30Fe10Cr10Al18. This work presents the potential of ML models to refine a huge design space containing thousands of unique compositions down to a single optimized composition that can then be experimentally studied in detail.
While ML techniques such as those discussed in this section can readily analyze extremely large data sets, their accuracy depends heavily on the robustness and comprehensive nature of experimentally verified training sets[77]. There is currently a severe lack of such high-fidelity datasets to accurately train ML models to ensure ML can accurately predict the properties of future alloy systems[92]. In the meantime, as these databases expand, the scientific community is also implementing other computational methods that do not rely so heavily on previous results to predict future alloying behavior. These methods include first-principles calculations, molecular dynamics (MD), and CALPHAD calculations and will be discussed in the following sections.
First-principles calculations
First-principles calculations (also called ab-initio) are computational methods that rely purely on fundamental quantum physical laws without additional assumptions[93]. The literature on first-principles methods is vast and presents a comprehensive overview beyond the scope of this work. This section will provide a sufficiently broad outline of the general concepts, advantages and disadvantages of these techniques pertinent to combinatorial studies of HEAs[93]. The main strength of these methods is that they do not require previous empirical observations of the predicted properties, and thus very little prior work is needed to implement them[94]. The most common practical implementation of ab-initio calculations is density functional theory (DFT) in the Khon-Sham formalism[94,95]. This method maps the quantum-mechanical many-electron Schrodinger equation onto an effective one-electron problem using electron density as a key variable. This mapping also requires the use of the exchange-correlation functional of the electron density which is not known for most systems and must be approximated either with the local density approximation (LDA)[96,97] or the generalized gradient approximation (GGA)[98-100]. Once these fundamental functions are calculated, the overall energy of the system can be calculated and used to determine the energy of formation for the possible phases of the system. This result can help researchers determine the stability of different phases to determine which phases are likely to form. It should be noted that in its initial state, DFT is a ground state theory and thus only provides the ground state energy at 0 K for a given configuration of atoms[94]. These results can be combined with thermodynamic concepts and statistical sampling techniques to bridge the gap between 0 K to a finite temperature[94].
Despite the strong predictive power of ab-initio calculations, they often suffer from high computational costs, which can significantly decrease the ability of researchers to explore the vast design space that is necessary to build accurate property maps for HEAs. To overcome this challenge, many researchers either combine first-principle calculations with more high-throughput methods like ML[101] or use new algorithms and models to improve the computational efficiency to the point where first-principles calculations can be used to explore hundreds to thousands of compositions in relatively short periods. Examples of such works will be discussed in this section.
One approach that is considered highly promising toward high fidelity and high throughput computations of HEAs is based on the small set of ordered structures (SSOS) containing several atoms[92]. This method works well to predict properties of equiatomic configurations of HEAs but loses computational efficiency when employed for non-equiatomic compositions. Sorkin et al. implemented a preselected set of small ordered structures (PSSOS) approach to address the issue of computational efficiency and used it to estimate the stability of BCC and FCC phases within the Al-Co-Cr-Fe-Ni system[92]. Traditionally the SSOS method uses a set of small, ordered structures (SOS) to model a HEA with a given composition. First, symmetry-unique SOS are constructed using non-conventional, non-primitive unit cells of cubic lattices. Each SOS has a unique pair correlation function. The complete set of possible SOS solutions is constructed and optimized using DFT. Then a small subset of SOS is selected by matching the pair correlation function of the target composition as a linear combination of the pair correlation functions of the selected SOS. This small set of SOS constitutes the solution of the SSOS. Screening the entire SOS solution space is impractical when studying HEAs, so the authors restricted their SOS space to those containing 5, 6, or 7 atoms. They selected the most frequent SOS structures in the solution set to further reduce the SOS space and only optimized those using DFT. This selection decreases the original SOS from over 50,000 sets to 1,500.
Through the above-mentioned process, the authors can predict the formation energy and density of the alloy system’s BCC and FCC phases of 8,801 compositions. This result is exemplified in Figure 5A, which shows a plot of the formation energy and density of the BCC phase with varying Al and Cr compositions. Here the marker color represents the Ni content, and the marker size represents the Co content. It can be seen that the addition of Al leads to a substantial decrease in the formation energy of the BCC phase. After calculating the same parameters for the FCC phase, the authors found that the difference in the formation energies of BCC and FCC (ΔEBCC→FCC = EBCC - EFCC) goes from positive to negative as the Al content increases, which is consistent with DFT calculations of the system. These results illustrate that the PSSOS method provides a new opportunity to achieve similar accuracy predictions of phase formations as DFT but with much cheaper computational costs, making this method highly suitable for high-throughput exploration of HEA space.
Figure 5. (A) Predicted formation energy and density per atom of BCC lattice structure in AlCoCrFeNi system calculated via the SSOS method as a function of Al and Cr content, the color denotes the Ni content, and marker size denotes the Co content. This figure is quoted with permission from Sorkin et al.[92]; (B) plot of predicted elastic constants (C11, C12, C44), Poisson ratio, and Bulk modulus to shear modulus ratio calculated with the VCA model as a function of Ti in the TixVNbMo system. This figure is quoted with permission from Chen[104]. BCC: Body-centered cubic; SSOS: small set of ordered structures.
Virtual crystal approximation (VCA) serves as a computationally efficient alternative to more complex first-principles methods like special quasirandom structure (SQS) and similar local atomic environment (SLAE). Normally, DFT methods must use approximations to study highly disordered systems[102]. The approximation is carried out by constructing a supercell that contains multiple disordered configurations with artificially imposed boundary conditions[102]. However, such calculations require large supercells that are computationally taxing to utilize in DFT calculations. VCA deals with this issue using a pseudo-potential that averages the properties of each atom in different positions in the lattice cell. Ramer and Rappe previously investigated multiple methods to produce the averaged pseudo-potential such as averaging the pseudo-potentials for each atom within the lattice and averaging ‘all-electron results’[103]. It was found that the averaging of ‘all-electron results’ provided the most accurate result when compared to experiments. This method involved averaging the Coulombic potentials and charge densities of the constituent atoms and then using these values to generate wavefunctions that are self-consistent solutions to the Kohn-Sham equation[103].
The computational efficiency of VCA makes it uniquely suited to explore HEA systems, as shown by Chen et al., who used the VCA method to explore the effect of Ti within the TixVNbMo system[104]. VCA only requires the construction and analysis of a primitive cell, while other DFT methods require the use of a supercell as previously discussed, making them much more difficult to calculate. Since VCA has previously achieved reliable results for studying RHEA systems, Chen et al. proposed that it is reasonable to implement it to analyze the mechanical properties of this RHEA. Figure 5B illustrates the effect of Ti content on the lattice elastic constants and elastic properties [Poisson ratio and ratio of the bulk modulus to the shear modulus (B/G)]. Looking at the lattice elastic constants, it is clear that C12 > C44 for all compositions, and the Cauchy pressure (Cp = C12 - C44) is positive for all the compositions. This suggests that the nature of the bonding for all these compositions remains metallic. The Born-Huang mechanical stability criterion is also met (C11 - C12 > 0, C11 + 2C12 > 0 and C44 > 0), which indicates that the BCC crystal structure remains stable for these compositions. The Poisson ratio and B/G ratio seem to both increase with increasing Ti. Both of these values have been suggested to correlate well with the ductility of a material, implying that higher Ti content improves ductility. Chen et al. also indicated that Young’s modulus (and hence yield strength) decreases with increasing Ti. To verify the accuracy of these results, the authors compared the properties of the equiatomic composition TiVNbMo to experimental values from literature and found a reasonable consistency.
New fist-principles methods such as Lederer-Toher-Vecchio-Curtarolo (LTVC) have been established over the last five years to provide novel approaches towards calculating solid solution phase stability in HEAs in order to guide future alloy discovery[105]. This method incorporates energy calculations into a mean-field statistical mechanics model, which uses order parameters to predict the transition temperature of a HEA system into a solid solution phase. The authors lay out the development of their protocol in 3 stages: (i) The automatic flow for material discovery (AFLOW)[106] repositories are used to train cluster expansion (CE) models[107] within the Alloy Theoretic Automated Toolkit (ATAT)[108] and estimate zero temperature energy configuration of atomic configurations, which are derivative structures from either FCC or BCC lattices, on which HEAs show solid solution formability; (ii) Then, the estimated atomic configurations are entered into a mean field statistical mechanical model called the generalized quasi-chemical approximation (GQCA)[109]; (iii) Finally, an order parameter is proposed by calculating the evolution of the probability of finding certain ordered configurations of atoms within the lattice.
To test this new method, the authors verified its accuracy by comparing its predictions to Monte Carlo simulations and experimental data for binary alloys. They also compared CALPHAD predictions via Thermo-calc for ternary alloys and experimental data from the literature. Once the method was considered reliable and accurate, the authors used it to predict the solid solution formation in many different alloys. They compared their predictions to the well-known empirical rules that usually inform the design of HEAs to form solid solutions. Figure 6A and B show the plots of the electronegativity and atomic size differences, as well as the VEC and atomic size differences. The large scatter of the green data points suggests that the LTVC method can be used to predict the formation of solid solutions beyond what is typically expected by the usual empirical rules. This study suggests that LTVC shows excellent potential to efficiently explore a large compositional space and discover new alloys that would not be considered under previous knowledge.
Figure 6. LTVC model predictions for quaternary and quinary alloys (green - predicted SS, blue - predicted SS and verified by experiments) plotted as a function of (A) the electronegativity difference and the atomic size difference; (B) the VEC and the atomic size difference. These figures are quoted with permission from Lederer et al.[105], copyright 2018, Elsevier. The effectiveness of the VEC rule previously used and the proposed rule from the work of Yang et al. in the Al-Co-Cr-Fe-Ni system[112], copyright 2022, Elsevier; (C) BCC structure (D) FCC structure. These figures are quoted with permission from Yang et al.[112], copyright 2022, Elsevier. BCC: body-centered cubic; FCC: face-centered cubic; LTVC: Lederer-Toher-Vecchio-Curtarolo; VEC: valence electron concentration; SS: solid solution.
As HEAs have been increasingly studied over the past decade, certain empirical rules have been established that correlate well with the observed properties[110]. In the past, it has been suggested that these empirical rules can provide a guideline surrounding the design of HEAs with desirable properties, such as the formation of single-phase solid solutions[111]. However, certain empirical rules, such as the VEC threshold for the stability of FCC and BCC solid solutions, have failed to maintain predictive accuracy over the years[112]. Yang et al. revisited this rule using special quasirandom structures (SQS) to investigate 180 compositions within the Al-Co-Cr-Fe-Ni alloy system[112]. The predictions of the phase selection between FCC and BCC were then compared to previous predictions made using the VEC of the alloy system. In their findings, Yang et al. argued that the threshold of VEC < 6.87 for the stability of the BCC phase could not accurately predict the phase formation in this system. The results presented by Yang et al. suggest that the FCC phase is stable when VEC < 8 and VEC < 5, while the BCC phase is most stable when 5 < VEC < 6.87. This finding reflects more accurately the trends illustrated in their work and is consistent with experimental data. The comparison for the accuracy of the two VEC rules is presented in Figure 6C and D, which shows that the new VEC rule has a superior prediction accuracy for both the BCC and FCC phases when the number of elemental alloy components increases from 1 to 4. It should be noted that this new rule also works well for quinary alloys but does not work well in predicting the dual-phase region. Further study is needed to produce more robust empirical rules that allow for simple rule-of-thumb predictions.
Molecular dynamics
Molecular dynamics (MD) simulations represent a powerful tool to explore and predict material properties of potentially useful materials before significant investments in experimental characterization are made. In MD simulations, the researchers typically define an MD box that outlines the boundary conditions of the system as well as the initial positions and velocities of each atom[113]. The ambient conditions of the simulated system must also be defined, such as temperature and pressure. Once it is initialized, the system is allowed to reach thermal equilibrium[113]. Then the microscopic trajectory of each atom is determined by Newton’s equations of motion depending on the potential energy functions utilized in defining the system[113,114]. The accuracy of simulated atom trajectory via MD simulations makes these methods well-suited to study the nucleation and evolution of defects such as vacancies, dislocations, grain boundaries, and twinning[115-117].
In the past, MD simulations have also been used to explore phase transformation, mechanical behavior, nucleation and crystallization processes within HEAs[118-120]. MD simulations can study much larger systems with faster computation times than ab-initio calculations because they use classical Newtonian mechanics versus the quantum mechanical interactions on which ab-initio methods are typically based. They can also accurately simulate non-equilibrium systems due to the rapid time scales over which a simulation is conducted[113]. Despite these impressive advantages, a known weakness of MD simulations is that their accuracies depend heavily on the accuracy of the potential energy functions used to define them. However, these potential energy functions must first be measured by experimentation or calculated via ab-initio methods, which can limit the applicability of MD simulations to novel systems that have not been studied before[113]. This section presents works that take advantage of the strengths of MD simulations to explore large composition and application spaces with relatively low computation times.
As previously discussed, many computational methods can be used to investigate and predict material properties, such as yield strength, hardness, and phase formation. However, MD simulation has the added benefit of allowing researchers to investigate deformation mechanisms within an alloy via simulation of atomic motion under various ambient and loading conditions[118]. This ability is especially important as it is very difficult and laborious to observe plastic deformation processes under experimental[118,121]. Pan et al. applied atomic-scale tensile MD simulations to a Fe80-xMnxCo10Cr10 alloy system to investigate transformation-induced plasticity (TRIP) and twinning-induced plasticity (TWIP) mechanisms in this system[121]. In this work, the atomic fraction of Mn, strain rate, and grain size were all adjusted to investigate each variable’s effect on the system’s deformation mechanisms[121]. Figure 7A shows a schematic illustration of the model where green dots represent the FCC phase and white dots denote grain boundaries. The FCC transforms into BCC and HCP during deformation, and this transformation was found to be most prevalent when x = 40. The addition of Mn also reduced the stacking fault energy, which facilitated twinning during deformation, leading to improved strain hardening. Interestingly the transformations and twinning mechanisms were suppressed for smaller nano-grain sizes, which Pan et al. attributed to the transformation from the intragranular evolution mechanism at larger grain sizes to the intergranular evolution mechanism at smaller grain sizes. This study shows the potential of MD simulations to explore compositional space and to provide a detailed analysis of deformation mechanisms before significant investments in experimental characterization.
Figure 7. (A) Constructed molecular dynamics model of Fe80-xMnxCo10Cr10 HEAs with FCC lattice structure and distribution of elements in the model. This figure is quoted from Pan et al.[121], copyright 2022, Elsevier; (B) simulation cell used in LAMMPS to calculate generalized stacking fault energy of the Co-Cr-Fe-Ni system. This figure is quoted with permission from Jarlov et al.[122], copyright 2022, Elsevier; (C) elemental distribution in the Co-Cr-Ni MEA system with different compositions produced by MD simulation. This figure is quoted with permission from Li et al.[123], copyright 2021, Elsevier. FCC: Face-centered cubic; HEA: high-entropy alloy; MD: molecular dynamics.
MD simulations can be used to investigate the relationship between the stacking fault energy and strengthening mechanisms within an alloy system. Understanding this relationship can then provide guidelines for designing new HEAs with tailored properties and deformation mechanisms suited to specific applications[122]. Jarlov et al. performed MD simulations using the Large-scale Atomic/Molecularly Massively Parallel Simulator (LAMMPS) to investigate the effect of the chemical composition in the Co-Cr-Fe-Ni alloy system on the generalized stacking fault energy (GSFE)[122]. The authors used this method to explore the system’s strengthening and deformation mechanisms during tensile tests. Figure 7B shows the simulated cell, and the planes marked as I, II, and III indicate the planes displaced during the tensile simulation. Based on the simulations, it was found that increasing Ni and Co contents led to an increase in the energy required to introduce stacking faults and deformation, while increasing Cr and Fe contents led to a decrease in the energy required to introduce these defects. When carrying out tensile simulations of the various compositions, it was found that the yield strength correlated linearly with the energy required to introduce intrinsic stacking faults. Thus, the strongest composition was identified as (CoCrNi)90Fe10, achieving the highest number of deformation twins. This result illustrates the power of MD simulations to optimize the alloy composition based on yield strength and tailoring of the simulated deformation mechanism.
While MD simulations can be powerful tools to predict the material properties of alloys, the high computational cost associated with these simulations makes it difficult to rapidly produce large datasets for high-throughput studies[123]. On the other hand, ML techniques are known for their potential to quickly and efficiently process and output huge amounts of data and thus offer a means to overcome the low data output of MD simulations. Li et al. combined high throughput MD simulation with ML to leverage both techniques’ strengths to explore an extensive data set and provide accurate and detailed information on the material properties[123]. MD simulations can produce highly accurate predictions of yield strength, but the data produced by these simulations have high dimensional input-low dimensional output characteristics. These properties make it challenging to produce mathematical models to predict the correlation between input factors and yield strength. On the other hand, ML techniques can produce enormous amounts of data. Still, their accuracy requires a large and robust set of training data that experimentation cannot do. Thus, Li et al. utilized high-throughput MD simulation to produce an extensive training data set to train an ANN that can almost fully explore the composition space of the Co-Cr-Ni medium entropy alloy (MEA) system[123]. Figure 7C shows examples of different MD simulation models prepared for this study. The predictions made by the ANN were shown to be highly accurate. This work highlights the potential for high throughput MD simulations used in tandem with ML techniques to produce vast amounts of highly accurate data that can efficiently identify optimal compositions within a large composition space, thereby overcoming the inherent weakness in each technique by leveraging the strengths of the other. Applying this method to other combinations of computational techniques may offer researchers new opportunities to expand the computational speed, size, and accuracy of future computational studies, which can accelerate alloy discovery far beyond the current state-of-the-art results.
The use of combining MD simulations with ML techniques was also explored by Zhang et al. to explore the non-equiatomic compositions within the Fe-Co-Cr-Ni-Mn alloy system[124]. In this case, the deformation of 100 compositions with a single-crystal structure was simulated in three different crystallographic directions, [100], [110], and [111]. The simulated stress-strain responses of these compositions are shown in Figure 8A. Three different ML techniques were then used to predict further the yield stress of non-equiatomic compositions within the alloy system. Unlike other ML tasks, the authors of this work used ML techniques to carry out binary classification of “Good” and “Weak” yield strength rather than quantitative prediction of yield strength. The advantage of this method is that ML programs trained with simulations of single crystals can be used to find optimized compositions that show promise as polycrystalline structures. Typically, polycrystalline models are much larger than single-crystal ones, which can make them more computationally expensive[125]. By leveraging the ability of ML classification techniques and the computational efficiency of high-throughput MD simulations of single crystals, the authors can produce highly efficient means to rapidly identify candidates for optimized compositions of HEA space. This technique was used again by Zhang et al. to carry out similar classification predictions for the Cu-Fe-Cr-Co-Ni alloy system[124]. It was again shown to be highly accurate and efficient at pointing out candidates with optimal yield strength[126]. This approach significantly refines the potential compositional space that experimentation needs to explore.
Figure 8. (A)MD simulated stress-strain response of single-crystal Fe-Co-Cr-Ni HEA system with different compositions (all elements are adjusted from 5 at. % to 35 at. %) loaded in different directions. This figure is quoted with permission from Zhang et al.[124], copyright 2021, Elsevier; (B) MD simulated stress-strain response of amorphous AlxCoCrFeNi (x = 1.0 and x = 2.0) HEAs at different temperatures. This figure is quoted with permission from Jiang et al.[127], copyright 2022, Elsevier. HEA: High-entropy alloy; MD: molecular dynamics.
While MD simulations are useful in exploring the compositional space of a system, they can also be used to study material performance within other design dimensions, such as application temperature. Jian et al. used MD simulations to study the effect of aluminum concentration, temperature, and strain rate in amorphous AlxCoCrFeNi HEAs to study their potential as low-density structural materials[127]. Figure 8B shows the stress-strain curves of two of the three simulated compositions ranging from 300 K to 1,200 K. For all three compositions, the yield strength and Young’s modulus both strongly depended on the temperature rather than the Al content. The temperature dependence of the yield strength originated from the high migration ability of atoms at higher temperatures, especially at 1,200 K, which was above the simulated glass transition temperature of about 1,100 K. The authors also varied the strain rate from
CALPHAD calculations
Phase diagrams are geometric representations of alloy systems under thermal equilibrium and typically denote the boundaries of composition and temperature where phase transformations are expected to occur[14]. These diagrams form the basis for studying solidification, crystal growth, and solid-solid phase transformations. Since the 1970s, the calculation of phase diagrams has become an integral part of alloy design, specifically through CALPHAD technology[14]. The technique relies on the minimization of the total Gibbs free energy of the system using the temperature, pressure, overall composition, and Gibbs energy function stored in databases[128].
The selection of the appropriate database is crucial for accurate calculations as the database should at least cover all the constituent binary and ternary sub-systems to provide accurate phase predictions for complicated alloy systems[129]. It should be noted that a current bottleneck in the field is the lack of comprehensive thermodynamic databases which cover large compositional and temperature spaces. Future experimental works are needed to help fill this gap. Recently, even first principle calculations have shown promise to build such databases with less effort than required for experimental characterization[129]. The current section provides examples of works that take advantage of the computational efficiency of CALPHAD methods to rapidly explore huge compositional spaces, which can reduce the large compositional spaces to ones that can be feasibly explored by experimentation.
One of the pioneering works to tackle the issue of combinatorial high-throughput studies using CALPHAD is carried out by Senkov et al.[130]. In this study, the authors used 9 different CALPHAD databases to calculate every equiatomic alloy containing 3-6 elements out of 26 elements[130]. This calculation resulted in screening 130,000 different alloy compositions to predict the phases at both their melting temperatures and 600 °C. Interestingly, Senkov et al. found that the proportion of alloys with solid solution (SS) microstructures decreased as the number of components increased, as seen in Figure 9A[130]. This contradicts the general notion that increasing the number of elements would increase the configurational entropy and thus promote SS formation. In order to investigate the cause of this discrepancy, Senkov et al. calculated the entropy of mixing (ΔSmix) and enthalpy of mixing (ΔHmix) for each composition which describes the Gibbs free energy for SS phases. They also calculated the entropy of formation (ΔSf) and enthalpy of formation
Figure 9. (A) Fractions of CALPHAD predicted single-phase solid solution, intermetallics, and solid solution and intermetallic equimolar alloys in 3 to 6 component alloy systems at the melting temperature (Tm) and at 600 °C. This figure is quoted with permission from Senkov et al.[130]; (B) two-dimensional projection of AlaCrbMocNbdTieV1-a-b-c-d-e phase diagram from CALPHAD showing compositions within two-dimensional space where a BCC solid solution phase forms at 800K. This figure is quoted with permission from Klaver et al.[131]. IM: Intermetallic; SS: solid solution.
Through the previous analysis, they explained that the configurational entropy increases with ln(N), where N is the number of elements, while the possible binary interactions increase with (N/2)∙(N-1). Thus, the number of binary interactions increases much faster than the configurational entropy, which increases the likelihood that an IM phase with a highly negative enthalpy of formation exists within a HEA system. Thus, the Gibbs free energy of possible IM phases decreases more rapidly than that of solid solution solutions as the number of elements increases. This work highlights the ability of large computational datasets to allow us to re-evaluate our fundamental assumptions of alloy design by providing large statistical datasets that reveal trends that may not be obvious from experimental testing.
Although many HEAs have been reported to form SS phases at lower temperatures, these are often metastable due to the inherent sluggish diffusion in HEAs. The fast computational speed of CALPHAD methods allows researchers to rapidly screen the composition phase for compositions that maintain a SS as the stable equilibrium phase even at low temperatures. Such methods have been utilized to predict the stable phases of 3 million compositions in 4 different alloy systems of AlCrMnNbTiV, AlCrMoNbTiV, AlCrFeTiV and AlCrMnMoTi[131]. This process was enabled by running approximately 100 calculations in parallel on single CPU cores in a computing cluster. This study aimed to identify various compositions that form single-phase solid solutions (SPSS) at low temperatures and then design compositions that are likely to exhibit good oxidation resistance. By incrementally adjusting the contents of various elements, the authors were able to investigate the effect of each element on the stability of SPSS. The alloy systems shown to have the most significant number of SPSS compositions were the AlCrMnNbTiV and AlCrMoNbTiV systems. Figure 9B shows the 2D projection of the compositional space explored in the AlCrMoNbTiV, where each red dot represents a composition with a predicted single-phase BCC microstructure. It was found that placing constraints to limit the Al and Cr contents can improve SPSS formation, as seen in the top 2 rows of Figure 9B but lowers the oxidation resistance. Thus, the optimal compositions found near the center of the high SPSS formation region and still maintaining a high oxidation resistance were Al25Cr7Mn25Nb1Ti1V41 or Al21Cr7Mn21Nb1Ti9V41. This study highlights the ability of high throughput CALPHAD methods to reduce a massive design space of over 3 million compositions down to a handful of promising candidates that can feasibly be explored even using conventional manufacturing methods.
The equiatomic Cantor alloy (CoCrFeMnNi) has been studied extensively in the past, including its deformation mechanism, phase formation, and mechanical properties at varying temperatures[132-134]. However, the non-equiatomic compositions have not been explored as deeply[135]. Assuming that a 1 at. % increment in any element’s atomic fraction constitutes a new alloy then the compositional space for a generic 5-element alloy system covers an excess of 106 unique compositions. Thus, CALPHAD or ML models are the best methods to screen through the massive composition space. However, the experimental databases on this system lack size and detail, and thus a ML approach cannot be adequately trained. For this reason, Conway et al. used high throughput CALPHAD methods to design composition within the Cantor alloy system (Co-Cr-Fe-Ni-Mn) that possesses a combination of high SPSS stability, good mechanical properties, and low material cost[135]. The high-throughput screening analyzed 1.78 million compositions where the elemental contents were gradually incremented by 1-2 at. % interval step. The phase fractions were calculated every 50 K between 500 K to 2,500 K to screen for compositions that produced thermally stable SPSS. Further constraints were applied to ensure every element was present in at least 10 at. %, and the Co and Ni contents were limited to 15 and 20 at. % to reduce the cost of the alloys. Twinning-induced plasticity (TWIP) and solid solution hardening (SSH) were fundamental strengthening mechanisms within this system. Thus, the authors used parameters within the TC-HEA database for their CALPHAD calculations of the SSH values and stacking fault energies (SFEs) for the screened compositions. Figure 10A shows the SFE and SSH plots in a quaternary diagram where the Co content was assumed constant at 10
Figure 10. (A) Quaternary phase diagrams at fixed 10 at. % Co illustrating explored composition space. The red circle points out the composition that is experimentally tested, and the red stars indicate the target compositions to maximize hardness (left) and minimize stacking fault energy (right). This figure is quoted with permission from Conway et al.[135]; (B) CSA predicted single-phase solid solution compositional spaces for FCC and BCC at 1,400 K, 1,450 K, and 1,500 K. This figure is quoted with permission from Abu-Odeh et al.[136], copyright 2018, Elsevier. BCC: Body-centered cubic; CSA: constraint satisfaction algorithm; FCC: face-centered cubic.
The process-structure-property-performance (PSPP) relationship is the central paradigm in materials science. The fundamental goal of many materials scientists is to use computation, theory and experimentation to establish causal trends between the individual elements of PSPP to systematically achieve better material performance. To that end, Abu-Odeh et al. contextualized alloy design as an inverse phase stability problem (IPSP)[136]. IPSP is defined as the need to identify the set of thermodynamic conditions that lead to the stabilization of desirable phases which produce high-performance materials. One such example is to provide the coordinates composition and temperature space that result in SPSS for HEAs. The approach Abu-Odeh et al. took to tackle this problem is described as a constraint satisfaction algorithm (CSA) which involves the use of ML protocols executed in tandem with CALPHAD calculations to satisfy specific material property criteria/constraints.
This method enables efficient exploration of a large composition region to identify regions of arbitrarily complex phase constitution characteristics. This approach has the potential to design alloy compositions of any phase fraction rather than just focusing on the discovery of SPSS, as previously shown in other works. Abu-Odeh et al. applied their framework to the Cantor alloy (Co-Cr-Fe-Ni-Mn) system, where they explored the regions of SPSS stability for both FCC and BCC phases. Figure 10B visually represents the change in FCC and BCC stability with increasing temperature for a ternary sub-section of the compositions explored. After confirming the outcomes of the SPSS regions in the quinary compositions of the system, the approach was expanded to search for precipitation hardening compositions in the Al-CoCrFeNi system by identifying composition regions that include minor secondary phases. It was expressed that the secondary phase would only be considered if it did not form via spinodal decomposition, as this would not lead to any significant precipitation hardening. With this technique, the authors could identify composition spaces most likely to exhibit precipitation-hardening behavior. They highlighted that providing more detailed constraints can further refine the predicted composition space to provide a target region that can be practically explored via experimental methods.
Comparison of computational methods
The previous categories of computational methods all serve important functions in the process of predicting and narrowing the huge compositional space of HEAs. To ensure efficient usage of computational resources and time, it is crucial for researchers to understand which method is most useful for their individual applications. This section offers a direct comparison between their individual strengths and weaknesses based on the previously discussed studies.
ML techniques have numerous advantages that researchers can use to explore many compositions at once. Firstly, the computational efficiency of most ML methods allows some studies to screen up to 105 compositions in a reasonable time frame[90,137]. The faster computation speed of ML than other computational techniques makes it particularly suited to exploring large composition spaces. Additionally, the ability to select various combinations of features as input variables, such as composition, atomic radius, valence electron concentration etc., gives ML a significant advantage in versatility allowing for pattern recognition between features that would normally not be possible with the human mind[82,138,139]. Despite the impressive capabilities, ML techniques rely heavily on large robust datasets to generate useful models[81,90,139]. Unfortunately, the relatively young age of the field of HEAs and the vast composition space means that the relative size of the currently available datasets is still quite small[48]. The small datasets limit the compositional regions where accurate ML models can be trained and applied[81,82]. The other common criticism of ML models is their lack of interpretability. ML models essentially act as a computational black box, meaning that even when they provide accurate predictions, the underlying physics is obscured by the complicated statistical calculations that are performed, making it difficult to build useful intuition from such models[78,79,87,140].
In contrast to the ML models, both first-principles and MD simulation methods rely primarily on well-known quantum mechanical and classical laws instead of statistical models[114,117,138]. This ensures that a strong fundamental understanding of the predicted properties can be extracted from such models. The reliance on fundamental physics also reduces the need for large training datasets as the required datasets are often already contained in readily available databases[125,141]. MD simulations also have the added benefit of illustrating the dynamic evolution of microstructures during an experiment, thereby providing atomic scale information on the phase transformation and deformation of materials during usage, which cannot be achieved using any other computational technique[127,142]. However, both first-principles and MD simulation methods are much more computationally expensive than ML and CALPHAD methods[138]. Thus, first-principles and MD techniques cannot explore as many compositions as ML and CALPHAD methods as seen in Table 1, where first-principles and MD can screen up to 104 and 103 compositions, respectively.
Comparison of pros, cons, and capabilities of various computational methods
| Computational method | Predicted Properties | Pros | Cons | Number of screened compositions | References |
| Machine learning | Elastic constants Phase formation Phase transformation temperature Hardness Tensile strength Compressive strength | High computational efficiency Versatility in predictive features | Requires large training sets Lack of physical interpretability Only gives statistical understanding | 105 | [48,78,79,81,82,87,90,137-139] |
| First-principles | Elastic constants Phase formation Phase transformation temperature | Low input information needed Provides fundamental understanding Atomic scale detail | Computationally expensive Time-consuming | 104 | |
| Molecular dynamics | Elastic constants Phase formation Phase transformation temperature Hardness Tensile strength Compressive strength | Provides fundamental understanding Atomic scale detail Dynamically simulate microstructure evolution | Computationally expensive Time-consuming Cannot provide macroscopic results | 103 | [114,115,125,127,141,142] |
| CALPHAD | Phase formation Phase transformation temperature | High computational efficiency High accuracy Easily interpretable | Only predicts equilibrium conditions No kinetic information | 106 |
Recent studies have attempted to overcome this flaw by combining first-principles calculations with ML to produce models that are computationally efficient and highly accurate and provide physical insight into chemical segregation and phase formation[143-145]. Leong et al. used a cluster expansion (CE) model, which expands the configurational energy of an alloy structure in terms of various atomic clusters[144]. This model was trained using data obtained through first-principles calculations. Once the configurational energy is calculated for the clusters in the test set, the authors calculate the probability of the nearest neighbor (NN) atomic pairing between the different atomic species in a Mo-V-Nb-Ti-Zr alloy system to predict the Warren-Cowley short-range order (SRO) parameters[144,146]. This SRO allows the authors to highlight the tendency of Zr to segregate and cluster leading to the formation of intermetallic phases below 1,400 K and single-phase solutions above 1,400 K.
Finally, CALPHAD methods are both computationally efficient and have sufficiently large databases to produce accurate predictions for many HEA compositions[147,148]. In fact, CALPHAD methods are able to screen more compositions than any of the other computational methods (up to 106 compositions) in a reasonable time span[135]. Despite this large computational efficiency, CALPHAD methods can only provide information about equilibrium phase formation and transformation temperatures which may not be representative of manufacturing or application conditions. This limitation is especially important for HEAs,c where sluggish diffusion limits the kinetics within the system, which can often lead to the formation of metastable phases that may not be expected under equilibrium conditions.
COMBINATORIAL ADDITIVE MANUFACTURING TO EXPLORE LARGE COMPOSITIONAL SPACE
After narrowing a target composition space using computational methods, the remaining candidate compositions are still too numerous to reasonably explore via traditional metallurgical techniques. Thus, high-throughput manufacturing techniques are needed to rapidly produce samples that cover the candidate composition region. Previous studies have utilized magnetron sputtering and diffusion multiples to produce combinatorial libraries[28,149-151]. However, as previously discussed, these techniques produce samples at micro- or nano-scale, which may not be representative of bulk materials.
Additionally, the cooling rates experienced during magnetron sputtering are orders of magnitude greater than the cooling rates in traditional manufacturing settings[35,36]. Thus, there is a need for a manufacturing technique that can produce vast compositional libraries at a bulk length scale with practically relevant cooling rates. Laser additive manufacturing (LAM) has shown great promise towards that end. Previously LAM has been used to produce alloys with improved properties compared to their conventionally manufactured counterparts[36,152-159]. Two main types of LAM are used in combinatorial studies, i.e., laser directed energy deposition (DED), also known as laser engineered net shaping (LENS), and laser powder-bed fusion (L-PBF)[160]. The DED process utilizes a carrier gas that allows the powder to flow continuously while shielding it from oxidation during deposition. A laser source simultaneously heats the material upon contact with the printing substrate or previous layer[37]. In the case of L-PBF, a flatbed of powder is deposited on a substrate. A laser is then used to melt the particles in a pattern determined by design software to form a part layer by layer[161].
Functionally graded materials
LAM can produce compositionally graded materials, making it a powerful tool for rapid combinatorial material exploration[160]. DED is the more common method used to produce graded materials, as the multiple nozzles can be coaxially aligned with the laser, ensuring that each nozzle’s flow rate can be individually adjusted to spatially control the deposited alloy composition[162,163]. By dynamically changing the flow rate during AM, a compositional gradient can be formed, allowing for the exploration of a large compositional space within the same sample [164,165]. This method is schematically illustrated in Figure 11A, where a compositionally graded wall is produced starting from pure Cantor alloy at the base and increasing the content of refractory metals with increasing the build height[166]. Pegues et al. used this method to add Nb, Ta, and Ti6Al4V to CoCrFeMnNi to produce 3 different materials libraries[166]. They explored the effect of these additions on the microstructure and mechanical properties of the resulting alloys. Utilizing this method allowed them to efficiently explore a large compositional space without producing large samples. Micro-hardness tests on all three libraries revealed that the addition of the refractory elements resulted in increased hardness, likely due to the formation of secondary intermetallic phases such as a Laves phase[166].
Figure 11. (A) Schematic illustration of high-throughput manufacturing of HEAs in a graded material under laser-directed energy deposition (L-DED). This figure is quoted with permission from Pegues et al.[166], copyright 2021, Elsevier; (B) schematic illustration of manufacturing a graded material under laser powder bed fusion (L-PBF) conditions. This figure is quoted with permission from Wen et al.[167], copyright 2021, Elsevier; (C) graded material library produced via L-DED in AlxCoCrFeNi. The graded HEA library is remelted to investigate the effects of composition and cooling rate. This figure is quoted with permission from Li et al.[171], copyright 2020, Elsevier. HEA: High-entropy alloy.
While DED is the most common method to produce gradient materials compositionally, Wen et al. used L-PBF to produce a gradient material, as shown in Figure 11B[167]. Normally, L-PBF is considered undesirable for compositionally graded materials as the powder composition cannot be systematically controlled once loaded in a chamber. Wen et al. addressed this issue by adding a partition within the powder hopper so that two different powders could be loaded together. Then a mixer is placed below the hopper that mixes powders along the width of the mixer. This mixture forms a compositional gradient in the laser scan plane when the powder bed is deposited. Thus, a horizontal compositional gradient forms rather than the typical vertical gradients achieved in DED combinatorial studies[168-170]. Wen et al. used CoCrFe medium entropy alloy and Inconel 718 as the feedstock powders to prove this new technique’s concept. At the pure CoCrFe end of the alloy gradient, a pure FCC phase structure was formed and as the Ni content increased due to the addition of Inconel 718, a secondary HCP phase was formed. The HCP phase content increased with increasing Ni content. The decrease in hardness occurred with increasing Ni-content, which is likely due to the larger sub-grain size observed near the Inconel 718 end.
Li et al. used DED to explore the effects of compositional and cooling rate changes on the microstructure and mechanical properties of the Al-Co-Cr-Fe-Ni alloy system [171]. First, they produced a pure CoCrFeNi substrate via casting. Then, they deposited varying amounts of Al on the substrate using a LENS system which formed different compositions of AlxCoCrFeNi along the substrate surface, ranging from x = 0.51 to 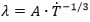 where λ is the cell size, A is a fitted parameter, and
where λ is the cell size, A is a fitted parameter, and 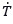 is the cooling rate. The microstructure refinement resulted in hardening following the Hall-Petch relationship. This work illustrates the potential for laser-based AM methods to rapidly and simultaneously explore the effects of composition and cooling rate on the phase evolution and mechanical properties of HEAs.
is the cooling rate. The microstructure refinement resulted in hardening following the Hall-Petch relationship. This work illustrates the potential for laser-based AM methods to rapidly and simultaneously explore the effects of composition and cooling rate on the phase evolution and mechanical properties of HEAs.
Teh et al. used DED to produce compositionally graded pillars within the Co-Fe-Ni alloy system[172]. By adjusting the content of each element along the build direction, the phase fraction of FCC vs. BCC was varied from pure BCC at the base of the pillar to dual phase FCC + BCC to pure FCC at the top. The hardness also varied with build height due to changes in composition and grain size caused by increasing the Ni concentration. They characterized the functional properties of each composition in addition to the mechanical properties by measuring the saturation magnetization, coercivity, and electrical resistivity. After analyzing the combination of properties, the authors presented a radar chart comparing some promising compositions to pure Fe, as shown in Figure 12A.
Figure 12. (A) Radar chart comparing properties of various promising compositions discovered from graded material library of the Co-Fe-Ni system. This figure is quoted with permission from Teh et al.[172], copyright 2022, Elsevier; (B) change in V concentration along the build direction for AlMoVxCrFe alloy. This figure is quoted with permission from Gwalani et al.[173], copyright 2019, Elsevier; (C) vickers hardness map of the side surface of graded CoCrFeNiTix HEA system. This figure is quoted with permission from Zhao et al.[174], copyright 2021, Elsevier. HEA: High-entropy alloy.
Gwalani et al. varied the V content in an AlMoCrFeVx (from x = 0 to x = 1) HEA system [Figure 12B][173]. The addition of V led to solid solution hardening, increasing the hardness monotonically from 485 HV at
Bulk materials library
While graded materials provide a convenient means to explore multiple compositions within a single sample, they cannot give a full picture of material performance due to the possible mixing between layers during LAM, which can be difficult to control. In this sense, bulk materials libraries can produce individual samples to be studied in further detail while maintaining a high-throughput approach if rapid characterization techniques can be applied. One such example is illustrated in Figure 13A, where Yu et al. used DED to produce a library of bulk samples using elemental Al powder and Cu50Zr50 powder in separate powder hoppers, as seen in Figure 13A[175]. This work aimed to find the optimal compositions and processing conditions to produce bulk metallic glass composites (BMGC). BMGCs are materials formed by adding a crystalline phase into a glassy amorphous matrix[176].
Figure 13. (A) Schematic of high-throughput fabrication and screening of combinatorial materials library and images of the printed library of Cu-Zr-Al alloy system. This figure is quoted with permission from Yu et al.[175], copyright 2021, Elsevier; (B) schematic of combinatorial material library fabrication and ultrasonic screening to rapidly estimate effective processing parameters of Zr51Ti5Ni10Cu25Al9 bulk metallic glass (BMG), adapted from Zhai et al.[177]; (C) schematic illustration of materials library produced with discrete dots of varying compositions. This figure is quoted with permission from Tsai et al.[178], copyright 2016, Elsevier; (D) schematic of DED processing of Fe-Ni-Cr-Mo bulk materials library. This figure is quoted with permission from Islam et al.[180], copyright 2021, AIP Publishing. DED: Directed energy deposition.
The crystalline phase helps hinder the propagation of shear bands and dissipate fracture energy, which can significantly improve the room temperature ductility of BMGCs compared to monolithic bulk metallic glasses[155]. In their work, BMGC samples were deposited and then remelted to produce initially deposited melt pools with similar dimensions and different cooling rates. An 11 × 11 sample library was produced where the Al content was adjusted from 0 at. % to 10 at. % along the x-direction while the laser power was varied along the y-direction from 150 W to 400 W. Finite element modeling (FEM) was used to estimate the cooling rates and XRD analysis was used to confirm the phase constitution. After identifying phases with both amorphous and crystalline phases, the authors defined a uniformity coefficient to estimate the sample that would be expected to show the highest ductility. This criterion arose because ductility is closely related to the spatial distribution and uniformity of the crystalline dendrites within the glassy matrix. The optimal composition contained 4 at. % Al and used a remelting power of 175 W.
The rapid cooling rates induced by laser-based AM techniques can encourage the formation of amorphous structures in additively manufactured alloys and hence offer a unique opportunity to study bulk metallic glass (BMG) formation[177]. Zhai et al. fabricated a library of one composition with varying processing conditions to rapidly determine the optimal conditions to produce a defect-free BMG[177]. The composition used was Zr51Ti5Ni10Cu25Al9. Using ultrasonic wave attenuation, they were able to rapidly determine the presence of defects, pores, or crystalline grain boundaries that may affect the performance of the BMG. This technique is schematically illustrated in Figure 13B. A laser power of 1,300 W and 600 mm/min was determined to provide the highest fraction of amorphous material while remaining defect-free. This work highlights the use of DED combined with ultrasonic wave attenuation to provide a non-destructive and easy way to rapidly investigate and verify the glass-forming ability of many compositions immediately after they are printed.
It is currently very difficult to predict the glass-forming ability (GFA) of an alloy composition. Thus, the current exploration of BMGs requires a high-throughput investigation similar to that of HEAs. For this reason, Tsai et al. deposited a combinatorial library of Cu-Zr-Ti to identify the composition with optimal GFA[178]. Figure 13C shows a schematic illustration of the construction of this library[178]. The library was built by depositing discrete hemispherical samples with varying Cu:Zr ratios between each row of samples. After the initial deposition, a layer of Ti was deposited with various feed rates and simultaneously melted onto the library. Each sample was remelted 2 more times to ensure the elements were fully melted and incorporated into each sample.
Once the library was prepared, each sample was remelted with different laser powers of 200 W, 240 W, and 280 W. Since a higher laser power leads to a lower cooling rate, compositions that maintain glassy microstructure with higher laser power should have higher GFA. Differential interference contrast (DIC) imaging under optical microscopy was used to screen for amorphous materials as samples with amorphous structures show a smooth liquid-like topography under DIC. At the same time, crystalline microstructures appear rough[179]. A total of 144 discrete samples were investigated, and 92 were identified as amorphous for the lowest power. Based on the previously mentioned criteria, the composition with the highest GFA was Cu51.7Zr36.7Ti11.6, as it showed a high fraction of amorphous microstructure and was located in the center of the region of compositions that exhibit an amorphous microstructure after remelting at 280 W. It was also pointed out that this method could be extended to alloy systems with even more components by using pre-alloyed powders. Thus, the procedure laid out by Tsai et al. illustrates a means to rapidly identify BMGs with excellent GFA within a given alloy system. In addition to the optimal composition, combinatorial studies can also be used to rapidly determine optimal printing parameters for a given alloy system. Islam et al. carried out such a study on 25 different compositions in the Fe-Ni-Cr-Mo alloy system to and define a normalized dimensionless parameter based on the energy input density from the laser and the material properties of the constituent atoms[180]. A schematic illustration of their experimental method is illustrated in Figure 13D.
Eutectic HEAs (EHEAs) combine design concepts from both HEAs and eutectic alloys and show great potential for structural applications due to their impressive combination of strength and ductility[156,181]. This combination of properties arises from a hard and soft phase which help provide strength and ductility, respectively. However, further optimization is possible through minor composition adjustments to achieve near-eutectic HEAs. Joseph et al. produced a library of bulk AlxCoCrFeNi2.1 samples using the DED method to analyze the effect of Al-content on the microstructure and mechanical properties of alloys with near-eutectic compositions[182]. Figure 14A presents the XRD peak patterns of the compositions explored and shows an increase in the B2 phase with increasing the Al content. Additionally, cast samples with the compositions of each phase were prepared. These allowed the authors to investigate samples with single-phase microstructures that were either purely FCC or purely B2 phase. After analyses of the phase fractions and compressive properties of each composition, it was found that the alloys’ yield strength followed a rule of mixtures based on the yield strength of the individual phases. This work highlights the ability of DED to provide large sample sets that allow for rapid characterization of multiple compositions that can elucidate strengthening trends within a system to achieve an optimal composition.
Figure 14. (A) X-ray diffraction profiles of AlxCoCrFeNi2.1 showing the change in FCC and BCC phase fractions with changing Al content. The inset shows an image of material library. This figure is quoted with permission from Joseph et al.[182], copyright 2020, Elsevier; (B) SEM images and EDS maps of Cr19Fe31Mn11Ni39, Cr28Fe23Mn20Ni29, and Cr42Fe17Mn20Ni21, from left to right. This figure is quoted with permission from Moorehead et al.[183], copyright 2021, Elsevier; (C) SEM images of the as-deposited CoCrFeNiNbx parallel to the build direction: (i) CoCrFeNiNb0; (ii) CoCrFeNiNb0.1; (iii) CoCrFeNiNb0.15; (iv) CoCrFeNiNb0.2; and perpendicular to the build direction: (v) CoCrFeNiNb0; (vi) CoCrFeNiNb0.1; (vii) CoCrFeNiNb0.15; and (viii) CoCrFeNiNb0.2. This figure is quoted with permission from Zhou et al.[9], copyright 2019, Elsevier. BCC: Body-centered cubic; FCC: face-centered cubic.
When testing the radiation damage resistance of a material, it is imperative to use bulk samples as the damage layer thickness is typically on the order of microns, and the compositional gradient struggles to maintain chemical homogeneity over large length scales. Additionally, thin-film-based materials typically form nano-grain microstructures, which artificially increase the radiation damage resistance of a material, making the results misleading compared to application conditions. Moorehead et al. printed a compositional library of Cr-Fe-Mn-Ni alloys to assess their irradiation properties[183]. It was found that Cr-rich compositions showed an increase in BCC phase fraction, while Fe and Ni-rich compositions showed higher FCC content, and Cr and Ni tended to segregate together preferentially. This trend can be seen in Figure 14B, where the compositions with a higher Cr content show more severe segregation. Nanoindentation was utilized as a high-throughput means to measure the effect of ion irradiation on the hardness of each composition. Radiation-induced hardening was found in all compositions with FCC, BCC, and FCC + BCC phases. The increase in hardness was consistently shown to be 1-1.5 GPa, with BCC-rich compositions showing the least increase in hardness. Additionally, Moorehead et al. found that compositions with a high Mn content may have a large amount of Mn depletion after homogenization due to the depressed melting point of high Mn-content alloys. Thus, the authors laid out a guideline to keep the Mn-content below 25 at. %. Finally, the time saved using the high throughput AM approach is highlighted compared to the traditional metallurgical approach of melting and casting. The authors state that traditional melting and casting could take up to 1-2 hours per composition compared to the 10 min per composition required by the DED method.
Zhou et al. utilized DED to rapidly produce samples with compositions CoCrFeNiNbx (referred to here as Nbx)[9]. The authors investigated the mechanical properties of each alloy composition and its correlation to the phase and microstructures present. Figure 14C shows SEM images of 4 compositions (Nb0, Nb0.1, Nb0.15, Nb0.2) prepared by DED. The top row shows images taken parallel to the building direction, while the bottom row shows images taken perpendicular to the building direction. The authors concluded that the addition of Nb to the CoCrFeNi system led to a transition from a columnar to an equiaxed structure due to the formation of a secondary Laves phase in addition to the primary FCC phase. The Laves phase also caused an increase in yield strength in the Nb0.2 composition more than three times that of the Nb-free composition while maintaining a ductility above 10%.
HIGH-THROUGHPUT CHARACTERIZATION TECHNIQUES
While high-throughput computational methods can narrow down the alloy design space and high-throughput manufacturing methods enable rapid fabrication of samples within the design space, high-throughput experimental methods are needed to characterize the manufactured materials’ properties to experimentally verify which set of composition and processing conditions ultimately leads to the target performance. This section focuses primarily on the different high-throughput methods which can rapidly characterize important material properties such as hardness, strength, ductility, phase and composition, magnetic hysteresis, saturation magnetization, and corrosion resistance.
Mechanical property characterization
Mechanical properties such as strength and ductility are crucial to assess the performance of a material for structural applications[184]. A few important criteria exist for a mechanical test considered to be useful for screening HEAs. First, the sample size and microstructure must represent bulk-like conditions[185]. Second, the test should include a dominant tensile component, as real application conditions often include some tensile stresses[185]. Microhardness and nanoindentation tests are the most common approach towards high-throughput screening of structural materials. These methods can quickly and accurately estimate bulk yield strength[185]. Nanoindentation can also offer broad insights into the post-yielding attributes through analysis of the stress-strain curves it produces[186]. The local nature of these two techniques also makes them highly useful in graded materials libraries where many compositions and microstructures can be manufactured in a single sample for rapid screening.
Here two example studies are provided that use microhardness testing to investigate the effect of composition on hardness. Jiang et al. produced various compositions of CoFeNixVMoy alloys to test the effects of composition and microstructure on the hardness[187]. This work concluded that an increase in the Mo content led to increased precipitation of the CoMo2Ni-type intermetallic phase. An increase in Ni content increased the FCC solid solution phase and decreased the hardness. Figure 15A depicts the hardness of the various compositions showing that the peak hardness was reached at the composition equiatomic CoFeNiVMo. Pegues et al. also used micro-hardness indentation to build a hardness map of a graded TaxCoCrFeMnNi sample, as shown in Figure 15B[166]. This map allowed them to rapidly determine the effect of Ta addition on the hardness of this Cantor alloy-based system. Higher Ta contents encouraged the formation of TaNi-rich intermetallic in the interdendritic region, which caused significant increases in hardness.
Figure 15. (A) Effects of Ni and Mo on Vickers hardness of CoFeNixVmoy. This figure is quoted with permission from Jiang et al.[187], copyright 2015, Elsevier; (B) TaxCoCrFeMnNi hardness map with associated elemental distribution. This figure is quoted with permission from Pegues
Although micro-indentation methods can provide reasonable data for screening materials, the most reliable method to investigate material properties is a lab-scale tension test with samples that conform to either the ASTM E8 standard or another equivalent internationally recognized standard. Here the authors of this review present one example from the literature and their own unpublished data to illustrate the typical results that can be achieved in a combinatorial HEA library. Ma et al. added Nb to the AlCoCrFeNi system, which led to the formation of Laves phase that increased the strength of the alloy while decreasing the ductility[188]. Tuning the Nb content allowed them to tune the compressive properties [Figure 15C]. This result indicates that the addition of intermetallic forming elements can be used to achieve a wide array of properties that can be optimized for application-specific uses. Following this design philosophy, the authors of this review recently used DED to produce CoCrFeNiTix alloys to achieve a composition with improved mechanical properties. The tensile stress-strain curves of our investigated CoCrFeNiTix HEAs are shown in Figure 15D. These results show that adding Ti to the base quaternary alloy increases the yield strength while decreasing the ductility until x = 0.2. Beyond this threshold, the yield strength and the ductility of the alloy drop simultaneously. It has been well established that the introduction of Ti into the CoCrFeNi system leads to the formation of brittle intermetallic phases that causes decreased ductility and increased hardness and yield strength[189-191]. The drop in yield strength from x = 0.2 to x = 0.25 is likely a result of defects that occurred during printing due to a higher fraction of brittle phases.
In order to fulfill the rapid testing needs of high-throughput experiments, a high degree of automation must be integrated into the characterization process to decouple experimental progress from the number of hours available to human researchers. To that end, Huang et al. developed a high-throughput tensile testing platform to automate the tensile testing procedure and increase the rate and which specimens can be characterized[192]. This method uses a large grip that is held onto the bottom of many dog-bone samples, and this grip is attached to a motorized table that moves the grip laterally into position. A top grip is aligned in the direction of travel, allowing for automated testing of many samples in a small-time frame. In the case of their work, Huang et al. tested many samples of 316L stainless steel printed through a combinatorial study of different printing conditions by L-PBF. This platform may also show great potential for combinatorial studies related to the compositions of HEAs by automating tensile testing of compositional libraries produced by laser-based AM.
Phase and composition analysis
XRD is a common tool used to analyze the phases present in a material. The following paragraph illustrates some examples of typical data extracted from XRD analysis in combinatorial studies. Chen et al. studied the phase evolution in (AlCoCrFeNi)100-xNix and (CoCrCuFeNi)100-xMox HEAs[193]. XRD analysis shows that when x is between 0 and 4 at. %, both alloys exhibited single-phase solid solution structure where the (AlCoCrFeNi)100-xNix alloy shows a BCC structure and the (CoCrCuFeNi)100-xMox alloy shows an FCC structure. As the Ni content increases, a dual-phase FCC/BCC structure forms, and the FCC phase fraction increases. On the other hand, when the Mo content increases beyond 4 at. %, the FCC/BCC structure also forms, and the BCC phase fraction increases with the Mo content. The XRD patterns of the Ni- and Mo-doped samples are shown in Figure 16A and B. Moorehead et al. used DED to produce a library of Mo-Nb-Ta-W HEAs, which were then examined via XRD[194]. The XRD patterns are shown in Figure 16C. In this case, all the compositions tested showed a full BCC phase.
Figure 16. (A) XRD patterns of (AlCoCrFeNi)100-xNix. This figure is quoted with permission from Chen et al.[193], copyright 2018, Elsevier; (B) XRD patterns of (CoCrCuFeNi)100-xMox. This figure is quoted with permission from Chen et al.[193], copyright 2018, Elsevier; (C) XRD patterns of 31 samples fabricated by L-DED in the Mo-Ta-Nb-W alloy system. This figure is quoted with permission from Moorehead et al.[194]; (D) XRD patterns of CoCrFeNiNbx printed in the authors’ lab.
However, energy dispersive spectroscopy (EDS) analysis showed that Nb was segregated to the interdendritic region. In order to tune the phase structure in a CoCrFeNiNbx alloy system, our group used DED by placing pre-alloyed CoCrFeNi powder in one powder feeder and pure Nb powder in another. Then, the feed rates from each feeder were adjusted to produce a graded material with increasing Nb along the build direction. The CoCrFeNiNbx compositions were selected as going from x = 0 to x = 1, where x was increased by about 0.1 for every 1 mm increase in height. Synchrotron XRD (SXRD) at the Cornell High Energy Synchrotron Source was then performed along the build direction to analyze the phase composition in each region. The beam size was maintained as 0.5 × 0.5 mm such that the measured phase compositions correspond accurately to the designed compositions. As the Nb content increased, an FCC/Laves dual-phase structure formed with the Laves phase volume fraction increased from 0% to 57% as the Nb content increased from 0 to 20 at. %. Figure 16D shows the SXRD results taken for each composition.
In addition to XRD analysis, EBSD can offer a means to probe phases at higher spatial resolution (around 200 nm for EBSD vs. about 1 mm for XRD), which may be especially important for gradient compositional libraries where the compositional change can be quite drastic over small length scales[185]. EBSD also has the advantage of being equipped onto SEM facilities. Thus, EDS analysis can often be carried out in parallel such that phase and composition can be resolved almost simultaneously. For experiments that include many phases and samples, there is a need to automate the phase analysis process to make the process more efficient[195,29]. Many groups have used high-throughput SXRD to rapidly identify phases in combinatorial material libraries[196]. The majority of these studies used thin films produced by magnetron sputtering[29,195,197,198]. However, there are almost no studies of large bulk materials that used similar high-throughput methods for phase structure analysis.
It should be noted that a bottleneck for the previously mentioned methods is the human intervention needed during data analysis. This analysis can require impractical time commitments when the number of compositions reaches hundreds or thousands. Thus, the development of automated systems for analyzing XRD, EBSD, and EDS data is crucial to ensure that experimental results of high-throughput experiments can be achieved in a timely manner. Machine learning has recently shown impressive results in this field by correctly indexing phases within an EBSD pattern without requiring human input to guess at the present phases[199]. Although this process has not been attempted for HEAs, it shows great promise to be applied to new materials. Extending this practice further to carry out more in-depth analysis, such as Rietveld refinement for XRD patterns, will greatly accelerate the development of future HEAs.
Magnetic property measurement
Tang et al. added Ho to a FeCoNi(CuAl)0.8 alloy to investigate the effect of the addition of rare earth (RE) element on the magnetic properties of this system[200]. The initial parent alloy showed a fully FCC structure, and adding Ho led to the formation of a secondary BCC phase. Increasing the atomic fraction of Ho led to an increase in the volume fraction of the BCC phase fraction and no change in the lattice parameter of the FCC phase. As shown in Figure 17A, increasing the Ho content led to lower energy losses via eddy currents and hysteresis until x = 0.05. Once x = 0.07, the energy losses increased substantially. The decrease in hysteresis loss is due to lower Cu segregation at the BCC-FCC phase boundaries with increasing Ho. This segregation leads to a lower magnetic domain pining effect, decreasing hysteresis losses[200]. At x = 0.07, the Cu and Ho tend to segregate heavily to phase boundaries, leading to higher hysteresis losses. The BCC phase shows thinner magnetic stripe domains than the FCC phase, which leads to lower eddy losses as the BCC phase fraction increases.
Figure 17. (A) Effect of Ho addition to FeCoNi(CuAl)0.8 on magnetic hysteresis response of this alloy measured at room temperature. This figure is quoted with permission from Tang et al.[200], copyright 2021, Elsevier; (B) saturation magnetization of FeCoNi(CuAl)x alloys as CuAl is added. This figure is quoted with permission from Zhang et al.[201], copyright 2017, Elsevier; (C) magnetization curves of NiAlFeCoxCr1-x. This figure is quoted with permission from Borkar et al.[202], copyright 2017, John Wiley and Sons; (D) magnetization curves of FeCoNi(MnAl)x. This figure is quoted with permission from Li et al.[203], copyright 2017, Elsevier.
Zhang et al. studied the effect of composition and phase fraction in a FeCoNi(CuAl)x alloy system on the magnetic and mechanical properties[201]. The general trend from Figure 17B shows that the saturation magnetization (Ms) decreases with increasing Cu and Al content and shows a slight increase from x = 0.8 to x = 0.9. Fe, Co, and Ni are all ferromagnetic elements, while Cu and Al are not, so the authors rationalize the decrease in Ms originating from the increase in non-ferromagnetic components. Borkar et al. also studied the effect of the Co/Cr ratio on the microstructure and magnetic properties of AlCoxCr1-xFeNi[202]. Increasing the Co/Cr ratio leads to increased Ms as the magnetization depends heavily on the composition, as shown in Figure 17C.
Li et al. adjusted the composition of a FeCoNi(MnAl)x to study the effect of composition on the magnetic properties of this material[203]. The results presented in Figure 17D show that the saturation magnetization decreases as the Cu and Al content increases to x = 0.5 and then increases as the Cu, and Al content increases further. The FeCoNi alloy shows a fully FCC structure, while the FeCoNi(MnAl)0.5 and FeCoNi(MnAl)0.75 show an FCC + BCC dual-phase structure, and the FeCoNi(MnAl) composition shows a nearly fully BCC structure. Also, the lattice parameter of the FCC phase increases as Mn and Al are added, and the lattice parameter of the BCC phase decreases. The authors explain that the magnetization of the BCC phase decreases with decreasing lattice parameters and the magnetization of the FCC phase decreases with increasing lattice parameters[203]. Thus, the FeCoNi(MnAl)0.5 composition shows the lowest magnetic performance because both phases show their lowest performance at that composition.
Corrosion resistance
Corrosion resistance is a crucial property when selecting materials for real-life applications. The degradation of materials due to corrosion leads to over $500 billion in repair and maintenance costs in the US alone[204]. The corrosion process is highly complicated and includes various mechanisms that depend on the type and concentration of the corrosive electrolyte, the composition and microstructure of the chosen material, the ambient temperature, and the time spent in service[185]. Due to the complexity of corrosion phenomena, there is currently no unifying computational model to predict corrosion resistance, and there are limited empirical models for certain systems. This challenge forces researchers to rely on experimental results to screen materials for corrosion resistance. Thus, high-throughput corrosion resistance methods are extremely important to characterize and screen HEAs for future applications. Typical high-throughput screening methods utilize multi-electrode arrays placed in a common electrolyte to allow multiple materials to be tested simultaneously[205,206]. Rapid characterization via wire resistance to indicate a reduction in the cross-sectional area has shown great potential to accelerate the analysis of corrosion resistance[207]. Additionally, optical characterization of the color change of a corroded substance can be correlated well with traditional polarization curves. It can thus provide an easy screening method without the need for in-depth analysis[208,209]. The remainder of this section will summarize the results of combinatorial studies on HEAs taken from the literature that illustrate the improvements in corrosion resistance achieved so far.
It is well known that Cr is a useful element to improve corrosion resistance, and this result has also been verified for many HEA systems[210]. Thus, a Cr-containing HEA system with elements that show a low thermal neutron absorption cross-section is a prime candidate for nuclear applications[210]. Xiang et al. studied the effect of Cr addition in a Mo0.5VNbTi system on the microstructure and properties, including corrosion resistance[210]. The corrosion resistance tests for the Mo0.5VNbTiCrx HEAs (x = 0, 0.25, 0.5, 0.75, 1.0, 1.5, and 2.0, denoted as Cr0, Cr0.25, Cr0.5, Cr0.75, Cr1.0, Cr1.5, and Cr2.0, respectively) was carried out in superheated steam at 400 °C at 10.3 MPa in a static autoclave which is in accordance with ASTM G2/G2M guidelines. The weight gain per unit surface area was measured after 10, 20, 30, 40, 50, 60, and 70 days. The weight gain for each sample was compared to that of Zr-4 alloy (Zr-1.41Sn-0.21Fe-0.10Cr), which is commonly used as fuel rod cladding in nuclear reactors due to its excellent corrosion resistance[210,211]. The results are depicted in Figure 18A, where the weight gain decreases with adding Cr, except for the Cr1.5 alloy, which may be due to defects. All the compositions outperform the Zr-4 alloy showing much lower weight gain. This HEA system shows significantly improved corrosion resistance compared to a state-of-the-art alloy used in current applications, illustrating the potential of HEAs to achieve incredible improvements in corrosion resistance properties.
Figure 18. (A) Weight gain of Mo0.5VNbTiCrx after corrosion test in superheated steam at 400 °C at 10.3 MPa pressure for 70 days, Zr-4 alloy is provided for comparison. This figure is quoted with permission from Xiang et al.[210], copyright 2020, Elsevier; (B) potentiodynamic polarization curves of Al2CrFeCoxCuNiTi HEA compared to Q235 steel. This figure is quoted with permission from Qiu et al.[212], copyright 2019, Elsevier; (C) potentiodynamic polarization curves of Al2CrFeCoCuTiNix HEAs and Q235 steel substrate. This figure is quoted with permission from Qiu et al.[213], copyright 2013, Elsevier; (D) potentiodynamic polarization curves of TixZrNbTaMo HEAs and Ti6Al4V. This figure is quoted with permission from Hua et al.[214], copyright 2021, Elsevier.
Q235 steel is a common structural steel used in many applications, but it often requires a coating to be used in corrosive environments[212]. A HEA coating with good corrosion resistance can offer protection to the Q235 steel without degradation to its mechanical properties[212]. Qiu et al. explored the effect of composition on corrosion resistance in the Al2CrFeCoxCuNiTi[212]. The addition of Co to the system leads to a more positive corrosion potential which implies a higher corrosion resistance especially compared to the control Q235 steel, as seen in Figure 18B. The authors mention that severe elemental segregation can lead to the formation of micro-potentials during potentiodynamic polarization tests which can lead to micro-corrosion and accelerate the corrosion process. The authors also note that the equiaxed grain structure observed in the HEAs also leads to improved corrosion resistance. Qiu et al. also conducted a similar study on Al2CrFeCoCuNixTi[213]. Their results are illustrated in Figure 18C. It was also found that the corrosion resistance increased with increasing Ni content and then decreased. The increase in corrosion resistance is because the Ni element has a high corrosion resistance which contributes to the improved corrosion resistance of the alloy. However, as the Ni content increases further beyond Ni1.0, the elemental segregation increases greatly, which leads to the formation of micro-potentials that accelerate the corrosion process.
Ti-Zr-based HEAs have been suggested as potential biomedical implant materials[214]. These implants invariably undergo friction wear over long periods, and the complex chemical environment of the human body also leads to corrosion. Thus, a comprehensive understanding of the corrosion and wear resistance of such HEAs is needed to assess their viability for use as implants. Hua et al. studied the corrosion resistance of TixZrNbTaMo HEAs and compared it to Ti-6Al-4V, which has long been favored for biomedical applications[215]. The corrosion resistance on these alloys is depicted through the potentiodynamic polarization curves in Figure 18D. The Ti0.5ZrNbTaMo composition shows the highest corrosion resistance[214]. SEM image analysis of all the tested compositions showed that no pitting occurred after the potentiodynamic polarization tests, which points to the high corrosion resistance of these alloys. Further surface analysis via XPS showed that the surface film of the HEAs is mainly composed of the Ti4+, Zr4+, Nb5+, Ta5+, Mo4+, and Mo6+ oxides, which indicates the formation of a passivation layer that protected the alloys from severe corrosion.
CONCLUSIONS AND FUTURE OUTLOOK
HEAs present abundant opportunities to search for new materials with properties and performance that can exceed traditional dilute alloys. While the potential for this new class of materials is promising, the vast composition and microstructure space is too large to explore efficiently via traditional metallurgical techniques based on trial-and-error approaches. This review article highlights important advances in combinatorial studies that either present high-throughput methods to rapidly filter out undesirable materials or provide insights into general rules of thumb to allow researchers to design high-performance materials more efficiently.
The ultimate goal is to ensure that researchers spend more time understanding how to design and manufacture high-performance HEAs for industrial applications and less time on repetitive sample preparation and characterization methods. Implementing efficient high-throughput methods can minimize the time spent studying sub-optimal alloy compositions, which maximizes the resources spent on improving the most promising alloys. First, this review explores the high-throughput computational techniques that can down-select the design space before experimental characterization is even attempted. Then, it presents works that use additive manufacturing as a solution to produce large combinatorial libraries of bulk sample materials at length scales comparable to those expected during service and applications. Finally, high-throughput material characterization is highlighted for rapid understanding of the relationships between composition, microstructure, and material properties. This review article serves as a guideline for developing workflows that can efficiently discover new high-performance HEAs. To this end, several research frontiers in the field are put forward:
1. Machine learning (ML) techniques can provide predictions of massive design space, but there currently exists a shortage of robust training sets for HEA compositions. Further investment in high-throughput computational techniques that can produce these robust databases, such as CALPHAD, first-principles calculations, and molecular dynamics simulation, is needed. Once these databases are sufficiently established, ML techniques can provide highly reliable predictions of the phase constitution for unknown compositions. They can even predict bulk properties such as yield strength and density.
2. Additive manufacturing provides a means to rapidly produce bulk samples of varying compositions and microstructures. However, AM materials are prone to defects that can significantly deteriorate performance. Further studies, including in-situ characterization during 3D printing, are needed to better characterize the small-scale physics, in-situ alloying chemistry, and macroscale defect formation to reduce the work needed in preliminary optimization.
3. Data collection and analysis of material characterization techniques need to be further automated to enable high-throughput characterization of enormous materials libraries without significant time investments from researchers. Such techniques as phase, composition and microstructure characterization may need to be carried out in parallel to maximize the efficient use of equipment with overlapping functionalities, such as SEM with EBSD capabilities. Additionally, data processing automation is critically needed to rapidly characterize the vast number of compositions that are explored in high-throughput experiments.
DECLARATIONS
AcknowledgmentsThis work is based upon research conducted at the Center for High Energy X-ray Sciences (CHESS), which is supported by the National Science Foundation under award (DMR-1829070). The authors are grateful to Katharine Shanks at CHESS for her support in data acquisition and analysis at the ID3A beamline.
Authors’ contributionsWriting: Mooraj S
Manuscript supervision and editing: Chen W
Availability of Data and MaterialsNot applicable.
Financial support and sponsorshipChen W acknowledges the support from National Science Foundation (DMR-2004429) and UMass Amherst Faculty Startup Fund.
Conflicts of interestAll authors declare that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2023.
REFERENCES
1. Oh HS, Kim SJ, Odbadrakh K, et al. Engineering atomic-level complexity in high-entropy and complex concentrated alloys. Nat Commun 2019;10:2090.
3. Cantor B, Chang I, Knight P, Vincent A. Microstructural development in equiatomic multicomponent alloys. Mater Sci Eng A 2004;375-377:213-8.
4. Yeh J, Chen S, Lin S, et al. Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv Eng Mater 2004;6:299-303.
6. Wu Q, Wang Z, Hu X, et al. Uncovering the eutectics design by machine learning in the Al-Co-Cr-Fe-Ni high entropy system. Acta Mater 2020;182:278-86.
7. Chanda B, Verma A, Das J. Nano-/ultrafine eutectic in CoCrFeNi(Nb/Ta) high-entropy alloys. Trans Indian Inst Met 2018;71:2717-23.
8. Zhang H, Liu P, Hou J, Qiao J, Wu Y. Prediction of strength and ductility in partially recrystallized CoCrFeNiTi0.2 high-entropy alloy. Entropy 2019;21:389.
9. Zhou K, Li J, Wang L, Yang H, Wang Z, Wang J. Direct laser deposited bulk CoCrFeNiNbx high entropy alloys. Intermetallics 2019;114:106592.
10. Poletti MG, Fiore G, Gili F, Mangherini D, Battezzati L. Development of a new high entropy alloy for wear resistance: FeCoCrNiW0.3 and FeCoCrNiW0.3 + 5 at.% of C. Mater Design 2017;115:247-54.
11. Xiao J, Tan H, Chen J, Martini A, Zhang C. Effect of carbon content on microstructure, hardness and wear resistance of CoCrFeMnNiCx high-entropy alloys. J Alloys Compd 2020;847:156533.
12. Cui Y, Shen J, Manladan SM, Geng K, Hu S. Wear resistance of FeCoCrNiMnAlx high-entropy alloy coatings at high temperature. Appl Surf Sci 2020;512:145736.
14. Li R, Xie L, Wang WY, Liaw PK, Zhang Y. High-throughput calculations for high-entropy alloys: a brief review. Front Mater 2020;7:290.
15. Yin Y, Chen Z, Mo N, et al. High-temperature age-hardening of a novel cost-effective Fe45Ni25Cr25Mo5 high entropy alloy. Mater Sci Eng A 2020;788:139580.
16. Ma Y, Wu S, Jia Y, et al. Hexagonal closed-packed precipitation enhancement in a NbTiHfZr refractory high-entropy alloy. Metals 2019;9:485.
17. Liu Z, Zhao D, Wang P, et al. Additive manufacturing of metals: microstructure evolution and multistage control. J Mater Sci Technol 2022;100:224-36.
18. Fu C, Li J, Bai J, et al. Effect of helium bubbles on irradiation hardening of additive manufacturing 316L stainless steel under high temperature He ions irradiation. J Nucl Mater 2021;550:152948.
19. Farshidianfar MH, Khajepour A, Gerlich A. Real-time control of microstructure in laser additive manufacturing. Int J Adv Manuf Technol 2016;82:1173-86.
20. Shamsaei N, Yadollahi A, Bian L, Thompson SM. An overview of Direct Laser Deposition for additive manufacturing; Part II: mechanical behavior, process parameter optimization and control. Addit Manuf 2015;8:12-35.
21. Derimow N, Clark T, Abbaschian R. Solidification processing and cooling rate effects on hexagonal Co22Cr18Cu20Mn16Ti24 high-entropy alloys. Mater Chem Phys 2020;240:122188.
22. Xu X, Guo S, Nieh T, Liu C, Hirata A, Chen M. Effects of mixing enthalpy and cooling rate on phase formation of AlxCoCrCuFeNi high-entropy alloys. Materialia 2019;6:100292.
24. Braeckman B, Boydens F, Hidalgo H, et al. High entropy alloy thin films deposited by magnetron sputtering of powder targets. Thin Solid Films 2015;580:71-6.
25. Al Hasan NM, Hou H, Sarkar S, et al. Combinatorial synthesis and high-throughput characterization of microstructure and phase transformation in Ni-Ti-Cu-V quaternary thin-film library. Engineering 2020;6:637-43.
26. Liu X, Zou P, Song L, et al. Combinatorial high-throughput methods for designing hydrogen evolution reaction catalysts. ACS Catal 2022;12:3789-96.
27. Ludwig A. Discovery of new materials using combinatorial synthesis and high-throughput characterization of thin-film materials libraries combined with computational methods. NPJ Comput Mater 2019;5:70.
28. Shi Y, Yang B, Rack PD, Guo S, Liaw PK, Zhao Y. High-throughput synthesis and corrosion behavior of sputter-deposited nanocrystalline Al (CoCrFeNi)100- combinatorial high-entropy alloys. Mater Design 2020;195:109018.
29. Kube SA, Sohn S, Uhl D, Datye A, Mehta A, Schroers J. Phase selection motifs in high entropy alloys revealed through combinatorial methods: large atomic size difference favors BCC over FCC. Acta Mater 2019;166:677-86.
30. Keil T, Utt D, Bruder E, Stukowski A, Albe K, Durst K. Solid solution hardening in CrMnFeCoNi-based high entropy alloy systems studied by a combinatorial approach. J Mater Res 2021;36:2558-70.
31. Geuser FD. High-throughput in-situ characterization and modeling of precipitation kinetics in compositionally graded alloys. Acta Mater 2015;101:1-9.
32. Zhang X, Xiang Y. Combinatorial approaches for high-throughput characterization of mechanical properties. J Materiomics 2017;3:209-20.
33. Wang Z, Zhang L, Li W, et al. A high-throughput approach to explore the multi-component alloy space: a case study of nickel-based superalloys. J Alloys Compd 2021;858:158100.
34. Zhu C, Li C, Wu D, et al. A titanium alloys design method based on high-throughput experiments and machine learning. J Mater Res Technol 2021;11:2336-53.
35. Liu YH, Fujita T, Aji DP, Matsuura M, Chen MW. Structural origins of Johari-Goldstein relaxation in a metallic glass. Nat Commun 2014;5:3238.
36. Li MX, Zhao SF, Lu Z, et al. High-temperature bulk metallic glasses developed by combinatorial methods. Nature 2019;569:99-103.
38. Ngo TD, Kashani A, Imbalzano G, Nguyen KT, Hui D. Additive manufacturing (3D printing): a review of materials, methods, applications and challenges. Compos B Eng 2018;143:172-96.
39. Snow Z, Nassar AR, Reutzel EW. Invited review article: review of the formation and impact of flaws in powder bed fusion additive manufacturing. Addit Manuf 2020;36:101457.
40. Clare A, Mishra R, Merklein M, et al. Alloy design and adaptation for additive manufacture. J Mater Process Technol 2022;299:117358.
41. Bandyopadhyay A, Traxel KD. Invited review article: metal-additive manufacturing - Modeling strategies for application-optimized designs. Addit Manuf 2018;22:758-74.
42. Zhang C, Ouyang D, Pauly S, Liu L. 3D printing of bulk metallic glasses. Mater Sci Eng R Rep 2021;145:100625.
43. Silva LJ, Souza DM, de Araújo DB, Reis RP, Scotti A. Concept and validation of an active cooling technique to mitigate heat accumulation in WAAM. Int J Adv Manuf Technol 2020;107:2513-23.
44. Dhinakaran V, Ajith J, Fathima Yasin Fahmidha A, Jagadeesha T, Sathish T, Stalin B. Wire arc additive manufacturing (WAAM) process of nickel based superalloys - a review. Mater Today 2020;21:920-5.
45. Kozamernik N, Bračun D, Klobčar D. WAAM system with interpass temperature control and forced cooling for near-net-shape printing of small metal components. Int J Adv Manuf Technol 2020;110:1955-68.
46. Hou P, Mooraj S, Champagne VK, et al. Effect of build height on temperature evolution and thermally induced residual stresses in plasma arc additively manufactured stainless steel. Metall Mater Trans A 2022;53:627-39.
47. Borkar T, Gwalani B, Choudhuri D, et al. A combinatorial assessment of AlxCrCuFeNi2 (0 < x < 1.5) complex concentrated alloys: microstructure, microhardness, and magnetic properties. Acta Mater 2016;116:63-76.
48. Miracle D, Senkov O. A critical review of high entropy alloys and related concepts. Acta Mater 2017;122:448-511.
49. Li Z, Raabe D. Strong and ductile non-equiatomic high-entropy alloys: design, processing, microstructure, and mechanical properties. JOM 2017;69:2099-106.
50. Choi W, Jung S, Jo YH, Lee S, Lee B. Design of new face-centered cubic high entropy alloys by thermodynamic calculation. Met Mater Int 2017;23:839-47.
51. Yeh JW. Recent progress in high-entropy alloys. Available from: https://www.researchgate.net/profile/Jien-Wei-Yeh/publication/245440481_Recent_progress_in_high-entropy_alloys/links/02e7e52456c6fbaec9000000/Recent-progress-in-high-entropy-alloys.pdf [Last accessed on 16 Mar 2023].
52. Li H, Lai J, Li Z, Wang L. Multi-sites electrocatalysis in high-entropy alloys. Adv Funct Mater 2021;31:2106715.
53. Marshal A, Pradeep K, Music D, Zaefferer S, De P, Schneider J. Combinatorial synthesis of high entropy alloys: introduction of a novel, single phase, body-centered-cubic FeMnCoCrAl solid solution. J Alloys Compd 2017;691:683-9.
54. Yao H, Qiao J, Hawk J, Zhou H, Chen M, Gao M. Mechanical properties of refractory high-entropy alloys: experiments and modeling. J Alloys Compd 2017;696:1139-50.
55. Zhang Y, Zhou Y, Lin J, Chen G, Liaw P. Solid-solution phase formation rules for multi-component alloys. Adv Eng Mater 2008;10:534-8.
56. Bao N, Zuo J, Du Z, Yang M, Jiang G, Zhang L. Computational characterization of the structural and mechanical properties of AlxCoCrFeNiTi1-x high entropy alloys. Mater Res Express 2019;6:096519.
57. Dong Y, Chen QS, Lu YP, Zhang PC, Li TJ. Effect of aging temperature on microstructure and hardness of CoCrFeNiTi0.5 high entropy alloy. Mater Sci Forum 2014;789:48-53.
58. Guo S, Ng C, Liu C. Anomalous solidification microstructures in Co-free AlxCrCuFeNi2 high-entropy alloys. J Alloys Compd 2013;557:77-81.
59. Chen J, Zhou X, Wang W, et al. A review on fundamental of high entropy alloys with promising high-temperature properties. J Alloys Compd 2018;760:15-30.
60. Stepanov N, Shaysultanov D, Ozerov M, Zherebtsov S, Salishchev G. Second phase formation in the CoCrFeNiMn high entropy alloy after recrystallization annealing. Mater Lett 2016;185:1-4.
61. Toda-caraballo I, Rivera-díaz-del-castillo PE. Modelling solid solution hardening in high entropy alloys. Acta Mater 2015;85:14-23.
63. Lee C, Chou Y, Kim G, et al. Lattice-distortion-enhanced yield strength in a refractory high-entropy alloy. Adv Mater 2020;32:e2004029.
64. Lee C, Song G, Gao MC, et al. Lattice distortion in a strong and ductile refractory high-entropy alloy. Acta Mater 2018;160:158-72.
65. Dirras G, Lilensten L, Djemia P, et al. Elastic and plastic properties of as-cast equimolar TiHfZrTaNb high-entropy alloy. Mater Sci Eng A 2016;654:30-8.
66. Owen L, Pickering E, Playford H, Stone H, Tucker M, Jones N. An assessment of the lattice strain in the CrMnFeCoNi high-entropy alloy. Acta Mater 2017;122:11-8.
67. Senkov O, Scott J, Senkova S, Miracle D, Woodward C. Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy. J Alloys Compd 2011;509:6043-8.
68. Guo S. Phase selection rules for cast high entropy alloys: an overview. Mater Sci Technol 2015;31:1223-30.
69. Zhang Y, Lu ZP, Ma SG, et al. Guidelines in predicting phase formation of high-entropy alloys. MRS Commun 2014;4:57-62.
70. Kottke J, Laurent-brocq M, Fareed A, et al. Tracer diffusion in the Ni-CoCrFeMn system: transition from a dilute solid solution to a high entropy alloy. Scr Mater 2019;159:94-8.
71. Mehta A, Sohn Y. Investigation of sluggish diffusion in FCC Al0.25CoCrFeNi high-entropy alloy. Mate Res Lett 2021;9:239-46.
72. Dąbrowa J, Danielewski M. State-of-the-art diffusion studies in the high entropy alloys. Metals 2020;10:347.
73. Sathiaraj G, Ahmed M, Bhattacharjee P. Microstructure and texture of heavily cold-rolled and annealed fcc equiatomic medium to high entropy alloys. J Alloys Compd 2016;664:109-19.
74. Bhattacharjee P, Sathiaraj G, Zaid M, et al. Microstructure and texture evolution during annealing of equiatomic CoCrFeMnNi high-entropy alloy. J Alloys Compd 2014;587:544-52.
75. Sathiaraj G, Bhattacharjee P. Effect of starting grain size on the evolution of microstructure and texture during thermo-mechanical processing of CoCrFeMnNi high entropy alloy. J Alloys Compd 2015;647:82-96.
76. Ranganathan S. Alloyed pleasures: multimetallic cocktails. Available from: http://eprints.iisc.ac.in/6189/1/Alloyed_pleasures.pdf [Last accessed on 16 Mar 2023].
77. Qiao L, Liu Y, Zhu J. A focused review on machine learning aided high-throughput methods in high entropy alloy. J Alloys Compd 2021;877:160295.
78. Butler KT, Davies DW, Cartwright H, Isayev O, Walsh A. Machine learning for molecular and materials science. Nature 2018;559:547-55.
79. Yang C, Ren C, Jia Y, Wang G, Li M, Lu W. A machine learning-based alloy design system to facilitate the rational design of high entropy alloys with enhanced hardness. Acta Mater 2022;222:117431.
80. Krishna YV, Jaiswal UK, Rahul RM. Machine learning approach to predict new multiphase high entropy alloys. Scr Mater 2021;197:113804.
81. Zhou T, Song Z, Sundmacher K. Big data creates new opportunities for materials research: a review on methods and applications of machine learning for materials design. Engineering 2019;5:1017-26.
82. Liu X, Xu P, Zhao J, Lu W, Li M, Wang G. Material machine learning for alloys: Applications, challenges and perspectives. J Alloys Compd 2022;921:165984.
83. Liu S, Kappes BB, Amin-ahmadi B, Benafan O, Zhang X, Stebner AP. Physics-informed machine learning for composition - process - property design: shape memory alloy demonstration. Appl Mater Today 2021;22:100898.
84. Yi W, Liu G, Lu Z, Gao J, Zhang L. Efficient alloy design of Sr-modified A356 alloys driven by computational thermodynamics and machine learning. J Mater Sci Technol 2022;112:277-90.
86. Nassar A, Mullis A. Rapid screening of high-entropy alloys using neural networks and constituent elements. Comput Mater Sci 2021;199:110755.
87. Risal S, Zhu W, Guillen P, Sun L. Improving phase prediction accuracy for high entropy alloys with machine learning. Comput Mater Sci 2021;192:110389.
88. Montavon G, Samek W, Müller K. Methods for interpreting and understanding deep neural networks. Digit Signal Process 2018;73:1-15.
89. Zhang Y, Wen C, Wang C, et al. Phase prediction in high entropy alloys with a rational selection of materials descriptors and machine learning models. Acta Mater 2020;185:528-39.
90. Vazquez G, Singh P, Sauceda D, et al. Efficient machine-learning model for fast assessment of elastic properties of high-entropy alloys. Acta Mater 2022;232:117924.
91. Purcell TAR, Scheffler M, Carbogno C, Ghiringhelli LM. SISSO++: A C++ implementation of the sure-independence screening and sparsifying operator approach. J Open Res Softw 2022;7:3960.
92. Sorkin V, Yu ZG, Chen S, Tan TL, Aitken ZH, Zhang YW. A first-principles-based high fidelity, high throughput approach for the design of high entropy alloys. Sci Rep 2022;12:11894.
93. Hautier G, Jain A, Ong SP. From the computer to the laboratory: materials discovery and design using first-principles calculations. J Mater Sci 2012;47:7317-40.
94. Ikeda Y, Grabowski B, Körmann F. Ab initio phase stabilities and mechanical properties of multicomponent alloys: a comprehensive review for high entropy alloys and compositionally complex alloys. Mater Charact 2019;147:464-511.
95. Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev 1965;140:A1133-8.
96. Ceperley DM, Alder BJ. Ground state of the electron gas by a stochastic method. Phys Rev Lett 1980;45:566-9.
97. Perdew JP. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys Rev B Condens Matter 1986;33:8822-4.
98. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett 1996;77:3865-8.
99. Perdew JP, Chevary JA, Vosko SH, et al. Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys Rev B Condens Matter 1992;46:6671-87.
100. Kim G, Diao H, Lee C, et al. First-principles and machine learning predictions of elasticity in severely lattice-distorted high-entropy alloys with experimental validation. Acta Mater 2019;181:124-38.
101. Rittiruam M, Noppakhun J, Setasuban S, et al. High-throughput materials screening algorithm based on first-principles density functional theory and artificial neural network for high-entropy alloys. Sci Rep 2022;12:16653.
102. Bellaiche L, Vanderbilt D. Virtual crystal approximation revisited: application to dielectric and piezoelectric properties of perovskites. Phys Rev B 2000;61:7877-82.
103. Ramer N, Rappe A. Application of a new virtual crystal approach for the study of disordered perovskites. J Phys Chem Solids 2000;61:315-20.
104. Chen L, Hao X, Wang Y, Zhang X, Liu H. First-principles calculation of the effect of Ti content on the structure and properties of TiVNbMo refractory high-entropy alloy. Mater Res Express 2020;7:106516.
105. Lederer Y, Toher C, Vecchio KS, Curtarolo S. The search for high entropy alloys: a high-throughput ab-initio approach. Acta Mater 2018;159:364-83.
106. Curtarolo S, Setyawan W, Hart GL, et al. AFLOW: an automatic framework for high-throughput materials discovery. Comput Mater Sci 2012;58:218-26.
107. Sanchez J, Ducastelle F, Gratias D. Generalized cluster description of multicomponent systems. Physica A 1984;128:334-50.
108. de Walle A, Asta M, Ceder G. The alloy theoretic automated toolkit: a user guide. Calphad 2002;26:539-53.
109. Berding MA, Sher A. Electronic quasichemical formalism: application to arsenic deactivation in silicon. Phys Rev B 1998;58:3853-64.
110. Jiang L, Lu Y, Jiang H, et al. Formation rules of single phase solid solution in high entropy alloys. Mater Sci Technol 2015; doi: 10.1179/1743284715y.0000000130.
111. Guo S, Ng C, Lu J, Liu CT. Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J Appl Phys 2011;109:103505.
112. Yang S, Liu G, Zhong Y. Revisit the VEC criterion in high entropy alloys (HEAs) with high-throughput ab initio calculations: a case study with Al-Co-Cr-Fe-Ni system. J Alloys Compd 2022;916:165477.
113. Zhou K & Liu B. Molecular dynamics simulation: fundamentals and applications. Academic Press; 2022.
114. Car R, de Angelis F, Giannozzi P, Marzari N. First-principles molecular dynamics. In: Yip S, editor. Handbook of Materials Modeling. Dordrecht: Springer; 2005. pp. 59-76.
115. Tang Y, Li D. Nano-tribological behavior of high-entropy alloys CrMnFeCoNi and CrFeCoNi under different conditions: a molecular dynamics study. Wear 2021;476:203583.
116. Yin S, Zuo Y, Abu-Odeh A, et al. Atomistic simulations of dislocation mobility in refractory high-entropy alloys and the effect of chemical short-range order. Nat Commun 2021;12:4873.
117. Fan Y, Wang W, Hao Z, Zhan C. Work hardening mechanism based on molecular dynamics simulation in cutting Ni-Fe-Cr series of Ni-based alloy. J Alloys Compd 2020;819:153331.
118. Li J, Fang Q, Liu B, Liu Y, Liu Y. Mechanical behaviors of AlCrFeCuNi high-entropy alloys under uniaxial tension via molecular dynamics simulation. RSC Adv 2016;6:76409-19.
119. Trong DN, Long VC, Ţălu Ş. Effects of number of atoms and doping concentration on the structure, phase transition, and crystallization process of Fe1-x-yNixCoy alloy: a molecular dynamic study. Appl Sci 2022;12:8473.
120. Xie L, Brault P, Thomann A, Yang X, Zhang Y, Shang G. Molecular dynamics simulation of Al-Co-Cr-Cu-Fe-Ni high entropy alloy thin film growth. Intermetallics 2016;68:78-86.
121. Pan Z, Fu Y, Wei Y, Yan X, Luo H, Li X. Deformation mechanisms of TRIP-TWIP medium-entropy alloys via molecular dynamics simulations. Int J Mech Sci 2022;219:107098.
122. Jarlöv A, Ji W, Zhu Z, et al. Molecular dynamics study on the strengthening mechanisms of Cr-Fe-Co-Ni high-entropy alloys based on the generalized stacking fault energy. J Alloys Compd 2022;905:164137.
123. Li J, Xie B, Fang Q, Liu B, Liu Y, Liaw PK. High-throughput simulation combined machine learning search for optimum elemental composition in medium entropy alloy. J Mater Sci Technol 2021;68:70-5.
124. Zhang L, Qian K, Huang J, Liu M, Shibuta Y. Molecular dynamics simulation and machine learning of mechanical response in non-equiatomic FeCrNiCoMn high-entropy alloy. J Mater Res Technol 2021;13:2043-54.
125. Morrissey LS, Nakhla S. Considerations when calculating the mechanical properties of single crystals and bulk polycrystals from molecular dynamics simulations. Mol Simul 2020;46:1433-42.
126. Zhang L, Qian K, Schuller BW, Shibuta Y. Prediction on mechanical properties of non-equiatomic high-entropy alloy by atomistic simulation and machine learning. Metals 2021;11:922.
127. Jiang J, Sun W, Luo N. Molecular dynamics study of microscopic deformation mechanism and tensile properties in AlxCoCrFeNi amorphous high-entropy alloys. Mater Today Commun 2022;31:103861.
128. Guruvidyathri K, Hari Kumar KC, Yeh JW, Murty BS. Topologically close-packed phase formation in high entropy alloys: a review of calphad and experimental results. JOM 2017;69:2113-24.
129. Gao MC. Design of high-entropy alloys. In: Gao MC, Yeh J, Liaw PK, Zhang Y, editors. High-entropy alloys. Cham: Springer International Publishing; 2016. pp. 369-98.
130. Senkov ON, Miller JD, Miracle DB, Woodward C. Accelerated exploration of multi-principal element alloys with solid solution phases. Nat Commun 2015;6:6529.
131. Klaver TPC, Simonovic D, Sluiter MHF. Brute force composition scanning with a CALPHAD database to find low temperature body centered cubic high entropy alloys. Entropy 2018;20:911.
132. Thurston KV, Gludovatz B, Hohenwarter A, Laplanche G, George EP, Ritchie RO. Effect of temperature on the fatigue-crack growth behavior of the high-entropy alloy CrMnFeCoNi. Intermetallics 2017;88:65-72.
133. Li YJ, Savan A, Ludwig A. Atomic scale understanding of phase stability and decomposition of a nanocrystalline CrMnFeCoNi Cantor alloy. Appl Phys Lett 2021;119:201910.
134. Zeng Z, Xiang M, Zhang D, et al. Mechanical properties of Cantor alloys driven by additional elements: a review. J Mater Res Technol 2021;15:1920-34.
135. Conway PL, Klaver T, Steggo J, Ghassemali E. High entropy alloys towards industrial applications: high-throughput screening and experimental investigation. Mater Sci Eng A 2022;830:142297.
136. Abu-odeh A, Galvan E, Kirk T, et al. Efficient exploration of the high entropy alloy composition-phase space. Acta Mater 2018;152:41-57.
137. Zhao DQ, Pan SP, Zhang Y, Liaw PK, Qiao JW. Structure prediction in high-entropy alloys with machine learning. Appl Phys Lett 2021;118:231904.
138. Schleder GR, Padilha ACM, Acosta CM, Costa M, Fazzio A. From DFT to machine learning: recent approaches to materials science-a review. J Phys Mater 2019;2:032001.
139. Zhou Z, Zhou Y, He Q, Ding Z, Li F, Yang Y. Machine learning guided appraisal and exploration of phase design for high entropy alloys. NPJ Comput Mater 2019:5.
141. Jiang J, Chen P, Qiu J, et al. Microstructural evolution and mechanical properties of AlxCoCrFeNi high-entropy alloys under uniaxial tension: a molecular dynamics simulations study. Mater Today Commun 2021;28:102525.
142. Wang L, Liu W, Zhu B, et al. Influences of strain rate, Al concentration and grain heterogeneity on mechanical behavior of CoNiFeAlxCu1-x high-entropy alloys: a molecular dynamics simulation. J Mater Res Technol 2021;14:2071-84.
143. Leong Z, Tan TL. Robust cluster expansion of multicomponent systems using structured sparsity. Phys Rev B 2019:100.
144. Leong Z, Ramamurty U, Tan TL. Microstructural and compositional design principles for Mo-V-Nb-Ti-Zr multi-principal element alloys: a high-throughput first-principles study. Acta Mater 2021;213:116958.
145. Fernández-caballero A, Wróbel JS, Mummery PM, Nguyen-manh D. Short-range order in high entropy alloys: theoretical formulation and application to Mo-Nb-Ta-V-W system. J Phase Equilib Diffus 2017;38:391-403.
146. Fontaine D. The number of independent pair-correlation functions in multicomponent systems. J Appl Crystallogr 1971;4:15-9.
147. Kattner UR. The calphad method and its role in material and process development. Tecnol Metal Mater Min 2016;13:3-15.
148. Zeng Y, Man M, Bai K, Zhang Y. Revealing high-fidelity phase selection rules for high entropy alloys: a combined CALPHAD and machine learning study. Mater Design 2021;202:109532.
149. Wu D, Tian Y, Zhang L, et al. Optimal design of high-strength Ti-Al-V-Zr alloys through a combinatorial approach. Materials 2018;11:1603.
150. Gumbmann E, De Geuser F, Deschamps A, Lefebvre W, Robaut F, Sigli C. A combinatorial approach for studying the effect of Mg concentration on precipitation in an Al-Cu-Li alloy. Scr Mater 2016;110:44-7.
151. Li Y, Jensen KE, Liu Y, et al. Combinatorial strategies for synthesis and characterization of alloy microstructures over large compositional ranges. ACS Comb Sci 2016;18:630-7.
152. Tang M, Pistorius PC, Narra S, Beuth JL. Rapid solidification: selective laser melting of AlSi10Mg. JOM 2016;68:960-6.
153. Aboutaleb AM, Mahtabi MJ, Tschopp MA, Bian L. Multi-objective accelerated process optimization of mechanical properties in laser-based additive manufacturing: case study on Selective Laser Melting (SLM) Ti-6Al-4V. J Manuf Process 2019;38:432-44.
154. Jung HY, Peter NJ, Gärtner E, Dehm G, Uhlenwinkel V, Jägle EA. Bulk nanostructured AlCoCrFeMnNi chemically complex alloy synthesized by laser-powder bed fusion. Addit Manuf 2020;35:101337.
155. Lu Y, Su S, Zhang S, et al. Controllable additive manufacturing of gradient bulk metallic glass composite with high strength and tensile ductility. Acta Mater 2021;206:116632.
156. Ren J, Zhang Y, Zhao D, et al. Strong yet ductile nanolamellar high-entropy alloys by additive manufacturing. Nature 2022;608:62-8.
157. Zhang S, Hou P, Mooraj S, Chen W. Printability of Zr41.2Ti13.8Cu12.5Ni10.0Be22.5 metallic glass on steel by laser additive manufacturing: a single-track study. Surf Coat Technol 2021;428:127882.
158. Wang YM, Voisin T, McKeown JT, et al. Additively manufactured hierarchical stainless steels with high strength and ductility. Nat Mater 2018;17:63-71.
159. Chen W, Voisin T, Zhang Y, et al. Microscale residual stresses in additively manufactured stainless steel. Nat Commun 2019;10:4338.
160. Li Z, Ludwig A, Savan A, Springer H, Raabe D. Combinatorial metallurgical synthesis and processing of high-entropy alloys. J Mater Res 2018;33:3156-69.
161. Santa-aho S, Kiviluoma M, Jokiaho T, et al. Additive manufactured 316L stainless-steel samples: microstructure, residual stress and corrosion characteristics after post-processing. Metals 2021;11:182.
162. Zhang C, Chen F, Huang Z, et al. Additive manufacturing of functionally graded materials: a review. Mater Sci Eng A 2019;764:138209.
163. del Val J, Arias-gonzález F, Barro O, et al. Functionally graded 3D structures produced by laser cladding. Procedia Manuf 2017;13:169-76.
164. Gwalani B, Gangireddy S, Shukla S, et al. Compositionally graded high entropy alloy with a strong front and ductile back. Mater Today Commun 2019;20:100602.
165. Li L, Wang J, Lin P, Liu H. Microstructure and mechanical properties of functionally graded TiCp/Ti6Al4V composite fabricated by laser melting deposition. Ceram Int 2017;43:16638-51.
166. Pegues JW, Melia MA, Puckett R, Whetten SR, Argibay N, Kustas AB. Exploring additive manufacturing as a high-throughput screening tool for multiphase high entropy alloys. Addit Manuf 2021;37:101598.
167. Wen Y, Zhang B, Narayan RL, et al. Laser powder bed fusion of compositionally graded CoCrMo-Inconel 718. Addit Manuf 2021;40:101926.
168. Shishkovsky I, Kakovkina N, Scherbakov V. Rapid TMC laser prototyping: Compositional and phase-structural sustainability via combinatorial design of titanium-based gradient alloy reinforced by nano-sized TiC or TiB2 ceramics. SPIE 2018;10523:172-7.
169. Traxel KD, Bandyopadhyay A. Influence of in situ ceramic reinforcement towards tailoring titanium matrix composites using laser-based additive manufacturing. Addit Manuf 2020;31:101004.
170. Gong X, Yabansu YC, Collins PC, Kalidindi SR. Evaluation of Ti-Mn alloys for additive manufacturing using high-throughput experimental assays and gaussian process regression. Materials 2020;13:4641.
171. Li M, Flores KM. Laser processing as a high-throughput method to investigate microstructure-processing-property relationships in multiprincipal element alloys. J Alloys Compd 2020;825:154025.
172. Teh WH, Chaudhary V, Chen S, et al. High throughput multi-property evaluation of additively manufactured Co-Fe-Ni materials libraries. Addit Manuf 2022;58:102983.
173. Gwalani B, Soni V, Waseem OA, Mantri SA, Banerjee R. Laser additive manufacturing of compositionally graded AlCrFeMoVx (x = 0 to 1) high-entropy alloy system. Opt Laser Technol 2019;113:330-7.
174. Zhao Y, Lau KB, Teh WH, et al. Compositionally graded CoCrFeNiTi high-entropy alloys manufactured by laser powder bed fusion: a combinatorial assessment. J Alloys Compd 2021;883:160825.
175. Yu Z, Zheng W, Li Z, et al. Accelerated exploration of TRIP metallic glass composite by laser additive manufacturing. J Mater Sci Technol 2021;78:68-73.
176. Wu Y, Wang H, Liu X, et al. Designing bulk metallic glass composites with enhanced formability and plasticity. J Mater Sci Technol 2014;30:566-75.
177. Zhai L, Lu Y, Zhao X, Wang L, Lu X. High-throughput screening of laser additive manufactured metallic glass via ultrasonic wave. Sci Rep 2019;9:17660.
178. Tsai P, Flores KM. High-throughput discovery and characterization of multicomponent bulk metallic glass alloys. Acta Mater 2016;120:426-34.
179. Tsai P, Flores KM. A combinatorial strategy for metallic glass design via laser deposition. Intermetallics 2014;55:162-6.
180. Islam Z, Nelaturu P, Thoma DJ. A dimensionless number for high-throughput design of multi-principal element alloys in directed energy deposition. Appl Phys Lett 2021;119:231901.
181. Zhang W, Liu L, Peng S, et al. The tensile property and notch sensitivity of AlCoCrFeNi2.1 high entropy alloy with a novel “steel-frame” eutectic microstructure. J Alloys Compd 2021;863:158747.
182. Joseph J, Imran M, Hodgson P, Barnett M, Fabijanic D. Towards the large-scale production and strength prediction of near-eutectic AlxCoCrFeNi2.1 alloys by additive manufacturing. Manuf Lett 2020;25:16-20.
183. Moorehead M, Nelaturu P, Elbakhshwan M, et al. High-throughput ion irradiation of additively manufactured compositionally complex alloys. J Nucl Mater 2021;547:152782.
184. Miracle D, Majumdar B, Wertz K, Gorsse S. New strategies and tests to accelerate discovery and development of multi-principal element structural alloys. Scr Mater 2017;127:195-200.
185. Miracle DB, Li M, Zhang Z, Mishra R, Flores KM. Emerging capabilities for the high-throughput characterization of structural materials. Annu Rev Mater Res 2021;51:131-64.
186. Pathak S, Kalidindi SR. Spherical nanoindentation stress-strain curves. Mater Sci Eng R Rep 2015;91:1-36.
187. Jiang L, Cao Z, Jie J, et al. Effect of Mo and Ni elements on microstructure evolution and mechanical properties of the CoFeNixVMoy high entropy alloys. J Alloys Compd 2015;649:585-90.
188. Ma S, Zhang Y. Effect of Nb addition on the microstructure and properties of AlCoCrFeNi high-entropy alloy. Mater Sci Eng A 2012;532:480-6.
189. Wang X, Liu Q, Huang Y, Xie L, Xu Q, Zhao T. Effect of Ti content on the microstructure and corrosion resistance of CoCrFeNiTix high entropy alloys prepared by laser cladding. Materials 2020;13:2209.
190. Shun T, Chang L, Shiu M. Microstructures and mechanical properties of multiprincipal component CoCrFeNiTix alloys. Mater Sci Eng A 2012;556:170-4.
191. Tong Y, Chen D, Han B, et al. Outstanding tensile properties of a precipitation-strengthened FeCoNiCrTi0.2 high-entropy alloy at room and cryogenic temperatures. Acta Mater 2019;165:228-40.
192. Huang K, Kain C, Diaz-vallejo N, Sohn Y, Zhou L. High throughput mechanical testing platform and application in metal additive manufacturing and process optimization. J Manuf Process 2021;66:494-505.
193. Chen R, Qin G, Zheng H, et al. Composition design of high entropy alloys using the valence electron concentration to balance strength and ductility. Acta Mater 2018;144:129-37.
194. Moorehead M, Bertsch K, Niezgoda M, et al. High-throughput synthesis of Mo-Nb-Ta-W high-entropy alloys via additive manufacturing. Mater Design 2020;187:108358.
195. Ren F, Pandolfi R, Van Campen D, Hexemer A, Mehta A. On-the-fly data assessment for high-throughput X-ray diffraction measurements. ACS Comb Sci 2017;19:377-85.
196. Long CJ, Bunker D, Li X, Karen VL, Takeuchi I. Rapid identification of structural phases in combinatorial thin-film libraries using X-ray diffraction and non-negative matrix factorization. Rev Sci Instrum 2009;80:103902.
197. Datye A, Alexander Kube S, Verma D, Schroers J, Schwarz UD. Accelerated discovery and mechanical property characterization of bioresorbable amorphous alloys in the Mg-Zn-Ca and the Fe-Mg-Zn systems using high-throughput methods. J Mater Chem B 2019;7:5392-400.
198. Zhao L, Jiang L, Yang L, et al. High throughput synthesis enabled exploration of CoCrFeNi-based high entropy alloys. J Mater Sci Technol 2022;110:269-82.
199. Kaufmann K, Zhu C, Rosengarten AS, Maryanovsky D, Wang H, Vecchio KS. Phase mapping in EBSD using convolutional neural networks. Microsc Microanal 2020;26:458-68.
200. Tang Y, Sun S, Lv M, et al. Effect of Ho addition on AC soft magnetic property, microstructure and magnetic domain of FeCoNi(CuAl)0.8Hox (x = 0-0.07) high-entropy alloys. Intermetallics 2021;135:107216.
201. Zhang Q, Xu H, Tan X, et al. The effects of phase constitution on magnetic and mechanical properties of FeCoNi(CuAl) (x = 0-1.2) high-entropy alloys. J Alloys Compd 2017;693:1061-7.
202. Borkar T, Chaudhary V, Gwalani B, et al. A combinatorial approach for assessing the magnetic properties of high entropy alloys: role of Cr in AlCoxCr1-xFeNi. Adv Eng Mater 2017;19:1700048.
203. Li P, Wang A, Liu C. Composition dependence of structure, physical and mechanical properties of FeCoNi(MnAl)x high entropy alloys. Intermetallics 2017;87:21-6.
204. Taylor CD, Lu P, Saal J, Frankel GS, Scully JR. Integrated computational materials engineering of corrosion resistant alloys. NPJ Mater Degrad 2018:2.
205. Taylor SR. The investigation of corrosion phenomena with high throughput methods: a review. Corros Rev 2011;29:135-51.
206. Muster T, Trinchi A, Markley T, et al. A review of high throughput and combinatorial electrochemistry. Electrochim Acta 2011;56:9679-99.
207. Whitfield MJ, Bono D, Wei L, Van Vliet KJ. High-throughput corrosion quantification in varied microenvironments. Corros Sci 2014;88:481-6.
208. White P, Smith G, Harvey T, et al. A new high-throughput method for corrosion testing. Corros Sci 2012;58:327-31.
209. Liu J, Liu N, Sun M, Li J, Sohn S, Schroers J. Fast screening of corrosion trends in metallic glasses. ACS Comb Sci 2019;21:666-74.
210. Xiang C, Fu H, Zhang Z, et al. Effect of Cr content on microstructure and properties of Mo0.5VNbTiCrx high-entropy alloys. J Alloys Compd 2020;818:153352.
211. Renčiuková V, Macák J, Sajdl P, Novotný R, Krausová A. Corrosion of zirconium alloys demonstrated by using impedance spectroscopy. J Nucl Mater 2018;510:312-21.
212. Qiu X. Corrosion behavior of Al2CrFeCoxCuNiTi high-entropy alloy coating in alkaline solution and salt solution. Results Phys 2019;12:1737-41.
213. Qiu X, Liu C. Microstructure and properties of Al2CrFeCoCuTiNix high-entropy alloys prepared by laser cladding. J Alloys Compd 2013;553:216-20.
214. Hua N, Wang W, Wang Q, et al. Mechanical, corrosion, and wear properties of biomedical Ti-Zr-Nb-Ta-Mo high entropy alloys. J Alloys Compd 2021;861:157997.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.




































Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].