Machine learning-accelerated first-principles predictions of the stability and mechanical properties of L12-strengthened cobalt-based superalloys
Abstract
As promising next-generation candidates for applications in aero-engines, L12-strengthened cobalt (Co)-based superalloys have attracted extensive attention. However, the L12 strengthening phase in first-generation Co-Al-W-based superalloys is metastable, and both its solvus temperature and mechanical properties still need improvement. Therefore, it is necessary to discover new L12-strengthened Co-based superalloy systems with a stable L12 phase by exploring the effect of alloying elements on their stability. Traditional first-principles calculations are capable of providing the crystal structure and mechanical properties of the L12 phase doped by transition metals but suffer from low efficiency and relatively high computational costs. The present study combines machine learning (ML) with first-principles calculations to accelerate crystal structure and mechanical property predictions, with the latter providing both the training and validation datasets. Three ML models are established and trained to predict the occupancy of alloying elements in the supercell and the stability and mechanical properties of the L12 phase. The ML predictions are evaluated using first-principles calculations and the accompanying data are used to further refine the ML models. Our ML-accelerated first-principles calculation approach offers more efficient predictions of the crystal structure and mechanical properties for Co-V-Ta- and Co-Al-V-based systems than the traditional counterpart. This approach is applicable to expediting crystal structure and mechanical property calculations and thus the design and discovery of other advanced materials beyond Co-based superalloys.
Keywords
INTRODUCTION
Ni-based superalloys have been widely used in the aviation, aerospace and petrochemical industries due to their superior combination of highly desirable properties, such as microstructural stability, mechanical properties and oxidation and thermal corrosion resistance at elevated temperatures[1,2]. The signature coherent γ/γ' two-phase precipitate microstructure can maintain the strength of the superalloys under high-temperature conditions[3]. However, due to the limitation of the melting temperature of elemental Ni
Nevertheless, to explore the high-dimensional composition and temperature space through the alloying strategy, the traditional experimental methods based on trial and error are labor intensive and time-consuming. In order to guide the design and discovery of new L12-strengthened Co-based superalloys with enhanced mechanical properties, the basic information, such as the crystal structures and atomic occupancies, of the L12 phase are highly desirable, which is defined as the site occupied by a doped TM. Through structural optimization and static calculations based on first-principles calculations, the ground-state static energy of the L12 phase at 0 K can be accurately calculated and the stable formation enthalpy and reaction energy of the L12 phase can then be derived[22,23]. First-principles calculations can also be combined with Hook’s law to predict the elastic constant of the supercell of Co-based superalloys, which allows for the prediction of the mechanical properties, such as the bulk, shear and elastic moduli[24,25]. However, the procedures of traditional first-principles calculations are tedious and require significant computational resources. In the case of a system with more than four elements, the number of nonequivalent sites for each element in the supercell will dramatically increase due to the increase in the types of elements, resulting in a significant increase in computational cost and a reduction in computational efficiency. Therefore, improving the computational efficiency to speed up alloy discovery requires an alternative approach[26].
To date, there has been a push towards big data and artificial intelligence in materials research[27,28]. Machine learning (ML) is a type of algorithm that can acquire new knowledge “automatically” like human beings, mine the existing data, extract key information, establish a predictive model that describes the relationship between influencing factors and a target property and use the model to predict new materials of new unknown systems[26]. ML-based methods have been widely used for assisting the design and discovery of a wide class of materials, including alloys, ceramics and composites, polymers, two-dimensional materials, organic-inorganic hybrids, and so on[29,30]. Using ML algorithms, new materials with excellent performance have been developed successfully and efficiently. However, most of the data used to train the models are collected from experimental studies[31-36]. Only a few studies have relied on data from first-principles calculations to train ML algorithms. For example, Guo et al. made efforts to establish and train ML models using the formation energies and lattice constants obtained from first-principles calculations of the
To overcome the limitations posed by the inherent low efficiency in predicting the crystal structure and mechanical properties of the L12 phase using conventional first-principles calculations, a ML-accelerated first-principles approach is proposed in the present work. First, ML algorithms are established and trained using the data provided by conventional density functional theory (DFT) calculations. A small number of predictions made by these ML models are then validated by the first-principles calculations and the resulting dataset is used for improving the ML models if necessary. Finally, the models are employed to predict the crystal structure and mechanical properties of the L12 phase. These predictions may provide a theoretical basis for the design and discovery of new L12-strengthed Co-based superalloys. In particular, it is found that the efficiency of this ML-assisted method is twice as fast as that based on conventional first-principles calculations alone.
CALCULATION METHOD
Iterative three-stage computations
In order to obtain the crystal structure and mechanical properties of the new L12-strengthened Co-based superalloys more efficiently, ML algorithms are combined with first-principles calculations to predict the properties of the superalloys mentioned above in three steps.
Before attempting to use ML algorithms, it is necessary to conduct a detailed analysis of the first-principles calculations to determine the concept of establishing the ML models, as shown in Figure 1. First, the types of TM dopants contained in the supercells are assumed and the relaxed structures of the L12 phase and its competing D019 phase are calculated through relaxation optimization. Second, the occupation tendency of the TM dopants in the L12 and D019 phases is evaluated to determine the occupancy that is defined as the site in a supercell occupied by a TM dopant in these two phases. Third, the stabilities of the L12 and D019 phases are compared in terms of the stable formation enthalpy, followed by the calculation of the mechanical properties for the L12 phase if it is more stable than the D019 phase.
Figure 1. Schematic workflow of ML-assisted first-principles calculations for designing L12-strengthened Co-based superalloys.
In this study, we propose a new type of approach for predicting the L12 phase crystal structure and mechanical properties based on ML algorithms in new Co-based superalloys in three steps, namely, occupied sites, stability prediction and mechanical property prediction, similar to the procedures of first-principles calculations mentioned above. Since the reaction energy and enthalpy of formation between different superalloy systems are incomparable numerically, the classification algorithm in ML should be selected to make a qualitative judgment rather than a quantitative prediction when predicting the occupancy of the doped TM atoms and the stability of the doped L12 and D019 phases.
First-principles calculations
Details of first-principles calculations
First-principles calculations are employed to generate data for training the ML model and verifying the ML model predictions, so as to improve the ML model iteratively. The details of the first-principles calculations are briefly summarized below. Generally, first-principles calculations can only deal with a completely ordered phase. If a completely ordered structure can be found and the correlation function of the structure is close to that of a disordered alloy, it is considered that the structure can reflect the configuration of the disordered alloy and the structure is used as the cell model of the disordered alloy in the calculation. The essence of the special quasi-random structure (SQS) method is to find a completely ordered structure to represent the disordered structure by matching the correlation function[38,39]. Therefore, we use the SQS method to construct 2 × 2 × 2 supercells of the Co-based superalloys and consider two types of structures for the Co-Al-W-, Co-V-Ti-, Co-V-Ir-, Co-V-Ta- and Co-Al-V-based systems, namely, the AuCu3 and Ni3Sn prototype structures corresponding to the L12 and D019 phases, respectively[39,40] (see Figure 2 for the L12 and D019 structures). In addition, the Alloy Theoretic Automated Toolkit (ATAT) is used to identify the nonequivalent positions in the supercells[41].
Figure 2. Crystal structures of (A) Co3(Al, W); (B) Co3(V, Ti); (C) Co3(V, Ir); (D) Co3(V, Ta) and (E) Co3(Al, V) of L12-ordered γ'-Co3(X, Y); and (F) Co3(Al, W); (G) Co3(V, Ti); (H) Co3(V, Ir); (I) Co3(V, Ta) and (J) Co3(Al, V) of D019-ordered γ'-Co3(X, Y). Sites #1, #2 and #3 represent Co and the X and Y dopants, respectively.
The Vienna Ab initio Simulation Package (VASP) is used to perform all the first-principles calculations with the projector augmented wave (PAW) method[42-46] and Perdew-Burke-Ernzerhoff (PBE) exchange-correlation functional using the generalized gradient approximation (GGA)[23]. During the structural relaxation, the criteria for the convergence of energy and maximum force are set to be 10-5 eV/atom and 10-3 eV/Å, respectively. The kinetic energy cutoff is set to 450 eV. Spin polarization is considered during the calculations because of the presence of the ferromagnetic Co. The Brillouin zones are sampled using
Reaction and stable formation energies of L12 and D019 structures
Determining the occupancy of the TM dopants in the L12 phase is a vital prerequisite for obtaining an accurate atomic configuration. The occupancy of an alloying element can be evaluated using the binding[23] and formation energies of the impurity[47]. Each system calculated contains three main elements, each of which is designated according to the name of the alloy system. For instance, Co, Al and W are the main elements #1, #2 and #3 in the Co-Al-W system, respectively. In order to discover the role played by each TM element, the reaction energy 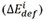 of the 3d, 4d or 5d TM element occupying sites #1, #2 and #3 in the supercells of each system is calculated as follows[48,49]:
of the 3d, 4d or 5d TM element occupying sites #1, #2 and #3 in the supercells of each system is calculated as follows[48,49]:
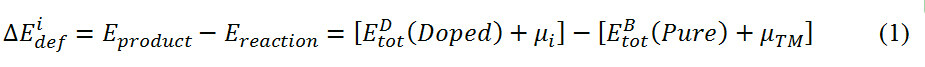
where 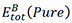 represents the energy of Co3(X, Y),
represents the energy of Co3(X, Y),  denotes the energy of TM-doped Co3(X, Y) and µi and µTMrepresent the chemical potential of the ith main and TM elements, respectively. The doping elements are energetically favorable to occupy the position(s) with the lowest reaction energy. Under Co-rich conditions, µCo denotes the energy of Co in the ground state[50]. Since we choose Co, CoAl, Co3W, Co3Ti, CoV3 and Co3Ta as reference compounds, µAL, µw, µTi, µTaandµVare calculated from the following relationships, respectively:
denotes the energy of TM-doped Co3(X, Y) and µi and µTMrepresent the chemical potential of the ith main and TM elements, respectively. The doping elements are energetically favorable to occupy the position(s) with the lowest reaction energy. Under Co-rich conditions, µCo denotes the energy of Co in the ground state[50]. Since we choose Co, CoAl, Co3W, Co3Ti, CoV3 and Co3Ta as reference compounds, µAL, µw, µTi, µTaandµVare calculated from the following relationships, respectively:
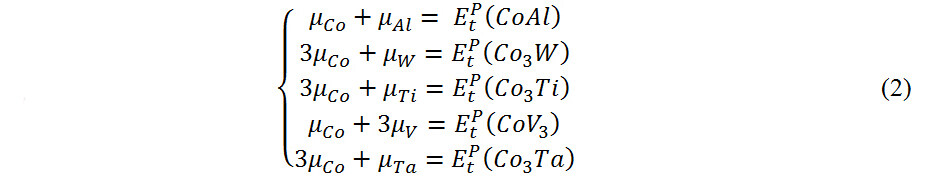
The stability of the L12 phase is then evaluated by comparing the stable formation enthalpy ΔHSof the TM-doped L12 and D019 phases, which can be calculated as follows[49,51]:
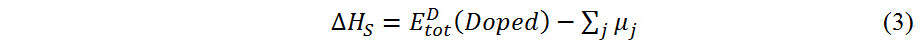
where µj is the chemical potential of element j.
Elastic properties from first-principles calculations
Elastic properties, such as the bulk (B), shear (G) and elastic moduli (E), can be calculated from the elastic constants, which can be computed according to the stress-strain energy curve method[52-56]. The calculation methods are presented in the Supporting Information (SI).
ML method
Dataset
The data for the L12 phase in the new Co-based superalloys with TM alloying elements are first generated by first-principles calculations. A total of 61 data from the Co-Al-W-, Co-V-Ti- and Co-V-Ir-based systems are collected for constructing a training set, which are all included in Supplementary Table 1[49,57]. The characteristics of the data are described briefly as follows:
(1) The microscopic characteristics of the elements are used to replace the names of the main and doping elements, including the melting point, boiling point, density, atomic weight, atomic radius, covalent radius, electronegativity and first ionization energy;
(2) For the occupancy prediction model, the microscopic characteristics of the main and doping elements are set as X and the occupancy of the doping elements are set as Y in the occupied site prediction models;
(3) For the L12 phase stability prediction model, the microscopic characteristics of the main and doping elements and the occupancy of the doping elements are set as X and the L12 phase stability is set as Y in the stability prediction models;
(4) For the mechanical properties of the L12 phase prediction model, the microscopic characteristics of the main and doping elements, the occupancy of the doping elements and the L12 phase stability are set as X and the mechanical properties are set as Y in the mechanical property prediction models of the L12 phase.
There are two research routes of choice:
Route I: Predict C11, C12 and C44 and then calculate the elastic properties, including B, G and E, according to Eqs. (1)-(10) in the SI;
Route II: Predict elastic properties, including B, G and E, directly.
ML model selection and performance evaluation
According to the “no free lunch” theory[58], no algorithm can be applied to all situations, i.e., one algorithm (algorithm A) outperforms another (algorithm B) on a specific data set and therefore algorithm A will be inferior to algorithm B on another specific data set. As a result, a variety of ML algorithms are first employed to predict the crystal structure and mechanical properties of the L12 phase, followed by a model performance evaluation and comparison. The algorithm with the best performance is selected for making predictions.
Random forest classification, gradient boosting classification (GBC), AdaBoost classification, a support vector machine, an artificial neural network (ANN), K-nearest neighbor classification and Gaussian process classification are selected to establish the classification models. In contrast, regression models are established using random forest regression, gradient boosting regression, AdaBoost regression, support vector regression, an ANN, K-nearest neighbor regression and Gaussian process regression.
All the ML algorithms are run through Python 3.0 and the sklearn package is used to carry out the calculations. All calculations are performed using a PC (Microsoft Windows 10, Intel Core (TM) i7-10875H, CPU 2.30 GHz, 16 GB of RAM).
The performance of the various ML algorithms mentioned above is compared using the K-fold cross-validation method. Since the test results of the K-fold cross-validation do not depend on the training set, the occurrence of overfitting can be avoided. The original data set is randomly divided into K equal subsets. One of the subsets is used as the test set, while the remaining ones consist of a new training set. Each subset should be used as a verification data set in turn, i.e., the above process is repeated K times. In this study, K is set to be ten[59,60].
The performance of a classification model is quantified by the so-called “accuracy”, which is the ratio of the total number of samples divided by the number of correct predictions, defined as:
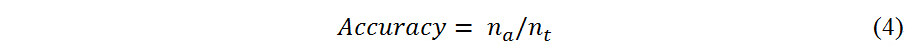
where ntand narepresent the total number of samples and the number of correct predictions, respectively. The criteria of accuracy need to be higher than 85%.
In this study, a principal component analysis (PCA) algorithm is also employed to reduce the dimensionality of the data. PCA is a statistical process that uses orthogonal transformation method to convert a series of observations of possible related variables into a set of linear independent variables referred to as principal components. A new feature vector 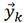 is defined by the following linear transformation:
is defined by the following linear transformation:
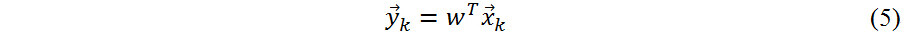
where WTis a matrix with orthonormal columns and 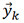 has fewer rows than
has fewer rows than 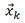 . The first three principal components are used to represent most of the information contained in more than 25 features[60,61].
. The first three principal components are used to represent most of the information contained in more than 25 features[60,61].
Several accuracy metrics, such as the coefficient of determination R, R2, mean absolute error (MAE) and root mean squared error (RMSE), were evaluated for the ML algorithms[26,60]:

where Y and 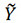 denote the true and predicted values of the targeted properties, respectively, n is the number size of the data, R value falls between (-1,1) and thus R2value falls within (0,1). The closer the value of R is to 1, the better the performance of the model prediction. MAE reflects the true error, while RMSE is more sensitive to outliers. A larger MAE value or a smaller RMSE value indicates that the model is under-fitting. The criteria of the R value need to be higher than 0.90, while the MAE and RMSE values are lower than 7.50 and 10.00, respectively.
denote the true and predicted values of the targeted properties, respectively, n is the number size of the data, R value falls between (-1,1) and thus R2value falls within (0,1). The closer the value of R is to 1, the better the performance of the model prediction. MAE reflects the true error, while RMSE is more sensitive to outliers. A larger MAE value or a smaller RMSE value indicates that the model is under-fitting. The criteria of the R value need to be higher than 0.90, while the MAE and RMSE values are lower than 7.50 and 10.00, respectively.
We evaluated the importance of the features with the relative importance (Ir) to measure the impact of these features on the occupancy of each doping element and the stability and mechanical properties of the L12 structure and it is given by:
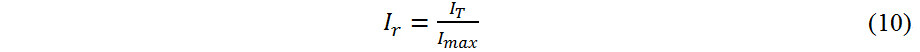
where IT is the importance of the feature calculated by the model and Imax is the highest importance calculated by the model among all the features. The values of Ir lie between 0 and 1.
Iterative ML model improvement
The performance of the selected ML algorithms is then iteratively improved through the interaction with the first-principles calculations. First, the selected algorithm is used to predict the target properties for a small amount of randomly chosen input data. Second, the predictions are verified using first-principles calculations. Third, if the accuracy of the models does not meet the requirements, the new data will be used as an additional dataset for re-training the ML model. The procedures above are repeated until the predefined precision is met. The improved models are then employed to predict all the remaining data (the workflow is schematically shown in Supplementary Figure 1).
RESULTS AND DISCUSSION
Establishment of ML models for predicting crystal structure and mechanical properties
Predicting dopant occupancy and stability of L12 structures
The occupancy of a TM dopant may significantly influence both the stability and mechanical properties of the L12 phase in Co-based superalloys[62]. In new Co-based superalloys, the D019 phase usually competes against the L12 phase[49]. The performance of various ML algorithms for predicting the dopant occupancy and stability of the L12 structures are evaluated using 10-fold cross-validation and the results are shown in Figure 3. The gradient boosting algorithm is found to have the highest accuracy (reaching 88.52% and 93.44% for occupancy and stability predictions, respectively) and is thus selected for predicting these two properties. The PCA classification results regarding the effect of TM dopant occupancy and the stability of L12 are shown in Figure 3 and their interpretation degrees are 92.05% and 93.44%, respectively. All the parameters of the ML algorithm are shown in Supplementary Table 2.
Figure 3. Ranking of prediction accuracies of (A) dopant occupancy and (B) L12 phase stability by different models. The GBC model has the highest accuracy (up to 88.52% and 93.44%, respectively). Prediction results of (C) occupied sites and (D) L12 phase stability from the model based on the GBC algorithm on the training set. Three features (main features #1, #2 and #3) are selected out of 25 using PCA for visualization (accuracy is 88.52%).
Predicting mechanical properties of L12 structure
The mechanical properties of the L12 phase in the new Co-based superalloys are the most important indicators of alloy properties. There are two routes for predicting them, as shown in Supplementary Figure 2. Route I sets C11, C12 and C44 as Y and calculates the mechanical properties, including B, G and E. Route II directly computes the mechanical properties, including B, G and E.
Route I: We start by presenting the results using route I. The performances of each regression algorithm are shown in Supplementary Figure 1. AdaBoost is found to outperform the others in predicting C11 and C44, considering the highest R values of 0.8880 and 0.8726 with the lowest MAE values of 7.5720 and 3.1180 and the lowest RMSE values of 10.110 and 3.9663, respectively. The performance of each ML model in predicting C12is relatively poor since its highest R value only reaches 0.6628 (see Supplementary Figure 3A-F). Supplementary Figure 3G-I show the prediction results of the AdaBoost regression model for C11, C12 and C44, which further proves that the prediction accuracy of the C12 model is low. B, G and E are calculated by C11, C12and C44, and because of the low accuracy of C12, the error of the B, G and E values calculated by the equations will be further amplified. Therefore, it is not needed to show the results of B, G and E.
Route II: Next, we present the results of the mechanical property predictions using route II. The performances of each ML algorithm are shown in Figure 4A-F. Compared with the rest of the ML models, the AdaBoost regression model has the best performance for B, G and E, with the highest R values of 0.8372, 0.9364 and 0.9354, the lowest MAE values of 2.4108, 1.8235 and 4.1253 and the lowest RMSE values of 5.1536, 2.5603 and 6.0385, respectively. The results of the predictions made using the AdaBoost regression algorithm are shown in Figure 4G-I.
Figure 4. Model performance of each regression model in terms of R, R2, MAE and RMSE on the training set by 10-fold cross-validation (route II): (A) R and R2 and (B) MAE and RMSE of bulk modulus (B); (C) R and R2 and (D) MAE and RMSE of shear modulus (G); (E) R and R2 and (F) MAE and RMSE of elastic modulus (E). Prediction results of mechanical properties of L12 phase in Co-based superalloys based on AdaBoost regression model (route II). The x-axis represents the true value and the y-axis represents the predicted value. When the true value is equal to the predicted value, the data will be distributed on a dashed line that passes through the origin and the slope of the dashed line is 1: (G) B; (H) G; (I) E.
Selection between two routes: Figure 5 compares the performance of the two routes. It can be found that the precision of C12 is relatively low and its highest R value only reaches 0.6628 in route I. The error of C11 is relatively large and its lowest MAE and RMSE values are 7.5720 and 10.110, respectively, which are much larger than those of other mechanical property prediction models. The value errors of B, G and E were calculated based on the predicted C11, C12 and C44 values using Eqs. (7)-(12) will be further enlarged. Therefore, the prediction results of C11, C12 and C44 are not discussed below.
Figure 5. Comparison of model performance of two routes based on Adaboost regression models. The warm color system (including vermeil, red and orange bars) represents the model performance of route I, while the cool color system (including blue, turquoise and cyan bars) represents the model performance of route II. (A) R and R2 of Adaboost regression models. (B) MAE and RMSE of Adaboost regression models.
Feature importance
The relative importance of different features on the dopant occupancy, stability of the L12 structures and the mechanical properties of the L12 phase are extracted from the gradient boosting classification and AdaBoost regression models, as shown in Figure 6. The names of the features are too long to be directly reflected in the figure and we therefore use codes to represent the full feature names, which are provided in Supplementary Table 3.
Figure 6. Calculated relative importance of different features on (A) dopant occupancy prediction based on gradient boosting classification model; (B) the stability of L12 structure prediction based on gradient boosting classification model; (C) bulk modulus prediction based on Adaboost regression model; (D) shear modulus prediction based on Adaboost regression model and (E) elastic modulus prediction based on Adaboost regression model. The ranking of the features is in accord with the related references.
The first ionization energy and electronegativity quantify the attraction between atoms and affect the distortion of the supercell, and are thus capable of evaluating the occupancy of a dopant in the supercell[63]. The covalent radius of a dopant affects the stability of the supercell[62]. The melting and boiling points of a dopant and the mechanical properties (such as bulk, shear and elastic moduli[64]) are correlated. It can be seen from Figure 6A that the values of relative importance for the electronegativity and the first ionization energy of the dopant are the highest, indicating that these two features predominantly determine the occupancy of the doped atom. Similarly, Figure 6B shows that the covalent radius and the first ionization energy of the dopant determine the stability of the L12 phase. Figure 6C indicates that the melting and boiling points of the dopant have the greatest influence on the mechanical properties, including the bulk, shear and elastic moduli.
Application of ML models for Co-based superalloys
The L12 phase exists at high temperatures in the Co-Al-W-, Co-V-Ti- and Co-V-Ir-based systems[1,6,65]. Building a new alloy system based on the properties of the major alloying elements is highly desirable. Ta can increase the L12 solvus temperature, while V can improve the strength of the alloy[66-68]. Herein, the trained ML models are employed to predict the crystal structure and mechanical properties of the L12 phase in new alloy systems containing V and Ta elements, such as the Co-V-Ta- and Co-Al-V-based systems. The prediction precision of the ML models without information for the Co-V-Ta- and Co-Al-V-based systems is usually low, so it is necessary to modify the models. The ML model modification precision is shown in Table 1.
Precision standard of ML model modification
| Prediction model | Indicator | Precision requirement of three pieces of data |
| Dopant occupancy models | Accuracy | 100% |
| L12 phase stability prediction models | Accuracy | 100% |
| Mechanical property prediction models | R | > 0.9 |
| MAE | < 5 | |
| RMSE | < 5 |
Co-V-Ta- and Co-Al-V-based systems
A rule is established where each round of random calculation verifies three data points for evaluating the model performance. In order to verify the prediction capability of the model for an unknown system, the calculated results of the Co-V-Ta-based system are added to the previous trained models as a new training set and the optimized models are used to predict the new Co-Al-V-based system. Through one round of iteration, the accuracy of the ML model for predicting dopant occupancy in the Co-V-Ta-based system is improved from 66.67% to 100%. The accuracy of the prediction in the Co-Al-V-based system reaches 100%, i.e., the model does not need to be modified. In addition, in order to verify the generalization ability of the ML model, we use first-principles calculations to compute the rest of the data that have not yet been verified. The results are compared with those predicted using the improved ML model. The results show that the prediction accuracy is improved from 80.00% to 95.00% for the Co-V-Ta-based system after only one-time model optimization. The accuracy of the Co-Al-V-based system is 95.24%. The PCA classification effect of the model is shown in Figure 7. The interpretation degrees of the Co-V-Ta- and Co-Al-V-based systems are 88.37% and 88.51%, respectively.
Figure 7. PCA classification result of occupied site prediction model based on GBC algorithm after one round of modification: (A) original Co-V-Ta-based system (accuracy reaches 80.00%); (B) modified Co-V-Ta-based system (accuracy reaches 95.00%); (C) original Co-Al-V-based system (accuracy reaches 95.24%).
The accuracy of the ML model for predicting the L12 phase stability in the Co-V-Ta-based system is improved from 66.67% to 100% through a one-round iteration. The accuracy of the prediction in the Co-Al-V-based system reaches 100%, i.e., the model does not need to be modified. As before, we use first-principles calculations to compute the rest of the data that have not yet been verified. The verified results show that the accuracy of model prediction in the Co-V-Ta-based system after one round of iteration is improved from 70.00% to 95.00%. The results show that the model predictions in the Co-Al-V-based system are all correct. The display effect of the PCA classification effect of the models is shown in Figure 8. The interpretation degrees of the Co-V-Ta- and Co-Al-V-based systems are 88.37% and 89.12%, respectively. It can be found that the modified gradient boosting algorithm is capable of making accurate predictions for both the occupancy of TM dopants and the stability of the L12 phase for both the Co-V-Ta- and Co-Al-V-based systems.
Figure 8. Display effect of PCA classification effect of L12 phase stability prediction model based on GBC algorithm after one round of modification: (A) original Co-V-Ta-based system (accuracy reaches 70.00%); (B) modified Co-V-Ta-based system (accuracy reaches 95.00%); (C) original Co-Al-V-based system (accuracy reaches 100%).
The iterative processes for improving the accuracy of the ML for predicting the mechanical property L12 phase are shown in Supplementary Figure 4. It can be found that the accuracy of model prediction is significantly improved.
The optimization processes of the ML models for predicting the mechanical properties of the L12 phase in the Co-V-Ta- and Co-Al-V-based systems are shown in Supplementary Figures 5 and 6, respectively. For a small amount of predicted data, it can be seen that the performance of the B, G and E models is significantly improved after only two rounds of model optimization. Specifically, through model optimization, the R values of B, G and E increase from 0.51937, 0.74161 and 0.9849 to 0.9852, 0.9801 and 0.9988, respectively. The MAE values of B, G and E decrease from 16.086, 13.693 and 31.824 to 1.5217, 1.2534 and 1.0340, respectively. The RMSE values decrease from 16.587, 13.729 and 31.858 to 1.8555, 1.4714 and 1.6157, respectively. The prediction accuracy of the B and G prediction models is low and the error of the E prediction model is relatively large before the models are modified. Compared with the Co-V-Ta-based system, the model performance of B, G and E can be greatly improved after only one round of modification. The R values of B, G and E increase from 0.9156, 0.7714 and 0.7807 to 0.9214, 0.9219 and 0.9981, respectively. The MAE values of B, G and E decrease from 13.283, 16.779 and 38.252 to 2.7629, 3.5654 and 4.3063, respectively. The RMSE values decrease from 13.398, 17.206 and 39.315, to 3.2245, 4.6005 and 4.7053, respectively. The prediction accuracy of the G prediction models is low and the error of the E prediction model is relatively large before the models are modified. In order to verify the generalization ability of the ML model, we calculate all the remaining data and verify the ML prediction results after two rounds of modification.
Figure 9 shows the overall prediction results of the modified mechanical performance models of the Co-V-Ta- and Co-Al-V-based systems and their model performances are shown in Figure 10. For the Co-V-Ta-based system, the R values of the B, G and E prediction models are 0.9556, 0.9114 and 0.9527, respectively, the MAE values are 2.4105, 1.8124 and 4.7547, respectively, and the RMSE values are 2.9600, 2.1988 and 5.6657, respectively. For the Co-Al-V-based system, the R values of the B, G and E prediction models are 0.9241, 0.9369 and 0.9369, respectively, the MAE values are 2.6882, 3.6844 and 6.4382, respectively, and the RMSE values are 3.4099, 4.4704 and 8.2324, respectively. Compared with the Co-V-Ta-based system, the modified Adaboost regression models have better prediction performance for the Co-Al-V-based system, which further proves that the ML model is capable of predicting the crystal structure and mechanical properties of the L12 phase in new Co-based superalloys.
Figure 9. Overall prediction results of modified mechanical performance models: (A) B; (B) G and (C) E of Co-V-Ta-based system; (D) B; (E) G and (F) E of Co-Al-V-based system.
Comparison of time cost and mechanical properties
It takes about two days for traditional first-principles calculations to compute a data point, while establishing a ML model requires five days. However, it takes less than a minute for the trained ML models to predict the calculation results. By comparing the calculation amount and time between the modified ML models and the traditional first-principles calculations, we find the prediction method based on ML algorithms can improve the calculation efficiency by more than double using the modified ML model, as shown in Table 2.
Comparison of time costs for first-principles calculations alone and ML-accelerated first principles calculations
| Task | Time | |
| Traditional DFT method | First-principles calculations | 92 days |
| ML-accelerated method | First-principles calculations | 22 days |
| Establish ML models | 5 days | |
| ML prediction | 1 minute | |
| Total | 27 days |
Comparison of the predicted B, G and E values for the Co-V-Ta-X and Co-Al-V-X systems with those for previous Co-Al-W-X and Co-V-Ti-X systems are shown in Figure 11. It can be seen that the mechanical properties of the Co-V-Ta-X and Co-Al-V-X system are generally higher than those of Co-Al-W-X and Co-V-Ti-X systems, except for the cases with Y, Zr and Re dopants. Using ML algorithms combined with first-principles calculations, two new systems (Co-V-Ta-X and Co-Al-V-X) with better mechanical properties than the previous systems are successfully and efficiently proposed.
SUMMARY
This work aims to address the challenges encountered by the traditional experimental approaches and first-principles calculation methods for the discovery of new Co-based superalloys (strengthened by L12 ordered precipitates), both of which are inefficient, time-consuming and labor-intensive when used alone.
A new approach is proposed that combines machine learning (ML) and first-principles calculations to speed up the prediction of crystal structure, phase stability and mechanical properties for systems, such as Co-V-Ta- and Co-Al-V-based alloys. This information is critical for developing new Co-based superalloys with superior properties at elevated temperatures. ML models are established and trained for predicting the site occupancy, phase stability and mechanical properties. Through iterative interactions between model predictions and validations using first-principles calculations, the ML models are further improved. Finally, the refined models are used to make accurate predictions for the crystal structure and mechanical properties for Co-V-Ta- and Co-Al-V-based systems.
The combination of ML and first-principles calculations may shed light on the rapid prediction of crystal structure and mechanical properties of other advanced materials beyond Co-based alloys.
DECLARATIONS
Author’s contributionsProject conception: Liu X, Wang C
Calculation task: Xi S, Yu J
Analysis: Xi S, Yu J, Bao L
Investigation: Xi S, Yu J, Bao L, Chen L, Li Z, Shi R
Draft Preparation: Xi S, Yu J, Shi R
Supervision: Liu X
Availability of data and materialsNot applicable.
Conflict of InterestAll authors declare that there are no conflict of interest.
Financial support and sponsorshipThis work was supported by the National Key R&D Program of China (No. 2020YFB0704503), the National Natural Science Foundation of China (Grant No. 52001098 and Grant No. 51831007), and the Key-Area Research and Development Program of GuangDong Province (Grant No. 2019B010943001), as well as the open research fund of Songshan Lake Materials Laboratory (2021SLABFK06).
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The author(s) 2022.
Supplementary MaterialsREFERENCES
1. Sims C. , Stoloff N., Hagel W. Superalloys II: High-temperature materials for aerospace and industrial power; 1987. Available from: https://www.researchgate.net/profile/James-Smialek/publication/283993132_High_Temperature_Oxidation_in_Superalloy/links/5829db5e08ae138f1bf2f305/High-Temperature-Oxidation-in-Superalloy.pdf [Last accessed on 14 Sep 2022].
2. Ruan J, Xu W, Yang T, et al. Accelerated design of novel W-free high-strength Co-base superalloys with extremely wide γ/γʹ region by machine learning and CALPHAD methods. Acta Materialia 2020;186:425-33.
3. Zhao S, Xie X, Smith GD, Patel SJ. Research and Improvement on structure stability and corrosion resistance of nickel-base superalloy INCONEL alloy 740. Mater Des 2006;27:1120-7.
5. Zhu J, Titus MS, Pollock TM. Experimental investigation and thermodynamic modeling of the Co-rich region in the Co-Al-Ni-W quaternary system. J Phase Equilib Diffus 2014;35:595-611.
6. Sato J, Omori T, Oikawa K, Ohnuma I, Kainuma R, Ishida K. Cobalt-base high-temperature alloys. Science 2006;312:90-1.
7. Miura S, Ohkubo K, Mohri T. Mechanical properties of Co-based L12 intermetallic compound Co3(Al,W). Mater Trans 2007;48:2403-8.
8. Kobayashi S, Tsukamoto Y, Takasugi T, et al. Determination of phase equilibria in the Co-rich Co-Al-W ternary system with a diffusion-couple technique. Intermetallics 2009;17:1085-9.
9. Yu Y, Wang C, Liu X, Ohnuma I, Kainuma R, Ishida K. Experimental determination of phase equilibria in the Co-Ti-Mo ternary system. Intermetallics 2008;16:1199-205.
10. Yao Q, Shang S, Hu Y, et al. First-principles investigation of phase stability, elastic and thermodynamic properties in L12Co3(Al,Mo,Nb) phase. Intermetallics 2016;78:1-7.
11. Qiang Y, Shang S, Kang W, et al. Phase stability, elastic, and thermodynamic properties of the L12(Co,Ni)3(Al,Mo,Nb) phase from first-principles calculations. J Mater Res 2017;32:1-9.
12. Kobayashi S, Tsukamoto Y, Takasugi T. Phase equilibria in the Co-rich Co-Al-W-Ti quaternary system. Intermetallics 2011;19:1908-12.
13. Kobayashi S, Tsukamoto Y, Takasugi T. The effects of alloying elements (Ta, Hf) on the thermodynamic stability of γ′-Co3(Al,W) phase. Intermetallics 2012;31:94-8.
14. Makineni S, Samanta A, Rojhirunsakool T, et al. A new class of high strength high temperature Cobalt based γ-γ′ Co-Mo-Al alloys stabilized with Ta addition. Acta Materialia 2015;97:29-40.
15. Makineni S, Nithin B, Chattopadhyay K. A new tungsten-free γ-γ’ Co-Al-Mo-Nb-based superalloy. Scripta Materialia 2015;98:36-9.
16. Makineni S, Nithin B, Chattopadhyay K. Synthesis of a new tungsten-free γ-γ′ cobalt-based superalloy by tuning alloying additions. Acta Materialia 2015;85:85-94.
17. Makineni SK, Nithin B, Palanisamy D, Chattopadhyay K. Phase evolution and crystallography of precipitates during decomposition of new “tungsten-free” Co(Ni)-Mo-Al-Nb γ-γ′ superalloys at elevated temperatures. J Mater Sci 2016;51:7843-60.
18. Chinen H, Omori T, Oikawa K, Ohnuma I, Kainuma R, Ishida K. Phase Equilibria and Ternary Intermetallic Compound with L12 Structure in Co-W-Ga System. J Phase Equilib Diffus 2009;30:587-94.
19. Chinen H, Sato J, Omori T, et al. New ternary compound Co3(Ge,W) with L12 structure. Scripta Materialia 2007;56:141-3.
20. Zenk CH, Povstugar I, Li R, et al. A novel type of Co-Ti-Cr-base γ/γ′ superalloys with low mass density. Acta Materialia 2017;135:244-51.
21. Im HJ, Makineni SK, Gault B, Stein F, Raabe D, Choi P. Elemental partitioning and site-occupancy in γ/γ′ forming Co-Ti-Mo and Co-Ti-Cr alloys. Scripta Materialia 2018;154:159-62.
22. Chen M, Wang C. First-principles investigation of the site preference and alloying effect of Mo, Ta and platinum group metals in γ′-Co3(Al,W). Scri Mater 2009;60:659-62.
23. Chen M, Wang C. First-principle investigation of 3d transition metal elements in γ′-Co3(Al,W). J Appl Phys 2010;107:093705.
24. Mao Z, Booth-morrison C, Sudbrack CK, Noebe RD, Seidman DN. Interfacial free energies, nucleation, and precipitate morphologies in Ni-Al-Cr alloys: calculations and atom-probe tomographic experiments. Acta Materialia 2019;166:702-14.
25. Xu W, Shang S, Wang C, et al. Accelerating exploitation of Co-Al-based superalloys from theoretical study. Mater Des 2018;142:139-48.
26. Yu J, Wang C, Chen Y, Wang C, Liu X. Accelerated design of L12-strengthened Co-base superalloys based on machine learning of experimental data. Mater Des 2020;195:108996.
28. Raccuglia P, Elbert KC, Adler PD, et al. Machine-learning-assisted materials discovery using failed experiments. Nature 2016;533:73-6.
29. Pilania G. Machine learning in materials science: From explainable predictions to autonomous design. Comp Mater Sci 2021;193:110360.
30. Yu J, Xi S, Pan S, et al. Machine learning-guided design and development of metallic structural materials. J Mater Inf 2021;1:9.
31. Liu P, Huang H, Antonov S, et al. Machine learning assisted design of γ′-strengthened Co-base superalloys with multi-performance optimization. npj Comput Mater 2020:6.
32. Swetlana S, Khatavkar N, Singh AK. Development of Vickers hardness prediction models via microstructural analysis and machine learning. J Mater Sci 2020;55:15845-56.
33. Ruan J, Liu X, Yang S, et al. Novel Co-Ti-V-base superalloys reinforced by L12-ordered γ′ phase. Intermetallics 2018;92:126-32.
34. Zou M, Li W, Li L, Zhao J, Feng Q. Machine learning assisted design approach for developing γ′-strengthened Co-Ni-base superalloys. 2020.
35. Li W, Li L, Antonov S, Wei C, Zhao J, Feng Q. High-throughput exploration of alloying effects on the microstructural stability and properties of multi-component CoNi-base superalloys. J Alloys Compd 2021;881:160618.
36. Tamura R, Osada T, Minagawa K, et al. Machine learning-driven optimization in powder manufacturing of Ni-Co based superalloy. Mater Des 2021;198:109290.
37. Guo J, Xiao B, Li Y, et al. Machine learning aided first-principles studies of structure stability of Co3(Al, X) doped with transition metal elements. Comp Mater Sci 2021;200:110787.
38. Zunger A, Wei S, Ferreira LG, Bernard JE. Special quasirandom structures. Phys Rev Lett 1990;65:353-6.
39. Jiang C. First-principles study of Co3(Al,W) alloys using special quasi-random structures. Scr Mater 2008;59:1075-8.
40. Asta M, Ozolins V, Woodward C. A first-principles approach to modeling alloy phase equilibria. JOM 2001;53:16-9.
41. de Walle A, Asta M, Ceder G. The alloy theoretic automated toolkit: a user guide. Calphad 2002;26:539-53.
42. Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys Rev B Condens Matter 1993;47:558-61.
43. Kresse G, Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys Rev B Condens Matter 1994;49:14251-69.
44. Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp Mater Sci 1996;6:15-50.
45. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B Condens Matter 1996;54:11169-86.
46. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B 1999;59:1758-75.
47. Dang H, Wang C, Shu X. Electronic structure of edge dislocation of core-doped Ti in Fe. Prog Nat Sci 2004;14:477-82.
48. Freysoldt C, Grabowski B, Hickel T, et al. First-principles calculations for point defects in solids. Rev Mod Phys 2014;86:253-305.
49. Xi S, Chen L, Bao L, et al. Effects of alloying elements on the atomic structure, elastic and thermodynamic properties of L12-Co3(V, Ti) compound. Mater Today Comm 2022;30:102931.
50. Xu W, Wang Y, Wang C, Liu X, Liu Z. Alloying effects of Ta on the mechanical properties of γ’ Co3(Al, W): A first-principles study. Scr Mater 2015;100:5-8.
51. Saal JE, Wolverton C. Thermodynamic stability of Co-Al-W L12 γ′. Acta Materialia 2013;61:2330-8.
52. Wang S, Ye H. Ab initio elastic constants for the lonsdaleite phases of C, Si and Ge. J Phys Condens Matter 2003;15:5307.
53. Shang S, Wang Y, Liu Z. First-principles elastic constants of α- and θ-Al2O3. Appl Phys Lett 2007;90:101909.
55. Anderson OL. A simplified method for calculating the debye temperature from elastic constants. J Phys Chem Sol 1963;24:909-17.
56. Chung DH, Buessem WR. The Voigt-Reuss-Hill (VRH) approximation and the elastic moduli of polycrystalline ZnO, TiO2 (Rutile), and α-Al2O3. J Appl Phys 1968;39:2777-82.
57. Liu X, Wang Y, Xu W, Han J, Wang C. Effects of transition elements on the site preference, elastic properties and phase stability of L12 γ′-Co3(Al, W) from first-principles calculations. J Alloys Compd 2020;820:153179.
58. Ho Y, Pepyne D. Simple explanation of the No-Free-Lunch theorem and its implications. J Optimiz The Appl 2002;115:549-70.
60. Yu J, Guo S, Chen Y, et al. A two-stage predicting model for γ′ solvus temperature of L12-strengthened Co-base superalloys based on machine learning. Intermetallics 2019;110:106466.
61. Belhumeur P, Hespanha J, Kriegman D. Eigenfaces vs. fisherfaces: recognition using class specific linear projection. IEEE Trans patt analys mach intell 1997;19:711-720.
62. Wang C, Zhang C, Wang Y, et al. Effects of transition elements on the structural, elastic properties and relative phase stability of L12 γ′-Co3Nb from first-principles calculations. Metals 2021;11:933.
63. Sanyal S, Waghmare UV, Hanlon T, Hall EL. Ni/boride interfaces and environmental embrittlement in Ni-based superalloys: a first-principles study. Mater Sci Engineer: A 2011;530:373-7.
64. Geng P, Li W, Zhang X, et al. A theoretical model for yield strength anomaly of Ni-base superalloys at elevated temperature. J Alloys Compd 2017;706:340-3.
65. Wang CP, Deng B, Xu WW, et al. Effects of alloying elements on relative phase stability and elastic properties of L12Co3V from first-principles calculations. J Mater Sci 2018;53:1204-16.
66. Bauer A, Neumeier S, Pyczak F, Göken M. Microstructure and creep strength of different γ/γ′-strengthened Co-base superalloy variants. Scr Mater 2010;63:1197-200.
67. Ruan J, Wang C, Yang S, et al. Experimental investigations of microstructures and phase equilibria in the Co-V-Ta ternary system. J Alloys Compd 2016;664:141-8.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.



























Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].