High-cycle fatigue S-N curve prediction of steels based on a transfer learning-guided convolutional neural network
Abstract
The evaluation and prediction of fatigue properties are crucial for metallic materials. Although the determination of S-N curves represents the most important methods for evaluating such properties, its fatigue testing is costly and time-consuming. Furthermore, fatigue testing involves different test conditions, thereby complicating the evaluation of the fatigue properties. This study develops a transfer convolutional neural network (TR-CNN) framework, in which the prediction of the reversed torsion S-N curves of steels is transferred from rotating bending S-N curves. In the TR-CNN framework, the source CNN models for rotating-bending curve prediction are first trained based on the composition and process conditions. Subsequently, based on the source models, the reversed torsion S-N curves are estimated by training the TR-CNN models based on only a small dataset. After proving the rationality of the framework, its universality with respect to different amounts of data is further investigated. The reversed torsion curves under small-sample conditions (22 samples) are predicted accurately by the TR-CNN. Additionally, the TR-CNN models remain accurate under varying amounts of data (22-112 samples), showing excellent generality for different amounts of fatigue data. The predictive capability of the TR-CNN models is improved by introducing tensile properties into the source models. The proposed TR-CNN framework can significantly reduce the cost of evaluating fatigue properties, and the prediction of S-N curves can be optimized by combining the transfer framework and low-cost properties related to fatigue.
Keywords
INTRODUCTION
The evaluation of the fatigue properties of metallic structural materials is of significant importance. The relationship between fatigue life and applied stress is the basis for fatigue analysis and anti-fatigue design, i.e., the stress-life approach. The resulting S-N curve is one of the most important methods to describe fatigue behavior. However, obtaining S-N curves via experimental testing remains costly and time-consuming. Furthermore, fatigue testing involves various test conditions, such as R-value and frequency, which further complicate the evaluation of fatigue properties. Therefore, modeling the prediction of S-N curves remains of significant interest.
Traditionally, various models have been developed for the prediction of fatigue properties. The Coffin–Manson and Basquin equations are two widely used classical models[1]. However, these models mainly rely on fitting of the testing data. Based on cumulative damage calculations[2-4], several models have been developed, such as the Palmgren–Miner linear damage rule, continuum damage mechanics, and energy-based models. Several models have also been developed based on the prediction of crack nucleation and growth[4-8]. Although they exhibit a high predictive ability, these models can only predict the lives of a limited number of alloys. The model parameters are usually determined experimentally or obtained from previous studies. Furthermore, most of the above models are again essentially based on fitting. Recently, the focus has been given to fatigue prediction using the unified mechanics theory (UMT) proposed by Basaran[9], which is a purely physics-based approach that does not require the fitting of an empirical evolution function[10,11]. The UMT has been validated for the fatigue prediction of metals in studies by Noushad et al.[12] and Egner et al.[13]. UMT-based models may represent a superior approach compared to traditional fitting-based fatigue models from a scientific point of view due to their combination of excellent accuracy and interpretability. Nonetheless, given the high cost of fatigue test data and the high demand for the rapid assessment of the fatigue properties of new materials, predictive models with better generality and practicability and the rapid assessment of fatigue without considering various parameters related to the mechanism are urgently required.
Some efforts have been made to directly build a relationship between material characteristics/loading conditions and fatigue properties via data-based machine learning (ML) to overcome the limitations of conventional models, as it does not require a clear knowledge of the mechanism[14-17]. For example, fatigue research based on ML has made significant progress in both fatigue strength prediction[18-24] and fatigue crack-driving force prediction[25]. Several researchers have recently developed ML-based models for fatigue life prediction[26-32]. Zhang et al. proposed a neuro-fuzzy-based ML method for predicting the high-cycle fatigue life of laser powder bed fusion stainless steel 316 L under different processing conditions, post-processing treatments, and cyclic stresses[26]. Similarly, Zhan et al. used several ML algorithms to establish models for predicting the fatigue life of 316 L with different additive manufacturing process parameters and fatigue loadings[27]. Furthermore, based on deep learning of long short-term memory networks, Yang et al. established a more general life-prediction method for the multiaxial fatigue of materials[30]. In a study by Maleki et al., a deep neural network was utilized for fatigue behavior prediction and analysis of a coated AISI 1045 mild carbon steel and AISI 316L stainless steel, which demonstrated a promising approach for deep learning in fatigue behavior modeling[31,32]. The above-mentioned works show that ML-based models present good applicability for the fatigue life prediction of different materials facing complex mechanisms and various conditions. However, few studies have focused on the continuous curves of fatigue performance, such as the S-N curve.
Recently, deep learning methods, such as convolutional neural networks (CNNs), have been applied to address the aforementioned problems. Kim et al. proposed a CNN-based prediction model of the transverse mechanical behavior (stress-strain curve) of unidirectional composites, with the predicted nonlinear curves showing excellent agreement with the results of finite element simulations[33]. Similarly, Yang et al. combined principal component analysis and CNNs to predict the entire stress-strain behavior of binary composites evaluated over the entire failure path[34]. Tu et al. proposed a predictive model combining the crystal plasticity finite element method and a deep neural network, which successfully predicted the stress-strain curve and yield strength of multi-phase additive manufactured stainless steels to within a 15% error[35]. Although the above studies achieved the accurate prediction of curves and demonstrated the excellent applicability of the CNN method, they were all based on large amounts of data (~1,000-100,000), which can be obtained based on computational approaches, such as finite element simulations. However, it is impractical to obtain such large amounts of data from fatigue testing for fatigue S-N curves. Specifically, at least hundreds of fatigue samples are required, meaning an unacceptable long-term cycle for data accumulation. Usually, only tens of existing curves are available for relatively new alloy systems, which is far from sufficient for training a reliable CNN model. Therefore, despite the promising prospects of CNNs, their further application in reliable fatigue prediction is inhibited by the lack of sufficient data and the high cost of additional data accumulation. The transfer learning concept may be introduced to address the aforementioned problem[36-40]. This concept can fully utilize the existing low-cost fatigue curves to handle small-sample curve prediction and has been previously applied to similar ML-based studies.
In this work, a transfer CNN (TR-CNN) predictive framework is proposed, in which the reversed torsion S-N curve prediction of low-alloy steels is transferred from the corresponding rotating bending S-N curves. In the framework, based on the source CNN models, which predict the rotating bending S-N curves with the steel composition and processing parameters as inputs (source task), the reversed torsion S-N curves are predicted by the TR-CNN models trained using only dozens of S-N curve examples (target task). The CNN approach in this framework is proven to be applicable for S-N curve prediction. The transfer method in the TR-CNN further helps to reduce the data requirements of the model and therefore reduces the cost of fatigue data accumulation, since a target S-N curve can be predicted using existing S-N curves and particularly low-cost data, like high-frequency fatigue.
MATERIALS AND METHODS
Dataset and data preprocessing
The Matnavi fatigue dataset built by the National Institute of Material Science (NIMS)[41] was used in the present work. In this dataset, the compositions, heat treatment conditions, and high-cycle S-N data of steels were recorded. Two datasets of rotating bending and reversed torsion fatigue, containing 411 and 141 samples, respectively, were collected. Each sample had 20 input features (composition and processing details) and a set of S-N data containing 13-20 data points. The complete datasets collected consist of data for carbon, low-alloy, spring, and stainless steel. The Matnavi dataset is high quality because all fatigue tests were performed at a single institution, with only small scattering within the data. Table 1 presents an overview of the dataset ranges.
Input and output ranges of various features in the database
| Inputs and outputs | Minimum | Maximum | Mean | Standard deviation | |
| Input | Carbon (wt.%) | 0.09 | 0.63 | 0.396 | 0.098 |
| Silicon (wt.%) | 0.16 | 2.05 | 0.306 | 0.254 | |
| Manganese (wt.%) | 0.32 | 1.6 | 0.825 | 0.289 | |
| Phosphorus (wt.%) | 0.004 | 0.031 | 0.017 | 0.005 | |
| Sulphur (wt.%) | 0.002 | 0.03 | 0.014 | 0.006 | |
| Nickel (wt.%) | 0.01 | 2.78 | 0.493 | 0.853 | |
| Chromium (wt.%) | 0.01 | 12.7 | 1.154 | 2.61 | |
| Copper (wt.%) | 0 | 0.26 | 0.061 | 0.049 | |
| Molybdenum (wt.%) | 0 | 0.24 | 0.061 | 0.085 | |
| Normalizing temperature (℃) | 30 | 900 | 820.47 | 188.76 | |
| Through hardening temperature (℃) | 30 | 975 | 833 | 136.5 | |
| Through hardening time (min) | 0 | 30 | 29.2 | 4.84 | |
| Cooling rate for through hardening (℃/s) | 0 | 24 | 11.76 | 7.15 | |
| Tempering temperature (℃) | 30 | 750 | 589.76 | 109.29 | |
| Tempering time (min) | 0 | 60 | 58.39 | 9.68 | |
| Cooling rate for tempering (℃/s) | 0 | 24 | 23.36 | 3.87 | |
| Reduction ratio (ingot to bar) | 289 | 5530 | 964.1 | 576.77 | |
| Area proportion of inclusions deformed by plastic work | 0 | 0.13 | 0.047 | 0.032 | |
| Area proportion of inclusions occurring in discontinuous array | 0 | 0.05 | 0.004 | 0.009 | |
| Area proportion of isolated inclusions | 0 | 0.06 | 0.009 | 0.012 | |
| Output | Rotating bending curves | 411 | |||
| Revered torsion curves | 141 |
For each set of S-N data, the data points were fitted to a curve based on the following equation from the JSMS-SD-6-04[42]:
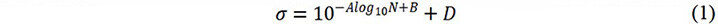
where σ represents the stress amplitude of loading, N represents the number of cycles to failure, and A, B and D are constants. Linear interpolation was further adopted to unify the data format before modeling. The cycle range of the fitted S-N curves was unified from 104 to 108. After interpolation, the curve containing 50 data points was regenerated, in which the stress amplitudes were evenly distributed along the logarithm of the cycles. Two sets of S-N data points in the dataset and the corresponding rotating bending and reversed torsion fitted curves are shown in Figure 1.
Figure 1. Preparation of S-N curves for two alloys in the dataset. Points and solid lines represent the S-N data points and fitted S-N curves, respectively.
For data preprocessing, the standard statistical z-score measurement for eliminating the dimensional differences of the features was used[43]. The inputs and outputs were normalized and the equation is given by:
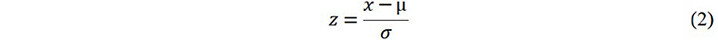
where z and x are the normalized and original values from the dataset, respectively, and µ and σ represent the mean and standard deviation of the original values for a certain dimensional feature, respectively. The importance of features on the rotating bending and reversed torsion curve prediction was investigated, which was measured by the mean decrease accuracy values for a random forest model. The results show that all input features have positive contributions to fatigue performance, as shown in Supplementary Figures 1 and 2. Therefore, further feature selection was not considered.
For the rotating-bending curves, a ratio of 4:1 was used to generate the training and testing sets from the dataset of 411 samples. Cross-validation was adopted to avoid the “lucky split” and the partitioning process was carried out randomly five times.
For the reversed torsion curves, from the initial dataset of 141 samples, 29 samples were selected as the validation set. Subsequently, 22 samples were randomly selected from the remaining 112 samples for TR-CNN model training and testing. Similarly, the above partitioning processes were carried out ten times randomly. In addition, to investigate the impact of data volumes on the predictive capability of the model, various subsets containing 33-112 samples were randomly selected for modeling. In the above cases, the same 4:1 ratio was used to generate the training and test sets.
Transfer CNN framework
In the present work, a TR-CNN framework was constructed, which treats the rotating bending S-N curves (source domain) as intermediate steps towards obtaining an estimate of the reversed torsion S-N curves (target domain). This process is schematically illustrated in Figure 2.
First, a source model for rotating-bending S-N curve prediction was trained via the CNN method using a relatively large dataset. In this model, twenty-dimensional features (compositions and processing parameters) reshaped into a 5 × 5 matrix were used as inputs of the CNN. For the reshaping process, the twenty-dimensional input values were sequentially filled into a 5 × 5 matrix and the value of the last five elements in the matrix was set to zero. The rotating bending S-N curve containing 50 data points formed the output.
Unlike some commonly used CNN model architectures, the complexity of the source CNN model was reduced by simplifying the architecture to adapt to small-sample characteristics. Furthermore, the pool layer was removed to reduce the loss of information during training. The sequence details of the layers in the source model are shown in Table 2. A 3 × 3 filter with was used and a dropout of 0.4 was considered to reduce overfitting.
Source CNN model architecture details
| Layer (type) | Shape |
| conv2d_1 (Conv2D) | (5, 5, 32) |
| conv2d_2 (Conv2D) | (5, 5, 64) |
| flatten_1 (Flatten) | 1600 |
| dense_1 (Dense) | 128 |
| dense_2 (Dense) | 64 |
| dropout_1 (Dropout) | 64 |
| dense_3 (Dense) | 50 |
A brief review of the calculation process of the CNN is provided. When the CNN is used in this work, the output volume of a convolutional layer is referred to as a feature map, since the purpose of these layers is to extract features from the input volume. The convolution operation can be written as:
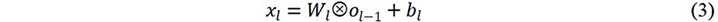
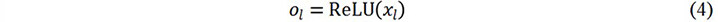
where ol-1 is the input volume of the lth convolutional layer or the output volume of the l-1th convolutional layer. The size of ol-1 is s × s × d, where s and d are the width and depth of the convolutional layer’s input volume, respectively. Wland blare the weight matrix and bias of the lth convolutional layer, respectively. At the end of each convolutional layer, an activation function is applied on the feature maps (xl) and then the output ol of the lth convolutional layer is obtained. A rectified linear unit (ReLU) is applied to the proposed CNN model as the nonlinear activation function, which can be expressed as:
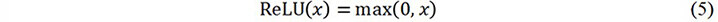
The feature map generated by the last convolutional layer is flattened into a vector. The vector is then fed to the first fully connected layer. The operation in the fully connected layer can be written as:

where the weight and bias of the kth fully connected layer are denoted by Wk and bk, respectively, and xk is the output of the lth fully connected layer. If a dropout is used, xk will go through the dropout layer. The final output of the model is further obtained via the output layer, which can be expressed as:
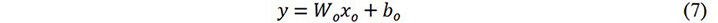
where Wo and bo are the weight matrix and bias of the last fully connected layer, respectively.
The target TR-CNN predictive model for reversed torsion curves was then constructed. The model was trained as follows: (1) Copy the convolutional layers and first fully connected layer of the source CNN model to the corresponding layers of the target TR-CNN model, which were called “transferred feature layers”. They remained frozen and did not participate in further training. (2) Initialize and train the remaining layers of the target TR-CNN model for fatigue strength prediction. For comparison, the corresponding NonTR-CNN (non-transfer) model was also trained. During training, the composition and processing parameters were directly coupled to the reversed torsion S-N curves without the rotating bending S-N curves as intermediate steps.
For the above CNN modeling, data preprocessing and model training were implemented using Keras and Scikit-learn. For training, the model was obtained after 1000 iterations, during which the loss function of the mean square error, a learning rate of 0.001, and the Adam optimizer were used.
The metrics used to evaluate the model performance are the mean absolute error (MAE) and squared correlation coefficient (R2), given by[16,44,45]:
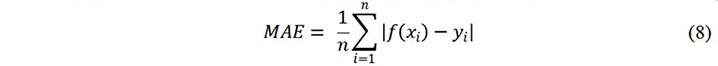
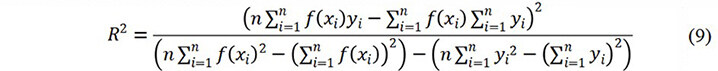
RESULTS
Prediction of rotating bending curves
Five CNN models were first built to predict the rotating-bending S-N curves based on the steel composition and processing parameters according to the transfer framework. Figure 3A shows the mean MAE results of the models for the training/testing sets. It is obvious that different partitions significantly affect the performance of the model. Therefore, it is important to select an appropriate model. Among these models, Model 2 exhibited the best prediction for the testing set and the lowest overfitting. Figure 3B presents the training history of Model 2. The training loss decreased rapidly with an increasing number of epochs and dropped to a low level after 50 epochs. Although there was slight overfitting, the loss for the test set was as low as 0.1 after 100 epochs and a sufficiently accurate model was obtained. Therefore, Model 2 was chosen as the source model for further modeling the reversed torsion curves in this study.
Figure 3. Performance of different source models. (A) MAE distribution of training set and testing set. (B) Training loss curves of source model.
Figure 4 shows a comparison between the predicted and actual S-N curves. The S-N curve prediction results for the eight systems chosen randomly from the training set are shown in Figure 4A and the corresponding results for the testing set are shown in Figure 4B. It can be observed that the predicted S-N curves are highly consistent with the actual curves. Similarly, the remaining curves in the dataset were also predicted accurately. In addition, fatigue strength is a significant property inferred from the S-N curve. The prediction results for the training and testing sets are shown in Figures 4C and D, respectively. The model performed well, with high R2 values of 99.46% and 96.22% for the training and testing sets, respectively. In summary, a reasonably accurate prediction was achieved based on the source CNN model, which demonstrates its excellent prediction capability and high applicability to fatigue curve modeling.
Prediction of reversed torsion curves
The TR-CNN models for the reversed torsion curves were further trained based on the source model. In addition, CNN models without transfer (NonTR-CNN) were also built to show how the TR framework can succeed in curve prediction using only a small dataset. As described in the Methods, the above process was implemented ten times according to different partitions for the dataset. The results of the model trained from one of the partitions (Part-2) are presented first.
Figure 5 shows the training history for the TR and NonTR-CNN models. The training and testing losses of the TR-CNN model dropped rapidly and an optimized model was obtained after ~300 iterations, with loss values of 0.08 and 0.14 at this time for the training and testing sets, respectively. However, the NonTR-CNN model consistently underperforms when various model parameters are used. At least 800 iterations are required and the loss values (0.17 and 0.22 for training and testing, respectively) are significantly higher than those of the TR-CNN. This indicates that the current dataset of 22 samples is not sufficient to directly train a reliable model. The training process of the TR-CNN can be implemented more efficiently and faster with the help of transfer learning.
The S-N curves in the validation set predicted by the TR-CNN and NonTR-CNN models are compared in Figure 6A, in which the results of six randomly chosen samples are shown. For the NonTR-CNN model, most curves deviated significantly from the actual curves and only a few curves, such as sample 5, were predicted accurately. In contrast, for the TR-CNN, the prediction results are consistent with the actual curves and the tendency of the curves can be well predicted, indicating a significant improvement over the NonTR model. The prediction results of the fatigue strength for the TR and NonTR models are shown in Figure 6B. With the help of a transfer, the fatigue strength of the vast majority of samples in the validation set was predicted more accurately than that of the NonTR model. Under the TR-CNN framework, the R2 and MAE values of the validation set are 89.96% and 12.17 MPa, respectively, which are significantly better than those of the NonTR-CNN (50.27% and 29.88 MPa). Figure 7A presents the MAE results of all 29 curves in the validation set predicted by the TR and NonTR models. For the Non-TR, the MAE value of most of the curves exceeds 10 MPa, which is unsatisfactory. Therefore, it is difficult to accurately predict the S-N curves for a CNN model directly trained based only on the current small dataset. In contrast, the TR-CNN framework exhibited better predictive capabilities with MAE values of ~10 MPa for most samples in the validation dataset. In addition to the results of Part-2, the TR and NonTR models trained according to the other partitions also have similar performances. Figure 7B shows the results of overfitting (the difference between the mean MAE values of the training and validation sets) for these models. All TR models exhibited a lower degree of overfitting compared to the NonTR models.
Figure 6. Comparison of prediction results for validation set by TR-CNN and NonTR-CNN models: (A) S-N curves; (B) fatigue strength.
Figure 7. Comparison of MAE results by TR and NonTR models: (A) validation set of Part-2; (B) overfitting of all partitions.
The above results demonstrate the advantages of the TR-CNN framework. Using the TR-CNN model, the fatigue data used to train a reliable model for reversed torsion curve prediction can be replaced with the already accumulated rotating bending data. Hence, the time and funding required for the data accumulation can be significantly reduced.
DISCUSSION
Universality of TR-CNN for different amounts of data
The predictive capability of the TR-CNN model was remarkable when trained using only 22 samples. The dependence of the model predictions on the fatigue data amounts for training is further investigated in this section. A series of fatigue data with varying samples from 33 to 112 was used to train the TR and NonTR models. Figure 8 shows the effects of the amount of fatigue data on the MAE of the validation set for the NonTR and TR models. Figure 8A shows the MAE distribution of all samples in the validation using Part-2. When the number of samples was less than 67, the MAE values of the NonTR model exhibited a large dispersion, indicating an obvious sensitivity to the fatigue data amount for the NonTR model. With an increasing amount of data for training, the MAE values gradually gathered at a lower interval. In comparison, for the TR model, the MAE values remained low over almost the entire range of 22–112 samples for training.
Figure 8. MAE results of validation set for NonTR and TR models trained with different fatigue data amounts. (A) MAE distribution of samples in one partition. (B) Mean MAE distribution with ten partitions.
Figure 8B presents the mean MAE results for the partitions, including the error bars. The mean prediction error of the NonTR-CNN decreased rapidly with increasing amounts of datasets from 22 to 78 samples. Thus, the model performance will be satisfactory with more data, exceeding 78 samples according to the statistical results, but more time and funding are required. However, the situation is different in the case of the TR models, where the mean MAE remains almost constant across the entire range, below 20 MPa, with relatively small error bars. This indicates the significant generality of the TR-CNN framework for various amounts of data. Thus, the TR-CNN is more suitable for obtaining the target S-N curves with the given limited amount of data. In summary, the presence of an intermediate model fed by a relatively larger number of other fatigue S-N data (i.e., rotating bending) can greatly contribute to linking the chemical composition/processing conditions to the reversed torsion curves, even when trained on a small dataset. Additionally, the data accumulation costs can be reduced substantially.
Optimization of curve prediction
In this section, efforts are made to help solve the problem of curve prediction under small-sample conditions from other perspectives. For the Non-TR model, hyperparameter modification and architecture improvement were considered to improve its predictive performance. On this basis, for the model hyperparameters, the dropout value, the number of neurons in the fully connected layer and the number of convolution kernels were adjusted; for the model architecture, the number of convolutional and fully connected layers were adjusted. However, the Non-TR model performance under different parameters is always unsatisfactory (their average MAE values are reasonably close, both at ~40 MPa, as shown in Supplementary Table 1.) and far worse than the TR model, which indicates that the traditional CNN model optimization method cannot solve the curve problem under the small sample dataset in this study. In contrast, the proposed TR framework solved this problem well, i.e., to obtain better predictive ability using unconventional CNN optimization methods (transfer learning guided by mechanic theory of S-N curves), which cannot be achieved by traditional CNN model optimization methods (such as optimizing only hyperparameters and architectures).
In addition, we further optimized the TR-CNN model architecture and demonstrated its good scalability. It is well known that quasi-static mechanical properties, such as tensile properties and hardness, are highly correlated with fatigue properties, such as fatigue strength, and various traditional empirical models have been established. For the dataset in the present work, a strong correlation exists between the tensile properties and two fatigue properties (fatigue strength of rotating bending and reversed torsion), as shown in Figures 9A and B. Furthermore, they are easier to obtain compared to fatigue data and hence carry a lower cost penalty. It may be a cost-effective strategy to predict the S-N curves by introducing tensile properties. To this purpose, in addition to the source model for rotating bending curve prediction, another source model for tensile properties prediction was constructed, in which the composition/processing parameters as the inputs and the three tensile properties (yield strength, ultimate tensile strength and total elongation) as the three-dimensional output. For the further TR-CNN framework, the transferred feature layers of two types of source models were copied and their last fully connected layers were concatenated. On this basis, a fully connected layer and an output layer were further added. A schematic diagram of the final architecture is shown in Figure 9C. The model parameters are consistent with the aforementioned TR-CNN models in the Results. Figure 9D presents the mean MAE results for the validation set of the TR models under various amounts of data after introducing tensile properties, with error bars. The predictive ability and stability of TR models have been improved significantly with the further help of the source models for tensile property prediction. In summary, the introduction of low-cost related properties, such as tensile properties, benefits greatly and thus can be further combined with the transfer framework.
Figure 9. Prediction results after introducing tensile properties. (A) Distribution of UTS, TEL and rotating bending fatigue strength of dataset. (B) Distribution of UTS, TEL and reversed torsion fatigue strength of dataset. (C) An optimized TR-CNN architecture incorporating a source model for tensile properties. (D) MAE results of basic TR models and TR models after introducing tensile properties.
CONCLUSIONS
In the present work, a deep learning-based transfer framework (TR-CNN) is proposed to provide an efficient method for reversed torsion S-N curve prediction under small-sample conditions. The proposed framework utilizes the correlations between rotating bending and reversed torsion fatigue. The main conclusions are as follows:
(1) The TR-CNN framework accurately predicts the reversed torsion curves under the condition of a small number of samples (22), which is significantly better than the NonTR model. Therefore, the demand for fatigue data has significantly decreased, resulting in a significant reduction in the cost of fatigue data accumulation. The transfer framework provides a basis for building an accurate S-N curve prediction.
(2) The TR model remained accurate under varying amounts of data (from 22 to 112), maintaining considerable advantages compared to the NonTR model, showing excellent generality given various fatigue data amounts.
(3) The predictive capability of the TR models was improved by introducing tensile properties into the source model. This is presented as an effective method to optimize the prediction of S-N curves by combining the transfer framework and low-cost properties related to fatigue. The proposed transfer framework combines certain physical interpretability and powerful data analysis capabilities and can be extended to small-sample prediction problems of other mechanical properties.
DECLARATIONS
Authors’ contributionsMade substantial contributions to the conception, supervision, and design of the study and performed manuscript editing and review: Xu W, Wang C
Performed machine learning modeling and data analysis and interpretation, as well as draft writing: Wei X
Provided professional guidance: Jia Z
Availability of data and materialsSupplementary materials are available from the Journal of Materials Informatics or from the authors.
Financial support and sponsorshipThis study was financially supported by the National Key R&D Program (No. 2021YFB3702404). The financial support provided by the National Natural Science Foundation of China (No. U1808208, 52171109) is gratefully acknowledged. The authors gratefully acknowledge the financial support provided by the Basic Scientific Research Funds of the Northeastern University (N2007011).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2022.
Supplementary MaterialsREFERENCES
1. Schijve J. Fatigue of structures and materials. . Springer Science & Business; 2001. Available from: https://citations.springernature.com/book?doi=10.1007/978-1-4020-6808-9 [Last accessed on 8 Jul 2022]
2. Fatemi A, Yang L. Cumulative fatigue damage and life prediction theories: a survey of the state of the art for homogeneous materials. Int J Fatigue 1998;20:9-34.
3. Hectors K, De Waele W. Cumulative damage and life prediction models for high-cycle fatigue of metals: a review. Metals 2021;11:204.
4. Santecchia E, Hamouda AMS, Musharavati F, et al. A review on fatigue life prediction methods for metals. Adv Mater Sci Eng 2016;2016:1-26.
6. Chan KS. A microstructure-based fatigue-crack-initiation model. Metall Mat Trans A 2003;34:43-58.
7. Venkataraman G, Chung Y, Nakasone Y, Mura T. Free energy formulation of fatigue crack initiation along persistent slip bands: calculation of S N curves and crack depths. Acta Metall Mater 1990;38:31-40.
8. Wu X. On Tanaka-Mura’s fatigue crack nucleation model and validation. Fatigue Fract Eng Mater Struct 2018;41:894-9.
9. Basaran C. Introduction to unified mechanics theory with applications. Springer Nature 2021:115-202.
10. Lee HW, Basaran C. A review of damage, void evolution, and fatigue life prediction models. Metals 2021;11:609.
11. Lee HW, Basaran C. Predicting high cycle fatigue life with unified mechanics theory. Mech Mater 2022;164:104116.
12. Jamal M N, Kumar A, Lakshmana Rao C, Basaran C. Low cycle fatigue life prediction using unified mechanics theory in Ti-6Al-4V alloys. Entropy (Basel) 2019;22:24.
13. Egner W, Sulich P, Mroziński S, Egner H. Modelling thermo-mechanical cyclic behavior of P91 steel. Int J Plast 2020;135:102820.
14. Zhang H, Fu H, He X, et al. Dramatically enhanced combination of ultimate tensile strength and electric conductivity of alloys via machine learning screening. Acta Mater 2020;200:803-10.
15. Zou C, Li J, Wang WY, et al. Integrating data mining and machine learning to discover high-strength ductile titanium alloys. Acta Mater 2021;202:211-21.
16. Shen C, Wang C, Wei X, Li Y, van der Zwaag S, Xu W. Physical metallurgy-guided machine learning and artificial intelligent design of ultrahigh-strength stainless steel. Acta Mater 2019;179:201-14.
17. Wang C, Shen C, Huo X, Zhang C, Xu W. Design of comprehensive mechanical properties by machine learning and high-throughput optimization algorithm in RAFM steels. Nucl Eng Technol 2020;52:1008-12.
18. Shiraiwa T, Miyazawa Y, Enoki M. Prediction of fatigue strength in steels by linear regression and neural network. Mater Trans 2018;60:189-98.
19. Choi D. Data-driven materials modeling with XGBoost algorithm and statistical inference analysis for prediction of fatigue strength of steels. Int J Precis Eng Manuf 2019;20:129-38.
20. Keprate A, Ratnayake RC. Data mining for estimating fatigue strength based on composition and process parameters. International Conference on Offshore Mechanics and Arctic Engineering: American Society of Mechanical Engineers; 2019. pp. V004T003A017. Available from: https://asmedigitalcollection.asme.org/OMAE/proceedings-abstract/OMAE2019/V004T03A017/1067629 [Last accessed on 8 Jul 2022]
21. Gautham BP, Kumar R, Bothra S, Mohapatra G, Kulkarni N, Padmanabhan KA. More efficient ICME through materials informatics and process modeling. In: Allison J, Collins P, Spanos G, editors. Proceedings of the 1st World Congress on Integrated Computational Materials Engineering (ICME). Hoboken: John Wiley & Sons, Inc.; 2011. pp. 35-42.
22. Agrawal A, Deshpande PD, Cecen A, Basavarsu GP, Choudhary AN, Kalidindi SR. Exploration of data science techniques to predict fatigue strength of steel from composition and processing parameters. Integr Mater Manuf Innov 2014;3:90-108.
23. Agrawal A, Choudhary A. An online tool for predicting fatigue strength of steel alloys based on ensemble data mining Int J Fatigue 2018. pp. 389-400.
24. Shiraiwa T, Briffod F, Miyazawa Y, Enoki M. Fatigue performance prediction of structural materials by multi-scale modeling and machine learning. In: Mason P, Fisher CR, Glamm R, Manuel MV, Schmitz GJ, Singh AK, Strachan A, editors. Proceedings of the 4th World Congress on Integrated Computational Materials Engineering (ICME 2017). Cham: Springer International Publishing; 2017. pp. 317-26.
25. Rovinelli A, Sangid MD, Proudhon H, Ludwig W. Using machine learning and a data-driven approach to identify the small fatigue crack driving force in polycrystalline materials. npj Comput Mater 2018:4.
26. Zhang M, Sun C, Zhang X, et al. High cycle fatigue life prediction of laser additive manufactured stainless steel: a machine learning approach. Int J Fatigue 2019;128:105194.
27. Zhan Z, Li H. Machine learning based fatigue life prediction with effects of additive manufacturing process parameters for printed SS 316L. Int J Fatigue 2021;142:105941.
28. Zhang X, Gong J, Xuan F. A deep learning based life prediction method for components under creep, fatigue and creep-fatigue conditions. Int J Fatigue 2021;148:106236.
29. Kalayci CB, Karagoz S, Karakas Ö. Soft computing methods for fatigue life estimation: a review of the current state and future trends. Fatigue Fract Eng Mater Struct 2020;43:2763-85.
30. Yang J, Kang G, Liu Y, Kan Q. A novel method of multiaxial fatigue life prediction based on deep learning. Int J Fatigue 2021;151:106356.
31. Maleki E, Unal O, Seyedi Sahebari SM, Reza Kashyzadeh K, Danilov I. Application of deep neural network to predict the high-cycle fatigue life of AISI 1045 Steel coated by industrial coatings. JMSE 2022;10:128.
32. Maleki E, Unal O, Guagliano M, Bagherifard S. Analysing the fatigue behaviour and residual stress relaxation of gradient nano-structured 316L steel subjected to the shot peening via deep learning approach. Met Mater Int 2022;28:112-31.
33. Kim D, Lim JH, Lee S. Prediction and validation of the transverse mechanical behavior of unidirectional composites considering interfacial debonding through convolutional neural networks. Composites Part B: Engineering 2021;225:109314.
34. Yang C, Kim Y, Ryu S, Gu GX. Prediction of composite microstructure stress-strain curves using convolutional neural networks. Mater Des 2020;189:108509.
35. Tu Y, Liu Z, Carneiro L, et al. Towards an instant structure-property prediction quality control tool for additive manufactured steel using a crystal plasticity trained deep learning surrogate. Mater Des 2022;213:110345.
37. Paul A, Jha D, Al-Bahrani R, et al. Transfer learning using ensemble neural networks for organic solar cell screening. In: 2019 International Joint Conference on Neural Networks (IJCNN): IEEE; 2019. pp. 1–8. Available from: https://ieeexplore.ieee.org/abstract/document/8852446 [Last accessed on 8 Jul 2022]
38. Yamada H, Liu C, Wu S, et al. Predicting materials properties with little data using shotgun transfer learning. ACS Cent Sci 2019;5:1717-30.
39. Kailkhura B, Gallagher B, Kim S, Hiszpanski A, Han TY. Reliable and explainable machine-learning methods for accelerated material discovery. npj Comput Mater 2019:5.
40. Jha D, Choudhary K, Tavazza F, et al. Enhancing materials property prediction by leveraging computational and experimental data using deep transfer learning. Nat Commun 2019;10:5316.
41. NIMS. Fatigue data sheet. Available from: https://smds.nims.go.jp/fatigue/ [Last accessed on 8 Jul 2022].
42. Sakai T, Sugeta A. Publication of the second edition of “Standard evaluation method of fatigue reliability for metallic materials” [Standard regression method of S-N curves]. J Soc Mat Sci 2005;54:37-43.
43. Jain A, Nandakumar K, Ross A. Score normalization in multimodal biometric systems. Pattern Recognition 2005;38:2270-85.
44. Maleki E. Artificial neural networks application for modeling of friction stir welding effects on mechanical properties of 7075-T6 aluminum alloy. IOP Conf Ser: Mater Sci Eng 2015;103:012034.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.


























Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].