Parameters optimization of electro-hydraulic power steering system based on multi-objective collaborative method

Taowen Cui; Shuaiyin Wang; Yuan Qu; Xiang Chen

doi:10.20517/ces.2022.57

Download PDF

Research Article | Open Access | 8 Mar 2023

Parameters optimization of electro-hydraulic power steering system based on multi-objective collaborative method

Views: 1229 | Downloads: 681 | Cited:

0

Taowen Cui^1,2

,

Shuaiyin Wang¹

, ...

Xiang Chen²

Complex Eng Syst 2023;3:3.

10.20517/ces.2022.57 | © The Author(s) 2023.

Author Information

Article Notes

Cite This Article

Abstract

Electro-hydraulic power steering (EHPS) systems are widely used in commercial vehicles due to their adjustable power assist and energy-saving advantages. In this paper, a dynamic model of the EHPS system is developed, and quantitative expressions for three evaluation indexes, steering road feel, steering sensibility and steering energy loss, are derived for the first time. A multi-objective collaborative optimization model of the EHPS system is then established, which consists of one total system and three parallel subsystems, based on collaborative optimization theory. Considering the coupled variables of each subsystem, the total system is optimized by a multi-objective algorithm, while the subsystems are optimized by a single-objective algorithm. The optimization results demonstrate that the average frequency domain energy of the steering road feel is increased by 69.1%, the average frequency domain energy of steering sensitivity is reduced by 19.2%, and steering energy consumption is reduced by 10.8% compared to the initial value. The non-dominated sorting genetic algorithm-II (NSGA-II) shows superior comprehensive performance compared to the other two multi-objective algorithms, and the optimization performance can be further improved by setting appropriate algorithm parameters.

Keywords

Electro-hydraulic power steering, multi-objective optimization, collaborative optimization, non-dominated sorting genetic algorithm-II

Download PDF 0 21

1. INTRODUCTION

As the focus on driving experience increases, research into vehicle steering systems has also gained attention. Traditional hydraulic power steering (HPS) systems provide assistance torque through an engine and offer a clear road feel, but have the disadvantage of high energy consumption. Electric power steering (EPS) systems provide adjustable assistance torque through a motor and have lower energy consumption, but the power-assisted range of EPS systems is narrow, limiting their application in vehicles with heavy front axle loads. Electric-hydraulic power steering (EHPS) systems combine the advantages of both systems, providing better road feel and lower energy consumption. Thus, EHPS systems have been widely used in commercial vehicles.

In recent years, research into EHPS systems has mainly focused on the control aspect^[1-6]. Neural network control algorithms have been applied to the steering assist control of EHPS systems to improve the driver's experience^[7]. Kim et al. proposed a design method for the steering motor speed of EHPS systems based on driver perception, which improved the driver's steering road feel and eliminated the catch-up effect^[8]. Lin et al. proposed a slip frequency control method for the steering motor of EHPS systems to effectively improve the response speed and accuracy of the steering motor^[9]. Ye et al. simplified the EHPS system and introduced the H2/H$$ \infty $$ control method to control the power assistance, which improves the anti-interference performance of the steering system^[10]. Hur et al. analyzed the characteristics of the interior permanent-magnet synchronous motor of EHPS systems and proposed precise control and real-time response control methods for the motor^[11].

However, current research rarely focuses on the steering experience of EHPS systems, and the optimization of the overall EHPS system is rarely reported. The evaluation indexes of EHPS systems involve not only steering flexibility and road feel, but also steering economy and other aspects with coupled effects^[12-14]. Therefore, the optimization of the EHPS system is essentially a multi-objective optimization problem (MOP).

Traditional multi-objective optimization algorithms usually set different weights for different indicators and sum them, thus transforming multi-objective optimization into single-objective optimization^[15]. However, these optimization algorithms show poorer performance in solving too many optimization objectives and non-convex optimization problems, and are prone to falling into local optima^[16]. As such, a number of intelligent optimization algorithms, such as non-dominated sorting genetic algorithm (NSGA) and NSGA-II, have been proposed and applied to satellite design and other fields^{[17, 18]}. Additionally, the collaborative optimization (CO) method can effectively solve complex optimization problems, with the obvious advantages of simplifying system decoupling and achieving parallel computation^[19-21]. The complex optimization model is divided into several subsystems according to the optimization objectives, and the coupling variables in the subsystems are coordinated by the consistency constraint^[22]. This is convenient for concurrent design, which is consistent with the modern industrial design structure^[23-25].

In this paper, steering road feel, steering sensitivity, and steering energy loss are taken as evaluation indexes. Considering the coupling factors of each subsystem, the multi-objective collaborative optimization method of the EHPS system is explored.

The rest of the paper is organized as follows. The dynamic model of the EHPS system is established in Section 2, and the three evaluation indexes of the steering system are derived for the first time. Section 3 establishes the multi-objective collaborative optimization model of the EHPS system and shows the multi-objective optimization results. Conclusions are given in Section 4.

2. SYSTEM DYNAMIC MODEL

The EHPS system consists of two parts: mechanical and hydraulic. The mechanical part includes a sequential connection of the steering wheel, steering column, rack and pinion, etc. The hydraulic part includes the oil tank, hydraulic pump, drive motor, rotary valve, and hydraulic cylinder. According to the vehicle speed and steering wheel torque, the drive motor drives the hydraulic pump at a certain speed to supply oil to the rotary valve and form a pressure difference on both sides. This pressure difference then provides adjustable assistance for the steering system through the hydraulic cylinder.

The EHPS system structure is shown in Figure 1.

Parameters optimization of electro-hydraulic power steering system based on multi-objective collaborative method

Figure 1. Structure of EHPS system. 1-Torque sensor; 2-rack and pinion; 3-hydraulic cylinder; 4- hydraulic pump; 5-drive motor; 6-rotary valve.

2.1. Steering model

The dynamics model of the EHPS system can be expressed as follows, which includes the steering wheel model, drive motor model, rack and pinion model, and steering resistance torque model^{[2, 8]}.

(1)

$$ \begin{eqnarray} \left\{\begin{array}{l} J_{s w} \ddot{\theta}_{s w}+B_{s w} \dot{\theta}_{s w} = T_{s w}-T_{s} \\ J_{m} \frac{d \omega}{d t}+B_{d} \omega = T_{m}-T_{c} \\ m_{o} \ddot{x}_{o}+B_{o} \dot{x}_{o} = F_{s s}+F_{h}-F_{r} \\ T_{r} = \frac{2 d k_{1}}{n_{1}}\left(\frac{a \omega_{r}}{u}+E_{1} \phi+\beta-\delta\right) \end{array}\right. \end{eqnarray} $$

where

$$ \begin{eqnarray*} \large \left\{\begin{array}{l} F_{h} = A_{p}(\frac{\rho}{8\left(C_{q} A_{2}\right)^{2}}\left(Q_{s}-A_{p} \frac{d x_{r}}{d t}\right)^{2}-\frac{\rho}{8\left(C_{q} A_{1}\right)^{2}}\left(Q_{s}+A_{p} \frac{d x_{r}}{d t}\right)^{2}) \\ q = 2 p_{b}\left[\pi\left(R_{2}^{2}-R_{1}^{2}\right)-\left(R_{2}-R_{1}\right) Z t\right] \\ p_{S} = \frac{\rho}{8\left(C_{q} A_{1}\right)^{2}}\left(Q_{s}+A_{p} \frac{d x_{r}}{d t}\right)^{2}+\frac{\rho}{8\left(C_{q} A_{2}\right)^{2}}\left(Q_{s}-A_{p} \frac{d x_{r}}{d t}\right)^{2} \\ T_{c} = \frac{q P_{s}}{2 \pi k_{p}} \end{array}\right. \end{eqnarray*} $$

2.2. Steering performance indexes

Considering the performance requirements of the EHPS system, steering road feel, steering sensibility, and steering energy loss are taken as the evaluation indexes. The quantitative formulas of the three evaluation indexes are derived as follows.

2.2.1. Steering road feel

In this paper, steering road feel is defined as a transfer function from steering resistance torque $$ T_{r} $$ to steering wheel torque $$ T_{sw} $$ , which reflects the efficiency of transmitting torque fluctuations from the road surface to the driver. Besides, the steering wheel angle $$ \theta_{s w} $$ is defined as 0 to reduce a degree of freedom and facilitate the analysis of the steering system.

It is assumed that the torque sensor can be simplified as a torsion bar spring, and the measured value of the torque sensor could be computed by

(2)

$$ \begin{eqnarray} T_{s} = K_{s}\left(\theta_{s w}-\theta_{p}\right) = -K_{s} \theta_{p} \end{eqnarray} $$

where $$ T_{sw} $$ is torque obtained by torque sensor.

According to the current control strategy, the current can be given by

(3)

$$ \begin{eqnarray} I = K T_{s} \end{eqnarray} $$

The torque $$ T_{m} $$ provided by the motor can be given by

(4)

$$ \begin{eqnarray} T_{m} = -K_{a} K K_{s} \theta_{p} \end{eqnarray} $$

Where $$ K_{a} $$ is the torque coefficient of the motor, $$ K $$ is power gain coefficient.

According to (1)-(4), steering road feel can be computed as follows.

(5)

$$ \begin{eqnarray} E(s) = \frac{T_{s w}(s)}{T_{r}(s)} = \frac{K_{s} q}{X_{1} s^{2}+Y_{1} s+Z_{1}} \end{eqnarray} $$

where

$$ \begin{eqnarray*} \large \left\{\begin{array}{l} X_{1}=\mathrm{m}_{r} r_{p}^{2} q+n_{2} J_{m} A_{p} r_{p} \\ Y_{1}=B_{r} q r_{p}^{2}+n_{2} B_{m} A_{p} r_{p}+\frac{\rho q^{2} n \eta_{v} A_{p}^{2} r_{p}^{2}}{2 C_{q}^{2} A_{1}^{2}} \\ Z_{1}=A_{p} r_{p} K K_{a} K_{s}+q K_{T T} \end{array}\right. \end{eqnarray*} $$

Generally, the effective road information frequency domain range is 0-40 Hz. Thus, steering road feel is measured by its average frequency power within this range.

(6)

$$ \begin{eqnarray} S_{c}=\frac{1}{2 \pi \omega_{0}} \int_{0}^{\omega_{0}}|E(j \omega)|^{2} d \omega \end{eqnarray} $$

2.2.2. Steering sensibility

Steering sensitivity reflects the response speed of a vehicle to steering action and has an important impact on vehicle safety at high speed.

The vehicle three degree of freedom differential equation can be described as^[17]

(7)

$$ \begin{eqnarray} \left\{\begin{array}{l} I_{z} \dot{\omega}_{r}-I_{x} \ddot{\phi}=N_{r} \omega_{r}+N_{\beta} \beta+N_{\phi} \phi+N_{\delta} \delta \\ m u\left(\omega_{r}+\dot{\beta}\right)-m_{s} h \ddot{\phi}=Y_{r} \omega_{r}+Y_{\beta} \beta+Y_{\phi} \phi+Y_{\delta} \delta \\ I_{x} \ddot{\phi}-m_{s} u\left(\omega_{r}+\dot{\beta}\right) h-I_{x} \dot{\omega}_{r}=L_{p} \dot{\phi}+L_{\phi} \phi \end{array}\right. \end{eqnarray} $$

where

$$ \begin{array}{l} N_{r} = -2 \frac{a^{2} k_{1}+b^{2} k_{2}}{u} \quad \quad N_{\beta} = -2 a k_{1}+2 b k_{2} \\ N_{\phi} = -2 a E_{1} k_{1}+2 b E_{2} k_{2} \quad N_{\delta} = 2 a k_{1} \\ Y_{r} = -2 \frac{k_{1} a-k_{2} b}{u} \quad \quad Y_{\beta} = -2\left(k_{1}+k_{2}\right) \\ Y_{\phi} = -2 k_{1} E_{1}-2 k_{2} E_{2} \quad \quad Y_{\delta} = 2 k_{1} \\ L_{\phi} = -[2 k_{1} E_{1} h + 2 k_{2} E_{2} h + 2(C_{21} + C_{23} + \frac{C_{a 1} + C_{a 2}}{d^{2}}) d^{2}-m_{s} g h] \\ L_{p} = -2\left(D_{21} + D_{23}\right) d^{2} \\ \end{array} $$

The following formula can be obtained by Laplace transformation of the above formula

(8)

$$ \begin{eqnarray} \large \left\{\begin{array}{l} \frac{\omega_{r}(s)}{\delta(s)}=\frac{A_{3} s^{3}+A_{2} s^{2}+A_{1} s+A_{0}}{B_{4} s^{4}+B_{3} s^{3}+B_{2} s^{2}+B_{1} s+B_{0}} \\ \frac{\beta(s)}{\delta(s)}=\frac{F_{3} s^{3}+F_{2} s^{2}+F_{1} s+F_{0}}{B_{4} s^{4}+B_{3} s^{3}+B_{2} s^{2}+B_{1} s+B_{0}} \\ \frac{\phi(s)}{\delta(s)}=\frac{H_{2} s^{2}+H_{1} s+H_{0}}{B_{4} s^{4}+B_{3} s^{3}+B_{2} s^{2}+B_{1} s+B_{0}} \end{array}\right. \end{eqnarray} $$

where

$$ \begin{eqnarray*} \begin{array}{l} A_{3} = -m u I_{x} N_{\delta}+h^{2} u m_{s}^{2} N_{\delta}-h u I_{x z} m_{s} Y_{\delta} \\ A_{2} = m u L_{p} N_{\delta}+I_{x} N_{\delta} Y_{\beta}-I_{x} N_{\beta} Y_{\delta} \\ A_{1} = m u L_{\phi} N_{\delta}-L_{p} N_{\delta} Y_{\beta}+L_{p} N_{\beta} Y_{\delta}-\text { hum }_{s} N_{\phi} Y_{\delta}+h_{s} N_{\delta} Y_{\phi} \\ A_{0} = -L_{\phi} N_{\delta} Y_{\beta}+L_{\phi} N_{\beta} Y_{\delta} \\ B_{4} = m u I_{x z}^{2}-m u I_{x} I_{z}+h^{2} u I_{z} m_{s}^{2} \\ B_{3} = m u I_{z} L_{p}+m u I_{x} N_{r}-h^{2} u m_{s}^{2} N_{r}+h I_{x z} m_{s} N_{\beta}+h u I_{x z} m_{s} Y_{r}-I_{x z}^{2} Y_{\beta}+I_{x} I_{z} Y_{\beta} \\ B_{2} = m u I_{z} L_{\phi}-m u L_{p} N_{r}-m u I_{x} N_{\beta}+h^{2} u m_{s}^{2} N_{\beta}+m u I_{x z} N_{\phi}+I_{x} N_{\beta} Y_{r}-I_{z} L_{p} Y_{\beta} \\ \quad -h u I_{x z} m_{s} Y_{\beta}-I_{x} N_{r} Y_{\beta}+h u I_{z} m_{s} Y_{\phi} \\ B_{1} = -m u L_{\phi} N_{r}+m u L_{p} N_{\beta}-L_{p} N_{\beta} Y_{r}+h^{h u m_{s}} N_{\phi} Y_{r}-I_{z} L_{\phi} Y_{\beta}+L_{p} N_{r} Y_{\beta}-I_{x z} N_{\phi} Y_{\beta} \\ \quad -\text { hum }_{s} N_{r} Y_{\phi}+I_{x z} N_{\beta} Y_{\phi} \\ B_{0} = m u L_{\phi} N_{\beta}-L_{\phi} N_{\beta} Y_{r}+L_{\phi} N_{r} Y_{\beta}-\text { hum }_{s} N_{\phi} Y_{\beta}+\text { hum }_{s} N_{\beta} Y_{\phi} \\ F_{3} = -h I_{x z} m_{s} N_{\delta}+I_{x z}^{2} Y_{\delta}-I_{x} I_{z} Y_{\delta} \\ F_{2} = m u I_{x} N_{\delta}-h^{2} u m_{s}^{2} N_{\delta}-I_{x} N_{\delta} Y_{r}+I_{z} L_{p} Y_{\delta}+h u I_{x z} m_{s} Y_{\delta}+I_{x} N_{r} Y_{\delta} \\ F_{1} = -m u L_{p} N_{\delta}+L_{p} N_{\delta} Y_{r}+I_{z} L_{\phi} Y_{\delta}-L_{p} N_{r} Y_{\delta}+I_{x z} N_{\phi} Y_{\delta}-I_{x z} N_{\delta} Y_{\phi} \\ F_{0} = -m u L_{\phi} N_{\delta}+L_{\phi} N_{\delta} Y_{r}-L_{\phi} N_{r} Y_{\delta}+h u m_{s} N_{\phi} Y_{\delta}-h u m_{s} N_{\delta} Y_{\phi} \\ H_{2} = -m u I_{x z} N_{\delta}-h u I_{z} m_{s} Y_{\delta} \\ H_{1} = -\text { hum }_{s} N_{\delta} Y_{r}+I_{x z} N_{\delta} Y_{\beta}+\text { hum }_{s} N_{r} Y_{\delta}-I_{x z} N_{\beta} Y_{\delta} \\ H_{0} = \text { hum }_{s} N_{\delta} Y_{\beta}-\text { hum }_{s} N_{\beta} Y_{\delta} \\ \end{array} \end{eqnarray*} $$

According to Formula (1) and (8), the transfer function from the rotation angle of steering wheel $$ \theta_{s w} $$ ($$ s $$ ) to the rotation angle of front wheel $$ \delta $$ ($$ s $$ ) can be expressed as

(9)

$$ \begin{eqnarray} \frac{\delta(s)}{\theta_{s w}(s)} & = & \frac{A_{p} r_{p} K K_{a} K_{s}+K_{s} q}{X_{2} s^{2}+Y_{2} s+Z_{2}+\frac{q 2 d k_{1}}{n_{2}}\left(\frac{a}{u} \frac{w_{r}(s)}{\delta(s)}+\frac{\beta(s)}{\delta(s)}+E_{1} \frac{\phi(s)}{\delta(s)}\right)} \end{eqnarray} $$

where

$$ \left\{\begin{array}{l} \mathrm{X}_{2}=\mathrm{m}_{r} r_{p}^{2} q n_{1}+n_{1} n_{2} J_{m} A_{p} r_{p} \\ Y_{2}=\left(B_{r} q r_{p}^{2}+n_{2} B_{m} A_{p} r_{p}+\frac{\rho q^{2} n \eta_{v} A_{p}^{2} r_{p}^{2}}{2 C_{q}^{2} A_{1}^{2}}\right) n_{1} \\ Z_{2}=\left(A_{p} r_{p} K K_{a} K_{s}+K_{s} q\right) n_{1}-\frac{2 q d k_{1}}{n_{1}} \\ \end{array}\right. $$

In this paper, the transfer function from the yaw velocity $$ \omega_{r} $$ ($$ S $$ ) to steering wheel $$ \theta_{s} $$ ($$ S $$ ) is defined as the steering sensitivity, expressed as

(10)

$$ \begin{eqnarray} \frac{\omega_{r}(s)}{\theta_{s w}(s)}=\frac{\omega_{r}(s)}{\delta(s)} \frac{\delta(s)}{\theta_{s w}(s)} \end{eqnarray} $$

Similar to steering road feel, the steering sensibility is also measured by the average frequency power in the range of 0-40 Hz and computed as

(11)

$$ \begin{eqnarray} F_{l}=\frac{1}{2 \pi \omega_{0}} \int_{0}^{\omega_{0}}\left|\frac{\omega_{r}(s)}{\theta_{h}(s)}\right|_{j=j \omega}^{2} d \omega \end{eqnarray} $$

2.2.3. Steering energy loss

Compared with traditional HPS systems, energy consumption of EHPS systems is greatly reduced. However, it still has a huge potential for energy saving. The schematic diagram of the energy flow of the EHPS system is shown in Figure 2.

Figure 2. The schematic diagram of energy flow.

The total energy of the steering system is supplied by the battery. One part of the energy is supplied to the ECU, and the energy loss is denoted as $$ P_{E-loss} $$ . The other part is supplied to the drive motor, which drives the hydraulic pump according to the ECU command. The energy loss of the drive motor is denoted as $$ P_{m-loss} $$ . The hydraulic pump pumps the hydraulic oil into rotary valve, and the energy losses of the two are denoted as $$ P_{p-loss} $$ and $$ P_{v-loss} $$ , respectively^{[9, 14]}. Thus, the total energy loss can be calculated as

(12)

$$ \begin{eqnarray} P = P_{E-loss}+P_{m-loss}+P_{p-loss}+P_{v-loss} \end{eqnarray} $$

where

$$ \left\{\begin{array}{l} P_{E-\text { loss }} = R_{a} i^{2}+\frac{U_{s}^{2}}{R_{\text {elec }}} \\ P_{m-\text { loss }} = \left[\frac{\frac{B_{v} \mathrm{n} \pi}{30}+T_{L_{o}}}{\mathrm{\; K}_{a}} \mathrm{r}_{\mathrm{a}}+\frac{\mathrm{k}_{\mathrm{e}} \mathrm{n} \pi}{30}-K_{a} \omega(t)\right] i \\ P_{p-\text { loss }} = \frac{\rho}{8 C_{q}^{2}}\left[\left(\frac{Q_{S}-A_{P} \dot{\theta}_{P} r_{P}}{A_{2}}\right)^{2}+\left(\frac{Q_{S}+A_{P} \dot{\theta}_{P} r_{P}}{A_{1}}\right)^{2}\right]\left(q n-Q_{S}\right) \\ P_{v-\text { loss }} = \frac{\rho}{8\left(C_{q} A_{1}\right)^{2}}\left(\frac{Q_{s}}{4}+A_{p} \frac{d x_{r}}{d t}\right)^{3}+\frac{\rho}{8\left(C_{q} A_{2}\right)^{2}}\left(\frac{Q_{s}}{4}-A_{p} \frac{d x_{r}}{d t}\right)^{3} \\ i = \frac{J_{m}}{K_{a}} \frac{d \omega(t)}{d t}+\frac{B_{d}}{K_{a}} \omega(t)+\frac{T_{c}}{K_{a}} \end{array}\right. $$

3. INTEGRATION OPTIMIZATION

As mentioned above, the optimization of EHPS system involves three evaluation indexes, steering road feel, steering sensitivity, and steering energy loss. Therefore, A multi-objective collaborative optimization model has been built, which simplifies the system decoupling, and the multi-objective optimization algorithm is applied to the model for a Pareto optimal solution set. Besides, the basic parameters of the EHPS system are shown in Table 1.

Table 1

The basic parameter of EHPS system

Name	Value	Name	Value
m/kg	4495	$$ C_{21} $$ /(N$$ \bullet $$ m/rad)	14, 130
$$ \rm{m}_{s} $$ /kg	3350	$$ C_{23} $$ /(N$$ \bullet $$ m/rad)	71, 200
$$ I_{x} $$ /kg$$ \bullet \rm{m}^{2} $$	2510	$$ C_{a1} $$ /(N$$ \bullet $$ m$$ \bullet $$ s/rad)	4, 000
$$ I_{xz} $$ /kg$$ \bullet \rm{m}^{2} $$	2810	$$ C_{a1} $$ /(N$$ \bullet $$ m$$ \bullet $$ s/rad)	3, 800
$$ I_{z} $$ /kg$$ \bullet \rm{m}^{2} $$	18800	$$ d $$ /m	0.23
$$ k_{1} $$ /(N/rad)	-2900	$$ J_{sw} $$ /kg$$ \bullet \rm{m}^{2} $$	0.04
$$ k_{2} $$ /(N/rad)	-2900	$$ C_{q} $$	0.62

3.1. Optimization model

Based on collaborative optimization theory, the main system is divided into three independent subsystems, which is convenient for parallel computation and reduces the optimization time. In the main system, three optimization objectives, steering road feel, steering sensibility and energy loss, are optimized by multi-objective optimization algorithm. Besides, the consistency constraint of design parameters is taken as the optimization goal of each subsystem, and the sequential quadratic programming (NLPQL) algorithm is used to optimize each system.

In this paper, the effective area of piston $$ A_{p} $$ , the moment of inertia of motor $$ J_{m} $$ , the stiffness coefficient $$ K_{s} $$ , the stator thickness $$ p_{b} $$ , the gap width of rotary valve and the radius of the rack and pinion $$ r_{p} $$ are selected as the optimization variables. The initial value and design scope of each variable are given in Table 2.

Table 2

The initial value and range of each variable

Design variable	Initial value	Lower	Upper
$$ A_{p} $$ ($$ \rm{m}^{2} $$ )	1.2$$ * 10^{-4} $$	0.5$$ *10^{-4} $$	2$$ *10^{-4} $$
$$ p_{b} $$ (m)	0.008	0.003	0.01
$$ K_{s} $$ (N/m)	80	30	150
$$ J_{m} $$ /kg$$ \bullet \rm{m}^{2} $$	5$$ * 10^{-3} $$	$$ 10^{-3} $$	$$ 10^{-2} $$
$$ r_{p} $$ (m)	0.05	0.01	0.1
$$ w $$ (m)	$$ 10^{-3} $$	$$ 10^{-4} $$	2$$ * 10^{-3} $$

The main system of optimization model is given by

(13)

$$ \begin{eqnarray} \left\{\begin{array}{l} Minimize \quad P \\ Minimize \quad F_{l} \\ Maximize \quad S_{c} \\ {Design} \quad {Variable} \quad {Bounds:} \\ \qquad \quad 3 \leq T_{p} \leq 5 \\ \quad Z_{L} \leq Z\left(A_{p}, p_{b}, K_{s}, J_{m}, r_{p}, w\right) \leq Z_{U} \\ \quad\quad R_{1, 2, 3} \leq 0.01 \\ \end{array}\right. \end{eqnarray} $$

where $$ T_{p} $$ is effective power torque, which is computed by

(14)

$$ \begin{eqnarray} T_{p} = A_{p} r_{p} p_{ab} \end{eqnarray} $$

where

$$ \begin{eqnarray*} \left\{\begin{array}{l} p_{ab} = \frac{\rho}{8\left(C_{q} A_{f 2}\right)^{2}}\left(q n \eta_{v}-A_{p} r_{p} \dot{\theta}_{p}\right)^{2}-\frac{\rho}{8\left(C_{q} A_{f 1}\right)^{2}}\left(q n \eta_{v}+A_{p} r_{p} \dot{\theta}_{p}\right)^{2} \\ A_{f 1} = N L[w+R\left(\theta_{z}-\theta_{p}\right)] \\ A_{f 2} = N L[w-R\left(\theta_{t}-\theta_{p}\right)] \end{array}\right.\\ \end{eqnarray*} $$

The first subsystem named as energy loss is given by

(15)

$$ \begin{eqnarray} \left\{\begin{array}{l} Minimize \\ R_{1} = \left(1-A_{p}^{\prime} / A_{p}\right)^{2}+\left(1-p_{b}^{\prime} / p_{b}\right)^{2} \\ \quad+\left(1-J_{m} / J_{m}^{\prime}\right)^{2}+\left(1-r_{p}^{\prime} / r_{p}\right)^{2}+ \left(1- w^{\prime} /w\right)^{2}\\ Design \quad Variable \quad Bounds: \\ \quad\quad 3 \leq T_{p}^{\prime} \leq 5 \\ \quad x_{L} \leq x\left(A_{p}^{\prime}, p_{b}^{\prime}, K_{s}^{\prime}, J_{m}^{\prime}, r_{p}^{\prime}, w^{\prime}\right) \leq x_{U} \end{array}\right. \end{eqnarray} $$

The second subsystem named as road feel is given by

(16)

$$ \begin{eqnarray} \left\{\begin{array}{l} Minimize \\ R_{2} = \left(1-A_{p}^{\prime \prime} / A_{p}\right)^{2}+\left(1-p_{b}^{\prime \prime} / p_{b}\right)^{2} \\ \quad +\left(1-r_{p}^{\prime \prime} / r_{p}\right)^{2}+\left(1-J_{m} / J_{m}^{\prime \prime}\right)^{2}+\left(1-K_{s}^{\prime \prime} / K_{s}\right)^{2} \\ Design \quad Variable \quad Bounds: \\ \quad\quad 3 \leq T_{p}^{\prime \prime} \leq 5 \\ \quad x_{L} \leq x\left(A_{p}^{\prime \prime}, p_{b}^{\prime \prime}, K_{s}^{\prime \prime}, J_{m}^{\prime \prime}, r_{p}^{\prime \prime}\right) \leq x_{U} \end{array}\right. \end{eqnarray} $$

The third subsystem named as steering sensibility is given by

(17)

$$ \begin{eqnarray} \left\{\begin{array}{l} Minimize \\ R_{3} = \left(1-A_{p}^{\prime \prime \prime} / A_{p}\right)^{2}+\left(1-p_{b}^{\prime \prime \prime} / p_{b}\right)^{2}+\left(1-K_{s}^{\prime \prime \prime} / K_{s}\right)^{2} \\ \quad +\left(1-J_{m}^{\prime \prime \prime} / J_{m}\right)^{2}+\left(1-r_{p}^{\prime \prime \prime} / r_{p}\right)^{2}+\left(1-w^{\prime \prime \prime} / w\right)^{2} \\ Design \quad Variable \quad Bounds: \\ \qquad \quad 3 \leq T_{p}^{\prime \prime \prime} \leq 5 \\ \quad x_{L} \leq x\left(A_{p}^{\prime \prime \prime}, p_{b}^{\prime \prime \prime}, K_{s}^{\prime \prime \prime}, J_{m}^{\prime \prime \prime}, r_{p}^{\prime \prime \prime}, w^{\prime \prime \prime}\right) \leq x_{U} \end{array} \right. \end{eqnarray} $$

According to the above models, the multi-objective collaborative optimization model of EHPS is showed in Figure 3.

Figure 3. Optimization model of EHPS.

3.2. Multi-objective optimization algorithm

The NSGA-II algorithm has excellent global search performance and is often used in multi-objective optimization. On the one hand, the NSGA-II introduces an elite strategy in the process of ranking, which avoids the loss of non-dominated individuals in the evolution process and speeds up the convergence speed of the algorithm. On the other hand, the NSGA-II improves the crowded-comparison approach, which ensures the diversity of the next generation and enhances the global exploratory capability of the algorithm.

The main steps of NSGA-II algorithm can be depicted as follows.

(1) Generate the initial population $$ P_{0} $$ at random and the size of $$ P_{0} $$ is $$ N $$ ;

(2) Calculate the fitness degree of each individual by fitness function, sorting all individuals according to non-dominated regulation;

(3) Generate the next population $$ Q_{t} $$ ($$ t $$ ) $$ \ge $$ 1 by crossover and mutation, and the size of $$ Q_{t} $$ is $$ N $$ . Forming a new population $$ R_{t} $$ consisted of $$ P_{t} $$ and $$ Q_{t} $$ ;

(4) Calculate the fitness degree and crowd degree for each individual. Then, select $$ N $$ individuals to constitute a new population $$ P_{t+1} $$ according to the non-dominated regulation;

(5) $$ t = t + 1 $$ ;

(6) Run Step 3 to Step 5 repeatedly until $$ t $$ equals to the maximum generation.

The flowchart of the NSGA-II algorithm is shown in Figure 4.

Figure 4. The flowchart of NSGA-II.

3.3. Optimization results

According to the established multi-objective collaborative optimization model of the EHPS system, the NSGA-II is applied to the main system for the overall optimization of evaluation indexes, and the NLPQL algorithm is applied to each subsystem for the consistency of design variables. Additionally, the multi-objective particle swarm optimization algorithm (MOPSO) and NCGA multi-objective optimization algorithms are applied to the main system, and the NSGA-II algorithm is used to optimize the whole EHPS system. The solution set distribution of the optimization results is shown in Table 3, and the multi-objective optimization results are shown in Table 4.

Table 3

The distribution of Pareto solutions

	Pareto solutions
NSGA-II
NSGA-II (CO)
MOPSO (CO)
NCGA (CO)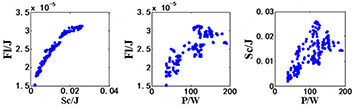

Table 4

Optimal result

Design variable	Initial value	NSGA-II	NSGA-II (CO)	MOPSO (CO)	NCGA (CO)
$$ A_{p} $$ ($$ \rm{m}^{2} $$ )	1.2$$ * 10^{-4} $$	1.21$$ * 10^{-4} $$	1.79$$ * 10^{-4} $$	1.24$$ * 10^{-4} $$	1.50$$ * 10^{-4} $$
$$ p_{b} $$ (m)	0.008	0.0034	0.0044	0.0035	0.0042
$$ K_{s} $$ (N/m)	80	32.45	31.7	41.4	36.2
$$ J_{m} $$ (kg$$ \cdot $$ $$ \rm{m}^{2} $$ )	6$$ * 10^{-3} $$	1.26$$ * 10^{-3} $$	1.82$$ * 10^{-3} $$	1.12 $$ * 10^{-3} $$	1.78 $$ * 10^{-3} $$
$$ r_{p} $$ (m)	0.06	0.037	0.032	0.034	0.021
$$ w $$ (m)	$$ 10^{-3} $$	5.88$$ * 10^{-4} $$	6.76 $$ * 10^{-4} $$	5.59$$ * 10^{-4} $$	5.27$$ * 10^{-4} $$
$$ F_{l} $$ ($$ J $$ )	3.24$$ *10^{-5} $$	2.81$$ * 10^{-5} $$	2.65 $$ * 10^{-5} $$	2.61$$ * 10^{-5} $$	3.13$$ * 10^{-5} $$
$$ S_{c} $$ ($$ J $$ )	0.016	0.023	0.027	0.021	0.026
$$ P $$ ($$ W $$ )	132.41	124.46	118.28	120.24	116.34

Table 4 shows the distribution of the Pareto solutions obtained by different multi-objective algorithms. It should be noted that all algorithms are executed 2000 times.

Firstly, multi-objective optimization method and multi-objective collaborative optimization method are compared. The distribution of the Pareto solutions obtained by only the NSGA-II is similar to the result by the NSGA-II with CO. 278 Pareto solutions are obtained by the NSGA-II with CO, and form a near-complete Pareto front. However, the number of Pareto solutions (104) obtained by the multi-objective optimization (NSGA-II) is too few to form a near-complete Pareto front. Furthermore, due to the insufficient number of solutions, poor non-dominant solutions cannot be eliminated, resulting in a low quality of the optimization solution set. Thus, it could be concluded that the multi-objective collaborative optimization has better solution set diversity and higher solution quality than the multi-objective optimization.

Secondly, the results obtained by CO combing with different multi-objective algorithms are compared. The MOPSO gets 53 Pareto solutions, while the NCGA and the NSGA-II have 269 and 278 Pareto solutions, respectively. Due to the neighborhood cultivation mechanism of the NCGA algorithm, excellent parent generations could be preserved in the next generation, which guarantees more Pareto solutions obtained, and the Pareto solutions distribution is more concentrated. In terms of NSGA-II algorithm, the elitist strategy is introduced; thus, excellent parent generations information could also be preserved in the next generation. Meanwhile, the sorting method based on crowding distance ensures that the Pareto solutions are distributed uniformly.

The optimization results are shown in Table 4. Through the multi-objective collaborative optimization method, the average frequency domain energy of steering sensibility is 2.65 $$ \times $$ $$ 10^{-5} $$ J, which is decreased by 19.2% compared with the initial value. The average frequency domain energy of the steering road feel is 0.027 J, and it is 1.69 times bigger than the initial value. Moreover, the steering energy loss is reduced to 118.28 W, which is reduced by 10.8% compared to the initial value. Besides, compared to the results by only the NSGA-II algorithm, the optimization objectives have been further improved by the NSGA-II algorithm with CO. The average frequency domain energy of steering sensitivity is further reduced by 5.69%. The average frequency domain energy of the steering road feel is further increased by 17.39%, and the steering energy loss is further reduced by 5.00%. Furthermore, the optimization by the NSGA-II algorithm with CO has the best comprehensive performance compared with the results obtained by CO with the other two multi-objective algorithms.

The Bode diagram of the steering road feel step response is shown in Figure 5. The amplitude in the 0-40 Hz range has been improved compared to that before optimization. Especially for the NSGA-II with CO method, it gets the highest average frequency domain energy among the optimization algorithms, which means that the information from the 0-40 Hz range of the road surface can be transmitted to the driver better.

Figure 5. Step response Bode diagram of steering road feel.

The Bode diagram of the steering sensibility step response is shown in Figure 6. Although the NSGA-II with CO method does not obtain the least steering sensibility, the optimization result obtained is still greatly improved compared to that before optimization.

Figure 6. Step response Bode diagram of steering sensibility.

Therefore, it could be concluded that multi-objective collaborative optimization can improve the steering road feel and reduce the steering sensitivity while improving the economy of the steering system. At the same time, the collaborative optimization of NSGA-II with CO has better solution sets diversity and comprehensive optimization results.

4. CONCLUSIONS

(1) On the basis of the EHPS system dynamics model and energy flow analysis, the evaluation index formula of the steering system is derived for the first time, including steering road feel, steering sensibility, and steering energy loss. In addition, considering the coupling relationship between subsystems, a multi-objective collaborative optimization model is established to achieve parallel computing.

(2) The multi-objective collaborative optimization further improves the performance of the EHPS system compared with the multi-objective optimization. Besides, the NSGA-II algorithm shows the best comprehensive performance in optimizing the design parameters of the EHPS system in the comparison of CO combing with multi-objective algorithms.

(3) The optimization results show that the EHPS system is optimized successfully and multiple evaluation indexes could be improved simultaneously. Besides, the optimization is beneficial for promoting the application of the EHPS system in the area of power steering and also serves as a good example for the optimization of electric power steering systems and active steering systems.

DECLARATIONS

Acknowledgments

The authors would like to thank the reviewers for their thoughtful comments and efforts towards improving our manuscript.

Authors' contributions

Conceptualization: Cui T

Experiment and analyze data: Cui T, Wang S

Manuscript drafting: Cui T, Chen X

Manuscript edition and review: Cui T, Wang S, Qu Y, Chen X

Availability of data and materials

Not applicable.

Financial support and sponsorship

The research presented within this article is supported by the Fundamental Research Funds for the Central Universities (Grant No. Jz2021HGQA0286).

Conflicts of interest

All authors declared that there are no conflicts of interest.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Copyright

Appendix for Nomenclature

REFERENCES

1. Liu C, Wang C, Zhao W, Guo Z. Displacement characteristics hierarchical control of electro-hydraulic compound steering for commercial vehicle. J Mech Eng Sci 2022;236:6395-409.

2. Guo ZQ, Wu HX, Zhao WZ, et al. Coordinated control strategy for vehicle electro-hydraulic compound steering system. J Automot Eng 2020;235:732-43.

3. Du H, Zhang QM, Chen SM, et al. Modeling, simulation, and experimental validation of electro-hydraulic power steering system in multi-axle vehicles. J Automot Eng 2019;233:317-32.

4. Zhang L, Wang Z, Ding X, Li S, Wang Z. Fault-tolerant control for intelligent electrified vehicles against front wheel steering angle sensor faults during trajectory tracking. IEEE Access 2021;9:65174-86.

5. Ding X, Wang Z, Zhang L. Hybrid control-based acceleration slip regulation for four-wheel-independent-actuated electric vehicles. IEEE Trans Transp Electrific 2021;7:1976-89.

6. Zhang L, Zhang Z, Wang Z, Deng J, Dorrell DG. Chassis coordinated control for full X-by-wire vehicles-a review. Chin J Mech Eng 2021;34:1-25.

7. Du H, Wang L, Chen JD, et al. Adaptive fuzzy radial basis function neural network integral sliding mode tracking control for heavy vehicle electro-hydraulic power steering systems. J Automot Eng 2020;234:872-86.

8. Lin L, Wang W, Liu ZQ. Modeling and simulation of slip frequency control for induction motor in electric vehicle EHPS system. Appl Mech Mater 2014;635-7:1251-5.

9. Kim SH, Min CS, Chong NC. Development of EHPS motor speed map using HILS system. IEEE Trans Veh Technol 2013;62:1553-67.

10. Ye M, Wang Q, Jiao S. Robust $$ \rm{H}_{2}/\rm{H}_{\infty}$$ control for the electrohydraulic steering system of a four-wheel vehicle. Math Probl Eng 2014;4:1-12.

11. Hur J. Characteristic analysis of interior permanent-magnet synchronous motor in electrohydraulic power steering systems. IEEE Trans Industr Inform 2008;55:2316-23.

12. Cui TW, Zhao WZ, Wang CY. Parametric optimization of a steering system based on dynamic constraints collaborative optimization method. Struct Multidiscipl Optim 2020;61:787-802.

13. Zhao WZ, Wang CY, Li YJ, et al. Integrated optimisation of active steering and semi-active suspension based on an improved memetic algorithm. Int J Veh Des 2015;67:388-405.

14. Crews JH, Mattson MG, Buckner GD. Multi-objective control optimization for semi-active vehicle suspensions. J Sound Vib 2011;330:5502-16.

15. Chen S, Shi T, Wang D, Chen J. Multi-objective optimization of the vehicle ride comfort based on kriging approximate model and NSGA-Ⅱ. J Mech Sci Technol 2015;29:1007-18.

16. Deb A, Srinivas GR, Chou CC. Development of a practical multi-disciplinary design optimization (MDO) algorithm for vehicle body design. SAE Tech Pap 2016;1:1537.

17. Cui TW, Zhao WZ, Tai K. Optimal design of electro-hydraulic active steering system for intelligent transportation environment. Energy 2021;214:118911.

18. Zhou PZ, Du JB, Lv ZH. Simultaneous topology optimization of supporting structure and loci of isolators in an active vibration isolation system. Comput Struct 2018;194:74-85.

19. Zhao WZ, Wang YQ, Wang CY. Multidisciplinary optimization of electric-wheel vehicle integrated chassis system based on steady endurance performance. J Clean Prod 2018;186:640-51.

20. Martins JRRA, Lambe AB. Multidisciplinary design optimization: a survey of architectures. AIAA J 2013;51:2049-75.

21. Park EJ, Luz LFD, Suleman A. Multidisciplinary design optimization of an automotive magnetorheological brake design. Comput Struct 2008;86:207-16.

22. Zadeh PM, Toropov VV, Wood AS. Metamodel-based collaborative optimization framework. Struct Multidiscipl Optim 2009;38:103-15.

23. Zhou G, Ma ZD, Cheng A, et al. Design optimization of a runflat structure based on multi-objective genetic algorithm. Struct Multidiscipl Optim 2015;51:1-9.

24. Huang H, An H, Wu W, Zhang L, Wu B, Li W. Multidisciplinary design modeling and optimization for satellite with maneuver capability. Struct Multidiscipl Optim 2014;50:883-98.

25. Mitra AC, Patil MV, Banerjee N. Optimization of vehicle suspension parameters for ride comfort based on RSM. J Inst Eng 2015;96:165-73.

Cite This Article

Research Article

Open Access

Parameters optimization of electro-hydraulic power steering system based on multi-objective collaborative method

Taowen Cui, ... Xiang Chen

How to Cite

Cui, T.; Wang S.; Qu Y.; Chen X. Parameters optimization of electro-hydraulic power steering system based on multi-objective collaborative method. Complex Eng. Syst. 2023, 3, 3. http://dx.doi.org/10.20517/ces.2022.57

Download Citation

If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click on download.

Export Citation File:

RIS BibTeX EndNote

Type of Import

Direct Import Indirect Import

Tips on Downloading Citation

This feature enables you to download the bibliographic information (also called citation data, header data, or metadata) for the articles on our site.

Citation Manager File Format

Use the radio buttons to choose how to format the bibliographic data you're harvesting. Several citation manager formats are available, including EndNote and BibTex.

Type of Import

If you have citation management software installed on your computer your Web browser should be able to import metadata directly into your reference database.

Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.

Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.

About This Article

Special Issue

This article belongs to the Special Issue Generalized Dynamics Modeling and Dynamics Control of Autonomous Driving Vehicle

Copyright

© The Author(s) 2023. Open Access This article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Data & Comments

Data

Views

1229

Downloads

681

Citations

0

Comments

0

21

Comments

Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.

⁰

Download PDF

Download XML 5 downloads

Cite This Article 26 clicks

Export Citation 48 clicks

Like This Article 21 likes

Share This Article

https://www.oaepublish.com/articles/ces.2022.57

Scan the QR code for reading!

See Updates

Contents

Figures

Parameters optimization of electro-hydraulic power steering system based on multi-objective collaborative method

Abstract

Keywords

1. INTRODUCTION

2. SYSTEM DYNAMIC MODEL

2.1. Steering model

2.2. Steering performance indexes

2.2.1. Steering road feel

2.2.2. Steering sensibility

2.2.3. Steering energy loss

3. INTEGRATION OPTIMIZATION

3.1. Optimization model

3.2. Multi-objective optimization algorithm

3.3. Optimization results

4. CONCLUSIONS

DECLARATIONS

Acknowledgments

Authors' contributions

Availability of data and materials

Financial support and sponsorship

Conflicts of interest

Ethical approval and consent to participate

Consent for publication

Copyright

REFERENCES

Cite This Article

How to Cite

Download Citation

Export Citation File:

Type of Import

Tips on Downloading Citation

Citation Manager File Format

Type of Import

About This Article

Special Issue

Copyright

Data & Comments

Data

Comments

Share This Article

See Updates

Committee on Publication Ethics

Portico

Committee on Publication Ethics

Portico