Environmentally friendly strategy for hybrid flow shop scheduling with the unrelated parallel machines
0Abstract
With the increasing environmental pressure, reducing the environmental impact on hybrid flow shops (HFS) has attracted extensive attention because of its broad industrial applications. The selection of machines in the implementation of HFS is a complex decision-making process that hinders the optimization efficiency in shops. However, this issue has not been addressed thoroughly. In light of this, a multi-objective mathematical model is formulated for the minimization of makespan and energy consumption of the hybrid flow shop scheduling problem (HFSP). The environmental performance of machines is calculated by the proposed evaluation index and is ranked on the basis of the integrated entropy and fuzzy technique for order performance by similarity to ideal solution method. Moreover, to solve the multi-objective model of HFSP, an improved differential evolution algorithm with a heuristic active decoding rule that incorporates the ranking of environmental performance of machines into the iterative process of the algorithm is presented. Finally, a case study is presented to evaluate the effectiveness of the proposed method and to prove the feasibility of the ranking-based differential evolution algorithm (RBDE). The result shows that the proposed RBDE outperforms RBNSGA-II and RBPSO in searching for non-dominated solutions that can solve the environmental production of HFSP effectively.
Keywords
INTRODUCTION
Excessive emissions of energy and resource increase carbon dioxide significantly, which is the main cause of ongoing climate change and global warming. Manufacturing has been among the top human activities worldwide that lead to large amounts of greenhouse gas (GHG) emissions, and environmentally friendly production in manufacturing can reduce energy consumption and carbon dioxide emissions effectively, which has aroused worldwide attention in industrial production and academics. Environmentally friendly production refers to the production or use of products that are not environmentally harmful, namely, everything from production should be favorable and safe for the planet in terms of products over their whole life cycle[1]. Nowadays, environmental scheduling is attracting increasing amounts of attention from numerous manufacturing companies to reduce their energy demand and negative environmental effects.
The hybrid flow shop scheduling problem (HFSP) indicated a combination of the classic flow-shop scheduling problem and the parallel machine scheduling problem, which was characterized by adjusting the processing sequence of jobs and allocating the parallel equipment reasonably[2]. With the pressure of environmental problems, the environmentally friendly production of HFSP has aroused extensive concerns[3,4]. HFSP takes the processing sequence and equipment as variables and obtains the optimal scheduling scheme with the principle of minimizing environmental impact through the effective optimization algorithm. Therefore, the efficient objective modeling, the reasonable processing sequence and equipment allocation, and the efficiency optimization algorithm have a decisive impact on environmental scheduling.
A lot of work has been dedicated to hybrid flow shop scheduling. To begin with, most previous work aimed at improving production efficiency from the perspective of multi-objective scheduling optimization, that is, the objective in HFSP is mainly focused on the minimization of makespan, the completion time, total tardiness, or others. For instance, Qin et al. proposed a mathematical model of the distributed heterogeneous hybrid flow shop problems with blocking constraints, and the optimization algorithm was developed to minimize the makespan of the hybrid flow shop[5,6]. Xu et al. proposed a shuffled frog-leaping algorithm to solve the hybrid flow-shop scheduling problem with makespan minimization[7]. Meng et al. addressed the hybrid flow shop scheduling problem with unrelated parallel machines, in which their objective focused on minimizing the makespan using eight mixed integer linear programming models[8]. Although production efficiency is essential, by no means should it be the only factor to be considered in manufacturing operations. Luo et al. considered not only production efficiency but also electric power cost with the presence of time-of-use electricity prices to improve production efficiency and reduce the energy consumption of hybrid flow shop[9]. Behnamian established the objective function of earliness, tardiness, makespan, and total worker employing costs considering the effects of learning, deterioration, and sequence-dependent setup times and proposed a colonial competitive algorithm to solve the hybrid flow shop scheduling problem[10]. With the increasing pressure of environmental problems, the energy saving and emission reduction strategy for scheduling has been proposed[11]. Qin et al considered not only the energy consumption of the processing time but also the idle and blocking times of all machines to realize to energy saving of the blocking hybrid flow shop[12]. Meng et al. established the idle energy-based model based on the modeling ideas of machine tools turning off and on to investigate the energy-conscious hybrid flow shop scheduling problem[13]. Li et al. developed a hybrid energy-aware multi-objective optimization algorithm that considered the setup energy consumption to solve the hybrid flow shop scheduling problem to minimize the energy consumption and the makespan simultaneously[14]. Generally, the decision maker needs more than a single criterion to reach the decision in real-life problems. With serious environmental pollution and strict environmental regulation, the multi-objective scheduling that considers the environmental problems and production demand of the industry has become the greatest challenge in HFSP.
Most previous research reported that the arrangement of parallel machines for various jobs quite affects the environmental performance of HFSP. According to the characteristic of parallel machines, the classic HFSP can be divided into three types, namely, the HFSP with identical parallel machines (HFSP-IPM), the HFSP with uniform machines (HFSP-UM), and the HFSP with unrelated parallel machines (HFSP-UPM). For HFSP-IPM, a job at a certain stage has the same speed, that is, each machine has an identical processing time. For HFSP-UM, the speed of parallel machines varies for each job at a stage, and the processing time is inversely proportional to the speed. HFSP-UPM is the most complex and close to real industrial manufacturing scheduling problems, which have wide engineering applications[13]. For HFSP-UPM, the processing time of a job on any parallel machine is independent and the production efficiency quite depends on the matching degree between the job and the machines[15]. Hence, to implement environmentally friendly production, the reasonable evaluation of environmental performance for the parallel machines becomes an urgent demand for scheduling[16]. The environmental performance of parallel machines can be evaluated from three aspects, i.e., environmental impact, technical performance and production cost[17]. The energy consumption of parallel machines was supposed to be the main source of environmental impact, which has been under extensive research. Drake et al. showed that there were significant amounts of energy associated with machine start-up and idling[18]. In light of this, Mouzon et al. proposed a greedy randomized adaptive search procedure integrated with the generic algorithm to solve the minimization of the total energy consumption of HFSP[19]. The result showed that a significant amount of energy can be saved when the non-bottleneck is turned off during a long idle time. Liu et al. presented an ultra-low idle state of machines by turning off some auxiliary parts in an idle state[20]. To calculate the energy consumption of machine tools with respect to various cutting parameters, the specific energy consumption (SEC) was generally recognized as an essential indicator. Besides, subsidiary materials, such as cutting fluid, also have an important influence on environmental impact[21]. For the production cost of parallel machines, the machining cost, the maintenance cost, etc., were generally investigated for optimizing the job scheduling of the workshop[10]. For technical performance, accuracy and reliability in terms of the basic requirements of production have been focused[22]. In addition, axes configurations, in particular at high-speed spindle rotations and high feed rates, have a significant variation of the dynamic properties for the machines[23]. To sum up, systematic environmentally friendly evaluation criteria for unrelated machines with respect to the above factors must be taken into account, and the environmental performance of machines should be qualified.
For the optimization of HFSP, the genetic algorithm[24], grey wolf algorithm[25], backtracking search algorithm[26], ant colony optimization[27], particle swarm optimization[28], and differential evolution algorithm[29] were developed. It is noted that the selection of machines for various jobs in HFSP was random in the iterations and the characteristics of machines have been oversimplified, which results in lower search efficiency. To overcome this problem, the local search method with a forward decoding method considering idle time[30,31], energy-saving capability[32], etc., was proposed. However, these methods are mostly applicable to single objective optimization, which did not apply to environmentally friendly production. Inspired by the No free lunch theorem, that is, the importance of utilizing problem-specific information to guide the search process of general-purpose algorithms. In view of the environmental performance of the machine tools, the information on the characteristics of machines can be exacted and incorporated into the selected meta-heuristic as a specialized local search module in HFSP to obtain the optimal scheduling scheme. This method can effectively narrow the search scope and improve search efficiency.
Based on the existing research on the hybrid flow shop scheduling, two key issues must be addressed: (1) comprehensive evaluation of the environmental performance of machines; (2) effective scheduling algorithm with respect to the environmental performance of machines. To rectify these deficiencies, in this paper, a strategy for hybrid flow shop scheduling with the ranking of the environmental performance of machines was established. The innovations of the approach are summarized as: (1) A multi-objective mathematical model for minimization of makespan and energy consumption was formulated with respect to the stages of processing, waiting and transportation considering the characteristics of the hybrid flow shop; (2) A multi-level environmentally friendly evaluation system for machines was developed with respect to the performance of ecological, economic, and technical. Subsequently, the environmental performance of the machines was ranked through the integrated entropy and fuzzy technique for order performance by similarity to the ideal solution (TOPSIS) method; (3) An improved differential evolution algorithm was presented to support the HFSP environmental scheduling with the heuristic active decoding rule referring to the ranking of the environmental performance of machines, which can narrow the search scope and accelerate the convergence speed.
The rest of this paper is organized as follows: The section of “PROBLEM FORMULATION” describes the characteristics of HFSP and establishes a multi-objective model for it. The section of “METHODOLOGY” describes the environmentally friendly evaluation criteria, the ranking method of the machines, and the ranking-based differential evolution (RBDE) algorithm. The section of “CASE STUDY” presents a case study to demonstrate the effectiveness of the developed method. Finally, the section of “CONCLUSION” discusses the conclusions and future work.
PROBLEM FORMULATION
The hybrid flow shop scheduling problem[33] was commonly described as a set of n (i = 1, 2, …, n) jobs that need to be processed at j (j = 1, 2, …, w) stages in series, as shown in Figure 1. The jobs to be performed for a given period are known and do not change, where stage j contains Mk (k = 1, 2, …, m) unrelated parallel machines and Mk ≥ 2 exists at no less than one stage. Each job should be processed at all stages sequentially and all jobs can be processed by any of the machines at each stage. The formal mathematical definition of the problem will be described in detail in the following sections.
Figure 1. Flowchart of HFSP.
Hybrid flow shop scheduling has been extensively examined to improve production efficiency. With the serious environmental problems, the assignment of machines and the sequence of operations were set as variables in the HFSP to minimize the makespan Tmake and energy consumption Econs. Moreover, the denotations of all the parameters for the hybrid flow-shop scheduling problem was shown in Table 1, and the hypotheses considered in this paper were summarized as follows:
Denotations of all the parameters for the hybrid flow-shop scheduling problem
| Index: | |
| i | Job number |
| j | Stage number |
| k | Machine number |
| Number: | |
| n | Number of total jobs |
| w | Number of total stages |
| m | Number of total machines |
| k* | Selected machine number for the next stage |
| Parameters: | |
| St(ijk) | Start time for the ith job of the jth stage at machine k |
| St(i+1)jk | Start time for the i+1th job of the jth stage at machine k |
| St(i(j+1)k*) | Start time for the ith job of the j+1th stage at machine k* |
| Sti(j+1) | Start time for the ith job of the j+1th stage at any machine |
| Stij | Start time for the ith job of the jth stage at any machine |
| Ft(ijk) | Completion time for the ith job of the jth stage at machine k |
| Ft(i(j+1)k*) | Completion time for the ith job of the j+1th stage at machine k* |
| Ft((i-1)jk) | Completion time for the i-1th job of the jth stage at machine k |
| Mk | Machine set |
| obj | Objective function |
| Tmake | Makespan |
| Econs | Total energy consumption |
| Pt(ijk) | Processing time for the ith job of the jth process at machine k |
| Pt(i(j+1)k*) | Processing time for the ith job of the j+1th process at machine k* |
| Tt(ijk) | Transportation time for the ith job of the jth stage at machine k to j+1th stage |
| TE(ijk) | Transportation energy consumption per unit time for the ith job of the jth stage at machine k to j+1th stage |
| d(jk) | The distance from the j stage at machine k to the machine tool in the next stage |
| V | Transportation speed |
| PE(ijk) | Processing energy consumption per unit time for the ith job of the jth process at machine k |
| WE(ijk) | Waiting energy consumption per unit time for the ith job of the jth process at machine k |
| Wt(ijk) | Waiting time for the ith job of the jth process at machine k |
| PEtotal | Total processing energy consumption |
| WEtotal | Total waiting energy consumption |
| TEtotal | Total transportation energy consumption |
| Tmax | The maximum makespan |
| Emax | The maximum energy consumption |
| Decision variables: | |
| Xijk | The decision variable of the ith job jth stage and kth machine tool |
(1) Jobs are independent and have equal priority.
(2) The job is transported to the next machine immediately after processing is finished processing in the previous machine.
(3) All jobs and machines are available at time zero.
(4) The machine cannot be turned off completely until it has finished all operations assigned to it.
(5) The order of operations for each job is predefined and cannot be modified.
(6) Pre-emption is not allowed, that is, no task can be interrupted before the completion of its current operation.
As emphasized by He et al., on average, a machine in the waiting phase consumes 13% of the energy in an
The total energy consumption was composed of the energy consumption for the processing stage PEtotal, waiting stage WEtotal and transportation stage TEtotal. PEtotal represents the energy consumption of the machine during the processing stage, which was associated with the processing power and processing time. WEtotalrefers to the energy consumed by machine tools when they are in standby state, that is, waiting to process the next job. TEtotal was determined by the transportation process of the jobs among different machines.
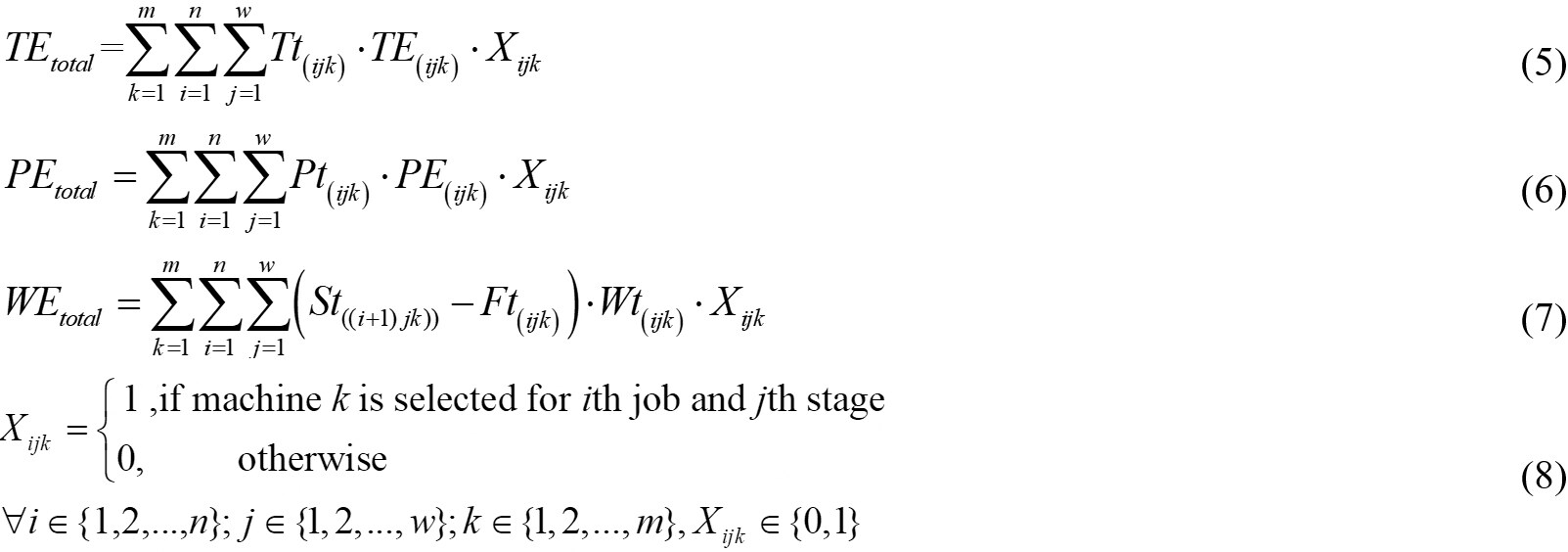
Mathematically, an integer linear programming model of the HFSP, which will be used throughout the paper, was formulated as follows.
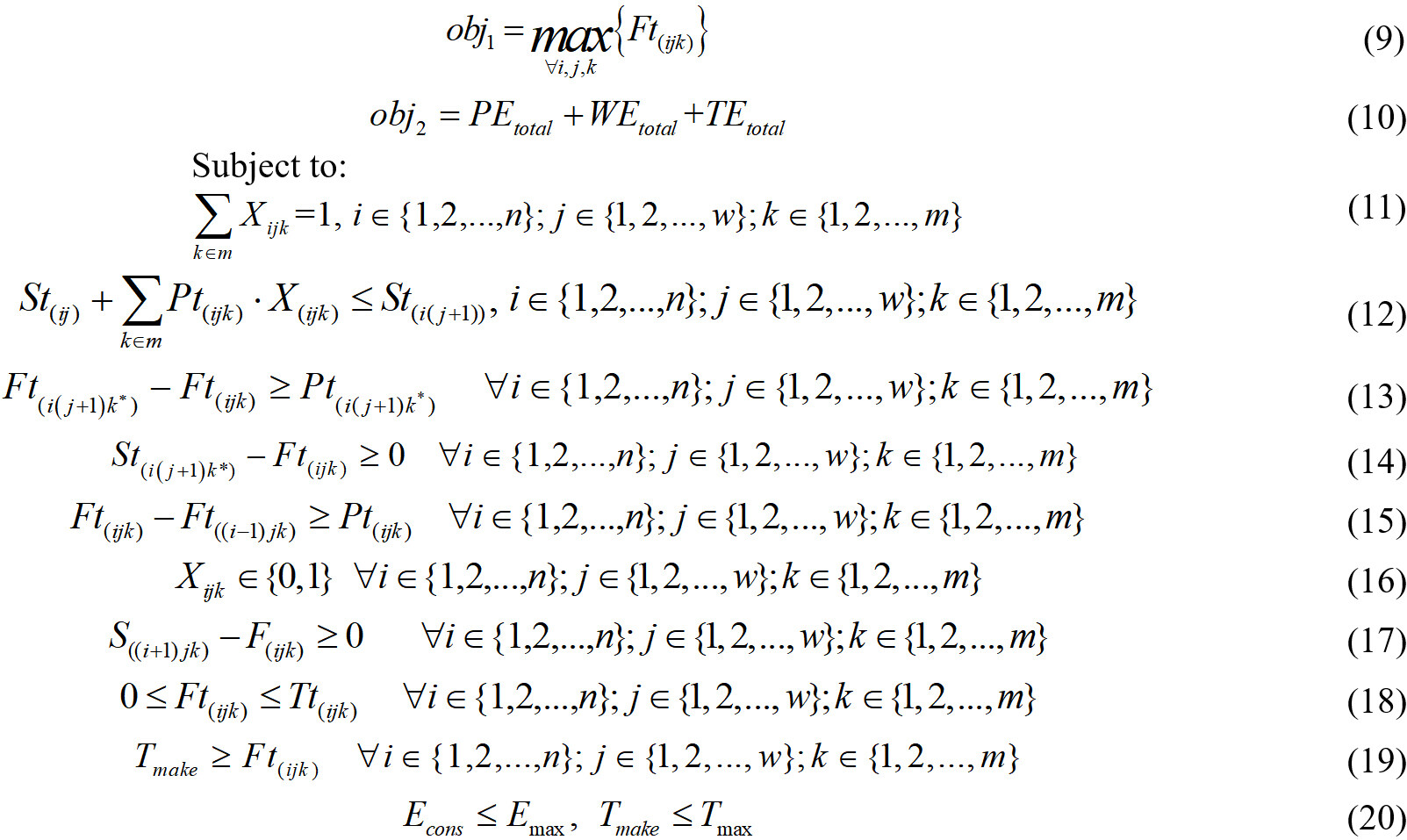
where Equations (9) and (10) are the objective functions. Equation (11) ensures that each operation is assigned to only one machine from its candidate parallel machines. Equation (12) means that the operations that belong to the same job satisfy the precedence. Equations (13) and (14) ensure that jobs are processed according to sequence constraints. Equation (15) governs that a machine can execute one operation at one time and becomes available for other operations only if the previous operation is completed. Equation (16) defines the assignment of jobs and the sequence of machines. Equation (17) represents the precedence relationship among various operations of a job. Equation (18) specifies that the completion time of each operation transported from one machine to another is greater than the completion time of the corresponding operation. Equation (19) implies that the makespan is equal to the maximum completion time of a schedule that includes the completion time of all jobs. Equation (20) guarantees that the production process meets the constraints of makespan and energy consumption in the hybrid flow shop.
METHODOLOGY
A novel method for environmental scheduling with respect to the characteristics of unrelated machines was proposed in this work. Figure 2 demonstrates the overall structure of the method. This method contains three key processes:
Figure 2. Flowchart of the proposed method.
(1) The environmentally friendly evaluation system of machines was constructed. The comprehensive environmentally friendly evaluation criteria were proposed in terms of the technical, economic, and ecological of machines.
(2) The machines were ranked on the basis of their environmental performance. The environmental performance of machines was recognized as a multi-level and multiple-indicator decision-making problem. An integrated entropy and fuzzy TOPSIS method were developed to rank the environmental performance of machines.
(3) The improved algorithm was proposed on the basis of the ranking of the environmental performance of machines. The active decoding method was presented according to the environmental performance of machines. Then, the RBDE algorithm was proposed to obtain the optimal scheduling solution efficiently.
Ranking of the environmental performance of machines
The environmentally friendly criteria are increasingly recognized as a useful tool for machine tool environmental performance assessment, which provides support for the improvement of the HFSP in fields such as ecological, technical, and economic improvement. Hence, a scientific and comprehensive environmentally friendly evaluation system is the prerequisite. From a systematic analysis of the characteristics of the machines and the current environmentally friendly indicators from the literature, a general environmentally friendly evaluation system that integrated technical, economic, and ecological performance was introduced.
The environmental performance evaluation of machines refers to the quantification of the technical indicator of production, the emissions of ecological, and the use of cost in the machining process, which is an overall consideration with multi-level and multiple indicators; the evaluation system is shown in Figure 3. The system was evaluated by three aspects described as follows.
Figure 3. The framework of the environmentally friendly evaluation system of machines.
(1) Technical performance. The technical indicators reflect the reliability and precision of the machines, which are the premises of checking whether the basic technical properties of the machine meet the technical indicator[36,37], such as reliability (N4) and precision (N3) when evaluating the technical performance[38]. The parameter configuration, such as the maximum spindle speed (N1) and feed rate (N2), could always be a factor for machine technical indicators.
(2) Economic performance. The economic indicator mainly includes the machining cost (N5), energy consumption cost (N6), and maintenance cost (N7). It does not only refer to the general cost of the product but also to the energy cost generated by electricity consumption in the processing.
(3) Ecological performance. The ecological indicator aims to reduce ecological environment destruction for the machine when it is processed. Generally, the major environmental impact was due to the energy consumption of the machines, and it can be characterized by the power of machines (working power N8 and waiting power N9) and SEC (N10). Besides, the cutting fluid (N11) is also an important factor in the environmental impact.
The selection of the machines in HFSP is typically a multi-criterion decision-making (MCDM) process. TOPSIS, as one of the most popular methods for solving MCDM problems, has been widely used. This method is based on the concept that the chosen alternative should have the shortest distance to the Positive Ideal Solution (PIS) (the solution which minimizes the cost criteria and maximizes the benefit criteria) and the farthest distance to the Negative Ideal Solution (NIS). Based on the construction of the multi-level system, the ranking of the environmental performance of machines was calculated by the integrated entropy fuzzy TOPSIS method[39,40]. The idea of the proposed method can be expressed in a series of three steps as follows.
Step1: Data preparation
The evaluation system covers the quantitative and qualitative indicators. For the qualitative ones, the linguistic variables were defined, and the corresponding membership function by the triangular fuzzy number was listed in Table 2. The decision matrix D was constructed by the decision maker by selecting the appropriate linguistic variables for the alternatives with respect to the criteria in accordance with Table 2. In addition, normalization was adopted to make all indicators conform to a norm or standard, and the influence of dimension was eliminated. The normalized value will be a positive value between 0 and 1, and the normalized process was recognized as three groups: benefit attributes, cost attributes, and non-monotonic attributes. Their details can be seen in Reference[41]. The normalized fuzzy-decision matrix denoted by R is shown in Equation (21).
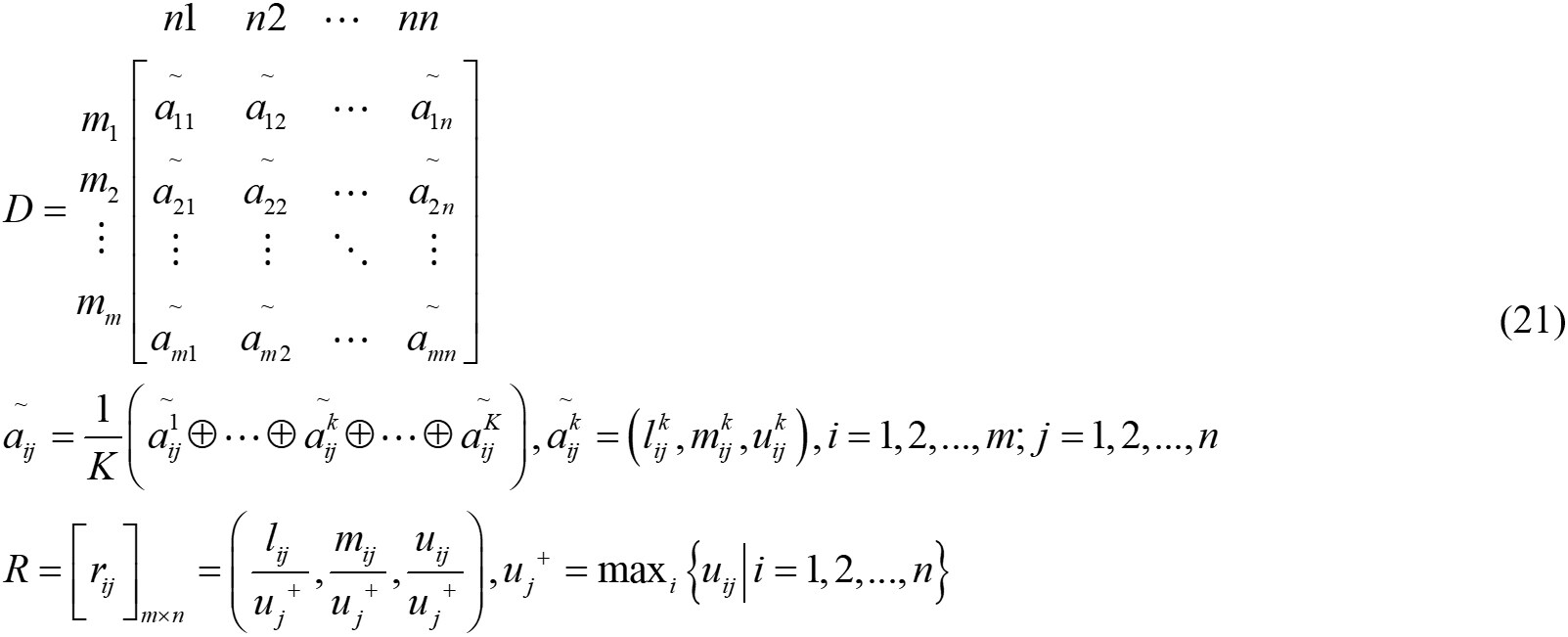
Membership function of linguistic scale
| Linguistic evaluation of parallel machines | Linguistic evaluation of the weight of criteria | Scale of fuzzy number |
| Very low (VL) | Little importance (VL) | (1,1,3) |
| Low (L) | Moderately important (MI) | (1,2,5) |
| Good (G) | Important (I) | (3,5,7) |
| High (H) | Very important (VI) | (5,7,8) |
| Excellent (Ex) | Absolutely important (AI) | (7,9,9) |
where aij is the value of the jth indicator of the ith machine tool. The value is determined by the attributes of the machine tool itself, which can be divided into qualitative and quantitative. The qualitative indicator is obtained from the proposed triangular fuzzy; m means the number of machines; n represents the indicators for the evaluation; K means the number of decision-makers.
Step2: Data processing
During the fuzzy comprehensive evaluation, the weight of the indicators wj is an essential step. This paper introduces the concept of “entropy” to solve the problem, and it is a quantitative measure of the amount of thermal energy not available to do work in a closed thermodynamic system. In information theory, entropy is a method used to measure the disorder degree of a system, which can measure the amount of information provided by data effectively. The detail of this method can be found in References[42,43]. The small entropy value indicates that the indicators provide a more effective amount of information, and the weight of the indicators is higher. The weighted normalized decision matrix V is shown as follows.
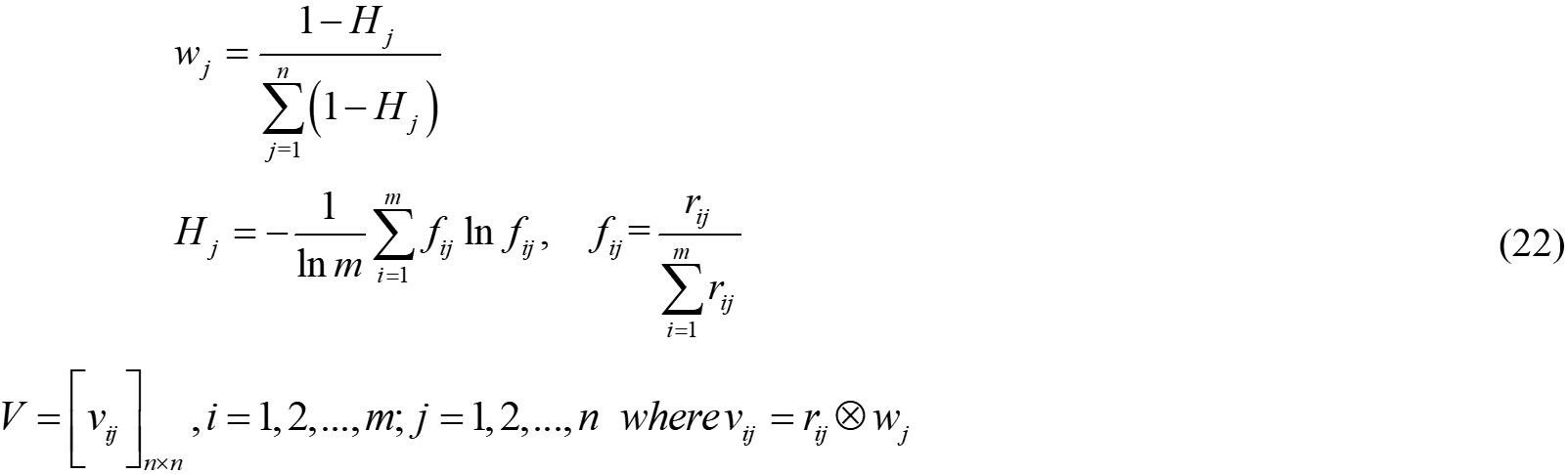
where wj is the weight of the indicators through the entropy method, and Hjrepresents the information entropy of the indicators.
Furthermore, the positive ideal and negative ideal solutions, i.e., PIS and NIS were respectively determined, and the PIS A+ (aspiration levels) and NIS A- (the worst levels) were defined as Equation (23). Then, the area compensation method[44] was proposed to measure the distances (di+ and di-) of each alternative to the A+ and A-.
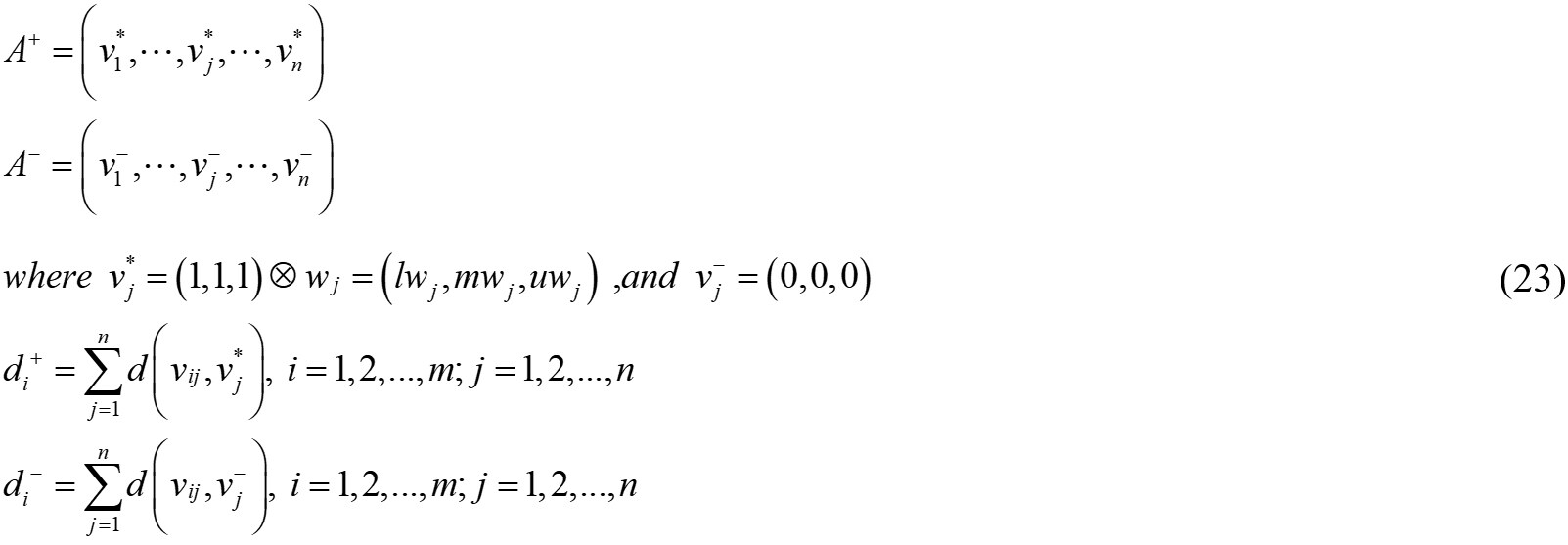
Step3: The ranking of the environmental performance of machines
The relative closeness to the ideal solution was calculated by Equation (24). Moreover, the order of the alternatives was obtained according to the descending order of the value of Ci, which means the ranking of the environmental performance of machines.
Differential evolution algorithm based on the environmental performance of machines
In HFSP, the selection of machines from unrelated parallel machines is an important decision-making process. Generally, the machines were randomly assigned, which increased the search space and was time-consuming. To handle this problem, a modified algorithm was proposed in accordance with the ranking of the environmental performance of machines in “Ranking of the environmental performance of machines”. This algorithm narrowed the search space and could obtain environmental scheduling solutions efficiently.
Differential Evolution (DE) refers to a stochastic direct search and global optimization algorithm that include genetic operations (i.e., differential mutation, crossover, and selection)[45,46]. It is a parallel search evolution strategy that is fairly fast and reasonably robust, which makes differential evolution a versatile tool today. Inspired by the No Free Lunch Theorem, the ranking of machines’ environmental performance was integrated with the DE by the heuristic decoding rule[47]. Hence, a ranking-based differential evolution algorithm (RBDE) was proposed to solve the hybrid flow-shop environmental scheduling problems. In this approach, the active decoding method was carried out and integrated into the iterations of the algorithm after the genetic operations. The selection pressure to the proper direction could be obtained to enhance its performance by accelerating the convergence speed in the iteration of DE. The procedures are described in detail below.
(1) Ranking-based active decoding rule
The decoding method is the key factor in decoding the iterative chromosome sequence into a reasonable production scheduling scheme, which has a great impact on the efficiency and accuracy of the solution. The heuristic active decoding rule proposed in this paper mainly refers to the directional selection of machines according to the environmental performance of machines. The machine with top-ranking environmental performance is more suitable for the jobs. Figure 4 presents the heuristic active decoding rule, in which the environmental performance of the parallel machines that correspond to the first process of job 2 is M3 > M2 > M1 > ...; therefore, M3 was selected for production after decoding. The pseudocode of the heuristic decoding process is shown in Table 3.
Figure 4. Heuristic active decoding rule.
Pseudocode of heuristic decoding process
| Algorithm1 Heuristic active decoding rule | |
| Input i, j//i means the number of jobs; j is the number of stages | |
| Output Select_M(i, j)//Select_M(i, j) represents the selected machine | |
| (1) | For i = 1 To n do |
| (2) | For j = 1 To w |
| (3) | Determined the parallel machines of the (i, j), namely as p_M(i, j); |
| (4) | Calculate the matching degree for the ith job of j stage Md (i, j) via section “METHODOLOGY”; |
| (5) | Ranking the environmental performance of machines, set the machine order as Set(i, j); |
| (6) | Selected machine Select_M(i, j) = min{Set(i, j)} |
| (7) | j++; |
| (8) | End For |
| (9) | i++; |
| (10) | End For |
(2) An improved DE following the decoding rule
Further, the proposed ranking-based heuristic active decoding rule was integrated with the differential evolution algorithm for HFSP environmental scheduling. The flowchart of the RBDE, which can realize the directional selection of the most environmental machines to accelerate the convergence speed, is illustrated in Figure 5. The detail was presented as follows:
Figure 5. Flowchart of the RBDE.
Step1: Initialization. Set simulation phase gen = 1, and initialize the population P0 = {p1, p2, …, pp} uniformly distributed in the search space. The scale factor of mutation and crossover operators were set as F and cr, respectively.
Step 2: Mutation. Difference strategy was carried out to realize individual variation, and the process can be described as:
Mu(NP) = xr1|(P0) + F·(xr2-xr3)|(P0)
where xr (P0) means the rth chromosome of the P0 population.
Step3: Crossover. Cross operation of P0 population and its mutant intermediates Cr(P0 + 1) was implemented as follows.
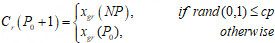
where rand (0, 1) is the random number that is evenly distributed between 0 and 1. xgr() represents the selection gene of the rth chromosome for the population.
Step5: Evaluation and Selection. The ranking-based active decoding method was applied for the selection of the machine for various jobs. The machine with the top ranking in environmental performance was probably selected for production. Then, the energy consumption and makespan could be calculated using the developed model [i.e., Equations (9) and (10)]. Moreover, the iteration process should satisfy the constraints of Equations (11)-(20). In this step, only non-dominated individuals were carried on to the next generations.
Step6: Stopping criteria. The evolution termination judgment was re-executed from Steps 2 to 5 until all termination conditions were met.
Step7: Report. Report the best individual outcome as the optimal solution.
CASE STUDY
A case was presented to testify the feasibility and effectiveness of the proposed methodology for environmental hybrid flow shop scheduling. In this case, four jobs were processed on 25 machines and each job requires 5 steps of operations. Five unrelated parallel machines exist in each process. The data were collected from Chongqing Machine Tool Co., Ltd, China.
Data preparation
The related information, including the job number, processing time, process power, and wait power, can be seen in Table 4. In addition, the environmental performance of each machine was evaluated and ranked using the integrated entropy and fuzzy TOPSIS method. The optimal scheduling solutions were obtained by the modified differential evolution algorithm with the objective of makespan and energy consumption and the variables of machine assignment and process sequence. In addition, the program was implemented in MATLAB 2016 and ran on an Intel Core i5 CPU (2.53 Ghz/8.00 G RAM) PC with a Windows 10 operation system, and the parameters and their selected values for the algorithm are summarized in Table 5.
The production information in HFSP
| Processes | Machines | Job1 | Job2 | Job3 | Job4 | Process power(kW) | Waiting power(kW) |
| Process 1 | M1 | 6 | 4.2 | 6.1 | 5.8 | 20 | 15 |
| M2 | 2.3 | 2.6 | 4.1 | 3.4 | 30 | 25 | |
| M3 | 4.2 | 3.2 | 5.6 | 4.3 | 25 | 20 | |
| M4 | 8.1 | 4.2 | 7.4 | 6.9 | 10 | 5 | |
| M5 | 1.5 | 2.6 | 3.6 | 2.8 | 35 | 30 | |
| Process 2 | M6 | 2.3 | 2.4 | 2.2 | 2.9 | 30 | 25 |
| M7 | 3.5 | 3.6 | 3.2 | 2.6 | 23 | 18 | |
| M8 | 4.3 | 4.3 | 4.8 | 3.6 | 18 | 13 | |
| M9 | 5.2 | 4.5 | 4.8 | 4.8 | 12 | 7 | |
| M10 | 6.1 | 5.2 | 5.6 | 5.1 | 8 | 5 | |
| Process 3 | M11 | 8.1 | 4.8 | 4.5 | 4.8 | 10 | 5 |
| M12 | 7.2 | 3.3 | 3.4 | 3.3 | 18 | 13 | |
| M13 | 3.1 | 2.5 | 1.5 | 1.9 | 35 | 30 | |
| M14 | 5.3 | 3.4 | 2.1 | 2.1 | 23 | 18 | |
| M15 | 9 | 5.3 | 5.3 | 5.6 | 8 | 5 | |
| Process 4 | M16 | 2.6 | 1.5 | 2.2 | 2.8 | 25 | 20 |
| M17 | 3.6 | 2.5 | 4.3 | 3.5 | 20 | 15 | |
| M18 | 3.8 | 1.9 | 3.4 | 3.5 | 23 | 18 | |
| M19 | 5.1 | 2.6 | 5.6 | 4.6 | 15 | 10 | |
| M20 | 6.2 | 3.9 | 6.3 | 5.3 | 10 | 5 | |
| Process 5 | M21 | 4.5 | 4.8 | 7.5 | 7.3 | 10 | 5 |
| M22 | 3.6 | 3.4 | 6.6 | 6.8 | 13 | 8 | |
| M23 | 2.7 | 3.5 | 5.8 | 5.6 | 15 | 10 | |
| M24 | 1.3 | 2.6 | 3.7 | 3.3 | 20 | 15 | |
| M25 | 1.5 | 2.6 | 4.8 | 4.6 | 18 | 13 |
Parameters of the proposed algorithm
| Parameters | Constraints |
| Initial population size | 100 |
| F | 0.5 |
| Cr | 0.3 |
| Stopping condition | Max iteration 200 or convergence‖△f‖ ≤ 10-3 |
The environmentally friendly evaluation information of each machine was measured in Table 6. The reliability of the technical performance was determined by the quality of the product, which was formulated by qualified rate Qr. The basic parameters, namely, the maximum spindle speed, feed rate and precision, were referred from the technical manual of the machines. The processing energy consumption of the environmental performance was related to SEC, which was determined by MRR[21]. The power of the working and waiting stage was listed in Table 4, and all the machines were dry-cutting in the case. The machining cost for the economic performance was measured by uup, the energy consumption was calculated by Equation (10), the value of the cost per unit energy consumption was set as 0.75 RMB/kW·h, and the maintenance cost when processing the 4 four jobs was close to zero.
Environmentally friendly evaluation information for the machines
| Processes | Machines | Job1 | Job2 | Job3 | Job4 |
| Qr/MRR/uup | Qr/MRR/uup | Qr/MRR/uup | Qr/MRR/uup | ||
| Process 1 | M1 | 0.90/22/1.67 | 0.87/25/1.67 | 0.89/50/1.67 | 0.96/27/1.67 |
| M2 | 0.75/30/3.00 | 0.79/32/3.00 | 0.92/58/3.00 | 0.92/34/3.00 | |
| M3 | 0.80/25/2.50 | 0.86/29/2.50 | 0.87/54/2.50 | 0.87/30/2.50 | |
| M4 | 0.91/20/1.00 | 0.91/21/1.00 | 0.95/38/1.00 | 0.82/21/1.00 | |
| M5 | 0.83/40/3.33 | 0.95/35/3.33 | 0.94/62/3.33 | 0.92/36/3.33 | |
| Process 2 | M6 | 0.80/35/3.67 | 0.93/54/3.67 | 0.91/35/3.67 | 0.89/36/3.67 |
| M7 | 0.85/32/3.00 | 0.89/523.00 | 0.86/32/3.00 | 0.91/31/3.00 | |
| M8 | 0.90/29/2.50 | 0.85/48/2.50 | 0.89/28/2.50 | 0.87/26/2.50 | |
| M9 | 0.79/25/2.17 | 0.78/45/2.17 | 0.84/26/2.17 | 0.95/21/2.17 | |
| M10 | 0.84/20/1.33 | 0.75/40/1.33 | 0.95/20/1.33 | 0.97/17/1.33 | |
| Process 3 | M11 | 0.85/38/1.67 | 0.92/25/1.67 | 0.84/15/1.67 | 0.88/32/1.67 |
| M12 | 0.79/45/2.00 | 0.97/27/2.00 | 0.86/18/2.00 | 0.95/37/2.00 | |
| M13 | 0.82/52/3.00 | 0.92/35/3.00 | 0.91/24/3.00 | 0.94/47/3.00 | |
| M14 | 0.94/48/2.50 | 0.89/32/2.50 | 0.82/22/2.50 | 0.86/45/2.50 | |
| M15 | 0.89/35/1.33 | 0.86/22/1.33 | 0.78/13/.33 | 0.87/26/1.33 | |
| Process 4 | M16 | 0.78/38/3.33 | 0.76/37/3.33 | 0.82/34/3.33 | 0.98/42/3.33 |
| M17 | 0.91/25/2.50 | 0.82/34/2.50 | 0.84/29/2.50 | 0.95/34/2.50 | |
| M18 | 0.82/32/3.00 | 0.84/30/3.00 | 0.91/32/3.00 | 0.85/39/3.00 | |
| M19 | 0.95/20/2.17 | 0.79/27/2.17 | 0.72/26/2.17 | 0.91/31/2.17 | |
| M20 | 0.92/17/1.83 | 0.83/25/1.83 | 0.85/24/1.83 | 0.87/24/1.83 | |
| Process 5 | M21 | 0.84/22/1.67 | 0.95/21/1.67 | 0.92/21/1.67 | 0.98/18/1.67 |
| M22 | 0.87/25/2.67 | 0.97/26/2.67 | 0.98/32/2.67 | 0.94/22/2.67 | |
| M23 | 0.91/28/3.00 | 0.89/30/3.00 | 0.91/37/3.00 | 0.87/24/3.00 | |
| M24 | 0.88/35/3.83 | 0.92/34/3.83 | 0.89/47/3.83 | 0.86/36/3.83 | |
| M25 | 0.85/32/3.50 | 0.93/32/3.50 | 0.95/43/3.50 | 0.93/31/3.50 |
RESULTS
Optimal value
To test the effectiveness of the methodology, we expanded the instance size by increasing the times of the data of jobs/processes/machines in Table 4. For simplicity of presentation, an instance with n jobs, s processes, and m machines was denoted as n × s × m. For each instance, the RBDE algorithm was run 50 times independently and took the average value of the solutions. The makespan and energy consumption of the energy-saving and high-efficiency solution obtained by the 12 instances of the simulation are shown in Table 7. The energy-saving point represents the average value of the lowest energy consumption in all optimization results. The high-efficiency point means the average value of the minimum makespan in all optimization results. It can be seen that the variation of energy consumption and makespan agrees with the variation trend of the objectives, as well as the variation trend of the instances. Moreover, it denoted the effectiveness of the proposed integer linear programming model and the algorithm.
Best-found results of RBDE with various instance
| No. | Instances | High-efficiency point | Energy-saving point | Running time (s) | ||
| Makespan(s) | Energy consumption (kWh) | Makespan(s) | Energy consumption (kWh) | |||
| 1 | 4 × 5 × 25 | 21 | 2404 | 22.9 | 1949 | 34.3 |
| 2 | 8 × 5 × 25 | 26.5 | 4067 | 33.8 | 3089 | 61.7 |
| 3 | 12 × 5 × 25 | 30.8 | 4900 | 38.2 | 4253 | 90.3 |
| 4 | 16 × 5 × 25 | 36.6 | 6051 | 40.3 | 5587 | 117.2 |
| 5 | 20 × 5 × 25 | 41.8 | 7113 | 50.2 | 6791 | 143.8 |
| 6 | 25 × 5 × 25 | 47.6 | 9315 | 56.7 | 8374 | 178.8 |
| 7 | 4 × 10 × 50 | 38.4 | 8249 | 39.9 | 6821 | 62.0 |
| 8 | 8 × 10 × 50 | 46.9 | 11,500 | 53.1 | 10,590 | 114.47 |
| 9 | 12 × 10 × 50 | 51.2 | 16,300 | 59.0 | 13,042 | 169.0 |
| 10 | 16 × 10 × 50 | 58.9 | 17,330 | 63 | 16,400 | 220.2 |
| 11 | 20 × 10 × 50 | 64.7 | 19,140 | 67 | 18,730 | 271.6 |
| 12 | 25 × 10 × 50 | 71.7 | 22,230 | 74.9 | 21,850 | 339.6 |
Analysis of the ranking of the environmental performance of machines
To visualize the performance of RBDE, the approximation of Pareto front solutions of NO3 and NO9 instances was selected for further illustration. It can be seen from Figure 6 that the results are distributed evenly and widely, thereby denoting the effectiveness of the proposed method. Moreover, the extreme points A, A’, B, B’ were selected from the obtained approximation of Pareto front solutions in Figure 6A and B to further assess the versatility of the proposed methodology, and the Gantt charts of the four test instances are shown in Figure 7.
Figure 6. Approximation of Pareto front solutions obtained by RBDE.
Figure 7. Gantt chart for the four instances.
As shown in Figure 7, the optimal processing sequence of the jobs in the four instances was optimized as: (A)-(8,10,9,2,4,3,1,6,5,7,12,11); (B)-(11,10,6,9,3,12,2,5,1,8,4,7); (C)-(12,4,2,11,3,10,8,6,9,7,1,5); (D)-(1,4,11,7,5,2,6,8,10,12,9,3), in which the legend for each color means the number of jobs in the hybrid flow shop. The ranking of the environmental performance of machines for each process for different jobs can be obtained according to section “METHODOLOGY”, as shown in Table 8, in which the high ranking of environmental performance means that the machine has better environmental performance and is easier to be selected. It can be seen from Figure 7A and B that the M1, M8, M9, M10, M13, M11, M18, M21 and M23 have low utilization in parallel machine tools, which demonstrated that the lower ranking of the environmental performance of machines was less likely to be selected for production. Besides, the results of the select machine in Figure 7C and D were double in Figure 7A and B, which was also consistent with the ranking of machines.
The ranking of the environmental performance of machines
| Processes | Machines | Ranking of the environmental performance of machines | |||
| Job1 | Job2 | Job3 | Job4 | ||
| Process 1 | M1 | 5 | 5 | 4 | 5 |
| M2 | 2 | 1 | 3 | 2 | |
| M3 | 3 | 4 | 5 | 4 | |
| M4 | 4 | 2 | 2 | 3 | |
| M5 | 1 | 3 | 1 | 1 | |
| Process 2 | M6 | 1 | 1 | 1 | 3 |
| M7 | 2 | 3 | 2 | 1 | |
| M8 | 3 | 5 | 3 | 2 | |
| M9 | 5 | 4 | 4 | 5 | |
| M10 | 4 | 2 | 3 | 4 | |
| Process 3 | M11 | 2 | 4 | 4 | 4 |
| M12 | 4 | 1 | 3 | 3 | |
| M13 | 5 | 2 | 1 | 1 | |
| M14 | 1 | 3 | 2 | 2 | |
| M15 | 3 | 5 | 5 | 5 | |
| Process 4 | M16 | 1 | 1 | 1 | 1 |
| M17 | 2 | 3 | 3 | 2 | |
| M18 | 3 | 2 | 2 | 3 | |
| M19 | 4 | 4 | 5 | 4 | |
| M20 | 5 | 5 | 4 | 5 | |
| Process 5 | M21 | 5 | 5 | 4 | 3 |
| M22 | 4 | 3 | 5 | 5 | |
| M23 | 3 | 4 | 3 | 4 | |
| M24 | 2 | 2 | 1 | 1 | |
| M25 | 1 | 1 | 2 | 2 | |
The assignment of job 1 was adopted to illustrate the feasibility of the method. The scatter diagram of the environmental performance value of the selected machine for job 1’s process was generated, as shown in Figure 8, which vividly illustrated the comparison of environmental performance value. As can be seen from Table 8, the machines with the high ranking of environmental performance are M2, M3, M5 in process1, M6, M7, M8 in process2, M11, M13, M14 in process3, M16, M17, M18 in process4, M23, M24 and M25. The selected machines of job 1 were M5, M8, M14, M18 and M25 according to the Gantt chart in Figure 7A, which means that all the operations avoid the machine tools with the lower ranking. It also reveals the effectiveness of the heuristic active decoding rule in solving environmental scheduling problems.
Figure 8. Scatter diagram of the environmental performance of the machines for job1.
Analysis of the proposed RBDE
In order to verify the effectiveness of the proposed RBDE, three algorithms were adopted for comparison, i.e., PSO, NSGA-II, and DE, and the machines of the instance were expanded to 100. For these algorithms, the population size is set as 100, the number of iterations is 200, and the detailed parameters are shown in Table 9. The running time, energy consumption, and makespan were set as criteria. Moreover, there are some differences in the optimization results of the algorithm, which cannot guarantee that the optimal optimization results can be obtained every time. Therefore, the standard deviation was introduced to reflect the stability of the optimization results of the algorithm. The comparison result is shown in Table 10.
Parameters of these algorithms
| Parameters | Constraints |
| Size of the population | 100 |
| Crossover rate | 0.8 |
| Mutation rate | 0.2 |
| Maximum generations | 200 |
| Threshold value | 0.001 |
| Number of particles in a swarm | 50 |
| Max number of iterations | 40 |
| Acceleration coefficients | 2 |
| Inertia coefficients (min, max) | 0.6, 0.9 |
The comparison of optimization results of PSO, NSGA-II, DE and RBDE
| No. | Instances | Running time | High-efficiency point | Energy-saving point | |||||||||
| Makespan/energy consumption/standard deviation | Makespan/energy consumption/standard deviation | ||||||||||||
| PSO | NSGA-II | DE | RBDE | PSO | NSGA-II | DE | RBDE | PSO | NSGA-II | DE | RBDE | ||
| 1 | 4 × 5 × 25 | 43.2 | 41.5 | 39.7 | 34.3 | 35.5/2617/8.95 | 34.7/2580/7.25 | 28.4/2479/5.85 | 21/2404/2.64 | 26.3/2104/8.95 | 23.4/2104/7.25 | 23.5/1986/5.85 | 22.9/1949/2.64 |
| 2 | 8 × 5 × 25 | 71.2 | 67.8 | 65.2 | 61.7 | 39.6/4325/10.32 | 36.2/4210/6.59 | 32.6/4125/4.63 | 26.5/4067/3.15 | 41.5/3207/10.32 | 40.5/3207/6.59 | 38.2/3145/4.63 | 33.8/3089/3.15 |
| 3 | 12 × 5 × 25 | 104.3 | 102.5 | 95.4 | 90.3 | 41.8/5312/9.76 | 41.3/5294/5.76 | 35.1/5203/5.32 | 30.8/4900/1.76 | 43.9/4425/9.76 | 44.2/4425/5.76 | 42.1/4327/5.32 | 38.2/4253/1.76 |
| 4 | 16 × 5 × 25 | 141.5 | 142.3 | 132.7 | 117.2 | 44.5/6294/8.36 | 45.8/6312/9.36 | 42.6/6254/8.8 | 36.6/6051/2.62 | 47.3/5618/8.36 | 48/5618/9.36 | 44.6/5596/8.80 | 40.3/5587/2.62 |
| 5 | 20 × 5 × 25 | 160.5 | 162.4 | 157.6 | 143.8 | 52.1/7386/11.1 | 53.6/7425/9.5 | 49.7/7211/9.2 | 41.8/7113/3.24 | 51.2/6791/11.1 | 54.6/6791/9.5 | 53.7/6810/9.2 | 50.2/6791/3.24 |
| 6 | 25 × 5 × 25 | 205.7 | 213.5 | 192.2 | 178.8 | 57.2/9483/17.19 | 60.2/9573/10.21 | 56.4/9462/8.57 | 47.6/9315/4.65 | 59.7/8510/17.19 | 61.2/8510/10.21 | 59.2/8421/8.57 | 56.7/8374/4.65 |
| 7 | 4 × 10 × 50 | 73.4 | 71.5 | 69.8 | 62.0 | 53.7/8627/12.35 | 51.4/8462/8.69 | 45.3/8351/7.98 | 38.4/8249/3.1 | 45.6/7125/12.35 | 42.3/7125/8.69 | 40.3/6932/7.98 | 39.9/6821/3.10 |
| 8 | 8 × 10 × 50 | 131.2 | 126.7 | 120.5 | 114.47 | 65.4/13011/15.51 | 63.5/12035/9.39 | 58.5/11798/8.65 | 46.9/11500/5.38 | 60.3/11742/15.51 | 57.9/11742/9.39 | 55.8/11620/8.65 | 53.1/10590/5.38 |
| 9 | 12 × 10 × 50 | 185.3 | 184.6 | 178.3 | 169.0 | 66.2/17684/10.98 | 65.7/17256/8.42 | 60.2/17001/7.21 | 51.2/16300/7.61 | 67.4/13965/10.98 | 65.3/13965/8.42 | 62.4/13872/7.21 | 59.0/13042/7.61 |
| 10 | 16 × 10 × 50 | 232.4 | 238.1 | 232.4 | 220.2 | 70.8/17925/10.34 | 71.9/18103/7.35 | 68.9/17856/6.89 | 58.9/17330/4.77 | 70.5/16492/10.34 | 71.2/16492/7.35 | 67.5/16475/6.89 | 63/16400/4.77 |
| 11 | 20 × 10 × 50 | 289.7 | 293.6 | 286.5 | 271.6 | 75.7/20473/11.32 | 76.3/20975/6.84 | 72.2/20113/5.32 | 64.7/19140/7.76 | 74.3/20112/11.32 | 75.6/20112/6.84 | 70.1/19023/5.32 | 67/18730/7.76 |
| 12 | 25 × 10 × 50 | 365.1 | 378.4 | 352.6 | 339.6 | 82.6/22868/17.08 | 85.4/23109/9.21 | 78.5/22870/6.38 | 71.7/22230/2.91 | 76.7/22367/17.08 | 79.1/22367/9.21 | 23.5/1986/5.85 | 74.9/21850/2.91 |
| 13 | 4 × 15 × 100 | 123.6 | 117.6 | 110.2 | 103.5 | 79.5/15953/9.67 | 81.6/15224/9.25 | 76.2/15005/8.35 | 57.6/15357/2.89 | 88.3/11923/14.32 | 87.7/12037/9.17 | 81.5/11984/9.21 | 59.7/11325/4.35 |
| 14 | 8 × 15 × 100 | 206.9 | 201.3 | 182.5 | 171.4 | 91.2/17105/12.68 | 89.3/17021/8.41 | 80.5/16981/6.57 | 65.4/16493/4.35 | 96.2/13398/11.38 | 94.8/13429/9.58 | 86.4/13369/7.36 | 69.6/12985/6.52 |
| 15 | 12 × 15 × 100 | 266.4 | 261.3 | 241.3 | 235.0 | 95.7/18936/13.57 | 92.6/18725/9.23 | 89.4/18116/8.51 | 73.2/17536/5.32 | 99.1/16813/12.69 | 98.4/17153/7.46 | 94.5/16211/8.29 | 79.5/14889/5.71 |
| 16 | 16 × 15 × 100 | 319.8 | 321.6 | 301.7 | 291.5 | 101.2/19031/12.35 | 105.8/19242/8.64 | 96.3/18927/7.32 | 79.2/18253/3.95 | 109.9/18137/11.98 | 110.4/18269/8.26 | 105.7/17675/6.24 | 87.2/16920/6.28 |
| 17 | 20 × 15 × 100 | 368.3 | 377.4 | 362.4 | 351.9 | 106.3/22763/10.68 | 110.7/23082/7.25 | 103.5/22563/6.87 | 85.6/21335/6.25 | 116.6/21057/10.52 | 121.4/21989/7.34 | 110.1/20132/4.58 | 97.5/18730/5.39 |
| 18 | 25 × 15 × 100 | 439.7 | 441.6 | 433.8 | 426.3 | 115.8/24069/16.59 | 118.6/24105/8.91 | 110.2/23948/7.14 | 91.1/23514/3.98 | 129.7/23150/15.87 | 132.4/23856/8.91 | 124.5/22854/7.13 | 103.2/21387/4.16 |
It can be seen from Table 10, the proposed RBDE performs better than other algorithms in terms of running time, the consumption of energy and makespan in both the high-efficiency point and the energy-saving point, which means that the RBDE has higher search efficiency and can obtain better scheduling scheme. The values of different criteria of four algorithms under different scales show that the proposed RBDE has more advantages in solving large-scale problems. Moreover, it can be observed from the results that RBDE has strong advantages in solving stability of scheduling problems of any instance comparing the standard deviation of optimization results of these algorithms. To sum up, the proposed RBDE has more advantages in solving HFSP.
Furthermore, in order to test the performance of the proposed algorithm, the heuristic rule was implanted in the Non-dominated sorting genetic algorithm-II (NSGA-II) and Particle Swarm optimization algorithm (PSO), namely RBNSGA-II and RBPSO. The ‘Max.’, ‘Avg.’, and ‘Min.’ columns represent the maximum, average, and minimum number of non-dominated solutions, respectively. It can be clearly found from Table 11 that the overall Avg, Max and Min yielded by RBDE were better than those generated by RBNSGA-II and RBPSO algorithms in the same running time for different scale problems. The reason can be explained by the fact that the proposed algorithm can take full of the non-dominated solutions to generate excellent offspring and the heuristic rule for iteration operators to disturb old individuals. Besides, in this paper, four performance metrics were utilized to evaluate the improved methods, i.e, convergence metric, uniformity performance, diversity metric, and hyper-volume.
Number of non-dominated solutions of each algorithm
| No. | Instance | RBDE | RBPSO | RBNSGA-II | ||||||
| Max | Min | Avg | Max | Min | Avg | Max | Min | Avg | ||
| 1 | 4 × 5 × 25 | 6 | 4 | 5.2 | 4 | 3 | 3.1 | 5 | 3 | 4.6 |
| 2 | 8 × 5 × 25 | 18 | 10 | 14.5 | 15 | 9 | 11.3 | 17 | 10 | 13.2 |
| 3 | 12 × 5 × 25 | 21 | 12 | 14.2 | 16 | 11 | 12.5 | 17 | 12 | 13.4 |
| 4 | 16 × 5 × 25 | 28 | 10 | 21.7 | 13 | 8 | 10.3 | 23 | 10 | 18.5 |
| 5 | 20 × 5 × 25 | 22 | 15 | 19.4 | 18 | 12 | 15.6 | 20 | 13 | 18.9 |
| 6 | 25 × 5 × 25 | 28 | 13 | 20.1 | 18 | 12 | 17.4 | 24 | 12 | 18.3 |
| 7 | 4 × 10 × 50 | 5 | 3 | 4.5 | 3 | 2 | 2.6 | 4 | 3 | 3.2 |
| 8 | 8 × 10 × 50 | 12 | 9 | 11.3 | 11 | 5 | 7.9 | 13 | 7 | 9.8 |
| 9 | 12 × 10 × 50 | 24 | 13 | 22.4 | 18 | 11 | 16.3 | 21 | 14 | 18.1 |
| 10 | 16 × 10 × 50 | 23 | 15 | 19.5 | 17 | 10 | 12.6 | 20 | 12 | 16.4 |
| 11 | 20 × 10 × 50 | 17 | 10 | 12.3 | 14 | 8 | 10.5 | 15 | 9 | 11.2 |
| 12 | 25 × 10 × 50 | 15 | 7 | 9.6 | 12 | 6 | 8.3 | 13 | 6 | 8.9 |
| 13 | 4 × 15 × 100 | 16 | 9 | 13.6 | 9 | 5 | 6.1 | 9 | 6 | 7.5 |
| 14 | 8 × 15 × 100 | 27 | 16 | 19.7 | 17 | 8 | 15.5 | 14 | 8 | 12.1 |
| 15 | 12 × 15 × 100 | 37 | 24 | 29.4 | 25 | 17 | 21.3 | 27 | 16 | 21.4 |
| 16 | 16 × 15 × 100 | 26 | 13 | 22.7 | 15 | 10 | 12.6 | 19 | 12 | 13.7 |
| 17 | 20 × 15 × 100 | 31 | 19 | 24.3 | 15 | 9 | 11.2 | 20 | 13 | 17.9 |
| 18 | 25 × 15 × 100 | 35 | 21 | 31.5 | 18 | 11 | 15.7 | 26 | 15 | 20.6 |
(1) convergence metric γ represents the distance between Pareto front P and the true Pareto-optimal front P*[48].
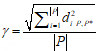
where |P| is the approximate Pareto-optimal front obtained by the specific algorithm, and dip, p* is the Euclidean distance between the ith solution in P and its closest neighbor in P*. P* refers to the true Pareto-optimal front. Since the true Pareto-optimal front P* is unknown for the test benchmarks, we merge the solutions obtained by all algorithms that we adopted and take the nondominated ones as P*.
(2) Uniformity Performance. Spacing Metric sp was used to measure the standard deviation of the minimum distance from each solution to others. The small value of spacing means that the distribution of the solutions in the Pareto solution set is more balance[49].
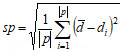
where di is the minimum distance from t point i on the Pareto frontier of the algorithm to the other points,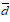 
is the average value of all distance di.
(3) Diversity metric △ measures the extent of spread achieved among the obtained solutions[48].
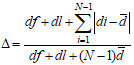
where df and dl are the Euclidean distances between the extreme solutions and the boundary solutions of the obtained non-dominated set. Assuming that there are N solutions on the best non-dominated front.
(4) Hyper-volume, HV. The volume of the region in the target space was enclosed by the non-dominant solution set and the reference point obtained by the algorithm. The larger the HV value, the better the comprehensive performance of the algorithm[50].
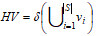
where δ is the Lebesgue measure, which was used to measure volume. |S| represents the number of non-dominated solution sets. vi means the Super volume composed of the reference point and the ith solution in the solution set.
Table 12 shows the statistical performance metrics obtained by the three algorithms. It was revealed from the table that RBDE outperforms RBNSAG-II and RBPSO for almost all the metrics, particularly for γ and sp, which means that RBDE can achieve the most proximity to the reference front. In terms of convergence γ, RBDE and RBPSO can quickly converge to a better value than RBNSAG-II. However, RBPSO is easy to fall into local convergence, and the universality and diversity of RBDE and RBNSGA-II (△ and HV) are significantly superior to the RBPSO. From the uniformity performance perspective (i.e, sp), it can be observed that the proposed RBDE and RBPSO outperform RBNSGA-II when the size is small. However, such an advantage will no longer exist if the problem size is larger. In the large-scale problems, the proposed RBDE and the RBNSGA-II can find more non-dominated solutions. In addition, RBDE can efficiently solve multi-objective HFSP problems, which means the proposed algorithms have better search ability than the others in this work.
Comparison of optimization results of the algorithms
| No. | Instance | RBDE | RBPSO | RBNSGA-II | |||||||||
| γ | Sp | △ | HV | γ | Sp | △ | HV | γ | Sp | △ | HV | ||
| 1 | 4*5*25 | 69.00 | 141.44 | 0.60 | 13.50 | 69.00 | 141.44 | 0.60 | 13.50 | 69.00 | 141.44 | 0.60 | 13.50 |
| 2 | 8*5*25 | 191.38 | 112.81 | 0.75 | 444.20 | 148.72 | 134.00 | 1.41 | 230.30 | 191.41 | 166.44 | 0.83 | 239.30 |
| 3 | 12*5*25 | 123.61 | 55.89 | 0.69 | 331.80 | 228.20 | 82.55 | 0.75 | 150.10 | 153.51 | 100.23 | 0.73 | 197.00 |
| 4 | 16*5*25 | 162.31 | 48.05 | 0.86 | 353.30 | 363.70 | 64.75 | 0.95 | 309.10 | 249.64 | 101.42 | 0.89 | 309.10 |
| 5 | 20*5*25 | 84.33 | 55.44 | 0.86 | 3879.00 | 276.67 | 86.66 | 0.97 | 1068.00 | 154.15 | 161.59 | 0.94 | 1506.40 |
| 6 | 25*5*25 | 80.38 | 85.16 | 0.61 | 966.50 | 267.86 | 195.66 | 0.94 | 333.80 | 140.72 | 98.15 | 0.92 | 949.30 |
| 7 | 4*10*50 | 35.00 | 37.79 | 0.07 | 37.00 | 35.00 | 37.79 | 0.07 | 37.00 | 35.00 | 37.79 | 0.07 | 37.00 |
| 8 | 8*10*50 | 94.42 | 163.86 | 0.85 | 135.00 | 94.42 | 163.86 | 0.85 | 135.00 | 94.42 | 163.86 | 0.85 | 135.00 |
| 9 | 12*10*50 | 103.75 | 173.27 | 0.67 | 312.00 | 128.33 | 249.99 | 0.75 | 120.00 | 113.76 | 181.53 | 0.73 | 247.00 |
| 10 | 16*10*50 | 112.31 | 158.39 | 0.72 | 321.78 | 267.82 | 205.69 | 0.74 | 125.42 | 198.53 | 176.33 | 0.74 | 273.25 |
| 11 | 20*10*50 | 323.00 | 123.57 | 0.73 | 347.00 | 761.25 | 196.00 | 0.80 | 136.00 | 453.75 | 180.19 | 0.74 | 146.00 |
| 12 | 25*10*50 | 150.00 | 94.44 | 0.52 | 439.50 | 350.47 | 125.62 | 0.79 | 376.81 | 236.00 | 82.82 | 0.73 | 409.00 |
| 13 | 4 × 15 × 100 | 29.72 | 92.31 | 0.71 | 52.36 | 29.72 | 98.72 | 0.61 | 52.36 | 29.72 | 105.72 | 0.65 | 52.36 |
| 14 | 8 × 15 × 100 | 52.69 | 113.62 | 0.87 | 97.25 | 50.37 | 116.21 | 0.92 | 78.69 | 52.09 | 120.62 | 0.91 | 78.69 |
| 15 | 12 × 15 × 100 | 98.51 | 149.73 | 0.79 | 305.43 | 90.35 | 158.15 | 0.84 | 205.73 | 83.12 | 160.44 | 0.83 | 287.75 |
| 16 | 16 × 15 × 100 | 157.32 | 171.81 | 0.62 | 317.68 | 234.51 | 189.63 | 0.79 | 247.61 | 201.31 | 177.52 | 0.72 | 354.27 |
| 17 | 20 × 15 × 100 | 251.86 | 188.40 | 0.76 | 367.93 | 347.25 | 192.76 | 0.85 | 183.64 | 417.53 | 185.35 | 0.81 | 217.62 |
| 18 | 25 × 15 × 100 | 231.60 | 163.12 | 0.84 | 397.25 | 302.72 | 181.37 | 0.97 | 217.98 | 310.42 | 170.37 | 0.95 | 241.01 |
To visualize the performance of these algorithms intuitively, the approximation of the Pareto front of the different scope of job instance, i.e., NO2, NO3, NO4, NO6, NO11 and NO12 are shown in Figure 9.
Figure 9. The approximation of Pareto front solutions of RBDE, RBNSGA-II and RBPSO algorithms. (●-RBDE, ◆-RBNSGA-II, 
-RBPSO)
As shown in Figure 9, the curves of these three schemes converge toward the approximation of the Pareto front, which gives an intuitive illustration of some results derived from the performance metrics. In addition, the RBDE algorithm performs the best among the three algorithms both in the quality and diversity of the solutions. These results also well explain the differences in the above-mentioned performance metrics for the three algorithms.
To sum up, the proposed RBDE algorithm was capable of providing better solutions than RBNSGA-II and RBPSO in terms of quality, running time and distribution of Pareto solutions. Besides, the heuristic active decoding rule of the proposed algorithm on the basis of the ranking of the environmental performance of machines can effectively narrow the research scope and improve search efficiency.
CONCLUSION
The accelerating use of energy and resource causes a significant increase in carbon dioxide, one of the foremost greenhouse gases (GHGs), which has radically contributed to the threat of global warming and climate change. In order to reduce the emissions for production, environmental scheduling has attracted worldwide attention. In this work, an environmental scheduling method is proposed to support the environmental production of the hybrid flow shop by evaluating and ranking the environmental performance of machines and integrating the active decoding rule for machine assignment into the differential evolution algorithm. In light of this, the environmental scheduling method can be elaborated and applied in terms of production timely and efficiently.
This method is suitable for environmental production in HFSP, which can be extended to other complex workshops, such as flexible flow shop scheduling problems. Moreover, efforts are expected to supplement the criteria of an environmentally friendly evaluation system, such as the social aspect. In future work, the multi-objective optimization tools are expected to be established to make use of to achieve comprehensive optimization by considering large numbers of variables and constraints, e.g., setup time of machines, limited resources, and requirements of customer order. The actual jobs-shop production to validate this method for environmental scheduling will be further discussed. Also, how to effectively avoid the problem that some machine tools are often selected and some are ignored in the production will further analyze.
DECLARATIONS
Authors’ contributionsConceived the methodology: Kong L, Wang L, Li F
Performed the manuscript: Kong L
Checked the data: Li J, Wang Y
Proofread manuscript: Cai Z, Zhou J
Availability of data and materialsAll data and materials used or analyzed during the current study are included in this manuscript.
Financial support and sponsorshipThis research was supported by the National Key R&D Program of China (Grant No. 2020YFB1711601), and the National Natural Science Foundation of China (Grant No. 52175473).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2023.
REFERENCES
1. Kong L, Wang L, Li F, Wang G, Fu Y, Liu J. A new sustainable scheduling method for hybrid flow-shop subject to the characteristics of parallel machines. IEEE Access 2020;8:79998-80009.
2. Miao Y, Lv X, Zhe C, Guo D. Application of self-adaptive evolution strategy DE algorithm based on optimal objective of due date in HFSP. 2015 IEEE Int Conf Cyber Technol Autom Control Intell Syst IEEE-CYBER; 2015. pp. 1491-5.
3. Ma Y, Li F, Wang L, Wang G, Kong L. Life cycle carbon emission assessments and comparisons of cast iron and resin mineral composite machine tool bed in China. Int J Adv Manuf Technol 2021;113:1143-52.
4. Kong L, Wang L, Li F, et al. A life-cycle integrated model for product Eco-design in the conceptual design phase. J Clean Prod 2022;363:132516.
5. Qin H, Han Y, Liu Y, Li J, Pan Q, Xue-han. A collaborative iterative greedy algorithm for the scheduling of distributed heterogeneous hybrid flow shop with blocking constraints. Expert Syst Appl 2022;201:117256.
6. Qin H, Han Y, Wang Y, Liu Y, Li J, Pan Q. Intelligent optimization under blocking constraints: A novel iterated greedy algorithm for the hybrid flow shop group scheduling problem. Knowl Based Syst 2022;258:109962.
7. Xu Y, Wang L, Wang S, Liu M. An effective shuffled frog-leaping algorithm for solving the hybrid flow-shop scheduling problem with identical parallel machines. Eng Optim 2013;45:1409-30.
8. Meng L, Zhang C, Shao X, Zhang B, Ren Y, Lin W. More MILP models for hybrid flow shop scheduling problem and its extended problems. Int J Prod Res 2020;58:3905-30.
9. Luo H, Du B, Huang GQ, Chen H, Li X. Hybrid flow shop scheduling considering machine electricity consumption cost. Int J Prod Econ 2013;146:423-39.
10. Behnamian J. Scheduling and worker assignment problems on hybrid flowshop with cost-related objective function. Int J Adv Manuf Technol 2014;74:267-83.
11. Zhao F, Ma R, Wang L. A self-learning discrete jaya algorithm for multiobjective energy-efficient distributed no-idle flow-shop scheduling problem in heterogeneous factory system. IEEE Trans Cybern 2022;52:12675-86.
12. Qin H, Han Y, Zhang B, et al. An improved iterated greedy algorithm for the energy-efficient blocking hybrid flow shop scheduling problem. Swarm Evol Comput 2022;69:100992.
13. Meng L, Zhang C, Shao X, Ren Y, Ren C. Mathematical modelling and optimisation of energy-conscious hybrid flow shop scheduling problem with unrelated parallel machines. Int J Prod Res 2019;57:1119-45.
14. Li J, Sang H, Han Y, Wang C, Gao K. Efficient multi-objective optimization algorithm for hybrid flow shop scheduling problems with setup energy consumptions. J Clean Prod 2018;181:584-98.
15. Novak A, Sucha P, Novotny M, Stec R, Hanzalek Z. Scheduling jobs with normally distributed processing times on parallel machines. Eur J Oper Res 2022;297:422-41.
16. Yepes-borrero JC, Perea F, Ruiz R, Villa F. Bi-objective parallel machine scheduling with additional resources during setups. Eur J Oper Res 2021;292:443-55.
17. Thies C, Kieckhäfer K, Spengler TS, Sodhi MS. Operations research for sustainability assessment of products: a review. Eur J Oper Res 2019;274:1-21.
18. Drake R, Yildirim MB, Twomey J, Whitman L, Ahmad J, Lodhia P. Data collection framework on energy consumption in manufacturing. Available from: https://soar.wichita.edu/bitstream/handle/10057/3422/Yildirim_2006.pdf?sequence=3&isAllowed=y [Last accessed on 10 Jan 2023].
19. Mouzon G, Yildirim MB, Twomey J. Operational methods for minimization of energy consumption of manufacturing equipment. Int J Prod Res 2007;45:4247-71.
20. Liu X, Wang L, Kong L, Li F, Li J. A hybrid genetic algorithm for minimizing energy consumption in flow shops considering ultra-low idle state. Procedia CIRP 2019;80:192-6.
21. Kong L, Wang L, Li F, et al. Multi-layer integration framework for low carbon design based on design features. J Manuf Syst 2021;61:223-38.
22. Dimitrov D, Karachorova V, Szecsi T. Accuracy and reliability control of machining operations on machining centres. Key Eng Mater 2014;615:32-8.
23. Brecher C, Fey M, Daniels M. Modeling of position-, tool- and workpiece-dependent milling machine dynamics. Available from: http://publications.rwth-aachen.de/record/661060/files/661060.pdf [Last accessed on 10 Jan 2023].
24. Salido MA, Escamilla J, Giret A, Barber F. A genetic algorithm for energy-efficiency in job-shop scheduling. Int J Adv Manuf Technol 2016;85:1303-14.
25. Feng Y, Zhou M, Tian G, et al. Target disassembly sequencing and scheme evaluation for cnc machine tools using improved multiobjective ant colony algorithm and fuzzy integral. IEEE Trans Syst Man Cybern Syst 2019;49:2438-51.
26. Lu C, Gao L, Pan Q, Li X, Zheng J. A multi-objective cellular grey wolf optimizer for hybrid flowshop scheduling problem considering noise pollution. Appl Soft Comput 2019;75:728-49.
27. Kang Y, Tang D. An approach to product solution generation and evaluation based on the similarity theory and ant colony optimisation. Int J Comput Integr Manuf 2014;27:1090-104.
28. Fang R, Popole Z. Multi-objective optimized scheduling model for hydropower reservoir based on improved particle swarm optimization algorithm. Environ Sci Pollut Res Int 2020;27:12842-50.
29. Tian G, Ren Y, Zhou M. Dual-objective scheduling of rescue vehicles to distinguish forest fires via differential evolution and particle swarm optimization combined algorithm. IEEE Trans Intell Transp Syst 2016;17:3009-21.
30. Wang L, Xu Y, Zhou G, Wang S, Liu M. A novel decoding method for the hybrid flow-shop scheduling problem with multiprocessor tasks. Int J Adv Manuf Technol 2012;59:1113-25.
31. Tian G, Ren Y, Feng Y, Zhou M, Zhang H, Tan J. Modeling and planning for dual-objective selective disassembly using and/or graph and discrete artificial bee colony. IEEE Trans Ind Inf 2019;15:2456-68.
32. Ding J, Song S, Wu C. Carbon-efficient scheduling of flow shops by multi-objective optimization. Eur J Oper Res 2016;248:758-71.
33. Tliba K, Diallo TML, Penas O, Ben Khalifa R, Ben Yahia N, Choley J. Digital twin-driven dynamic scheduling of a hybrid flow shop. J Intell Manuf ; doi: 10.1007/s10845-022-01922-3.
34. He Y, Li Y, Wu T, Sutherland JW. An energy-responsive optimization method for machine tool selection and operation sequence in flexible machining job shops. J Clean Prod 2015;87:245-54.
35. Lu C, Gao L, Li X, Pan Q, Wang Q. Energy-efficient permutation flow shop scheduling problem using a hybrid multi-objective backtracking search algorithm. J Clean Prod 2017;144:228-38.
36. Strantzali E, Aravossis K, Livanos GA. Evaluation of future sustainable electricity generation alternatives: the case of a Greek island. Renew Sust Energ Rev 2017;76:775-87.
37. Sahabuddin M, Khan I. Multi-criteria decision analysis methods for energy sector’s sustainability assessment: robustness analysis through criteria weight change. Sustain Energy Technol Assess 2021;47:101380.
38. He B, Luo T, Huang S. Product sustainability assessment for product life cycle. J Clean Prod 2019;206:238-50.
39. Tian G, Zhang H, Zhou M, Li Z. AHP, gray correlation, and TOPSIS combined approach to green performance evaluation of design alternatives. IEEE Trans Syst Man Cybern Syst 2018;48:1093-105.
40. Memari A, Dargi A, Akbari Jokar MR, Ahmad R, Abdul Rahim AR. Sustainable supplier selection: a multi-criteria intuitionistic fuzzy TOPSIS method. J Manuf Syst 2019;50:9-24.
41. Shih H, Shyur H, Lee ES. An extension of TOPSIS for group decision making. Math Comput Model 2007;45:801-13.
42. Liu X, Yang X, Lei M. Optimisation of mixed-model assembly line balancing problem under uncertain demand. J Manuf Syst 2021;59:214-27.
43. Tiwari V, Jain PK, Tandon P. An integrated Shannon entropy and TOPSIS for product design concept evaluation based on bijective soft set. J Intell Manuf 2019;30:1645-58.
44. Wang X, Chan HK, Li D. A case study of an integrated fuzzy methodology for green product development. Eur J Oper Res 2015;241:212-23.
45. Zhao F, Zhao L, Wang L, Song H. An ensemble discrete differential evolution for the distributed blocking flowshop scheduling with minimizing makespan criterion. Expert Syst Appl 2020;160:113678.
46. Liu W, Gong Y, Chen W, Liu Z, Wang H, Zhang J. Coordinated charging scheduling of electric vehicles: a mixed-variable differential evolution approach. IEEE Trans Intell Transp Syst 2020;21:5094-109.
47. Li L, Wang Y, Xu Y, Lin K. Meta-learning based industrial intelligence of feature nearest algorithm selection framework for classification problems. J Manuf Syst 2022;62:767-76.
48. Luo S, Zhang L, Fan Y. Energy-efficient scheduling for multi-objective flexible job shops with variable processing speeds by grey wolf optimization. J Clean Prod 2019;234:1365-84.
49. Li X, Lu C, Gao L, Xiao S, Wen L. An effective multiobjective algorithm for energy-efficient scheduling in a real-life welding shop. IEEE Trans Ind Inf 2018;14:5400-9.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Kong L, Li F, Wang L, Li J, Wang Y, Cai Z, Zhou J. Environmentally friendly strategy for hybrid flow shop scheduling with the unrelated parallel machines. Green Manuf Open 2023;1:8. http://dx.doi.org/10.20517/gmo.2022.10
AMA Style
Kong L, Li F, Wang L, Li J, Wang Y, Cai Z, Zhou J. Environmentally friendly strategy for hybrid flow shop scheduling with the unrelated parallel machines. Green Manufacturing Open. 2023; 1(2): 8. http://dx.doi.org/10.20517/gmo.2022.10
Chicago/Turabian Style
Kong, Lin, Fangyi Li, Liming Wang, Jianfeng Li, Yitong Wang, Zekang Cai, Jiaxuan Zhou. 2023. "Environmentally friendly strategy for hybrid flow shop scheduling with the unrelated parallel machines" Green Manufacturing Open. 1, no.2: 8. http://dx.doi.org/10.20517/gmo.2022.10
ACS Style
Kong, L.; Li F.; Wang L.; Li J.; Wang Y.; Cai Z.; Zhou J. Environmentally friendly strategy for hybrid flow shop scheduling with the unrelated parallel machines. Green. Manuf. Open. 2023, 1, 8. http://dx.doi.org/10.20517/gmo.2022.10
About This Article
Copyright
Data & Comments
Data
0
Cite This Article 10 clicks
Like This Article 21
likes
Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.