A prediction approach of fiber laser surface treatment using ensemble of metamodels considering energy consumption and processing quality
, ... Abstract
Laser surface treatment (LST) is essential for advanced manufacturing but is extremely energy intensive. Being energy-aware is imperative as the industry pays increasing attention to energy management and environmental protection. However, existing literature mainly focuses on the laser-material interaction in LST, while few studies have considered energy consumption when investigating the processing quality. In this article, three metamodels (Kriging, RBF, and SVR) are integrated into an ensemble of metamodels (EM) by suitable weight coefficients, and the EM incorporates the predictive advantages of different metamodels. The EM establishes the relationship between laser process parameters (laser power, scan speed, and defocusing amount) and three outputs (total energy consumption, surface roughness, and depth-width ratio of LST track). The effectiveness of the presented prediction approach is validated by the leave-one-out method and additional experiments. Furthermore, the main influences of process parameters on the three outputs are studied. According to the technique for order preference by similarity to an ideal solution (TOPSIS), the optimal process parameter is Group No. 2, with the relative closeness of 78.04%, while the worst one is Group No. 13, with the relative closeness of 2.21%. The presented prediction approach can serve as a reliable foundation in the energy-aware application of laser processing.
Keywords
INTRODUCTION
Recent years have witnessed the growing importance and urgency of energy-saving and environmental protection in manufacturing. Statistics from the International Energy Agency (IEA) indicate that, among energy-consuming industries, manufacturing activity contributes over 33% of the total energy consumption in countries of the Organization for Economic Cooperation and Development (OECD)[1,2]. In addition, manufacturers are urged to make tangible efforts to enhance energy efficiency to gradually achieve green manufacturing, and related legislation is being introduced to promote this transition[3]. Therefore, energy awareness in processing is becoming increasingly critical, and further understanding of energy consumption should be uncovered to enhance economic gains while minimizing environmental influences.
Laser surface treatment (LST) is recently one of the most popular methods of heat treatment, since LST effectively improves surface performance and prolongs the service life of parts[4-8]. LST without added materials encompasses laser surface quenching (LSQ) and laser surface melting (LSM) techniques[4]. During LST, the surface temperature of the workpiece increases quickly to temperatures above the point of critical transformation (austenization or melting temperature), and the self-excited cooling quickly makes the surface layer change into new phases with fine microstructure and high dislocation density[4,5]. Compared with traditional heat treatment techniques, the benefits of LST include low thermal deformation, homogeneous microstructures, little limitation on the shape complexity of the part, no need for intermediate cooling media, and controllable quality[4,5,9]. Thus, LST plays an increasingly prominent role in the heat treatment area and has been widely applied in many fields, such as metallurgy, railway, machinery manufacturing, and aerospace[10-13]. However, LST involves complicated coupling variations including temperature, stress, and microstructure transformation[5]. Changes in parameters, such as exposure time, the power of laser beam, and geometry and energy distribution of beam, can lead to different processing results[9,14]. The prediction for LST involves revealing the non-linear correlation between the laser process parameters and the processing results, which is traditionally addressed based on experience and the trial-and-error method with a long development cycle. Although experimental results are of great value to researchers, the vast cost and time required for experiments are prohibitive. Furthermore, output results other than known sample points within the process window are difficult to obtain due to the lack of adequate information.
To address this, various modeling approaches are used for prediction and optimization in LST, among which metamodeling is effective in revealing the relationship between process parameters and processing qualities[5,9,15-18]. Zhang et al. used non-linear equations of the Taylor series to establish the relationships between the laser process parameters and surface hardening effects (wear resistance, hardness, hardening depth, and surface roughness), and then applied particle swarm optimization (PSO) to achieve the hardening requirement and the high efficiency[18]. Lambiase et al. predicted the hardness of the laser hardened surface using an artificial neural network (ANN), where the analytical model of temperature history was used[19]. Colombini et al. employed the response surface method (RSM) to construct the functions between inputs (focal length, laser beam speed, and temperature) and outputs (hardness and geometry of the laser hardened zone) in laser quenching, and then performed the optimization based on the functions[9].
Some researchers have studied the energy consumption and environmental impact of other laser processing methods[2,20-22]. However, existing literature on LST mainly focuses on the laser-material interaction, and few articles consider the energy consumption of LST when investigating the processing quality. In addition, every metamodel has specific merits and demerits[23], and no stand-alone metamodel is the most efficient in all applications[24,25]. Thus, if an unsuitable metamodel is chosen, an accurate result is hard to obtain. Randomly selecting a metamodel may increase the possibility of suboptimal results[26,27]. The accuracy of the individual metamodel mostly hinges on the specific training data used and characteristics of the problems faced, and it is therefore likely that the selected metamodels turn out to be less accurate with new sample points[23,26].
To overcome the drawbacks aforementioned, three different metamodels, namely Kriging, radial basis function (RBF), and support vector regression (SVR), are integrated into an ensemble of metamodels (EM) to reduce the risk of adopting an inappropriate individual metamodel. Furthermore, both the energy awareness and the processing quality are investigated in this work. Three-factor and four-level experiments were designed and carried out. The EM constructs the correlation between laser process parameters and processing results (including total energy consumption, surface roughness, and depth-width ratio of processing track) for the prediction in fiber LST. In addition, verification experiments show the effectiveness of the presented prediction approach.
EXPERIMENTAL DETAILS
Experimental platform and materials
The shield disc cutter is subjected to severe friction and wear processes during the tunneling[28], and a surface with high hardness helps to improve its tribological performance[29,30]. The commercially available shield disc cutter is used as the workpiece, which is named KDCMSV special steel and offered by Wuhan Engineering Drilling Tool Co., Ltd. Based on the H13 die steel material, the manufacturer appropriately increases the content of alloying elements such as C, Cr, Mo, and V to produce the special material for the shield disc cutter, and the main components are shown in Table 1. Additionally, the mechanical properties of the KDCMSV special steel are as follows: hardness of 56.8 HRC, ultimate tensile strength of 1890 Mpa, yield strength of 1705 Mpa, and impact toughness of 17.8 J/cm2. The quenching and tempering treatment is performed on the whole part of the shield disc cutter, and the schematic diagram of the process is shown in Figure 1. Specifically, the shield disc cutter was first heated to 1080 ℃ for 2 h, and then subjected to oil quenching. After that, it was washed with cold water for 30 min, then heated to 550 ℃ for 5 h, and finally air-cooled to room temperature. The workpiece was cut from the shield disc cutter using wire-electrode cutting and used for the LST experiments. The dimensions of the workpiece are shown in Figure 2, and it can be observed that there is micro-texture produced by turning processing on the workpiece surface, resulting in the surface with the average RA of 7.12 μm. Figure 3 indicates the schematic diagram of the LST process, and the focal length is 250 mm. Figure 4 shows the integrated platform of LST processing and energy consumption metering, which contains IPG fiber laser system (power range from 400 to 4000 W), ABB six-axis robot, chiller system, VICTOR-5000 smart power meter (SPM), and other auxiliary equipment.
Figure 1. The schematic diagram of the quenching and tempering process of the shield disc cutter.
Figure 2. The dimensions of the workpiece and the shield disc cutter.
Figure 3. The schematic diagram of the fiber LST process. LST: Laser surface treatment.
Figure 4. The platform of fiber LST processing and energy consumption metering. LST: Laser surface treatment.
The main components of KDCMSV special steel
| Element | C | Si | Mn | P | S | Cr | Ti | V | Mo |
| wt.% | 0.5 | 0.8 | 0.7 | 0.015 | 0.005 | 5.5 | 0.5 | 1.2 | 1.8 |
Design of experiment
The laser process parameters have significant effects on the cross-sectional profile of the laser treated zone. Based on pre-tests and related literature[5,9,12], the laser process parameters that significantly affect the LST results are laser power (LP), scan speed (SS), and defocusing amount (DA). To investigate the effects of process parameters on the energy consumption and the processing quality, the design of experiment (DOE) is carried out, and the L16 (43) Taguchi matrix with three factors and four levels is used. Table 2 lists the values and levels of the laser process parameters.
Levels and values of process parameters of the L16 (43) experiments
| Factor levels | Process parameters | ||
| LP / W | SS / (mm·s–1) | DA / cm | |
| 1 | 400 | 45 | 3 |
| 2 | 500 | 50 | 4 |
| 3 | 600 | 55 | 5 |
| 4 | 700 | 60 | 6 |
Evaluation criteria and experimental results
Total energy consumption
In this work, the metering system of energy consumption is developed, which consists of SPM (also named power quality analyzer) and the curvilinear integral procedure based on MATLAB. Specifically, the SPM is applied to obtain real-time power by measuring the electric current and voltage. After that, the power is converted to energy consumption based on the integral calculation. To measure the electric current of each system and piece of equipment, the current clamp of the SPM is mounted outside the current bus. In addition, the voltage measuring line of the SPM is linked to measuring the electric voltage, as shown in Figure 4. The measurement range of voltage is from 1 to 1000 V, while that of current is from 10 mA to 3000 A, and the measurement errors are less than 1%. The total energy consumption (TEC) of the LST platform is mostly made up of the energy consumed by the fiber laser system, the chiller system, the ABB robot, and the gas extraction system[31]. The energy consumed by the gas extraction system varies little when different laser process parameters are used[31]. Thus, it can be ignored in the investigation of the relationship between energy consumption and process parameters[32-34]. Therefore, The TEC consists of the total energy used by the three systems during the metering cycle:
where ECl, ECc, and ECr are the energy consumed by the fiber laser system, the chiller system, and the ABB robot system, respectively.
Processing quality
For the heat treatment of common quenching and tempering, two requirements need to be met to achieve grain refinement[5,9,12]: (1) The heating temperature reaches above the critical temperature of austenite transformation Ac1. (2) The cooling rate is larger than the critical rate of martensitic transformation. LST has a large heating and cooling rate, which can make the workpiece fully complete the above phase transition. Specifically, the rapid heating makes the initial ferrite/pearlite phase quickly transform into the austenite phase. After the heat source passes, the heat is rapidly carried away by the surrounding cooler metal, which is called the “self-quenching effect”[9]. The large cooling rate makes the temperature of the laser treated zone lower than the martensite starting temperature, which avoids reverse transformations[12,35]. This results in the formation of fine microstructures on the laser treated surface[9], thereby improving the surface hardness and wear resistance of the workpiece[29]. The profile geometry of the treated zone processed by the LST is shown in Figure 5, where the depth of LST zone (DZ) and the width of LST zone (WZ) are indicated. There are many quality evaluation indicators for LST, including cutting performance, process defects, and some cross-section geometries. This study is limited to only selecting depth-width ratio (DWR) and surface roughness (R) as the indicators of quality evaluation.
Figure 5. The cross-section of the LST zone. LST: Laser surface treatment; WZ: the width of LST zone; DZ: the depth of LST zone.
(a) Depth-width ratio
The cross-section geometry is widely used as the evaluation indicator to reflect the quality of laser processing[32,36,37]. Furthermore, the DWR is often of interest in LST[5,9,36]. Specifically, too large DWR can introduce the crack defect since it is accompanied by excessive energy density. Besides, too large DWR affects the processing efficiency due to the insufficient width of LST track on the workpiece surface. In contrast, too small DWR often leads to a small depth of penetration of LST zone. Thus, a suitable DWR value is beneficial in LST. This work selects the DWR as an indicator to evaluate the LST processing result since DWR can indicate characteristics of the cross-section of the LST zone, given as
(b) Surface roughness
The goal of LST is to raise the surface temperature over the critical transition threshold, specifically the austenitizing temperature (solid-state transformation) for LSQ and the melting temperature for LSM[4]. During the LSQ and LSM processes, liquid-to-solid and solid-to-solid transformations occur in the laser treated zone, which can promote the generation of residual stresses. The residual stresses result from differences in the expansion and contraction ratios of the molten metal, heat-affected zone, and metal substrate, as well as volume variations of the phase transformation reactions (transformational stresses)[38]. Thus, LST can significantly affect the surface roughness of the processed workpiece[18,39-41]. The higher surface roughness of the laser treated region on steel workpieces often leads to worse wear performance[42,43]. In general, the LSQ (or laser hardening) process causes a slight increase in R; however, when the laser energy intensity increases, melting can be observed within the processed region, and the LSM process leads to a significant increase in R due to the severe distortion of surfaces[39]. Minimal distortion and low cracking tendency of the laser treated surface are considered as the ideal criteria of LST for tools and components subjected to friction and wear processes[39,44]. The low value of surface roughness agrees with the criteria, as distortions and cracks usually lead to large surface roughness. Therefore, in this work, R is taken as an indicator of processing quality, and a low R value is desired.
The R value of each experiment was measured by a confocal microscope. The one-dimensional formula of surface roughness for a surface with a profile length L can be expressed as
where f(x) is the variation of local surface height at the point x compared with the average height of the whole profile with the assumption that the whole profile is even[45]. fm is the height of m positions along the profile length L, and the surface roughness can be formulated as
The surface roughness can easily be extended to the two-dimensional surface profile. The R of a specific area with m × n measured variations fi,jcan be calculated as
Experimental results
The LST experiments were conducted with the laser process parameters listed in Table 2. An alcohol solution containing 4% (volume fraction) of nitric acid was used to reveal the LST zone. Next, the geometries of the LST zone were measured and recorded. Table 3 lists the specific laser process parameters and their experimental results.
Fiber LST process parameters and experimental results
| No. | Process parameters | Experimental results | |||||
| LP (W) | SS (mm/s) | DA (cm) | TEC (104 J) | R (μm) | DWR | ||
| 1 | 400 | 45 | 4 | 6.348 | 14.670 | 0.143 | |
| 2 | 400 | 50 | 5 | 6.142 | 9.785 | 0.146 | |
| 3 | 400 | 55 | 6 | 5.968 | 7.040 | 0.087 | |
| 4 | 400 | 60 | 3 | 5.923 | 14.630 | 0.130 | |
| 5 | 500 | 45 | 5 | 6.513 | 7.640 | 0.100 | |
| 6 | 500 | 50 | 4 | 6.340 | 13.680 | 0.171 | |
| 7 | 500 | 55 | 3 | 6.202 | 15.890 | 0.172 | |
| 8 | 500 | 60 | 6 | 5.988 | 7.090 | 0.074 | |
| 9 | 600 | 45 | 6 | 6.678 | 8.970 | 0.102 | |
| 10 | 600 | 50 | 3 | 6.538 | 17.240 | 0.190 | |
| 11 | 600 | 55 | 4 | 6.333 | 7.980 | 0.128 | |
| 12 | 600 | 60 | 5 | 6.158 | 7.600 | 0.101 | |
| 13 | 700 | 45 | 3 | 6.947 | 17.880 | 0.193 | |
| 14 | 700 | 50 | 6 | 6.632 | 6.980 | 0.113 | |
| 15 | 700 | 55 | 5 | 6.463 | 9.330 | 0.133 | |
| 16 | 700 | 60 | 4 | 6.327 | 11.040 | 0.173 | |
PROPOSED APPROACH
Ensemble of metamodels
Various metamodels have been widely used in many engineering applications recently[23,46,47]. Metamodeling can uncover the underlying relationship between input and output variables, given as
where x is the input variables, y is the outputs,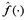 
is the metamodeling method, α is the coefficient vector, and ε is the stochastic parameter. Every metamodel has specific merits and demerits[23], and no individual metamodel is proven to be the most effective for all applications[24]. If an unsuitable individual metamodel is chosen, the accurate result is hard to obtain. In this work, three kinds of metamodels (Kriging, RBF, and SVR) are integrated into the EM with weight coefficients, given as
where x is the inputs (unknown point),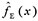 
is the predictive output from the EM, 
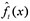(i = 1, 2, 3) are the predictive outputs from the three individual metamodels (Kriging, RBF, and SVR), and ωi (i = 1, 2, 3) are the corresponding weight coefficients of them, respectively. The Supplementary Materials describe the details of Kriging, RBF, and SVR metamodels.
In this work, the leave-one-out (LOO) cross-validation method is used to evaluate the accuracy of the three individual metamodels and the established EM. The average error under the LOO method (AELOO) and maximum error under the LOO method (MELOO) are taken as two evaluation indicators, which can be formulated as
where m is the quantity of sample points,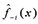 
is the predicted value based on the metamodel trained using all data without the ith sample point, and fi(x) is the experimental value. Lower AELOO and/or MELOO values indicate the metamodel is more accurate. A larger weight coefficient should be assigned to a more accurate metamodel. In this work, AELOO is employed to generate the weight coefficients of Kriging, RBF, and SVR. Based on AELOO, the two metamodels with better accuracy are selected and integrated into the EM for the predictions, while the metamodel with the largest AELOO among the three is discarded. The weight coefficient of the most accurate metamodel is assigned as the largest weight coefficient.
Framework of the proposed approach
In this work, the presented EM aims to fit the relationship between laser process parameters (LP, SS, and DA) and LST processing results (TEC, R, and DWR). Figure 6 shows the overall framework of the proposed method, which mainly includes three parts: DOE, the establishment of EM, and the validation of EM. Specifically, LST experiments with sample points generated using the Taguchi matrix are carried out. Next, the three processing results are taken as the evaluation criteria, and then used to establish Kriging, RBF, and SVR metamodels. After that, the weight coefficients of three individual metamodels are determined according to AELOO and then used in the construction of EM. Furthermore, the accuracy of the established EM is validated by both the LOO method and additional experiments.
Figure 6. The overall framework of the proposed method. LST: Laser surface treatment; EM: ensemble of metamodels; RBF: radial basis function; SVR: support vector regression; AELOO: average error under the LOO method; LOO: leave-one-out.
RESULTS AND DISCUSSIONS
Construction of EM
In this work, Equations and are used to evaluate the accuracy of Kriging, RBF, and SVR. The AELOO and MELOO of three metamodels for the three responses (TEC, R, DWR) are shown in Figure 7. Among the three metamodels, the one with the largest AELOO is discarded (weight coefficients of 0%), while the weight coefficients of the metamodels with the smallest and second smallest AELOO are 66.67% (two-thirds) and 33.33% (one-third), respectively. According to trial-and-error and experience, such a weight coefficient assignment method is simple and efficient in most cases.
Figure 7. AELOO and MELOO of the four metamodels for the three responses: (A) TEC; (B) R; and (C) DWR. AELOO: Average error under the LOO method; MELOO: maximum error under the LOO method; LOO: leave-one-out; RBF: radial basis function; SVR: support vector regression; EM: ensemble of metamodels.
Furthermore, in the validation of EM phase shown in Figure 6, additional experiments are used to validate the accuracy of EM. The accuracy threshold can refer to the relevant indicators in other literature: energy consumption[32], cross-section geometry[48,49], and surface roughness[45]. The maximum relative errors of 3%, 35%, and 35% are, respectively, set as the accuracy threshold of metamodels for TEC, R, and DWR in this work. If the accuracies of metamodels for the three responses meet the requirement, then the assignment of the weight coefficients for the metamodel construction is appropriate.
In addition, the color diagrams of the three responses (TEC, R, and DWR) based on EMs are provided in Figure 8 to show the relationship between the input and output variables in the LST process. EM is employed to predict and demonstrate the response values at different locations in the design space of process parameters. As shown by the legends of Figure 8, the magnitude of the value is represented by the difference in color. In each color subplot, it can be observed that different input process parameters (or sample points) lead to different response values. That is, the processing results of LST vary with the different inputs. Besides, one group of process parameters results in different colors in different subplots since different response values of TEC, DWR, and R are obtained.
Figure 8. Color diagrams of EMs: (A) TEC; (B) R; and (C) DWR. LST: Laser surface treatment; LP: laser power; SS: scan speed; TEC: the total energy consumption; R: surface roughness; DWR: depth-width ratio; EM: ensemble of metamodels.
Validation of EM
The AELOO and MELOO of the EMs are calculated and compared with Kriging, RBF, and SVR, as shown in Figure 7. For TEC, EM has lower errors than RBF and SVR in both AELOO and MELOO; For R, the accuracy of EM is second and only inferior to RBF in AELOO, while the MELOO of EM is lower than that of RBF; and, for DWR, the AELOO of EM ranks in second place, while the MELOO of EM performs the best among the four models. Overall, EM never has the worst accuracy for the three different responses, which shows that the proposed approach can effectively reduce the probability of randomly selecting an unsuitable metamodel. The constructed EMs are employed to predict three output responses under the LOO method. For each cross-validation, the 15 samples in Table 3 are used as the training dataset, while the remaining set of samples is used for testing. Figure 9 shows the comparison of experimental values (EV) and predictive values (PV) from EMs. The statistical indicators (R2) between EV and PV under the LOO cross-validation method of TEC, R, and DWR were calculated as 0.641, 0.543, and 0.363, respectively.
Figure 9. Experimental values and predictive values from EMs under the LOO method. TEC: The total energy consumption; R, surface roughness; DWR: depth-width ratio; EM: ensemble of metamodels; LOO: leave-one-out; EV: experimental values; PV: predictive values.
Four additional experiments were carried out to evaluate the accuracy of the EMs. Table 4 lists the laser process parameters and output responses of these additional experiments (named Nos. 1-4). The relative error (RE) is used to assess the difference between the PV and the EV. The RE is formulated as
Figure 10. Experimental values and predictive values from EMs: (A) TEC; (B) R; and (C) DWR. TEC: The total energy consumption; R: surface roughness; DWR: depth-width ratio; EV: experimental values; PV: predictive values; RE: relative error; EM: ensemble of metamodels.
Figure 11. Geometry of the cross-section and topography of the upper surface of the additional validations: (A) No. 1 and (B) No. 2. R: Surface roughness; WZ: the width of LST zone; DZ: the depth of LST zone; DWR: depth-width ratio.
Laser process parameters and output responses of the four additional experiments
| No. | LP (W) | SS (mm/s) | DA (cm) | TEC (104 J) | R (μm) | DWR |
| 1 | 400 | 50 | 4 | 6.168 | 11.87 | 0.154 |
| 2 | 600 | 50 | 4 | 6.512 | 15.46 | 0.138 |
| 3 | 700 | 55 | 5 | 6.463 | 10.56 | 0.112 |
| 4 | 550 | 55 | 5 | 6.229 | 8.32 | 0.144 |
Main effects of process parameters
The experimental results show that the process parameters (LP, SS, and DA) have obvious impacts on TEC, R, and DWR. As shown in Figure 12, the influences of process parameters are evaluated based on the main effect analysis. The horizontal back dashed line in each subfigure represents the average value of the main effect of the four levels. The δ value is shown in each subfigure to reflect the maximum influence on the processing results (TEC, R, and DWR) under the parameters at different levels. A larger value of δ represents a larger main effect. The δ values of mean TEC (104 J) for LP, SS, and DA are, respectively, 0.497, 0.523, and 0.086. It can be observed that both LP and WS have significant influences on TEC, while DA has little effect on TEC. A decrease in LP and an increase in SS can effectively decrease TEC. For the response R, the δ of the mean value (μm) for LP, SS, and DA are, respectively, 1.084, 2.230, and 8.890, while the δ of mean DWR for LP, SS, and DA are, respectively, 0.026, 0.036, and 0.077. For both R and DWR, the most important factor among the three process parameters is DA. An increase in DA would lead to a significant decrease in R and DWR, and a larger LP can result in a larger DWR. More specifically, when DA increases and other parameters remain unchanged, the diameter of the laser spot on the workpiece surface becomes larger, which leads to more dispersion of the laser energy and less energy received per unit area. Thus, an LST track with a smaller depth and larger width would be obtained, resulting in a smaller DWR, and vice versa. When LP increases and other parameters remain unchanged, the energy density increases, which causes the depth of the laser processing zone to become significantly larger, thereby increasing the DWR[18,37]. In addition, when DA increases or LP decreases, the laser energy density decreases, and the processing effect of LST is weakened; thus, the phase transformation and distortion of the treated surface are reduced, which reduces R significantly.
Figure 12. Main effects of process parameters on the three responses: (A) TEC; (B) R; and (C) DWR. TEC: The total energy consumption; R: surface roughness; DWR: depth-width ratio; LP: laser power; SS: scan speed; DA: defocusing amount.
Multi-response evaluation using TOPSIS
Commonly used methods for evaluating and ranking the process parameters in laser processing include TOPSIS method[22,50-52], integrated goal method[53-55], and normalization and weighting method[56]. TOPSIS is proposed to obtain the best decision based on the compromise solution principle[57], and it can be employed as a comprehensive evaluation method for multiple attribute decision-making[58]. TOPSIS can eliminate the influence of dimensions from different indicators in the calculation process. Thus, the closeness of each decision solution to the positive ideal solution (S+) and the negative ideal solution (S-) can be calculated. The optimal compromise solution is defined as the one closest to the S+ and farthest from the S-[59]. Based on the experiments in Table 3, the TOPSIS approach is employed. For the responses TEC and R, smaller values are preferred, while too large or too small DWR values are undesirable; thus, the criterion is defined as follows:
where DWR’ is the average DWR of the 16 sets of experiments in Table 3. The weight coefficients of the three criteria (TEC, R, and DWR*) are set as 40%, 40%, and 20%, respectively.
Figure 13 shows the rank order of the relative closeness Ci for the 16 sets of experiments based on the TOPSIS approach. A higher Ci represents that the evaluated alternative is closer to S+ and performs better in the comprehensive evaluation. The sequence of the optimal experiments is listed as: 2, 11, 12, 3, 15, 4, 8, 14, 5, 16, 1, 9, 6, 7, 10, and 13. The best three among the 16 sets of process parameters in Table 3 are Group Nos. 2, 11, and 12, with the relative closenesses of 78.04%, 74.94%, and 71.78%, respectively. The worst experiment is Group No. 13 with the relative closeness of 2.21%. Considering the practical application, the TOPSIS scores can be obtained for multiple groups of experiments, which can provide a theoretical basis for the final selection of more reasonable process parameters[22]. Therefore, Group Nos. 2, 11, and 12 of process parameters are recommended considering the energy consumption and the processing quality. In general, selecting reasonable process parameters to obtain processing results with low TEC and suitable DWR and R is an effective way to improve the application of LST.
Figure 13. The relative closeness of 16 sets of experiments using the TOPSIS approach. TOPSIS: Technique for order preference by similarity to an ideal solution.
CONCLUSION
In this work, a prediction approach based on EM is presented and used in the fiber LST process. Three metamodels (Kriging, RBF, and SVR) are integrated into the EM by suitable weight coefficients. The complex relationships between the process parameters and three LST results (TEC, R, and DWR) are established by the EM. The reliability of the presented prediction approach is validated by the LOO method and additional experiments. The influences of process parameters on three output results are studied. The four conclusions are summarized:
1. The EM can effectively decrease the risk of randomly selecting an unsuitable metamodel and performs well in the prediction.
2. The main effect analysis shows that both LP and WS have significant influences on TEC, while DA is the most important factor for R and DWR.
3. According to the TOPSIS approach, the sequence of the optimal experiments is listed as: 2, 11, 12, 3, 15, 4, 8, 14, 5, 16, 1, 9, 6, 7, 10, and 13. The optimal process parameter is Group No. 2, with the relative closeness of 78.04%, while the worst one is Group No. 13, with the relative closeness of 2.21%.
4. The presented prediction approach considering both the energy consumption and the processing quality can serve as a reliable foundation in the energy-aware application of the LST process.
The proposed prediction approach can also be applied to other experimental results (tensile strength, hardness, etc.) in LST, as well as other laser processing technologies, such as laser welding and selective laser melting.
DECLARATIONS
Authors’ contributionsInvestigation: Zhang C
Conceptualization: Wu J, Li C, Cao H
Methodology: Wu J, Cao H
Experiments: Wu J
Data analysis: Wu J
Technical support: Cao H
Writing original draft: Wu J
Review and editing: Zhang C, Jiang P
Supervision: Zhang C, Jiang P
Funding acquisition: Zhang C, Jiang P
Project administration: Jiang P
Resources: Li C, Cao H
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis research was partially supported by the Project of International Cooperation and Exchanges NSFC (Grant No. 51861165202), the National Natural Science Foundation of China (Grant Nos. 51575211, 51705263, 51805330), the 111 Project of China (Grant No. B16019). The authors thank the experimental support from the Experiment Center for Advanced Manufacturing and Technology in the School of Mechanical Science & Engineering of HUST.
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2022.
Supplementary MaterialsREFERENCES
1. International Energy Agency. Energy efficiency indicators: database and documentation, 2017. Available from: https://doi.org/10.1787/9789264284234-en [Last accessed on 30Aug 2022].
2. He Y, Xiong J, Li Y, Tian X, Jiang P. Process parameter selection for laser welding of aluminium alloy from the perspective of energy effectiveness. J Eng Manufact 2022;236:1574-88.
3. Du Y, Yi Q, Li C, Liao L. Life cycle oriented low-carbon operation models of machinery manufacturing industry. J Clean Prod 2015;91:145-57.
4. Catalán N, Ramos-moore E, Boccardo A, Celentano D. Surface laser treatment of cast irons: a review. Metals 2022;12:562.
5. Yu Z, Li C, Chen Z, Li Y, Han X. Sensitivity analysis of laser quenching parameters of ASTM 1045 of disk laser based on response surface method. Met Mater Int 2021;27:1236-51.
6. Singh A, Harimkar SP. Laser surface engineering of magnesium alloys: a review. JOM 2012;64:716-33.
7. Chai L, Wu H, Zheng Z, et al. Microstructural characterization and hardness variation of pure Ti surface-treated by pulsed laser. J Alloys Compd 2018;741:116-22.
8. Chai L, Zhu Y, Hu X, et al. A strategy to introduce gradient equiaxed grains into Zr sheet by combining laser surface treatment, rolling and annealing. Script Mater 2021;196:113761.
9. Colombini E, Sola R, Parigi G, Veronesi P, Poli G. Laser quenching of ionic nitrided steel: effect of process parameters on microstructure and optimization. Metall and Mat Trans A 2014;45:5562-73.
10. Cao X, Shi L, Cai Z, Liu Q, Zhou Z, Wang W. Investigation on the microstructure and damage characteristics of wheel and rail materials subject to laser dispersed quenching. Appl Surf Sci 2018;450:468-83.
11. Chen Z, Zhu Q, Wang J, Yun X, He B, Luo J. Behaviors of 40Cr steel treated by laser quenching on impact abrasive wear. Opt Laser Technol 2018;103:118-25.
12. Li Z, Tong B, Zhang Q, Yao J, Kovalenko V. Microstructure refinement and properties of 1.0C-1.5Cr steel in a duplex treatment combining double quenching and laser surface quenching. Mater Sci Eng 2020;776:138994.
13. Zheng Y, Hu Q, Li C, et al. A novel laser surface compositing by selective laser quenching to enhance railway service life. Tribol Int 2017;106:46-54.
14. Ki H, So S. Process map for laser heat treatment of carbon steels. Opt Laser Technol 2012;44:2106-14.
15. Palmieri FL, Ledesma RI, Dennie JG, et al. Optimized surface treatment of aerospace composites using a picosecond laser. Comp Part B 2019;175:107155.
16. Alikhani S, Kazemi Zahabi M, Javad Torkamany M, Hasan Nabavi S. Time-dependent 3D modeling of the thermal analysis of the high-power diode laser hardening process. Opt Laser Technol 2020;128:106216.
17. Steen WM, Courtney C. Surface heat treatment of EnS steel using a 2kW continuous-wave CO2 laser. Metal Technol 1979;6:456-62.
18. Zhang T, Li L, Liang F, Yang B. Parameter optimization of laser die-surface hardening using the particle swarm optimization technique. Int J Adv Manuf Technol 2008;36:1104-12.
19. Lambiase F, Di Ilio A, Paoletti A. Prediction of laser hardening by means of neural network. Procedia CIRP 2013;12:181-6.
20. Li Y, Xiong M, He Y, Xiong J, Tian X, Mativenga P. Multi-objective optimization of laser welding process parameters: the trade-offs between energy consumption and welding quality. Opt Laser Technol 2022;149:107861.
21. Zhu Y, Peng T, Jia G, Zhang H, Xu S, Yang H. Electrical energy consumption and mechanical properties of selective-laser-melting-produced 316L stainless steel samples using various processing parameters. J Clean Prod 2019;208:77-85.
22. Cao H, Li Y, Li H, Zhang C, Ge W, Xing B. Multi-objective response evaluation for carbon emission and welding performance of laser welding process. Int J Adv Manuf Technol 2022;121:3005-23.
23. Wang GG, Shan S. Review of metamodeling techniques in support of engineering design optimization. J Mechan Design 2007;129:370-80.
24. Goel T, Haftka RT, Shyy W, Queipo NV. Ensemble of surrogates. Struct Multidisc Optim 2007;33:199-216.
25. Wu J, Zhang C, Lian K, Sun J, Zhang S. Processing parameter optimization of fiber laser beam welding using an ensemble of metamodels and MOABC. Front Mech Eng 2022;17:47.
26. Acar E. Effect of error metrics on optimum weight factor selection for ensemble of metamodels. Expert Syst Appl 2015;42:2703-9.
27. Song X, Sun G, Li G, Gao W, Li Q. Crashworthiness optimization of foam-filled tapered thin-walled structure using multiple surrogate models. Struct Multidisc Optim 2013;47:221-31.
28. Elbaz K, Shen S, Zhou A, Yin Z, Lyu H. Prediction of disc cutter life during shield tunneling with AI via the incorporation of a genetic algorithm into a GMDH-type neural network. Engineering 2021;7:238-51.
29. Zhang X, Lin L, Xia Y, et al. Experimental study on wear of TBM disc cutter rings with different kinds of hardness. Tunn Undergr Space Technol 2018;82:346-57.
30. Wu J, Yu A, Chen Q, Wu M, Sun L, Yuan J. Tribological properties of bronze surface with dimple textures fabricated by the indentation method. J Eng Tribol 2020;234:1680-94.
31. Huang Z, Cao H, Zeng D, Ge W, Duan C. A carbon efficiency approach for laser welding environmental performance assessment and the process parameters decision-making. Int J Adv Manuf Technol 2021;114:2433-46.
32. Wu J, Lian K, Deng Y, Jiang P, Zhang C. Multi-objective parameter optimization of fiber laser welding considering energy consumption and bead geometry. IEEE Trans Automat Sci Eng 2021.
33. Peng T, Chen C. Influence of energy density on energy demand and porosity of 316L stainless steel fabricated by selective laser melting. Int J of Precis Eng and Manuf -Green Tech 2018;5:55-62.
34. Li J, Cao L, Hu J, Sheng M, Zhou Q, Jin P. A prediction approach of SLM based on the ensemble of metamodels considering material efficiency, energy consumption, and tensile strength. J Intell Manuf 2022;33:687-702.
35. Molian PA. Laser surface heat treatment of AISI 4340 steel: a microstructural study. Mater Sci Eng 1981;51:253-60.
36. Nasrollahi V, Penchev P, Batal A, Le H, Dimov S, Kim K. Laser drilling with a top-hat beam of micro-scale high aspect ratio holes in silicon nitride. J Mater Proc Technol 2020;281:116636.
37. Yang Y, Cao L, Wang C, Zhou Q, Jiang P. Multi-objective process parameters optimization of hot-wire laser welding using ensemble of metamodels and NSGA-II. Rob Compt-Int Manuf 2018;53:141-52.
38. Fernández-vicente A, Pellizzari M, Arias J. Feasibility of laser surface treatment of pearlitic and bainitic ductile irons for hot rolls. J Mater Proc Technol 2012;212:989-1002.
39. Zammit A, Abela S, Betts JC, Grech M. Discrete laser spot hardening of austempered ductile iron. Surf Coat Technol 2017;331:143-52.
40. Roy S, Zhao J, Shrotriya P, Sundararajan S. Effect of laser treatment parameters on surface modification and tribological behavior of AISI 8620 steel. Tribol Int 2017;112:94-102.
41. Babič M, Calì M, Nazarenko I, et al. Surface roughness evaluation in hardened materials by pattern recognition using network theory. Int J Interact Des Manuf 2019;13:211-9.
42. Yazici O, Yilmaz S. Investigation of effect of various processing temperatures on abrasive wear behaviour of high power diode laser treated R260 grade rail steels. Tribol Int 2018;119:222-9.
43. Lesyk D, Martinez S, Mordyuk B, et al. Combining laser transformation hardening and ultrasonic impact strain hardening for enhanced wear resistance of AISI 1045 steel. Wear 2020;462-463:203494.
44. Pantelis D, Pantazopoulos G, Antoniou S. Wear behavior of anti-galling surface textured gray cast iron using pulsed-CO2 laser treatment. Wear 1997;205:178-85.
45. Strano G, Hao L, Everson RM, Evans KE. Surface roughness analysis, modelling and prediction in selective laser melting. J Mater Proc Technol 2013;213:589-97.
46. Cao L, Li J, Hu J, Liu H, Wu Y, Zhou Q. Optimization of surface roughness and dimensional accuracy in LPBF additive manufacturing. Opt Laser Technol 2021;142:107246.
47. Cai X, Qiu H, Gao L, Li X, Shao X. A hybrid global optimization method based on multiple metamodels. EC 2018;35:71-90.
48. Rong Y, Zhang Z, Zhang G, et al. Parameters optimization of laser brazing in crimping butt using Taguchi and BPNN-GA. Opt Laser Eng 2015;67:94-104.
49. Kanti K, Srinivasa Rao P. Prediction of bead geometry in pulsed GMA welding using back propagation neural network. J Mater Proc Technol 2008;200:300-5.
50. Akbari M, Shojaeefard MH, Asadi P, Khalkhali A. Hybrid multi-objective optimization of microstructural and mechanical properties of B4C/A356 composites fabricated by FSP using TOPSIS and modified NSGA-II. Trans Nonf Metal Soc China 2017;27:2317-33.
51. Akbari M, Asadi P, Zolghadr P, Khalkhali A. Multicriteria optimization of mechanical properties of aluminum composites reinforced with different reinforcing particles type. J Proc Mech Eng 2018;232:323-37.
52. Gopinath C, Lakshmanan P, Palani S. Fiber laser microcutting on duplex steel: parameter optimization by TOPSIS. Mater Manuf Proc 2022;37:985-94.
53. Gao Z, Shao X, Jiang P, et al. Parameters optimization of hybrid fiber laser-arc butt welding on 316L stainless steel using Kriging model and GA. Opt Laser Technol 2016;83:153-62.
54. Jiang P, Cao L, Zhou Q, Gao Z, Rong Y, Shao X. Optimization of welding process parameters by combining Kriging surrogate with particle swarm optimization algorithm. Int J Adv Manuf Technol 2016;86:2473-83.
55. Zhou Q, Rong Y, Shao X, Jiang P, Gao Z, Cao L. Optimization of laser brazing onto galvanized steel based on ensemble of metamodels. J Intell Manuf 2018;29:1417-31.
56. Zhang F, Zhou T. Process parameter optimization for laser-magnetic welding based on a sample-sorted support vector regression. J Intell Manuf 2019;30:2217-30.
57. Hwang C, Yoon K. Methods for multiple attribute decision making. Multiple attribute decision making. Berlin: Springer Berlin Heidelberg; 1981. pp. 58-191.
58. Omrani H, Alizadeh A, Emrouznejad A. Finding the optimal combination of power plants alternatives: A multi response Taguchi-neural network using TOPSIS and fuzzy best-worst method. J Clean Prod 2018;203:210-23.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Wu J, Zhang C, Jiang P, Li C, Cao H. A prediction approach of fiber laser surface treatment using ensemble of metamodels considering energy consumption and processing quality. Green Manuf Open 2023;1:3. http://dx.doi.org/10.20517/gmo.2022.04
AMA Style
Wu J, Zhang C, Jiang P, Li C, Cao H. A prediction approach of fiber laser surface treatment using ensemble of metamodels considering energy consumption and processing quality. Green Manufacturing Open. 2023; 1(1): 3. http://dx.doi.org/10.20517/gmo.2022.04
Chicago/Turabian Style
Wu, Jianzhao, Chaoyong Zhang, Ping Jiang, Congbo Li, Huajun Cao. 2023. "A prediction approach of fiber laser surface treatment using ensemble of metamodels considering energy consumption and processing quality" Green Manufacturing Open. 1, no.1: 3. http://dx.doi.org/10.20517/gmo.2022.04
ACS Style
Wu, J.; Zhang C.; Jiang P.; Li C.; Cao H. A prediction approach of fiber laser surface treatment using ensemble of metamodels considering energy consumption and processing quality. Green. Manuf. Open. 2023, 1, 3. http://dx.doi.org/10.20517/gmo.2022.04
About This Article
Copyright
Data & Comments
Data
Cite This Article 41 clicks
Like This Article 14
likes
Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.