Local causal pathway discovery for single-cell RNA sequencing count data: a benchmark study
Abstract
Aim: Recent developments in single-cell RNA sequencing (scRNAseq) and analysis have revealed regulatory behaviors not previously described using bulk analysis. scRNAseq features resolution at the level of the individual cell and provides opportunities for identifying cell type-specific gene regulatory networks. The technology promises to discover biomarkers and targeted treatments with enhanced effectiveness and reduced side effects. Pathway reverse engineering and causal algorithms have been validated in bulk sequencing transcriptomic data successfully for gene regulatory network reconstruction. In the current study, we evaluated the performance of local causal discovery algorithms for de novo reconstruction of local gene regulatory networks tailored to scRNAseq count data.
Method: We benchmarked the performance of the state-of-the-art local causal discovery algorithm generalized local learning with five conditional independent tests in controlled conditions (simulated count data) and real-world single-cell RNA sequencing datasets.
Results: The simulation study showed that local causal discovery methods with appropriate conditional independence tests could result in excellent discovery performance (given a sufficient sample size). As expected, various conditional independence tests possess different power-sample characteristics. The discovery performance for all tested conditional independence tests on real-world data is relatively low, potentially due to imperfect standards or deviation of simulated data distribution from real-world data.
Conclusion: Our findings provide insights and practical guidance for applying causal discovery methods to single-cell RNAseq data for gene regulatory network reconstruction.
Keywords
INTRODUCTION
Unlike diagnosis and outcomes prediction, where correlational relationships are often sufficient, predicting responses to a treatment critically depends on knowledge of the causes of biological processes. Gene regulatory networks describe the causal and mechanistic interactions between transcription factors and genes and are, therefore, critical for treatment discovery and precision treatment selection. Many gene regulatory pathways (e.g., functional components of regulatory networks) were derived for biological systems under many different conditions based on bulk gene expression and other data, and several have led to targeted treatments, especially in cancer[1].
Recent developments in single-cell RNA sequencing (scRNAseq) analysis have revealed regulatory behaviors not previously described using bulk analysis[2-4]. Regarding intra-tumor heterogeneity, analysis of glioblastomas showed that one tumor contains individual cells that resemble the four bulk gene expression molecular subtypes (proneural, neural, classical, and mesenchymal), revealing diverse regulatory programs within the same tumor[5]. Concerning tumor immune function, scRNAseq analysis of the breast tumor microenvironment observed a continuum of T cell states, leading to a new understanding of immune responses to tumors[6]. Highlighting the potential clinical utility of scRNAseq data, several scRNAseq-based studies suggested a link between the transcriptomic profile of specific cell subpopulations and patient-level cancer outcomes[5,7,8]. scRNAseq identified subgroups of drug-resistant cells[9,10] and expression profiles linked to resistance[11]. One case study provided evidence for the ability of scRNAseq to identify treatment-refractory mechanisms and treatment selection for surviving tumor cells[12].
Bulk gene expression data has fundamental limitations compared to single-cell data. When the regulation of a gene by a transcription factor is present in one cell type but not another, there is an obligatory signal attenuation owing to a lower signal-to-noise ratio. Separating cell types via scRNAseq promises to deliver a better ability to dissect the regulatory relationship than bulk sequencing. Another problem is that there are relationships with opposite orientations within cell types, which, when aggregated, are also attenuated and may vanish entirely[13]. Additional distribution-related artifacts may occur, such as Berkson Fallacy type mixtures where spurious associations and those with reversed directions can emerge[14]. scRNAseq operates at the resolution of the individual cell and can overcome these problems; it provides opportunities for identifying cell type-specific gene regulatory networks that can result in targeted treatments with better effectiveness and fewer side effects[15] than those that derive from bulk analyses.
Deducing or modeling gene regulatory networks at the single-cell level from scRNAseq data is an active pursuit of the bioinformatics community. Several methods have been developed in various biological model systems leveraging single-cell transcriptome profiling datasets[16-20]. SCOUP infers gene regulation networks by modeling the cell dynamics as ordinary differential equations with pseudo-time as the temporal reference[21]. TENET utilizes transfer entropy to approximate the strength of causal relationships between genes and predict large-scale gene regulatory cascades/relationships from scRNAseq data[22].
Furthermore, ordering cells according to pseudo-time may not be appropriate in specific cell populations, limiting these methods’ applicability. There are other limitations in methods that do not depend on pseudo-time, such as the SCENIC[24], including the reliance on correlational relationships (e.g., coexpression) for the discovery of causal mechanisms and the dependence on databases of known regulatory relationships. To summarize, these methods are not based on mathematically sound theories to guarantee reliable causal inference from observational data and are thus only heuristic. Finally, benchmark studies showed that the performance of these methods was moderate[25].
Formal causal inference methods exist for general distributions and have been tested in biological discovery and bulk gene expression data[26-31]. The current study aims to assess the performance of formal causal inference methods for regulatory network reconstruction using scRNAseq data. To apply these methods to scRNAseq data, one needs to consider that these are multivariate count data requiring appropriate statistical tests of association and conditional independence. Various statistics and machine learning methods have been introduced for modeling this type of data. Concerning identifying statistical relationships among count variables, such as correlation and difference between groups, the most straightforward variety of the method is transforming count data to Gaussian distributions such that one can leverage existing statistical methods designed for Gaussian data. The data transformation methods are simple and widely adopted in applied research, despite the debate over their effectiveness[32-35]. We explored log transformation in the current study (see the METHOD section for detail). Other methods include models specifically designed for modeling count data, such as the Poisson regression[35]. We examined the conditional independence test based on the Poisson regression.
Another class of methods utilizes non-parametric models to infer relationships among count data. These methods make no distributional assumptions and thus can be applied to count data[35]. In our study, we explored two methods that fit into this category, the kernel conditional independence test[36] and the partial distance correlation test[37] (see the METHODS section for detail).
More closely related to causal pathway/regulatory network discovery is learning Bayesian networks over multivariate count variables. Initial work for modeling multivariate count variables focused on modeling the multivariate joint distribution, similar to how multivariate Gaussian distributions can be modeled. However, due to the nature of the count data, this approach is problematic because the density of the joint distribution for count data is only normalizable if the coefficients specifying the model are non-positive[38,39]. Various modifications, such as truncation and modifying the base measures of the Poisson distribution, have been implemented to mitigate this issue[40]. Another way to address the normalization problem is to circumvent it by modeling the distribution of each variable as a local conditional Poisson distribution given the local neighborhood of the variable without requesting a consistent joint distribution. Most of the more recent work in this domain uses this approach.
The details for local neighborhood selection, one key component of this variety of methods, varies across studies. Allen and Han approximated the local neighborhood by fitting L1 penalized Poisson or log-normal regressions[41,42]. Hadji heuristically inferred the local neighborhood via functional gradient descent, i.e., boosting[43]. These approaches for local neighborhood selection are essential feature selection approaches that optimize for reconstructing the conditional density (i.e., predictivity) while penalizing for the size of the local neighborhood. They are not leveraging the causal nature of the data generation process and, therefore, do not guarantee the discovery of local causality.
Based on the literature, we chose to model the distribution of each count variable as a local conditional Poisson distribution given its local neighborhood. However, instead of using predictive feature selection approaches for local neighborhood selection, as employed by previous studies, we utilized local causal discovery methods for local neighborhood identification. Causal discovery methods (in contrast to predictive feature selection methods and scRNAseq-specific regulatory network reconstruction methods based on pseudo-time or coexpression) guarantee the discovery of causal relationships under broad distributional assumptions[44].
We focused on local causal discovery methods for the following reasons. First, local causal neighborhood discovery is conducive to modeling the Poisson conditional density for each variable. Second, local causal discovery methods uncover (arguably) the most important causal relationships around a gene, i.e., its direct causes and direct effects. Third, the local causal discovery methods are more sample-efficient than global causal discovery methods and have excellent scalability to networks with millions of vertices.
The causal discovery methods used here identify causal relationships by examining the statistical properties in the data using conditional independence tests, following the frameworks of Pearl et al.[44] and
METHOD
Local causal discovery within the generalized local learning framework
Several causal structure discovery methods have been used for de novo reconstruction of gene regulatory networks using bulk gene expression data with success[26-30]. In this study, we used a family of causal structure discovery methods called the generalized local learning (GLL) causal discovery methods to reconstruct the gene regulatory network based on scRNAseq data. The GLL can be adapted to numerous distributions and application domains while guaranteeing that the causal structure discovered will be correct under broad assumptions.
In general, the algorithms in the GLL framework take two inputs: (1) a dataset D with a set of variables V and sample size N; and (2) a target (i.e., response) variable of interest T∈V. The output of the algorithm is the local causal structure around T.
The GLL framework can be instantiated in many ways, giving rise to existing state-of-the-art and novel algorithms. Different instantiations of the GLL can discover different components of the local causal structure. For example, the GLL-PC sub-family discovers the direct causes and direct effects of the target of interest, whereas the GLL-MB sub-family discovers the Markov boundary of the target of interest, consisting of the direct causes, direct effects, and direct causes of the direct effects. In the current study, intending to identify the target’s direct causes and direct effects, we chose to instantiate the GLL-PC family, more specifically, as the HITON-PC algorithm[46-48].
The GLL algorithmic framework is sound under well-defined and sufficient conditions. Moreover, it is computationally efficient and applicable to datasets of very high dimensionalities (i.e., millions of variables using modest computing equipment). Empirically, benchmark studies on simulated and various real-world data demonstrated that GLL outperforms other methods with excellent local structure reconstruction accuracy given moderate sample sizes[46,47]. GLL algorithms have been applied to many real-world data for causal discovery and feature selection with great success[49-53]. In addition, GLL algorithms can be used for global causal discovery through local-to-global learning[46,47] and equivalent class discovery[54].
Conditional independence tests
The GLL algorithm framework infers the local causal neighborhood of the target of interest via systematically examining the statistical dependencies and independencies in the data using statistical tests of conditional independence. Briefly, a pair of variables X and Y are conditionally independent given variable set Z, if P(X|Y, Z) = P(X|Z), where P(Z) > 0. Intuitively, knowing the value of variable Y does not provide more information regarding X, if we already know Z. The conditional independence relationship is connected to a causal relationship under the faithfulness condition and the causal Markov condition[44,55], e.g., in a faithful causal network. A variable X is the direct cause or the direct effect of a variable T if and only if X and T are conditionally dependent given all subsets of observed variables, excluding X and T[45].
The GLL algorithm framework leverages this foundational principle of causality to identify a target variable’s direct causes and effects. Its search strategy optimizes for correct statistical inference given the available sample size and computational efficiency. To identify a variable’s direct cause and direct effects, the GLL algorithm conducts multiple conditional independence tests among variables iteratively. The error incurred on individual conditional independence tests would affect the quality of the discovery. In general, the error rate of a conditional independence test (like any statistical test) depends on the assumptions of the test, effect size, sample size, and the trade-off between type I (false positive rate) and type II error (false negative rate).
The comparative advantage of various conditional independence tests for local causal discovery leveraging count data (such as the scRNAseq data) has not been characterized systematically in the literature. Therefore, we evaluated five conditional independence tests on systematically generated simulated and real datasets. The five conditional independence tests include:
● Fisher: this is the classical Fisher’s z test. This test uses Fisher’s z-transformation of the partial correlation and tests for zero partial correlation between variable X and T, given variables in the conditioning set, assuming linear additive relationships among variables and Gaussian noise[56]. We chose to evaluate Fisher’s test even though it is not appropriate for count data because of its simplicity and previously reported good empirical performance in datasets that violate test assumptions[47].
● Log-Fisher: the Fisher’s z test is applied to log-transformed count data. The log transformation of count data reduces the over-dispersion and is often applied to count data before subsequent analysis. Although the appropriateness of log transformation for count data has been under debate[33], we evaluated this method owing to its simplicity and prevalence of log transformation in the literature[57-60].
● Poisson CI test: conditional independence test based on Poisson regression. It tests for non-zero partial correlations between X and T conditioned on variables in the conditioning set based on two Poisson regressions[35]: the first with T as the dependent variable and X and the variables in the conditioning set as the independent variables, the second with X as the dependent variable; and T as well as the variables in the conditioning set as the independent variables. The overall test is considered significant if either of the two tests is significant, indicating statistical dependence.
● Kernel conditional independence (KCI) test: Kernel-based conditional independence test. This test does not explicitly estimate the conditional or joint densities of the variables in question but computes test statistics based on kernel matrixes of the variables. This test does not make assumptions regarding the distribution of the variables or about the functional relationships among the variables[36]. Notably, the KCI test is designed for continuous variables. Even though count data violate the test assumption, we choose to test its empirical performance.
● Partial distance correlation (pdcor) test: partial distance correlation test is a test for zero partial distance correlation for variable sets X and T conditioned on Z. Although the test can handle three variable sets of arbitrary dimensions, for our purpose (of testing the independence between X and T given Z), X and T would always have a fixed dimension of one. The partial distance correlation does not have distributional assumptions regarding the variables and can capture non-linear dependenceies[37].
Simulated data experiments
We systematically simulated the count dataset to test the performance of different conditional independence tests for local causal discovery under various conditions that affect the discoverability of causal structure. The following simulation conditions were explored: network structure, the form of the data generation function, the signal-to-noise ratio, and the sample size.
Network structure
The task of qualitative causal discovery is to learn the causal structure that generates the data distribution from the analysis of experimental data or from an observational sample from that data distribution. The goal of quantitative causal discovery is to estimate the magnitude of causal effects that variable manipulations have on some target variable of interest using experimental or observational modeling methods. We focused on the discovery process based on observational data. Local causal discovery aims to learn the local causal structure (e.g., direct causes and direct effects) of a target variable.
Therefore, the first step in our data generation process is to generate a network structure that encodes a set of causal relationships among variables. Specifically, we generated random directed acyclic graphs (DAGs) with a specified number of vertices (NV)and a number of directed edges (NE). Each vertex in a DAG corresponds to a variable in its generated data. Each directed edge represents the direct causal relationship between the pair of variables connected by the edge, i.e., X → Y represents variable X is a direct cause of variable Y. The DAG encodes all the causal relationships (direct and indirect) among the set of variables generated from it. We generated four types of DAGs with different numbers of nodes (NV), number of edges (NE), and different densities: (1) NV = 20, NE = 20; (2) NV = 20, NE = 50; (3) NV = 200, NE = 200; (4) NV = 200, NE = 500.
Data generation functions
Given the qualitative causal information encoded in the generated DAG, the second step in the data generation process is to define the quantitative causal relationship among variables. Most studies in the statistical and machine learning literature generate multivariate Poisson data in two ways: (1) using the Poisson distribution; and (2) using the Poisson LogNormal distribution. We generate data using both methods because it is unknown which method better approximates true multivariate Poisson data observed in various domains.
The first method specifies the conditional distribution of a variable Vi given its parents Pa(Vi) as a Poisson distribution, with the Poisson λ determined by the weighted sum of the values of the parents and an intercept term:
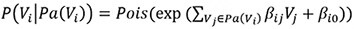
The second data generation method uses the Poisson-LogNormal distribution which contains a latent multivariate normal distribution over the variables U, with the corresponding observed count variables V being conditionally Poisson distributed:
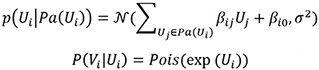
It is worth noting that the exponential function in the conditional distribution for the Poisson and Poisson LogNormal distributions. Due to the exponential function, some choices of β will result in extremely large values for Vi. Therefore, we constrained the coefficients’ value to better reflect real-world distributions. In addition, we generated positive and negative coefficients to represent positive and negative causal effects, paralleling the up- and downregulations observed in true scRNAseq data. The distribution of β in our simulated studies is shown in Supplementary Section S1.
Signal-to-noise ratio concerning causal effect sizes
We explored two signal-to-noise conditions to study the effect of the signal-to-noise ratio of causal effect size on the local causal discovery. As specified in the previous section, the data generated is considered to have a low noise condition. We also generated data with added noise (low signal-to-noise ratio) by randomly selecting 30% of the data and permuting them per variable, referred to as the high noise condition. This strategy injects additional noise while preserving the marginal distribution.
Sample size
We study the effect of sample size by examining simulated data of sample sizes of 100, 500, and 1000 observational units.
Summary of simulation conditions
To summarize, we explored four types of network structure, two types of data generation functions, and two signal-to-noise ratios, resulting in 4 × 2 × 2 = 16 types of data generation processes. To reduce artifacts due to (and assess the variability of) simulated datasets, each data generation process was repeated 50 times to produce 16 × 50 = 800 datasets. Each simulated dataset contained 1000 samples. To test the influence of sample sizes, subsamples of 100, 500, and 1000 were sampled from each simulated dataset. Local causal discovery with different conditional independence tests was conducted on each data sample.
Experiments with real-world data
We analyzed two single-cell RNAseq datasets to reconstruct the local causal neighborhood of transcription factors. For the THP-1 dataset, the scRNAseq data was obtained from Park (2021)[61] (GSE176294), and we used the network described in Tomaru (2009)[62] as the gold standard. The gold standard was developed with knock-down experiments and transcription factor binding experiments. For the Yeast dataset, the scRNAseq was obtained from Jackson (2020)[63], and we used the network developed in Tchourine (2018)[64] as the gold standard. This gold standard was derived by combining binding and expression information from various sources. The description of these datasets is displayed in Table 1. The coverage of the scRNAseq datasets and their corresponding gold standards differed; therefore, we focused on the overlapping gene sets and the regulatory relationships among them. We conducted local causal discovery on each dataset and examined the effect of sample sizes by sampling ten sets of samples of sizes 100, 5000, and 1000.
Application of GLL for local causal discovery
The GLL algorithm instantiated with the five conditional independence tests was applied to individual variables in each data sample (simulated and real-world data) for local causal discovery. The output of the GLL algorithm is the estimated local causal neighborhood of the variable in questions from the data sample given by the specific conditional independence test. The pseudo-code and detailed discussions regarding the GLL algorithm have been described previously[46,47]. We implemented the GLL algorithm using MATLAB.
Performance evaluation
The true local causal neighborhood of a variable consists of its direct causes and direct effects. The performance of local causal discovery is evaluated by comparing the discovered local causal neighborhood to the true local causal neighborhood. Because a variable is either in the local neighborhood of another variable or is not (i.e., a binary decision where being in the local neighborhood is considered positive), we chose metrics for binary classification for performance evaluation. Specifically, we computed the following metrics: sensitivity, specificity, positive predictive value (PPV), negative predictive value, and F1 score. The metrics were computed using each variable as a target separately. The mean and variability were reported.
As stated in the previous sections, for the simulated data, the true local neighborhood is determined by the true network structure that generated the data. The true network was obtained from the prior literature for the actual data.
RESULTS
Simulated data experiments
We compared the performance of GLL instantiated with five different conditional independence tests for local causal discovery across all simulation conditions and multiple performance metrics. We reported sensitivity [Figure 1], specificity [Figure 2], and PPV [Figure 3] in the main text. Figures reporting negative predictive values and the F1 score are in Supplementary Section S2.
Figure 1. Local causal neighborhood discovery sensitivity for various conditional independence tests and simulation conditions. The numerical value represents the mean sensitivity of a gven conditional independence test for a given simulation condition over 50 randomly generated datasets. We colored the cells according to their sensitivity to aid the inspection of the figure. Deeper red indicates better performance, and deeper yellow indicates worse performance. Bolded cells indicate the best performance among the five conditional independence tests for a given simulation condition.
Figure 2. Specificity of local causal neighborhood discovery for various conditional independence tests and simulation conditions. Cells were colored according to the performance to aid the inspection of the figure. Deeper red indicates better performance, and deeper yellow indicates worse performance. Bolded cells indicate the best performance among the five conditional independence tests for a given simulation condition.
Figure 3. PPV of local causal neighborhood discovery for various conditional independence tests and simulation conditions. Cells were colored according to the performance to aid the inspection of the figure. Deeper red indicates better performance, and deeper yellow indicates worse performance. Bolded cells indicate the best performance among the five conditional independence tests for a given simulation condition.
Figure 4. Local causal neighborhood discovery performance measured by sensitivity, specificity, and PPV for various conditional independence tests and real-world datasets. Cells were colored according to the performance to aid the inspection of the figure. Deeper red indicates better performance, and deeper yellow indicates worse performance. Bolded cells indicate the best performance among the five conditional independence tests for a given sample size and dataset.
The sensitivity metric is the number of true positives over the total number of positives. In our case, it is the number of identified neighbors that are true neighbors over the total number of neighbors for a vertex. Higher sensitivity indicates that the algorithms identify a higher proportion of true neighbors. The Poisson conditional independence test (PoissonCI) achieved the best sensitivity in 35 out of 48 simulation conditions nominally. In the remaining 13 of 48 simulation conditions, pdcor achieved the best sensitivity.
As the sample size increases, the sensitivity of all conditional independence tests improves, as evidenced by Figure 1. The discovery of local causal edges in smaller scRNA data is achievable with high sensitivity using the Poison or Fisher tests and a sample size of 500 or more. Adding additional noise to the data decreased the sensitivity of all conditional independence tests. We could not directly compare the performances using Poisson vs. the Poisson LogNormal data generation function in our simulation setting because the signal-to-noise ratio in the two conditions differed. However, our results showed that all five conditional independence tests could achieve similar sensitivity for simulated data generated from the two data generation functions.
Moreover, the sensitivity for the simulation condition generated from graphs with the same edge-to-vertex ratio but a different number of vertices (NV) and a number of edges (NE) were comparable (e.g., NV = 20, NE = 20 vs. NV = 200, NE = 200; NV = 20, NE = 50 vs. NV = 200, and NE = 500). This effect was observed in other benchmark studies on local causal discovery algorithms on non-count data[46,47]. Comparing low- and high-edge density given the same number of vertices (e.g., NV = 20, NE = 20 vs. NV = 20,
In summary, as evidenced by Figure 1, the discovery of local causal edges in networks with lower edge-to-vertex ratio (NV = 20, NE = 20 and NV = 200, and NE = 200) is achievable with good sensitivity by using either the Poison or Fisher tests and sample size 500 or more. In higher density networks (NV = 20,
Turning to specificity (the number of true negatives over the total number of negatives), nominally, the KCI test achieved the best performance in 42 of 48 simulation conditions. In the remaining six of 48 simulation conditions, Fisher’s test (Fisher) achieved the best performance.
As the sample size increases, the specificity of all conditional independence tests decreases in general, as expected. However, for the sample size tested, the influence of sample size on specificity is small. Adding additional noise to the data resulted in similar specificity for the Poisson data generation function but increased specificity for the Poisson LogNormal data generation function. It is worth noting that the mean difference in specificity among the conditional independence tests is relatively low (< 0.02) within each simulation condition with the data generated using the Poisson data generation function. However, when the data are generated with the Poisson log normal data generation function, the specificity for PoissonCI, the most sensitive conditional independence test in most conditions, is lower than other conditional independence tests.
In summary, as evidenced by Figure 2, the discovery of local causal edges in scRNA data is achievable with very high specificity using any examined methods.
PPV is the number of true positives over the number of predicted positives. In our case, it is the number of identified neighbors that are true neighbors over the number of identified neighbors. A higher PPV indicates that a higher proportion of the identified neighbors are true. For PPV, Fisher’s test (Fisher) nominally achieved the best performance in 41 out of 48 simulation conditions. In the remaining seven conditions, the KCI test achieved the best performance.
PPV increased as the sample size increased and decreased as more noises were added to the data. Unlike sensitivity and specificity, PPV is mathematically affected by the prior (i.e., the NE over pairs of vertices in our setting); as a result, we observed a decrease in the positive predictive value when the NV in the graph increased.
In summary, as evidenced by Figure 3, the discovery of local causal edges in a network with a small NV is achievable with high PPV using Fisher’s tests and to a comparable degree by other tests except for the pdcor test with a sample size larger or equal to 500. The PPV is substantially reduced in data with a higher NV, and the KCI and Fishers’ tests performed better.
Real-world data experiments
We applied GLL with different conditional independence tests to two real-world scRNAseq datasets for local causal discovery. We subsampled these datasets to assess the change in performance as a function of sample size (core results in Figure 4, all results in Supplementary Section S3). The pdcor test achieved the best sensitivity for all datasets and sample sizes in the real-world data. The KCI test achieved the best specificity for all datasets and sample sizes. The KCI is often the best for PPV (in three of six experimental conditions).
In these two datasets, not all methods performed as well as in simulated data, suggesting that the data are unusually hard outliers or that the gold standards are not as precise as needed (see DISCUSSION).
DISCUSSION
We tested the performance of local causal discovery algorithms equipped with different conditional independence for reconstructing the local causal neighborhood based on simulated and real-world scRNAseq data.
To our knowledge, this study is the first where local causal discovery algorithms and conditional independence tests were benchmarked on systematically generated count data. Our simulation study showed that local causal discovery methods with appropriate conditional independence tests could result in excellent discovery performance given a sufficient sample size. Different conditional independence tests, as expected, have different power-sample characteristics. Therefore, the best conditional independence test depends on the discovery task. When one wishes to discover as many true neighbors as possible (maximizing sensitivity), the Poisson conditional independence test and Fisher’s test has an advantage for networks with low edge-to-vertex ratios. In contrast, the Poisson conditional independence test, Fisher’s test, and the KCI test have an advantage for networks with higher edge-to-vertex ratios. Our simulation study provides general guidance for choosing a conditional independence test for local causal discovery given count data.
Although the primary goal of our simulation study was to compare the effectiveness of various conditional independence tests for local causal discovery given count data under laboratory (i.e., controlled and simulated) analysis conditions, it can also help in experiment planning[65,66]. For example, our results on simulated data can help answer questions such as, “is scRNAseq data from one hundred cells sufficient for identifying the local causal neighborhood given specific conditional independence tests and desired level of performance metrics?” Across all simulation conditions, we found that sensitivity, PPV, and F1 score increased substantially when the sample size increased from 100 to 500, while the difference in performance for these metrics was less drastic when the sample size increased from 500 to 1000. For datasets with a larger number of vertices and edges (e.g., for simulated data where NV = 200 and NE = 500), the performance was less than ideal even at a sample size of 1000.
Several directions for future work can be taken to expand and enrich the results of the current study. First, despite being a systematic benchmark study for local causal discovery utilizing various conditional independence tests for count data, this benchmark study only explored a subspace of the available methods for single-cell regulatory network reconstruction. We did not compare the local causal discovery method with previously reported methods that utilize non-causal techniques for neighborhood identification[21-24,41-43]. In general, methods not designed for causal discovery have (as expected) underperformed causality-optimized methods[46,47]; however, they might be advantageous for specific performance metrics (e.g., trading low specificity and many false positives for higher sensitivity). Second, a major difficulty in evaluating causal discovery methods on real-world data is the lack of suitable gold standards[67]. Despite the increasing availability of scRNAseq data, high-quality gold standards are scarce. The gold standards[62,64] we used in our study were constructed from the bulk level rather than single-cell data.
Furthermore, they were derived from studies limited to a partial set of genes. These limitations may explain the performance gap in our results between simulated and real data. More analyses must be conducted as more real-life datasets with reliable true direct causality gold standards become available. Using gold standards constructed from single-cell data or conducting experimental validations based on the local causal neighborhoods discovered by different algorithms would produce a more accurate evaluation of the performance of the algorithms. Finally, our data simulation methods do not capture all the complexities in real-world single-cell data. This limitation might contribute to the large difference between the results from the simulated data and the real-world study. Future studies using simulations that generate data that better approximate the scRNAseq data (e.g., resimulation methods) for developing and benchmarking methods are desired.
Until the understanding of the performance of various discovery methods is fully characterized, we propose that in situations where experiments do not meet apparent requirements for good discovery performance (e.g., small sample size, large edge-to-vertex ratio for sensitivity, and a large number of vertexes for PPV), based on our results, a more exploratory attitude and careful (i.e., not over-interpreted) examination of results is warranted. Similarly, experimental validation of the results is warranted when analysis operates in high-PPV regions.
In conclusion, the current study is the first to systematically evaluate the performance of the local causal discovery algorithm given different conditional independence tests on simulated count data with empirical results in real-world scRNAseq data. It provides an initial set of insights for designing analyses and choosing discovery methods in research involving scRNAseq data for gene regulatory network reconstruction.
DECLARATIONS
Authors’ contributionsConception and design: Ma S, Aliferis C
Data analysis: Bieganek C, Ma S, Tourani R
Interpretation of data: Ma S, Tourani R, Aliferis C, Wang J
Writing and editing the manuscript: Ma S, Aliferis C, Wang J, Tourani R
Availability of data and materialsData supporting the findings are either shared in the paper’s main text or the Supplementary Material.
Financial support and sponsorshipThe efforts of Drs. Ma S., Wang J., and Aliferis C. were partly supported by the University of Minnesota Clinical and Translational Science Institute grant 5UL1TR002494, the Minnesota Tissue Mapping Center of Cellular Senescence, grant 1U54AG076041, and the Midwest Murine-Tissue Mapping Center (MM-TMC) grant 1U54AG079754-01. Dr. Wang J. gratefully acknowledges support from the UMN Masonic Cancer Center and NCI grants P30CA077598 and U54AG079754.
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable
Consent for publicationNot applicable
Copyright© The Author(s) 2023.
Supplementary MaterialsREFERENCES
1. Cheng Y, He C, Wang M, et al. Targeting epigenetic regulators for cancer therapy: mechanisms and advances in clinical trials. Signal Transduct Target Ther 2019;4:62.
2. Mallory XF, Edrisi M, Navin N, Nakhleh L. Methods for copy number aberration detection from single-cell DNA-sequencing data. Genome Biol 2020;21:208.
3. Soneson C, Robinson MD. Bias, robustness and scalability in single-cell differential expression analysis. Nat Methods 2018;15:255-61.
4. Arzalluz-Luque Á, Conesa A. Single-cell RNAseq for the study of isoforms-how is that possible? Genome Biol 2018;19:110.
5. Patel AP, Tirosh I, Trombetta JJ, et al. Single-cell RNA-seq highlights intratumoral heterogeneity in primary glioblastoma. Science 2014;344:1396-401.
6. Azizi E, Carr AJ, Plitas G, et al. Single-cell map of diverse immune phenotypes in the breast tumor microenvironment. Cell 2018;174:1293-1308.e36.
7. Jang JS, Li Y, Mitra AK, et al. Molecular signatures of multiple myeloma progression through single cell RNA-Seq. Blood Cancer J 2019;9:2.
8. Mitra AK, Mukherjee UK, Harding T, et al. Single-cell analysis of targeted transcriptome predicts drug sensitivity of single cells within human myeloma tumors. Leukemia 2016;30:1094-102.
9. Kim KT, Lee HW, Lee HO, et al. Single-cell mRNA sequencing identifies subclonal heterogeneity in anti-cancer drug responses of lung adenocarcinoma cells. Genome Biol 2015;16:127.
10. Horning AM, Wang Y, Lin CK, et al. Single-cell RNA-seq reveals a subpopulation of prostate cancer cells with enhanced cell-cycle-related transcription and attenuated androgen response. Cancer Res 2018;78:853-64.
11. Tirosh I, Izar B, Prakadan SM, et al. Dissecting the multicellular ecosystem of metastatic melanoma by single-cell RNA-seq. Science 2016;352:189-96.
12. Lee HW, Chung W, Lee HO, et al. Single-cell RNA sequencing reveals the tumor microenvironment and facilitates strategic choices to circumvent treatment failure in a chemorefractory bladder cancer patient. Genome Med 2020;12:47.
13. Chu T, Glymour C, Scheines R, Spirtes P. A statistical problem for inference to regulatory structure from associations of gene expression measurements with microarrays. Bioinformatics 2003;19:1147-52.
14. Berkson J. Limitations of the application of fourfold table analysis to hospital data. Int J Epidemiol 2014;43:511-5.
16. Grubman A, Chew G, Ouyang JF, et al. A single-cell atlas of entorhinal cortex from individuals with Alzheimer’s disease reveals cell-type-specific gene expression regulation. Nat Neurosci 2019;22:2087-97.
17. Regev A, Teichmann SA, Lander ES, et al. Science forum: the human cell atlas. Elife 2017;6:e27041.
18. Rozenblatt-Rosen O, Stubbington MJT, Regev A, Teichmann SA. The human cell atlas: from vision to reality. Nature 2017;550:451-3.
19. Schiller HB, Montoro DT, Simon LM, et al. The human lung cell atlas: a high-resolution reference map of the human lung in health and disease. Am J Respir Cell Mol Biol 2019;61:31-41.
20. Wagner J, Rapsomaniki MA, Chevrier S, et al. A single-cell atlas of the tumor and immune ecosystem of human breast cancer. Cell 2019;177:1330-1345.e18.
21. Matsumoto H, Kiryu H. SCOUP: a probabilistic model based on the Ornstein-Uhlenbeck process to analyze single-cell expression data during differentiation. BMC Bioinform 2016;17:232.
22. Kim J, T Jakobsen S, Natarajan KN, Won KJ. TENET: gene network reconstruction using transfer entropy reveals key regulatory factors from single cell transcriptomic data. Nucleic Acids Res 2021;49:e1.
23. Deshpande A, Chu LF, Stewart R, Gitter A. Network inference with Granger causality ensembles on single-cell transcriptomics. Cell Rep 2022;38:110333.
24. Aibar S, González-Blas CB, Moerman T, et al. SCENIC: single-cell regulatory network inference and clustering. Nat Methods 2017;14:1083-6.
25. Pratapa A, Jalihal AP, Law JN, Bharadwaj A, Murali TM. Benchmarking algorithms for gene regulatory network inference from single-cell transcriptomic data. Nat Methods 2020;17:147-54.
26. Ma S, Kemmeren P, Gresham D, Statnikov A. De-novo learning of genome-scale regulatory networks in
27. Ma S, Kemmeren P, Aliferis CF, Statnikov A. An evaluation of active learning causal discovery methods for reverse-engineering local causal pathways of gene regulation. Sci Rep 2016;6:22558.
28. Friedman N, Nachman I, Peer D. Learning bayesian network structure from massive datasets: The “sparse candidate” algorithm. arXiv 2013:1301.6696.
29. Maathuis MH, Kalisch M, Bühlmann P. Estimating high-dimensional intervention effects from observational data. Ann Statist 2009:37.
30. Sachs K, Perez O, Pe’er D, Lauffenburger DA, Nolan GP. Causal protein-signaling networks derived from multiparameter single-cell data. Science 2005;308:523-9.
31. Spirtes P, Glymour C, Scheines R, et al. Constructing Bayesian network models of gene expression networks from microarray data. 2000;1390833.
33. St-Pierre AP, Shikon V, Schneider DC. Count data in biology-Data transformation or model reformation? Ecol Evol 2018;8:3077-85.
34. Ives AR, Freckleton R. For testing the significance of regression coefficients, go ahead and log-transform count data. Methods Ecol Evol 2015;6:828-35.
35. Cameron AC, Trivedi PK. Regression analysis of count data. Cambridge: Cambridge University Press; 2013.
37. Székely GJ, Rizzo ML. Partial distance correlation with methods for dissimilarities. Ann Statist 2014;42:2382-412.
38. Yang E, Allen G, Liu Z, Graphical models via generalized linear models. .
39. Yang E, Ravikumar P, Allen GI, Liu Z. On graphical models via univariate exponential family distributions. J Mach Learn Res 2015;16:3813-47.
40. Yang E, Ravikumar PK, Allen GI, Liu Z. .
41. Allen GI, Liu Z. A local poisson graphical model for inferring networks from sequencing data. IEEE Trans Nanobiosci 2013;12:189-98.
42. Han SW, Zhong H. Estimation of sparse directed acyclic graphs for multivariate counts data. Biometrics 2016;72:791-803.
43. Hadiji F, Molina A, Natarajan S, Kersting K. Poisson dependency networks: gradient boosted models for multivariate count data. Mach Learn 2015;100:477-507.
44. Pearl J. Causality. Cambridge University Press. 2009. Available from: https://www.cambridge.org/core/books/causality/B0046844FAE10CBF274D4ACBDAEB5F5B [Last accessed on 23 Feb 2023].
45. Spirtes P, Glymour C, Scheines R. Causation, prediction, and search. Berlin, Germany: Springer-Verlag; 1993.
46. Aliferis CF, Statnikov A, Tsamardinos I, Mani S, Koutsoukos XD. Local causal and markov blanket induction for causal discovery and feature selection for classification Part I: algorithms and empirical evaluation. J Mach Learn Res 2010;11:171-234. https://jmlr.org/papers/volume11/aliferis10a/aliferis10a.pdf [Last accessed on 23 Feb 2023]
47. Aliferis CF, Statnikov A, Tsamardinos I, Mani S, Koutsoukos XD. Local causal and markov blanket induction for causal discovery and feature selection for classification Part II: analysis and extensions. J Mach Learn Res 2010;11:235-84. Available from: https://www.jmlr.org/papers/volume11/aliferis10b/aliferis10b.pdf [Last accessed on 23 Feb 2023]
48. Aliferis CF, Tsamardinos I, Statnikov A. HITON: a novel markov blanket algorithm for optimal variable selection. AMIA Annu Symp Proc 2003;2003:21-5.
49. Saxe GN, Ma S, Ren J, Aliferis C. Machine learning methods to predict child posttraumatic stress: a proof of concept study. BMC Psychiatry 2017;17:223.
50. Galatzer-Levy IR, Ma S, Statnikov A, Yehuda R, Shalev AY. Utilization of machine learning for prediction of post-traumatic stress: a re-examination of cortisol in the prediction and pathways to non-remitting PTSD. Transl Psychiatry 2017;7:e0.
51. Gunlicks-Stoessel M, Klimes-Dougan B, VanZomeren A, Ma S. Developing a data-driven algorithm for guiding selection between cognitive behavioral therapy, fluoxetine, and combination treatment for adolescent depression. Transl Psychiatry 2020;10:321.
52. Winterhoff B, Kommoss S, Heitz F, et al. Developing a clinico-molecular test for individualized treatment of ovarian cancer: the interplay of precision medicine informatics with clinical and health economics dimensions. AMIA Annu Symp Proc 2018;2018:1093-102.
53. Statnikov A, McVoy L, Lytkin N, Aliferis CF. Improving development of the molecular signature for diagnosis of acute respiratory viral infections. Cell Host Microbe 2010;7:100-1.
54. Statnikov A, Lytkin NI, Lemeire J, Aliferis CF. Algorithms for discovery of multiple markov boundaries. J Mach Learn Res 2013;14:499-566.
56. Fisher RA. The distribution of the partial correlation coefficient. Metron 1924;3:329-32. Available from: https://digital.library.adelaide.edu.au/dspace/handle/2440/15182 [Last accessed on 23 Feb 2023]
57. Kobak D, Berens P. The art of using t-SNE for single-cell transcriptomics. Nat Commun 2019;10:5416.
58. Pombo Antunes AR, Scheyltjens I, Lodi F, et al. Single-cell profiling of myeloid cells in glioblastoma across species and disease stage reveals macrophage competition and specialization. Nat Neurosci 2021;24:595-610.
59. Melsted P, Booeshaghi AS, Liu L, et al. Modular, efficient and constant-memory single-cell RNA-seq preprocessing. Nat Biotechnol 2021;39:813-8.
60. Townes FW, Hicks SC, Aryee MJ, Irizarry RA. Feature selection and dimension reduction for single-cell RNA-Seq based on a multinomial model. Genome Biol 2019;20:295.
61. Park HT, Park WB, Kim S, Lim JS, Nah G, Yoo HS. Revealing immune responses in the Mycobacterium avium subsp. paratuberculosis-infected THP-1 cells using single cell RNA-sequencing. PLoS One 2021;16:e0254194.
62. Tomaru Y, Simon C, Forrest AR, et al. Regulatory interdependence of myeloid transcription factors revealed by Matrix RNAi analysis. Genome Biol 2009;10:R121.
63. Jackson CA, Castro DM, Saldi GA, Bonneau R, Gresham D. Gene regulatory network reconstruction using single-cell RNA sequencing of barcoded genotypes in diverse environments. Elife 2020;2020:9.
64. Tchourine K, Vogel C, Bonneau R. Condition-Specific Modeling of Biophysical Parameters Advances Inference of Regulatory Networks. Cell Rep 2018;23:376-88.
65. Murphy KR, Myors B, Wolach A. .
66. Kummerfeld E, Willianms L, Ma S. Power analysis for causal discovery. Res Square 2022:PPR553586.
67. Kummerfeld E, Woolf T, Glad W, Sebag M, Ma, S. Important topics in causal analysis: summary of the caws 2021 round table discussion. In Causal Analysis Workshop Series (PMLR); 2021, pp. 52-4. Available from: https://proceedings.mlr.press/v160/kummerfeld21a/kummerfeld21a.pdf [Last accessed on 23 Feb 2023].
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Special Topic
Copyright
Data & Comments
Data





















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].