A large-scale task scheduling algorithm based on clustering and duplication
Abstract
Aim: Our research aims to explore a fast and efficient scheduling algorithm. The purpose is to schedule large-scale tasks on a limited number of processors reasonably while improving resource utilization.
Methods: This paper proposes a clustering and duplication-based method for large-scale task scheduling on a limited amount of processors. We cluster large-scale task to reduce the scale of the task in our method at first. Second, duplication-based task scheduling is carried out. Third, we optimize the local effect more precisely by deduplication in the last stage.
Results: We compare our algorithm with the state-of-the-art algorithms in the article. The results demonstrate that our scheduling scheme obtains about 30% optimization compared to existing large-scale scheduling methods and runs roughly ten times faster than existing duplication-based algorithms when scheduling large-scale tasks to a limited number of processors as compared to similar algorithms.
Conclusion: In this paper, we propose a task scheduling algorithm that can decrease the scheduling time of large- scale tasks on a limited number of processors and speed up the global execution time of the task. Further, we will study large-scale task scheduling on heterogeneous processor clusters.
Keywords
Introduction
Task parallelization and distributed computing are growing in popularity as the speed of computer development decreases and the demand for computing power increases. Applications such as Deep Learning and graph analytics require multiple computational resources (e.g., CPU/GPU, network bandwidth, memory)[1]. Device placement requires proper scheduling of existing resources in edge computing[2,3]. Therefore, a scheduler that allocates resources reasonably and efficiently so that tasks can be completed as soon as possible and maximizes resource utilization is needed.
Applications such as these are commonly modelled as large-scale Directed Acyclic graphs (DAG), in which nodes denote tasks and edges denote inter-task dependencies. Usually, the nodes of these DAG range in the tens of thousands, and we call such task scheduling large-scale task scheduling. Large-scale task scheduling is a significant and challenging area of research in computer science. Task scheduling systems need to balance the execution time of tasks and available computing resources to enable applications to be executed in the shortest time and maximize resource utilization. The demands on computer resources while executing a task vary significantly due to the different characteristics of the task. Some tasks demand a significant CPU for computation, while others have more requirements for IO operations. Meanwhile, there are many criteria used to evaluate the effectiveness of task scheduling - for example, fairness, low latency and high throughput. So there is hardly a method that can balance so many factors at the same time. It is a dynamic scheduling problem if task nodes come sequentially in time. If the tasks are specified, and all task-related information is known before schedule, then that is a static scheduling problem. The scheduling problem is a widely acknowledged NP-hard problem. Thus, researchers have proposed various solutions to the scheduling for different application cases. In this paper, we focus on large-scale static task scheduling on limited processors.
DAG scheduling is known as the static task scheduling problem[4-9]. Scheduling can be done statically during compilation since data such as task execution time, task dependencies, and communication costs are known about the application. We model the application as a DAG, with nodes denoting a task and edges denoting the dependencies between tasks. There are a certain number of processors available to schedule these tasks. We also know the task’s execution time and its time to transmit between tasks (if they are assigned to different processors). DAG scheduling aims to assign tasks to a reasonable number of processors so that the whole task completion time (makespan) is minimized.
The existing algorithms can be divided into three categories: list scheduling[5,7,10-13], cluster-based scheduling[5,14], and task duplication-based scheduling[4,6,15]. Some researchers also proposed mixed algorithms[5,16,17]. Through analysis, we find that the list-based scheduling algorithm is simple and easy to implement. However, it leads to a waste of computational resources, which is not acceptable. The duplication-based task scheduling algorithm performs well when scheduling small-scale tasks with a thousand nodes or less. Nevertheless, once the scale of the graph grows large, e.g., tens of thousands of nodes, it will take a long time because it usually has high algorithmic complexity. The clustering-based task scheduling algorithm is based on a bottom-up clustering approach, in which atomic tasks form clusters. We argue that the decisions in this method are local and cannot take into account the global structure of the graph. In addition, clustering-based tasks tend to be better with an adequate number of processors, leading to a waste of computational resources. The mixed algorithm[5,16,17] combines task clustering with list-based scheduling or duplication-based scheduling. For duplication-based scheduling[4,6,15] are achieved by allowing the assignment of a single task to multiple clusters to carry out task duplication, which can reduce the communication cost. Our approach can also be viewed as a mix of clustering and task duplication scheduling, where the task duplication part of the decision is limited by cluster scheduling.
In this paper, we propose a new large-scale Task Deduplication-based Partition Algorithm and Task Duplication (TDPATD) scheduling algorithm to reduce the complexity of task duplication-based (TDB) scheme[4,6,15] and accelerate large-scale task scheduling on a limited number of processors. TDPATD applies a DAG partitioning algorithm to cluster tasks with complex dependencies and generates new tiny task clusters at first. Subsequently, TDPATD applies an improved task duplication strategy to schedule the task clusters and obtains a better scheduling scheme. Lastly, the scheduling scheme is applied to the large-scale task clusters. Fine-grained task scheduling optimization is carried out to eliminate duplicate tasks to attain an ideal result.
The main contributions of our TDPATD are as follows:
Enhanced task initialization assignment algorithm: Large-scale task scheduling indicates that the number of tasks is much greater than the number of available processors. Existing duplication-based algorithms could not properly tackle this case. We strengthened the existing algorithm to satisfy this scenario.
Fine-grained optimization: We check the task on each processor and then remove the qualifying tasks to improve the global completion time since DAG partition and task duplication may generate duplicate execution of tasks when the scheduling of tasks is completed.
New parameters for algorithm: We define several parameters used in TDPATD to clarify better what we are accomplishing.
We compared TDPATD with state-of-the-art algorithms, including TDCA[4], which is a task duplication-based algorithm, BL_EST and BL_ETF[5], a list-based scheduling algorithm, and BL_EST_PART and BL_ETF_PART[5], which are mixed clustering and list-based scheduling algorithms. In addition, TDCA with a small amount of improvement based on clustering is also compared. Moreover, a DAG generator is used to cover different types of DAGs to evaluate our algorithms. We have investigated our algorithm on datasets from different sources, and extensive experiments have demonstrated that TDPATD can achieve better results when dealing with large-scale task scheduling. It can also achieve satisfactory results when dealing with small and mid-scale scheduling tasks.
The organizational structure of this paper is as follows. In Section 2, we discussed the background of this work. In Section 3, we introduced the details of TDPATD. We present the experimental results and analysis in Section 4. The conclusion is stated in Section 5.
Background
Model
We use the DAG graph to represent the task model. Let G = ⟨V, E⟩ be a directed acyclic graph, where V is a set of points denoted as V = {vi| vi ∈ N}, and each element represents a task node. N = |V| represents the total number of tasks. E is the set of edges denoted as E = {vi, vj | vi ≠ vj and vi, vj ∈ V} . The set of parent nodes of each vertex is denoted as Parent(vi) = {vj |⟨vj, vi⟩ ∈ E}, and the set of child nodes is denoted as Child(vi) = {vj |⟨vi, vj⟩ ∈ E}. If Parent(vi) = ø is the empty set, then node vi is a root node. Similarly, if Child(vj) = ø is empty, then node vi is a leaf node. The execution time of task vi on the processor is denoted as wi, W is the set of task execution times. The communication time of the task ⟨vi, vj⟩ is denoted as c(i, j) . When the partition is executed on a DAG, the partition result is denoted by PT. We record the node correspondence between the new diagram and the original DAG by subscripts and corresponding values. pt(i) indicates the partition number where the node vi is located in the original DAG.
The computing platform is a homogeneous cluster of identical processing units, called processors, denoted as P communicating through a fully connected homogeneous network. We enforce the realistic duplex singleport communication model, where at any point in time, each processor can, in parallel, execute a task, send multiple data, and receive multiple data. Each task needs to be assigned to a processor according to a priority constraint. In contrast, tasks are non-preemptive and atomic: processors execute only one task each time, and the execution of a task cannot be interrupted. The mapping between tasks and assigned processors is denoted as si, where i ∈ V, and si is the number of the task processor. The execution time of the task on the processor is wi. In addition, any ⟨vi, vj⟩ ∈ E, task vj cannot be dealed before task vi finished. Then the time that task vj needs to wait on processor sj for the computation results of task vi to be transferred over is c(i, j) if the processors si ≠ sj. The communication between processors is a duplex multi-port model. Specifically, each processor can process tasks, send data as well as receive data in parallel at any given time. Tasks, send data, and receive data at any given time, and can send and receive data between multiple processors simultaneously. Our goal is to minimize the global execution time (makespan) of the whole task through proper resource utilization. The formula for the makespan is available in Tables 1 and 2.
Parameters and interpretations
| i. j | Number of task in the DAG, also known as nodes. |
| Parent(i) | Set of parents of task vi.(i.e., all nodes that send data to node i). |
| Child(i) | Set of children of task vi.(i.e., all nodes that i send data to ). |
| W | Set of weght fot all nodes. |
| wi | Weight of task vi. (Also represent the execution time on the processor. ) |
| P | Set of processor available. |
| δ(i, j, p, q) | Communication cost from vi to vj. δ = 0 when p = q. |
| est(i, p) | When task i is assigned to processor p, the earliest start time for task i. |
| ect(i, p) | When task i is assigned \o proceisor p, the earliest complete time for task i. |
| pat(p, i) | Based on the current schedule, processor p’s available time for task i. |
| rst(i, p) | Based on the current schedule, the run-time start time for task i on processor p. |
| rct(i, p) | Based on the current schedule, the run-time complete time for task i on processor p. |
List and interpretation of formulas
| Eq. No. | Formula for calculation of parameters |
|---|---|
| 1 | 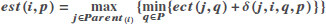 |
| Earliest start time of task vi on processor p. | |
| 2 | ect(i,p) = est(i,p) + wi |
| Earliest completion time of task vi on processor p. | |
| 3 | pat(i,p) = 0 |
| Processor avaliable time for the first task vi on schedule array sch. | |
| 4 | pat(i,p) = pat(p,rct(sch[index(sch,i)- 1],p)) |
| index(sch,i) means get node i’s subscript in the schedule array sch. | |
| 5 | 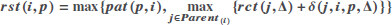 |
| In the simulation, the processor that completed node j will be recorded, here Δ represents the processor. | |
| 6 | rct(i,p) =rst(i,p) + wi |
| The run-time completion time of task vi on processor p. | |
| 7 | makespan = max{rct(i,θ) |vi ∈ {vi |Child(j) = ø} |
| θ mean the processor that vi assigned to. |
Related work
Task scheduling is classified into dynamic scheduling and static scheduling, and dag task scheduling belongs to static task scheduling. Methods of static task scheduling can be roughly divided into three categories: (1) List-based scheduling methods; (2) clustering-based scheduling methods; and (3) task duplication-based scheduling methods.
A priority is allocated to each task initially for the list-based scheduling method[5,7,10-13,18,19]. The priority list is formed in the order of descending priority, and then the task list is assigned to the processors in order. These algorithms differ in terms of how the priority levels are defined or how the tasks are assigned to the processors. Shin et al.[20] defined three task priority levels, namely, S-Level, T-Level, and B-Level. S-Level, also known as static level, is the most extended path length from the current node to the exiting node regardless of the communication cost between tasks. B-Level, also known as bottom or next level, calculates the longest path from the current node to the exit node considering the communication cost. T-Level (top-level or top rank) is the length of the longest path (including the communication cost) from the entry node to the current node. Heuristic algorithms based on list scheduling are usually easy to implement and understand. Generally, list-based scheduling algorithms also have lower complexity, but their solutions are not as effective as the other two types of scheduling algorithms.
The tasks are partitioned into clusters at first, and the tasks from the same cluster are scheduled as a block in the cluster-based scheduling method[5,21-24]. Clusters usually consist of tasks with strong correlation. The nature of the method is that tasks are grouped together on the same processor which are strongly correlated and the communication time between tasks on the same processor is quite negligible. Then the cluster will be scheduled to an unlimited number of processors which eventually are put altogether into the number of processors available. The cluster-based scheduling scheme works better when the actual number of available processors does not fall short of the number of clusters.
The underlying logic behind the TDB[4,6,8,15] scheduling algorithm is to reduce communication costs by assigning some tasks to multiple processors redundantly. In duplication-based scheduling, different strategies are available to select the ancestor nodes to be duplicated. Some algorithms clone the direct ancestors (e.g., TANH[6]) only, while others try to clone all possible ancestors (e.g., TDCA[4]).
The mixed algorithm[5,13,16,25-27] combines task clustering with list-based scheduling or duplication-based scheduling. Existing list-based scheduling algorithms (e.g., LDCP[7], HEFD[13]) will duplicate the previous tasks in order to reduce communication costs. For duplication-based scheduling[4,6] are achieved by allowing assignment of a single task to multiple clusters to carry out task duplication, which can reduce the communication cost. Our approach is close to cluster-based scheduling, as we partition the tasks into K ≥ p clusters at first, with p being the number of processors available. In the next step, we will schedule the tasks based on the task duplication method. Finally, we conduct more fine-grained task duplication checks. Thus, our approach can also be viewed as a mix of clustering and task duplication scheduling, where the task duplication part of the decision is limited by cluster scheduling.
Method
We describe the details of the TDPATD in this section. The proposed algorithm includes several vital parameters and three phases. In the first phase, TDPATD generates a specific partition by DAGP[28]. Then we can get a new graph by the partition information. The partition algorithm will ensure that the new graph is directed and acyclic. In the second phase, we generate an original scheduling scheme based on an improved algorithm of TDCA[4] since TDCA is better for the case when there are enough processors. Then the new graph is mapped back to the original graph according to the partition information. This step can ensure that the execution time will not increase, which will be proved later. Finally, the deduplication will occur based on the new schedule. Figure 1 shows the global process diagram of our strategy. We will explain it in more detail later.
Figure 1. Global process diagram of Task Deduplication-based Partition Algorithm and Task Duplication (TDPATD). G1 and G2 denote origin Directed Acyclic graphs (DAG) and clustered DAG, respectively. PT indicates the partition result. Nodes with the same color belong to the same partition, sch denotes scheduling scheme based on DAG. The gray dots denote unnecessary nodes in sch for G1, which will delete later. From p1 to pn denotes the number of processors.
Partition and clustering
First, we will partition the original DAG graph by a partitioning algorithm and obtain the PT mentioned in Section 2.1. This step is primarily a partitioning algorithm based on DAGP, which guarantees that the partitioning results will be a directed acyclic graph. In this process, we can control the number of partitions based on the number of processors available. In the clustering process, we will get a new graph based on the current partition information. The rules for generating the new graph are specified as follows. First, the total weight of the partition is calculated, i.e., the weights of all nodes in the same partition are summed. Because the weights of the nodes refer to the execution time of the task on the processor, the execution time does not vary due to clustering. The following formula calculates the weights of partition k:
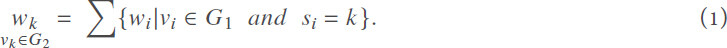
Then in the second stage, the communication time between partitions will be calculated. There are several possible candidates here: (1) the sum of node communication weights between partitions; (2) the average of node communication weights between partitions; and (3) the maximum value of node communication between partitions. The first case calculation rule modeled that the processor can only process tasks and send data serially. The second calculation method considers the communication situation as a whole, which is in the case that the communication weights are more evenly distributed and have a smaller distribution. However, the new graph is no longer accurate if there are extreme cases, such as a communication cost in a subinterval that is significantly above the average, which will have a negative impact on our later strategies. We adopt the third solution in this paper, which is suitable for the model of multi-port duplex communication. The communication cost between and is calculated as follows:
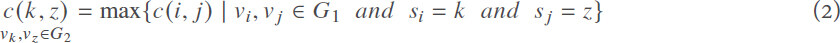
The negative impact due to taking the maximum value will be optimized in the Deduplication phase. In the third step, the connectivity between the partitions will be obtained by calculation. In the new DAG, the node numbers are the ones of the previous partitions, making it easier for the mapping process later. For example, partition 1 and partition 2, correspond to node 1 and node 2 in the new graph. if there exists any node in partition 1 that needs to communicate to the node in partition 2, then node 1 needs to communicate to node 2 in the new graph. The new graph should have a directed edge between node 1 and node 2 . This value takes the communication weight value obtained in the second step.
Scheduling
In the task scheduling phase, the solution we use is primarily based on TDCA, a duplication-based scheduling algorithm. At the same time, We have made some improvements to adapt our algorithm: TDCA is better when the number of processors is sufficient. TDCA does not give a suitable solution when the processors are fully occupied, but there are still a large number of tasks to be assigned. Considering that we mainly deal with large-scale task scheduling, the number of tasks is much larger than the number of available processors. So we made some changes. We stop the initialization method of TDCA when there are no available processors. Based on the existing scheduling scheme, we calculate the RCT of the task assigned and then assign the task to the processor with the smallest RCT. A more detailed description of the algorithm is given in Algorithm 1.
After the task initialization, we will get a task scheduling based on the new DAG. The task scheduling algorithm is based on TDCA. In this paper, some parameters are tuned to get better scheduling results. All the parameters we use and the formulas are shown in Tables 1 and 2. We will further optimize the scheduling scheme after we obtain it.
Deduplication
It is more challenging to optimize the scheduling scheme based on the new graph further. Before further optimizing makespan, the scheduling scheme needs to be applied to the original graph. The difference is that 3.2 generates a new dag graph based on partitioning, while the work to be done here is to decompose the nodes in the scheduling scheme to the nodes in the original graph that make up the partition based on the partition information. Here it will make the makespan further reduced. Since our scheduling is based on task duplication scheduling, the same task is processed more than once on different processors. Before mapping back to the original graph, the nodes of the same partition are regarded as a block. The granularity of tasks is smaller after mapping back to the original graph. Then there will be some tasks that will be repeatedly executed. So, we can remove the duplicate tasks to improve the global completion time. More specifically, we simulate the execution of tasks on each processor based on the existing task scheduling scheme. When executing to a task vi on processor p, the task will be computed on the assigned processor p at first, and then the completion time rct(i, p) of the task on the assigned processor p will be recorded in the completion list. Then we check the completion of that task in the completion list. It means there is a possibility that the same task is repeatedly computed on different processors several times if the task is completed more than once. Further, we deal with this case. We find the processor where each task is assigned to first. Then we find the first child node of that task assigned to the same processor and record the communication weight θ between them. This process is usually done very quickly because the task arrangement is based on an incremental BLevel arrangement, and the BLevel values of the parent and child nodes do not differ very much. Then we make a comparison, which is illustrated here by the example that task i has completed the computation on both processors p, q. Then we check if any of the tasks satisfy the following equation:

δ here refers to the communication delay from task i to the first child node on processor q. If the equation holds, it means that the task i assigned on processor q is unnecessary since task i has already completed its computation on processor p, and the result is transferred to q earlier than i completes on q. So we can remove task i on processor q. This process works better when more completion records are found. A more exact description of this algorithm is in Algorithm 2.
Complexity analysis
The meanings of the symbols are explained at the beginning, n and m denote the number of nodes and edges, respectively. Similarly λ and θ denote the number of nodes and edges of the DAG after clustering, respectively. By p, we denote the number of processors.
In the partition stage, we use the DAGP [28] partition algorithm, which has a time complexity of O (n + m). The complexity of the cluster is O (n + m). In the task scheduling phase, our strategy is similar to TDGA[4]. The complexity is O (pθλ + p2θ). Moreover, the complexity is effortless to calculate in the mapping phase, which is O (n). In the deduplication phase, we can calculate the complexity to be O (p2n), which is described in Algorithm 2.
To sum up, the overall time complexity of TDPATD is O (m + pθλ + p2θ + p2n). We know that the complexity of TDCA is O (pmn + p2m). When the number of processors is constant, and the number of task nodes is much larger than the number of processors, i.e., n ≫ p, our complexity can be considered as O (m + n + θλ), while the complexity of TDCA is O (mn). It can be seen from the above equation that our algorithm has a great advantage in time.
Trace of TDPATD
We will use a small instance to illustrate the process of TDPATD in this section. The DAG we use is shown in Figure 2. The connection relationship between them and the communication time is given in the figure. Also, the weights of the nodes are in Table 3. We will schedule the tasks to 2 processors. We partition the DAG by DAGP[28] firstly. Here we partition the original dag G1 into 5 parts, and the partition results are shown in Figure 2. The same color belongs to the same partition. Then we clustered the original graph into a new dag graph G2 based on the partition information. We can calculate the weight of task v1 in the new graph G2 according to the rules of clustering:
Figure 2. The origin DAG G1 and partition result. Nodes with the same color belong to the same partition.
Weight of nodes for origin DAG G1
| Nodes | v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 | v10 | v11 | v12 | v13 | v14 | v15 |
| Weight | 62 | 67 | 88 | 43 | 40 | 75 | 80 | 74 | 40 | 60 | 69 | 63 | 78 | 39 | 31 |
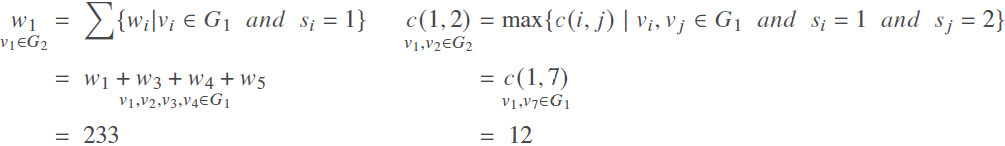
The cost of communication from node v1 to node v2 can be obtained by calculating. The remaining data in the G2 are available through the same calculation steps. The full calculation results are shown in Figure 3 and Table 4.
Weight of nodes for new DAG G2
| Nodes | v1 | v2 | v3 | v4 | v5 |
| Weight | 233 | 80 | 144 | 204 | 248 |
Next, we schedule G2 to our two processors based on our strategy. The scheduling results are shown in Figure 4. Then, we apply this scheduling scheme to the original graph G1. The results are shown in Figure 5. We observe that task v1, v3 and v5 are assigned on both processes. Next, we will check the possibility of deleting them.
During the Deduplication phase, we will simulate the execution of the scheduling scheme on the processor. We remove and update the scheduling scheme if we find any tasks that match the conditions. First, we simulate the execution of processor 1. It can be seen that processor 1 does not need to accept data from other processors before it can complete all assigned tasks. We can get rct(3,1) = 217 and rct(12,1) = 437. Next, we simulate the execution of processor 2. After the processor has computed task v3 . We find that there are two completion messages for task v3. Then check if there is a possibility to delete one of them. Then we find that task v3 on processor 2 is qualifying because rct(3,2) = 305 > rct(3,1) + c(3,9) = 244 holds. Then we remove task v3 from processor 2. A similar case occurs again when processor 2 completes task v5. As a result of the calculation, there exists a task that meets the condition because the equation rct(5,1) = 331 > rct(5,2) + c(5,12) = 281 holds. We remove task v5 from processor 1 and update the scheduling scheme. Attention, all tasks after task v5 on processor 1 need to be re-simulated for computation. In the end, our scheduling scheme is shown in Figure 6.
Results
DataSet
We have evaluated instances coming from two sources. The program generates the first set we use to generate the various types of graphs we need. The specific generation process will be described in detail later. The second set is from the work of Lin et al.[2]. This set contains 7 instances of graphs, each having 200 to 8000 nodes. We used four DAGs generated by widely used DNN models. The DNN models include BERT (with 3. 6, 128 transformer layers), ResNet-50[2].
There are several important parameters for our generation procedure which we will explain in detail. The first is the number of tasks n, i.e., the number of vertices in the DAG graph. Then the next is the communication computation ratio, CCR. graph height, which is the number of layers of the graph levels. AOD, the average out-degree. CDR, the communication data packet range. The steps of our graph generation are as follows. In addition, there are two critical parameters used in our strategy. The proc indicates the number of available processors, and part is the number of partitions. The part is also interpreted as the number of nodes in the clustered DAG graph G2.
Generate the count of node in every level. We obtain the results directly since both the first and the last layer of the graph contain only one node. Then (n-2) nodes are randomly and uniformly distributed into the remaining layers.
Generate the out degree and weight of node. In this step we generate the exit degree information for each node in each layer starting from the first layer. The out degree matches the normal distribution with a mean value of the configured parameters. The process will not stop until the bottom second layer, because the penultimate layer has only one outgoing edge of the node, pointing to the exit node. The last layer has only exit nodes, and the exit node out degree is 0. we consider both the ideal AOD and the number of nodes in the next layer when generating the out degree for each node. If the number of nodes is sufficient, the random generation is performed with the AOD as the mean value. Otherwise, we judge whether the generated number of nodes is within the reality, and if not, they are rounded off and regenerated. At the same time, we randomly generate weight for each node according to the configuration of CDR and CCR. Here the distribution of weight follows distribution.
Connect nodes in adjacent level. This process connects the nodes between the layers and then the entire DAG. We ensure that the difference in the in-degrees of the nodes in the connected layers is not greater than one when establishing connections between layers to ensure the balance of the whole graph. For the first layer, the entry node will establish a directed edge with each second layer node. For the penultimate layer, each node will establish a directed edge with the exit node. Also, we will generate the edge weight for each generated directed edge, that is, the communication time between tasks, based on the CCR and CDR.
Ensure the connections among multiple levels. There may occur a case that a node does not have a parent node or child node in the actual process of generating the graph. We finally check each node’s parent node and child node (except the entry node and the exit node). We will randomly choose a parent node in the node’s upper level to create a directed edge if the in-degree of the node is 0. If the node out-degree is 0, a child node is randomly selected among the nodes in the next layer of that node to create a directed edge. By doing so, we ensure that the final graph is directed and acyclic.
Baselines
BL_EST[5]
The logic of the algorithm is relatively simple. First, all the tasks that can be executed immediately are put into the ready queue. Generally, the tasks in the queue are usually the entry tasks after initialization. All completed tasks are put into the completion queue. The task will be put into the waiting queue if any parents are not in the completion queue. When a processor is available, the first task in the ready queue will be assigned.
ETF[5]
EFT is a dynamic priority-based list scheduler. For tasks in the ready queue, the algorithm calculates the earliest start time for each task on a different processor. Unlike BL_EST, which assigns processors directly, ETF considers the actual time that a task gets executed on a processor, which is relatively better than BL_EST However, its time complexity is higher than the latter.
BL_EST_PART and ETF_PART[5]
These two are mixed scheduling algorithms of clusters and lists. The main concept of this algorithm is to partition tasks into a certain number of clusters first and then schedule them. The detailed algorithm for scheduling is basically similar to BL_EST and ETF, but tasks belonging to the same cluster will be assigned to the same processor. This is an algorithm with a balanced performance.
B_Deduplication
This is half of our algorithm, which does not contain the results of deduplication. The work of B_Deduplication (before deduplication) mainly optimizes the algorithm for initializing the task queue. We set this baseline to emphasize the practical part of our work.
Comprehensive comparison
The parameters of the DAG graphs and the parameters of the algorithm involved in the experiments are as follows:
Number of nodes n ∈ {4000, 5000, 6000, 7000, 8000, 9000, 10000}.
Communication-computation ratio CCR∈ {0.5, 1, 1.5, 2, 2.5, 5, 7}.
Processor number proc ∈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20}.
Partation num part ∈ {400, 500, 600, 700, 800, 900, 1000, 1200}.
We evaluated the effect of the different number of partitions on the performance of our strategy in the first experiment. It should be noted that we cannot exhaustively explore all the possibilities due to the large parameter space. Thus we adopted reasonable configurations in each experiment except the variable under investigation. As shown in Figure 7, the performance of our algorithm is not so good when the number of partitions is small. As the number of partitions increases, the advantage of our strategy is exposed. Our method performs equally well on the real dataset, as shown in Figure 8. According to the experiments, the all-around performance of TDPATD exceeds the traditional clustering-based algorithm when the ratio of the number of nodes to the number of partitions does not go beyond 20. The improvement in the performance of our algorithm over baseline is about 30% to 40% when the number of partitions is reasonable. Moreover, the data for ETF and BL_EST remain unchanged in Figure 7 for the reason that the number of partitions does not affect these two strategies.
In the second experiment, we investigated the effect of CCR on makespan. As shown in Figure 9, our algorithm performs well and produces a satisfactory makespan when the CCR is within a reasonable range. The performance of our algorithm tends to be the same as the baseline algorithm, and the effect of the deduplication fades out when the CCR is greater than 5. In our strategy, we will remove node vi from p if vi has generated results on other processors and the transfer time to p is faster than executing vi directly. As the time for communication between tasks grows, fewer tasks will be qualified in this case. So the experiment meets expectations. Second, in this experiment, we observe that the effect of deduplication is noticeable. The makespan is primarily consistent with the effect of the baseline when no task is being done with the deduplication, which is a further indication that our work is practical.
We investigated the effect of the number of processors on the makespan in the third experiment. We found that the baseline algorithm is not very sensitive to the number of processors. As the number of processors we set increases, the actual number of occupied processors does not produce any additional variation. We found that the baseline algorithm is not very sensitive to the number of processors. As the number of processors increases, the actual number of occupied processors will settle at a specific value. Our analysis of the possible reasons for this phenomenon is that the communication time incurred by scheduling the cluster to other processors will be longer than the computation time of the processors because the communication time on the same processor is almost negligible. The results are shown in Figure 10, which indicates that our algorithm can obtain about 30% optimization compared to the baselines. The makespan decreases, but the rate of change tends to zero as the number of processors increases.
Figure 10. Comparison of makespan on number of processor. TDPATD can obtain better results when the number of available processors is growing.
In the fourth experiment, we investigated the effect of the number of nodes on the makespan. Figure 11 shows that when the number of partitions is fixed, the performance of our algorithm gradually decreases as the number of tasks increases, which corroborates the conclusion of the first experiment indirectly.
In addition, we compare it with the traditional duplication-based scheduling algorithm. When TDCA[4] runs tens of thousands of node graphs (large-scale DAG), it takes too long, so we tested it with small-scale graphs. The results are shown in Figure 12. We first compare our method with TDCAs makespan. We find that our method and TDCAs makespan are pretty similar when the number of available processors is small. At the same time, our method runs an order of magnitude faster than TDCA. Both our method and TDCA show a promising trend when the number of processors is larger. As the number of available processors increases, the running time of TDCA decreases, and the running time of our method increases. Our method runtime is an order of magnitude faster than the traditional replication algorithm. A comparison of our strategy and TDCA is shown in Figure 13, where a deep neural network model models the dataset. The experimental results are within our expectations since TDCA is more adept at handling a small and sufficient number of processors cases.
Figure 12. Comparison of makespan and running time for TDCA and TDPATD on the graph with node 1000 TDPATD has outstanding advantages in running speed.
Figure 13. Results for makespan with different number of nodes on the bert dataset. TDPATD has practically comparable results on the realistic data set.
In general, the experiments satisfy our expectations predominantly. Compared with traditional algorithms, the advantage of our algorithm is self-evident when the graph size is larger and fewer processors are available. The number of partitions and CCR have a significant impact on our algorithm. The impact of the number of nodes on the algorithm depends on the number of partitions. The number of processors affects the experimental results in a way.
Conclusions
For large-scale DAG task scheduling, we propose a new algorithm. The algorithm mixes cluster-based scheduling and duplication-based scheduling. The cluster-based scheduling algorithm can significantly reduce the complexity and running time of the algorithm when dealing with large-scale scheduling tasks. However, there is a loss of scheduling effectiveness as a consequence. Therefore, we apply the duplication-based task scheduling method based on clustering to reduce the loss of scheduling effect due to clustering. Moreover, we optimize the task queue initialization strategy of TDCA to make it more suitable for our algorithm. In addition, we define several new parameters pat, rst, and rct. By calculating the rct of the task, we can further optimize the scheduling scheme during the simulation stage. More importantly, we carry out another task deduplication work after that and remove the unnecessary tasks generated by the previous scheduling to improve the effectiveness of our strategy. Upon experimental analysis, our strategy excels when the tasks satisfy (1) the normal range of CCR (no more than 5); and (2) the number of available processors is small. It indicates that our strategy can avoid the waste of resources while optimizing the effect of large-scale task scheduling. Further, we will investigate large-scale task scheduling on heterogeneous processor clusters. Also, we consider using parallel approaches to speed up this work in the future. We hope that there will be more research and progress in the future.
Declarations
Authors’ contributionsMade substantial contributions to conception and design of the study and performed data analysis and interpretation: Huang W, Shi Z, Xiao Z
Funding acquisition, project administration, provide research resources, and supervision: Chen C, Li K
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was supported by Natural Science Foundation of Hunan Province (No. 2020JJ5083).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2021.
REFERENCES
1. Parravicini A, Delamare A, Arnaboldi M, et al. DAG-based scheduling with resource sharing for multi-task applications in a polyglot GPU runtime. 2021 IEEE International Parallel and Distributed Processing Symposium (IPDPS) Portland, OR, USA. IEEE; 2021. pp. 111-20.
2. Lin P, Shi Z, Xiao Z, et al. Latency-driven model placement for efficient edge intelligence service. IEEE Trans Serv Comput 2021; doi: 10.1109/TSC.2021.3109094.
3. Liu L, Tan H, Jiang SHC, et al. Dependent task placement and scheduling with function configuration in edge computing. 2019 IEEE/ACM 27th International Symposium on Quality of Service (IWQoS) Phoenix, AZ, USA. IEEE; 2019. pp. 1-10.
4. He K, Meng X, Pan Z, et al. A novel task-duplication based clustering algorithm for heterogeneous computing environments. IEEE Trans Parallel Distrib Syst 2018;30:2-14.
5. Özkaya MY, Benoit A, Uçar B, et al. A scalable clustering-based task scheduler for homogeneous processors using dag partitioning. 2019 IEEE International Parallel and Distributed Processing Symposium (IPDPS) Rio de Janeiro, Brazil. IEEE; 2019. pp. 155-65.
6. Bajaj R, Agrawal DP. Improving scheduling of tasks in a heterogeneous environment. IEEE Trans Parallel Distrib Syst 2004;15:107-18.
7. Daoud MI, Kharma N. A high performance algorithm for static task scheduling in heterogeneous distributed computing systems. J Parallel Distrib Comput 2008;68:399-409.
8. Kwok YK, Ahmad I. Static scheduling algorithms for allocating directed task graphs to multiprocessors. ACM Comput Surv 1999;31:406-71.
9. Chowdhury P, Chakrabarti C. Static task-scheduling algorithms for battery-powered dvs systems. IEEE Trans Very Large Scale Integr VLSI Syst 2005;13:226-37.
10. Chronaki K, Rico A, Casas M, et al. Task scheduling techniques for asymmetric multi-core systems. IEEE Trans Parallel Distrib Syst 2016;28:2074-87.
11. Omara FA, Arafa MM. Genetic Algorithms for Task Scheduling Problem. In: Abraham A, Hassanien A, Siarry P, Engelbrecht A, editors. Foundations of Computational Intelligence Volume 3. Berlin: Springer Berlin Heidelberg; 2009. pp. 479-507.
12. Liu GQ, Poh KL, Xie M. Iterative list scheduling for heterogeneous computing. J Parallel Distrib Comput 2005;65:654-65.
13. Tang X, Li K, Liao G, et al. List scheduling with duplication for heterogeneous computing systems. J Parallel Distrib Comput 2010;70:323-9.
14. Palis MA, Liou JC, Wei DSL. Wei Task clustering and scheduling for distributed memory parallel architectures. IEEE Trans Parallel Distrib Syst 1996;7:465-5.
15. Zhang W, Hu Y, He H, et al. Linear and dynamic programming algorithms for real-time task scheduling with task duplication. J Supercomput 2019;75:494-509.
16. Taheri G, Khonsari A, Entezari-Maleki R, et al. A hybrid algorithm for task scheduling on heterogeneous multiprocessor embedded systems. Appl Soft Comput 2020;91:106202.
17. McCreary CL, Khan AA, Thompson JJ, et al. A comparison of heuristics for scheduling dags on multiprocessors. Proceedings of 8th International Parallel Processing Symposium Cancun, Mexico. IEEE: 1994. pp. 446-51.
18. Radulescu A, Van Gemund AJC. Low-cost task scheduling for distributed-memory machines,”. IEEE Trans Parallel Distrib Syst 2002;13:648-58.
19. Topcuoglu H, Hariri S, Wu MY. Performance-effective and low-complexity task scheduling for heterogeneous computing. IEEE Trans Parallel Distrib Syst 2002;13:260-74.
20. Shin KS, Cha MJ, Jang MS, et al. Task scheduling algorithm using minimized duplications in homogeneous systems. J Parallel Distrib Comput 2008;68:1146-56.
21. Wang H, Sinnen O. List-scheduling versus cluster-scheduling. IEEE Trans Parallel Distrib Syst 2018;29:1736-49.
22. Kanemitsu H, Hanada M, Nakazato H. Clustering-based task scheduling in a large number of heterogeneous processors. IEEE Trans Parallel Distrib Syst 2016;27:3144-57.
23. Kwok YK, Ahmad I. Dynamic critical-path scheduling: an effective technique for allocating task graphs to multiprocessors. IEEE Trans Parallel Distrib Syst 1996;7:506-21.
24. Wu MY, Gajski DD. Hypertool: a programming aid for message-passing systems. IEEE Trans Parallel Distrib Syst 1990;1:330-43.
25. Daoud MI, Kharma N. A high performance algorithm for static task scheduling in heterogeneous distributed computing systems. J Parallel Distrib Comput 2008;68:399-409.
26. Liu CH, Li CF, Lai KC, et al. A dynamic critical path duplication task scheduling algorithm for distributed heterogeneous computing systems. 12th International Conference on Parallel and Distributed Systems - (ICPADS’06) Minneapolis, MN. IEEE; 2006. p. 8.
27. Ranaweera S, Agrawal DP. A task duplication based scheduling algorithm for heterogeneous systems. Proceedings 14th International Parallel and Distributed Processing Symposium Cancun, Mexico. IEEE; 2000. pp. 445-50.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
































Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].