Observer-based H∞ consensus for linear multi-agent systems subject to measurement outliers
Abstract
The consensus problem has a crucial role in theoretical and practical aspects of interconnected systems, for instance in smart computing field. This paper is concerned with the observer-based H∞ consensus problem for a class of linear multi-agent systems subject to measurement outliers. In the addressed observer-based H∞ consensus problem, measurement outliers can affect the estimation accuracy and thus affect the consensus performance. To assuage the impact of measurement outliers, a control protocol based on an observer containing a saturation function with variable saturation limits is proposed. The purpose of this paper is to find a solution to the addressed H∞ consensus problem for a class of linear multi-agent systems subject to measurement outliers by designing an observer-based control protocol such that multi-agent systems can fulfill the H∞ consensus performance over a finite horizon. With the aid of Lyapunov theory, the sufficient condition is established to guarantee that the consensus error dynamic system satisfies the H∞ consensus performance. Then, the linear matrix inequality (LMI) approach is used to obtain the desired parameters of the observer-based control protocol. Finally, the effectiveness of the proposed control protocol is verified in a simulation environment.
Aim: The purpose of this study is to find a solution to the addressed H∞ consensus problem for a class of linear multi-agent systems subject to measurement outliers.
Methods: By choosing a suitable Lyapunov function, the sufficient condition is obtained, which can guarantee the consensus error dynamic system satisfying the given H∞ consensus performance. The LMI approach is employed to design the desired controller. With Matlab LMI toolbox, a numerical example was conducted to demonstrate the effectiveness of the proposed observer-based control protocol in the simulation environment.
Results: A satisfactory consensus performance can be guaranteed for multi-agent systems subject to measurement outliers under the proposed observer-based control protocol. The constructed saturation function with variable saturation limits can mitigate the effect of measurement outliers by dynamically regulating saturation limits. Compared with the traditional observer-based control protocol, in this paper, the proposed observer-based control protocol shows robustness against measurement outliers.
Conclusion: A solution to the addressed multi-agent consensus problem subject to measurement outliers was found by designing an observer-based consensus controller. The obtained results can be extended to sensor networks, neural networks, and nonlinear multi-agent systems.
Keywords
Introduction
A smart computing system is usually composed of a number of smart mobile nodes. To maintain the prespecific system performance requirement in the presence of certain sudden cases, researchers have employed many intelligent methods to cope with the computing problem for different types of practical systems. With the development of science and technology, the study of the smart computing problem for interconnected systems has become a hot research topic, and much effort has been made in many application fields, such as smart grids[1]. It is worth mentioning that the consensus problem has shown a crucial role in theoretical and practical aspects of interconnected systems and has stirred up a wave of research (see[2,3]).
In the past few decades, the research on collective behaviors of multiple networked agents has attracted attention owing to the wide range of practical applications referring to robotics, satellite networks, unmanned vehicles, sensor networks, and so on. Consensus, as one of the most typical collective behaviors, aims to let the states of a group of homogeneous or heterogeneous agents in light of the local shared neighboring information reach a common value[4,5]. Focusing on the consensus control problem, researchers in different research fields have made great efforts and numerous research results have been published (see[6] and the references therein). To cater to the robustness requirement of multi-agent systems, the H∞ consensus problem is put forward in ref.[7], which is extended to the H∞ consensus control problem in ref.[8]. Until now, the H∞ consensus problem has been studied deeply and many remarkable results have been published (see, e.g.,[9-16]). In particular, the H∞-consensus control problem under round-robin protocol is studied for a class of linear multi-agent systems in ref.[15]. Further, in ref.[16], the leader–follower H∞-consensus problem is investigated for a class of nonlinear multi-agent systems under semi-Markovian switching topologies with partially unknown transition rates.
In light of the given network topology, how to design an efficient H∞ consensus control protocol is a pivotal issue for the individual agent[17]. Under the state-feedback-based control protocol, one agent in multi-agent systems, by using its own state information and the state information shared by its neighboring agents, can make its state converge to a given common state. Because of the simpleness and convenience of design, the state-feedback-based consensus control problem has obtained widely attention[6,18]. Unfortunately, in practical engineering, it is sometimes difficult to attain the full state information. Instead, observer-type distributed consensus control protocols, as one type of the measurement-based control protocols, have been developed.
In recent decades, the observer-based H∞ consensus problem for multi-agent systems has attracted a large amount of research attention, and many remarkable research results have been published in the literature (see, e.g.[4,19-21]). In ref.[19], a robust yet reliable consensus control law against actuator faults is proposed, under which the desired control performance can be ensured. In ref.[4], the observer-type event-triggered H∞ consensus control problem is studied in a finite-time horizon for a class of discrete time-varying multi-agent systems subject to external disturbances and missing measurements.
In the above-mentioned studies, the impacts of missing measurements, actuator faults, and redundant channels on multi-agent consensus performance have been investigated. In practical applications, it is noted that outlier is another common phenomenon mainly originating from sensor or communication failures, disturbances in the environment, human errors, and so on, which will contaminate the measurements and thus affect the control performance. To mitigate the effect of measurement outliers, several research efforts have been made (see[22-26]). For example, in[22], a novel observer including a saturation function with variable saturation limits is constructed. Based on the results, the state estimation problem for neural networks is studied in ref.[23] and the fault detection problem is considered in T-S fuzzy system in ref.[26]. In addition, the method proposed for outliers detection in wireless sensor networks has been studied, which is implemented within a hierarchical multi-agent framework in ref.[27]. It is worth mentioning that the H∞ consensus control problem based on such a novel observer for linear multi-agent systems has not yet gained adequate attention, and this constitutes the main motivation of this paper.
Based on above discussions, in this paper, the observer-based H∞ consensus problem is studied for a class of linear multi-agent systems subject to measurement outliers. The main contributions of this paper are summarized as follows: (1) measurement outliers are considered for the first time for linear multi-agent consensus control problem; (2) a saturation function with variable saturation limits is introduced to the observer; and (3) a novel observer-based control protocol is proposed, under which linear multi-agent systems subject to measurement outliers can achieve H∞ consensus performance over a finite horizon.
Problem formulation
Consider a multi-agent system with N agents under a fixed network topology. Let  be a directed graph including a node set
be a directed graph including a node set 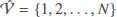 and an edge set
and an edge set 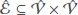 . If an edge exists between nodes i and j, we denote
. If an edge exists between nodes i and j, we denote 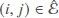 and node j is called a neighbor of node i and vice versa; if no edge exists between nodes i and j, it means
and node j is called a neighbor of node i and vice versa; if no edge exists between nodes i and j, it means 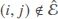 . Let
. Let 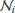 denote all neighbors of node i. Moreover, define the Laplacian matrix
denote all neighbors of node i. Moreover, define the Laplacian matrix 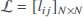 with lij = −1 if
with lij = −1 if 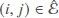 , lij = 0 if
, lij = 0 if 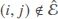 , and
, and 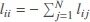 .
.
Consider a discrete linear multi-agent system with N agents. The dynamics of ith agent can be expressed by
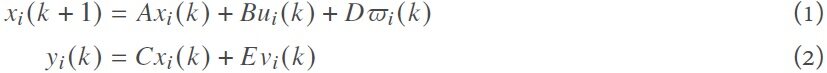
where 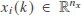 is the state,
is the state, 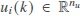 is the control input,
is the control input, 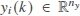 is the measurement output,
is the measurement output,  and
and 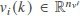 are the system noise and measurement disturbance, respectively, which are assumed to belong to l2 [0, M]. A, B, C, D, and E are known time-invariant matrices with appropriate dimensions.
are the system noise and measurement disturbance, respectively, which are assumed to belong to l2 [0, M]. A, B, C, D, and E are known time-invariant matrices with appropriate dimensions.
In this paper, we consider a case that outliers may occur in the measurement. In practical applications, outliers may originate from sensor or communication failures, disturbances in the environment, human errors, and so on. To mitigate the effect of measurement outliers, we construct an observer-based control protocol of the following form for agent i:
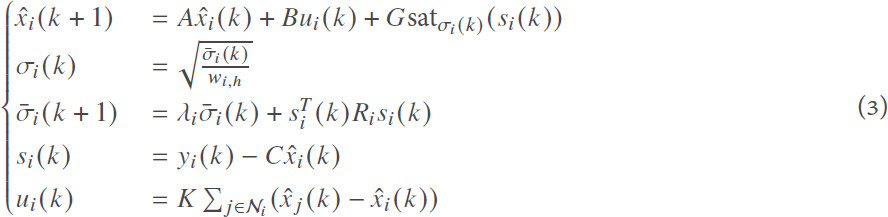
where x̂i(k) is the state of the observer i, σi(k) = [σi,1(k), σi,2(k),..., σi,h(k)]T (h = 1, 2,..., ny) denotes the variable non-negative saturation limit vector, si(k) = [si,1(k), si,2(k),..., si,h(k)]T is the innovation vector, and satσi(k)(si(k)) is a saturation function of the following form:
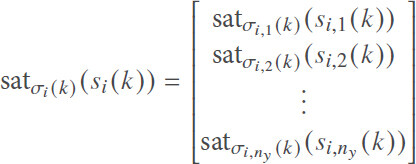
with satσi,h(k)(si,h(k)) = max {-σi,h(k), min {σi,h(k), si,h(k)}} being a saturation function. The scalars λi ∈ [0, 1), wi,h > 0 matrices  , and G and K are controller parameters to be designed below. Define Wi = diag(wi, 1, wi, 2,..., wi, ny).
, and G and K are controller parameters to be designed below. Define Wi = diag(wi, 1, wi, 2,..., wi, ny).
An auxiliary variable qi(k) is introduced to simplify the notation expression, which is defined as follows:

Denote
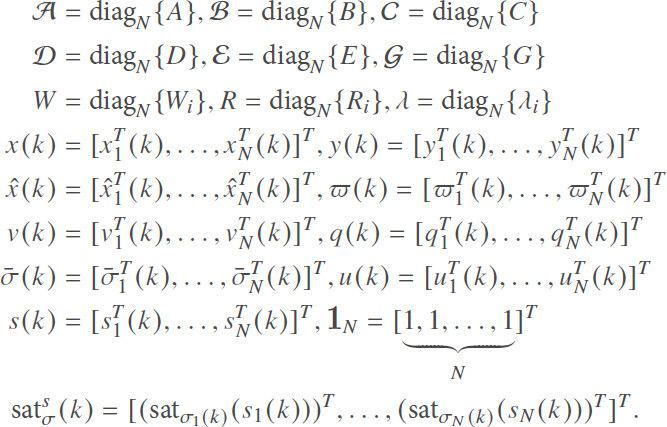
Then, Equations (1) and (2) can be rewritten as follows:
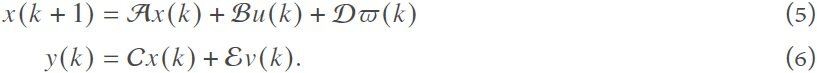
The proposed observer-based control protocol in Equation (3) can be rewritten as follows:

Then, the augmented auxiliary variable q(k) has the following form:

By defining e(k) = x(k) − x̂(k) and combining Equations (5)–(8), the following error dynamic system can be obtained:
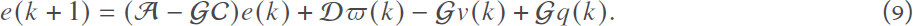
Denote
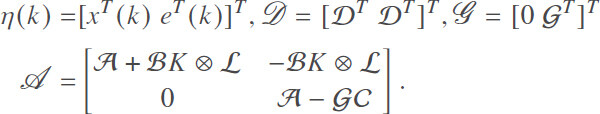
Then, it follows from Equations (5) and (9) that
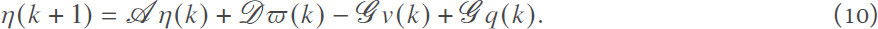
Definition 1Given the positive definite matrix U = UT > 0 and the disturbance attenuation level γ > 0, if the following inequality

holds, where  , it is said that the multi-agent system in Equation (1) can achieve the H∞consensus performance index in Equation (11) over a finite horizon [0, M].
, it is said that the multi-agent system in Equation (1) can achieve the H∞consensus performance index in Equation (11) over a finite horizon [0, M].
In this paper, our objective is to design appropriate parameter matrices and scalars {G, λi, Ri,Wi, K} for the proposed observer-based control protocol in Equation (3) such that the multi-agent system in Equation (1) can achieve consensus.
Main results
In this section, a solution is found to the addressed multi-agent consensus problem by properly designing the desired controller in Equation (3). The following theorem gives a sufficient condition under which the augmented system in Equation (10) can achieve the given H∞ consensus performance in Equation (11).
Firstly, we give the following assumption and lemma which are useful to obtain our main results.
Assumption 1The matrix B is a full-column rank matrix, i.e., rank (B) = cB.
For the matrix B, there exist two orthogonal matrices 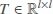 and
and  , such that
, such that

where 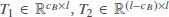 , and Λ = diag{Λ1, Λ2,..., ΛCB} with Λj (j = 1, 2, . . ., cB) being nonzero singular values of B.
, and Λ = diag{Λ1, Λ2,..., ΛCB} with Λj (j = 1, 2, . . ., cB) being nonzero singular values of B.
Lemma 1Assume the matrix 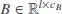 is a full-column rank matrix. If matrix P1has the structure
is a full-column rank matrix. If matrix P1has the structure
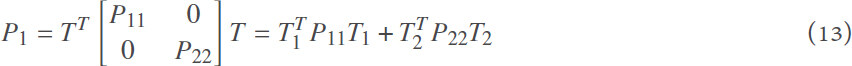
where 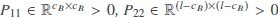 , and the definitions of T1and T2are given in Equation (12), then a nonsingular matrix
, and the definitions of T1and T2are given in Equation (12), then a nonsingular matrix  satisfies BP0 = P1B.
satisfies BP0 = P1B.
Theorem 1Consider the linear multi-agent system in Equation (1) and let the disturbance attenuation level γ, a positive definite matrix U, and controller parameters {G, K} be given. The augmented system in Equation (10) can achieve the H∞consensus performance in Equation (11) if there exist a positive definite matrix P and some controller parameter matrices and scalars {λi, Ri,Wi}, under the initial condition 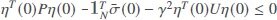 , satisfying the following LMI:
, satisfying the following LMI:

where
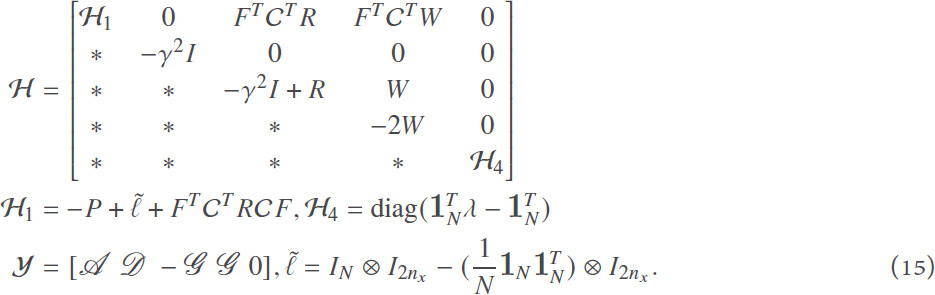
proof 1Construct the following Lyapunov-like functional function for the augmented system in Equation (10):
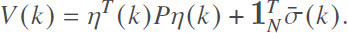
Then, one has
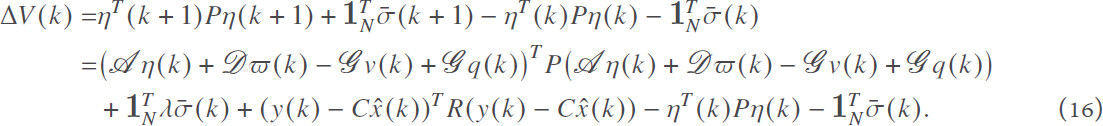
According to Lemma 1.6 in[28], the following sector constraint condition can be obtained:
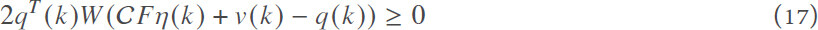
where F = [0 I].
Taking the H∞consensus performance in Equation (11) into consideration, it follows from Equations(16)and(17)that

where 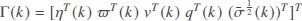 and
and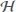 and
and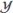 are given in Equation (15).
are given in Equation (15).
By noticing the initial condition 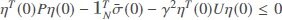 , we have from Equation (18) that the H∞consensus performance requirement in Equation (11) is achieved when Equation (14) holds. The proof is now complete.
, we have from Equation (18) that the H∞consensus performance requirement in Equation (11) is achieved when Equation (14) holds. The proof is now complete.
According to the results in Theorem 1, the sufficient condition guaranteeing the augmented system in Equation (10) achieves the H∞ consensus performance in Equation (11) is obtained. Thus, we are now ready to design the parameters of the proposed controller in Equation (3) in terms of the following theorem.
Theorem 2Consider the linear multi-agent system in Equation (1) and let the disturbance attenuation level γ and a positive definite matrix U be given. The augmented system in Equation (10) can achieve the H∞consensus performance in Equation (11) if there exist a positive definite matrix P = diag{P1, P2} with 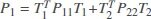 ,
, 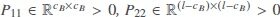 , T1and T2being given in Equation (12), and some parameter matrices and scalars {G, λi, Ri,Wi, K0}, under the initial condition
, T1and T2being given in Equation (12), and some parameter matrices and scalars {G, λi, Ri,Wi, K0}, under the initial condition 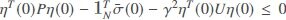 , satisfying the following LMI:
, satisfying the following LMI:

where
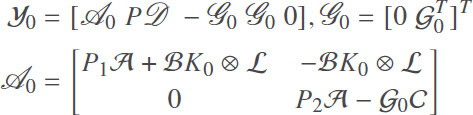
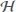 is given in Equation (15).
is given in Equation (15).
Moreover, the parameters of desired controller are given by
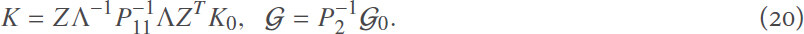
proof 2Noting Assumption 1 and Lemma 1, we can obtain that there exists a nonsingular matrix 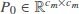 that satisfies BP0 = P1B. Then, we can obtain P0as follows:
that satisfies BP0 = P1B. Then, we can obtain P0as follows:

Let P1B = BP0, K0 = P0K and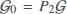 ; then, in light of the Schur complement lemma, Equation (19) can easily be obtained from Equation (14). The proof of this theorem is now complete.
; then, in light of the Schur complement lemma, Equation (19) can easily be obtained from Equation (14). The proof of this theorem is now complete.
In Equation (3), by letting σi (k) = σ → ∞ (i = 1, 2, . . ., N), the following general control protocol can be obtained for agent i:
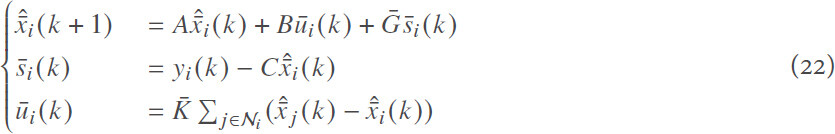
By defining 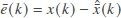 and combining Equations (5), (5) and (22), we can obtain
and combining Equations (5), (5) and (22), we can obtain
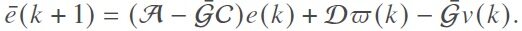
Denote
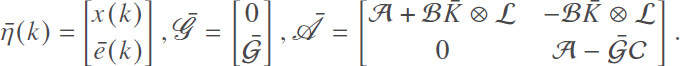
Then, we obtain
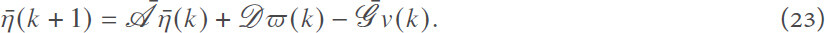
The following corollary can guarantee that the augmented system in Equation (23) satisfies the following H∞ consensus performance requirement
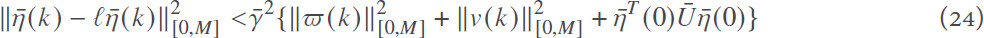
where Ū = ŪT> 0 is a positive definite matrix and ȳ> 0 is the disturbance attenuation level, which means that the consensus performance of multi-agent system in Equation (1) can be guaranteed.
Corollary 1Consider the multi-agent system Equation (1) and let the disturbance attenuation level ȳ and a positive definite matrix Ū be given. The augmented system in Equation (23) achieves the H∞consensus performance requirement in Equation (24) if there exist a positive definite matrixP̄ = diag {P̄1, P̄2} with  ,
,  , T̄1 and T̄2 being given in Equation (12), and some parameter matrices {Ḡ, K̄0} under the initial conditionP̄ - γ̄2Ū ≥ 0, satisfying the following LMI:
, T̄1 and T̄2 being given in Equation (12), and some parameter matrices {Ḡ, K̄0} under the initial conditionP̄ - γ̄2Ū ≥ 0, satisfying the following LMI:
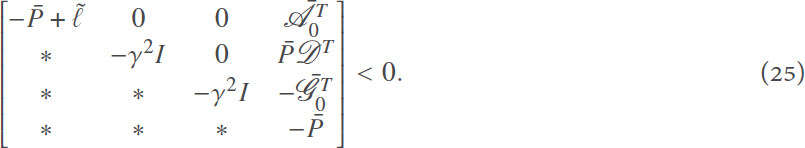
Moreover, the parameters of desired controller are given by
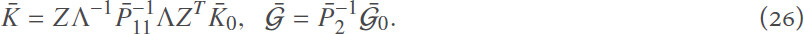
proof 3By lettingσi(k) = σ → ∞, wi(k) → 0, Ri(k) = 0, and λi(k) = 0 (i = 1, 2, . . ., N), the proof of this corollary can be obtained directly from Theorem 2.
Remark 1The main contribution of this paper is that a novel observer containing a saturation function with variable saturation limits is introduced into the designed consensus control protocol. Because of the constraint of saturation function with variable saturation limits, the saturation limits can dynamically change when outliers occur. Based on such merit, the designed control protocol can mitigate the effect of measurement outliers effectively.
Remark 2Thus far, a solution to the addressed H∞consensus problem for a class of linear multi-agent systems subject to measurement outliers has been found by designing an observer-based control law. The main results have been derived and shown in Equations (1) and (2). For the case of measurement without outliers, the corresponding result is given in Corollary 1. In the next section, a numerical example is provided in a simulation environment to verify the effectiveness of the proposed consensus control protocol.
Illustrative example
In this section, a numerical example is provided to verify the effectiveness of the proposed control protocol in Equation (3).
Consider multi-agent systems including five agents. Given the Laplacian matrix as 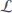 = [2 −1 −1 0 0; −1 3 − 1 − 1 0; −1 − 1 4 − 1 − 1; 0 − 1 − 1 3 − 1; 0 0 − 1 − 1 2], the ith agent’s state is xi (k) = [xi,1 (k) xi,2 (k)]T and its dynamics is given in Equation (1) with
= [2 −1 −1 0 0; −1 3 − 1 − 1 0; −1 − 1 4 − 1 − 1; 0 − 1 − 1 3 − 1; 0 0 − 1 − 1 2], the ith agent’s state is xi (k) = [xi,1 (k) xi,2 (k)]T and its dynamics is given in Equation (1) with
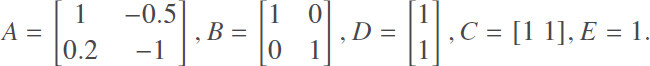
The length of finite horizon M is set as M = 100. γ is chosen as γ = 1.5. xi (0) and x̂i(0) (i = 1, 2,..., 5) obey the uniform distribution on the interval [−2, 2]. Set σ̄(0), and ϖi(k), and vi(k) as σ̄(0) = 1, ϖi(k) = e-10k sin(10k), and vi(k) = e−10k cos(10k) (i = 1, 2, . . ., 5), respectively.
The outliers considered in measurements are unit pulse signals, which enter the second agent at k = 60 and the fourth agent at k = 80. Next, by making a comparison between the results of Theorem 2 and Corollary 1, the effectiveness of the proposed control protocol in Equation (3) can be demonstrated. In terms of the results of Theorem 2 and Corollary 1, by employing MATLAB LMI toolbox, the solutions of LMIs in Theorem 2 can be obtained as follows:
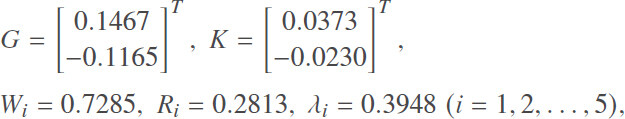
and then the simulation results are shown in Figure 1–5, which depict the compared state trajectories of five agents, the evolution profiles of σi(k), and the compared consensus errors, respectively.
From the simulation results employing the results of Corollary 1, we can see that outliers can affect the consensus performances of the second fourth agents and their neighboring agents. The variable σ2(k) can change dynamically when outliers of k = 60 occur such that the effect of outliers is weakened. For the fourth agent, the variable σ4(k) can change dynamically once outliers occur. Based on this merit, when outliers occur, the proposed control protocol in Equation (3) can have satisfactory performance. For the first, third, and fifth agents without the effect of outliers, variables σl(k) (l = 1, 3, 5) converge to zero. For the consensus error  , at k = 60 and k = 80, in terms of results in Corollary 1, consensus errors of the second and fourth agents and their neighboring agents have relatively large fluctuations. In light of the results in Theorem 2, the fluctuations of consensus errors of the second and fourth agents and their neighboring agents are very small. The simulation results demonstrate the effectiveness of the proposed control protocol Equation (3).
, at k = 60 and k = 80, in terms of results in Corollary 1, consensus errors of the second and fourth agents and their neighboring agents have relatively large fluctuations. In light of the results in Theorem 2, the fluctuations of consensus errors of the second and fourth agents and their neighboring agents are very small. The simulation results demonstrate the effectiveness of the proposed control protocol Equation (3).
Moreover, to demonstrate the usefulness of the proposed control protocol in Equation (3), we choose the outliers obeying the zero mean Gaussian noise with covariance 10. The simulation results are shown in Figures 6–10. From the simulation results, we can see that the proposed control protocol has a satisfactory performance against the different types of measurement outliers.
Figure 6. State trajectories xi,1 (k) of five agents subject to measurement outliers (Gaussian noise).
Figure 7. State trajectories xi,2 (k) of five agents subject to measurement outliers (Gaussian noise).
Conclusion
In this paper, the observer-based H∞ consensus problem for a class of linear multi-agent systems subject to measurement outliers is investigated. To mitigate the effect of measurement outliers, a novel control protocol based on an observer including a saturation function with variable saturation limits is proposed. Under the proposed observer-based control protocol, multi-agent systems can achieve the H∞ consensus performance index over a finite horizon. Finally, by making a comparison with the general observer-based control protocol, the effectiveness of the proposed control protocol was verified in a simulation environment. Future research directions may be devoted to an extension of the results obtained to nonlinear multi-agent systems and multi-agent systems with variable number of agents. Moreover, the obtained results can also be extended further to more practical research fields, such as sensor networks, neural networks, and multiple mobile robot system.
Declarations
Authors’ contributionsMade substantial contributions to conception and design of the study and performed data analysis and interpretation: Lu Y, Zhang N
Performed data acquisition, as well as provided administrative, technical, and material support: Karimi HR
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was partially funded by the Italian Ministry of Education, University and Research through the Project “Department of Excellence LIS4.0-Lightweight and Smart Structures for Industry 4.0”.
Conflicts of interestAll authors declared that there are no conflicts of interest.
AcknowledgmentsAnyone who contributed towards the article but does not meet the criteria for authorship, including those who provided professional writing services or materials, should be acknowledged. Authors should obtain permission to acknowledge from all those mentioned in the Acknowledgments section. This section is not added if the author does not have anyone to acknowledge.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2021.
REFERENCES
1. Loia V, Terzija V, Vaccaro A, Wall P. An Affine-Arithmetic-Based Consensus Protocol for Smart-Grid Computing in the Presence of Data Uncertainties. IEEE Trans. Ind Electron 2015;62:2973-82.
2. Formato G, Troiano L, Vaccaro A. Achieving consensus in self-organizing multi agent systems for smart microgrids computing in the presence of interval uncertainty. J Ambient Intell Human Comput 2014;5:821-8.
3. Yang Z, Wu W, Li H, Zhou Y. Consensus in Smart Computing Systems Proc IEEE International Conference on Smart Computing. IEEE 2017.
4. Xu W, Wang Z, Ho DWC. Finite-horizon
5. Zhang D, Xu Z, Karimi HR, Wang QG, Yu L. Distributed
6. Qin J, Ma Q, Shi Y, Wang L. Recent advances in consensus of multi-agent systems: A brief survey. IEEE Trans Ind Electron 2017;64:4972-83.
7. Shen B, Wang Z, Hung YS. Distributed
8. Liu Y, Jia Y.
9. Lin P, Jia Y, Li L. Distributed robust
10. Mo L, Jia Y.
11. Saboori I, Khorasani K.
12. Wang X, Yang GH. Distributed reliable
13. Wang Z, Ding D, Dong H, Shu H.
14. Zhang H, Feng G, Yan H, Chen Q. Observer-based output feedback event-triggered control for consensus of multi-agent systems. IEEE Trans Ind Electron 2014;61:4885-94.
15. Song J, Han F, Fu H, Liu H. Finite-horizon distributed
16. He M, Mu J, Mu X.
17. Wang L, Wang Z, Wei G, Alsaadi FE. Observer-based consensus control for discrete-time multiagent systems with coding-decoding communication protocol. IEEE T Cybern 2019;49:4335-45.
18. Qin J, Gao H, Yu C. On discrete-time convergence for general linear multi-agent systems under dynamic topology. IEEE Trans Autom Control 2014;59:1054-9.
19. Chen J, Zhang W, Cao Y-Y, Chu H. Observer-based consensus control against actuator faults for linear parameter-varying multi-agent systems. IEEE Trans Syst Man Cybern: Syst 2017;47:1336-47.
20. Gao L, Cui Y, Chen W. Admissible consensus for descriptor multi-agent systems via distributed observer-based protocols. J. Frankl Inst 2017;354:257-76.
21. Wang HD, Wu H-N. Distributed consensus observer-based
22. Alessandri A, Zaccarian L. Stubborn state observers for linear time-invariant systems. Automatica 2018;88:1-9.
23. Lu C, Wu M, He Y. Stubborn state estimation for delayed neural networks using saturating output errors. IEEE Trans Neural Netw Learn Syst 2020;31:1982-94.
24. Mao J, Ding D, Wei G. Distributed stubborn-set-membership filtering with a dynamic event-based scheme: The Takagi-Sugeno fuzzy framework. Int J. Adapt Control Signal Process 2020; doi: 10.1002/acs.3209.
25. Shen Y, Wang Z, Shen B, Dong H. Outlier-resistant recursive filtering for multisensor multirate networked systems under weighted try-once-discard protocol. IEEE T. Cybern ; doi: 10.1109/TCYB.2020.3021194.
26. Wang X, Yang GH. Observer-based fault detection for T-S fuzzy systems subject to measurement outliers. Neurocomputing 2019;335:21-36.
27. Gil P, Martins H, Januario F. Detection and accommodation of outliers in wireless sensor networks within a multi-agent framework. Appl Soft Comput 2016;42:204-14.
28. Tarbouriech S, Garcia G, da Silva JMG, Queinnec I. Stability and stabilization of linear systems with saturating actuators. London: Springer; 2011.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.







 subject to measurement outliers (unit pulse).
subject to measurement outliers (unit pulse).
 subject to measurement outliers (unit pulse).
subject to measurement outliers (unit pulse).



 subject to measurement outliers (Gaussian noise).
subject to measurement outliers (Gaussian noise).
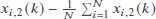 subject to measurement outliers (Gaussian noise).
subject to measurement outliers (Gaussian noise).











Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].