Forecasting day-ahead spot electricity prices using deep neural networks with attention mechanism
, Abstract
This paper presents a novel approach to forecast hourly day-ahead electricity prices. In recent years, many predictive models based on statistical methods and machine learning (deep learning) techniques have been proposed. However, the approach presented in this paper focuses on the problem of constructing a fair and unbiased model. In this considered case, unbiased means that the model can increase prediction accuracy and decrease categorical bias across different data clusters. For this purpose, a model combining techniques such as long short-term memory (LSTM) recurrent neural network, attention mechanism, and clustering is created. The proposed model’s main feature is that the attention weights for LSTM hidden states are calculated considering a context vector given for each sample individually as the cluster center to which the sample belongs. In training mode, the samples are iteratively (one time per epoch) clustered based on representation vectors given by the attention mechanism. In the empirical study, the proposed model was applied and evaluated on the Nord Pool market data. To confirm that the model decreases categorical bias, the obtained results were compared with results of similar LSTM models but without the proposed attention mechanism.
Keywords
Introduction
Since the early 1990s, energy markets have play increasingly important roles in the power systems worldwide because of the deregulation process. Forecasting energy demand and day-ahead prices is a vital issue for all market participants.Accurate day-ahead price forecasting in the spot market helps the power suppliers adjust their bidding strategies to achieve the maximum benefit. On the other hand, consumers can derive a plan to maximize their utilities using the electricity purchased from the pool or use self-production to protect themselves against high prices[1].
Time series of electricity prices tend to have complex features such as nonstationarity, nonlinearity, and high volatility, making energy price forecasting difficult. One of the widely used and most powerful model groups is the time series models. Weron[2-4] reviewed the approaches to modeling and forecasting day-ahead electricity prices. He also found that an approach where each hour is forecasted separately gives better results than an approach where forecasts are made for the whole day at once. However, both approaches are equally popular. Common statistical methods are: autoregressive (AR) and autoregressive with exogenous inputs (ARX) models[5], double seasonal Holt–Winter (DSHW) models[6], threshold ARX (TARX) models[7,8], autoregressive integrated moving average (ARIMA) models[9,10], semi/nonparametric models[5,11], generalized autoregressive conditional heteroscedasticity (GARCH)-based models[12-14], and dynamic regression (DR) and transfer function (TF) models[15]. Next to statistical models, computational intelligence techniques are widely used in electricity price forecasting due to their strong nonlinear modeling capabilities. Szkuta et al.[16] proposed a three-layered ANN with back-propagation for modeling and predicting the Victorian electricity market data. Wang et al.[17] proposed a neural-network-based approach to predict system marginal prices, also considering weekend and public holidays as input. The cascaded neural network structure for market-clearing price prediction in the New England market was presented by Zhang et al.[18]. Over the last decade, several innovations have been introduced in the field of neural networks that have led to deep learning development. Forecasting electricity prices using deep learning techniques, e.g., deep recurrent neural networks, is also presented in many papers[19–24].
Electricity prices display a set of relatively unique attributes: a constant balance between production and consumption[25]; dependence of the consumption on time, e.g., the hour of the day, day of the week, and time of the year; load and generation that is influenced by external weather conditions[25] ; and influence of neighboring markets[4]. Due to these characteristics, as shown in many studies, errors of forecasting are different in different groups of data[22-26]. Natural data groups are those resulting from data division by time, e.g., according to the seasons, months, days of the week, or hour of the day. Other groups that are more difficult to identify are those resulting from the division of data according to external factors, such as weather conditions (temperature or wind force) and fuel prices, e.g. natural gas, oil, and coal. Each of these groups may be represented by a different number of samples in the dataset in practice. It has also been shown that algorithms trained based on biased data lead to algorithmic discrimination[27,28]. Recently, comparative tests have emerged to quantify discrimination[29,30], as well as datasets designed to evaluate these algorithms[31]. Therefore, this article takes the challenge of integrating debiasing capabilities directly into a model during a training process that adjusts automatically and unattended to training data deficiencies. This approach includes a comprehensive deep learning algorithm that simultaneously learns to forecast electricity prices for the next day and the clustering of the training data in an unsupervised manner.
Methods
Before proposing the deep learning algorithm for prediction and the training procedure, the problem specification, LSTM recurrent network, and attention mechanism are introduced.
Problem Statement
Consider the problem of prediction future values. Let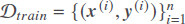 
be a set of paired training data samples consisting of features (present and past values) 
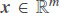and future values 
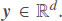The aim is to find a functional mapping of f : X
Y parameterized by θ that minimizes some loss 
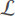(θ) over given training dataset. In other words, we consider solving the following optimization problem:
For new test sample, (x,y), the predictor should output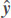 
= fθ(x) where 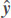is almost equal to y. Now, assume that each sample also has an associated latent vector 
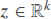which represents hidden features of the sample[32]. The notion of a biased predictor can be formalized as follows[33] :
Definition 1A predictor, fθ(x), is biased if its prediction changes after being exposed to additional sensitive feature inputs. It means that a predictor is fair with respect to a set of latent features,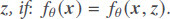 
A good example to understand this is the facial detection problem considered by Amini et al.[33]. When deciding whether an image contains a face or not, a person’s skin color, gender, and even age are the primary latent variables and should not influence the classifier's decision. To ensure the reliability of the classifier with respect to different latent variables, the dataset should contain roughly uniform samples in the hidden space. In other words, the training dataset should equally represent different categories over the latent space. Note that this is different from claiming that the dataset should be balanced for the classes. Moreover, in time series forecasting, it is an even more natural situation due to the lack of division into classes. However, methods proposed in the literature[33-35] to generate training data that are more “fair” by resampling or generating new samples are difficult to apply to time series.
LSTM recurrent network
The LSTM was introduced by Sepp Hochreiter and Jurgen Schmidhuber in 1997[36]. Unlike traditional recurrent neural networks, an LSTM network is well-suited to learn from experiences to identify and predict the time series when there are very long time lags with unknown size. The main feature of LSTM is the ability to remove or add information to the cell state, carefully regulated by three different structures called gates, namely input, forget, and output gates. As shown in Figure 1, the state of each cell (ct–1) passes through the LSTM cell to generate a state for the next step (ct). Gates are a way to let information along the state flow optionally. They have been composed of a sigmoid or tanh neural net layer and a pointwise multiplication operation.
Figure 1. The detailed structure within a LSTM cell [22].
The mathematical functions of three gates are defined as:
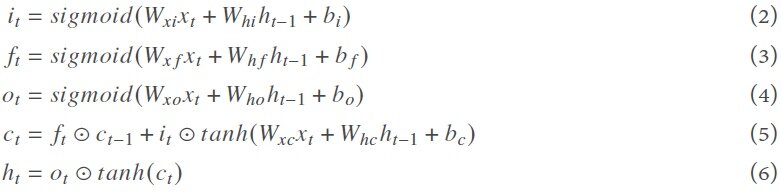
where it is the input gate, which controls how much information of input (xt) and previous hidden state (ht–1) is allowed to pass into the memory cell; ft is the forget gate, which controls how much information is forgotten before passing though the cell; ot is the output gate, which controls how much information from the current memory cell can be output to the hidden state; ct represents the cell state generated as an additional variable for the cell; W is the weight matrix; and b is the biases to each layer. The symbol 
represents the operation of pointwise multiplication[22].
Encoder–decoder with attention
Based on LSTM units, encoder–decoder networks[37] have become popular due to their success in machine translation. The main idea is to encode the source sentence as a fixed-length vector and use the decoder to generate a translation. One problem with encoder–decoder networks is that their performance will deteriorate rapidly as the input sequence’s length increases[38]. In time series analysis, especially when we work with high-frequency time series, this could be a concern. To resolve this issue, the attention-based encoder–decoder network[39] employs an attention mechanism to select parts of hidden states across all the time steps. Attention is a mechanism that provides a richer encoding of the source sequence to construct a context vector that the decoder can then use. The main difference between the encoder–decoder with attention mechanism and the encoder–decoder model is that a different context vector ct is computed for every time step t of the decoder. Let hi, i = 1,2, ..., k be a hidden states of encoder; then, the context vector ct is computed as a weighted sum of these hidden states hi
The weight αti of each hidden state hi is computed by
where
is an alignment model that scores how well the inputs around position i and the output at position t match. The score is based on the previous hidden state st–1 of the decoder and the ith hidden state of the input sentence. The model fatt could be a feedforward neural network that is jointly trained with all the other components of the system.
LSTM with attention for forecasting electricity prices
In this work, we propose to apply the LSTM deep neural network (LSTM-DNN) with a specific attention mechanism to predict the electricity day-ahead price. The architecture of the proposed model is shown in Figure 2.
Figure 2. Architecture of the proposed model for forecasting electricity day-ahead prices.
Preprocessing and input/output
Figure 3 shows the high volatility of the Nord Pool market’s electricity price in the SE1 region. Figure 3 shows that all prices are positive, and sometimes extremely high prices appear. The extremely high prices can be caused by shortages of power supply in the system. However, those extreme values of the price occur infrequently. For instance, for the SE1 region, during seven years from 22 January 2013 to 31 December 2019, prices higher than 66 EUR/MWh (higher than mean plus three sigmas) occur less than 1% of the time. Therefore, to reduce the effect of abnormal events on the prediction performance, we refine the extreme prices into specific values. Its neighbor prices interpolate the prices higher than the mean plus three sigmas. After redefining the prices, we also transform prices by using the natural logarithm as follows:
Figure 3. The electricity price of the Nord Pool market in SE1 region during seven years from 22 January 2013 to 31 December 2019 (60,840 h).
where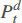 
is the electricity price on day d at time step t.
As inputs, we can use various variables: historical prices or loads, weather conditions, holidays, the day of the week, oil prices, etc. Our research assumes that the price discounts everything, so all the factors mentioned above should already be included in the price. Hence, we use as input only historical prices. The actual price values on day d are denoted as:
The predicted price values at day d are represented as:
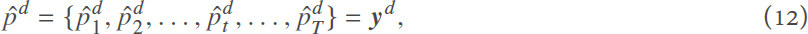
where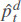 
is the predicted price at time step t. T can be 24 for an hourly market (as in our case) and 48 for a half-hourly market. As an input to the LSTM cell to predict the prices for the day d + 1, we use all the prices in the L days before:
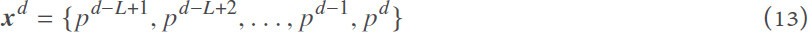
LSTM Encoder with attention and clustering
To generate a vector of latent features for each sample, each sample is projected into feature space by feeding it through the LSTM encoder with an attention mechanism twice. The LSTM encoder is a simple LSTM model that has a single hidden layer of LSTM units. This model returns the sequences of hidden states hl (l = 1,2,...,L) and it has one hyperparameter latent_dim, which determines the dimension of the vectors hl, z, and c. The model used to perform the Attn block’s attention score is the traditional multilayer perceptron (MLP) neural network with one hidden layer with latent_dim neurons and hyperbolic tangent (tanh) as the activation function. The input of the model is concatenation of vectors hl and c. The output is the vector ai of attention weights. Each example is passed through the attention mechanism with the context vector c set to zero in the first run. Next, on the set of vectors z, generated in this way, the clustering algorithm (k-means) is performed with a given hyperparameter for the number of clusters (cl_num). Then, in the second run, each sample is passed through an attention mechanism with the context vector c set to the cluster center to which the sample belongs. Finally, the vector z generated in this way for each sample is passed to the predictive model.
Predictor
As a simple prediction model, the model for predicting day-ahead prices is the MLP neural network with one hidden layer with the rectified linear unit (ReLu) activation function in the hidden layer and a linear activation function in the output layer. The input of the model is vector z and the output is the vector y of day-ahead prices that we intend to forecast. The model has one hyperparameter neurons_num, which determines the number of neurons of the hidden layer.
Training
In the proposed model, all parts of the model are jointly trained by minimizing the mean absolute percentage error (MAPE), defined as the average absolute difference between the actual value and the forecast value divided by the actual value:
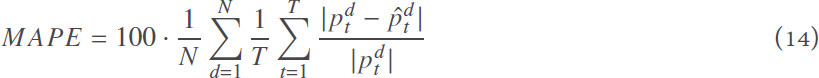
where 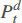an 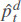are actual and forecast price on day d at time step t, respectively.
The mean absolute percentage error’s choice over the mean square error is made for a simple reason: because electricity prices have large spikes, the Euclidean norm would emphasize the spiky prices. As an optimizer, we choose the Adam algorithm[40], a stochastic gradient descent method[41] that uses adaptive learning rates. With the Adam algorithm, the training procedure also considers early stopping[42] by monitoring the error on the validation dataset to avoid overfitting.
Empirical study
In this section, we perform the empirical study to evaluate the proposed model and analyze the various models’ obtained results. Our goal is to confirm that the proposed attention mechanism with clustering improves forecasts’ accuracy and makes the model more unbiased. To do so, we evaluate three architecture of the model:
The simple vanilla LSTM model is the proposed model without attention mechanism and clustering; the vector z passed to predictive model is set to the last hidden state of LSTM, z = hL.
The LSTM encoder with attention is the proposed model with attention but without clustering; the context vector c is set to zero.
The proposed model, which is described in the previous sections.
Data
For this research, we consider the public Nord Pool1 day-ahead market covering electricity prices from six countries divided into 14 regions, namely Sweden (SE1, SE2, SE3, and SE4), Finland (FI), Norway (Oslo, Kr.sand, Bergen, Molde, Tr.heim, and Troms), Estonia (EE), Lithuania (LV), and Latvia (LT), in the period from January 2013 to December 2019. The data are prepared using preprocessing techniques described in Section Preprocessing and Input/Output, including a deal with too high prices and log-transformation of prices.
The data are divided into three sets:
Training set (1 January 2013 to 31 December 2017): These data are used for training the models.
Validation set (1 January 2017 to 31 December 2018): These data are used to select the optimal model (early stopping).
Test set (1 January 2018 to 31 December 2019): These data, which are not used at any step during the model training process, are employed as the out-of-sample data to compare the models.
There are 24 electricity prices per day. Hence, the training dataset comprises 602,808 data points to predict. Both validation and test datasets comprise 122,640 data points to predict each.
Hyperparameters
The hyperparameters that should be chosen for the model are described above with the proposed model’s architecture. To choose optimal values for hyperparameters, we conducted a grid search over tunable parameters. As a result, for the sake of conciseness in this paper, we present the results obtained for optimal configurations of hyperparameters: L = 21, latent_dim = 64, neurons_num = 128, and three different cl_num ∈ {10,20, 30}, to show the impact of numbers of clusters.
Results
To compare and analyze the various predictors’ predictive accuracy, we compute their MAPE on the test set. Models were re-trained from scratch five times each for added statistical robustness of results. It is important to note that the predictors are not re-estimated when new data are available, i.e., the models were trained on data from 2013 to 2017, while the test data cover 2019. The obtained results are listed in Table 1 and shown in Figure 4. The example of forecasted prices is illustrated in Figure 5.
Comparison of the predictive accuracy of the various forecasters by means and standard deviations of MAPE (%) computed for different groups of data resulting from the division of data by region and time.
| Model | cl_nutn | Overall | Regions | Seasons | Months | |||
| Mean | Std | Mean | Std | Mean | Std | |||
| LSTM | 0 | 13.87073 | 13.87073 | 7.43098 | 13.81929 | 6.87106 | 13.80947 | 13.86471 |
| LSTM att | 0 | 13.48047 | 13.48047 | 7.10680 | 13.43214 | 6.51909 | 13.42175 | 12.92929 |
| Proposed | 10 | 13.42228 | 13.42228 | 7.07100 | 13.37356 | 6.58061 | 13.36267 | 12.89435 |
| Proposed | 20 | 13.36895 | 13.36895 | 6.98201 | 13.32102 | 6.42634 | 13.31264 | 12.71844 |
| Proposed | 30 | 13.32764 | 13.32764 | 6.89610 | 13.27935 | 6.38002 | 13.27071 | 12.74699 |
| Model | cl_num | Dayweeks | Hours | Peaks | ||||
| Mean | Std | Mean | Std | Mean | Std | |||
| LSTM | 0 | 13.87974 | 4.94078 | 13.10990 | 1.84422 | 13.71895 | 3.95523 | |
| LSTM att | 0 | 13.48865 | 4.38670 | 12.72462 | 1.46363 | 13.43393 | 3.80945 | |
| Proposed | 10 | 13.43036 | 4.47882 | 12.59082 | 1.57140 | 13.33455 | 3.73537 | |
| Proposed | 20 | 13.37693 | 4.41302 | 12.67355 | 1.60619 | 13.29039 | 3.49958 | |
| Proposed | 30 | 13.33565 | 4.37444 | 12.66831 | 1.50792 | 13.27910 | 3.39811 | |
Figure 4. Increased performance and decreased categorical bias with the proposed model for season category.
Figure 5. Forecasted prices for a random selected week from test data.
To demonstrate debiasing, we quantified prediction performance on individual categories. Specifically, we considered different data groups resulting from data division by region and date and time (seasons, months, day weeks, hours, and peaks). From the results shown in Table 1, we can make various observations. As expected, the column “Overall” shows that adding an attention mechanism improved predictions, and adding clustering improved them even more. There is also a dependency that increasing the number of clusters improves prediction. Moreover, for almost all divisions, the proposed model turned out to be the most unbiased predictor. As we can see, the standard deviation is then the smallest and, in most cases, decreases as the number of clusters increases. The only exception is the division into hours, which may result from the fact that forecasts are made for the whole day, not individually for each hour. As shown in Figure 4, a greater force of debiasing (increasing cl_num) improved the predictions for the “spring” category. This suggests that our model may debias for a qualitative feature such as the season, which has a significant impact on its usefulness in improving forecasting models’ reliability. Contrary to the trend observed with spring days, the prediction errors in the “summer” category increase with an increasing number of clusters; we suspect that it may be related to other external factors. Additionally, the “autumn” and “winter” categories’ errors remained almost constant for both the biased and debiased models and were much better than those of the other categories. This suggests that our proposed model does not sacrifice performance on categories that already have high precision. As confirmed by Figure 4, the overall precision increased with an increased debiasing power (increasing cl_num). Error bars (standard error of the mean) are shown in order to visualize the statistical significance of differences between the trained models. It is also worth noting that the differences in the quality of forecasts between the categories are significant, confirming the need to develop methods to eliminate these issues.
Conclusion
In this paper, the LSTM deep neural network with attention mechanism and clustering is devised for electricity market day-ahead price forecasting, which considers a context vector given for each sample individually as the cluster center to which the sample belongs. By learning the latent variables in an unsupervised manner, we can scale this approach to large datasets without labeling them in a training set. We applied our proposed model to forecasting day-ahead electricity prices. Given a biased training dataset, our models show increased prediction accuracy and decreased categorical bias across various data categories compared to similar models but without the proposed mechanisms. The next step in our research will be to also include external factors (e.g., production, consumption, weather conditions, and oil prices) as input data and to extend the model with a decoder module based on the Variational Autoencoder model. These activities could contribute to achieving even better predictions and improve the learning phase of latent structures in the data.
Declarations
Authors’ contributionsMade substantial contributions to conception and design of the study and made implementation and performed data analysis and interpretation: Marszałek A, Burczynski T
Availability of data and materialsNot applicable.
Financial support and sponsorshipNone.
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2021.
REFERENCES
1. Amjady N, Keynia F. Day ahead price forecasting of electricity markets by a mixed data model and hybrid forecast method. International Journal of Electrical Power & Energy Systems 2008;30:533-46.
2. Weron R. Modeling and Forecasting Electricity Loads and Prices: A Statistical Approach. Chichester: Wiley; 2006.
3. Weron R. Forecasting Wholesale Electricity Prices: A Review of Time Series Models. In: Milo W, Wdowinski P, editors. FINANCIAL MARKETS: PRINCIPLES OF MODELLING, FORECASTING AND DECISION-MAKING. Lodz: FindEcon Monograph Series, WUL; 20082.
4. Weron R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. International Journal of Forecasting 2014;30:1030-1081.
5. Weron R, Misiorek A. Forecasting spot electricity prices: A comparison of parametric and semiparametric time series models. International Journal of Forecasting 2008;24:744-63.
6. Cruz A, Muñoz A, Zamora JL, Espínola R. The effect of wind generation and weekday on Spanish electricity spot price forecasting. Electric Power Systems Research 2011;81:1924-35.
7. Misiorek A, Trueck S, Weron R. Point and Interval Forecasting of Spot Electricity Prices: Linear vs. Non-Linear Time Series Models. Studies in Nonlinear Dynamics & Econometrics 22 Sep 2006;10. Available from: https://www.degruyter.com/view/journals/snde/10/3/article-snde.2006.10.3.1362.xml.xml.
8. Kristiansen T. Forecasting Nord Pool day-ahead prices with an autoregressive model. Energy Policy 2012;49:328 - 332. Special Section: Fuel Poverty Comes of Age: Commemorating 21 Years of Research and Policy. Available from: http://www.sciencedirect.com/science/article/pii/S0301421512005381.
9. Crespo Cuaresma J, Hlouskova J, Kossmeier S, Obersteiner M. Forecasting electricity spot-prices using linear univariate time-series models. Applied Energy 2004;77:87-106.
10. Yang Z, Ce L, Lian L. Electricity price forecasting by a hybrid model, combining wavelet transform, ARMA and kernel-based extreme learning machine methods. Applied Energy 2017;190:291-305.
11. Vilar JM, Cao R, Aneiros G. Forecasting next-day electricity demand and price using nonparametric functional methods. International Journal of Electrical Power & Energy Systems 2012;39:48-55.
12. Knittel CR, Roberts MR. An empirical examination of restructured electricity prices. Energy Economics 2005;27:791-817.
13. Garcia RC, Contreras J, van Akkeren M, Garcia JBC. A GARCH forecasting model to predict day-ahead electricity prices. IEEE Transactions on Power Systems 2005;20:867-74.
14. Diongue AK, Guégan D, Vignal B. Forecasting electricity spot market prices with a k-factor GIGARCH process. Applied Energy 2009;86:505-10.
15. Nogales FJ, Contreras J, Conejo AJ, Espinola R. Forecasting Next-Day Electricity Prices by Time Series Models. IEEE Power Engineering Review 2002;22:58-8.
16. Szkuta BR, Sanabria LA, Dillon TS. Electricity price short-term forecasting using artificial neural networks. IEEE Transactions on Power Systems 1999;14:851-7.
17. Wang AJ, Ramsay B. A neural network based estimator for electricity spot-pricing with particular reference to weekend and public holidays. Neurocomputing 1998;23:47-57.
18. Li Zhang, Luh PB, Kasiviswanathan K. Energy clearing price prediction and confidence interval estimation with cascaded neural networks. IEEE Transactions on Power Systems 2003;18:99-105.
19. Peng L, Liu S, Liu R, Wang L. Effective long short-term memory with differential evolution algorithm for electricity price prediction. Energy 2018;162:1301-14.
20. Lago J, De Ridder F, De Schutter B. Forecasting spot electricity prices: Deep learning approaches and empirical comparison of traditional algorithms. Applied Energy 2018;221:386-405.
21. Zhu Y, Dai R, Liu G, Wang Z, Lu S. Power Market Price Forecasting via Deep Learning. In: IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society; 2018. pp. 4935-39.
22. Jiang L, Hu G. Day-Ahead Price Forecasting for Electricity Market using Long-Short Term Memory Recurrent Neural Network. In: 2018 15th International Conference on Control, Automation, Robotics and Vision (ICARCV); 2018. pp. 949-54.
23. Brusaferri A, Matteucci M, Portolani P, Vitali A. Bayesian deep learning based method for probabilistic forecast of day-ahead electricity prices. Applied Energy 2019;250:1158-75.
24. Peng L, Zhu Q, Lv SX, Wang L. Effective long short-term memory with fruit fly optimization algorithm for time series forecasting. Soft Computing 2020;10.
25. Shahidehpour M, Yamin H, Li Z. 1. In: Market Overview in Electric Power Systems. John Wiley & Sons, Ltd; 2002. pp. 1-20. Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/047122412X.ch1.
26. Tan Z, Zhang J, Wang J, Xu J. Day-ahead electricity price forecasting using wavelet transform combined with ARIMA and GARCH models. Applied Energy 2010;87:3606-10.
27. Bolukbasi T, Chang KW, Zou J, Saligrama V, Kalai A. Man is to Computer Programmer as Woman is to Homemaker? Debiasing Word Embeddings. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. NIPS'16. Red Hook, NY, USA: Curran Associates Inc.; 2016. pp. 4356-4364.
28. Caliskan A, Bryson J, Narayanan A. Semantics derived automatically from language corpora contain human-like biases. Science 2017;356:183-6.
29. Kilbertus N, Rojas-Carulla M, Parascandolo G, Hardt M, Janzing D, et al. Avoiding Discrimination through Causal Reasoning. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. NIPS'17. Red Hook, NY, USA: Curran Associates Inc.; 2017. pp. 656-666.
30. Hardt M, Price E, Srebro N. Equality of Opportunity in Supervised Learning. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. NIPS'16. Red Hook, NY, USA: Curran Associates Inc.; 2016. pp. 3323-3331.
31. Buolamwini J, Gebru T. Gender Shades: Intersectional Accuracy Disparities in Commercial Gender Classification. In: Friedler SA, Wilson C, editors. Proceedings of the 1st Conference on Fairness, Accountability and Transparency. vol. 81 of Proceedings of Machine Learning Research. New York, NY, USA: PMLR; 2018. pp. 77-91.
32. Zemel R, Wu Y, Swersky K, Pitassi T, Dwork C. Learning Fair Representations. In: Dasgupta S, McAllester D, editors. Proceedings of the 30th International Conference on Machine Learning. vol. 28 of Proceedings of Machine Learning Research. Atlanta, Georgia, USA: PMLR; 2013. pp. 325-33.
33. Amini A, Soleimany AP, Schwarting W, Bhatia SN, Rus D. Uncovering and Mitigating Algorithmic Bias through Learned Latent Structure. In: Proceedings of the 2019 AAAI/ACM Conference on AI, Ethics, and Society. AIES '19. New York, NY, USA: Association for Computing Machinery; 2019. pp. 289-295.
34. Nguyen GH, Bouzerdoum A, Phung SL. A supervised learning approach for imbalanced data sets. In: 2008 19th International Conference on Pattern Recognition; 2008. pp. 1-4.
35. Sattigeri P, Hoffman SC, Chenthamarakshan V, Varshney KR. Fairness GAN: Generating datasets with fairness properties using a generative adversarial network. IBM Journal of Research and Development 2019;63:31-9.
36. Hochreiter S, Schmidhuber J. Long Short-Term Memory. Neural Computation 1997;9:1735-80.
37. Kalchbrenner N, Blunsom P. Recurrent Continuous Translation Models. In: Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing. Seattle, Washington, USA: Association for Computational Linguistics; 2013. pp. 1700-9. Available from: https://www.aclweb.org/anthology/D13-1176.
38. Cho K, van Merrienboer B, Bahdanau D, Bengio Y. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches. CoRR 2014 Oct. Available from: http://arxiv.org/abs/1409.1259..
39. Bahdanau D, Cho K, Bengio Y. Neural Machine Translation by Jointly Learning to Align and Translate; 2016.
40. Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. In: Bengio Y, LeCun Y, editors. 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings; 2015. Available from: http://arxiv.org/abs/1412.6980.
41. Bottou L. Large-Scale Machine Learning with Stochastic Gradient Descent. In: Lechevallier Y, Saporta G, editors. Proceedings of COMPSTAT’2010. Heidelberg: Physica-Verlag HD; 2010. pp. 177-86.
Cite This Article
Open Access
, Tadeusz BurczynskiHow to Cite
Marszałek, A.; Burczynski T. Forecasting day-ahead spot electricity prices using deep neural networks with attention mechanism. . J. Smart. Environ. Green. Comput. 2021, 1, 21-31. http://dx.doi.org/10.20517/jsegc.2021.02
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.