Curvature-guided assembly of nonconvex nanocrystals into chiral Kagome superlattices

INTRODUCTION

The self-assembly of colloidal nanoparticles into superlattices with intricate structures that emulate or exceed the complexity of natural materials is an enduring objective^[1,2]. Present research predominantly focuses on isotropic spherical or polyhedral nanocrystals^[3-5], which are prone to form densely packed structures due to their high symmetry, such as cubic lattices. Nonetheless, the directional control over their interactions is restricted, making it difficult to achieve low-symmetry, low-density special lattices. In contrast, anisotropic nonconvex nanoparticles can transcend conventional symmetry constraints, facilitating long-range ordered and precise assembly. A breakthrough led by Dong's group from the Department of Chemistry at Fudan University, in collaboration with theoretical and international teams, demonstrates that nonconvex nanocrystals - specifically dumbbell-shaped particles (nanodumbbells, NDs) - enable unprecedented control over directional interactions via curvature complementarity. This strategy unlocks the formation of intricate two-dimensional (2D) superlattices, including chiral Kagome structures, through entropy-driven depletion forces and geometric self-recognition^[6]. The work bridges atomic-level precision and colloidal assembly, offering a robust framework for programmable metamaterials.

NONCONVEX BUILDING BLOCKS: DESIGN AND ASSEMBLY

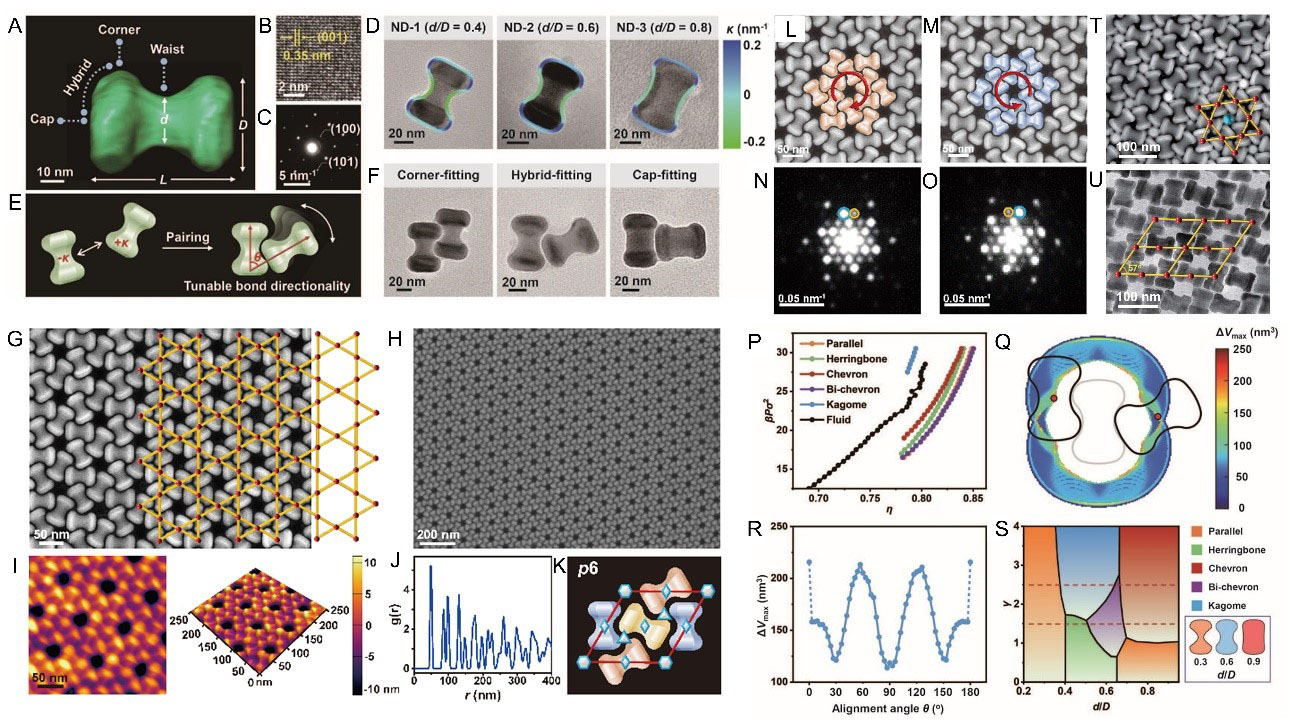
Dong's group synthesized colloidal NaYF₄:Yb/Er@NaGdF₄@NaNdF₄ NDs with tunable concave waists and convex heads [Figure 1A-C]. By varying the waist-to-head width ratio (d/D), they modulated the concavity (0.4-0.9), which dictated local curvature profiles [Figure 1D]. These NDs exhibit self-complementary "lock-and-key" interactions: concave waists selectively bind to convex heads of neighboring particles [Figure 1E]. Three distinct fitting modes emerged-corner, hybrid, and cap fitting-depending on d/D [Figure 1F]. High-concavity NDs (d/D < 0.55) favored corner fitting, while moderate-concavity NDs (0.55 < d/D < 0.65) adopted hybrid modes, enabling diverse lattice symmetries.

Figure 1. Numbbell-shaped nanoparticles self-assemble into chiral Kagome superlattices and their formation mechanism. (A-F) Morphology and structure of 2D ND superlattices with different local curvature; (G-H) Microstructure of Kagome lattices self-assembled from NDs; (L-O) Planar chirality of left- and right-handed Kagome lattices; (P-S) Formation mechanism of Kagome lattices. (T-U) AB₃-type binary superlattices and open oblique lattices self-assembled from NDs. Reproduced from Reference^[6] with permission. 2D: Two-dimensional; ND: nanodumbbell.

CHIRAL KAGOME LATTICES: PRECISION AND STABILITY

A hallmark achievement was the self-assembly of high-quality Kagome superlattices [Figure 1G-I], a non-close-packed structure with p6 symmetry and planar chirality. The Kagome lattice, composed of vertex-sharing triangles and hexagons, formed via hybrid fitting of moderate-concavity NDs (d/D ≈ 0.6). Each ND interlocked with four neighbors at 60° alignment angles, creating trihexagonal motifs [Figure 1J and K]. Strikingly, the lattice exhibited handedness, with alternating left- and right-handed domains [Figure 1L and M]. The asymmetry in the intensity of the diffraction spots of the corresponding selected area electron diffraction (SAED) further indicates the planar chirality of the Kagome lattice [Figure 1N and O]. Radial distribution functions and grazing-incidence X-ray scattering confirmed long-range translational order of Kagome lattice.

DEPLETION INTERACTIONS: OVERCOMING KINETIC TRAPS

The team identified depletion forces as critical drivers of assembly. Introducing free oleic acid as depletants enhanced concave-convex attractions, overcoming steric hindrance and kinetic traps [Figure 1P-S]. Monte Carlo simulations revealed that purely hard-core interactions favored dense phases (e.g., chevron lattices), while depletion stabilized the low-density Kagome lattice by maximizing overlap volumes (ΔV_max) at specific orientations. Theoretical phase diagrams predicted Kagome stability within 0.55 < d/D < 0.65, aligning with experiments.

EXPANDING COMPLEXITY: BINARY AND LOW-DENSITY SUPERLATTICES

The design principle extends beyond single-component systems. Co-assembling NDs of varying sizes yielded AB₃-type binary superlattices, where small NDs occupied voids in a Kagome framework [Figure 1T]. Additionally, engineering NDs with dual concave sites enabled open oblique lattices (packing fraction ~ 59%), highlighting multivalent bonding versatility [Figure 1U].

CONCLUSION AND OUTLOOK

This work establishes nonconvex nanocrystals as a powerful platform for programmable self-assembly. The team has innovated the theoretical framework for colloidal self-assembly by utilizing curvature-guided depletion to facilitate “lock-and-key” precision assembly of nonconvex particles, such as NDs. This advancement has elevated “curvature engineering” to a new paradigm for directional bonding design. Combined theoretical calculations with experimental validation, they demonstrated that chiral Kagome lattices (characterized by low symmetry and low filling fraction) are the thermodynamically stable phase, challenging the traditional notion that “dense packing is the most stable state”. This breakthrough paves the way for metamaterials with tailored optical, mechanical, topological or electronic properties. The mechanical and topological properties of the superlattices are controlled by altering the curvature of the building blocks, whereas the optical and electrical properties may be tuned by modulating band structure, exchanging ligands, and forming heterojunctions.

Future efforts aim to explore novel architectures, design multicomponent systems, and validate potential applications. Based on the complementary assembly patterns driven by curvature utilizing dumbbell-shaped nanoparticles, curvature gradient-gradated nonconvex particles (such as trigonal clusters or star-shaped particles) can be designed to achieve hierarchical ordered structures, such as spiral Kagome phase. The single-component superlattice system is extended to multicomponent systems, designing multifunctional superlattices and verifying the universality of the curvature-driven principle. Moreover, the unique geometric configurations and electronic structures of these superlattices endow them with potential applications in quantum computing, catalysis, and optoelectronic sensing, providing a foundation for the development of related devices to showcase their prospects. As nonconvex building blocks bridge the gap between atomic and colloidal assembly, they herald a new era in bottom-up nanotechnology.