Construction of an explicit rutting model for asphalt pavement considering aging factors
Abstract
Under different time and space conditions, the rutting evolution of asphalt pavement has a complex nonlinear relationship with axle load, temperature, humidity and material. How to express the rutting evolution of asphalt pavement systematically and explicitly has always been a difficult problem in the industry. In this paper, the I-R-F model is proposed for the first time, which can express the rutting evolution of all semi-rigid asphalt pavement forms explicitly. Compared with other mature explicit model frameworks, the structure is more standard, parameters are simplified and the fitting accuracy is higher. The proposed model has improved the rutting fitting accuracy on semi-rigid asphalt roads by an average of 0.018. It is obtained by improving the R-F model framework in the previous research results of the author, introducing the influence factors of ultraviolet aging to correct the model, and further performing Complementary Ensemble Empirical Mode Decomposition with Adaptive Noise and wavelet packet threshold denoising on the RIOHTrack data, ultimately achieving a good fitting effect for rutting evolution.
Keywords
1. INTRODUCTION
The semi-rigid asphalt pavement has the advantages of high bearing capacity, good anti-deformation performance, strong frost resistance, and ease of local material utilization. Therefore, the semi-rigid asphalt pavement has become the main form of asphalt pavement in many countries. With the development of the transportation industry, the semi-rigid asphalt pavement has exhibited rutting and cracking phenomena. Thus, it is particularly important to study the evolution mechanism of the semi-rigid pavement. Rutting is one of the main failure forms of semi-rigid asphalt pavement, and it is also the main research content of this paper. Rutting increases as traffic loads increase, while rutting deepens longitudinally, further threatening the base and even the subbase. To solve the rutting problem, it is not only necessary to develop anti-rutting materials, but also to analyze related internal and external factors affecting rutting, master its evolution law, further guide pavement design, and solve the rutting problem from the source[1-3]. Based on the previous work, the corresponding theoretical system has been established in this research field, and it can guide the design better [4]. However, there are still some practical phenomena, such as lack of data, insufficient data mining and imperfect theoretical system, which lead to some practical difficulties, such as the accuracy of the current asphalt pavement rutting prediction model is not high enough and the design life error of asphalt pavement is large.
Since the 1960s, the research on rutting of asphalt pavements has gradually gained attention and been promoted. The main types of models include mechanical models based on mechanical theories, empirical models driven mainly by data, mechanical-experimental models combining artificial intelligence and mechanical theories, etc.The research method of mechanical model is based on elastic layered theory, combined with viscoelastic theory and material performance parameters, the stress and strain law of pavement structure is calculated, and rutting prediction model is obtained. The model forms mainly include viscoelastic model [5, 6], viscoelastic-plastic model [7, 8], viscoelastic-plastic damage model, [9, 10] and so on. Although the mechanical model has the strongest theoretical basis, it is difficult to select the mechanical model and accurately confirm the constitutive parameters due to the limitation of practical engineering background and data. The empirical model research method is based on the statistical methods and the actual pavement observation or accelerated loading test data, combined with the actual pavement condition; through statistical regression analysis, the empirical model of asphalt pavement rutting prediction is established. Based on American Association of State Highway and Transportation Officials 56 (AASHTO) test road data, full-scale loop data and indoor loop test data, relevant scholars obtained rut curves of different working conditions and different structures, respectively. In recent years, scholars, through artificial neural network research, also achieved a good rutting prediction effect [11, 12], by combining the machine learning model approach, some explicit model results were obtained[13]. The rutting prediction model established by empirical model method has good accuracy for specific external environments, pavement structures and materials. However, the practical problems of inaccurate and missing data often cause the empirical model to fail to systematically characterize the rutting evolution process. The mechanical-empirical model method is to establish the empirical relationship equation between rutting depth and pavement structure and material parameters through the mechanical theory of elastic layered system or viscoelastic-plastic system, combined with the relevant indoor and outdoor test data. Based on the research of mechanical theory, the dynamic expression of the stress-strain response model is realized by modifying the test data. The representative prediction models of this model method include Monismith model and AASHTO 2002 model [14-18]. The mechanical-empirical model combines the advantages of mechanical and empirical methods. The RIOHTrack full-scale ring data used in this paper plays a key role in the implementation of the model. In this paper, the relevant mechanical models are used for reference, and statistical methods are used to fit and modify the model, and finally the corresponding model effect is obtained.
In addition to the mechanical evolution of asphalt pavement under the action of compound force, the aging of asphalt material caused by internal and external factors also has a certain impact on the rutting evolution and research of asphalt pavement. The main factors affecting asphalt aging include external environmental factors such as temperature, air, light and precipitation. Asphalt aging is a gradual process, and the aging rate directly affects the service life of asphalt pavement. The physical changes and chemical reactions in the aging process of asphalt materials cause bitumen to become brittle and hard gradually, which further affects the deformation resistance and fatigue properties of asphalt binders, thus affecting the durability of the pavement [19]. Therefore, the durability of asphalt pavement can be improved by analyzing the mechanism of asphalt aging and the relationship between different aging modes and fatigue performance of asphalt pavement, and taking corresponding solutions. Thermo-oxygenation is one of the main processes of aging. In addition to thermal oxygen, ultraviolet (UV) light is another cause of asphalt aging. The main difference between UV aging and thermal oxygen aging is that the way of chemical bond fracture is different. Thermal oxygen causes the thermal decomposition and fracture of the chemical bond inside the polymer material. Under the action of UV, all kinds of chromogenic groups inside the material absorb UV light energy and change from the ground state to the excited state, causing the chemical bond to fracture. The primary oxidation products (such as carboxyl and peroxide groups) produced by UV radiation are unstable, which further accelerates the aging of asphalt. Due to the action of UV light, the internal groups of asphalt molecules are interrupted, and the asphalt components changed [20, 21]. Compared with other aging factors of asphalt pavement caused by rutting, the UV aging factor is more in line with the rutting evolution characteristics of asphalt pavement. Its actual measurement data is easier to collect. Moreover, through data analysis and comparison, its effect is remarkable. Therefore, this paper adopts the UV aging factor for the research. The aging process of asphalt mixture under UV light has the characteristics of saturation state, and the Verhulst model can specifically describe the evolution process of physical properties with the characteristics of saturation state [22, 23]. In this paper, the Verhulst model is used to establish the nonlinear equation of asphalt mixture road performance index under different UV irradiation times.
RIOHTrack is the first full-scale road test ring in China. After years of demonstration, design and construction, the civil construction system of full-scale road test ring road was officially completed in November 2015. The data used in this study is mainly from the RIOHTrack full-scale ring data. The data used in this paper covers temperature, humidity, load, radiation and other data related to rutting research, which was collected after 56 million measurements, and is also the most authoritative full-scale track test data in China [24]. On the basis of the research of RIOHTrack full-scale ring data,
At present, no scholar has been able to effectively propose an explicit rutting evolution model that can effectively represent the rutting evolution law and simultaneously cover the aging mechanism of asphalt materials. In order to anticipate and comprehensively predict the needs of material aging development and rutting and inflection points prediction in advance, this paper innovatively superposes the aging factor into the
After introducing the research status of asphalt route rutting. In Section 2, the asphalt pavement data denoising method and the superimposed aging mechanism are introduced, and the improved asphalt pavement rutting model
2. MODEL STUDY
2.1. Theory of denoising analysis
The measured data of RIOHTrack have the characteristics of unknown distribution, high noise and nonlinearity. To better fit the distribution and effectively build the rutting prediction model, it is necessary to perform the denoising analysis on the measured test data.
Commonly used denoising methods include nonlinear median filter, mathematical morphology, singular value decomposition, Empirical Mode Decomposition (EMD), wavelet transform [26], etc. The signal smoothing effect of the nonlinear median filter is poor. The denoising performance of mathematical morphology filter is determined by its transform type and the shape and size of the structuring element, but the actual pulse signal size is unknown. The smoothness of the signal after singular value decomposition is not good, and the noise content is high after reconstruction. {EMD} is easy to produce mode aliasing and boundary effects, so that Intrinsic Mode Functions (IMFs) of different scales contain similar components. The power quality signal denoising method based on {EMD} directly discards the decomposed IMF1[27, 28]. On the one hand, it cannot retain the high-frequency characteristics of the original signal; on the other hand, it does not consider the influence of end effects and mode aliasing. Ensemble Empirical Mode Decomposition (EEMD) improved from {EMD} was proposed for signal denoising[29], although mode aliasing was reduced, it was at the cost of loss of calculation accuracy. The Complementary Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN), can effectively reduce the reconstruction error[30].
Wavelet transform is a localized time-frequency analysis tool, which can decompose the signal into wavelet coefficients of different frequency bands, respectively representing the outline and details of the signal. Wavelet transform [31] only decomposes the low-frequency band of the signal. Wavelet packet transform is a more widely used wavelet transform, which can decompose both low-frequency and high-frequency signals without increasing data redundancy and data loss. The noise of rutting data is mainly distributed in high-frequency signals, so wavelet packet transformation is more effective for denoising rutting data of asphalt roads.
If the first few high-frequency IMFs obtained by EMD decomposition of the noisy power quality signal are directly discarded, it will cause the loss of high-frequency information and incomplete elimination of high-frequency noise. Due to the complex characteristics of asphalt pavement data such as unknown distribution, non-stationary and nonlinearity, the CEEMDAN noise reduction algorithm combined with wavelet packet adaptive threshold is applied in this paper[32]. CEEMDAN is improved on the basis of EMD, and borrows the idea of adding Gaussian noise in EEMD method and cancelling noise by multiple superposition and average, which is suitable for processing non-stationary and nonlinear signals. Wavelet packet adaptive threshold denoising method combines wavelet packet transform with adaptive threshold to make the data denoising have certain adaptability. The noisy signal is set as follows:
where x(t) is the original signal, and e(t) is the noise signal.
The overall denoising implementation steps are as follows:
(1) Perform {CEEMDAN} decomposition on
(2) The correlation coefficient method is used to screen out the first few {IMFs} components that need to be denoised by wavelet packet adaptive threshold.
(3) Threshold noise reduction is performed on the sieved {IMFs}.
(4) The signal after threshold processing is reconstructed with the remaining {IMFs}, and the denoised signal is obtained.
2.2. Improved R-F model
The
where
The experimental results show that the fatigue life of asphalt pavement will be reduced due to the aging of asphalt material [33]. With the occurrence of fatigue phenomena such as micro-cracks on asphalt pavement, rutting phenomenon will be intensified under the continuous action of vehicle load. To a certain extent, the aging of asphalt materials accelerates the evolution of rutting, so it is necessary to use asphalt aging as an auxiliary variable to characterize rutting and the aging problem of asphalt pavement needs to be paid attention to.
In order to better study the rutting inflection point effect caused by material aging damage and establish a more universal asphalt rutting evolution model, this paper mainly considers the UV aging factor to conduct supplementary research on road rutting. At the same time, the correlation between thermal oxygen effect and material selection is stronger and more complex, and the relevant measured data is lacking.
In this paper, Verhulst model is used to establish a nonlinear equation characterizing the UV aging properties of asphalt mixture [34], and the parameters in the model are further estimated. Two characteristic values, UV aging rate and UV aging residual index, are proposed to measure the change of UV aging properties of asphalt mixture, in order to provide theoretical basis for asphalt pavement maintenance and technology.
Because the Verhulst model has a good performance in characterizing the evolution process of saturation states, it is adopted to fit the nonlinear aging process of asphalt mixtures under UV radiation. The Verhulst model is expressed as follows:
where
Solving the above ordinary differential equation, we obtain
where
When
Let
which is the nonlinear equation of pavement performance of asphalt mixture under different UV irradiation time.
For Equation 6, when
On the basis of
where
In this paper, a rutting evolution model framework of
3. MODEL APPLICATION
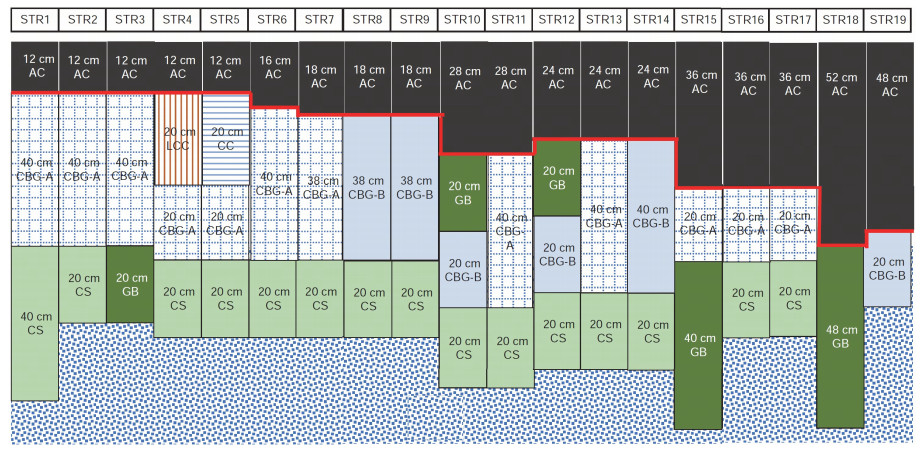
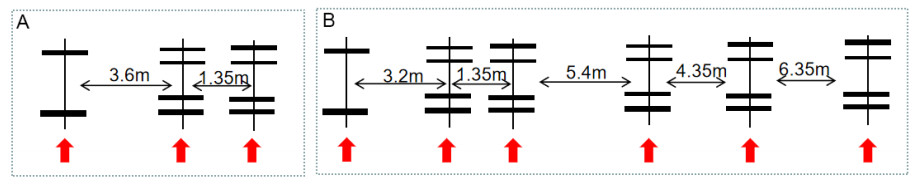
As shown in Figure 1, all the structures of RIOHTrack full-scale ring road include 3 semi-rigid foundation roads with a thin asphalt layer, 4 conventional semi-rigid foundation roads, 2 rigid composite roads, 2 flip structure roads, 6 thick asphalt structure roads and 2 full-layer structure roads, totaling 6 structural forms and 19 structural pavements. The thickness of different pavement structures varies from 68 cm to 100 cm. The relevant pavement structure is composed of different asphalt mixture surface layers and base materials, cement stabilization materials and graded gravel base materials [35]. The asphalt concrete structural layer thickness of these pavement structures is 12, 16, 18, 24, 28, 36, 48 cm (or 52 cm), and its material is mainly SBS modified asphalt, and the main material of the base is cement stabilized graded gravel and cement stabilized soil, which basically covers all the structures and thickness of the current high-grade highway. The operation of the ring road is achieved through the loading of trucks for 12 h each day. The loading of the towed truck, which used the pattern shown in Figure 2A in 2017 and 2018, has changed to the pattern shown in Figure 2B since 2019 [36]. The performance test of the loop includes two types: real-time monitoring and periodic testing. The real-time monitoring includes the all-weather collection of stress and strain information inside the structure at the frequency of 2000Hz, the inductive vehicle axle load monitoring, and the internal and external environmental monitoring of the structure.
Figure 1. The RIOHTrack ring road has a total of 19 structures, which include a thin asphalt layer semi-rigid foundation road, a conventional semi-rigid foundation road, a rigid composite road, a flip structure road, a thick asphalt structure road, and a full thickness structure road. Taking the structure of STR 1 as an example, it consists of a 12cm asphalt concrete surface layer, a 40cm cement stabilized graded gravel layer, and a 40cm cement stabilized soil layer[25]
Figure 2. The loading data of the tow truck adopts different axle load wheelbase at different times. (A) shows the loading situation from 2017 to 2018, while (B) represents the loading situation from 2019 onwards
The data of semi-rigid asphalt pavement are studied in this paper, and the research results have reference significance for other subgrade pavement forms. The seven tracks STR1-STR3 and STR6-STR9, as shown in Figure 1, all have the structural characteristics of semi-rigid asphalt pavement, but the thickness of each layer, the total thickness and the material selection of each layer are different. The data used in the article is prior to October 2021, when more than 56 million measurements were taken.
3.1. Model fitting
Considering the application prospect and data basis comprehensively, this paper selects semi-rigid asphalt pavement data to study. Considering the nonlinear and non-stationary characteristics of asphalt pavement data, this paper adopts the CEEMDAN and wavelet adaptive threshold denoising method.
Under the framework of the improved rutting prediction model 8 for asphalt pavement, according to the data calculation, the paper considers its maximum polynomial degree to be 9, and builds a rutting evolution model for asphalt pavement with axle load:
where
Using the above denoised data, the relevant parameters, statistical analysis results and fitting effects are obtained as follows.
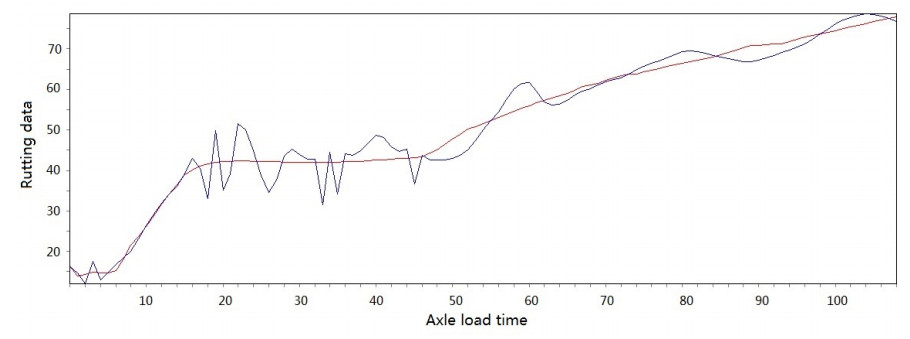
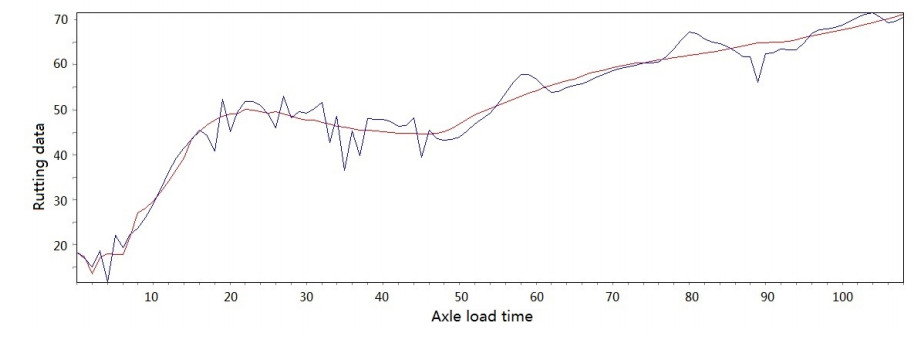
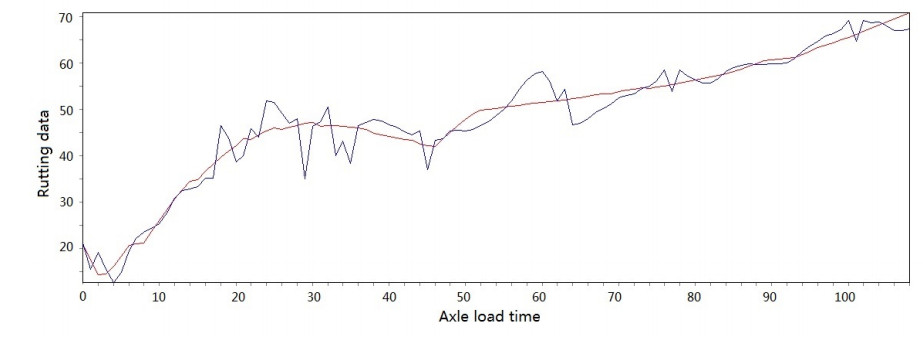
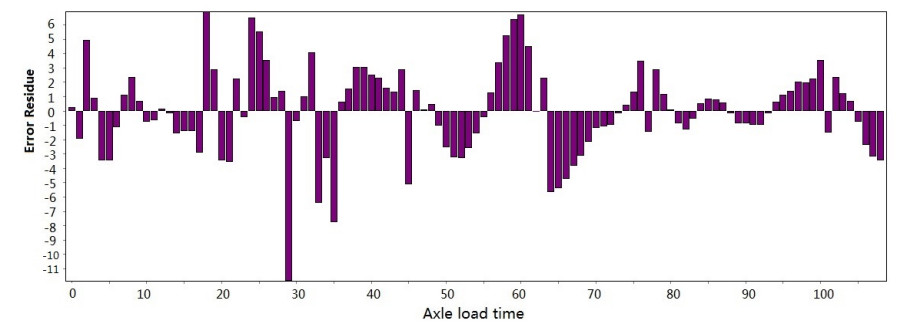
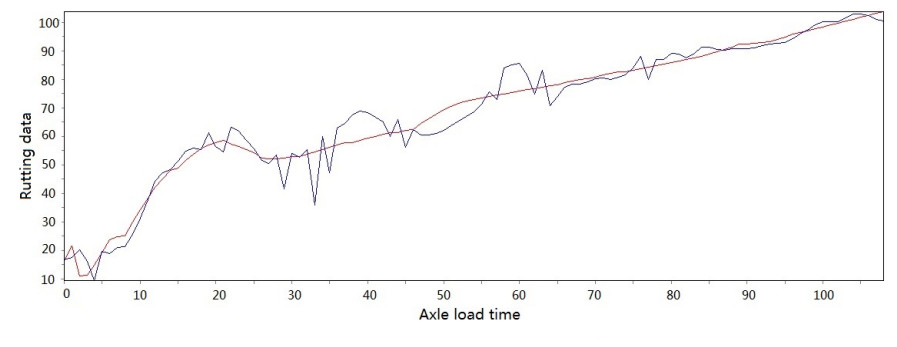
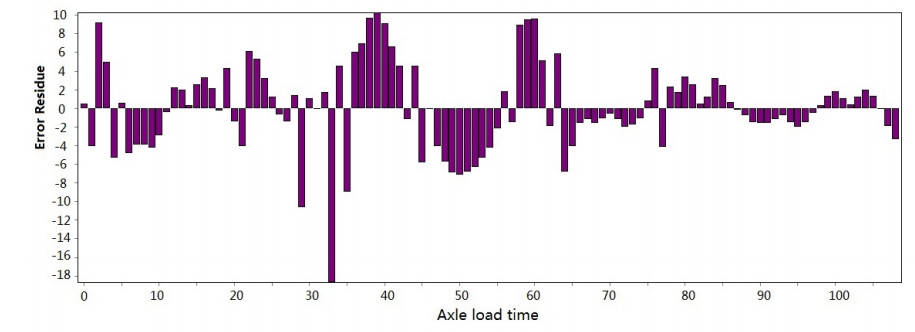
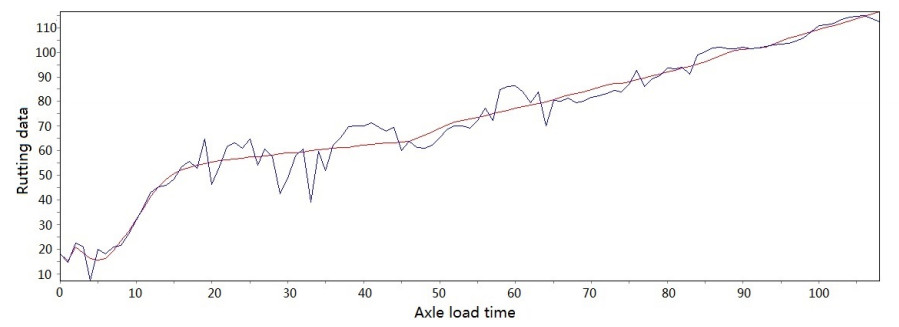
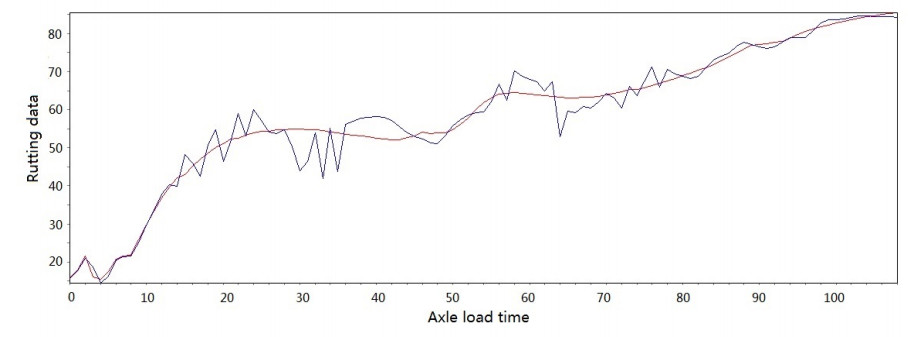
The performance of the improved model in each road section and the statistics are detailed in Table 1. From the perspective of the determination coefficient value, the model effect is very obvious.
The model's effectiveness can be judged based on the coefficient of determination. The maximum value is 0.966, and the minimum value is 0.951
| Statistics/track number | 1 | 2 | 3 | 6 | 7 | 8 | 9 |
| 0.964 | 0.963 | 0.962 | 0.951 | 0.962 | 0.966 | 0.964 | |
| RMSE | 2.522 | 3.360 | 2.719 | 2.966 | 4.567 | 4.86 | 3.368 |
| SSE | 693.228 | 1230.617 | 805.658 | 958.804 | 2273.135 | 2574.807 | 1236.708 |
| DC | 0.964 | 0.963 | 0.965 | 0.962 | 0.9617 | 0.9664 | 0.964 |
| Chi-Square | 9.532 | 13.989 | 9.569 | 10.828 | 23.753 | 24.673 | 11.656 |
| F-Statistic | 2868.984 | 2803.308 | 2717.709 | 2077.293 | 2687.691 | 3078.81 | 2840.410 |
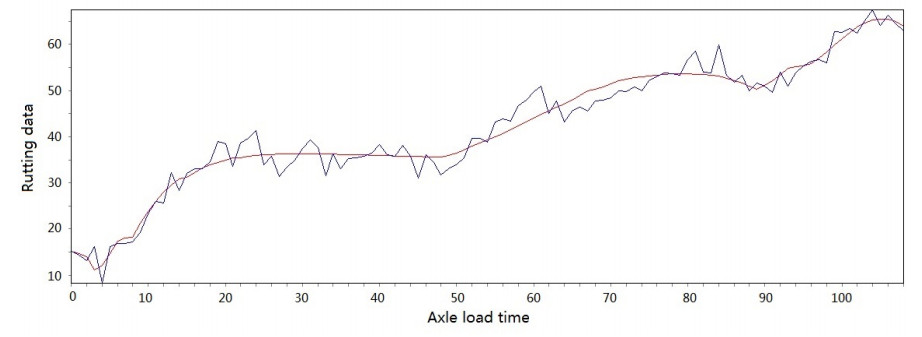
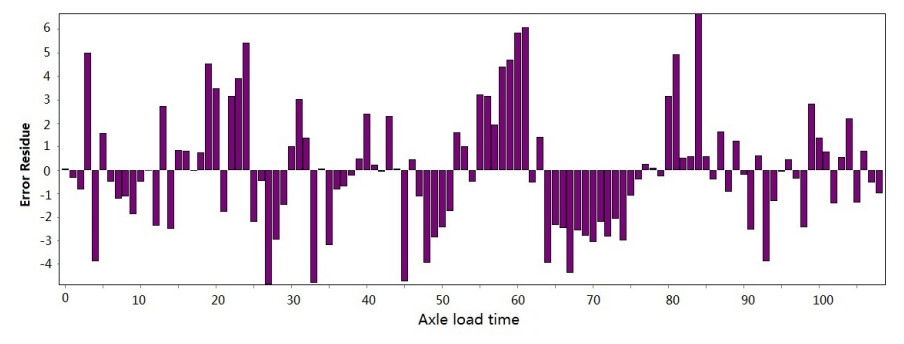
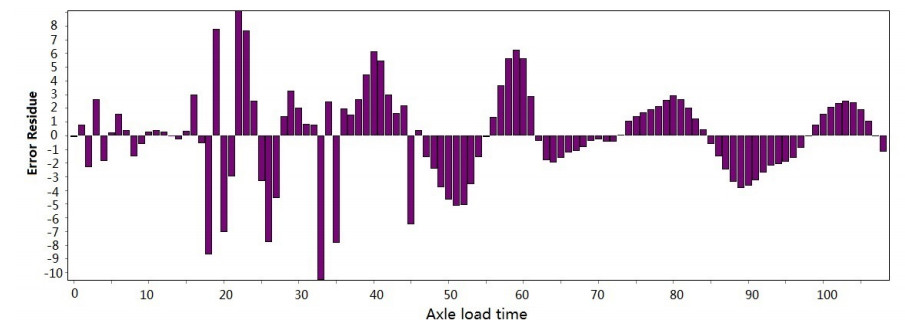
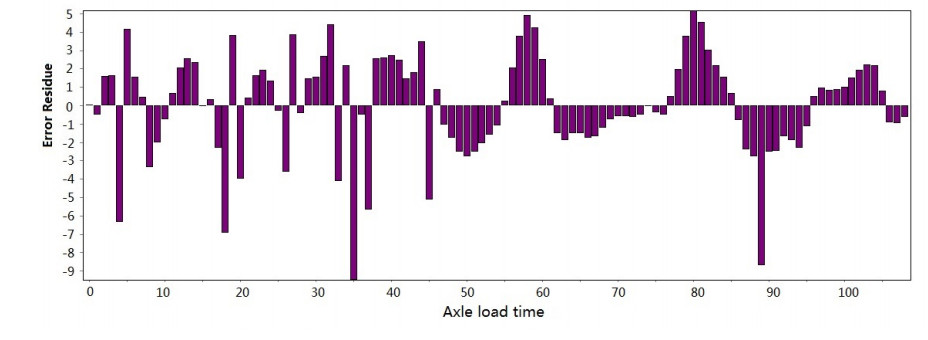
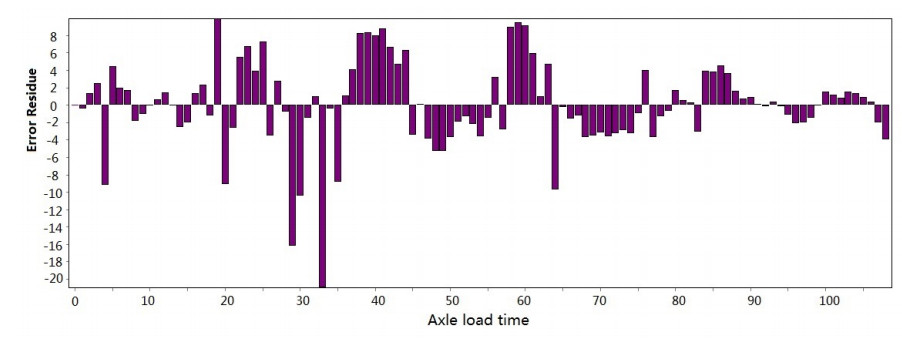
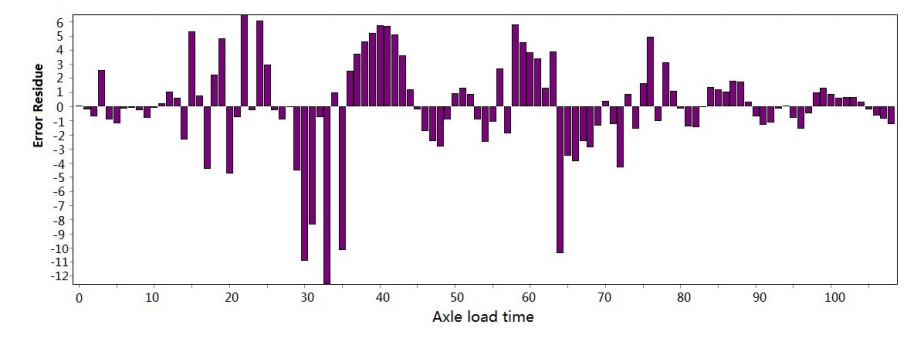
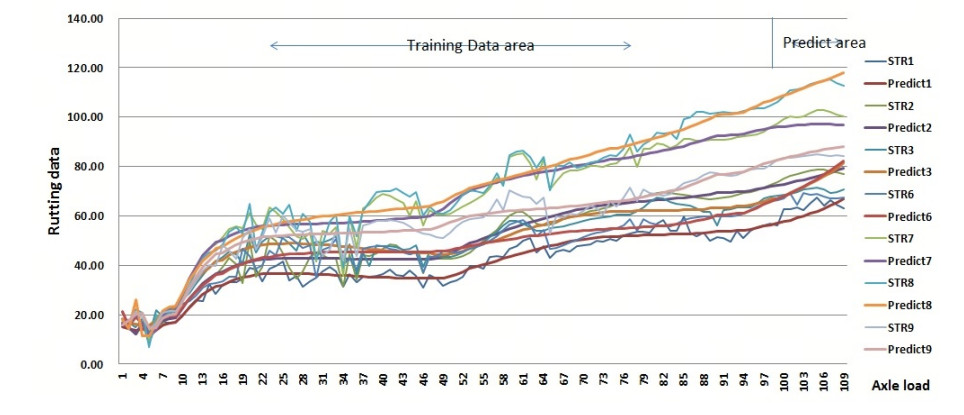
Figure 3-Figure 16 show the fitting performance and residual plot of the rutting evolution model on each semi-rigid asphalt pavement, respectively, and the comparison between the paper model and other excellent models after data denoising is presented in Table 2.
The coefficients of determination
| Models/track number | 1 | 2 | 3 | 6 | 7 | 8 | 9 |
| 0.964 | 0.963 | 0.962 | 0.951 | 0.962 | 0.966 | 0.964 | |
| 0.935 | 0.951 | 0.933 | 0.935 | 0.947 | 0.959 | 0.947 | |
| 0.935 | 0.944 | 0.905 | 0.842 | 0.935 | 0.899 | 0.922 | |
| 0.912 | 0.936 | 0.892 | 0.885 | 0.929 | 0.946 | 0.910 |
3.2. Convergence analysis
In this section, by setting (17) as the loss function, we further utilize the Levenberg-Marquardt optimization method to effectively fit the evolutionary data.
where,
After calculating and iterating based on the measured rut evolution data, the values of the loss function gradually stabilized on each type of pavement structure. The values were 2.522, 3.360, 2.719, 2.966, 4.567, 4.86, 3.368, respectively. At this point, the model has fully converged, demonstrating the effective convergence effect of the constructed model.
The data calculation and parameter solution in this article were accomplished using a nonlinear programming software. Through this process, the convergence perform ance of the model was effectively verified.
3.3. Prediction effect
In order to verify the model prediction effect, the training set and the test set are divided by time as the boundary. Based on the time axis, the data from the last 10% of the period is selected as the test set, covering 10 samplings from June 2021 to October 2021, with a span of over 7 million standard axle loads and representing the rutting changes over this period. The interval between each two samplings is approximately 770, 000 standard axle loads. The training set and test set are divided based on the characteristics and performance of the rutting model.
The specific prediction effect diagram is shown in Figure 17. For the prediction results of unknown domain data, the loss function values reached 3.31, 3.23, 6.55, 8.71, 4.58, 2.61 and 2.19, respectively.
Using the model in this article for data processing and analysis, the obtained determination coefficients are 0.962, 0.965, 0.952, 0.925, 0.959, 0.965, 0.961; the RMSE values are 2.624, 3.288, 3.149, 3.948, 4.774, 4.994, 3.513 and the SSE values are 750.276, 1178.665, 1080.756, 1699.361, 2484.613, 2718.441, 1344.879, reflecting a good prediction effect.
3.4. Comparative analysis
Based on improved Burgers model and the JTG D50-2017 design specification framework, under the actual measurement data, the contents of the improved model framework
(1)
where
(2) The
where
Through data noise reduction, data analysis, and model parameter fitting, the effect of improved
4. CONCLUSIONS
In this paper, through data mining and comparative analysis, the value of the
Based on the empirical model of mechanics, this paper innovatively proposes the
Due to the reasons of basic data and material selection, the aging factor of the improved model has not considered the effect of thermal oxidation, which needs further study and demonstration. At the same time, the model needs to be further validated and analyzed under different road structures, axle loads, temperatures, humidity and radiation environments to further enhance the generalization ability of the model.
DECLARATIONS
Authors' contributions
Substantial contributions to conceptualization and methodology of the study and writing, visualization: Kou, B.; Cao, J.; Shi, Z.
Formal analysis, methodology and validation, along with data analysis: Huang, W.; Ma, T.
Review and editing: Gong, Y.
All authors have read and agreed to the published version of the manuscript.
Availability of data
The data that has been used is confidential.
Financial support and sponsorship
This work is supported by the National Key Research and Development Project of China under Grant (No. 2020YFA0714300), the National Natural Science Foundation of China under Grant (No. 61833005) and the Open Project of Key Laboratory of Transport Industry of Comprehensive Transportation Theory (Nanjing Modern Multimodal Transportation Laboratory) of China under Grant (No. MTF2023004).
Conflicts of interest
This manuscript underwent a double-blind peer review process. Cao, J. is an Advisory Board Member of the journal Complex Engineering Systems. Cao, J. was not involved in any steps of editorial processing, notably including reviewers' selection, manuscript handling, and decision making, while the other authors have declared that they have no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Suh, Y. C.; Cho, N. H.; Mun, S. Development of mechanistic cempirical design method for an asphalt pavement rutting model using APT. Constr. Build. Mater. 2011, 25, 1685-90.
2. Zhu, H. R.; Sun, L. Mechanistic rutting prediction using a two-stage viscoelastic viscoplastic damage constitutive model of asphalt mixtures. J. Eng. Mech. 2013, 139, 1577-91.
3. Prez, I.; Gallego, J. Rutting prediction of a granular material for base layers of low-traffic roads. Constr. Build. Mater. 2010, 24, 340-5.
4. Zheng, J.; Lv, S.; Liu, C. Technical system, key scientific problems and technical frontier of long-life pavement. Chin. Sci. Bull. 2020, 65, 3219-27.
5. Wu, W. B.; Xu, Z. H.; Tian, X. G.; Zhang, S. Q. Viscoelastic property of aging asphalt mixture and parameters determination method. In: 2010 International Conference on Measuring Technology and Mechatronics Automation; 2010, pp. 1083-6.
6. Mun, S.; Chehab, G. R.; Kim, Y. R. Determination of time-domain viscoelastic functions using optimized interconversion techniques. Road. Mater. Pavement. Des. 2007, 8, 351-65.
7. Tashman, L.; Masad, E.; Zbib, H.; Little, D.; Kaloush, K. Anisotropic viscoplastic continuum damage model for asphalt mixes. Geotech. Spec. Publ. 2004, 123, 111-25.
8. You, T.; Al-Rub, R. K. A.; Masad, E. A.; Kassem, E.; Little, D. N. Three-dimensional microstructural modeling framework for dense-graded asphalt concrete using a coupled viscoelastic, viscoplastic, and viscodamage model. J. Mater. Civ. Eng. 2013, 26, 607-21.
9. Darabi, M. K.; Al-Rub, R. K. A.; Masad, E. A.; Huang, C. V. Thermodynamic based model for coupling temperature dependent viscoelastic, viscoplastic, and viscodamage constitutive behavior of asphalt mixtures. Int. J. Numer. Anal. Methods. Geomech. 2012, 36, 817-54.
10. Al-Rub, R. K. A.; You, T.; Masad, E. A. Mesomechanical modeling of the thermo-viscoelastic, thermo-viscoplastic, and thermo-viscodamage response of asphalt concrete. Int. J. Adv. Eng. Sci. Appl. Math. 2011, 3, 14-33.
11. Fares, A.; Zayed, T.; Abdelkhalek, S.; Faris, N.; Muddassir, M. Rutting measurement in asphalt pavements. Automat. Constr. 2024, 161, 105358.
12. Archilla, A. R.; Madanat, S. Development of a pavement rutting model from experimental data. J. Transp. Eng. 2000, 126, 291-9.
13. Kou, B.; Cao, J.; Shi, Z.; Huang, W.; Ma, T.; Gong, Y. Construction of data-driven explicit rutting evolution model for asphalt pavement. Appl. Math. Stat. 2025, 2, 5.
14. Ban, H.; Im, S.; Kim, Y. R. Nonlinear viscoelastic approach to model damage-associated performance behavior of asphaltic mixture and pavement structure. Can. J. Civ. Eng. 2013, 40, 313-23.
15. Zhang, Y.; Luo, X.; Deng, Y.; et al. Evaluation of rutting potential of flexible pavement structures using energy-based pseudo variables. Constr. Build. Mater. 2020, 247, 118391.
16. Gandomi, A. H.; Alavi, A. H.; Mirzahosseini, M. R.; Nejad, F. M. Nonlinear genetic-based models for prediction of flow number of asphalt mixtures. J. Mater. Civ. Eng. 2010, 23, 248-63.
17. Abd, D. M.; Ahmed, T. M.; Ahmed, T. Y. Characterization of rutting resistance of warm-modified asphalt mixtures tested in a dynamic shear rheometer. J. Mech. Behav. Mater. 2023, 32, 20220277.
18. Hafeez, I. Rutting prediction model of asphalt concrete mixtures using uniaxial repeated creep test. Kuwait. J. Sci. Eng. 2011, 38, 45-61.
19. Dave, E. V.; Buttlar, W. G.; Paulino, G. H. Asphalt pavement aging and temperature dependent properties through a functionally graded viscoelastic model, Part-Ⅱ: applications; 2009, PP. 53-8.
20. Chvez-Valencia, L. E.; Manzano-Ramírez, A.; Alonso-Guzmán, E.; Contreras-García, M. E. Modelling of the performance of asphalt pavement using response surface methodology the kinetics of the aging. Build. Sci. 2007, 42, 933-9.
21. Petersen, J.; Harnsberger, P. Asphalt aging: dual oxidation mechanism and its interrelationships with asphalt composition and oxidative age hardening. Transp. Res. Rec. J. Trans. Res. Board. 1998, 1638, 47-55.
22. Zhang R. Regional logistics demand analysis based on gray system theory: a case study of Hangzhou city. In: 2010 Third International Conference on Knowledge Discovery and Data Mining. 9-10 January 2010.
23. Song, Y. H.; Nie, D. X. Verhulst model for predicting foundation settlement. Rock. Soil. Mech. 2003, 24, 123-6.
24. Wang, X. D.; Zhou, G. L.; Liu, H. Y.; Qing, X. Key points of RIOHTRACK testing road design and construction. J. Highw. Transp. Res. Dev. 2020, 14, 1-16.
25. Kou, B.; Cao, J. D.; Huang, W.; Ma, T. The rutting model of semi-rigid asphalt pavement based on RIOHTRACK full-scale track. Math. Biosci. Eng. 2023, 20, 8124-45.
26. Kopsinis, Y.; McLaughlin, S. Development of EMD-based denoising methods inspired by wavelet thresholding. IEEE. T. Signal. Proces. 2009, 57, 1351-62.
27. Han, G.; Zhang, J. W.; Zhu, X. Research on denosing of power quality disturbance detection and location based on EEMD adaptive thresholding. Electr. Meas. Instrum. 2014, 51, 45-9.
28. Liu, G.; Chen, L.; Qian, Z.; Zhang, Y.; Ren, H. Rutting prediction models for asphalt pavements with different base types based on riohtrack full-scale track. Constr. Build. Mater. 2021, 305, 124793.
29. Li, F.; Zhang, B.; Verma, S.; et al. Seismic signal denoising using thresholded variational mode decomposition. Explor. Geophys. 2017, 49, 450-61.
30. Yeh, J. R.; Shieh, J. S.; Huang, N. E. Complementary ensemble empirical mode decomposition: a novel noise enhanced data analysis method. Adv. Adap. Data. Anal. 2010, 2, 135-56.
31. Tikkanen, P. Nonlinear wavelet and wavelet packet denoising of electrocardiogram signal. Biol. Cybern. 1999, 80, 259-67.
32. Yang, Y.; Li, S.; Li, C.; He, H.; Zhang, Q. Research on ultrasonic signal processing algorithm based on CEEMDAN joint wavelet packet thresholding. Measurement. 2022, 201, 111751.
33. Zhu, G. J.; Wu, S. P.; Liu, R. Study on the fatigue property for aged asphalt mixtures by using four point bending tests. Mater. Sci. Forum. 2009, 614, 289-94.
34. He, X.; Hochstein, D.; Ge, Q.; et al. Accelerated aging of asphalt by UV photo-oxidation considering moisture and condensation effects. J. Mater. Civ. Eng. 2018, 30, 1-12.
35. Wang, Y.; Yan, J.; Huang, W.; Rutkowski, L.; Cao, J. Variable-order fractional derivative rutting depth prediction of asphalt pavement based on the riohtrack full-scale track. Sci. China. Inform. Sci. 2022, 66, 152205.
36. Wang, X. D.; Zhang, L.; Zhou, X. Y.; Xiao, Q.; Shan, L. Y. Research progress of RIOHTrack in China. In: 6th International Conference on Accelerated Pavement Testing (APT), 2020; pp. 21-31.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data
















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].