Critical nodes identification in complex networks: a survey
Abstract
Complex networks have become essential tools for understanding diverse phenomena in social systems, traffic systems, biomolecular systems, and financial systems. Identifying critical nodes is a central theme in contemporary research, serving as a vital bridge between theoretical foundations and practical applications. Nevertheless, the intrinsic complexity and structural heterogeneity characterizing real-world networks, with particular emphasis on dynamic and higher-order networks, present substantial obstacles to the development of universal frameworks for critical node identification. This paper provides a comprehensive review of critical node identification techniques, categorizing them into seven main classes: centrality, critical nodes deletion problem, influence maximization, network control, artificial intelligence, higher-order and dynamic methods. Our review bridges the gaps in existing surveys by systematically classifying methods based on their methodological foundations and practical implications, and by highlighting their strengths, limitations, and applicability across different network types. Our work enhances the understanding of critical node research by identifying key challenges, such as algorithmic universality, real-time evaluation in dynamic networks, analysis of higher-order structures, and computational efficiency in large-scale networks. The structured synthesis consolidates current progress and highlights open questions, particularly in modeling temporal dynamics, advancing efficient algorithms, integrating machine learning approaches, and developing scalable and interpretable metrics for complex systems.
Keywords
1. Introduction
Complex networks and systems are fundamental to diverse fields, including social network analysis, urban traffic modeling [1], biomolecular structure analysis [2], and financial systems [3], where understanding the interplay between network structure, system architecture, and functionality is a central research focus [4]. A typical network consists of nodes, representing entities within a real system, and edges, which encode relationships between them. By leveraging graph structures to model real-world systems, researchers can systematically analyze the interactions that govern their dynamics. A key challenge in complex network research is identifying important nodes, a topic that has garnered significant attention due to its broad applications. In neural brain networks, neurons are interconnected through nerve fibers, and the transmission of signals enables autonomous decision-making. In transportation networks, identifying critical nodes aids in traffic prediction, optimization, and infrastructure planning. Similarly, in epidemiological networks, infections originating from a few individuals can rapidly propagate through contact links, posing significant risks to public health. In communication networks, detecting key nodes enhances resource allocation and strengthens network security. Likewise, in social networks, pinpointing influential individuals or communities facilitates targeted marketing and improves user engagement. Advances in structural analysis and feature extraction continue to refine our understanding of network robustness, efficiency, and optimization, shedding light on the fundamental principles that govern complex systems.
Recent years have seen a growing number of review articles providing systematic overviews of node importance in complex networks. Various terms - such as key nodes, critical nodes, important nodes, and influence-maximizing nodes - have been used to describe structurally and functionally significant elements, leading to the development of a wide range of methods for assessing node importance in different contexts. For instance, Liu et al. [5] reviewed advances in node influence ranking by considering both network structure and diffusion dynamics, analyzing the strengths, limitations, and applicability of different approaches. Ren et al. [6] introduced over 30 methods for identifying important nodes, categorizing them based on criteria such as node neighbors, network paths, feature vectors, and contraction techniques. Their study evaluated node importance from the perspectives of network robustness, vulnerability, and diffusion dynamics, yet the effectiveness of these methods remains constrained by network size and computational complexity. Lalou et al. [7] focused on the Critical Node Deletion Problem (CNDP), classifying solution algorithms based on problem variants and constraints related to network fragmentation. While their work systematically examined the impact of node removal on network connectivity and vulnerability, its applicability to dynamic and real-world networks remains an open challenge. More recent reviews have explored influence maximization (IM) and node ranking in greater depth. Hafiene et al. [8] addressed the IM problem in social networks, aiming to select a set of users that maximize influence spread. However, existing IM approaches often struggle with high computational costs and scalability in large-scale networks. Zhang et al. [9] classified influential node ranking methods (INRM) and compared validation models based on cascade failure, linear threshold, and epidemic processes, yet integrating these models with real-time applications remains a challenge. Li et al. [10] summarized key challenges in diffusion models, such as computational complexity and parameter tuning, and examined how reinforcement learning and graph learning improve efficiency and generalizability. Nevertheless, machine learning-based approaches often require extensive training data and careful model selection. Jaouadi et al. [11] provided a comprehensive classification of IM models, highlighting their evolution from static to dynamic networks and emerging trends in handling large-scale systems, though trade-offs between accuracy and efficiency remain a concern. In addition to traditional network models, recent efforts have extended node importance analysis to high-order networks. Liu et al. [12] reviewed statistical indices for hypergraphs and simplicial complexes, introducing physically meaningful measures such as degree-dependent indicators, clustering coefficients, centrality metrics, and entropy-based indices. These studies highlight the diversity of methods for evaluating node importance, as well as significant progress in influence propagation, network robustness, and higher-order structures. However, most previous reviews have focused on specific types of network structures, such as static or higher-order networks, and there is still a lack of comprehensive and unified analyses covering multiple network forms. From the perspective of application scenarios, including IM and network fragmentation, the importance of nodes in relation to network control and stability has been largely overlooked. Similarly, from a methodological perspective, while centrality measures, node deletion strategies, and infection models have been discussed, systematic reviews of machine learning-based approaches and comprehensive index-based methods remain insufficient. This paper provides a comprehensive review of recent advances in identifying critical nodes in complex networks. Our key contributions are as follows:
● Categorization of application scenarios: From the application scenario oriented perspective of key nodes, this study systematically classifies existing methods into three key categories as depicted in Figure 1: (1) topological representation, which assesses node importance by structural metrics such as degree, eigenvalues, and path-based centrality; (2) IM, where the goal is to select a set of Top-
● Bridging gaps in existing surveys: Despite prior studies focusing on specific aspects such as centrality, influence propagation, and critical node deletion problems, there exists a lack of unified discourse regarding the methods and application scenarios of machine learning techniques in recent years. As presented in Table 1, this study bridges this gap by integrating artificial intelligence methods. These methods will be classified based on their methodological foundations and practical applications. Via comparative analysis, the study underscores the advantages, limitations, and applicability of these methods across different network types.
Comparison of existing studies on critical node identification across different methodological aspects
| Centrality | CNDP | IM | Control | AI | Higher-order | Dynamic | |
| Liu et al. [5] | √ | × | × | × | × | × | × |
| Ren et al. [6] | √ | × | × | × | × | × | × |
| Lalou et al. [7] | × | √ | × | × | × | × | × |
| Hafiene et al. [8] | × | × | × | √ | × | × | × |
| Zhang et al. [9] | × | × | × | × | × | × | × |
| Li et al. [10] | × | × | √ | × | × | × | × |
| Jaouadi et al. [11] | × | × | √ | × | × | × | √ |
| Liu et al. [12] | × | × | × | × | × | √ | × |
| Chen et al. (Ours) | √ | √ | √ | √ | √ | √ | √ |
● Comprehensive review of methodologies: From a methodological standpoint, this study analyzes nine key node identification techniques across various network structures and dynamic environments as tabulated in Table 2. This includes traditional topology-based approaches (e.g., centrality and shortest paths), optimization and control-based frameworks, information diffusion models, machine learning-driven methods, and recent advances in dynamic and higher-order networks.
Overview of structure, categorization and contributions
| Ranking methods | Categories | Details and contributions |
| Neighbors-based | 2.1 Degree centrality | Focus on local structural features, including node degrees, coreness, neighbor influence, and cohesive subgraphs, providing intuitive and efficient influence estimation. |
| 2.2 K-shell decomposition | ||
| 2.3 H-index | ||
| 2.4 K-truss | ||
| 2.5 Structural hole | ||
| 2.6 Neighborhood similarity | ||
| Eigenvector-based | 3.1 Eigenvector centrality | Utilize spectral properties and iterative propagation principles to assess global influence, emphasizing connections to other influential nodes. |
| 3.2 Katz centrality | ||
| 3.3 Pagerank algorithm | ||
| 3.4 Voting mechanism | ||
| Path-based | 4.1 Betweenness centrality | Measure node importance based on shortest paths, traversal distances, or probabilistic walks, capturing both local and global topological information. |
| 4.2 Closeness centrality | ||
| 4.3 Random walk | ||
| Control-optimization based | 5.1 Network control | Formulate node selection as optimization or control problems, identifying key nodes for structural stability, synchronization, or influence maximization. |
| 5.2 Maximization of connected component | ||
| 5.3 Minimization of pair connectivity | ||
| 5.4 Minimum spanning tree | ||
| Machine learning-based | 6.1 Information entropy | Leverage machine learning models, including classical, deep, and reinforcement learning, to learn influence patterns from structural or dynamic features. |
| 6.2 Clustering coefficient | ||
| 6.3 Machine learning | ||
| 6.4 Reinforcement learning | ||
| Comprehensive index-based | 7.1 Gravity formula | Integrate multiple metrics or criteria into unified indices, achieving more balanced and adaptable node ranking by considering multiple dimensions of importance. |
| 7.2 Multiple metrics | ||
| 7.3 Topsis and entropy-weight | ||
| Information propagation-based | 8.1 Diffusion model | Estimate node influence through simulation or modeling of propagation dynamics, linking rankings to spreading. |
| 8.2 Dynamical sensitivity | ||
| High-order networks | Capture complex relational patterns beyond pairwise links to improve influence identification accuracy. | |
| Dynamic networks | Address temporal evolution of networks to track time-dependent variations in node importance. | |
In this paper, we conduct a structured and comprehensive study of this field. We not only review the existing identification of key nodes in the network and the understanding of application scenarios from the perspective of network structure, methodology, and application scenario, but also discuss key challenges and unresolved issues. Note that the definitions of symbols used in this paper are provided in Table 3.
Table of symbols
| Symbol | Definition |
| G | Graph |
| Set of nodes | |
| Set of edges, eij denotes an edge connecting nodes vi and vj | |
| Number of nodes | |
| Number of edges | |
| Set of first-order neighbors of node v | |
| Set of first-order and second-order neighbors of node v | |
| dij | Path between vertices vi and vj |
| Shortest path length between two nodes | |
| Adjacency matrix | |
| Degree of vertex vi | |
| Triangle formed by nodes vi, vj, and vk | |
| Eigenvector of the network |
2. Neighbors-Based Ranking Methods
In complex network analysis, the contribution of neighbors can better measure the importance of nodes, and the essence of the node's position and role in the network can be captured through domain information. This section discusses node ranking methods based on the neighbor information of nodes in the network topology as displayed in Table 4. They can provide a detailed perspective on node importance by considering the local network structure, strike a balance between computational efficiency and accuracy, and are suitable for large-scale networks.
Comparison of neighbors-based ranking methods
| Title | Related works | Advantages/Disadvantages |
| Degree centrality | [13-17] | |
| [18-25] | ||
| H-index | [26-29] | |
| K-truss | [30,31] | |
| Structural hole | [32-37] | |
| Neighborhood similarity | [38-42] |
2.1. Degree centrality
In the study of social network structures, Bavelas et al. [13] introduced the concept of centrality, and Nieminen et al. [14] addressed the complex and cumbersome calculation of point centrality metrics by proposing a direct measure of node importance through the adjacency matrix. Specifically, the degree of node vi is defined as follows:
The advantage of this metric is that it is intuitive and easy to understand, with simple computation. However, the node degree metric cannot have comparability across networks of different scales. Building on this, the concept of degree centrality for the entire network is introduced, defined as:
The improved metric enables comparisons across networks of varying sizes. Intuitively, a node with more neighbors is likely to be more influential. However, this metric only considers the local state of node vi and cannot take into account the local environment of the node. To address the limitations of high computational cost and low local relevance in centrality measures, Chen et al. [15] introduced semi-local centrality (SLC), which incorporates the degrees of both first and second-order neighbors with flexible parameters. While degree centrality performs effectively in scenarios with low diffusion probabilities, SLC is better suited for larger diffusion probabilities, capturing broader network influence. To mitigate the sensitivity of centrality measures to diffusion probabilities, Ma et al. [16] proposed Laplacian centrality, which measured node influence by the energy change of a network after node removal. It can be easily computed using node degree, significantly reducing computational complexity and offering good scalability, though it only considered nodes and their first-order information. Zhu et al. [17] introduced an Improved Laplacian Centrality (ILC) based on the self-consistency concept, incorporating global topological structure information.
2.2. K-shell decomposition
Kitsak et al. [18] proposed the
To distinguish the importance of nodes within the same
Extensive numerical simulations have shown that in some networks, nodes with high
2.3. H-index
H-index is originally designed to gauge the impact of academic journals and researchers. Lü et al. [26] extended the H-index to measure node importance in networks. The H-index of node
where
2.4. K-truss
Cohen et al. [30] introduced the concept of K-truss decomposition for a given unweighted undirected network. Let
where
2.5. Structural hole
Yu et al. [32] introduced the concept of "structural hole" to identify key nodes in a network by defining a node influence matrix
where
where
In contrast, while the
2.6. Neighborhood similarity
In a network, two similar nodes are more likely to be interested in transmitting the same information, and the likelihood of information propagating through the edges between the nodes is higher. Wang et al. [38] defined the similarity between nodes
where
3. Eigenvector-Based Ranking Methods
Eigenvector-based methods evaluate node importance by considering both the number and influence of connections through eigenvector analysis and iterative computation as detailed in Table 5. These methods extend beyond simple neighbor counting by incorporating the significance of connected nodes. They are extensively used in social network analysis to identify influential entities, in web search algorithms for page ranking, and in biological networks to detect critical components. The key strength of these methods lies in their ability to capture the recursive nature of importance: a node is deemed important if it is connected to other important nodes. This property enables more accurate assessment of node significance compared to approaches based solely on local neighborhood information. Nevertheless, such methods entail several limitations, including high computational cost, sensitivity to parameter settings, and the necessity for cautious interpretation across diverse network contexts.
Comparison of eigenvector-based ranking methods
| Title | Related works | Advantages/Disadvantages |
| Eigenvector centrality | [43-49] | |
| Katz centrality | [50,51] | |
| PageRank algorithm | [52-56] | |
| Voting mechanism | [57-62,63] |
3.1. Eigenvector centrality
Eigenvector Centrality (EC) takes into account the importance of a node's neighbors [43,44]. It uses the eigenvectors and eigenvalues of the network's adjacency matrix to measure the importance of nodes. The main idea is to assume that the importance of node
where
To address eigenvector centrality's localization issue, which concentrates weight on a few nodes, Martin et al. [48] introduced a method based on a non-backtracking matrix. This method avoids localization while yielding similar results to eigenvector centrality in dense networks. Zhong et al. [49] combined Jaccard similarity with the dissimilarity between nodes and proposed the eigen-centrality from the differences and similarities of structure (ECDS) centrality method, which takes the weighted sum of the centralities of its neighboring nodes to form an iterative formula similar to the eigenvector centrality.
3.2. Katz centrality
Katz centrality [50] extended eigenvector centrality by adding a constant term to describe the importance of the central node itself. It is defined as:
where
3.3. Pagerank algorithm
Traditional ranking methods for webpages rely on "keyword density", but this can be undermined by "malicious keywords." Page et al. [52] proposed the core algorithm of Google's search engine, Pagerank. The value of node
where
where
To address the limitations of PageRank, such as its failure to incorporate node attributes or external information, Yang et al. [53] described the frequency and duration of contact between nodes in a directed weighted network to capture the importance of nodes based on their in-degrees and out-degrees. They proposed the Two-Way-PageRank method to identify important nodes in directed weighted networks. Hsu et al. [54] introduced the AttriRank model, which integrates node attribute similarity into the ranking process. This model utilizes random walks, capturing associations between nodes based on both network structure and attribute similarity. The random walk is framed as a Markov chain, with a transition matrix that balances information propagation across the network and node attributes. Building on this, Sheng et al. [55] proposed the Trust-PageRank (TPR) algorithm, which combines attribute similarity and trust values, defined through structural degree ratios. TPR effectively merges node attributes and network structure to refine node rankings. Su et al. [56] introduced a cascade failure and directionally weighted PageRank method tailored for power grid networks. This approach incorporates grid connectivity, electrical topology, and power flow direction, thus enhancing the grid's resilience by mitigating the impact of cascading failures.
3.4. Voting mechanism
To address the parameter adjustment issue in the PageRank algorithm, Lü et al. [57] introduced a background node
After traversing all the nodes in the network, the LR value is obtained. Compared to PageRank, LR has stronger robustness in resisting spammer attacks and random interference. Building on this, Li et al. [58] introduced the weight-LeaderRank algorithm for weighted networks, which modifies the standard random walk by incorporating a biased random walk. This adjustment ensures that neighboring nodes receive higher scores, thereby improving the identification of influential propagators. To address the issue of overlapping influence in methods such as PageRank, ClusterRank, and
Building on the information of node neighborhood within the network topology, Kumar et al. [60] proposed the NCVoteRank method, which adjusts the voting weights according to the core degree of neighboring nodes, adding flexibility to the voting framework. Sun et al. [61] enhanced this concept by introducing the weight-VoteRank method, which incorporates both the number of neighbors and edge weights, allowing for a more nuanced measure of node importance in weighted networks. Li et al. [62] further refined the VoteRank algorithm with the introduction of Linearity and Importance (DIL) [63]. This method initializes node scores and voting abilities based on local importance, and updates the voting capabilities of neighbors in each round. Through iterative voting, the Top-
4. Path-Based Ranking Methods
Path-based ranking methods assess node importance through the analysis of paths connecting nodes, taking into account their positions and roles within network connectivity and information dissemination. These methods characterize the global structure and connection patterns of networks by evaluating shortest paths, average distances, and random walk processes as detailed in Table 6. Applications include identifying intermediaries and pivotal communicators in social networks, locating critical hubs in transportation systems, and understanding material or information transfer mechanisms in biological networks. The primary advantage of these approaches lies in their capability to capture the global influence of nodes and highlight those that function as bridges or central connection points within the network. However, these methods are computationally intensive, particularly for large-scale networks, necessitating simplifications or approximations to ensure practical feasibility.
Comparison of path-based ranking methods
| Title | Related works | Advantages/Disadvantages |
| Betweenness centrality | [64-73] | |
| Closeness centrality | [74-78] | |
| Random walk | [79-81] |
4.1. Betweenness centrality
Freeman et al. [64] reviewed traditional centrality measures to determine the importance of nodes in social networks. Based on the connectivity between nodes, they introduced Betweenness Centrality (BC), which measures the importance of a node by counting the number of shortest paths that pass through the node. It is defined as:
where
where the network diameter is the maximum eccentricity value among all nodes in the network
To address the high time complexity of betweenness centrality, Song et al. [68] introduced load centrality (LC), which measures the change in network paths after node removal to assess the node's impact on connectivity. Ventresca et al. [69] developed the CNDP algorithm, which determines node connectivity and capacity based on path length, the number of paths, and network scale. Many real-world networks display hierarchical and modular structures. Zhang et al. [70] proposed a multi-scale node importance metric using a kernel function, where bandwidth determines the range of interactions. Small bandwidth captures short-range interactions, while large bandwidth highlights long-range interactions, offering insights into node influence across different scales during dynamic processes. In power systems, Yang et al. [71] introduced the Electric Observability Capability Index (EOCI) and the Electrical Dynamic Characteristics Index (EkI) to identify critical nodes influencing power system observability and controllability. Kianian et al. [72] used degrees and independent influence paths to approximate influence propagation, reducing computational cost by pruning insignificant nodes. Xiao et al. [73] applied Local Average Shortest Path with extended Neighborhood concept (LASPN) theory to identify critical nodes, combining local average shortest paths and extended neighborhoods for efficient processing in large-scale networks.
4.2. Closeness centrality
To address the interference of special values in paths, Freeman et al. [74] introduced Closeness Centrality by calculating the average distance of a node to all other nodes in the network. The smaller the average shortest distance
In a connected network, the smaller the average distance between a node and all other nodes in the network, the larger the closeness centrality of that node. This can be understood as determining the importance of a node by the average transmission time of information in the network. To improve closeness centrality for network efficiency, Latora et al. [75] extended betweenness centrality to disconnected networks and proposed the EFF index. However, this approach requires calculating the distances between all node pairs, which is computationally expensive for large networks. To reduce this complexity, Salavati et al. [76] applied the Louvain community detection algorithm to identify network communities. By maximizing modularity, they extracted community structures and selected key nodes using betweenness centrality. They also introduced a method to identify gateway nodes linking communities and reduced computation by focusing on a subset of special nodes. Okamoto et al. [77] proposed the RAND algorithm to estimate average node distances efficiently. It selects top candidate nodes based on these estimates and ranks them precisely, balancing computational efficiency with accuracy. Sheng et al. [78] introduced the global and local structure(GLS) method, which calculates the influence of nodes by considering common neighbors and structural characteristics. This method combines local and global structural influence based on their information exchange capabilities.
4.3. Random walk
Currently, methods for identifying key nodes based on heuristic centrality measures are used only for specific network topologies or unique dynamic models for analysis and demonstration. Iannelli et al. [79] proposed a method based on the random walk effective distance
where
5. Control-Optimization Based Ranking Methods
Control optimization-based ranking methods identify key nodes by employing network control theory and optimization techniques. These methods aim to characterize the influence of nodes on network dynamics, controllability, and connectivity, offering valuable insights for applications in security, robustness enhancement, and regulation of dynamic processes as detailed in Table 7. In security, they help detect vulnerable links and improve resilience against attacks. In infrastructure networks, they aid in designing effective control strategies. The primary advantage of these approaches lies in their ability to offer a dynamic and interactive perspective on node importance, revealing the impact of individual nodes on overall network functionality and stability. However, these methods face challenges such as high computational complexity and control and optimization theory.
Comparison of control optimization-based ranking methods
| Title | Related works | Advantages/Disadvantages |
| Network control | [82-107] | |
| Maximization of connected Component optimization | [108-121] | |
| Minimization of pair Connectivity optimization | [122-139] | |
| Minimum spanning tree | [140-145] | |
5.1. Network control
Existing research has highlighted the importance of specific nodes in regulating network dynamics and functionality. Li et al. [82] employed the Watts-Strogatz propagation model to explore spreading mechanisms in small-world networks. Their analysis of delayed control propagation with linear and nonlinear feedback controllers demonstrated how network parameters influence stability and oscillatory behavior. Ghosh et al. [83] emphasized the critical role of dynamic synchronization in maintaining global network coherence. Their findings showed that proper weighting procedures significantly enhance synchronization in static complex networks, with key nodes exerting disproportionate influence on system stability. D'Souza et al. [84] proposed a framework for network control that integrates node dynamics and macroscopic network properties, refining control strategies through higher-order interactions. Liu et al. [85] developed analytical tools to assess the controllability of arbitrary directed networks, establishing that the number of driver nodes required for full control is primarily dictated by the network's degree distribution. Their work uncovered a fundamental relationship between network structure and control feasibility: sparse, heterogeneous networks are the most difficult to control, whereas dense, homogeneous networks require fewer driver nodes. The controllability of a system governed by linear time-invariant dynamics:
where
which seeks the control input
The eigenvalues of the Laplacian matrix play a critical role in pinning control and network controllability, directly influencing the selection of optimal driver nodes for synchronizing large-scale networks. Yu et al. [89] proposed a distributed adaptive strategy that adjusts coupling weights based on local node dynamics to achieve synchronization, later extending their work to establish synchronization criteria for various network topologies, including strongly and weakly connected graphs [90]. Ding et al. [91] demonstrated that denser and more homogeneous networks exhibit superior controllability, with controlled nodes typically having lower in-degree than the network average. Amani et al. [92] introduced the Eigenvalue Sensitivity Index (ESI), which ranks nodes using extremal Laplacian eigenvectors to estimate their importance in pinning control. They further developed a computationally efficient method based on sensitivity analysis of the Laplacian matrix to identify near-optimal driver nodes [93]. Liu et al. [94] evaluated pinning effectiveness via the smallest eigenvalue of the grounded Laplacian, linking controllability to network structure. Several optimization strategies have been investigated. Wang et al. [95] achieved full network control through structural perturbations using a single driver node. Bof et al. [96] showed that energy-efficient control depends on the left and right Perron eigenvectors of the network matrix. Zhou et al. [97] proposed the ControlRank metric, validating degree-based rankings in scale-free networks. Liu et al. [98] refined driver node selection by prioritizing nodes with the largest eigenvector components corresponding to the dominant Laplacian eigenvalue. Bomela et al. [99] applied the Moore–Penrose pseudoinverse of the Laplacian to identify Most Influential Nodes (MIN) in oscillatory networks. Recent studies have emphasized minimal intervention strategies. Jiang et al. [100] showed that large-scale synchronization can often be achieved with minimal control effort or higher-order interactions. Sun et al. [101] analyzed optimal control in reaction-diffusion networks, revealing the influence of topology and diffusion parameters on epidemic dynamics. Collectively, these works highlight the strong interdependence between spectral properties, network structure, and dynamic processes, underscoring the value of targeted interventions for achieving efficient and robust network control.
The contribution of network edges, including loops, to overall network dynamics is fundamentally governed by the eigenvector corresponding to the smallest nonzero eigenvalue of the Laplacian matrix, known as the Fiedler vector. The cumulative effect of all edges is encapsulated in the network's algebraic connectivity, which dictates synchronization and diffusion properties. Zhang et al. [102] analyzed the impact of adding feedback edges in directed acyclic graphs (DAGs) on consensus behavior in multi-agent systems. They identified disruptive feedback edges that degrade convergence speed and formulated a necessary and sufficient condition for their identification. Mo et al. [103] extended this by introducing a topology-based optimization framework for directed graphs, enabling the systematic selection of edges that enhance convergence. They demonstrated that in strongly connected weighted digraphs, the second smallest Laplacian eigenvalue remains real and established conditions for edge selection that improve consensus dynamics. Jiang et al. [104] proposed a method to assess the importance of loops in complex networks, ranking key loops based on their influence on the Fiedler value. Similarly, Cao et al. [105] developed a theoretical framework for synchronization acceleration by optimizing directed edge placement and weights. They derived a necessary and sufficient condition for selecting edges that enhance convergence, allowing efficient identification through Laplacian eigenspace computations. Zhang et al. [106] reaffirmed the existence of disruptive feedback edges in DAGs and explicitly constructed conditions for their identification. Gao et al. [107] further examined how weighted edge additions influence algebraic connectivity in directed graphs, proving that changes in Laplacian eigenvalues are localized within subgraphs containing the added edges. Their findings underscore the dependence of algebraic connectivity on edge weight, range, and distribution along network paths. These studies further reveal how interventions of network edges and cycles control dynamic behavior, highlighting the role of spectral properties in optimizing synchronization and controllability.
5.2. Maximization of connected component
In a network, there exists a set of important nodes that influence the network's robustness and connectivity. By removing these nodes or attacking the network, we can identify a critical set of nodes. Deleting this set of nodes can minimize or maximize the connectivity components (such as the largest connected component or node pair connectivity) in the remaining network, which is known as the Critical Nodes Deletion Problem. Aringhieri et al. [108] designed a general framework to address several classic critical node problems (CNPs), specifically: (1) Pairwise connectivity: Minimize the number of connected node pairs in the remaining network by deleting up to
Thulasiraman et al. [110] evaluated node value using cut vertices and edges for network diagnostics and security, employing link testing and node connection statistics. In protein interaction networks, Boginski et al. [111] aimed to identify key nodes by solving the Cardinally Constrained-CNDP (CC-CNDP), defined as minimizing the set of deleted nodes
where
Furthermore, Arulselvan et al. [113] proposed a risk management-based method to detect a set of nodes that, when deleted, cause the connectivity index of the resulting subgraph to fall below a threshold. This problem is defined as the cardinality-constrained critical node problem (CC-CNP) and modeled as an integer linear programming (ILP) problem, which is solved using a heuristic genetic algorithm. In social networks, there exists a set of
To address the high computational costs of greedy algorithms on large networks. Wang et al. [118] developed a community-based greedy algorithm using node edge weights for propagation speed, incorporating information diffusion for community detection and dynamic programming to identify influential nodes. Lam et al. [119] used simulations in the NetLogo multi-agent environment to identify critical infrastructure components, assessing node failure impacts via attack scenarios and the giant component metric. Ventresca et al. [120] proposed a depth-first search method with
5.3. Minimization of pair connectivity
To minimize pairwise connectivity by removing a fixed number of nodes, Di Summa et al. [122] proposed an ILP model with non-polynomial constraints, as follows:
where constraint (1) limits the number of deletions to
In small-scale networks, heuristic algorithms are commonly used to identify critical nodes that impact connectivity. Arulselvan et al. [123] employed a combinatorial heuristic integrating integer programming to efficiently minimize pairwise connectivity by selectively removing nodes. Similarly, Shen et al. [124] introduced an adaptive algorithm that identifies critical nodes without requiring full recalculations after topological changes, enhancing efficiency and response speed. Ventresca et al. [125] developed an approximation algorithm for undirected, unweighted graphs, combining ILP with randomized rounding. By handling vertex and triangle inequality constraints separately, their method effectively reduces subgraph connectivity while capping the number of deleted nodes at
To address the complexity and accuracy balance in identifying critical nodes in large-scale networks, Pullan et al. [128] proposed a Greedy Randomized Adaptive Search Procedure (GRASP) with Path Relinking. The algorithm introduces an evolutionary path relinking mechanism during the path search process. It was shown that the GRASP with Path Relinking is more efficient than algorithms such as neighborhood search and simulated annealing in solving the CNDP. Addis et al. [129] proposed a "hybrid" heuristic algorithm based on the basic greedy algorithm. By combining two greedy rules, "node addition and deletion, " the algorithm addresses the CNDP problem of removing K nodes to minimize the residual network connectivity. The algorithm alternates between node addition and deletion operations in the feasible solution space, effectively avoiding local optimal solutions. Chen et al. [130] focused on the critical node fragmentation problem in weighted networks. They proposed a non-convex mixed-integer quadratic programming (MIQP) model for undirected weighted networks. A greedy algorithm is employed to approximate the optimal solution, and the algorithm iteratively selects K critical nodes (Critical Node Set, CNS) that cause the most significant decrease in network pairwise connectivity, identifying the critical node combination that maximizes network performance.
To mitigate the high computational complexity of the critical node deletion problem, Ventresca et al. [131] employed a population-based incremental learning algorithm combined with combinatorial simulated annealing to detect critical nodes, leveraging depth-first search to minimize pairwise connectivity. For dense networks where pairwise connectivity computations remain
Recent studies have focused on optimizing critical node detection and network robustness under adversarial conditions. Zhang et al. [135] formulated the Critical Node Detection problem in interdependent networks as a Bi-objective Optimization Problem (BICND) and designed a method integrating single-layer and multi-layer network transfer. This approach reduced algorithmic complexity while enhancing accuracy in identifying critical nodes. Fortz et al. [136] proposed a compact integer programming formulation for the node attack optimization problem using pseudo-components within a two-level model, addressing performance limitations of prior iterative methods. Jiang et al. [137] introduced the EBC method, leveraging loop structures to assess network robustness against targeted attacks and precisely identify edges critical to resilience. Kouam et al. [138] simulated adversarial behavior to evaluate node influence, modeling attack progression toward the target. Zhou et al. [139] examined the NP-hard nature of the protection node problem and optimized key node selection via an influence redundancy mechanism. By minimizing the adjacency matrix's spectral radius after key node removal, they demonstrated submodular properties in the objective function and achieved an approximation ratio of
5.4. Minimum spanning tree
Chen et al. [140] evaluated the relative importance of two sets of nodes by comparing the number of spanning trees in the remaining network after node deletion. The fewer the number of spanning trees in the corresponding network after removing a set of nodes and their associated edges, the more important that set of nodes is considered to be. This method is simple to compute and provides a more accurate reflection of node importance. When the network size is large, the algorithm complexity of solving the problem increases. To improve the solving efficiency, the objective function is decomposed into multiple subproblems. Di Summa et al. [141] studied the minimization of the number of connected node pairs in the remaining graph after node deletion, designing the network as a tree structure to extend the solution to the CNP subproblem. Hermelin et al. [142] discussed the Critical Node Cut (CNC) problem: given a graph
Regarding the linear framework of the network traffic and connectivity constraint problem, Addis et al. [143] focused on the combinatorial problem of node deletion. They provided a dynamic programming recursive method for solving the tree decomposition problem based on graphs, which can solve the CNP problem in polynomial time on general and special graphs (split graphs, bipartite graphs, and the complements of bipartite graphs). Aringhieri et al. [144] proposed two metaheuristics based on iterative local search and variable neighborhood search frameworks to achieve maximum fragmentation of graphs. They designed two computationally efficient neighborhoods, evaluated different exploration strategies, and found that the improved strategy produced a large number of new best solutions. Using betweenness centrality, they were able to reduce the runtime without compromising the solution quality. Wang et al. [145] combined the advantages of the minimum spanning tree (MST) structure and the minimum connected dominating set (MCDS) properties, introducing edge weight normalization to calculate the connection strength between nodes. They defined the MCDS efficiency (SEW) and excluded non-critical endpoints, further distinguishing node importance.
6. Machine Learning-based Ranking Methods
Machine learning-based ranking methods have transformed the identification of influential nodes in complex networks by leveraging advanced techniques such as information entropy, clustering coefficients, graph neural networks, and reinforcement learning to capture intricate structural patterns and relationships. These methods find applications in diverse domains, including social network analysis, information diffusion, network security, and infrastructure management as detailed in Table 8. Compared to traditional approaches, machine learning enables more accurate and nuanced assessment of node importance, while also being capable of handling large-scale networks and capturing nonlinear dependencies that conventional methods may overlook. However, these approaches introduce new challenges, such as the requirement for extensive training data, dependence on model design and generalization capability, and limitations in computational resources.
Comparison of machine learning-based ranking methods
| Title | Related works | Advantages/Disadvantages |
| Information entropy | [146-156] | |
| Clustering coefficient | [157-164] | |
| Graph conventional network | [168,169,171,172] | |
| Graph embeddings | [173-180] | |
| Graph attention network | [181-187] | |
| Graph contrast learning | [188-190] | |
| Graph neural networks | [191-195] | |
| Reinforcement learning | [196-208] |
6.1. Information entropy
Entropy-based measures quantify the uncertainty or diversity in information propagation and have been widely applied to assess node centrality. Nikolaev et al. [146] introduced entropy centrality, which evaluates a node's potential for dissemination via discrete Markov processes. Specifically, a node's entropy centrality is defined as
The term
Other studies have leveraged entropy in various contexts. Nitt et al. [148] proposed a degree centrality mapping entropy (ME) to identify critical nodes through local interactions. Similarly, Fu et al. [149] defined global node information entropy based on the
Network entropy is typically used to characterize the amount of information encoded in a network structure. Based on the assumption that removing more important nodes may lead to greater structural changes, Ai et al. [153] defined node importance as the change in network entropy before and after its removal. Wu et al. [154] proposed
6.2. Clustering coefficient
The clustering coefficient is a crucial factor in determining the local influence of nodes. Chen et al. [157] combined the number of node neighbors, the influence of neighbor nodes, and the clustering coefficient to propose the ClusterRank method for local node importance ranking, specifically defined as:
The local clustering coefficient
To overcome the limitations of undirected graphs in representing conditional independence, Dablander et al. [161] developed a causal framework based on DAGs. Assuming the Markov condition holds, they introduced the concept of "faithfulness" to ensure that the DAG accurately captures variable independencies. They further quantified causal impacts using Average Causal Effect (ACE) and Kullback-Leibler (KL) divergence. Their findings indicate that eigenvector centrality outperforms traditional metrics in predicting the causal influence of nodes within such networks. Liu et al. [162] integrated latent group information in power systems by developing the Group-Driven Framework for Identifying Critical Nodes (GDF-ICN) algorithm. This framework combines the structural and operational states of power systems with node group affiliations, iteratively optimizing group partitions around critical nodes. A fuzzy closeness metric is incorporated to enhance the description of group structure, while leveraging clustering effects to bolster the robustness of critical node identification. Wang et al. [163] proposed an influential node evaluation algorithm grounded in information entropy theory. By defining metrics based on the number of triangles and edge weights, they introduced the concept of edge entropy weights - capturing differences in edge weights and their influence on neighboring nodes. This approach integrates k-core metrics to characterize local node influence, with higher entropy values indicating greater complexity and overall influence within the network. Zhang et al. [164] presented a novel method focused on maximizing the range of influence. Their approach constructs an information transmission probability matrix, which quantifies the probability of information transfer between arbitrary node pairs.
6.3. Machine learning
Machine learning offers a powerful framework for identifying influential nodes by reframing the problem as a regression task. These methods leverage supervised learning algorithms trained on node labels derived from epidemic model simulations and traditional centrality measures, capturing complex relationships between network structure and propagation potential. Zhao et al. [165] employed information infection vectors to encode topological characteristics and infection dynamics across diverse propagation scenarios. Using node labels obtained from susceptible-infected-recovered (SIR) model simulations, they trained classifiers and regressors - including Naïve Bayes, decision trees, random forests, Support Vector Machines (SVM), k-Nearest Neighbors (KNN), logistic regression, and Multilayer Perceptron (MLP) - to predict node importance. Yang et al. [166] introduced a network-aware local centrality index (NLC) that integrates topology with node embeddings. Applying DeepWalk to project network structures into a low-dimensional space, they incorporated third-order neighborhood information to refine influence estimation. Rezaei et al. [167] further advanced this paradigm by engineering collective node features - spanning connectivity, degree, and coreness measures - and training an SVR model with an RBF kernel, demonstrating the efficacy of tailored feature representations in predicting node influence. However, existing models face limitations in feature representation and scalability. The development of deep learning and graph neural network approaches provides a powerful new framework for analyzing node attributes and quantifying influence.
Graph conventional network: Zhao et al. [168] pioneered the deep learning framework InfGCN based on graph convolutional networks (GCN). InfGCN constructs node structural features - including degree, closeness, betweenness, and clustering coefficient - and builds a fixed neighbor network via BFS. By training with actual infection rate vectors from SIR model simulations, InfGCN minimizes the error between predicted and actual infection rates to accurately estimate node influence. Similarly, Kumar et al. [169] adopted the Stru2vec node embedding algorithm [170] along with a message-passing neural network (MPNN) to process node embeddings and SIR-based influence vectors, identifying the Top-
Graph embeddings: Wei et al. [173] focused on reducing computational complexity. They selected candidate nodes based on shell connections and topological features, then used deep learning to generate low-dimensional vectors for calculating propagation dependency. Keikha et al. [174] proposed Deep learning for Information Maximization(DeepIM) (an algorithm using deep learning techniques for influence maximization problem), which extracts global and local structural features via CARE, constructs custom paths, and employs Word2vec to learn node feature vectors for measuring user relevance. Bouyer et al. [175] presented Embedding Technique for Influence Maximization (ETIM), combining shell decomposition, graph embedding, and local structure features to decrease computation. Wu et al. [176] constructed node features using rule-equivalent similarity and Graph Convolutional Networks. Ahmad et al. [177] proposed frameworks (LCNN) that merge CNNs with local node representations and multi-scale metrics. Rashid et al. [178] introduced the GN model, integrating deep learning and probabilistic properties via Graph Convolutional Networks to detect overlapping communities and key nodes. Xiong et al. [179] proposed the AGNN algorithm, fusing autoencoders with GNNs to generate topological feature embeddings through GCN and optimizing the ranking prediction model using listMLE. Yu et al. [180] developed methods region-based CNNs (RCNN) that integrate GCNs and CNN-based adjacency features for effective critical node detection.
Graph attention network: Most existing node importance assessments in knowledge graphs fail to fully utilize available information and cannot capture node relationships and attribute features. To address this, Park et al. [181] developed graph estimation node importance (GENI) that uses predicate-aware attention mechanisms and flexible centrality adjustments to aggregate node and neighbor information across multiple GNN layers. It updates node embeddings via an aggregation function with a nonlinear transformation and maps these to importance scores using a scoring neural network. GENI also incorporates node in-degree centrality to adjust importance estimates. Define a GNN with
where
Graph contrast learning: Recent advancements in contrastive learning have improved node importance estimation by integrating multiview representations and attention mechanisms. Liu et al. [188] addressed the limitations of single-graph models by introducing the Multiview Contrastive Representation Learning (MCRL) framework, which employs dual graph encoders and contrastive learning to derive multi-perspective node representations. This approach enhances the estimation of node importance by comparing embeddings generated through GCN and graph attention mechanisms (GAT). By incorporating a positive-negative sampling strategy, MCRL identifies nodes that maintain both high similarity and distinctiveness across multiple structural views - key indicators of importance. Building on this concept, Zhang et al. [189] developed the Label-Contrastive Pretraining (LICAP) model, which employs hierarchical sampling to prioritize top-ranked nodes. LICAP utilizes a Predicate-Aware Graph Attention Network (PreGAT) to refine node embeddings, ensuring robust differentiation between influential and peripheral nodes. Meanwhile, Shu et al. [190] proposed node importance evaluation in heterogeneous network based on attention mechanism and graph contrastive learning method (AGCL), a contrastive learning framework for heterogeneous networks that leverages attention mechanisms to quantify both local and global node importance. By extracting structural features through contrastive learning and computing importance weights via attention mechanisms, AGCL offers a comprehensive approach to evaluating node influence in complex networks.
Graph neural networks: Huang et al. [191] introduced HIN Importance Value Estimation Network (HIVEN), a GNN-based framework designed for heterogeneous information networks (HINs). By integrating a heterogeneous information aggregator and a meta-path-based mechanism, HIVEN effectively captures the structural and relational intricacies of HINs, improving both accuracy and efficiency in node ranking. Building on structural knowledge integration, Chen et al. [192] developed SKES (Deep Structural Knowledge Exploitation and Synergy), which incorporates node centrality and similarity metrics to learn high-dimensional feature distributions. SKES refines importance predictions using optimal transport theory, enabling precise characterization of node significance within heterogeneous graphs. Similarly, Lin et al. [193] leveraged Large Language Models (LLMs) in the LLMs Empowered Node Importance Estimation (LENIE) framework to enhance semantic representations in knowledge graphs. By employing a clustering-based triplet sampling strategy and node-specific adaptive prompts, LENIE enriches node embeddings, thereby improving the initialization of node importance estimation models. Higher-order network structures have also been incorporated into learning-based ranking methods. Zhao et al. [194] proposed HONNMA, a high-order neural network framework that employs motif attention to capture complex topological dependencies. This model encodes interactions through a weighted motif adjacency matrix and refines node embeddings using a skip-connected architecture, allowing for more robust node importance estimation. Addressing the Critical Node Detection Problem, Michos et al. [195] applied Hopfield Neural Networks (HNN) to optimize network resilience. By reformulating as an energy minimization task, their approach identifies critical nodes by converging toward stable network states with minimal energy.
6.4. Reinforcement learning
Reinforcement learning influences key node selection by using rewards and penalties to guide the process, treating the impact of nodes - whether on overall network performance or individual propagation capability - as the value incentive. In this framework, the objective is to identify a set of important nodes by either maximizing or minimizing a value-based objective function. To tackle high time complexity in critical node identification, Fan et al. [196] proposed the FInding key players in complex Networks through DEep Reinforcement learning (FINDER) framework. It minimizes the accumulated normalized connectivity (ANC) through a node deletion strategy. The ANC is defined as:
where
To address information diffusion features in node importance analysis, several studies have integrated reinforcement learning with graph-based methods. Jaques et al. [198] used a multi-agent reinforcement learning framework with counterfactual reasoning and measures such as KL divergence to assess the impact of alternative actions on other agents, identifying influential nodes. Chen et al. [199] proposed DeepELE, combining graph embeddings with reinforcement learning in a susceptible-infected-susceptible (SIS) model. Each node is assigned a diffusion weight, and a state–action value function evaluates the network-wide infection impact after node removal, selecting key nodes by minimizing an objective function. Li et al. [200] introduced Deep learnIng-baSed influenCe maximization (DISCO), combining network embedding with deep reinforcement learning for various node-related problems. Chen et al. [201] developed ToupleGDD, an end-to-end deep reinforcement learning framework coupling three graph neural networks with a double deep Q-network for parameter learning, addressing IM while overcoming limitations such as narrow IM formulations and low scalability. Ling et al. [202] introduced DeepIM, generating latent representations of seed sets in a data-driven manner to capture diverse information diffusion patterns, and designing a novel objective function for optimal seed sets under flexible node centrality constraints. Li et al. [203] presented deeP reInforcement leArning-based iNfluence maximization (PIANO), merging deep reinforcement learning with network embedding to estimate node influence, providing a pre-trained model pool for direct application. Uthayasuriyan et al. [204] introduced Differential Evolution-Reinforcement Learning (DERL), integrating differential evolution with Deep Q Network (DQN)-based reinforcement learning, and Li et al. [205] proposed AdaRisk, a risk-adaptive deep reinforcement learning framework for detecting fragile nodes in uncertain graphs. Xu et al. [206] developed HEDRL-IM, reformulating IM in hypergraphs as a network weight optimization task solved via deep Q-networks, integrating evolutionary algorithms and propagation simulation. Zhu et al. [207] proposed BiGDN, employing bidirectional neighborhood aggregation and integrating deep reinforcement learning with multi-head attention for robust node representations. Ahmad et al. [208] developed CoreQ, using K-core decomposition and Q-learning to identify candidate seed nodes.
7. Comprehensive Index Based Ranking Methods
Comprehensive index ranking methods evaluate node importance by integrating multiple network attributes and advanced analytical techniques. These methods combine various centrality measures, gravity models, and decision-making frameworks to overcome the limitations of single-indicator approaches and provide a more holistic assessment of node significance in complex networks. These indicators are widely applied across domains such as social network analysis, biological networks, transportation systems, and infrastructure management. The primary advantage of these methods is their ability to incorporate diverse structural and functional indicators, thereby offering a more nuanced characterization of node importance. However, they also introduce challenges, including increased computational complexity and careful selection and integration of relevant indicators.
7.1. Gravity formula
The law of universal gravitation has been innovatively applied in network science. By defining the gravitational constant multiplied by the product of the masses of two nodes divided by the square of the distance between the nodes, the centrality and statistical indicators of nodes are considered as "mass", and the shortest distance between nodes is used as the distance, thus constructing a new framework for measuring node importance. Ma et al. [209] combined the K-shell index of nodes and the shortest path between nodes to identify important nodes in the network through the gravitational calculation formula, defining the importance of node
where
In addition, Li et al. [211] proposed the Local Gravity Model (LGM), which extends the basic gravity model to include neighborhood information; nodes surrounded by neighbors with high
A single centrality measure often fails to fully capture the importance of nodes in a network. To address this, researchers have introduced weighted models based on gravitational principles, incorporating multiple attributes to assess node influence. Wang et al. [217] enhanced the gravity model method by integrating
To mitigate the high computational cost of shortest path calculations, researchers have proposed alternative approaches that approximate or replace shortest path metrics with more efficient methods. Zhao et al. [224] employed random walks to estimate node distances, using degree centrality as a proxy for node influence. Extending this idea, Zhao et al. [225] introduced the Network Embedding and Gravity Model (NEGM), which replaces shortest path lengths with Euclidean distances derived from Node2Vec embeddings. Similarly, Shang et al. [226] defined a probabilistic distance using Markov chain-based transition probabilities, capturing latent inter-node relationships without computing exact shortest paths. Beyond shortest path approximations, alternative gravity-based models have been proposed. Curado et al. [227] introduced a method leveraging return-based random walks and effective distance to capture both static and dynamic network topologies. Yang et al. [228] refined interaction range definitions by incorporating an adaptive truncation radius and considering all-channel paths instead of shortest path constraints. Chen et al. [229] proposed the Degree Centrality Gravity Model (DCGM) model, integrating degree and average neighbor degree to enhance influence estimation. Further advancements address asymmetric interactions and multilayer structures. Meng et al. [230] developed the Asymmetric Attraction Model (AAM), transforming adjacency matrices into asymmetric attraction matrices to capture directional dependencies. Xu et al. [231] introduced the communicability-based adaptive gravity model (CAGM), incorporating influence probability,
7.2. Multiple metrics
To address challenges in identifying critical nodes arising from varied network structures and densities, researchers have developed composite centrality measures that integrate multiple metrics. For instance, Comin et al. [235] proposed a comprehensive centrality index that balances global and local characteristics by analyzing three different information propagation strategies. De Arruda et al. [236] further explored dynamic propagation by proposing the Random Walk Accessibility (RWA) expansion indicator, based on nine centrality measures, to assess the ability of nodes to spread information in both spatial and non-spatial networks. To integrate multiple centrality measures, Hu et al. [237] adopted linear discriminant analysis to integrate eigenvector, betweenness, closeness, degree centrality, and mutual information, developing a multi-metric evaluation algorithm. Hu et al. [238] then proposed the node importance contribution correlation matrix (NICCM) method, constructing a contribution matrix that defines importance by combining efficiency with weighted contributions.
Several studies have integrated multiple centrality measures to enhance prediction accuracy. Bucur et al. [239] combined statistical classifiers into composite metrics, demonstrating high predictive power in SIR epidemic models. Wei et al. [240] developed a heterogeneous mean-field model incorporating betweenness, degree, H-index, and core degree, showing that betweenness-based immunization strategies are effective in BA networks, whereas degree-based strategies perform well in real networks. An et al. [241] introduced the DIRCI method, leveraging dynamic influence scope, network layer centrality, and community centrality for critical node identification in multilayer networks. Wu et al. [242] proposed radiation centrality, which models information dissipation using attenuation and scattering theories. Other approaches combine local and global structural features. Cao et al. [243] introduced INLGC, integrating local network constraint coefficients with global community structure. Kopsidas et al. [244] merged centrality measures from different transport networks to assess metro station criticality. Wang et al. [245] proposed a multi-factor information matrix centrality algorithm, incorporating node influence, neighbor influence, and feedback-based mutual influence. Lei et al. [246] developed the Weighted Information Index (WII), which utilizes second-order neighbor information to construct an information distribution vector. Ullah et al. [247] introduced NPIC, integrating neighborhood and path information, while Zhang et al. [248] employed the Comprehensive Voting Ranking (CVR) algorithm, incorporating mutual information and k-center clustering to identify critical nodes in urban rail networks. Several iterative and hybrid models have also been proposed. Lee et al. [249] developed the Balanced Iterative Influence (BII) algorithm, iteratively combining local structural information with global influence. Esfandiari et al. [250] introduced HNPR, which integrates
To address the challenge of distinguishing nodes within the same
7.3. Topsis and entropy-weight
The TOPSIS method integrates multiple centrality metrics, offering a comprehensive and objective approach to evaluate node importance. Du et al. [268] proposed a new method for assessing node importance in complex networks using the TOPSIS method. A decision matrix
where
The entropy weight method and empowerment method enhance the highest attribute in the comprehensive evaluation system, increasing the distinction of relative tightness. Chen et al. [273] introduced an adjustable TOPSIS method to address the entropy weight method's tendency to overemphasize attributes with high data diversity. This method incorporates a weight coefficient to modulate the influence of entropy weights on the evaluation outcomes. Ishfaq et al. [274] employed the entropy weight technique to assign objective weights to each criterion and then applied TOPSIS to rank nodes. Yang et al. [275] proposed a local centrality indicator that incorporates multi-layer neighbor and clustering coefficient information. When combined with grey relational analysis (GRA) and the SIR model, this indicator more accurately identifies key nodes compared to traditional weighted TOPSIS. Vega-Oliveros et al. [276] introduced the multi-centrality index (MCI) for document keyword extraction by optimizing the combination of centrality indicators. Lu et al. [277] used relative entropy and gray relational degree to improve node evaluation in power networks. Zhang et al. [278] proposed a Multi-attribute Critic Network Decision Indicator (MCNDI) that integrates the H-index, closeness centrality, and other metrics using the objective CRITIC method for weighting. Ju et al. [279] introduced the Multi-Criteria Compromise Ranking Method (VIKOR) combined multiple rail transit networks into a multi-layer regional network, determined centrality criterion weights using an objective method.
8. Information Propagation Based Ranking Methods
Ranking methods based on information propagation assess node importance by simulating and analyzing the spread of information or disease across the static network as illustrated in Table 9. These methods offer valuable insights into dynamic spreading processes and are widely applied in social network analysis, public health disease control, and marketing strategies. Their main advantage lies in capturing both structural and dynamic aspects of diffusion, enabling a more realistic evaluation of node information maximization. However, they also face several challenges, including the difficulty of accurately modeling propagation dynamics, high computational demands for large-scale networks, and the need for domain-specific knowledge to interpret results effectively.
Comparison of comprehensive index-based and information propagation based ranking methods
| Title | Related works | Advantages/Disadvantages |
| Gravity formula | [209-234] | |
| Topsis and entropy-weight multiple metrics | [235-255,257-259,261-279] | |
| Information propagation method | [280-309] |
8.1. Diffusion model
Diffusion-based ranking methods assess node influence by modeling information or disease spread. Macdonald et al. [280] applied the SIR model to compare centrality metrics, demonstrating that eigenvector centrality effectively identifies high-impact spreaders above a critical infection threshold. Borgatti et al. [281] introduced the KPP-POS and KPP-NEG algorithms: KPP-POS optimizes information flow by maximizing average diffusion efficiency, while KPP-NEG disrupts network connectivity by removing key nodes, enhancing influence identification for targeted dissemination. Zhuge et al. [282] proposed Topological Centrality (TC), iteratively updating node and edge weights to quantify influence, with a stable weight of 1 indicating centrality. Aral et al. [283] applied randomized experiments and a continuous-time proportional hazards model to distinguish individual influence from peer susceptibility. Addressing location-aware IM, Li et al. [284] developed approximation-ratio greedy algorithms: a boundary greedy method leveraging upper and lower bounds for Top-
To overcome the limitations of traditional centrality metrics in assessing the spreading capability of non-topologically dominant nodes, Lawyer et al. [285] introduced the Expected Force (EXP) metric, which incorporates entropy to model the distribution of infectiousness across multiple propagation rounds. Similarly, Chen et al. [286] proposed three diffusion-based indicators - NEGD, diffusion speed, and diffusion scale - where NEGD, defined as the ratio of Expected Geodesic Distance (EGD) to Largest Geodesic Distance (LGD), quantifies overall propagation efficiency. Although these methods effectively identify influential nodes within local neighborhoods, they do not guarantee global optimality. Robinaugh et al. [287] improved influence estimation by introducing single-step and multi-step expected impact measures for analyzing psychopathology networks. Bozorgi et al. [288] proposed the INCIM algorithm, which combines local propagation dynamics with global network structure to evaluate both inter- and intra-community influence under the linear threshold model. Meanwhile, Holme et al. [289] investigated outbreak size, vaccination effects, and information diffusion using SIR simulations. Collectively, these diffusion-based approaches simulate the spread of information or disease to assess node influence, integrating both local and global network characteristics to offer practical solutions for identifying critical nodes in diverse network environments.
Recent advances further enhance influence estimation. Yin et al. [290] leveraged Compressed Sensing Theory (CST) to frame node identification as sparse signal reconstruction, applying the SIR model for efficient target detection. He et al. [291] proposed the Two-stage Iterative Framework for the Influence Maximization in social networks (TIFIM), combining descending iteration and top-advantage metrics for seed node selection. Tulu et al. [292] developed the Node Willingness and Influence (NWI) algorithm, integrating network structure and interaction frequency for key spreader detection. Zhong et al. [293] introduced the Improved Information Entropy (IIE) method, leveraging higher-order neighborhoods and weighted entropy to refine node importance. Li et al. [294] employed a Spearman-like correlation to enhance ranking precision, outperforming degree and betweenness centrality. Gong et al. [295] proposed the Probability-Driven Structure-Aware (PDSA) algorithm, which updates influence estimates via graph traversal in the IC model. Wang et al. [296] introduced the HGIM method, constructing a heterogeneous propagation graph to integrate topology with diffusion cascades. To model dynamic influence, Mohammadi et al. [297] proposed the Two-Sided Sign-Aware Matching (TSM) framework, incorporating trust and reciprocity in signed networks. Wang et al. [298] introduced the Dynamic Propagation Probability (DPP) model, redefining neighbor influence within a three-hop neighborhood. Xu et al. [299] developed the Local Propagation Probability (LPP) model, integrating hierarchical propagation influence across different orders.
For large-scale networks, Ai et al. [300] proposed the spreading probability centrality (SPC) method, which balances network connectivity with propagation precision by defining infection probabilities within a truncated radius. Zareie et al. [301] optimized key node selection using the Gray-golf algorithm, incorporating second-order neighbor effects for propagation efficiency. Chen et al. [302] introduced the Dynamic Influence Seed Selection (DYISSE) method, integrating two-hop triangular influence measures for robust diffusion estimation. Fink et al. [303] introduced virus centrality, leveraging weighted directed networks to estimate propagation potential. Sun et al. [304] further refined IDME by integrating neighborhood similarity and centrality. Ullah et al. [305] proposed the Local Structure System (LSS), which incorporates
8.2. Dynamical sensitivity
Liu et al. [307] have proposed the dynamic sensitive centrality (DSC) by integrating topological features and dynamic characteristics, considering a discrete time spreading model in which an infected node will infect its neighbors with a spreading rate
Define
9. High-order Networks Based Ranking Methods
Unlike traditional pairwise connections as Graph in Figure 2A, high-order networks, such as simplicial complexes and hypergraphs as shown in Figure 2B and C. Centrality measures typically used in conventional networks can be extended by integrating higher-order relationships, leading to the development of novel node importance metrics. Recent advancements in hypergraph-based ranking methods have improved node importance estimation by integrating higher-order relationships. Kapoor et al. [310] extended degree centrality to hypergraphs, defining weighted degree centrality as the sum of weights of hyperedges connecting a node to others. Specifically, given a hypergraph
where
In terms of hypergraph eigenvector centrality, Benson et al. [316] extended eigenvector centrality to uniform hypergraphs using tensor Perron-Frobenius theory. Zhao et al. [317] introduced higher-order centrality measures incorporating low-order network metrics. These metrics incorporate low-order network metrics to more accurately assess the relative importance of clusters in higher-order structures. Li et al. [318] proposed an electrostatic field-based algorithm to identify seed node sets in hypergraphs. Xie et al. [319] introduced Local gravity-based centrality in hypergraphs(LHGC), which incorporates node degree and higher-order distance in a gravitational model. The lack of research on higher-order relationships in dynamic networks has been addressed by Zhao et al. [320] developed centrality matrices for Pagerank, Hub, and Authority by adjusting weights of network motifs at different orders.
Beyond binary network models, simplicial complexes, composed of
10. Dynamic Networks Based Ranking methods
Recent research has focused on developing ranking methods for dynamic networks [Figure 2D] to better capture the evolving nature of node interactions and improve node importance estimation. Kim et al. [327] introduced the time-ordered graph to simplify dynamic networks into static networks of directed flow. They expanded traditional centrality measures, such as degree, betweenness, and closeness to dynamic graphs using the following definitions:
where
In the realm of multilayer temporal networks, Lü et al. [330] developed the ECMSim method, utilizing a fourth-order tensor to capture node similarity and PageRank for tensor-based networks. They further refined this approach with Multilayer temporal eigenvector centrality based on cosine similarity index (MTEIGBC) and Multilayer temporal PageRank centrality based on cosine similarity index (MTPRBC) centralities [331], which employ cosine similarity to rank nodes across multiple dimensions including layers and timestamps. Expanding upon these concepts, Lü et al. [332] extend the classical HITS to multilayer temporal networks as MT-HITS centrality. This method incorporates inter-layer similarity coefficients and solves tensor equations to define centrality vectors across multiple dimensions. Bi et al. [333] adapted the gravitational model to dynamic networks through the Temporal Gravity Model (TGM). TGM defines temporal distance based on both network structure and temporal order, integrating static centrality measures with their dynamic extensions.
To address the limitations of fixed constants in multilayer coupled networks, Jiang et al. [334] developed the enhanced similarity index (ESI) to assess interlayer coupling in multilayer networks, moving beyond fixed constants. By integrating node neighbors across two time layers and introducing an attenuation factor, they created a decay-based super adjacency matrix (ASAM) to identify key node pairs affecting the largest connected component in temporal networks. Taylor et al. [335] integrated centrality matrices from different network layers into a joint
To track influential nodes in dynamic social networks, Song et al. [339] framed the problem as IM in dynamic environments. They proposed an upper-limit exchange greedy algorithm, which optimizes influence coverage by replacing nodes in the previously identified set of influential nodes, thus enabling efficient continuous tracking as the network evolves. Building on these ideas, Huang et al. [340] extended dynamic sensitivity to temporal networks by introducing Temporal Dynamic Sensitivity Centrality (TDC), which highlights that both the topology and dynamics of the network affect node spread. Additionally, Huang et al. [341] defined a super-evolution matrix to model temporal network structures, effectively reducing computational complexity by transforming the problem of calculating eigenvector centrality into the computation of eigenvectors from low-dimensional matrices. Additionally, Qu et al. [342] introduced the Temporal Information Gathering (TIG) process, which defines node importance based on four key factors: time information gathering depth, time distance matrix, initial information, and a weighting function. Furthermore, Arebi et al. [343] proposed a method based on temporal centrality measures to identify the minimum driver nodes set (MDS) that can fully control the network. Meanwhile, Li et al. [344] proposed a temporal information fusion model, which successfully identifies critical nodes in dynamic power information networks from both a topological and informational perspective.
To address the high settlement cost of temporal Katz centrality, Zhang et al. [345] introduced the Two-stage Attention-based Temporal Knowledge Graph Convolutional Network (TATKC). This framework combines temporal attention mechanisms with MLP to predict node ranking, enhancing performance through normalization and neighbor node sampling strategies. Similarly, Yu et al. [346] constructed a feature matrix based on neighborhood information and used the SIR model to identify key nodes in temporal networks. By employing network embedding and machine learning, they proposed the MLI algorithm, which transforms the identification of key nodes into a regression problem. In addition, Yu et al. [347] proposed a framework that combines GCN and RNN to identify nodes with optimal propagation capabilities, considering the sequential topology of temporal networks. Furthermore, Wang et al. [348] modeled node propagation as a hierarchical infection process, proposing Hierarchical Structure Influence (HSI), which quantifies a node's propagation potential across the entire network.
11. Summary and Discussion
In this review, we have systematically examined the concepts and methodologies associated with identifying important, critical, influential, and key nodes in complex networks and systems. Existing research has been broadly categorized into three main classes: structurally important nodes, highly influential nodes in information spreading, and critical nodes under performance constraints. In static networks, traditional centrality measures, such as degree, betweenness, and clustering coefficient, have provided the foundation for assessing node importance. However, the advent of dynamic, multilayer, and higher-order network models has given rise to a new generation of metrics, including spatio-temporal coupling indicators, propagation-based dynamic centralities, and hypergraph-based approaches. These methods have deepened our understanding of node roles and spreading mechanisms, particularly in contexts where interactions evolve over time and across multiple layers. Furthermore, models that incorporate coupling effects, edge weight dynamics, temporal features, and information fusion have enabled more robust identification of critical nodes in complex, real-world settings. Such advances have demonstrated practical relevance across diverse domains, including social networks, biological networks, power grid networks, transportation networks, and geographical networks.
Despite these developments, significant challenges persist in accurately pinpointing key nodes within real-world networks characterized by heterogeneity and dynamic complexity. The following areas require fulture direction: (1) Dynamic network evolution patterns: Existing methods often merely extend static indicators to dynamic networks, with insufficient study on the evolution patterns of key nodes and their spatial distribution in dynamic networks. This limits the exploration of potential patterns in complex systems. Additionally, researchers should focus more on identifying and inferring higher-order structures and dynamics in higher-order networks. (2) Efficient algorithm development: As networks grow in scale and complexity, there is an urgent need for efficient algorithms with low computational overhead. Many existing heuristic methods for node removal lack scalability and are ill-suited to large, dynamically evolving systems. Research should focus on developing real-time tracking algorithms, influence estimation techniques, and control strategies tailored to dynamic and multilayer networks. (3) Integration of machine learning and data-driven approaches: Recent advances in machine learning and data-driven methods, such as network embedding and deep learning, provide new perspectives for node importance identification. The emergence of novel network data structures such as semantic text attribute graphs and knowledge graphs offers opportunities to combine traditional centrality measures with modern machine learning models. This integration can enhance prediction accuracy and adaptability in recommendation systems, databases, and other applications. (4) Cross-domain applications and validation: Most current node importance measures are context-specific, limiting their generalizability. Developing a unified framework that accounts for structural, dynamic, and higher-order features is essential. Different domains (e.g., social networks, biological systems, power grids, transportation networks) have distinct definitions and requirements for key nodes. Future research should emphasize interdisciplinary collaboration, validate theoretical models with real-world datasets, and develop customized solutions for specific scenarios. In conclusion, the identification of key nodes in complex networks is a vibrant research area with significant theoretical and practical implications. Addressing the aforementioned challenges and future directions will contribute to a deeper understanding of complex systems and enable more effective solutions for real-world problems.
DECLARATIONS
Acknowledgments
We acknowledge Prof. Guanrong Chen from City University of Hong Kong for insightful discussions. We also would like to express our great appreciation to the editors and reviewers.
Authors' contributions
Conceived and designed the study, and wrote the manuscript: Chen, D.; Chen, J.
Performed the literature collection, analysis, and contributed to the writing and revision of the manuscript: Zhang, X.; Jia, Q.; Liu, X.; Sun, Y.
Contributed to the discussion and provided significant feedback on the manuscript: Lü, L.
Supervised the research, provided overall guidance, and revised the manuscript: Yu, W.
All authors have read and agreed to the published version of the manuscript.
Availability of data and materials
Not applicable.
Financial support and sponsorship
This work has received funding from the National Key R&D Program of China under Grant 2022ZD0120004, the Zhishan Youth Scholar Program, the National Natural Science Foundation of China under Grants 62233004, 62273090, and 62073076, and the Jiangsu Provincial Scientific Research Center of Applied Mathematics under Grant BK20233002.
Conflicts of interest
This manuscript underwent a double-blind peer review process. Yu, W. serves as the Editor-in-Chief of Complex Engineering Systems, Chen, D. and Lü, L. are members of its Editorial Board. None of them were involved in any part of the editorial process for this manuscript, including reviewer selection, handling, or decision-making, while the other authors have declared that they have no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Akbarzadeh, M.; Estrada, E. Communicability geometry captures traffic flows in cities. Nat. Hum. Behav. 2018, 2, 645-52.
2. De Domenico, M. More is different in real-world multilayer networks. Nat. Phys. 2023, 19, 1247-62.
3. Bardoscia, M.; Barucca, P.; Battiston, S.; et al. The physics of financial networks. Nat. Rev. Phys. 2021, 3, 490-507.
4. Yu, W.; Chen, D.; Liu, H.; et al. Systems science in the new era: intelligent systems and big data. Sci. China. Inf. Sci. 2024, 67, 136201.
5. Liu, J. G.; Ren, Z.; Guo, Q.; Wang, B. Research progress on node importance ranking in complex networks. Acta. Phys. Sin. 2013, 62, 178901.
6. Ren, X.; Lü, .; L, . Review of ranking nodes in complex networks. Chin. Sci. Bull. 2014, 59, 1175-97.
7. Lalou, M.; Tahraoui, M. A.; Kheddouci, H. The critical node detection problem in networks: a survey. Comput. Sci. Rev. 2018, 28, 92-117.
8. Hafiene, N.; Karoui, W.; Romdhane, L. B. Influential nodes detection in dynamic social networks: a survey. Expert. Syst. Appl. 2020, 159, 113642.
9. Zhang, B.; Zhao, X.; Nie, J.; et al. Epidemic model-based network influential node ranking methods: a ranking rationality perspective. ACM. Comput. Surv. 2024, 56, 1-39.
10. Li, Y.; Gao, H.; Gao, Y.; Guo, J.; Wu, W. A survey on influence maximization: from an ml-based combinatorial optimization. ACM. Trans. Knowl. Discov. Data. 2023, 17, 1-50.
11. Jaouadi, M.; Romdhane, L. B. A survey on influence maximization models. Expert. Syst. Appl. 2024, 248, 123429.
12. Liu, B.; Zeng, Y.; Yang, R.; Lü, .; L, . Fundamental statistics of higher-order networks: a survey. Acta. Phys. Sin. 2024, 73, 128901.
15. Chen, D.; Lü, L.; Shang, M. S.; Zhang, Y. C.; Zhou, T. Identifying influential nodes in complex networks. Phys. A. 2012, 391, 1777-87.
16. Ma, Y.; Cao, Z.; Qi, X. Quasi-Laplacian centrality: a new vertex centrality measurement based on Quasi-Laplacian energy of networks. Phys. A. 2019, 527, 121130.
17. Zhu, X.; Hao, R. Identifying influential nodes in social networks via improved Laplacian centrality. Chaos. Soliton. Fract. 2024, 189, 115675.
18. Kitsak, M.; Gallos, L. K.; Havlin, S.; et al. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888-93.
19. Zeng, A.; Zhang, C. J. Ranking spreaders by decomposing complex networks. Phys. Lett. A. 2013, 377, 1031-35.
20. Li, C.; Wang, L.; Sun, S.; Xia, C. Identification of influential spreaders based on classified neighbors in real-world complex networks. Appl. Math. Comput. 2018, 320, 512-23.
21. Liu, J. G.; Ren, Z. M.; Guo, Q. Ranking the spreading influence in complex networks. Phys. A. 2013, 392, 4154-59.
22. Zareie, A.; Sheikhahmadi, A. A hierarchical approach for influential node ranking in complex social networks. Expert. Syst. Appl. 2018, 93, 200-211.
23. Ibnoulouafi, A.; El Haziti, M.; Cherifi, H. M-centrality: identifying key nodes based on global position and local degree variation. J. Stat. Mech. 2018, 2018, 073407.
24. Liu, Y.; Tang, M.; Zhou, T.; Do, Y. Core-like groups result in invalidation of identifying super-spreader by k-shell decomposition. Sci. Rep. 2015, 5, 9602.
25. Liu, Y.; Tang, M.; Zhou, T.; Do, Y. Improving the accuracy of the k-shell method by removing redundant links: from a perspective of spreading dynamics. Sci. Rep. 2015, 5, 13172.
26. Lü, L.; Zhou, T.; Zhang, Q. M.; Stanley, H. E. The H-index of a network node and its relation to degree and coreness. Nat. Commun. 2016, 7, 10168.
27. Liu, Q.; Zhu, Y. X.; Jia, Y.; et al. Leveraging local h-index to identify and rank influential spreaders in networks. Phys. A. 2018, 512, 379-91.
28. Gao, L.; Yu, S.; Li, M.; Shen, Z.; Gao, Z. Weighted h-index for identifying influential spreaders. Symmetry 2019, 11, 1263.
29. Zareie, A.; Sheikhahmadi, A. EHC: extended H-index centrality measure for identification of users' spreading influence in complex networks. Phys. A. 2019, 514, 141-55.
30. Cohen, J. Trusses: cohesive subgraphs for social network analysis. National Security Agency Technical Report; 2008. Available from: https://www.researchgate.net/publication/242103824_Trusses_Cohesive_Subgraphs_for_Social_Network_Analysis[Last accessed on 10 Jul 2025].
31. Malliaros, F. D.; Rossi, M. E. G.; Vazirgiannis, M. Locating influential nodes in complex networks. Sci. Rep. 2016, 6, 19307.
32. Yu, F.; Xia, X.; Li, W.; et al. Critical node identification for complex network based on a novel minimum connected dominating set. Soft. Comput. 2017, 21, 5621-29.
33. Yu, H.; Cao, X.; Liu, Z.; Li, Y. Identifying key nodes based on improved structural holes in complex networks. Phys. A. 2017, 486, 318-27.
34. Xu, H.; Zhang, J.; Yang, J.; Lun, L. Identifying important nodes in complex networks based on multiattribute evaluation. Math. Probl. Eng. 2018, 2018, 8268436.
35. Liu, Y.; Wang, J.; He, H.; Huang, G.; Shi, W. Identifying important nodes affecting network security in complex networks. Int. J. Distrib. Sens. Netw. 2021, 17, 1550147721999285.
36. Zhao, Z.; Li, D.; Sun, Y.; Zhang, R.; Liu, J. Ranking influential spreaders based on both node k-shell and structural hole. Knowl. Based. Syst. 2023, 260, 110163.
37. Ma, J.; Kong, L.; Li, H. An effective edge-adding strategy for enhancing network traffic capacity. Phys. A. 2023, 609, 128321.
38. Wang, P.; Xu, B.; Wu, Y.; Zhou, X. Link prediction in social networks: the state-of-the-art. Sci. China. Inf. Sci. 2015, 1, 1-38.
39. Lu, P.; Zhang, Z. Critical nodes identification in complex networks via similarity coefficient. Mod. Phys. Lett. B. 2022, 36, 2150620.
40. Ai, J.; He, T.; Su, Z. Identifying influential nodes in complex networks based on resource allocation similarity. Phys. A. 2023, 627, 129101.
41. Rao, K. V.; Chowdary, C. R. CBIM: community-based influence maximization in multilayer networks. Inf. Sci. 2022, 609, 578-94.
42. Tong, T.; Yuan, W.; Jalili, M.; Dong, Q.; Sun, J. A novel ranking approach for identifying crucial spreaders in complex networks based on Tanimoto Correlation. Expert. Syst. Appl. 2024, 255, 124513.
43. Bonacich, P. Factoring and weighting approaches to clique identification. J. Math. Sociol. 1971, 92, 1170-82.
45. Ilyas, M. U.; Radha, H. Identifying influential nodes in online social networks using principal component centrality. In: 2011 IEEE International Conference on Communications. IEEE; 2011. pp. 1-5.
46. Estrada, E.; Rodríguez-Velázquez, J. A. Subgraph centrality in complex networks. Phys. Rev. E. 2005, 71, 056103.
47. Ahajjam, S.; El Haddad, M.; Badir, H. LeadersRank: towards a new approach for community detection in social networks. In: 2015 IEEE/ACS 12th International Conference of Computer Systems and Applications; 2015. pp. 1-8.
48. Martin, T.; Zhang, X.; Newman, M. E. Localization and centrality in networks. Phys. Rev. E. 2014, 90, 052808.
49. Zhong, L.; Shang, M.; Chen, X.; Cai, S. M. Identifying the influential nodes via eigencentrality from the differences and similarities of structure. Phys. A. 2018, 510, 77-82.
51. Zhang, Y.; Bao, Y.; Zhao, S.; Chen, J.; Tang, J. Identifying node importance by combining betweenness centrality and katz centrality. In: 2015 International Conference on Cloud Computing and Big Data; 2015. pp. 354-57.
52. Page, L.; Brin, S.; Motwani, R.; Winograd, T. The pagerank citation ranking: bring order to the web. Stanford University; 1998. Available from: http://ilpubs.stanford.edu:8090/422/[Last accessed on 10 Jul 2025].
53. Yang, Y.; Xie, G.; Xie, J. Mining important nodes in directed weighted complex networks. Discrete. Dyn. Nat. Soc. 2017, 2017, 9741824.
54. Chinchi, H.; Yian, L.; Wenhao, C.; Minghan, F.; Shoude, L. Unsupervised ranking using graph structures and node attributes. In Proceedings of the tenth ACM International Conference on Web Search and Data Mining; 2017. pp. 771-79.
55. Sheng, J.; Zhu, J.; Wang, Y.; Wang, B.; Hou, Z. Identifying influential nodes of complex networks based on trust-value. Algorithms 2020, 13, 280.
56. Su, Q.; Chen, C.; Sun, Z.; Li, J. Identification of critical nodes for cascade faults of grids based on electrical PageRank. Glob. Energy. Interconnect. 2021, 4, 587-95.
57. Lü, L.; Zhang, Y. C.; Yeung, C. H.; Zhou, T. Leaders in social networks, the delicious case. PLoS. One. 2011, 6, e21202.
58. Li, Q.; Zhou, T.; Lü, L.; Chen, D. Identifying influential spreaders by weighted LeaderRank. Phys. A. 2014, 404, 47-55.
59. Zhang, J.; Chen, D.; Dong, Q.; Zhao, Z. Identifying a set of influential spreaders in complex networks. Sci. Rep. 2016, 6, 27823.
60. Kumar, S.; Panda, B. S. Identifying influential nodes in social networks: neighborhood Coreness based voting approach. Phys. A. 2020, 553, 124215.
61. Sun, H.; Chen, D.; He, J.; Ch'ng, E. A voting approach to uncover multiple influential spreaders on weighted networks. Phys. A. 2019, 519, 303-12.
62. Li, Y.; Yang, X.; Zhang, X.; Xi, M.; Lai, X. An improved voterank algorithm to identifying a set of influential spreaders in complex networks. Front. Phys. 2022, 10, 955727.
63. Liu, J.; Xiong, Q.; Shi, W.; Shi, X.; Wang, K. Evaluating the importance of nodes in complex networks. Phys. A. 2016, 452, 209-19.
64. Freeman, L. C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35-41.
66. Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D. U. Complex networks: structure and dynamics. Phys. Rep. 2006, 424, 175-308.
67. Lü, Z.; Zhao, N.; Xiong, F.; Chen, N. A novel measure of identifying influential nodes in complex networks. Phys. A. 2019, 523, 488-97.
68. Song, Z.; Duan, H.; Ge, Y.; Qiu, X. A novel measure of centrality based on betweenness. In 2015 Chinese Automation Congress; 2015. pp. 174-78.
69. Ventresca, M.; Aleman, D. Efficiently identifying critical nodes in large complex networks. Comput. Soc. Netw. 2015, 2, 1-16.
70. Zhang, J.; Xu, X.; Li, P.; Zhang, K.; Small, M. Node importance for dynamical process on networks: a multiscale characterization. Chaos 2011, 21.
71. Yang, D.; Sun, Y.; Zhou, B.; Gao, X.; Zhang, H. Critical nodes identification of complex power systems based on electric cactus structure. IEEE. Syst. J. 2020, 14, 4477-88.
72. Kianian, S.; Rostamnia, M. An efficient path-based approach for influence maximization in social networks. Expert. Syst. Appl. 2021, 167, 114168.
73. Xiao, Y.; Chen, Y.; Zhang, H.; et al. A new semi-local centrality for identifying influential nodes based on local average shortest path with extended neighborhood. Artif. Intell. Rev. 2024, 57, 115.
74. Freeman, L. C. Centrality in social networks: Conceptual clarification. Soc. Netw. 2002, 1, 238-63.
75. Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701.
76. Salavati, C.; Abdollahpouri, A.; Manbari, Z. Ranking nodes in complex networks based on local structure and improving closeness centrality. Neurocomputing 2019, 336, 36-45.
77. Okamoto, K.; Chen, W.; Li, X. Ranking of closeness centrality for large-scale social networks. In Proceedings of the 2nd Annual International Workshop on Frontiers in Algorithmics. Heidelberg: Springer-Verlag; 2008. p. 186-95.
78. Sheng, J.; Dai, J.; Wang, B.; et al. Identifying influential nodes in complex networks based on global and local structure. Phys. A. 2020, 541, 123262.
79. Iannelli, F.; Mariani, M. S.; Sokolov, I. M. Influencers identification in complex networks through reaction-diffusion dynamics. Phys. Rev. E. 2018, 98, 062302.
80. Dong, J.; Ye, F.; Chen, W.; Wu, J. Identifying influential nodes in complex networks via semi-local centrality. In 2018 IEEE International Symposium on Circuits and Systems; 2018. pp. 1-5.
81. Kermarrec, A. M.; Le Merrer, E.; Sericola, B.; Trédan, G. Second order centrality: distributed assessment of nodes criticity in complex networks. Comput. Commun. 2011, 34, 619-28.
82. Li, X.; Wang, X. Controlling the spreading in small-world evolving networks: stability, oscillation, and topology. IEEE. Trans. Autom. Control. 2006, 51, 534-40.
83. Ghosh, D.; Frasca, M.; Rizzo, A.; et al. The synchronized dynamics of time-varying networks. Phys. Rep. 2022, 949, 1-63.
84. D'Souza, R. M.; di Bernardo, M.; Liu, Y. Controlling complex networks with complex nodes. Nat. Rev. Phys. 2023, 5, 250-62.
85. Liu, Y.; Slotine, J. J.; Barabási, A. L. Controllability of complex networks. Nature 2011, 473, 167-73.
86. Ding, J.; Wen, C.; Li, G. Key node selection in minimum-cost control of complex networks. Phys. A. 2017, 486, 251-61.
87. Lu, J.; Liu, R.; Lou, J.; Liu, Y. Pinning stabilization of Boolean control networks via a minimum number of controllers. IEEE. Trans. Cybern. 2019, 51, 373-81.
88. Zhu, S.; Cao, J.; Lin, L.; Lam, J.; Azuma, S. I. Toward stabilizable large-scale Boolean networks by controlling the minimal set of nodes. IEEE. Trans. Autom. Control. 2023, 69, 174-88.
89. Yu, W.; DeLellis, P.; Chen, G.; Di Bernardo, M.; Kurths, J. Distributed adaptive control of synchronization in complex networks. IEEE. Trans. Autom. Control. 2012, 57, 2153-58.
90. Yu, W.; Chen, G.; Lu, J.; Kurths, J. Synchronization via pinning control on general complex networks. SIAM. J. Control. Optim. 2013, 51, 1395-416.
91. Ding, J.; Tan, P.; Lu, Y. Z. Optimizing the controllability index of directed networks with the fixed number of control nodes. Neurocomputing 2016, 171, 1524-32.
92. Amani, A. M.; Jalili, M.; Yu, X.; Stone, L. Finding the most influential nodes in pinning controllability of complex networks. IEEE. Trans. Circuits. Syst. Ⅱ. 2017, 64, 685-89.
93. Amani, A. M.; Jalili, M.; Yu, X.; Stone, L. Controllability of complex networks: choosing the best driver set. Phys. Rev. E. 2018, 98, 030302.
94. Liu, H.; Xu, X.; Lu, J. A.; Chen, G.; Zeng, Z. Optimizing pinning control of complex dynamical networks based on spectral properties of grounded Laplacian matrices. IEEE. Trans. Syst. Man. Cyber. Syst. 2018, 51, 786-96.
95. Wang, W.; Ni, X.; Lai, Y.; Grebogi, C. Optimizing controllability of complex networks by minimum structural perturbations. Phys. Rev. E. 2012, 85, 026115.
96. Bof, N.; Baggio, G.; Zampieri, S. On the role of network centrality in the controllability of complex networks. IEEE. Trans. Control. Netw. Syst. 2016, 4, 643-53.
97. Zhou, J.; Yu, X.; Lu, J. A. Node importance in controlled complex networks. IEEE. Trans. Circuits. Syst. Ⅱ. 2018, 66, 437-41.
98. Liu, H.; Wang, B.; Lu, J.; Li, Z. Node-set importance and optimization algorithm of nodes selection in complex networks based on pinning control. Acta. Phys. Sin. 2021, 70, 056401.
99. Bomela, W.; Sebek, M.; Nagao, R.; et al. Finding influential nodes in networks using pinning control: centrality measures confirmed with electrochemical oscillators. Chaos 2023, 33, 093128.
100. Jiang, Q.; Zhou, J.; Li, B.; Liu, H.; Lu, J. A. Pinning synchronization of a complex network: nodes, edges and higher-order edges. Europhys. Lett. 2024, 147, 61001.
101. Sun, G. Q.; He, R.; Hou, L. F.; et al. Optimal control of spatial diseases spreading in networked reaction-diffusion systems. Phys. Rep. 2025, 1111, 1-64.
102. Zhang, H. T.; Chen, Z.; Mo, X. Effect of adding edges to consensus networks with directed acyclic graphs. IEEE. Trans. Autom. Control. 2017, 62, 4891-97.
103. Mo, X.; Chen, Z.; Zhang, H. T. Effects of adding a reverse edge across a stem in a directed acyclic graph. Automatica 2019, 103, 254-60.
104. Jiang, S.; Zhou, J.; Small, M.; Lu, J. A.; Zhang, Y. Searching for key cycles in a complex network. Phys. Rev. Lett. 2023, 130, 187402.
105. Cao, H.; Zhang, H. T.; Xie, L. Synchronization acceleration of networked systems via edge addition to single-root weighted digraphs. IEEE. Trans. Autom. Control. 2024, 70, 1730-44.
106. Zhang, H. T.; Cao, H.; Chen, Z. A necessary and sufficient condition of an interfering reverse edge for a directed acyclic graph. IEEE. Trans. Autom. Control. 2022, 67, 4885-91.
107. Gao, S.; Zhang, S.; Chen, X. Effects of adding edges on the consensus convergence rate of weighted directed chain networks. IEEE. Trans. Autom. Control. 2025, 70, 4077-84.
108. Aringhieri, R.; Grosso, A.; Hosteins, P.; Scatamacchia, R. A general evolutionary framework for different classes of critical node problems. Eng. Appl. Artif. Intell. 2016, 55, 128-45.
109. Alozie, G. U.; Arulselvan, A.; Akartunalı, K.; Pasiliao Jr, E. L. Efficient methods for the distance-based critical node detection problem in complex networks. Comput. Oper. Res. 2021, 131, 105254.
111. Boginski, V.; Commander, C. W. Identifying. critical. nodes. in. protein-protein. interaction. networks;. 2008..
112. Karygiannis, A.; Antonakakis, E.; Apostolopoulos, A. Detecting critical nodes for MANET intrusion detection systems. In Second International Workshop on Security, Privacy and Trust in Pervasive and Ubiquitous Computing; 2006. pp. 9-15.
113. Arulselvan, A.; Commander, C. W.; Shylo, O.; Pardalos, P. M. Cardinality-constrained critical node detection problem. Performance Models and Risk Management in Communications Systems; 2011, pp. 79-91.
114. Li, C.; Lin, S.; Shan, M. Finding influential mediators in social networks. In Proceedings of the 20th International Conference Companion on World Wide Web; 2011, pp. 75-6.
115. Ventresca, M.; Harrison, K. R.; Ombuki-Berman, B. M. An experimental evaluation of multi-objective evolutionary algorithms for detecting critical nodes in complex networks. In European Conference on the Applications of Evolutionary Computation. Springer; 2015, pp. 164-76.
116. Veremyev, A.; Boginski, V.; Pasiliao, E. L. Exact identification of critical nodes in sparse networks via new compact formulations. Optim. Lett. 2014, 8, 1245-59.
117. Ren, T.; Li, Z.; Qi, Y.; et al. Identifying vital nodes based on reverse greedy method. Sci. Rep. 2020, 10, 4826.
118. Wang, Y.; Cong, G.; Song, G.; Xie, K. Community-based greedy algorithm for mining top-k influential nodes in mobile social networks. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2010. pp. 1039-48.
119. Lam, C. Y.; Lin, J.; Sim, M. S.; Tai, K. Identifying vulnerabilities in critical infrastructures by network analysis. Int. J. Crit. Infrastruct. 2013, 9, 190-210.
120. Ventresca, M.; Aleman, D. A fast greedy algorithm for the critical node detection problem. In: International Conference on Combinatorial Optimization and Applications. Springer; 2014. pp. 603-12.
121. Tang, J.; Zhang, R.; Wang, P.; et al. A discrete shuffled frog-leaping algorithm to identify influential nodes for influence maximization in social networks. Knowl. Based. Syst. 2020, 187, 104833.
122. Di Summa, M.; Grosso, A.; Locatelli, M. Branch and cut algorithms for detecting critical nodes in undirected graphs. Comput. Optim. Appl. 2012, 53, 649-80.
123. Arulselvan, A.; Commander, C. W.; Elefteriadou, L.; Pardalos, P. M. Detecting critical nodes in sparse graphs. Comput. Oper. Res. 2009, 36, 2193-200.
124. Shen, Y.; Dinh, T. N.; Thai, M. T. Adaptive algorithms for detecting critical links and nodes in dynamic networks. In: 2012 IEEE Military Communications Conference; 2012. pp. 1-6.
125. Ventresca, M.; Aleman, D. A derandomized approximation algorithm for the critical node detection problem. Comput. Oper. Res. 2014, 43, 261-70.
126. Dinh, T. N.; Thai, M. T. Assessing attack vulnerability in networks with uncertainty. In: 2015 IEEE Conference on Computer Communications; 2015. pp. 2380-88.
127. Sarker, S.; Veremyev, A.; Boginski, V.; Singh, A. Critical nodes in river networks. Sci. Rep. 2019, 9, 11178.
128. Pullan, W. Heuristic identification of critical nodes in sparse real-world graphs. J. Heuristics. 2015, 21, 577-98.
129. Addis, B.; Aringhieri, R.; Grosso, A.; Hosteins, P. Hybrid constructive heuristics for the critical node problem. Ann. Oper. Res. 2016, 238, 637-49.
130. Chen, W.; Jiang, M.; Jiang, C.; Zhang, J. Critical node detection problem for complex network in undirected weighted networks. Phys. A. 2020, 538, 122862.
131. Ventresca, M. Global search algorithms using a combinatorial unranking-based problem representation for the critical node detection problem. Comput. Oper. Res. 2012, 39, 2763-75.
132. Shen, Y.; Nguyen, N. P.; Xuan, Y.; Thai, M. T. On the discovery of critical links and nodes for assessing network vulnerability. IEEE/ACM. Trans. Netw. 2012, 21, 963-73.
133. Ventresca, M.; Aleman, D. A region growing algorithm for detecting critical nodes. In: International Conference on Combinatorial Optimization and Applications. Springer; 2014. pp. 593-602.
134. Yin, H.; Hou, J.; Gong, C. A mixed strength decomposition method for identifying critical nodes by decomposing weighted social networks. Europhys. Lett. 2023, 142, 61003.
135. Zhang, L.; Zhang, H.; Feng, X.; Yang, H.; Cheng, F. An evolutionary multitasking method for multi-objective critical node detection on interdependent networks. IEEE. Trans. Cognit. Commun. Netw. 2025, 11, 607-20.
136. Fortz, B.; Mycek, M.; Pióro, M.; Tomaszewski, A. Min-max optimization of node-targeted attacks in service networks. Networks 2024, 83, 256-88.
137. Jiang, W.; Li, P.; Li, T.; Fan, T.; Zhang, C. Identifying vital edges based on the cycle structure in complex networks. Phys. Lett. A. 2025, 530, 130137.
138. Kouam, W.; Hayel, Y.; Deugoué, G.; Kamhoua, C. A novel centrality measure for analyzing lateral movement in complex networks. Phys. A. 2025, 658, 130255.
139. Zhou, M.; Liu, H.; Liao, H.; Liu, G.; Mao, R. Finding the key nodes to minimize the victims of the malicious information in complex network. Knowl. Based. Syst. 2024, 293, 111632.
140. Zhao, J.; Liu, X.; Guo, J. Evaluation method for node importance of communication network based on complex network analysis. In: Communications, Signal Processing, and Systems. Singapore: Springer; 2019.
141. Di Summa, M.; Grosso, A.; Locatelli, M. Complexity of the critical node problem over trees. Comput. Oper. Res. 2011, 38, 1766-74.
142. Hermelin, D.; Kaspi, M.; Komusiewicz, C.; Navon, B. Parameterized complexity of critical node cuts. Theor. Comput. Sci. 2016, 651, 62-75.
143. Addis, B.; Di Summa, M.; Grosso, A. Identifying critical nodes in undirected graphs: complexity results and polynomial algorithms for the case of bounded treewidth. Discrete. Appl. Math. 2013, 161, 2349-60.
144. Aringhieri, R.; Grosso, A.; Hosteins, P.; Scatamacchia, R. Local search metaheuristics for the critical node problem. Networks 2016, 67, 209-21.
145. Wang, H.; Shan, Z.; Ying, G.; et al. Evaluation method of node importance for power grid considering inflow and outflow power. J. Mod. Power. Syst. Clean. Energy. 2017, 5, 696-703.
146. Nikolaev, A. G.; Razib, R.; Kucheriya, A. On efficient use of entropy centrality for social network analysis and community detection. Soc. Netw. 2015, 40, 154-62.
147. Zareie, A.; Sheikhahmadi, A.; Jalili, M. Influential node ranking in social networks based on neighborhood diversity. Future. Gener. Comput. Syst. 2019, 94, 120-29.
148. Nitt, G. Using mapping entropy to identify node centrality in complex networks. Phys. A. 2016, 453, 290-97.
149. Fu, Y. H.; Huang, C. Y.; Sun, C. T. Identifying super-spreader nodes in complex networks. Math. Probl. Eng. 2015.
150. Guo, C.; Yang, L.; Chen, X.; et al. Influential nodes identification in complex networks via information entropy. Entropy 2020, 22, 242.
151. Xu, M.; Wu, J.; Liu, M.; et al. Discovery of critical nodes in road networks through mining from vehicle trajectories. IEEE. Trans. Intell. Trans. Syst. 2018, 20, 583-93.
152. Tulu, M. M.; Hou, R.; Younas, T. Identifying influential nodes based on community structure to speed up the dissemination of information in complex network. IEEE. Access. 2018, 6, 7390-401.
153. Ai, X. Node importance ranking of complex networks with entropy variation. Entropy 2017, 19, 303.
154. Wu, Y.; Dong, A.; Ren, Y.; Jiang, Q. Identify influential nodes in complex networks: a k-orders entropy-based method. Phys. A. 2023, 632, 129302.
155. Tong, T.; Dong, Q.; Sun, J.; Jiang, Y. Vital spreaders identification synthesizing cross entropy and information entropy with kshell method. Expert. Syst. Appl. 2023, 224, 119928.
156. Li, Y.; Cai, W.; Li, Y.; Du, X. Key node ranking in complex networks: a novel entropy and mutual information-based approach. Entropy 2019, 22, 52.
157. Chen, D. B.; Gao, H.; Lü, L.; Zhou, T. Identifying influential nodes in large-scale directed networks: the role of clustering. PLoS. One. 2013, 8, e77455.
158. Gao, S.; Ma, J.; Chen, Z.; Wang, G.; Xing, C. Ranking the spreading ability of nodes in complex networks based on local structure. Phys. A. 2014, 403, 130-47.
159. Yang, L.; Song, Y.; Jiang, G. P.; Xia, L. L. Identifying influential spreaders based on diffusion K-truss decomposition. Int. J. Mod. Phys. B. 2018, 32, 1850238.
160. Zareie, A.; Sheikhahmadi, A.; Jalili, M.; Fasaei, M. S. K. Finding influential nodes in social networks based on neighborhood correlation coefficient. Knowl. Based. Syst. 2020, 194, 105580.
161. Dablander, F.; Hinne, M. Node centrality measures are a poor substitute for causal inference. Sci. Rep. 2019, 9, 6846.
162. Liu, Y.; Song, A.; Shan, X.; Xue, Y.; Jin, J. Identifying critical nodes in power networks: a group-driven framework. Expert. Syst. Appl. 2022, 196, 116557.
163. Wang, B.; Zhang, J.; Dai, J.; Sheng, J. Influential nodes identification using network local structural properties. Sci. Rep. 2022, 12, 1833.
164. Zhang, X.; Zhu, J.; Wang, Q.; Zhao, H. Identifying influential nodes in complex networks with community structure. Knowl. Based. Syst. 2013, 42, 74-84.
165. Zhao, G.; Jia, P.; Huang, C.; Zhou, A.; Fang, Y. A machine learning based framework for identifying influential nodes in complex networks. IEEE. Access. 2020, 8, 65462-71.
166. Yang, X.; Xiong, Z.; Ma, F.; et al. Identifying influential spreaders in complex networks based on network embedding and node local centrality. Phys. A. 2021, 573, 125971.
167. Rezaei, A. A.; Munoz, J.; Jalili, M.; Khayyam, H. A machine learning-based approach for vital node identification in complex networks. Expert. Syst. Appl. 2023, 214, 119086.
168. Zhao, G.; Jia, P.; Zhou, A.; Zhang, B. InfGCN: identifying influential nodes in complex networks with graph convolutional networks. Neurocomputing 2020, 414, 18-26.
169. Kumar, S.; Mallik, A.; Khetarpal, A.; Panda, B. Influence maximization in social networks using graph embedding and graph neural network. Inf. Sci. 2022, 607, 1617-36.
170. Ribeiro, L. F.; Saverese, P. H.; Figueiredo, D. R. struc2vec: learning node representations from structural identity. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2017. pp. 385-94.
171. Zhang, M.; Wang, X.; Jin, L.; Song, M.; Li, Z. A new approach for evaluating node importance in complex networks via deep learning methods. Neurocomputing 2022, 497, 13-27.
172. Liu, C.; Cao, T.; Zhou, L. Learning to rank complex network node based on the self-supervised graph convolution model. Knowl. Based. Syst. 2022, 251, 109220.
173. Wei, P.; Zhou, J.; Yan, B.; Zeng, Y. ENIMNR: enhanced node influence maximization through node representation in social networks. Chaos. Soliton. Fract. 2024, 186, 115192.
174. Keikha, M. M.; Rahgozar, M.; Asadpour, M.; Abdollahi, M. F. Influence maximization across heterogeneous interconnected networks based on deep learning. Expert. Syst. Appl. 2020, 140, 112905.
175. Bouyer, A.; Beni, H. A.; Oskouei, A. G.; et al. Maximizing influence in social networks using combined local features and deep learning-based node embedding. Big. Data. 2024.
176. Wu, Y.; Hu, Y.; Yin, S.; et al. A graph convolutional network model based on regular equivalence for identifying influential nodes in complex networks. Knowl. Based. Syst. 2024, 301, 112235.
177. Ahmad, W.; Wang, B.; Chen, S. Learning to rank influential nodes in complex networks via convolutional neural networks. Appl. Intell. 2024, 54, 3260-78.
178. Rashid, Y.; Bhat, J. I. OlapGN: a multi-layered graph convolution network-based model for locating influential nodes in graph networks. Knowl. Based. Syst. 2024, 283, 111163.
179. Xiong, Y.; Hu, Z.; Su, C.; Cai, S. M.; Zhou, T. Vital node identification in complex networks based on autoencoder and graph neural network. Appl. Soft. Comput. 2024, 163, 111895.
180. Yu, E.; Wang, Y.; Fu, Y.; Chen, D.; Xie, M. Identifying critical nodes in complex networks via graph convolutional networks. Knowl. Based. Syst. 2020, 198, 105893.
181. Park, N.; Kan, A.; Dong, X. L.; Zhao, T.; Faloutsos, C. Estimating node importance in knowledge graphs using graph neural networks. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2019. pp. 596-606.
182. Park, N.; Kan, A.; Dong, X. L.; Zhao, T.; Faloutsos, C. Multiimport: inferring node importance in a knowledge graph from multiple input signals. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2020. pp. 503-12.
183. Munikoti, S.; Das, L.; Natarajan, B. Scalable graph neural network-based framework for identifying critical nodes and links in complex networks. Neurocomputing 2022, 468, 211-21.
184. Ge, K.; Han, Q. B. Node importance estimation for knowledge graphs based on multi-perspectives attention fusion mechanism. Int. J. Pattern. Recognit. Artif. Intell. 2024, 38, 2459017.
185. Chen, X.; Lei, P. I.; Sheng, Y.; Liu, Y.; Gong, Z. Social influence learning for recommendation systems. In Proceedings of the 33rd ACM International Conference on Information and Knowledge Management; 2024. pp. 312-22.
186. Liu, Z.; Qiu, H.; Guo, W.; Zhu, J.; Wang, Q. NIE-GAT: node importance evaluation method for inter-domain routing network based on graph attention network. J. Comput. Sci. 2022, 65, 101885.
187. Kou, J.; Jia, P.; Liu, J.; Dai, J.; Luo, H. Identify influential nodes in social networks with graph multi-head attention regression model. Neurocomputing 2023, 530, 23-36.
188. Liu, L.; Zeng, W.; Tan, Z.; Xiao, W.; Zhao, X. Node importance estimation with multiview contrastive representation learning. Int. J. Intell. Syst. 2023, 2023, 5917750.
189. Zhang, T.; Hou, C.; Jiang, R.; et al. Label informed contrastive pretraining for node importance estimation on knowledge graphs. IEEE. Trans. Neural. Networks. Learn. Syst. 2025, 36, 4462-76.
190. Shu, J.; Zou, Y.; Cui, H.; Liu, L. Node importance evaluation in heterogeneous network based on attention mechanism and graph contrastive learning. Neurocomputing 2025, 626, 129555.
191. Huang, C.; Fang, Y.; Lin, X.; et al. Estimating node importance values in heterogeneous information networks. In: 2022 IEEE 38th International Conference on Data Engineering; 2022. pp. 846-58.
192. Chen, Y.; Fang, Y.; Wang, Q.; Cao, X.; King, I. Deep structural knowledge exploitation and synergy for estimating node importance value on heterogeneous information networks. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2024. pp. 8302-10.
193. Lin, X.; Zhang, T.; Hou, C.; et al. Node importance estimation leveraging LLMs for semantic augmentation in knowledge graphs. arXiv 2024.
194. Zhao, X.; Yu, H.; Huang, R.; et al. A novel higher-order neural network framework based on motifs attention for identifying critical nodes. Phys. A. 2023, 629, 129194.
195. Michos, I.; Neocleous, K.; Papadopoulou Lesta, V. Critical node detection in sparse graphs using hopfield neural networks. In Proceedings of the 13th Hellenic Conference on Artificial Intelligence; 2024. pp. 1-4.
196. Fan, C.; Zeng, L.; Sun, Y.; Liu, Y. Finding key players in complex networks through deep reinforcement learning. Nat. Mach. Intell. 2020, 2, 317-24.
197. Tan, X.; Zhou, Y.; Zhou, M.; Fu, Z. Learning to detect critical nodes in sparse graphs via feature importance awareness. IEEE. Trans. Autom. Sci. Eng. 2024, 22, 3772-82.
198. Jaques, N.; Lazaridou, A.; Hughes, E.; et al. Social influence as intrinsic motivation for multi-agent deep reinforcement learning. In: International Conference on Machine Learning; 2019. pp. 3040-49. Available from: https://proceedings.mlr.press/v97/jaques19a.html[Last accessed on 10 Jul 2025].
199. Chen, P.; Fan, W. Identifying critical nodes via link equations and deep reinforcement learning. Neurocomputing 2023, 126871.
200. Li, H.; Xu, M.; Bhowmick, S. S.; et al. Disco: influence maximization meets network embedding and deep learning. arXiv 2019.
201. Chen, T.; Yan, S.; Guo, J.; Wu, W. ToupleGDD: a fine-designed solution of influence maximization by deep reinforcement learning. IEEE. Trans. Comput. Soc. Syst. 2023, 11, 2210-21.
202. Ling, C.; Jiang, J.; Wang, J.; et al. Deep graph representation learning and optimization for influence maximization. arXiv 2023.
203. Li, H.; Xu, M.; Bhowmick, S. S.; et al. PIANO: influence maximization meets deep reinforcement learning. IEEE. Trans. Comput. Soc. Syst. 2022, 10, 1288-300.
204. Uthayasuriyan, A.; Chandran, G. H.; Kavvin, U. V.; Mahitha, S. H.; Jeyakumar, G. Adaptive hybridization of differential evolution and DQN-reinforcement learning to solve the influence maximization problem in social networks. Int. J. Intell. Eng. Syst. 2024, 17, 109-25.
205. Li, F.; Xu, Z.; Cheng, D.; Wang, X. AdaRisk: risk-adaptive deep reinforcement learning for vulnerable nodes detection. IEEE. Trans. Knowl. Data. Eng. 2024, 36, 5576-90.
206. Xu, L.; Ma, L.; Lin, Q.; et al. Influence maximization in hypergraphs based on evolutionary deep reinforcement learning. Inf. Sci. 2025, 698, 121764.
207. Zhu, W.; Zhang, K.; Zhong, J.; Hou, C.; Ji, J. BiGDN: an end-to-end influence maximization framework based on deep reinforcement learning and graph neural networks. Expert. Syst. Appl. 2025, 270, 126384.
208. Ahmad, W.; Wang, B. A learning-based influence maximization framework for complex networks via K-core hierarchies and reinforcement learning. Expert. Syst. Appl. 2025, 259, 125393.
209. Ma, L.; Ma, C.; Zhang, H.; Wang, B. Identifying influential spreaders in complex networks based on gravity formula. Phys. A. 2016, 451, 205-12.
210. Maji, G.; Namtirtha, A.; Dutta, A.; Malta, M. C. Influential spreaders identification in complex networks with improved k-shell hybrid method. Expert. Syst. Appl. 2020, 144, 113092.
211. Li, Z.; Huang, X. Identifying influential spreaders in complex networks by an improved gravity model. Sci. Rep. 2021, 11, 22194.
212. Li, S.; Xiao, F. The identification of crucial spreaders in complex networks by effective gravity model. Inf. Sci. 2021, 578, 725-49.
213. Liu, F.; Wang, Z.; Deng, Y. GMM: a generalized mechanics model for identifying the importance of nodes in complex networks. Knowl. Based. Syst. 2020, 193, 105464.
214. Yang, X.; Xiao, F. An improved gravity model to identify influential nodes in complex networks based on k-shell method. Knowl. Based. Syst. 2021, 227, 107198.
215. Li, H.; Shang, Q.; Deng, Y. A generalized gravity model for influential spreaders identification in complex networks. Chaos. Solitons. Fractals. 2021, 143, 110456.
216. Fei, L.; Zhang, Q.; Deng, Y. Identifying influential nodes in complex networks based on the inverse-square law. Phys. A. 2018, 512, 1044-59.
217. Wang, J.; Li, C.; Xia, C. Improved centrality indicators to characterize the nodal spreading capability in complex networks. Appl. Math. Comput. 2018, 334, 388-400.
218. Li, Z.; Ren, T.; Ma, X.; et al. Identifying influential spreaders by gravity model. Sci. Rep. 2019, 9, 8387.
219. Yan, X.; Cui, Y.; Ni, S. J. Identifying influential spreaders in complex networks based on entropy weight method and gravity law. Chin. Phys. B. 2020, 29, 048902.
220. Wang, Y.; Li, H.; Zhang, L.; Zhao, L.; Li, W. Identifying influential nodes in social networks: centripetal centrality and seed exclusion approach. Chaos. Soliton. Fract. 2022, 162, 112513.
221. Yang, P.; Zhao, L.; Dong, C.; Xu, G.; Zhou, L. AIGCrank: a new adaptive algorithm for identifying a set of influential spreaders in complex networks based on gravity centrality. Chin. Phys. B. 2023, 32, 058901.
222. Zhu, S.; Zhan, J.; Li, X. Identifying influential nodes in complex networks using a gravity model based on the H-index method. Sci. Rep. 2023, 13, 16404.
223. Liu, Y.; Cheng, Z.; Li, X.; Wang, Z. An entropy-based gravity model for influential spreaders identification in complex networks. Complexity 2023, 2023, 6985650.
224. Zhao, J.; Wen, T.; Jahanshahi, H.; Cheong, K. H. The random walk-based gravity model to identify influential nodes in complex networks. Inf. Sci. 2022, 609, 1706-20.
225. Zhao, N.; Liu, Q.; Wang, H.; et al. Estimating the relative importance of nodes in complex networks based on network embedding and gravity model. Comput. Inf. Sci. 2023, 35, 101758.
226. Shang, Q.; Deng, Y.; Cheong, K. H. Identifying influential nodes in complex networks: effective distance gravity model. Inf. Sci. 2021, 577, 162-79.
227. Curado, M.; Tortosa, L.; Vicent, J. F. A novel measure to identify influential nodes: return random walk gravity centrality. Inf. Sci. 2023, 628, 177-95.
228. Yang, P.; Meng, F.; Zhao, L.; Zhou, L. AOGC: an improved gravity centrality based on an adaptive truncation radius and omni-channel paths for identifying key nodes in complex networks. Chaos. Soliton. Fract. 2023, 166, 112974.
229. Chen, D.; Su, H. Identification of influential nodes in complex networks with degree and average neighbor degree. IEEE. J. Emerg. Sel. Top. Circuits. Syst. 2023, 13, 734-42.
230. Meng, L.; Xu, G.; Dong, C. An improved gravity model for identifying influential nodes in complex networks considering asymmetric attraction effect. Phys. A. 2025, 657, 130237.
231. Xu, G.; Dong, C. CAGM: a communicability-based adaptive gravity model for influential nodes identification in complex networks. Expert. Syst. Appl. 2024, 235, 121154.
232. Li, Z.; Tang, J.; Zhao, C.; Gao, F. Improved centrality measure based on the adapted PageRank algorithm for urban transportation multiplex networks. Chaos. Soliton. Fract. 2023, 167, 112998.
233. Lü, L.; Zhang, T.; Hu, P.; et al. An improved gravity centrality for finding important nodes in multi-layer networks based on multi-PageRank. Expert. Syst. Appl. 2024, 238, 122171.
234. Chi, K.; Wang, N.; Su, T.; Yang, Y.; Qu, H. Measuring the centrality of nodes in networks based on the interstellar model. Inf. Sci. 2024, 678, 120908.
235. Comin, C. H.; da Fontoura Costa, L. Identifying the starting point of a spreading process in complex networks. Phys. Rev. E. 2011, 84, 056105.
236. De Arruda, G. F.; Barbieri, A. L.; Rodríguez, P.M.; et al. Role of centrality for the identification of influential spreaders in complex networks. Phys. Rev. E. 2014, 90, 032812.
237. Hu, F.; Liu, Y. Multi-index algorithm of identifying important nodes in complex networks based on linear discriminant analysis. Mod. Phys. Lett. B. 2015, 29, 1450268.
238. Hu, P.; Fan, W.; Mei, S. Identifying node importance in complex networks. Phys. A. 2015, 429, 169-76.
239. Bucur, D. Top influencers can be identified universally by combining classical centralities. Sci. Rep. 2020, 10, 20550.
240. Wei, X.; Zhao, J.; Liu, S.; Wang, Y. Identifying influential spreaders in complex networks for disease spread and control. Sci. Rep. 2022, 12, 5550.
241. An, Z.; Hu, X.; Jiang, R.; Jiang, Y. A novel method for identifying key nodes in multi-layer networks based on dynamic influence range and community importance. Knowl. Based. Syst. 2024, 305, 112639.
242. Wu, H.; Deng, H.; Li, J.; Wang, Y.; Yang, K. Hunting for influential nodes based on radiation theory in complex networks. Chaos. Soliton. Fract. 2024, 188, 115487.
243. Cao, M.; Wu, D.; Du, P.; Zhang, T.; Ahmadi, S. Dynamic identification of important nodes in complex networks by considering local and global characteristics. J. Complex. Netw. 2024, 12, cnae015.
244. Kopsidas, A.; Kepaptsoglou, K. Identification of critical stations in a Metro system: a substitute complex network analysis. Phys. A. 2022, 596, 127123.
245. Wang, Y.; Zhang, L.; Yang, J.; Yan, M.; Li, H. Multi-factor information matrix: a directed weighted method to identify influential nodes in social networks. Chaos. Soliton. Fract. 2024, 180, 114485.
246. Lei, M.; Liu, L.; Ramirez-Arellano, A. Weighted information index mining of key nodes through the perspective of evidential distance. J. Comput. Sci. 2024, 78, 102282.
247. Ullah, A.; Sheng, J.; Wang, B.; Din, S. U.; Khan, N. Leveraging neighborhood and path information for influential spreaders recognition in complex networks. J. Intell. Inf. Syst. 2024, 62, 377-401.
248. Zhang, J.; Zhou, Y.; Wang, S.; Min, Q. Critical station identification and robustness analysis of urban rail transit networks based on comprehensive vote-rank algorithm. Chaos. Soliton. Fract. 2024, 178, 114379.
249. Lee, Y.; Wen, Y.; Xie, W.; et al. Identifying influential nodes on directed networks. Inf. Sci. 2024, 677, 120945.
250. Esfandiari, S.; Fakhrahmad, S. M. The collaborative role of K-shell and PageRank for identifying influential nodes in complex networks. Phys. A. 2025, 658, 130256.
251. Chen, L.; Rezaeipanah, A. SFIMCO: scalable fair influence maximization based on overlapping communities and optimization algorithms. Neurocomputing 2025, 129687.
252. Zhang, K.; Pu, Z.; Jin, C.; Zhou, Y.; Wang, Z. A novel semi-local centrality to identify influential nodes in complex networks by integrating multidimensional factors. Eng. Appl. Artif. Intell. 2025, 145, 110177.
253. Mo, H.; Gao, C.; Deng, Y. Evidential method to identify influential nodes in complex networks. J. Syst. Eng. Elect. 2015, 26, 381-87.
254. Xu, G. Q.; Miao, J. L.; Dong, C. LGP-DS: a novel algorithm for identifying influential nodes in complex networks based on multi-dimensional evidence fusion. Europhys. Lett. 2025, 149, 21003.
255. Sheikhahmadi, A.; Nematbakhsh, M. A.; Zareie, A. Identification of influential users by neighbors in online social networks. Phys. A. 2017, 486, 517-34.
256. Wang, Z.; Zhao, Y.; Xi, J.; Du, C. Fast ranking influential nodes in complex networks using a k-shell iteration factor. Phys. A. 2016, 461, 171-81.
257. Wang, Z.; Du, C.; Fan, J.; Xing, Y. Ranking influential nodes in social networks based on node position and neighborhood. Neurocomputing 2017, 260, 466-77.
258. Sheikhahmadi, A.; Nematbakhsh, M. A. Identification of multi-spreader users in social networks for viral marketing. J. Inf. Sci. 2017, 43, 412-23.
259. Yang, F.; Li, X.; Xu, Y.; et al. Ranking the spreading influence of nodes in complex networks: an extended weighted degree centrality based on a remaining minimum degree decomposition. Phys. Lett. A. 2018, 382, 2361-71.
260. Namtirtha, A.; Dutta, A.; Dutta, B.; Sundararajan, A.; Simmhan, Y. Best influential spreaders identification using network global structural properties. Sci. Rep. 2021, 11, 2254.
261. Ullah, A.; Wang, B.; Sheng, J.; et al. Identification of nodes influence based on global structure model in complex networks. Sci. Rep. 2021, 11, 6173.
262. Ullah, A.; Wang, B.; Sheng, J.; et al. Identifying vital nodes from local and global perspectives in complex networks. Expert. Syst. Appl. 2021, 186, 115778.
263. Hu, H.; Sun, Z.; Wang, F.; Zhang, L.; Wang, G. Exploring influential nodes using global and local information. Sci. Rep. 2022, 12, 22506.
264. Wang, F.; Sun, Z.; Gan, Q.; et al. Influential node identification by aggregating local structure information. Phys. A. 2022, 593, 126885.
265. Mukhtar, M. F.; Abal Abas, Z.; Baharuddin, A. S.; et al. Integrating local and global information to identify influential nodes in complex networks. Sci. Rep. 2023, 13, 11411.
266. Yang, Q.; Wang, Y.; Yu, S.; Wang, W. Identifying influential nodes through an improved k-shell iteration factor model. Expert. Syst. Appl. 2023, 238, 122077.
267. Qiu, F.; Yu, C.; Feng, Y.; Li, Y. Key node identification for a network topology using hierarchical comprehensive importance coefficients. Sci. Rep. 2024, 14, 12039.
268. Du, Y.; Gao, C.; Hu, Y.; Mahadevan, S.; Deng, Y. A new method of identifying influential nodes in complex networks based on TOPSIS. Phys. A. 2014, 399, 57-69.
269. Liu, Z.; Jiang, C.; Wang, J.; Yu, H. The node importance in actual complex networks based on a multi-attribute ranking method. Knowl. Based. Syst. 2015, 84, 56-66.
270. Hu, J.; Du, Y.; Mo, H.; Wei, D.; Deng, Y. A modified weighted TOPSIS to identify influential nodes in complex networks. Phys. A. 2016, 444, 73-85.
271. Li, M.; Zhou, S.; Wang, D.; Chen, G. Identifying influential nodes based on resistance distance. J. Comput. Sci. 2023, 67, 101972.
272. Dong, C.; Xu, G.; Meng, L.; Yang, P. CPR-TOPSIS: a novel algorithm for finding influential nodes in complex networks based on communication probability and relative entropy. Phys. A. 2022, 603, 127797.
274. Ishfaq, U.; Khan, H. U.; Iqbal, S. Identifying the influential nodes in complex social networks using centrality-based approach. Comput. Inf. Sci. 2022, 34, 9376-92.
275. Yang, P.; Xu, G.; Chen, H. Multi-attribute ranking method for identifying key nodes in complex networks based on GRA. Int. J. Mod. Phys. B. 2018, 32, 1850363.
276. Vega-Oliveros, D. A.; Gomes, P. S.; Milios, E. E.; Berton, L. A multi-centrality index for graph-based keyword extraction. Inf. Proc. Manag. 2019, 56, 102063.
277. Lu, M. Node importance evaluation based on neighborhood structure hole and improved TOPSIS. Comput. Netw. 2020, 178, 107336.
278. Zhang, Y.; Lu, Y.; Yang, G.; Hang, Z. Multi-attribute decision making method for node importance metric in complex network. Appl. Sci. 2022, 12, 1944.
279. Ju, Y.; Li, Z.; Chen, Y.; Feng, R. A novel method to evaluation node importance in multilayer regional rail transit network. In: International Conference on Intelligent Transportation Engineering. Springer; 2021. pp. 295-307.
280. Macdonald, B.; Shakarian, P.; Howard, N.; Moores, G. Spreaders in the network sir model: an empirical study. arXiv 2012.
281. Borgatti, S. P. Identifying sets of key players in a social network. Comput. Math. Org. Theory. 2006, 12, 21-34.
282. Zhuge, H.; Zhang, J. Topological centrality and its e-Science applications. J. Am. Soc. Inf. Sci. Technol. 2010, 61, 1824-41.
283. Aral, S.; Walker, D. Identifying influential and susceptible members of social networks. Science 2012, 337, 337-41.
284. Li, G.; Chen, S.; Feng, J.; Tan, K. L, Li, W. S. Efficient location-aware influence maximization. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data; 2014. pp. 87-98.
286. Chen, X. Critical nodes identification in complex systems. Complex. Intell. Syst. 2015, 1, 37-56.
287. Robinaugh, D. J.; Millner, A. J.; McNally, R. J. Identifying highly influential nodes in the complicated grief network. J. Abnorm. Psychol. 2016, 125, 747.
288. Bozorgi, A.; Haghighi, H.; Zahedi, M. S.; Rezvani, M. INCIM: a community-based algorithm for influence maximization problem under the linear threshold model. Inf. Proc. Manag. 2016, 52, 1188-99.
289. Holme, P. Three faces of node importance in network epidemiology: exact results for small graphs. Phys. Rev. E. 2017, 96, 062305.
290. Yin, H.; Zhang, A.; Zeng, A. Identifying hidden target nodes for spreading in complex networks. Chaos. Soliton. Fract. 2023, 168, 113103.
291. He, Q.; Wang, X.; Lei, Z.; et al. TIFIM: a two-stage iterative framework for influence maximization in social networks. Appl. Math. Comput. 2019, 354, 338-52.
292. Tulu, M. M.; Hou, R.; Younas, T. Vital nodes extracting method based on user's behavior in 5G mobile social networks. J. Netw. Comput. Appl. 2019, 133, 39-50.
293. Zhong, L.; Bai, Y.; Tian, Y.; et al. Information entropy based on propagation feature of node for identifying the influential nodes. Complexity 2021, 2021, 5554322.
294. Li, P.; Liu, K.; Li, K.; Liu, J.; Zhou, D. Estimating user influence ranking in independent cascade model. Phys. A. 2021, 565, 125584.
295. Gong, Y.; Liu, S.; Bai, Y. A probability-driven structure-aware algorithm for influence maximization under independent cascade model. Phys. A. 2021, 583, 126318.
296. Wang, Y.; Zheng, Y.; Liu, Y. HGIM: Influence maximization in diffusion cascades from the perspective of heterogeneous graph. Appl. Intell. 2023, 53, 22200-22215.
297. Mohammadi, S.; Nadimi-Shahraki, M. H.; Beheshti, Z.; Zamanifar, K. Improved information diffusion models based on a new two-sided sign-aware matching framework in complex networks. Chaos. Soliton. Fract. 2024, 187, 115298.
298. Wang, J.; Sun, S. Identifying influential nodes: a new method based on dynamic propagation probability model. Chaos. Soliton. Fract. 2024, 185, 115159.
299. Xu, G.; Meng, L. A novel algorithm for identifying influential nodes in complex networks based on local propagation probability model. Chaos. Soliton. Fract. 2023, 168, 113155.
300. Ai, J.; He, T.; Su, Z.; Shang, L. Identifying influential nodes in complex networks based on spreading probability. Chaos. Soliton. Fract. 2022, 164, 112627.
301. Zareie, A.; Sheikhahmadi, A.; Jalili, M. Identification of influential users in social network using gray wolf optimization algorithm. Expert. Syst. Appl. 2020, 142, 112971.
302. Chen, G.; Zhou, S.; Liu, J.; Li, M.; Zhou, Q. Influential node detection of social networks based on network invulnerability. Phys. Lett. A. 2020, 384, 126879.
303. Fink, C. G.; Fullin, K.; Gutierrez, G.; et al. A centrality measure for quantifying spread on weighted, directed networks. Phys. A. 2023, 626, 129083.
304. Sun, Z.; Sun, Y.; Chang, X.; et al. Finding critical nodes in a complex network from information diffusion and Matthew effect aggregation. Expert. Syst. Appl. 2023, 233, 120927.
305. Ullah, A.; Shao, J.; Yang, Q.; et al. Lss: a locality-based structure system to evaluate the spreader's importance in social complex networks. Expert. Syst. Appl. 2023, 228, 120326.
306. Corsin, J.; Zino, L.; Ye, M. An evidence-accumulating drift-diffusion model of competing information spread on networks. Chaos. Soliton. Fract. 2025, 192, 115935.
307. Liu, J. G.; Lin, J.; Guo, Q.; Zhou, T. Locating influential nodes via dynamics-sensitive centrality. Sci. Rep. 2016, 6, 21380.
308. Mo, H.; Deng, Y. Identifying node importance based on evidence theory in complex networks. Phys. A. 2019, 529, 121538.
309. Du, Z.; Tang, J.; Qi, Y.; et al. Identifying critical nodes in metro network considering topological potential: a case study in Shenzhen city - China. Phys. A. 2020, 539, 122926.
310. Kapoor, K.; Sharma, D.; Srivastava, J. Weighted node degree centrality for hypergraphs. In: 2013 IEEE 2nd Network Science Workshop; 2013. pp. 152-55.
311. Lee, J.; Lee, Y.; Oh, S. M.; Kahng, B. Betweenness centrality of teams in social networks. Chaos 2021, 31, 061108.
312. St-Onge, G.; Iacopini, I.; Latora, V.; et al. Influential groups for seeding and sustaining nonlinear contagion in heterogeneous hypergraphs. Commun. Phys. 2022, 5, 25.
313. Xie, M.; Zhan, X. X.; Liu, C.; Zhang, Z. K. An efficient adaptive degree-based heuristic algorithm for influence maximization in hypergraphs. Inf. Proc. Manag. 2023, 60, 103161.
314. Lee, J.; Goh, K. I.; Lee, D. S.; Kahng, B. (k, q)-core decomposition of hypergraphs. Chaos. Soliton. Fract. 2023, 173, 113645.
315. Mancastroppa, M.; Iacopini, I.; Petri, G.; Barrat, A. Hyper-cores promote localization and efficient seeding in higher-order processes. Nat. Commun. 2023, 14, 6223.
316. Benson, A. R. Three hypergraph eigenvector centralities. SIAM. J. Math. Data. Sci. 2019, 1, 293-312.
317. Zhao, Y.; Li, C.; Shi, D.; Chen, G.; Li, X. Ranking cliques in higher-order complex networks. Chaos 2023, 33, 073139.
318. Li, S.; Li, X. Influence maximization in hypergraphs: a self-optimizing algorithm based on electrostatic field. Chaos. Soliton. Fract. 2023, 174, 113888.
319. Xie, X.; Zhan, X.; Zhang, Z.; Liu, C. Vital node identification in hypergraphs via gravity model. Chaos 2023, 33, 013104.
320. Zhao, X.; Yu, H.; Liu, S.; Cao, X. A general higher-order supracentrality framework based on motifs of temporal networks and multiplex networks. Phys. A. 2023, 614, 128548.
321. Battiston, F.; Cencetti, G.; Iacopini, I.; et al. Networks beyond pairwise interactions: Structure and dynamics. Phys. Rep. 2020, 874, 1-92.
322. Goldberg, T. E. Combinatorial Laplacians of simplicial complexes; 2002. Available from: https://pi.math.cornell.edu/goldberg/Papers/CombinatorialLaplacians.pdf[Last accessed on 10 Jul 2025].
323. Estrada, E.; Ross, G. J. Centralities in simplicial complexes. J. Theor. Biol. 2018, 438, 46-60.
324. Serrano, D. H.; Hern'andez-Serrano, J.; G'omez, D. S. Simplicial degree in complex networks. Chaos. Soliton. Fract. 2020, 137, 109839.
326. Estrada, E.; Knight, P. A. A. first. course. in. network. theory. 2015.
327. Kim, H.; Anderson, R. Temporal node centrality in complex networks. Phys. Rev. E. 2012, 85, 026107.
328. Tsalouchidou, I.; Baeza-Yates, R.; Bonchi, F.; Liao, K.; Sellis, T. Temporal betweenness centrality in dynamic graphs. Int. J. Data. Sci. Anal. 2020, 9, 257-72.
329. Elmezain, M.; Othman, E. A.; Ibrahim, H. M. Temporal degree-degree and closeness-closeness: a new centrality metrics for social network analysis. Mathematics 2021, 9, 2850.
330. Lü, L.; Zhang, K.; Zhang, T.; et al. Eigenvector centrality measure based on node similarity for multilayer and temporal networks. IEEE. Access. 2019, 7, 115725-33.
331. Lü, .; L., Zhang. K.; Zhang, T.; et al. PageRank centrality for temporal networks. Phys. Lett. A. 2019, 383, 1215-22.
332. Lü, L.; Zhang, K.; Bardou, D.; et al. HITS centrality based on inter-layer similarity for multilayer temporal networks. Neurocomputing 2021, 423, 220-35.
333. Bi, J.; Jin, J.; Qu, C.; et al. Temporal gravity model for important node identification in temporal networks. Chaos. Soliton. Fract. 2021, 147, 110934.
334. Jiang, J. L.; Fang, H.; Li, S. Q.; Li, W. M. Identifying important nodes for temporal networks based on the ASAM model. Phys. A. 2022, 586, 126455.
335. Taylor, D.; Myers, S. A.; Clauset, A.; Porter, M. A.; Mucha, P. J. Eigenvector-based centrality measures for temporal networks. Multiscale. Model. Simul. 2017, 15, 537-74.
336. Tao, L.; Kong, S.; He, L.; et al. A sequential-path tree-based centrality for identifying influential spreaders in temporal networks. Chaos. Soliton. Fract. 2022, 165, 112766.
337. Chen, B.; Hou, G.; Li, A. Temporal local clustering coefficient uncovers the hidden pattern in temporal networks. Phys. Rev. E. 2024, 109, 064302.
338. Pan, R. K.; Saramäki, J. Path lengths, correlations, and centrality in temporal networks. Phys. Rev. E. 2011, 84, 016105.
339. Song, G.; Li, Y.; Chen, X.; He, X.; Tang, J. Influential node tracking on dynamic social network: An interchange greedy approach. IEEE. Trans. Knowl. Data. Eng. 2016, 29, 359-72.
340. Huang, D. W.; Yu, Z. G. Dynamic-Sensitive centrality of nodes in temporal networks. Sci. Rep. 2017, 7, 41454.
341. Huang, Q.; Zhao, C.; Zhang, X.; Wang, X.; Yi, D. Centrality measures in temporal networks with time series analysis. Europhys. Lett. 2017, 118, 36001.
342. Qu, C.; Zhan, X.; Wang, G.; Wu, J.; Zhang, Z. K. Temporal information gathering process for node ranking in time-varying networks. Chaos 2019, 29, 033116.
343. Arebi, P.; Fatemi, A.; Ramezani, R. An effective approach based on temporal centrality measures for improving temporal network controllability. Cyber. Syst. 2022, 56, 1-20.
344. Li, Y.; Zhao, Y.; Xu, T.; Wu, S. Node importance research of temporal CPPS networks for information fusion. IEEE. Trans. Reliab. 2023, 73, 1291-301.
345. Zhang, T.; Fang, J.; Yang, Z.; Cao, B.; Fan, J. TATKC: a temporal graph neural network for fast approximate temporal Katz centrality ranking. In: Proceedings of the ACM on Web Conference 2024, 2024. pp. 527-38.
346. Yu, E.; Fu, Y.; Chen, X.; Xie, M.; Chen, D. Identifying critical nodes in temporal networks by network embedding. Sci. Rep. 2020, 10, 12494.
347. Yu, E.; Fu, Y.; Zhou, J.; Sun, H.; Chen, D. Predicting critical nodes in temporal networks by dynamic graph convolutional networks. Appl. Sci. 2023, 13, 7272.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data





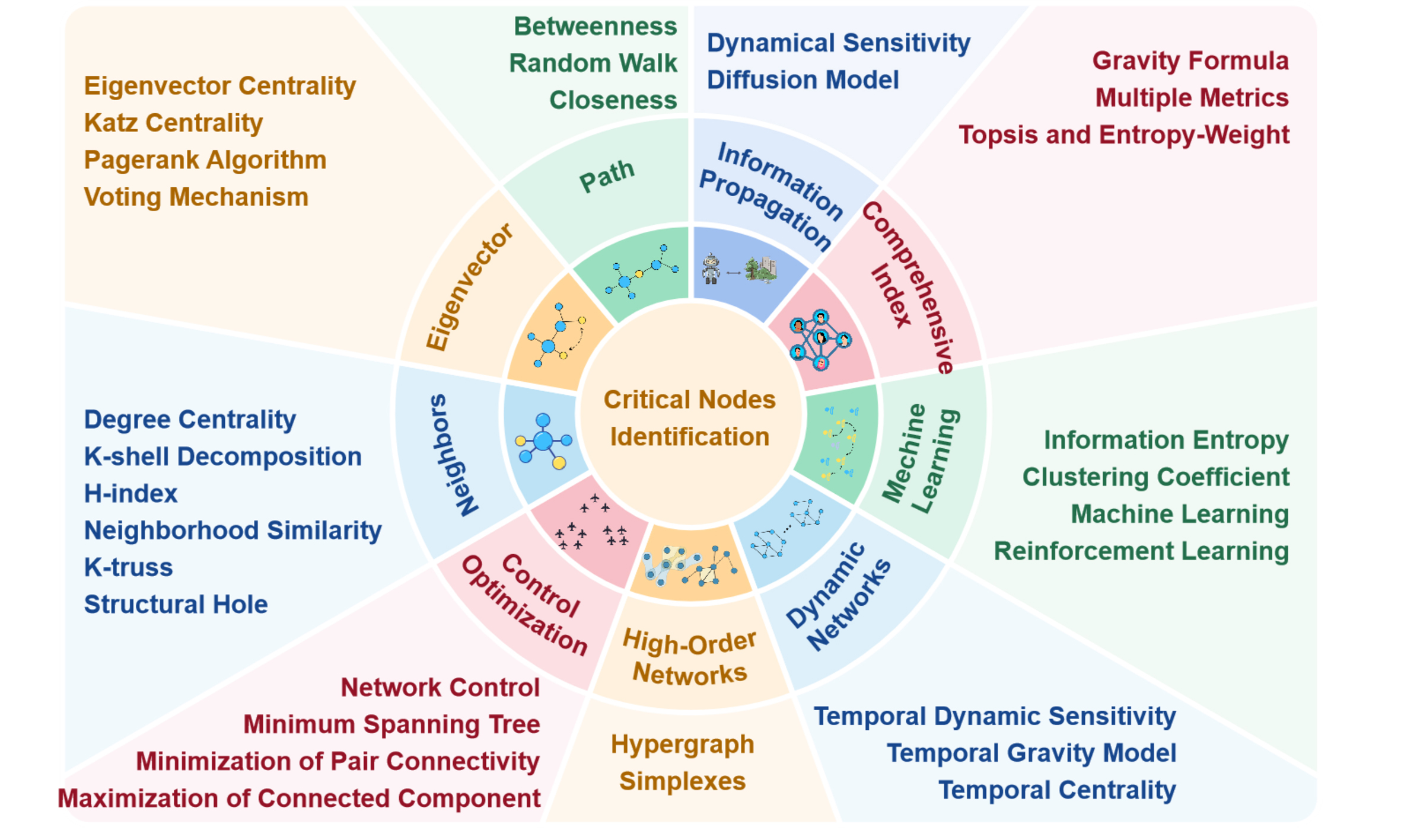
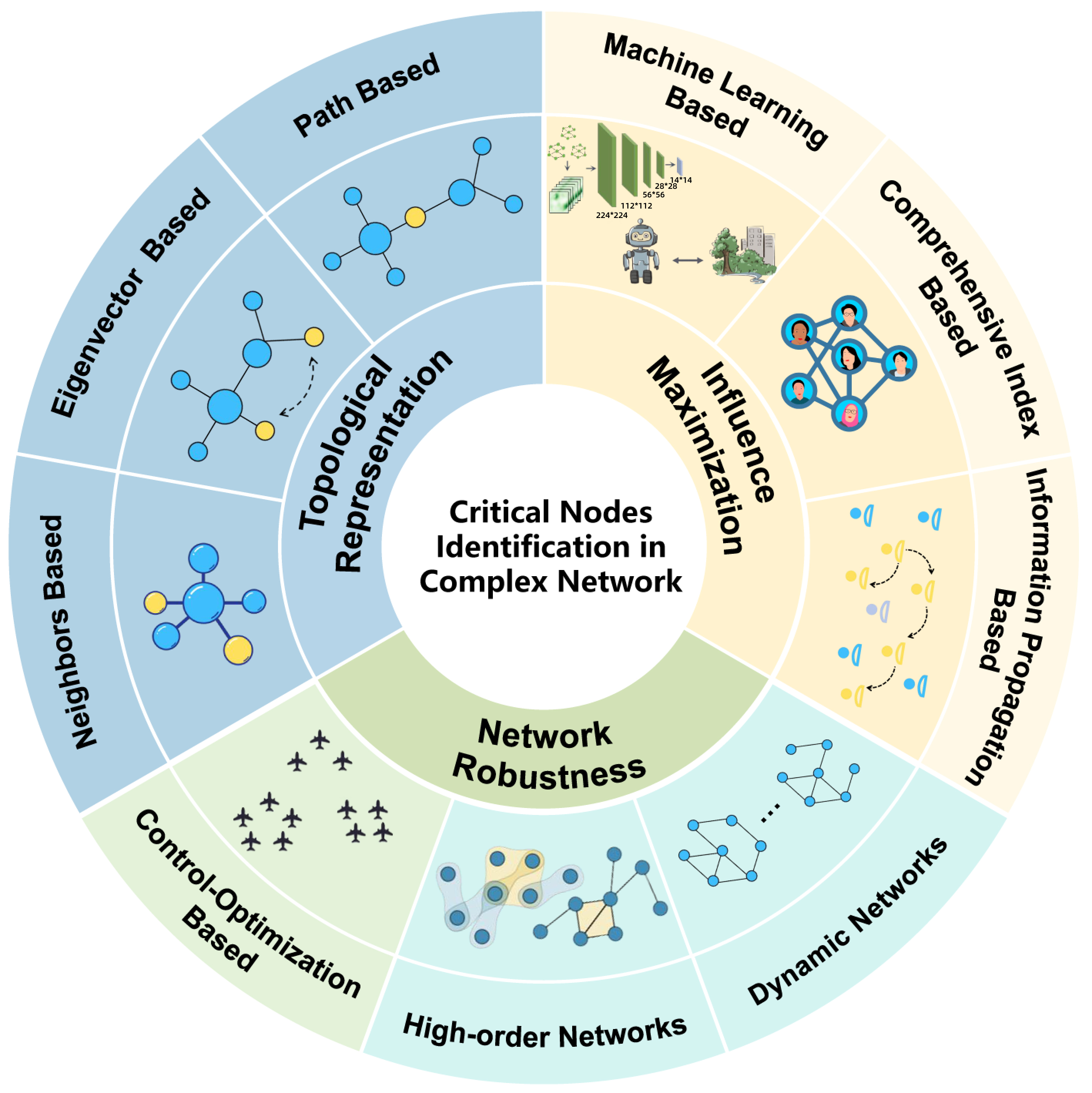
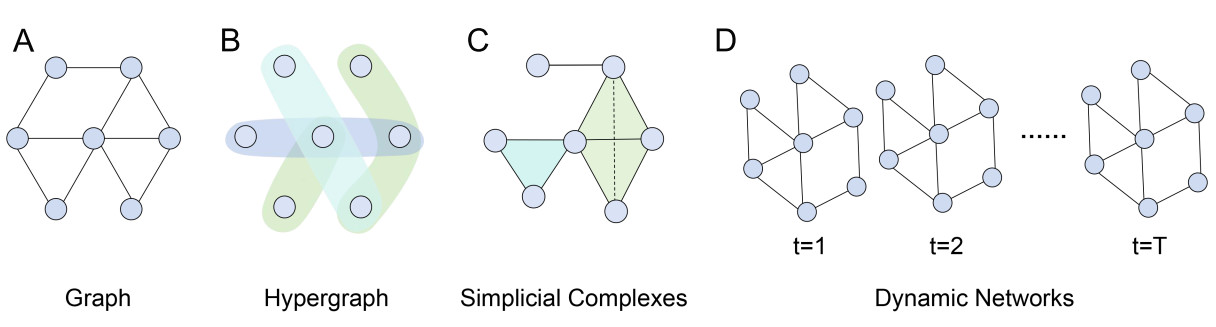











Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].