RF-NSGA-II framework for inverse design of high-performance Mg-Gd-based magnesium alloys
Abstract
An inverse design framework, RF-NSGA-II, is developed using machine learning (ML) methods and a multi-objective co-optimization strategy. It enables intelligent design of chemical compositions and processing parameters for thermo-mechanical treatments based on desired mechanical properties of Mg alloys. Using a database of extruded Mg-Gd and Mg-Y-based alloys, RF-NSGA-II integrates an optimized forward model with a non-dominated sorting genetic algorithm II (NSGA-II). The forward model is constructed by evaluating the performance of different ML algorithms, with the random forest (RF) algorithm experimentally validated to accurately describe the relationship between chemical composition and mechanical properties. RF-NSGA-II simultaneously optimizes multiple mechanical properties, and validation through experimental measurements demonstrates its effectiveness. Using target mechanical properties as inputs, chemical compositions and processing parameters for solid-solution treatment and extrusion are efficiently determined for a high-strength Mg-11.5Gd-6.0Y-1.0Zn-0.2Mn (wt.%) alloy and a high-ductility Mg-2.5Gd-1.0Zn (wt.%) alloy, achieving tensile strength/elongation values of 417 MPa/3.2% and 223 MPa/34%, respectively. These results provide a transparent and effective route for the inverse design of advanced Mg alloys based on desired mechanical properties.
Keywords
INTRODUCTION
Magnesium (Mg) alloys are promising lightweight structural materials for engineering applications in aerospace, automotive, and transportation due to their low density and high specific strength and stiffness[1-3]. However, the relatively low strength and ductility of Mg alloys severely limit their widespread applications[4,5]. The incorporation of rare earths (RE) into the Mg matrix has been demonstrated to significantly enhance the mechanical properties. Particularly, Mg alloys containing Gadolinium (Gd) and Yttrium (Y) show exceptional potential for high-performance applications owing to their excellent solid solution strengthening and age hardening effects[6-10]. The synergistic interaction of Zn, Zr, and Mn with RE elements (Gd/Y) can further enhance the alloy performance by facilitating the formation of a long-period stacking ordered phase (LPSO)[11,12], secondary phase particles[13], and the refined microstructure[14]. Additionally, thermomechanical processes such as extrusion can further improve the mechanical properties of Mg alloys by refining the microstructure through dynamic recrystallization and precipitation phase modulation[9,15,16].
Generally, the development of high-performance Mg alloys depends on the synergistic interaction of alloying elements, processing techniques, and other pertinent variables. As the array of alloying elements expands and processing technologies evolve, the interplays between them become very complex and are not straightforward to understand. This dynamic interaction complicates the correlation between mechanical properties of Mg alloys and their compositional and processing parameters. Currently, the design of Mg alloys predominantly relies on an experimental trial-and-error approach, which is laborious and inefficient. Traditional thermodynamic and kinetic models, based on well-established physical principles, provide reliable predictions when the underlying mechanisms are clear. Nevertheless, they often face challenges in modeling complex, multi-factor coupled systems and obtaining the necessary critical parameters. Given this context, there is an urgent necessity to devise a novel method capable of rapidly capturing the relationship between the mechanical properties of Mg alloys and their composition-processing parameters. To this end, the present study proposes a novel machine learning (ML)-based inverse design framework. It integrates the random forest (RF) and non-dominated sorting genetic algorithm II (NSGA-II), which enables rapid multi-objective optimization and provides a transparent route for the inverse design of advanced Mg alloys.
ML, a rapidly emerging data-driven technology, effectively uncovers implicit relationships within extensive datasets. It is distinguished by its low computational cost and short development cycle[17]. ML has been widely applied across various domains of computer science, including computer vision[18,19] and natural language processing[20]. In the field of materials, there has been growing interest in ML for compound discovery, structural property prediction, new materials discovery, and pharmaceutical molecular design. In a recent study, Rahnama et al. employed a decision tree regression algorithm to predict the hydrogen weight percentage of hydrogen storage metal hydrides[21]. Liu et al. accurately predicted the structure of 891 ABO3 compounds with 94.6% accuracy using a gradient boosting decision tree (GBDT)[22]. In addition, Ghorbani et al. systematically compared several ML algorithms, including Lasso, kernel ridge regression, RF, and neural networks, for predicting tensile properties, providing valuable insights into alloy performance modeling[23]. These applications highlight the potential of ML in the field of materials science, particularly in predicting alloy properties and guiding design optimization. By effectively describing the relationship between material composition and properties, ML facilitates the understanding of the underlying laws governing material-related properties and thus avoids the unnecessary expenditure associated with redundant research[24]. Meanwhile, significant progress has been made in ML-based alloy inverse design research, including the development of global optimization methods[25], active learning[26,27], and generative networks[28,29]. It should be noted that Bayesian optimization has recently evolved beyond traditional global extremum search to address goal-oriented inverse design tasks[30]. Qin et al. combined two expectation improvement (EI) functions to efficiently capture the complex relationship between the ultimate tensile strength (UTS) and electrical conductivity, enabling the ML-based inverse design of Cu-Ni-Si alloys[31]. Padhy et al. developed a multi-objective Bayesian optimization (MOBO)-based inverse design strategy to combine the magnetic, electrical, and mechanical properties to accurately design Fe-Co-Ni alloys[32]. However, the application of ML to Mg alloys remains relatively limited, as research in this area is still in its early stages and mainly focuses on predicting their structures and properties rather than on alloy design.
In recent years, high-performance Mg alloys, particularly those based on Gd and Y, have attracted considerable attention. The resulting body of reliable data provides a solid foundation for applying ML to their design. Developing effective methods for designing such alloys can help overcome the efficiency bottleneck caused by extensive experimental testing and characterization. To achieve simultaneous optimization of multiple mechanical properties, advanced multi-objective optimization strategies are therefore essential. Ghorbani et al. implemented an active learning framework that combined Gaussian process regression with Bayesian optimization to efficiently optimize the multi-objective performance of strength and ductility in Mg alloys, providing valuable technical insights for the field[33]. In contrast, the present study establishes a novel ML-based framework that enables rapid inverse screening and multi-objective optimization of Mg alloy compositions and processing parameters. Unlike Bayesian optimization methods, which rely on iterative sampling and are suited for data-scarce scenarios, the proposed RF-NSGA-II (RF combined with NSGA-II) framework adopts a global search strategy that fully exploits existing database resources. Moreover, it yields the complete set of Pareto-optimal solutions in a single run, providing diverse candidate alloys for efficient materials design.
The present work develops an inverse design framework for Mg-Gd-based alloys by employing ML and a multi-objective co-optimization strategy. Based on the collected data for extruded Mg-Gd and Mg-Y alloys and the identification of key compositional and processing parameters, the optimized forward model was developed by evaluating the performance of multiple ML algorithms, including RF, eXtreme gradient boosting, support vector regression (SVR), and multilayer neural networks. It properly describes the relationship between chemical composition and mechanical properties, including tensile yield strength (TYS), UTS, and elongation (EL). The NSGA-II is then implemented to simultaneously optimize essential mechanical properties using the established forward model, which is validated through experimental measurements. Furthermore, the inverse design framework is adopted to efficiently develop advanced Mg-Gd-based alloys tailored to the desired mechanical properties.
MATERIALS AND METHODS
Data preparation
The dataset employed in present work was compiled from a wide range of published experimental studies on extruded Mg-Gd and Mg-Y-based alloys. The key parameters considered include alloy composition (types and contents of alloying elements), processing parameters [solid solution temperature (ST), solid solution time (St), extrusion temperature (ET), and extrusion ratio (ER)], and mechanical properties (TYS, UTS, and EL). The raw data was cleaned to remove missing and duplicate entries, and feature selection was performed, resulting in approximately 400 available data points. The variation ranges (minimum and maximum limits) of each feature variable are summarized in Table 1. It is worth noting that the lower bounds for the alloying elements were set to zero to preserve a broader design space and avoid artificially excluding potentially high-performance compositions, particularly in the absence of well-defined critical concentration thresholds.
Minimum and maximum limits of feature variables for Mg-Gd and Mg-Y-based alloys
| Variables | Min | Max | Variables | Min | Max |
| Gd (wt.%) | 0 | 15.5 | ST (°C) | 350 | 560 |
| Y (wt.%) | 0 | 7.2 | St (h) | 2 | 48 |
| Zn (wt.%) | 0 | 6.2 | ET (°C) | 250 | 505 |
| Zr (wt.%) | 0 | 1.0 | ER | 3.9 | 89.0 |
| Mn (wt.%) | 0 | 2.2 | TYS (MPa) | 73 | 425 |
| Nd (wt.%) | 0 | 6.5 | UTS (MPa) | 157 | 483 |
| Er (wt.%) | 0 | 9.1 | EL (%) | 1.5 | 63.0 |
Model methods
Four ML models - SVR, artificial neural networks (ANNs), RF, and eXtreme gradient boosting tree (XGBoost) - were implemented to evaluate their efficiency in constructing the forward model for describing the relationship between chemical composition and mechanical properties. In comparison, SVR is a versatile ML algorithm well suited for addressing intricate nonlinear challenges in high-dimensional spaces through the use of kernel tricks[34,35]. ANNs are adept at handling complex nonlinear problems by performing linear and nonlinear transformations with various neuron activation functions[36,37]. Both the RF and XGBoost achieve regression or classification tasks by constructing ensembles of decision trees - either in parallel or sequentially - and demonstrate strong capability in handling high-dimensional, nonlinear data[38]. Moreover, by incorporating random feature selection and regularization, they mitigate overfitting and exhibit good generalization performance[39,40].
The NSGA is widely utilized in multi-objective intelligent optimization algorithms due to its stable performance[41]. In addition, NSGA-II introduces fast non-dominated sorting, crowding distance sorting, and an elitism strategy, which significantly enhance computational efficiency and population diversity while improving the quality of evolved solutions[42]. Compared to single-objective optimization, multi-objective optimization considers multiple performance metrics in alloy design. It also provides the decision-maker with a range of Pareto-optimal solutions[43], offering flexibility in selecting the most suitable design solution based on specific applications. Furthermore, multi-objective optimization may reveal unconventional material combinations or processing methods that are difficult to identify under a single-objective optimization framework, thus offering novel pathways for materials innovation.
Experimental methods
To validate the predictions for the ML-based models, a great variety of Mg-Gd-based alloys were produced via gravity casting, and their compositions were determined using inductively coupled plasma (ICP) analysis. The casting ingots were fabricated as columnar ingots with a diameter of 80 mm and a height of
RF-NSGA-II framework
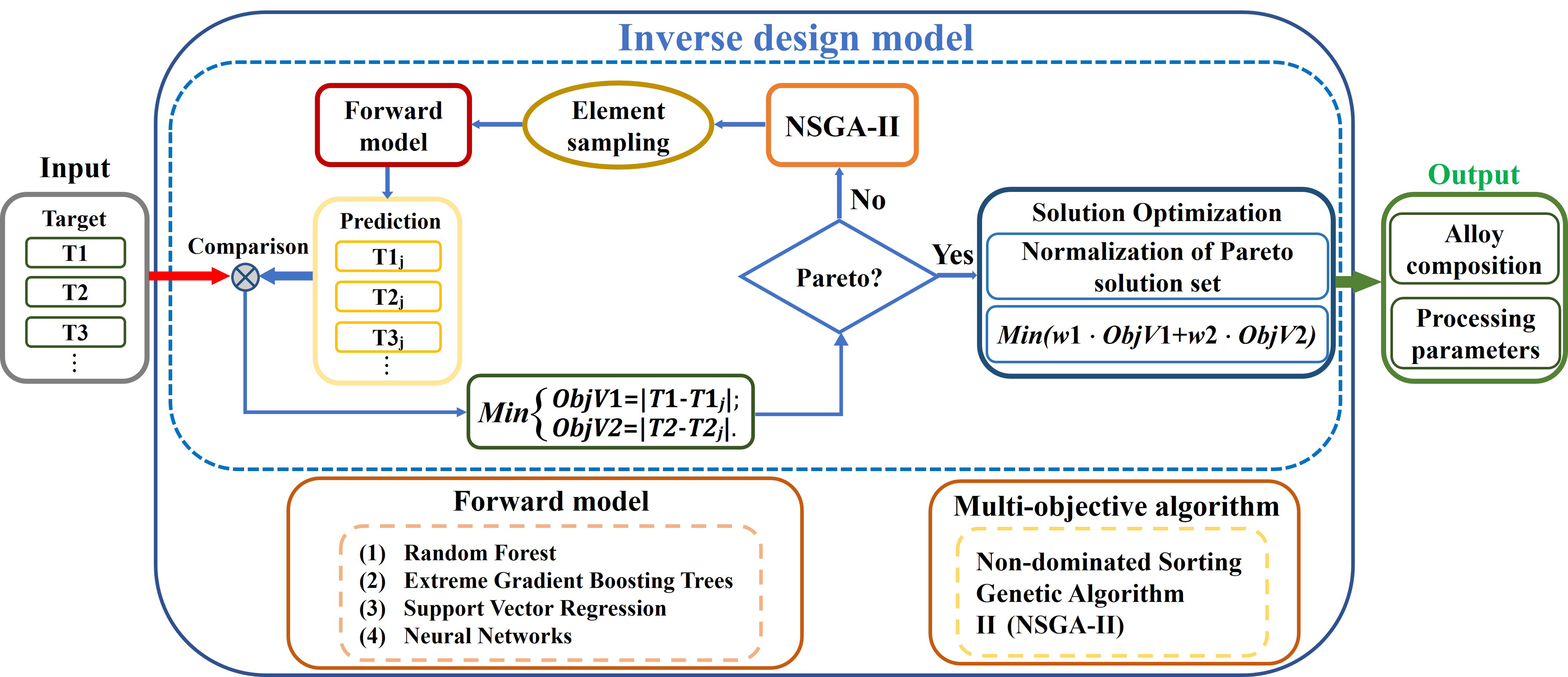
Figure 1 illustrates the proposed inverse design framework for Mg alloys. It comprises a forward model that describes the relationship between chemical composition and mechanical properties, a NSGA-II for multi-objective optimization, and Pareto-optimal solution screening for alloy selection. The framework takes specific mechanical property targets as inputs and outputs optimized alloy compositions and processing parameters. Specifically, the forward model is established by evaluating the performance of different ML methods. Then, the NSGA-II algorithm searches for candidate solutions within the compositional and processing parameter space, aligned with the input dimensions of the forward model. These candidate solutions are fed into the forward model to predict TYS, UTS, and EL for the given composition and processing parameters. Subsequently, the absolute error between the predicted and target values is minimized by updating candidate solutions through non-dominated sorting, population selection, crossover, and mutation. After several iterations, the Pareto-optimal solution set is obtained. Finally, the Pareto-optimal solutions are normalized to eliminate order-of-magnitude differences between objectives, calculated as[44]:
Figure 1. Inverse design framework based on NSGA-II and ML methods. NSGA-II: Non-dominated sorting genetic algorithm II; ML: machine learning.
where Y′ and Y represent the normalized and original objective values, respectively, while Ymin and Ymax are the minimum and maximum values of this objective in the Pareto-optimal solution set.
Therefore, the optimal Pareto solution is selected by minimizing Y′ of different targeted properties, such as UTS and EL, as:
Where F indicates the weighted sum of the normalized objective values; wUTS and wEL represent the importance weights of UTS and EL, respectively (∑wi = 1), reflecting the priority assigned to the accuracy of inverse design for each property[44,45]. In this study, the weights for UTS and EL are both set to 0.5, indicating equal emphasis on the accuracy of their inverse design to achieve a balanced optimization between strength and ductility.
RESULTS AND DISCUSSION
Forward model
To establish the optimal regression model for TYS, UTS, and EL of Mg-Gd-based alloys, four different ML algorithms - SVR, ANN, RF, and XGBoost - were implemented based on Python 3.9 using Scikit-learn and xgboost ML open-source libraries. The predictive capability of different ML algorithms was evaluated using the coefficient of determination (R2) and the mean absolute error (MAE). In the modeling process, standardization was employed to scale the dataset and eliminate the effect of numerical differences on the predictions. In addition, to ensure the robust model evaluation, the effects of data division and algorithm hyperparameters on prediction errors were considered, and a five-fold cross-validation protocol was implemented for the optimization of model parameters.
To evaluate the predictive capability of different ML algorithms, Figure 2 compares the predicted and actual values of TYS, UTS, and EL for Mg-Gd and Mg-Y-based alloys within both training and testing datasets. The R2 and MAE values are presented in Table 2. For TYS, both RF and XGBoost exhibit comparable high R2 values, while RF achieves a lower prediction error on the test set (MAE = 21.0 MPa). For UTS prediction, RF markedly outperforms the other three algorithms on the test set, achieving R2 = 0.90 and MAE =
Figure 2. Predictive accuracy of TYS, UTS, and EL from (A-C) RF, (D-F) XGBoost, (G-I) SVR and (J-L) multilayer neural networks. TYS: Tensile yield strength; UTS: ultimate tensile strength; EL: elongation; RF: random forest; XGBoost: eXtreme gradient boosting tree; SVR: support vector regression.
Comparison of the performance of different ML algorithms
| Algorithm | Evaluation metric | Training set | Testing set | ||||
| TYS | UTS | EL | TYS | UTS | EL | ||
| RF | R2 | 0.95 | 0.96 | 0.91 | 0.89 | 0.90 | 0.84 |
| MAE | 13.1 | 10.2 | 2.0 | 21.0 | 16.5 | 3.2 | |
| XGB | R2 | 0.97 | 0.96 | 0.97 | 0.89 | 0.87 | 0.81 |
| MAE | 10.4 | 10.3 | 1.2 | 22.3 | 18.5 | 3.3 | |
| SVR | R2 | 0.94 | 0.9 | 0.86 | 0.85 | 0.87 | 0.75 |
| MAE | 9.2 | 14.0 | 3.0 | 23.0 | 18.3 | 3.4 | |
| MLP | R2 | 0.90 | 0.96 | 0.86 | 0.86 | 0.83 | 0.81 |
| MAE | 18.4 | 9.5 | 2.7 | 23.0 | 22.2 | 3.7 | |
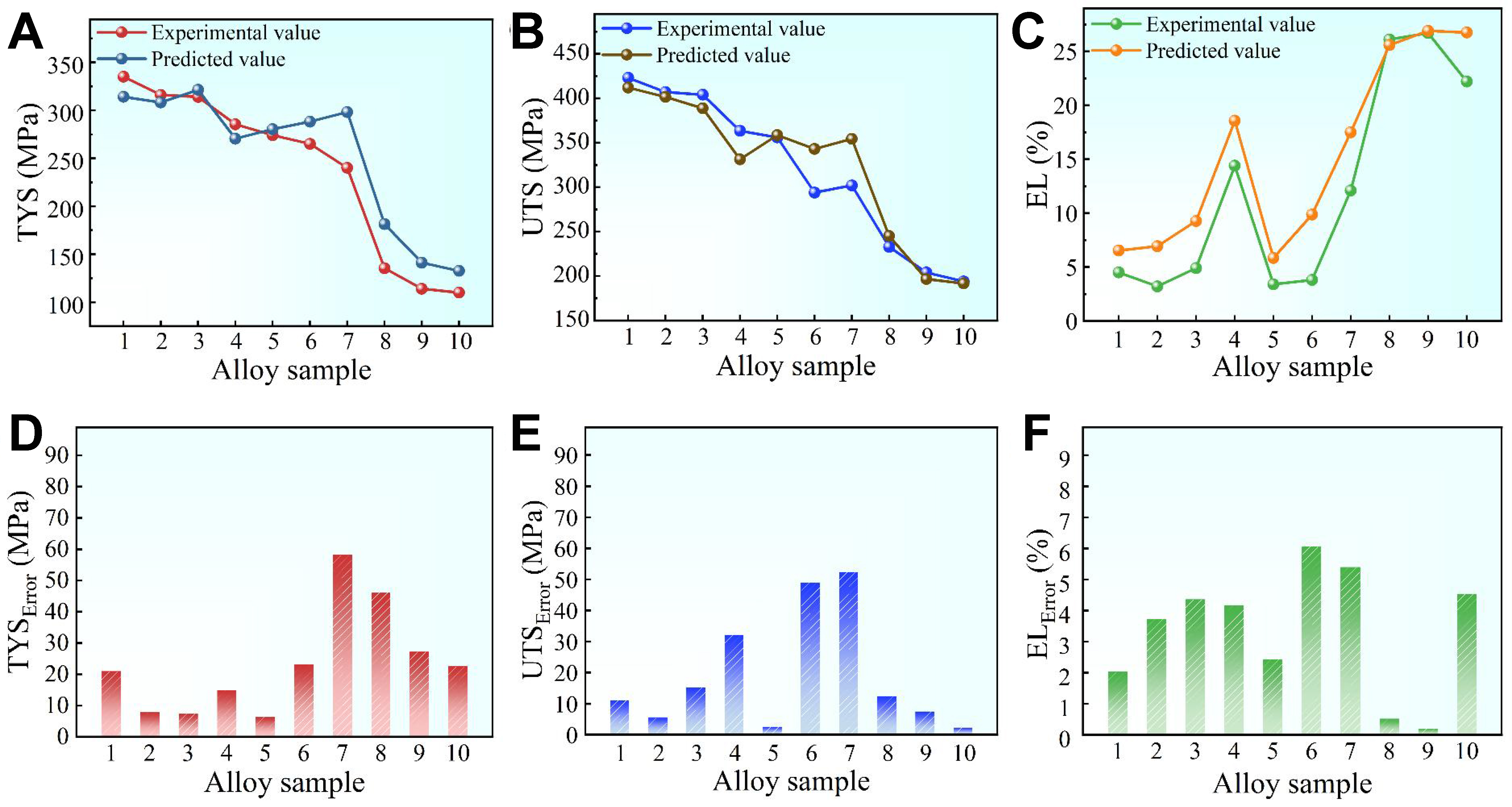
To further verify the predictive ability of the RF model, ten different Mg-Gd-based alloys were prepared and tested for tensile mechanical properties. The chemical compositions and processing parameters are shown in Table 3. It should be noted that the selected alloys span a wide range of compositional and processing conditions to ensure representative validation samples. To compare with experimental measurements, the TYS, UTS, and EL are predicted using the established RF forward model with the parameters listed in Table 3. Figure 3A-C compares the experimentally measured TYS, UTS, and EL with the predictions from the RF forward model for various high-strength and high-ductility alloys, demonstrating strong agreement between predicted and measured mechanical properties of Mg-Gd-based alloys. The absolute prediction errors of the RF forward model are illustrated in Figure 3D-F. Specifically, the predictive discrepancies for UTS and TYS are less than 30 MPa for most alloys, while the prediction error for EL is mainly below 4%. On average, the prediction discrepancies of TYS, UTS, and EL are 23.5 MPa (~9.8%), 19.0 MPa (~6.0%), and 3.3%, respectively. Although a few samples exhibit slightly larger deviations, the errors are randomly distributed across all test cases, without evident bias toward specific compositional or processing conditions. It suggests that the RF model maintains robust predictive stability and generalizability across different regions of the input feature space.
Figure 3. Comparison between the RF predictions and experimental measurements of mechanical properties (A-C) for different high-strength and high-ductility alloys, and the corresponding absolute errors between the prediction and measurements (D-F). RF: Random forest.
The actual chemical composition and processing parameters of the alloys
| No. | Composition (wt.%) | Processing parameters | |||||||||
| Gd | Y | Zn | Zr | Mn | Nd | Er | ST (°C) | St (h) | ET (°C) | ER | |
| 1 | 12.3 | 6.2 | 1.4 | 0.3 | 514 | 21 | 420 | 15 | |||
| 2 | 11.0 | 5.4 | 1.0 | 0.5 | 520 | 12 | 420 | 11 | |||
| 3 | 10.4 | 7.8 | 2.8 | 0.8 | 514 | 30 | 437 | 22 | |||
| 4 | 11.1 | 0.5 | 1.1 | 0.9 | 540 | 12 | 415 | 22 | |||
| 5 | 15.5 | 0.1 | 1.9 | 0.2 | 5.0 | 4.0 | 510 | 22 | 395 | 14 | |
| 6 | 12.4 | 0.1 | 1.9 | 0.3 | 6.2 | 0.3 | 510 | 18 | 450 | 10 | |
| 7 | 11.2 | 0.8 | 1.8 | 0.3 | 2.0 | 540 | 5 | 400 | 22 | ||
| 8 | 1.8 | 0.2 | 1.2 | 0.1 | 489 | 7 | 390 | 22 | |||
| 9 | 2.9 | 0.7 | 0.2 | 0.5 | 2.8 | 540 | 8 | 390 | 22 | ||
| 10 | 2.6 | 0.7 | 0.2 | 0.4 | 2.5 | 540 | 8 | 420 | 22 | ||
Inverse model
In accordance with the inverse design framework described in Figure 1, the inverse design model was established by integrating the forward model based on RF algorithm and NSGA-II model in Python 3.9 relying on Geatpy2.7 evolutionary algorithm open-source tool. Considering the strong correlation between TYS and UTS, the objective functions of the model are defined as the absolute prediction error of UTS
where P denotes the predicted value of the forward model, T represents the target properties, which correspond to the input parameters of the inverse design model. Namely, when AEUTS = 0 and AEEL = 0, the target properties are perfectly achieved by the designed chemical composition and processing parameters. In order to facilitate the analysis of the performance of the model, the reference condition is set as a binary array (0, 0).
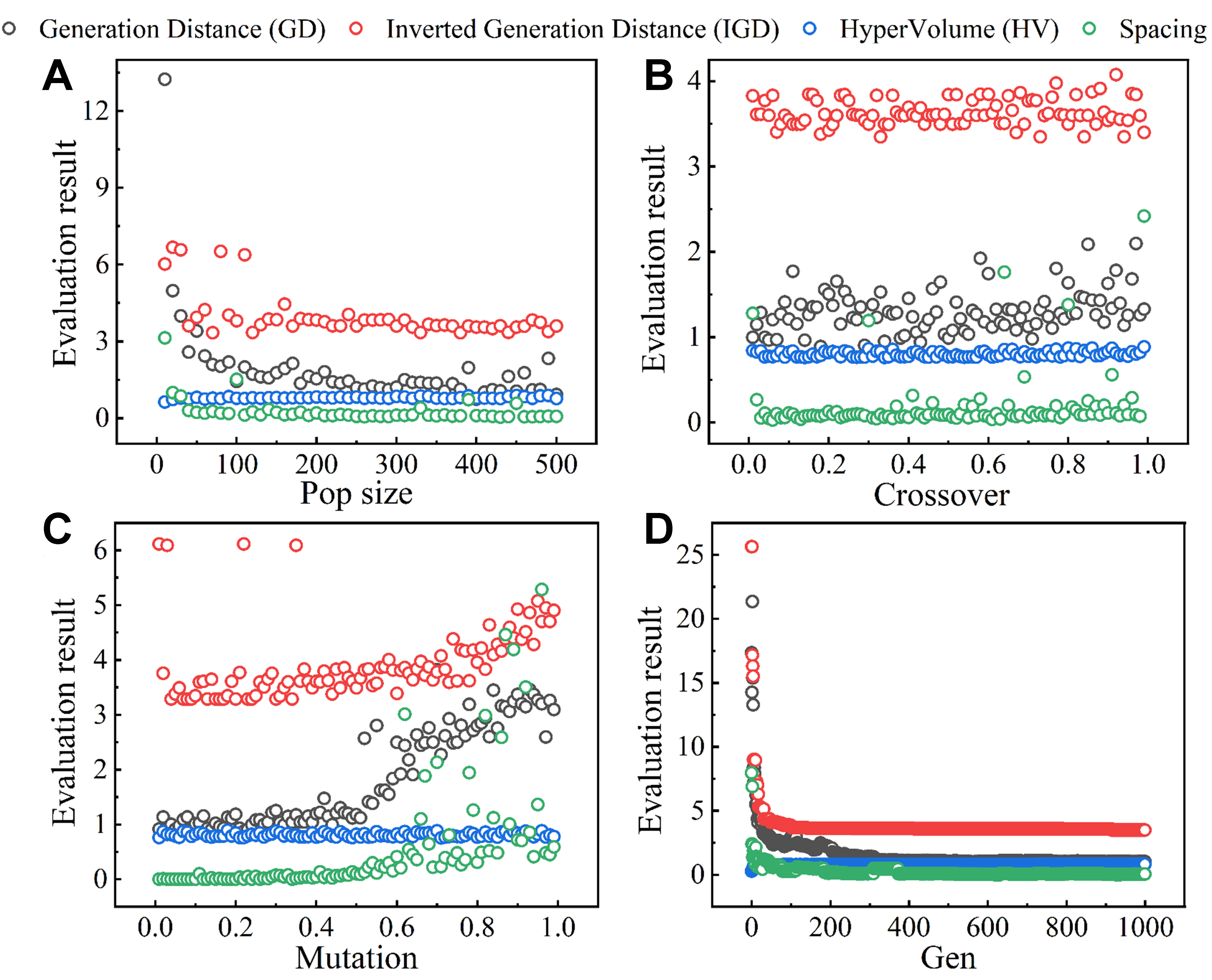
The population size (Pop size), Crossover, Mutation, and the number of generations (Gen) in NSGA-II exhibit an important influence on the efficiency of optimization process, which in turn affects the stability of the inverse design model. In order to prevent local optimum entrapment during modeling, a cyclic traversal method was employed to investigate the effects of the four parameters on model stability. Accordingly, the performance is evaluated using indicators such as generation distance (GD), inverse generation distance (IGD), hypervolume (HV) and spacing.
Figure 4 illustrates how model stability changes with variations in Pop size, crossover, mutation, and Gen. The effect of Pop size on the four assessment indicators [Figure 4A] shows a marked decline in both GD and IGD as Pop size increases, stabilizing at a low level once the population exceeds 300. The irregular fluctuations in HV are likely due to the built-in reference point setting, which randomly initializes a different reference value each cycle. Nonetheless, the overall trend of HV increases with Pop size. When the population reaches 200, the spacing decreases significantly, approaching nearly zero. Systematic evaluation demonstrates that both convergence efficiency and solution quality in the inverse design model are positively correlated with Pop size, with satisfactory stability achieved when the Pop size exceeds 300.
Figure 4. Changes of GD, IGD, HV, and spacing with (A) population size, (B) crossover, (C) mutation, and (D) number of population genetic generations in inverse design model. GD: Generation distance; IGD: inverse generation distance; HV: hypervolume.
The effects of mutation and crossover probabilities are further examined, as illustrated in Figure 4B and C, respectively. The findings indicate that at relatively low mutation probabilities, the model exhibits good convergence and less impact on overall solution quality, as evidenced by fluctuations in the HV metrics at higher levels. This suggests that the variations in mutation probability have a limited effect on the solution quality, indicating that the solution obtained by the NSGA-II algorithm is in good agreement with the real solution. When the mutation probability exceeds 0.5, the uniformity of the solution diminishes and the stability is compromised. This indicates that the NSGA-II algorithm exhibits enhanced convergence efficiency under lower mutation probabilities, resulting in optimization results that are closer to the true values. Conversely, the variation of the crossover probability shows a negligible effect on all four indicators. The HV value remains high and close to 1, while the GD and spacing values remain low. This indicates that the quality of the solution set and the coverage of the objective space are maintained at an optimal level.
To enable computationally efficient alloy design, the optimization of Gen was systematically analyzed. The number of selection, crossover, and mutation operations performed by the model increases with the number of the Gen. It should be noted that configurations with inadequately low Gen may induce insufficient exploration of the target space, and result in local optimization. As illustrated in Figure 4D, the degrees of convergence, diversity, and uniformity of the model are markedly enhanced, while the stability of the model is essentially maintained up to 300 generations. Consequently, the optimal parameter settings for the Mg alloy inverse model are Pop size = 300, Mutation = 0.5, Crossover = 0.7, and Gen = 300.
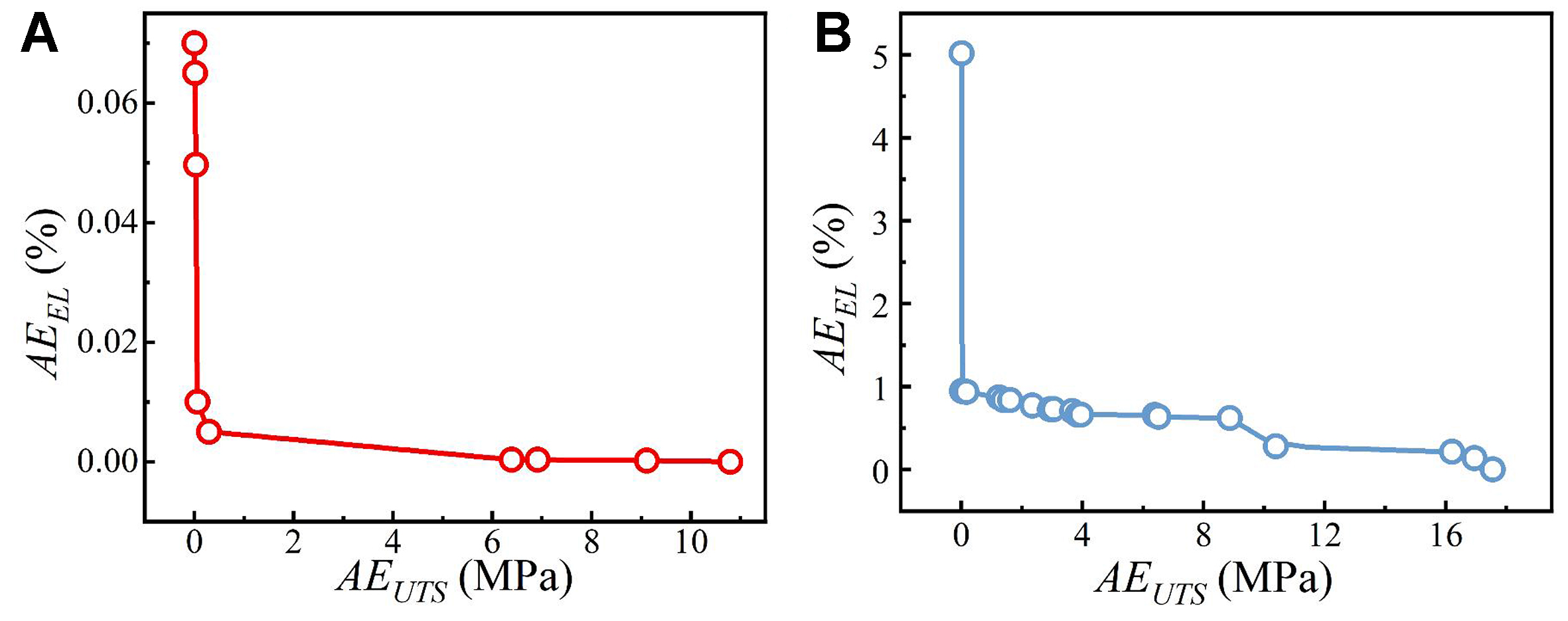
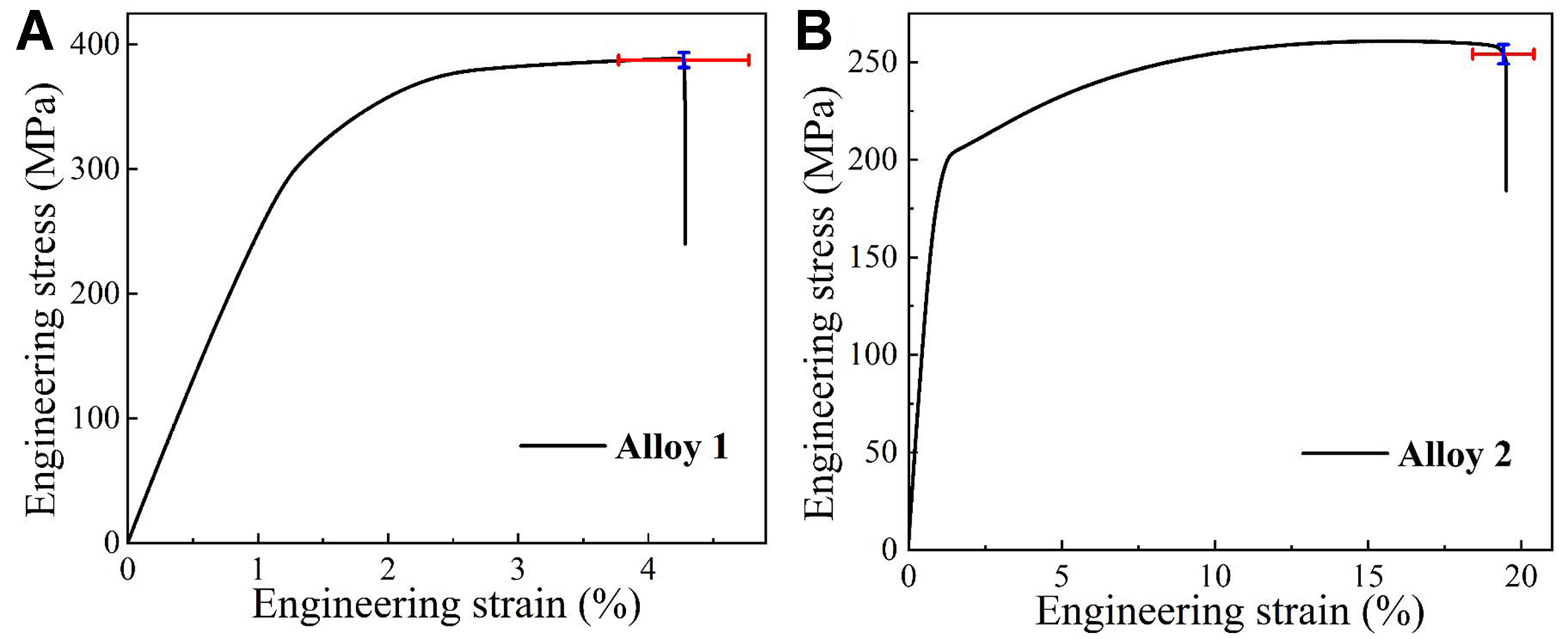
In order to verify the design capability of the developed RF-NSGA-II framework, we applied the model to alloy design using two different target properties as inputs: Alloy 1: UTS = 400 MPa; EL = 5% and Alloy 2: UTS = 250 MPa; EL = 20%. Figure 5 illustrates the Pareto frontier optimization results for the two alloys. It is clear that the non-dominated solutions obtained by the model show a relatively small error from the target properties. Specifically, the non-dominated solutions for Alloy 1 show small deviations of less than
Figure 5. The Pareto front of validation alloys generated by the RF-NSGA inverse design model: (A) Alloy 1 with the target UTS =
The predicted composition and processing parameters from the RF-NSGA inverse design model
| Alloy | Composition (wt.%) | Processing parameters | Predicted | Target | ||||||||
| Gd | Y | Zn | Mn | ST (°C) | St (h) | ET (°C) | ER | UTS/MPa | EL/% | UTS/MPa | EL/% | |
| Alloy 1 | 11.0 | 5.8 | 1.1 | 0.1 | 515 | 16 | 455 | 10 | 400.3 | 5.1 | 400 | 5 |
| Alloy 2 | 2.4 | 0.0 | 1.5 | 0.0 | 490 | 20 | 400 | 22 | 250.1 | 19.1 | 250 | 20 |
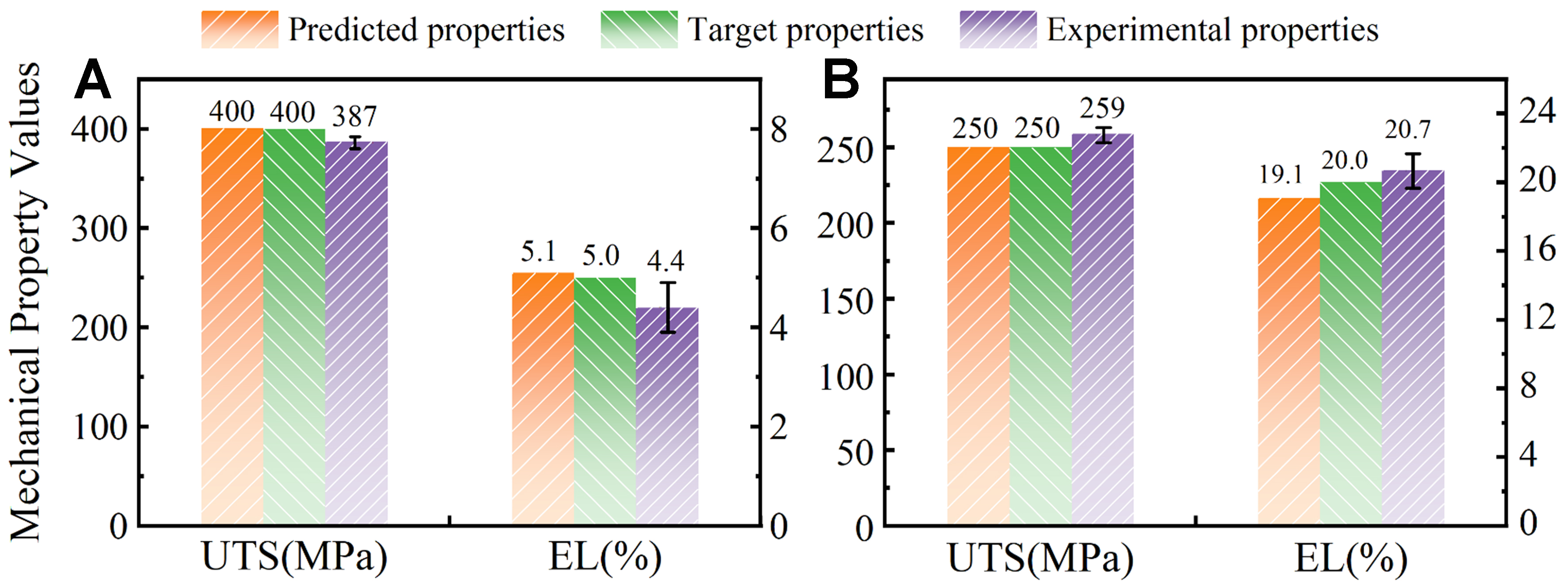
To verify the predictions, the two designed Mg alloys are experimentally fabricated and processed according to the chemical composition and processing parameters listed in Table 4. The experimentally measured engineering stress-strain curves of both alloys are shown in Figure 6. The measured UTS and EL are
Inverse design of high-performance Mg-Gd-based alloy
For data-centric ML methods, the ability to effectively guide high-performance alloy design at or beyond existing dataset boundaries represents a critical aspect of practical application. In this context, the established RF-NSGA inverse design model was employed to design Mg-Gd-based alloys at the edge of the dataset to achieve improved mechanical properties. Given the potential of different combinations of chemical compositions and processing parameters at the data edge to reach target properties, the inverse design process was configured with an expanded decision space, as detailed in Table 5. It should be noted that, although the decision space was broadened to some extent, the compositional and processing parameters remained within physically and technologically reasonable limits.
The expanded decision space used for the inverse design of high-performance Mg-Gd-based alloys
| Range | Composition (wt.%) | Processing parameters | ||||||
| Gd | Y | Zn | Mn | ST (°C) | St (h) | ET (°C) | ER | |
| Min | 0 | 0 | 0 | 0 | 400 | 5 | 290 | 5 |
| Max | 15 | 7 | 4 | 2 | 560 | 30 | 460 | 40 |
Using the established RF-NSGA inverse design model, two Mg-Gd-based alloys with high strength and ductility were designed. The target properties for the two alloys were set as UTS values of 450 and 250 MPa, paired with EL values of 5% and 40%, respectively. To ensure design stability, five independent inverse design runs were conducted. The optimized chemical compositions and processing parameters were then selected by comparing their deviations from the target values.
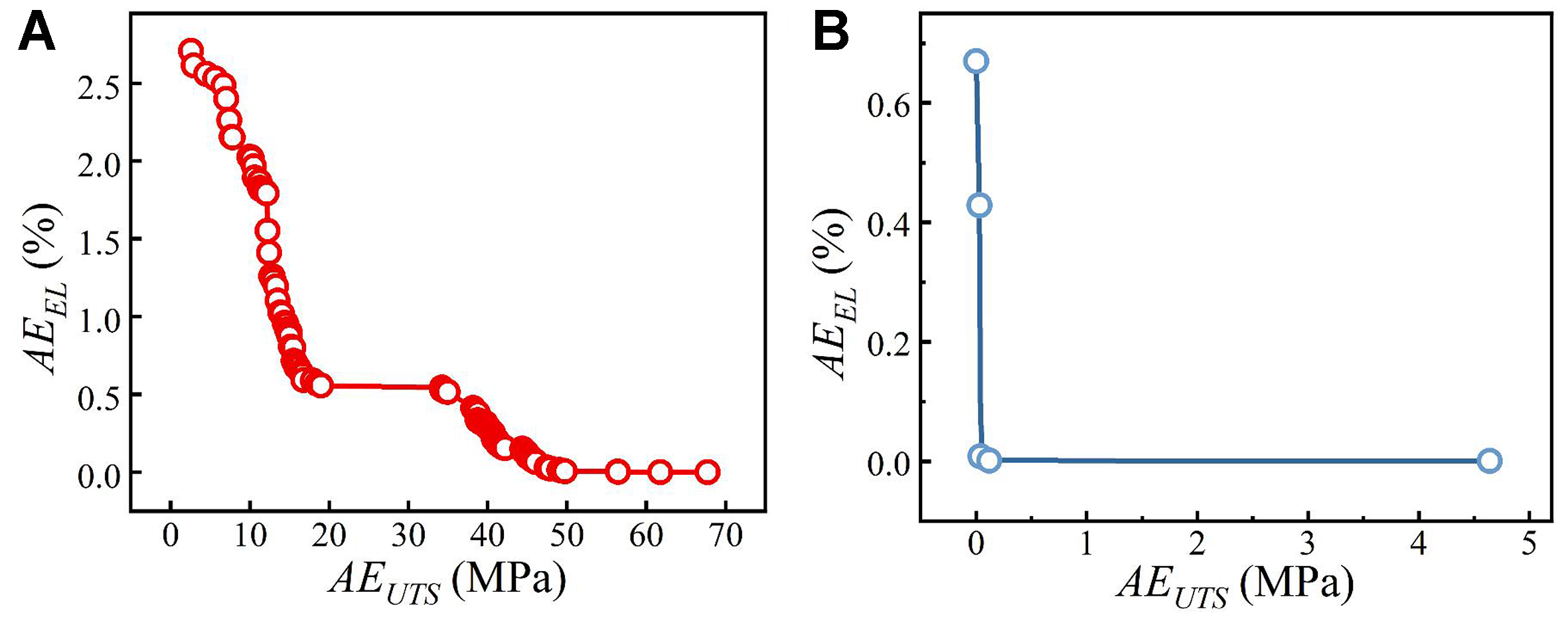
Figure 8 shows the Pareto optimal frontiers calculated by the inverse model for the two alloys. In comparison, the non-dominated solutions for high-strength alloys are rather scattered, indicating an increased challenge in the balance between strength and ductility. The designed chemical composition and process parameters for both alloys are shown in Table 6. Accordingly, the high-strength alloy is Mg-11.5Gd-6.0Y-1.0Zn-0.2Mn (VW126, wt.%) containing relatively high RE content of 17.5 wt.%. The high-ductility alloy is Mg-2.5Gd-1.0Zn (VZ31, wt.%) containing relatively low RE content of 2.5 wt.%. It should be noted that the UTS of the designed VW126 alloy is slightly below the target value (~11.3 MPa) due to the limited data available for high-strength alloys within the established dataset.
Figure 8. The Pareto front of high-performance Mg-Gd-based alloys generated by the RF-NSGA inverse design model: (A) high-strength alloy with the target UTS = 450 MPa and EL = 5%; and (B) high-ductility alloy with the target UTS = 250 MPa and EL = 40%. RF: Random forest; NSGA: non-dominated sorting genetic algorithm; UTS: ultimate tensile strength; EL: elongation.
Prediction of the compositions, process parameters, and mechanical properties of high-performance Mg-Gd-based alloys from the inverse design model
| Alloy | Composition (wt.%) | Processing parameters | Predicted | Target | ||||||||
| Gd | Y | Zn | Mn | ST (°C) | St (h) | ET (°C) | ER | UTS/MPa | EL/% | UTS/MPa | EL/% | |
| VW126 | 11.5 | 6.0 | 1.1 | 0.2 | 512 | 12 | 400 | 13 | 438.7 | 6.8 | 450 | 5 |
| VZ31 | 2.5 | 0.0 | 0.9 | 0.0 | 547 | 13 | 410 | 28 | 250.1 | 40.0 | 250 | 40 |
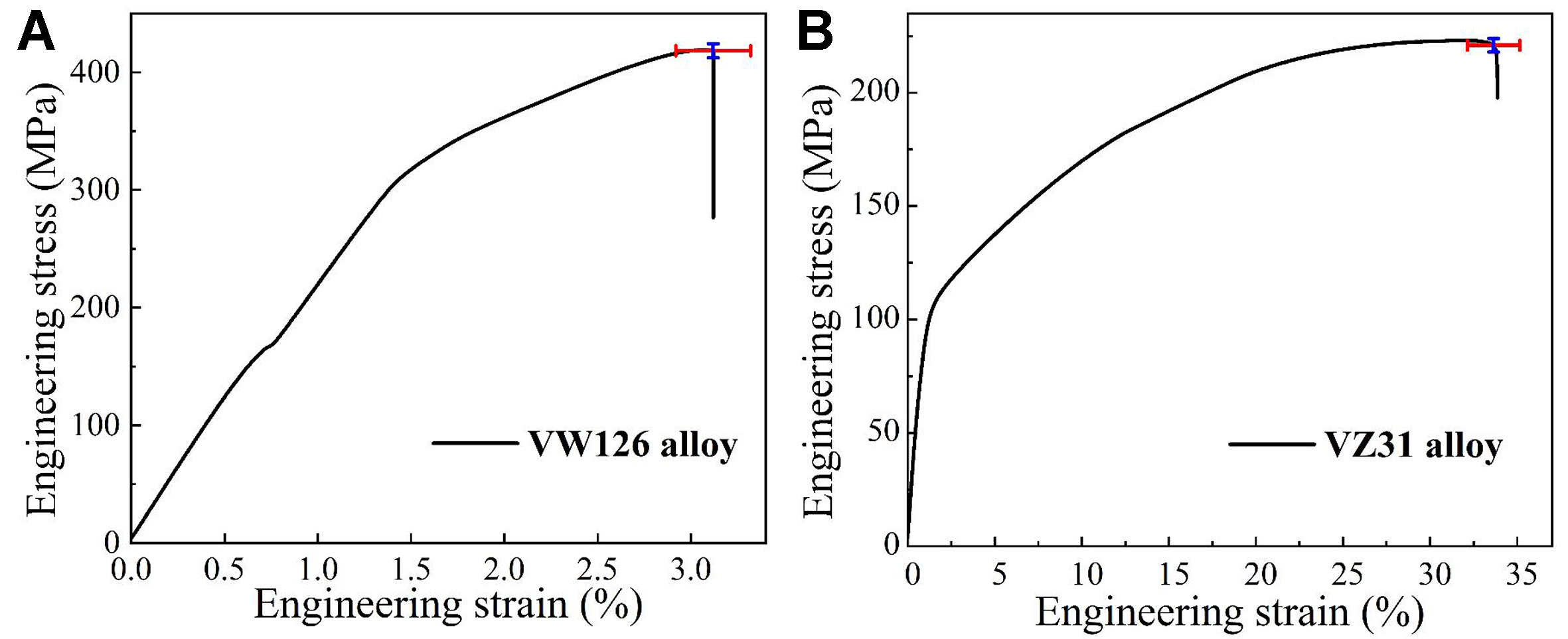
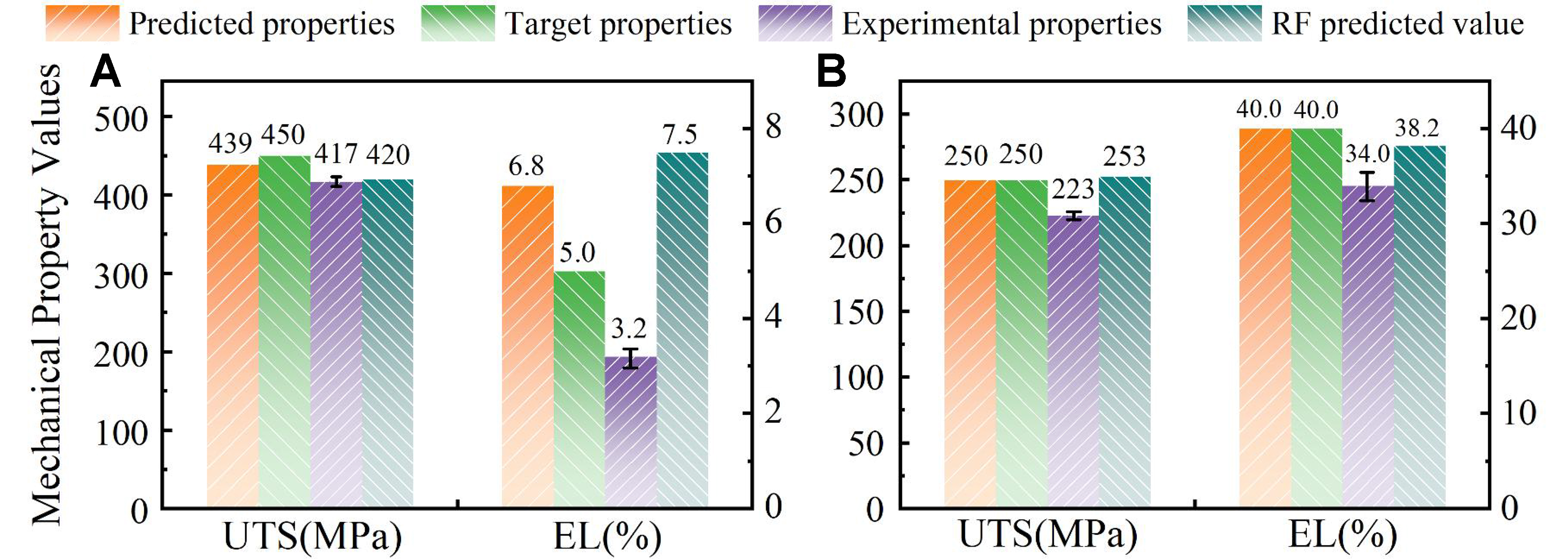
Based on the predictions from the inverse design model, VW126 and VZ31 alloys were prepared for mechanical property tests. The actual compositions of the designed alloys and the process parameters applied in practical experiments are shown in Table 7. It should be noted that the ER applied in the experiments was slightly different from the designed ones for simplification. The tensile stress-strain curves of the two alloys at room temperature are illustrated in Figure 9. Three repetitive tests were performed for each alloy to ensure reliability. The averaged UTS and EL of the VW126 alloy were experimentally measured to be 417 MPa and 3.2%, respectively, while those of the VZ31 alloy were 223 MPa and 34.0%. For comparison without any potential uncertainties, the RF forward model was applied to predict the mechanical properties for the designed alloys with the inputs shown in Table 7. Figure 10 compares the experimentally measured mechanical properties with the target values, the predictions from the RF-NSGA inverse design model, and the RF model predictions based on the experimental input parameters. It is clear that the deviations in UTS and EL between the predictions from the inverse design model and the experimental measurements are 21.7 MPa and 3.6% for the VW126 alloy, and 27.1 MPa and 6.0% for the VZ31 alloy. It is worth noting that using absolute error to evaluate EL is more appropriate, as the relatively low EL values can lead to an overestimation of deviations when using relative error in the low-value range. With the inputs used in the experiments (which slightly differ from the designed ones), the deviations in UTS and EL between the predictions from the RF forward model and the experimental results are further reduced to 3.5 MPa and 4.3% for the VW126 alloy, and 29.7 MPa and 4.2% for the VZ31 alloy. Therefore, the established inverse design model exhibits relatively high reliability for the efficient design of high-strength and high-ductility Mg-Gd-based alloys. The present advances provide a transparent route for the inverse design of advanced Mg alloys based on the desired mechanical properties. It should be noted that, although the current study focuses on Mg-Gd-based alloys, the proposed inverse design framework is inherently generalizable to other alloy systems with appropriate modifications to the input parameters.
Figure 9. Room-temperature tensile stress-strain curves of high-performance Mg-Gd-based alloys designed by the inverse design model: (A) VW126 alloy and (B) VZ31 alloy.
Figure 10. Comparison of mechanical properties from experimental measurements, inverse design mode, target properties, and the RF model with the inputs applied practically in experiments for (A) VW126 alloy and (B) VZ31 alloy. RF: Random forest.
Chemical composition and processing parameters applied practically in the experiments
| Alloy | Composition (wt.%) | Processing parameters | ||||||
| Gd | Y | Zn | Mn | ST (°C) | St (h) | ET (°C) | ER | |
| VW126 | 11.4 | 6.2 | 1.2 | 0.3 | 515 | 12 | 400 | 10 |
| VZ31 | 2.7 | 0.0 | 0.9 | 0.0 | 545 | 13 | 410 | 25 |
CONCLUSIONS
To achieve the intelligent design of chemical composition and processing parameters of thermo-mechanical treatments based on the desired mechanical properties of Mg alloys, an inverse design framework is developed by employing ML methods and a multi-objective co-optimization strategy. The framework is validated by experimental measurements and applied to the efficient design of advanced Mg-Gd-based alloys. The main findings are summarized as follows:
(1) A forward model is established by evaluating the performance of different ML algorithms. Among them, the RF algorithm is demonstrated to accurately describe the relationship between chemical composition and mechanical properties for Mg-Gd and Mg-Y-based alloys. Its generalization capability is further validated by experimental measurements.
(2) The RF-NSGA-II framework is established by integrating the optimized forward model with the NSGA-II for Mg alloys. It enables the inverse determination of alloy compositions and processing parameters based on target properties. The efficiency of the model is further validated by experimental measurements.
(3) The RF-NSGA-II framework is successfully applied to intelligent design of a high-strength Mg-11.5Gd-6.0Y-1.0Zn-0.2Mn (wt.%) alloy and a high-ductility Mg-2.5Gd-1.0Zn (wt.%) alloy. The experimentally measured UTS and EL of these alloys are 417 MPa and 3.2%, and 223 MPa and 34.0%, respectively. The present findings demonstrate a transparent and effective route for the inverse design of advanced Mg alloys with tailored mechanical properties.
DECLARATIONS
Authors’ contributions
Investigation, data curation and analysis, conceptualization, figure preparation, writing - original draft: Cheng, Y.; Wang, L.
Conceptualization, funding acquisition, data curation, resources, supervision, project administration, writing - review and editing: Dong, Z.
Methodology, data processing, figure preparation: Zheng, Z.; Xia, Z.
Methodology; writing - review and editing: Bai, S.; Song, J.
Funding acquisition; writing - review and editing, Project administration: Jiang, B.
Availability of data and materials
Raw data that support the findings are available from the corresponding author upon reasonable request.
Financial support and sponsorship
None.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Luo, X.; Yang, H.; Zhou, J.; et al. Achieving outstanding heat-resistant Mg-Gd-Y-Zn-Mn alloy via introducing RE/Zn segregation on α-Mn nanoparticles. Scr. Mater. 2023, 236, 115672.
3. Mordike, B. L.; Ebert, T. Magnesium: properties - applications - potential. Mater. Sci. Eng. A. 2001, 302, 37-45.
4. Joost, W. J.; Krajewski, P. E. Towards magnesium alloys for high-volume automotive applications. Scr. Mater. 2017, 128, 107-12.
5. Shah, S.; Liu, M.; Khan, A.; et al. Twinning aspects and their efficient roles in wrought Mg alloys: a comprehensive review. J. Magnes. Alloys. 2024, 12, 2201-30.
6. Li, Y.; Zhang, A.; Li, C.; et al. Recent advances of high strength Mg-RE alloys: alloy development, forming and application. J. Mater. Res. Technol. 2023, 26, 2919-40.
7. Jiang, B.; Dong, Z.; Zhang, A.; Song, J.; Pan, F. Recent advances in micro-alloyed wrought magnesium alloys: theory and design. Trans. Nonferrous. Met. Soc. China. 2022, 32, 1741-80.
8. Calado, L. M.; Carmezim, M. J.; Montemor, M. F. Corrigendum: Rare earth based magnesium alloys - a review on WE series. Front. Mater. 2022, 9, 858921.
9. Wang, H.; Luo, X.; Zhang, D.; Qiu, C.; Chen, D. High-strength extruded magnesium alloys: a critical review. J. Mater. Sci. Technol. 2024, 199, 27-52.
10. Ning, J.; Gao, B.; Yuan, X.; Zhou, J.; Tang, G.; Chen, L. Strength and ductility improvement in a heterostructured Mg-Gd-Y alloy with inversely-gradient hardness distribution. Jf. Mater. Res. Technol. 2024, 28, 3781-93.
11. Li, Y.; Yang, C.; Zeng, X.; Jin, P.; Qiu, D.; Ding, W. Microstructure evolution and mechanical properties of magnesium alloys containing long period stacking ordered phase. Mater. Charact. 2018, 141, 286-95.
12. Zhou, J.; Luo, X.; Yang, H.; et al. Introducing lamellar LPSO phase to regulate room and high-temperature mechanical properties of Mg-Gd-Y-Zn-Zr alloys by altering cooling rate. J. Mater. Res. Technol. 2023, 24, 7258-69.
13. Chen, J.; Ji, C.; Huang, Q.; et al. Formation mechanism of W phase and its effects on the mechanical properties of Mg−Dy−Zn alloys. J. Magnes. Alloys. 2025, 13, 2174-89.
14. Wu, G.; Tong, X.; Wang, C.; Jiang, R.; Ding, W. Recent advances on grain refinement of magnesium rare-earth alloys during the whole casting processes: a review. J. Magnes. Alloys. 2023, 11, 3463-83.
15. Xue, K.; Luo, Z.; Xia, S.; Dong, J.; Li, P. Study of microstructural evolution, mechanical properties and plastic deformation behavior of Mg-Gd-Y-Zn-Zr alloy prepared by high-pressure torsion. Mater. Sci. Eng. A. 2024, 891, 145953.
16. Jiang, Y.; Le, Q.; Zhu, Y.; et al. Review on forming process of magnesium alloy characteristic forgings. J. Alloys. Compd. 2024, 970, 172666.
17. Wei, J.; Chu, X.; Sun, X.; et al. Machine learning in materials science. InfoMat 2019, 1, 338-58.
18. Zhang, C. C.; Zhang, K.; Ni, R.; Liu, H.; Shen, J. Unleashing the potential of machine learning: an exploration of state-of-the-art algorithms and real-world applications in computer vision. In 2023 Congress in Computer Science, Computer Engineering, & Applied Computing (CSCE), Las Vegas, USA. July 24-27, 2023. IEEE; 2023. pp. 422-5.
19. Kate, C.; Kalpana, C.; Sharma, A.; Yadav, A. S.; Kumar, A.; Kumar, S. S. Investigation of machine learning algorithms for pattern recognition in image processing. In 2023 5th International Conference on Inventive Research in Computing Applications (ICIRCA) Coimbatore, India. August 03-05, 2023. IEEE; 2023. pp. 898-904.
20. Sharma, H.; Jindal, H.; Devi, B. Advancements in natural language processing: techniques and applications. In 2023 International Conference on Advanced Computing & Communication Technologies (ICACCTech), Banur, India. December 23-24, 2023. IEEE; 2023. pp. 61-5.
21. Rahnama, A.; Zepon, G.; Sridhar, S. Machine learning based prediction of metal hydrides for hydrogen storage, part I: prediction of hydrogen weight percent. Int. J. Hydrogen. Energy. 2019, 44, 7337-44.
22. Liu, H.; Cheng, J.; Dong, H.; et al. Screening stable and metastable ABO3 perovskites using machine learning and the materials project. Comput. Mater. Sci. 2020, 177, 109614.
23. Ghorbani, M.; Boley, M.; Nakashima, P.; Birbilis, N. A machine learning approach for accelerated design of magnesium alloys. Part A: alloy data and property space. J. Magnes. Alloys. 2023, 11, 3620-33.
24. Fu, Z.; Liu, W.; Huang, C.; Mei, T. A review of performance prediction based on machine learning in materials science. Nanomaterials 2022, 12, 2957.
25. Lee, K.; Song, Y.; Kim, S.; et al. Genetic design of new aluminum alloys to overcome strength-ductility trade-off dilemma. J. Alloys. Compd. 2023, 947, 169546.
26. Li, J.; Zhang, Y.; Cao, X.; et al. Accelerated discovery of high-strength aluminum alloys by machine learning. Commun. Mater. 2020, 1, 74.
27. Xue, D.; Balachandran, P. V.; Hogden, J.; Theiler, J.; Xue, D.; Lookman, T. Accelerated search for materials with targeted properties by adaptive design. Nat. Commun. 2016, 7, 11241.
28. Qian, C.; Tan, R. K.; Ye, W. Design of architectured composite materials with an efficient, adaptive artificial neural network-based generative design method. Acta. Mater. 2022, 225, 117548.
29. Debnath, A.; Krajewski, A. M.; Sun, H.; et al. Generative deep learning as a tool for inverse design of high entropy refractory alloys. J. Mater. Inf. 2021, 1, 3.
30. Tian, Y.; Li, T.; Pang, J.; et al. Materials design with target-oriented Bayesian optimization. npj. Comput. Mater. 2025, 11, 1704.
31. Qin, Z.; Zhao, H.; Zhang, S.; et al. Design of high performance Cu-Ni-Si alloys via a multiobjective strategy based on machine learning. Mater. Today. Commun. 2024, 39, 108833.
32. Padhy, S. P.; Chaudhary, V.; Lim, Y. F.; et al. Experimentally validated inverse design of multi-property Fe-Co-Ni alloys. iScience 2024, 27, 109723.
33. Ghorbani, M.; Boley, M.; Nakashima, P. N. H.; Birbilis, N. An active machine learning approach for optimal design of magnesium alloys using Bayesian optimisation. Sci. Rep. 2024, 14, 8299.
34. Mazaheri, A.; Kamkar, S. Webpage saliency prediction using a single layer support vector regressor. In 2024 10th International Conference on Artificial Intelligence and Robotics (QICAR). 2024. pp. 80-3.
35. Mi, X.; Tian, L.; Tang, A.; et al. A reverse design model for high-performance and low-cost magnesium alloys by machine learning. Comput. Mater. Sci. 2022, 201, 110881.
36. Uhrig, R. E. Introduction to artificial neural networks. In Proceedings of IECON ’95 - 21st Annual Conference on IEEE Industrial Electronics, Orlando, USA. November 06-10, 1995. IEEE; 1995. pp. 33-7.
37. Choi, R. Y.; Coyner, A. S.; Kalpathy-Cramer, J.; Chiang, M. F.; Campbell, J. P. Introduction to machine learning, neural networks, and deep learning. Transl. Vis. Sci. Technol. 2020, 9, 14.
38. Li, Z.; Li, S.; Birbilis, N. A machine learning-driven framework for the property prediction and generative design of multiple principal element alloys. Mater. Today. Commun. 2024, 38, 107940.
39. Liu, B.; Mazumder, R. Randomization can reduce both bias and variance: a case study in random forests. arXiv 2024, arXiv:2402.12668. Available online: https://doi.org/10.48550/arXiv.2402.12668. (accessed 10 Nov 2025).
40. Chen, T.; Guestrin, C. XGBoost: a scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016. Association for Computing Machinery; 2016. pp. 785-94.
41. Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE. Trans. Evol. Computat. 2002, 6, 182-97.
42. Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE. Access. 2021, 9, 57757-91.
43. Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221-48.
44. Marler, R. T.; Arora, J. S. Survey of multi-objective optimization methods for engineering. Struct. Multidisc. Optim. 2004, 26, 369-95.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Special Topic
Copyright
Data & Comments
Data


















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].